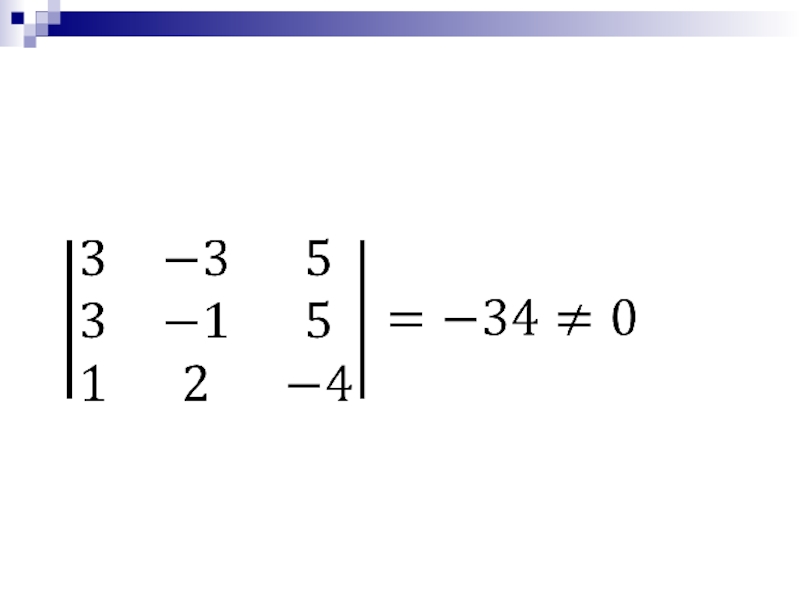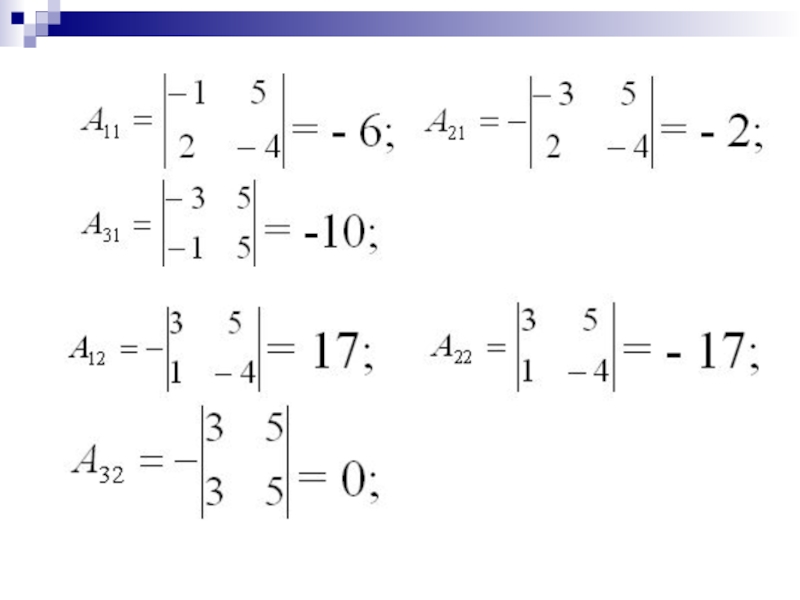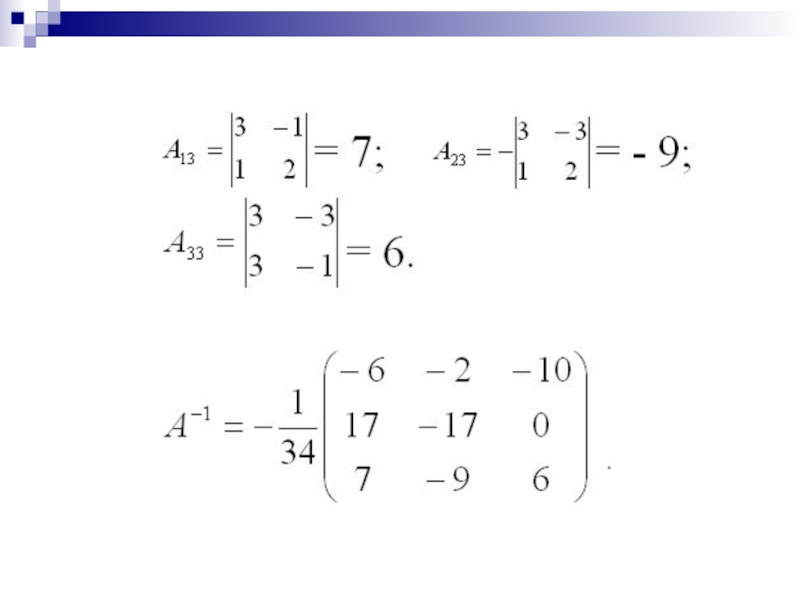Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина МАТЕМАТИКА
Содержание
- 1. Дисциплина МАТЕМАТИКА
- 2. Разделы математики1.Линейная и векторная алгебра2. Аналитическая геометрия3.Функции.
- 3. ППИ,1 курс1 семестр: 1 лекция (2 ч);
- 4. Балльно-рейтинговая система 1 курсОн-лайн 1 лекции 5
- 5. МАТЕМАТИКА Раздел 1. ЛИНЕЙНАЯ и ВЕКТОРНАЯ
- 6. ЛИТЕРАТУРА (ППИ)Худякова М.М., Фалькова О.Н,
- 7. Учебные вопросы. 1. Линейные операции над матрицами.
- 8. Введение в дисциплинуЛинейная алгебра – раздел
- 9. 1 Учебный вопрос. Линейные операции над матрицами.
- 10. Определение . Числовой матрицей размерности mn
- 11. Принятые обозначения матрицы:Прописные буквы латинского алфавита A,
- 12. Определение . Матрицы A и B называются
- 13. Определение. Матрица называется квадратной матрицей, если число
- 14. Определение. Квадратная матрица называется диагональной матрицей, если
- 15. Сложение и вычитание матрицСложение и вычитание матриц
- 16. Пример . Даны матрицы Найти C=А +B.Решение
- 17. Свойства сложенияA+B=B+A(A+B)+C=A+(B+C)A+0=A, где O – нулевая матрица такой же размерности, как и матрица A.
- 18. Умножение матрицы на числоЭто матрица, полученная умножением соответствующих элементов на данное число
- 19. Транспонирование матриц Определение. Матрицу AT называют
- 20. Умножение матриц Определение. Произведением матрицы Am×n
- 21. Пример умножения матриц
- 22. Учебный вопрос. Определители второго и третьего
- 23.
- 24. Если порядок матрицы равен трем (n =3),
- 25. 1 способ) Данную формулу можно запомнить приписав
- 26. Или, 2 способ) используем правило треугольников:В этой
- 27. Пример. Вычислить определитель приписыванием первых двух столбцовРешение.
- 28.
- 29. Пример . Для определителя |A| укажем некоторые миноры и алгебраические дополнения:
- 30. Учебный вопрос Свойства определителя.
- 31. Свойства определителей. (дз)1.
- 32. Алгоритм вычисления определителя методом приведения его к треугольному виду.
- 33. 6. Определитель не изменится, если к элементам
- 34. 8.Определитель, все элементы i-ой строки (столбца) которого
- 35. Учебный вопрос .Разложение определителя по элементам строки или столбца матрицы (теорема Лапласа).
- 36. Определение. Определителем матрицы n-го порядка называется
- 37. Теорема Лапласа.Определитель матрицы n-го порядка равен сумме
- 38.
- 39. Слайд 39
- 40. Слайд 40
- 41. Алгоритм вычисления определителя методом эффективного понижения порядка.
- 42. Раздел 1. ЛИНЕЙНАЯ и ВЕКТОРНАЯ АЛГЕБРА
- 43. ЛИТЕРАТУРА (ППИ)Данко П.Е., Попов А.Г и др.
- 44. Учебный вопрос . Алгоритм отыскания обратной матрицы
- 45. Определение. Квадратная матрица называется вырожденной матрицей, если
- 46. Теорема об обратной матрицеЕсли квадратная матрица А
- 47. Формула для обратной матрицы 3-его порядка:
- 48. Алгоритм составления обратной матрицы:1)2)
- 49. Пример. Найти матрицу, обратную данной А =
- 50. Воспользуемся формулой
- 51.
- 52. Слайд 52
- 53. Слайд 53
- 54. Скачать презентанцию
Разделы математики1.Линейная и векторная алгебра2. Аналитическая геометрия3.Функции. Дифференциальное исчисление.---------------------------------------------4. Интегральное исчисление.5. Дифференциальные уравнения. Ряды.6. Теория вероятностей и математическая статистика.
Слайды и текст этой презентации
Слайд 1Дисциплина МАТЕМАТИКА
Лектор: Юлия Абдулловна Ахкамова,
доцент кафедры математики и методики обучения математике ЮУрГГПУ
Слайд 2Разделы математики
1.Линейная и векторная алгебра
2. Аналитическая геометрия
3.Функции. Дифференциальное исчисление.
---------------------------------------------
4. Интегральное
исчисление.
5. Дифференциальные уравнения. Ряды.
6. Теория вероятностей и математическая статистика.
Слайд 3ППИ,1 курс
1 семестр:
1 лекция (2 ч);
практ.занятий (6
ч и зачет).
Контрольная работа, зачет
2 семестр:
3 лекции (6
ч);3 практ. занятий (6 ч);
консультаций (3 ч).
Экзамен ( 6 ч)
Слайд 4Балльно-рейтинговая система 1 курс
Он-лайн 1 лекции 5 баллов (max 1*5=5);
3
лаб. занятия по 5 баллов(max 3*5=15); Контрольная работа №1 задачи 1,3а,б.в,8 (max 60);
Защита-обсуждение занятий или кр (электронного варианта) max 10 баллов);
Зачетная работа до 20 баллов .
60 баллов и выше «Зачтено»,
Слайд 5МАТЕМАТИКА Раздел 1.
ЛИНЕЙНАЯ и ВЕКТОРНАЯ АЛГЕБРА
Лекция № 1.
Матрицы. Действия
над матрицами. Определители и их свойства.
Слайд 6ЛИТЕРАТУРА (ППИ)
Худякова М.М., Фалькова О.Н,
Основы высшей математики.
Данко П.Е., Попов А.Г и др. Высшая математика в
упражнениях и задачах, части I,II.-------------------------------------------------------------------
Баврин И.И. Высшая математика.
Шолохович Ф.А. Высшая математика в кратком изложении.
Слайд 7Учебные вопросы.
1. Линейные операции над матрицами. Произведение и транспонирование матриц.
2. Вычисление ранга матрицы путем приведения её к треугольному
виду.3. Метод Гаусса систем линейных алгебраических уравнений.
4.Построение выпуклого многоугольника.
Слайд 8 Введение в дисциплину
Линейная алгебра – раздел алгебры, изучающий линейные
и векторные пространства. Исторически первым разделом линейной алгебры была теория
линейных уравнений.Именно в связи с решением систем линейных уравнений возникли понятия матрицы и определителя.
Слайд 91 Учебный вопрос. Линейные операции над матрицами. (Правило сложения , вычитания
матриц. Правило умножения матрицы на число.)
Произведение и транспонирование матриц.
Слайд 10Определение . Числовой матрицей размерности mn называется прямоугольная таблица
чисел
состоящая из m строк и n столбцов:
Числа
называются элементами матрицы A,i – номер строки, j – номер столбца, на пересечении которых стоит элемент aij.
Слайд 11Принятые обозначения матрицы:
Прописные буквы латинского алфавита A, B, C, …
Am×n
,если хотят указать размерность матрицы.
Пример .
Матрица может
состоять из одного столбца или из одной строки, и даже из одного элемента. Слайд 12Определение . Матрицы A и B называются равными матрицами, если
они одинаковой размерности и все их соответствующие элементы aij и
bij равны, т.е. aij=bij.Замечание. Равными могут быть только матрицы одинаковой размерности.
Слайд 13Определение. Матрица называется квадратной матрицей, если число её строк равно
числу её столбцов, т.е. m=n.
Определение. Главной диагональю квадратной матрицы называется
линия, вдоль которой расположены элементы a11 , a22, a33, … , ann . Определение. Матрица называется нулевой матрицей, если все её элементы равны нулю.
Слайд 14Определение. Квадратная матрица называется диагональной матрицей, если на главной диагонали
расположены числа, отличные от нуля, вне главной диагонали - нули.
Определение.
Диагональная матрица, на главной диагонали которой стоят единицы, а остальные элементы – нули, называется единичной матрицей.Слайд 15Сложение и вычитание матриц
Сложение и вычитание матриц определено только для
матриц одинаковой размерности.
Определение. Суммой (разностью) матриц Am×n и Bm×n
одинаковой размерности является матрица Cm×n той же размерности, каждый элемент которой cij равен сумме (разности) соответствующих элементов этих матрицСлайд 17Свойства сложения
A+B=B+A
(A+B)+C=A+(B+C)
A+0=A, где O – нулевая матрица такой же размерности,
как и матрица A.
Слайд 18Умножение матрицы на число
Это матрица, полученная умножением соответствующих элементов на
данное число
Слайд 19 Транспонирование матриц
Определение. Матрицу AT называют транспонированной матрицей к
данной матрице А, если элементы каждой строки матрицы А стали
элементами столбцами матрицы AT под тем же номером.Слайд 20 Умножение матриц
Определение. Произведением матрицы Am×n на матрицу Bn×k
называется матрица
Cm×k= A·B , имеющая m строк
и k столбцов, у которой элемент cij равен сумме произведений элементов i-й строки матрицы A и j-го столбца матрицы B. Замечание:
Произведение матриц существует только для согласованных матриц, т.е. когда первый множитель имеет число столбцов, равное числу строк второго множителя.
Слайд 22 Учебный вопрос. Определители второго и третьего порядков, их вычисление .
(Правило вычисления определителя II порядка. Правило треугольников вычисления определителя III порядка
.)Слайд 24Если порядок матрицы равен трем (n =3), то определителем третьего
порядка назовем число, вычисленное по формуле:
Слайд 251 способ) Данную формулу можно запомнить приписав к определителю первые
два столбца.
Со знаком плюс берутся произведения элементов стоящих на
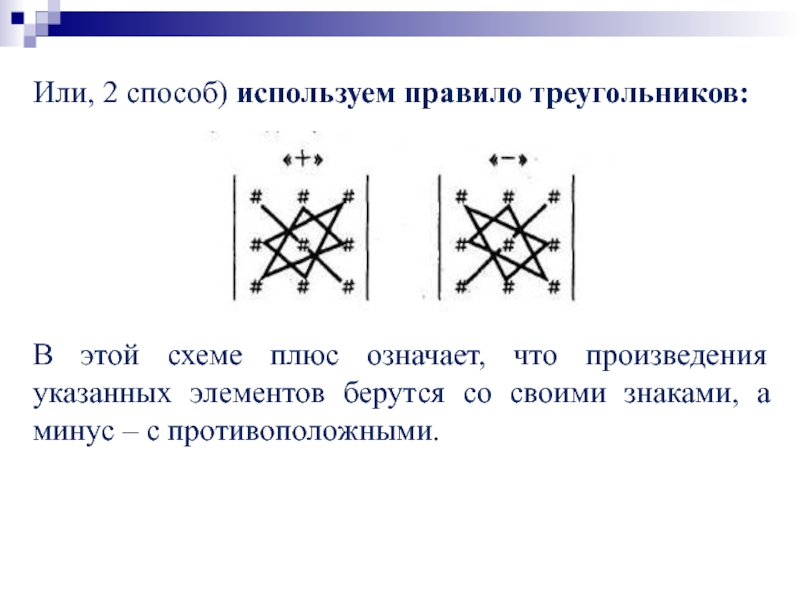
главной диагонали и на диагоналях, параллельных к ней, со знаком минус – произведения элементов на побочной диагонали и диагоналей, параллельных к ней.Слайд 26Или, 2 способ) используем правило треугольников:
В этой схеме плюс означает,
что произведения указанных элементов берутся со своими знаками, а минус
– с противоположными.Слайд 31Свойства определителей. (дз)
1. При транспонировании матрицы
ее определитель не изменяется:
2. При перестановке двух строк (столбцов)
матрицы ее определитель меняет знак на противоположный. 3. Определитель с двумя равными или пропорциональными строками (или столбцами) равен нулю.
4. Если все элементы некоторой строки (столбца) определителя имеют общий множитель, то его можно вынести за знак определителя.
5. Определитель с нулевой строкой (или столбцом) равен нулю.
Слайд 33
6. Определитель не изменится, если к элементам одной строки (столбца)
прибавить соответствующие элементы другой строки (столбца), умноженные на одно и
то же число (не равное нулю).7. Определитель диагональной матрицы равен произведению элементов на главной диагонали.
С помощью свойств 6-7 определитель можно привести к треугольному виду и легко вычислить. (долгий процесс)
Слайд 348.Определитель, все элементы i-ой строки (столбца) которого представляют сумму двух
слагаемых, равна сумме двух определителей, все элементы которых, кроме i-ой
строки (столбца), те же, что и в исходном, а в i-ой строке (столбце) первого определителя стоят первые слагаемые, в i-ой строке (столбце) второго определителя – вторые.Слайд 35Учебный вопрос .
Разложение определителя по элементам строки или столбца матрицы
(теорема Лапласа).
Слайд 36
Определение. Определителем матрицы n-го порядка называется число, которое сопоставляется квадратной
матрице n-го порядка, получаемое по определенному правилу (Теорема Лапласа).
Слайд 37Теорема Лапласа.
Определитель матрицы n-го порядка равен сумме произведений элементов какой-либо
строки (или столбца) на их алгебраические дополнения.
Слайд 41Алгоритм вычисления определителя методом эффективного понижения порядка.
1) Выбрать «ряд» определителя
(строку или столбец), содержащий нуль ( используя свойства определителей можем
получить нуль ).2) Вычислить алгебраические дополнения элементов этого «ряда».
3) Применить теорему Лапласа для вычисления данного определителя.
Слайд 42Раздел 1.
ЛИНЕЙНАЯ и ВЕКТОРНАЯ АЛГЕБРА
Обратная матрица. Ранг матрицы. Основные
сведения о СЛУ. Методы решения СЛУ.
Слайд 43ЛИТЕРАТУРА (ППИ)
Данко П.Е., Попов А.Г и др. Высшая математика в
упражнениях и задачах, части I,II.
-------------------------------------------------------------------
Баврин И.И. Высшая математика.
Шолохович Ф.А.
Высшая математика в кратком изложении.Слайд 45Определение. Квадратная матрица называется вырожденной матрицей, если её определитель равен
нулю.
Квадратная матрица А называется невырожденной матрицей,
если | A
| ≠ 0.Определение. Матрица А-1 называется обратной матрицей к матрице A, если А-1∙A = A∙А-1 = E.