Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина: Надежность и диагностика систем электроснабжения Тема : расчёт
Содержание
- 1. Дисциплина: Надежность и диагностика систем электроснабжения Тема : расчёт
- 2. m N
- 3. m- число резервных элементов системы;N- число рабочих
- 4. Появление отказов в системе будем рассматривать как
- 5. В общем случае могут отказывать и элементы,
- 6. 2. Математическое описание задачи.Суть задачи состоит в
- 7. Предположим, что при отказе любого из элементов
- 8. Интенсивность отказа системы (из числа рабочих и
- 9. Интенсивность восстановления равна К ν, если количество
- 10. В момент времени t+Δt система может находиться
- 11. В момент времени t система
- 12. Вероятность того, что к моменту t+Δt система
- 13. Для определения коэффициента готовности системы в любой,
- 14. Все события, описанные данной системой дифференциальных уравнений,
- 15. Данная система дифференциальных уравнений может быть решена
- 16. С учётом сказанного, система алгебраических уравнений, определяющая
- 17. Из 11.10 с учётом 11.8 имеем:
- 18. Определим коэффициент готовности, как вероятность застать в
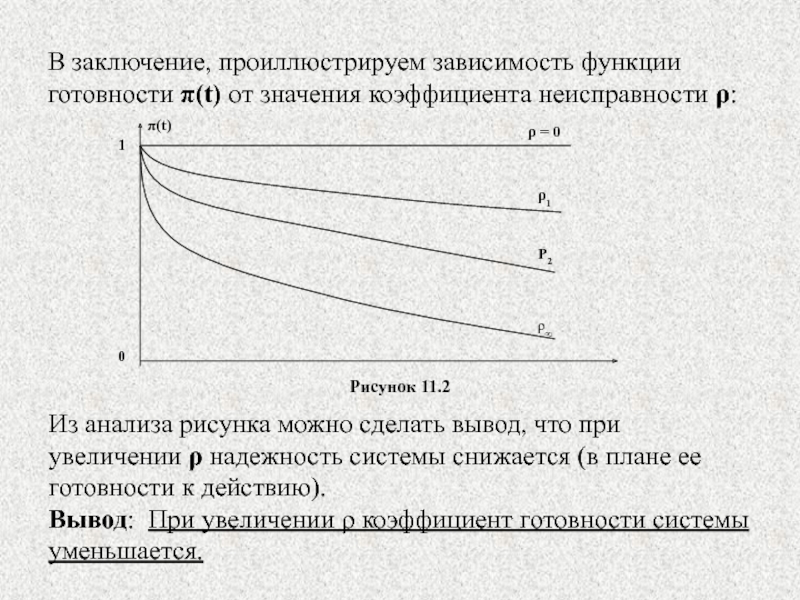
- 19. В заключение, проиллюстрируем зависимость функции готовности π(t)
- 20. Рассмотрим некоторые частные случаи: Случай
- 21. Используя формулы 11.12 и 11.11 получим:
- 22. Таким образом в этом случае коэффициент готовности
- 23. Случай 2. Если общее число однотипных элементов,
- 24. Случай 3. Резервирование горячее, но работает лишь
- 25. Коэффициент готовности системы равен:
- 26. Случай 4. Резервирование холодное, работают m +1
- 27. Если же элементы отказывают и в неработоспособном
- 28. Случай 5. Резервирование холодное, работает одна ремонтная
- 29. в случае отказов и в нерабочем состоянии
- 30. Выводы: Для расчета коэффициента готовности системы можно
- 31. Специально для кафедры ЭЭС от доцента
- 32. Скачать презентанцию
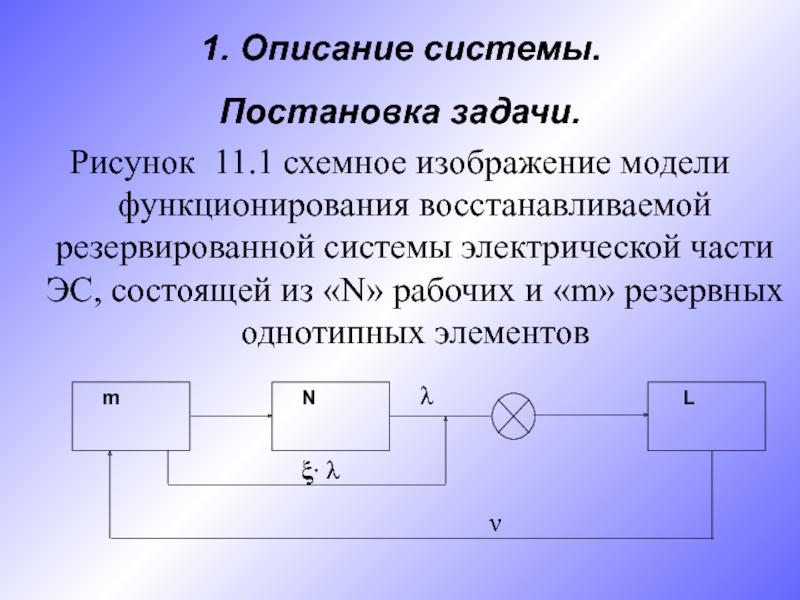
m N L1. Описание системы. Постановка задачи.Рисунок 11.1 схемное изображение модели функционирования восстанавливаемой резервированной системы электрической части ЭС, состоящей из «N» рабочих и «m» резервных однотипных
Слайды и текст этой презентации
Слайд 1Дисциплина: Надежность и диагностика систем электроснабжения Тема: расчёт коэффициента готовности восстанавливаемой
резервированной системы , состоящей из однотипных элементов.
Слайд 2 m
N
L
1. Описание системы.
Постановка задачи.
Рисунок 11.1 схемное изображение модели функционирования восстанавливаемой резервированной системы
электрической части ЭС, состоящей из «N» рабочих и «m» резервных однотипных элементовλ
∙ λ
ν
Слайд 3m- число резервных элементов системы;
N- число рабочих элементов системы;
L- число
элементов обслуживающей системы;
[лямбда]- интенсивность отказов элементов системы;
[ню]- интенсивность
восстановления отказавших элементов системы[кси]- коэффициент использования резерва.
=1, если резервирование горячее; =0, если резервирование холодное (отсутствуют отказы в этом состоянии);
в общем случае: 0 < = < = 1
очередь на востановление
Слайд 4Появление отказов в системе будем рассматривать как простейший поток однородных
событий, появляющихся со средней интенсивностью λ, рассматриваемой как параметр этого
потока. Обслуживание рассматриваемой системы будем характеризовать показательным законом распределения времени восстановления с интенсивностью восстановления ν.Задача поставленная перед системой, выполняется группой из N элементов. При отказе любого из элементов этой группы, он мгновенно замещается резервным, а отказавший элемент отправляется на восстановление.
Обслуживающая система состоит из L-элементов. При занятости всех обслуживающих элементов, отказавший элемент становится в очередь на восстановление.
После восстановления элемент возвращается в резерв с частотой .
Слайд 5В общем случае могут отказывать и элементы, находящиеся в резерве
с частотой *λ. Тогда они также направляются на восстановление в
обслуживающую систему.Следует отметить, что в данной задаче восстановление повышает надёжность системы в смысле увеличения её готовности к действию, а так же повышает вероятность безотказной работы системы в целом. Объясняется это следующим образом: чем быстрее происходит восстановление, тем более количество резервных элементов!
Слайд 62. Математическое описание задачи.
Суть задачи состоит в следующем: система выходит
из строя если откажут m+1 элементов.
Считаем, что система находится в
состоянии Ек , когда число отказавших элементов равно К. Очевидно что в состояниях Е0, Е1,...,Еm система работоспособна. Состояние Еm+1 является состоянием отказа системы.Состояние Еm+2 ,...,Es – cчитается невозможным, если невозможны новые отказы в отказавшей системе, где S – общее число однотипных элементов, циркулирующих в системе.
При S>N + m, некоторые из элементов находятся в нерабочем состоянии (на ремонте или в очереди на ремонт).
Слайд 7Предположим, что при отказе любого из элементов работающей группы, он
замещается резервом. Это допущение учитывается при составлении таблицы группы технических
средств для указания минимально необходимого количества технических средств в группе для обеспечения нормальной работы системы. Менее этого количества элементов опускаться нельзя, иначе наступит отказ группы и системы в целом.Слайд 8
Интенсивность отказа системы (из числа рабочих и резервных элементов), находящейся
в состоянии Ек равна:
Nλ + (m - k) λ = nk λ; (11.1) Откуда:
nk = N + (m - k) ; (11.2)
Где:
λ – интенсивность отказа резервного элемента;
0 < = < = 1;
Слайд 9Интенсивность восстановления равна К ν, если количество ремонтных бригад не
менее m+1 и ν, если в работе находится лишь одна
бригада.Обозначим вероятность застать систему в произвольный момент времени t в состоянии Ек через Рк(t).
Для определения Рк(t) составляется система дифференциальных уравнений конечного порядка по следующему алгоритму:
Берётся момент времени с малым приращением Δt и находится вероятность Рк(t+Δt)
Слайд 10В момент времени t+Δt система может находиться в состоянии Ек
при следующих трёх условиях:
В момент времени t система находится в
состоянии Ек и за время Δt не происходит никаких изменений с её элементами. Вероятность такого события равна:Рк(t) * (1-nkλ Δt)*(1-k ν Δt) (11.3)
Где:
– коэффициент использования резервного элемента;
nk = N + (m - k) – расчётная величина;
k – число отказов из m – резервных элементов;
(1 – nk λ Δt) – вероятность того, что за время Δt в системе не возникнет ни одного отказа;
(1 - k ν Δt) – вероятность того, что не один отказавший элемент за время Δt не будет восстановлен;
k ν – интенсивность восстановления, если количество ремонтных бригад не менее: m+1, и ν – если работает лишь одна ремонтная бригада;

![Дисциплина: Надежность и диагностика систем электроснабжения Тема : расчёт m- число резервных элементов системы;N- число рабочих элементов системы;L- число элементов m- число резервных элементов системы;N- число рабочих элементов системы;L- число элементов обслуживающей системы; [лямбда]- интенсивность отказов элементов](/img/thumbs/81111d0ef4e80787fee2ef039372a126-800x.jpg)