Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина: МАТЕМАТИКА Лектор: Ахкамова Юлия Абдулловна доцент кафедры
Содержание
- 1. Дисциплина: МАТЕМАТИКА Лектор: Ахкамова Юлия Абдулловна доцент кафедры
- 2. ЛЕКЦИЯ № 19 Формула полной
- 3. ЛИТЕРАТУРА Гмурман В.Е. Теория вероятностей и математическая статистика, Высшее образование,2006, с. 50-63.
- 4. ЛИТЕРАТУРА Шолохович Ф.А. Высшая математика в кратком
- 5. УЧЕБНЫЕ ВОПРОСЫ1.Теоремы о повторении опытов. Определение вероятности
- 6. УЧЕБНЫй ВОПРОСТеоремы о повторении опытов. -Определение вероятности
- 7. Теоремы о повторении опытов. Рассмотрим многократное
- 8. Формула Бернулли. Если вероятность появления
- 9. Пример.Вероятность изготовления стандартной детали равна 0,9. Какова
- 10. Слайд 10
- 11. Приближенные формулы в схеме Бернулли Локальная теорема
- 12. Пример.Вероятность поражения мишени стрелком равна р=0,8. Найти
- 13. Слайд 13
- 14. Интегральная теорема Муавра-Лапласа Если вероятность р наступления
- 15. где
- 16. Пример.
- 17. Формула Пуассона При большом числе n испытаний
- 18. Пример.Вероятность угадывания 6 номеров в спортлото (6
- 19. Слайд 19
- 20. Слайд 20
- 21. Определение вероятности появления события
- 22. событие А не наступит ни разу произойдет хотя бы раз ( не менее одного)
- 23. Отклонение относительной частоты от вероятности
- 24. УЧЕБНЫЙ ВОПРОСТеорема о полной вероятности, формула Байеса.
- 25. Теорема о полной вероятности.Пусть имеется группа событий
- 26. Пусть А - некоторое событие, которое может
- 27. Пример.На трех станках изготавливаются одинаковые детали, причем
- 28. Решение.Обозначим через А событие – наудачу взятая
- 29. Найдем вероятности этих гипотез. Поскольку на первом
- 30. Искомую вероятность того, что наудачу взятая деталь
- 31. Пусть в результате проведения эксперимента появилось событие
- 32. Пример.Рассмотрим приведенную выше задачу о деталях, только
- 33. Решение.По формуле БайесаИмеем
- 34. УЧЕБНЫЙ ВОПРОСВиды случайных величин и их числовые характеристики.
- 35. Под случайной величиной (С.В.) понимается числовая величина,
- 36. Случайные величиныДискретныеНепрерывные
- 37. Определение. Дискретной С.В. называют случайную величину, которая
- 38. Основные числовые характеристики С.В.МатематическоеожиданиеМ(Х)ДисперсияD(Х)Среднееквадратическоеотклонениеσ(Х)
- 39. где : Математическое ожидание
- 40. Основные формулы, определяющие числовые характеристики С.В.
- 41. Функция распределенияУниверсальным законом распределения С.В. любого типа
- 42. Определение. Случайная величина Х называется непрерывной, если
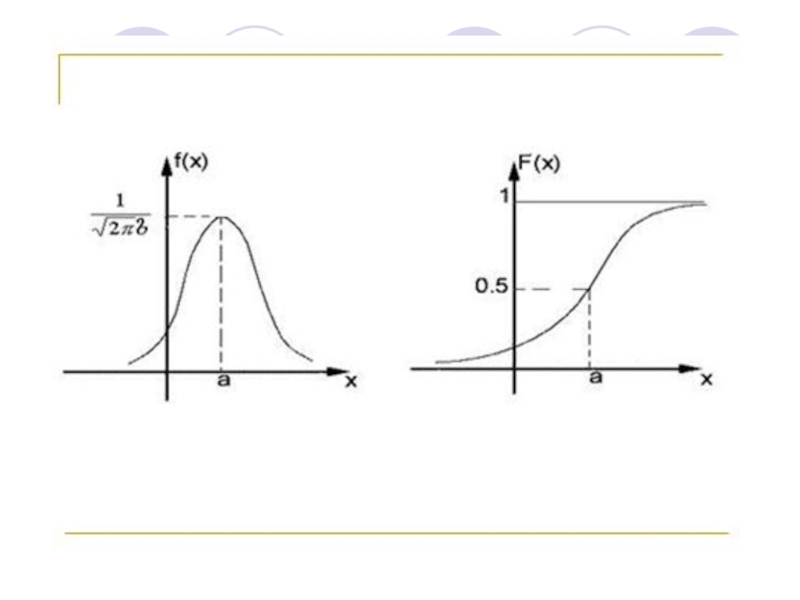
- 43. Нормальное распределениеС. В. имеет нормальное распределение с
- 44. Слайд 44
- 45. Задание на самоподготовкуГмурман В.Е. Теория вероятностей и математическая статистика, Высшее образование,2009, с. 30-51.
- 46. Скачать презентанцию
ЛЕКЦИЯ № 19 Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их числовые характеристики, виды распределений .
Слайды и текст этой презентации
Слайд 1Дисциплина:
МАТЕМАТИКА
Лектор: Ахкамова Юлия Абдулловна
доцент кафедры математики и
методики обучения математике ЮУрГГПУ
Слайд 2 ЛЕКЦИЯ № 19 Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия
дискретной и непрерывной величин, их числовые характеристики, виды распределений
.
Слайд 3
ЛИТЕРАТУРА
Гмурман В.Е.
Теория вероятностей
и математическая
статистика,
Высшее образование,
2006,
с. 50-63.
Слайд 4ЛИТЕРАТУРА
Шолохович Ф.А. Высшая математика в кратком изложении.
Баврин И.И. Высшая
математика.
Данко П.Е., Попов А.Г и др. Высшая математика в упражнениях
и задачах, часть II. 
Слайд 5
УЧЕБНЫЕ ВОПРОСЫ
1.Теоремы о повторении опытов.
Определение вероятности появления события не
менее «m» раз и не менее одного раза в «n»
опытах.2.Теорема о полной вероятности, формула Байеса.
Слайд 6
УЧЕБНЫй ВОПРОС
Теоремы о повторении опытов.
-Определение вероятности появления события не
менее «m» раз и не менее одного раза в «n»
опытах.
Слайд 7 Теоремы о повторении опытов.
Рассмотрим многократное повторение одного и того
же испытания, в котором может либо наступить, либо не наступить
событие А. Вероятность появления А в каждом из испытаний постоянна, равна р.Такие испытания называются "схемой повторных независимых испытаний" или "схемой Бернулли".
Слайд 8Формула Бернулли.
Если вероятность появления события A в
каждом испытании постоянна, то вероятность того, что событие А произойдёт
ровно k раз в n независимых испытаниях вычисляется по формуле Бернулли,
где р – вероятность появления события А,
q=1–p
Слайд 9Пример.
Вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что
среди 10 деталей окажется более 1 нестандартной?
Слайд 11Приближенные формулы в схеме Бернулли
Локальная теорема Муавра-Лапласа
Если вероятность р
наступления события А в каждом испытании постоянна и отлична от
0 и 1, а число испытаний достаточно велико, то вероятность того, что событие А произойдёт ровно k раз в n независимых испытаниях,
где
; φ(-х)=φ(х); для значений этой функции составлены специальные таблицы.
Слайд 12Пример.
Вероятность поражения мишени стрелком равна р=0,8. Найти вероятность того, что
при n= 100 выстрелах мишень будет поражена ровно k =
86 раз.
Слайд 14Интегральная теорема Муавра-Лапласа
Если вероятность р наступления события А в
каждом испытании постоянна и отлична от 0 и 1, то
вероятность появления события А не менее k1 раз и не более k2 раза при достаточно большом количестве испытаний n:
Слайд 15где
- функция Лапласа,
её значения приведены в специальных таблицах;
Ф(-х) = - Ф(х);
Ф(х>5)=0,5.
Слайд 17Формула Пуассона
При большом числе n испытаний и сравнительно малой
вероятности р наступления события А в каждом испытании выполняется приближен-ное
равенствогде λ = np.
Слайд 18Пример.
Вероятность угадывания 6 номеров в спортлото (6 из 49) равна
7,2· 10-8. При подсчете оказались заполненными 5 млн. карточек. Какова
вероятность того, что никто не угадал все 6 номеров? Какое наименьшее количество карточек нужно заполнить, чтобы с вероятностью не менее 0,9 хотя бы один угадал 6 номеров?
Слайд 21 Определение вероятности появления события не менее «m» раз и
не менее одного раза в «n» опытах.
Вероятность того, что
в n испытаниях событие наступит:не более m раз
Не менее m раз
Слайд 25Теорема о полной вероятности.
Пусть имеется группа событий В1, В2,..., Вn,
обладающая следующими свойствами:
1) все события попарно несовместны:
Вi ∩ Вj = Ø ; i ≠ j;2) их объединение образует пространство элементарных исходов :
=В1 U В2 U ... U Вn.
В этом случае будем говорить, что В1, В2,..., Вn образуют полную группу событий. Такие события назовём гипотезами.
Слайд 26
Пусть А - некоторое событие, которое может наступить лишь при
появлении одного из событий Вi . Тогда имеет место формула
полной вероятности:P(A)=P(В1)∙P(A/ В1)+P(В2)∙P(A/В2)+...+P(Вn)∙P(A/Вn)
В1
В2
В4
В3
Вn
Слайд 27Пример.
На трех станках изготавливаются одинаковые детали, причем на первом вырабатывается
50% всех деталей, на втором – 30% и на третьем
– 20%. При этом, вероятность появления брака с первого станка составляет 0,05, со второго – 0,08, с третьего – 0,1. Найти вероятность того, что наудачу взятая деталь соответствует стандарту.
Слайд 28Решение.
Обозначим через А событие – наудачу взятая деталь соответствует стандарту.
Возможны следующие предположения (гипотезы):
В1- деталь
изготовлена на первом станке;В2 - деталь изготовлена на втором станке;
В3 - деталь изготовлена на третьем станке.
Слайд 29Найдем вероятности этих гипотез.
Поскольку на первом станке вырабатывается 50%
всех деталей, то Р(В1) =0,5 ;
Р(В2) =
0,3; Р(В3) = 0,2.Найдем условные вероятности события А:
Р(А/В1) = 1 - 0,05 = 0,95.
Р(А/В2) = 1 - 0,08 = 0,92.
Р(А/В3) = 1 - 0,1 = 0,9.
Слайд 30Искомую вероятность того, что наудачу взятая деталь соответствует стандарту, находим
по формуле полной вероятности:
Р(А)=Р(В1)·Р(А/В1)+Р(В2)·Р(А/В2)+ +Р(В3)·Р(А/В3)=
=0,5·0,95+0,3·0,92+0,2·0,9 = =0,475 + 0,276
+ 0,18 = 0,931.
Слайд 31Пусть в результате проведения эксперимента появилось событие A. Если необходимо
оценить вклад какого-либо события Вi в реализацию события A, то
используется формула Байеса оценки вероятности гипотезы после опытаИспользуя для знаменателя формулу полной вероятности, получим
Слайд 32Пример.
Рассмотрим приведенную выше задачу о деталях, только изменим вопрос задачи.
Пусть наудачу взятая деталь соответствует стандарту.
Найти вероятность того,
что эта деталь изготовлена на третьем станке.
Слайд 35Под случайной величиной
(С.В.) понимается числовая величина, которая в результате
опыта может принять то или иное значение, причем заранее неизвестно
какое именно.Например:
Число родившихся детей в течение суток в городе N.
Количество бракованных изделий в данной партии.
Число произведённых выстрелов до первого попадания.
Дальность полёта артиллерийского снаряда.
Слайд 37Определение. Дискретной С.В. называют случайную величину, которая прини-мает только конечное
или счетное число значений х1, х2, ... с вероятнос-тями р1,
р2, ... соответственно, при этомр1+р2 + ... = 1.
Определение. Непрерывной С.В.называют случайную величину, возможные значения которой непрерывно заполняют числовую ось или некоторый её отрезок.
Слайд 38Основные числовые
характеристики С.В.
Математическое
ожидание
М(Х)
Дисперсия
D(Х)
Среднее
квадратическое
отклонение
σ(Х)
Слайд 39 где :
Математическое ожидание С.В. Х
М(Х)
называют средним значением С.В. Математическое ожидание показывает какое значение С.В.
можно ожидать в среднем при проведении серии опытов.Дисперсией D(X) случайной величины Х называется математическое ожидание её отклонения от математического ожидания
Слайд 41Функция распределения
Универсальным законом распределения С.В. любого типа является функция распределения
С.В.– вероятность того, что значение С.В. будет меньше некоторого вполне
определенного текущего значения х:F(x) = P(X < x).
Слайд 42Определение. Случайная величина Х называется непрерывной, если её функция распределения
F(х) (интегральная функция распределения) непрерывна в любой точке и дифференцируема
всюду, кроме, быть может, отдельных точек.Определение. Плотностью распределения (дифференциальной функцией распределения) непрерывной случайной величины Х называется производная её функции распределения
Слайд 43Нормальное распределение
С. В. имеет нормальное распределение с параметрами а и
σ, если её плотность распределения задаётся формулой
Функция распределения имеет вид
Слайд 45Задание на самоподготовку
Гмурман В.Е. Теория вероятностей и математическая статистика, Высшее
образование,2009, с. 30-51.
