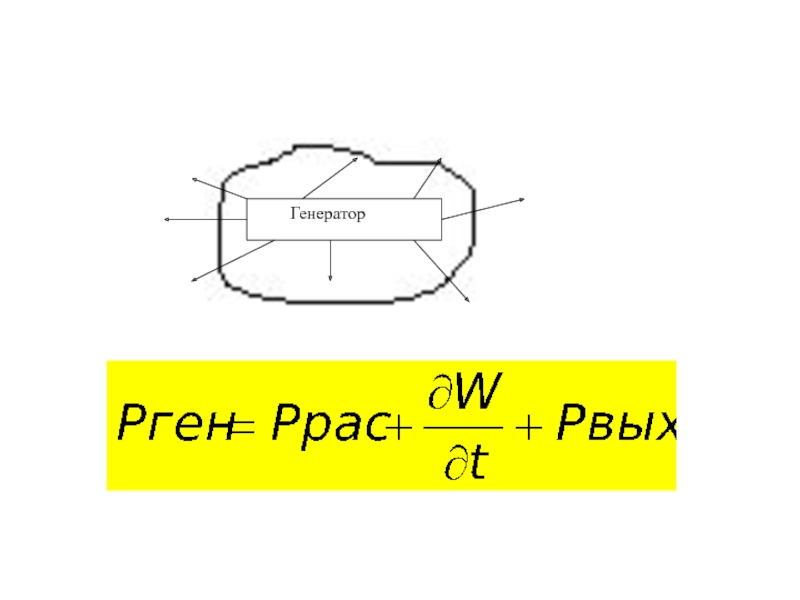
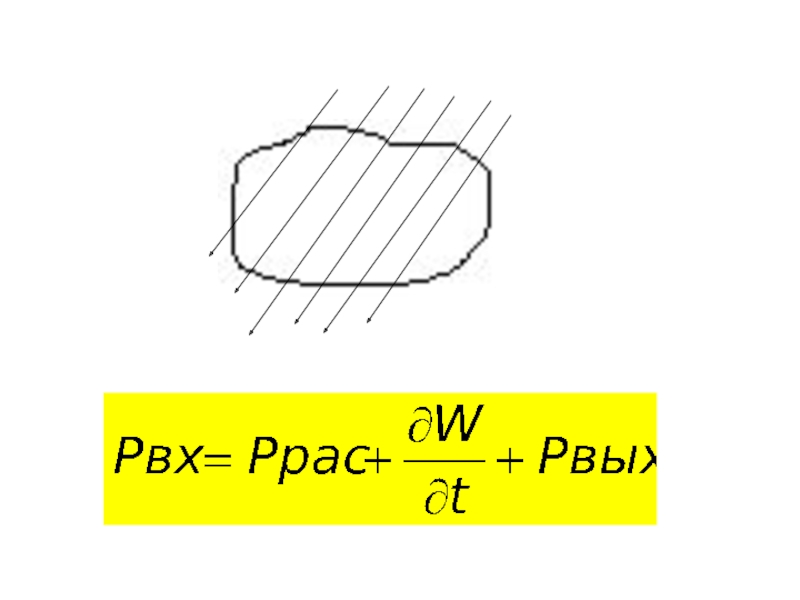
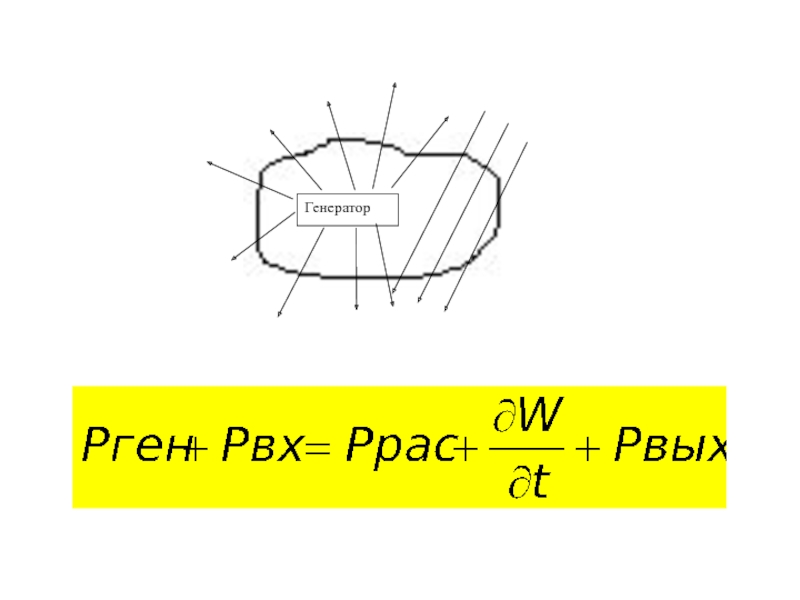
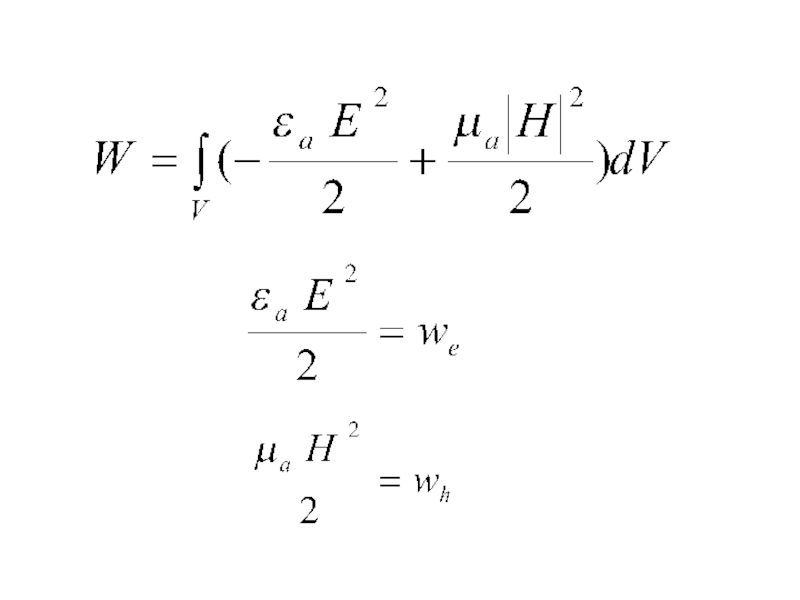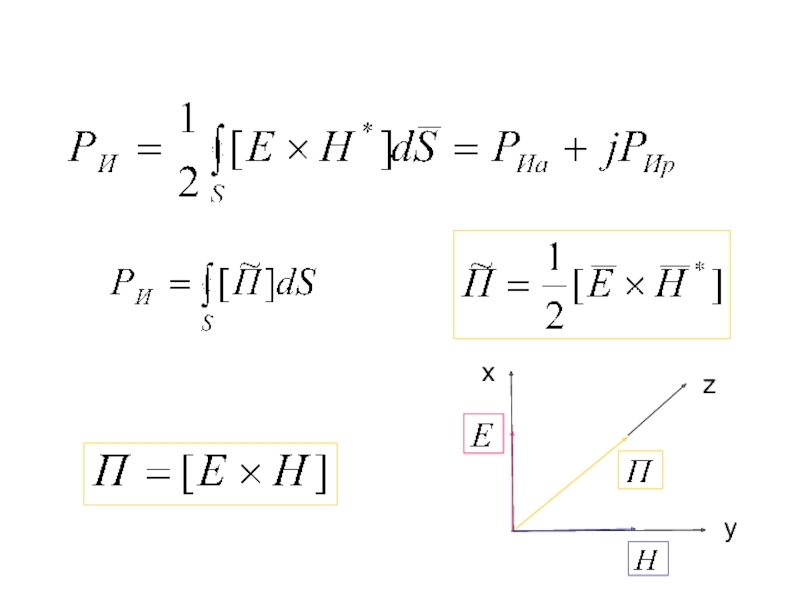с.18...29]:
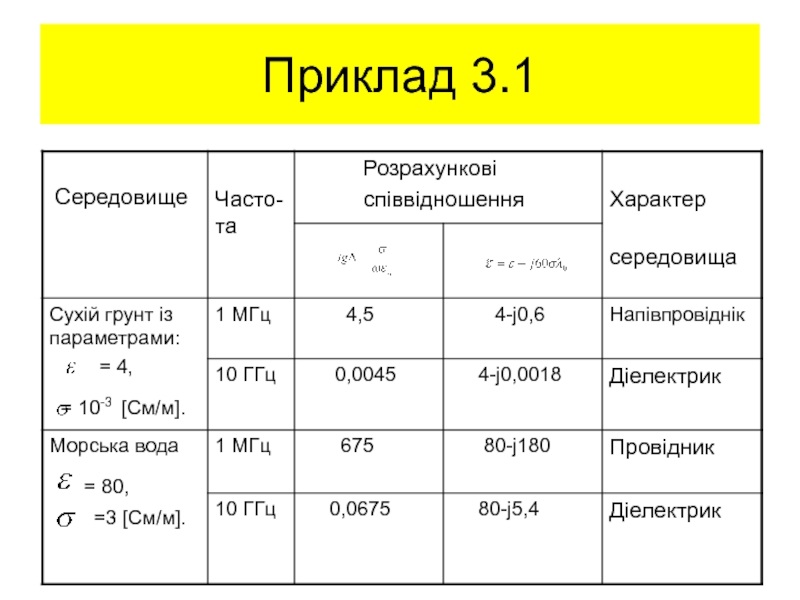
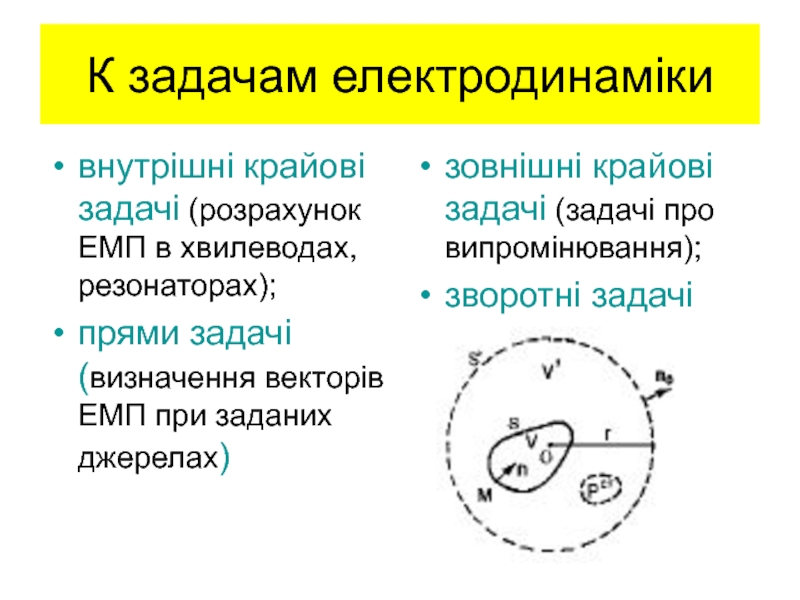
матеріальні рівняння та класифікація середовищ;
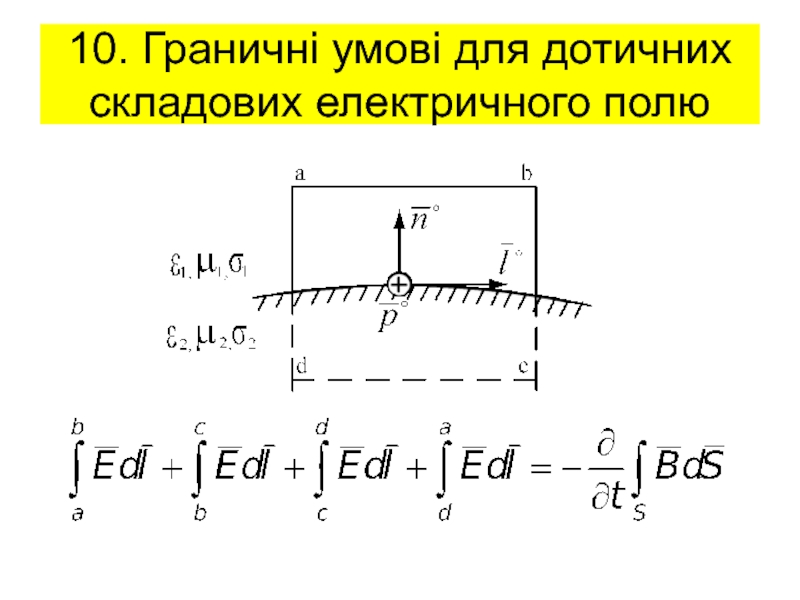
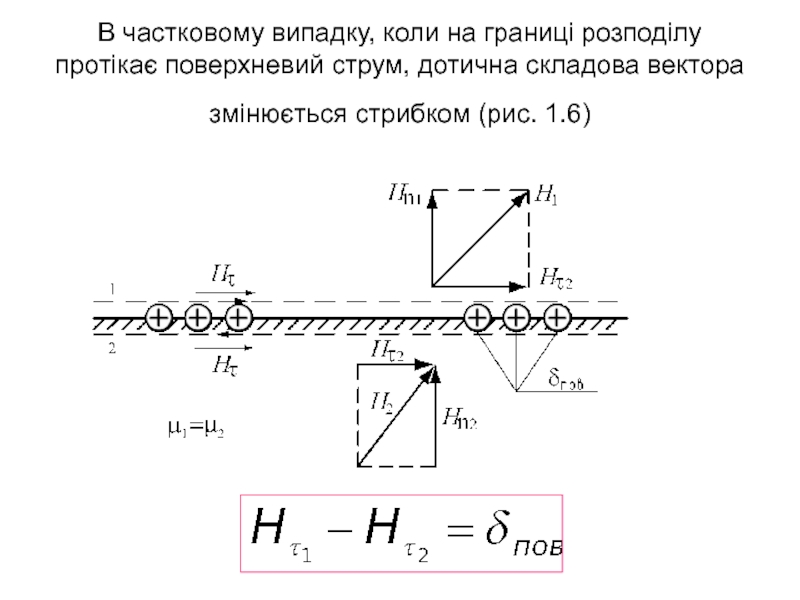
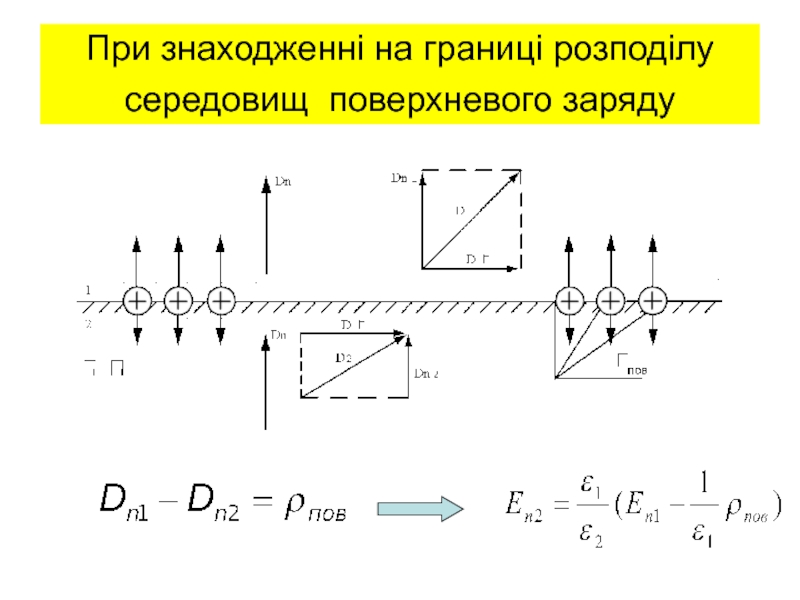
граничні умови для дотичних і
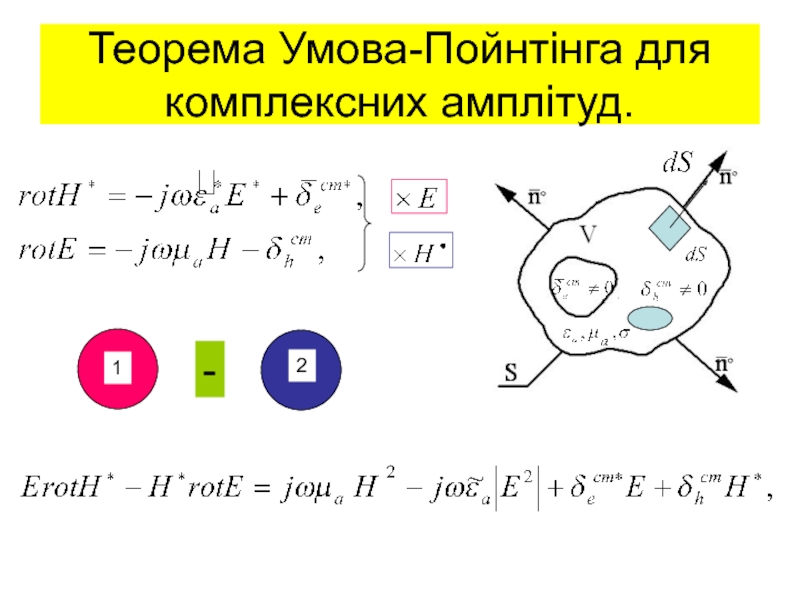
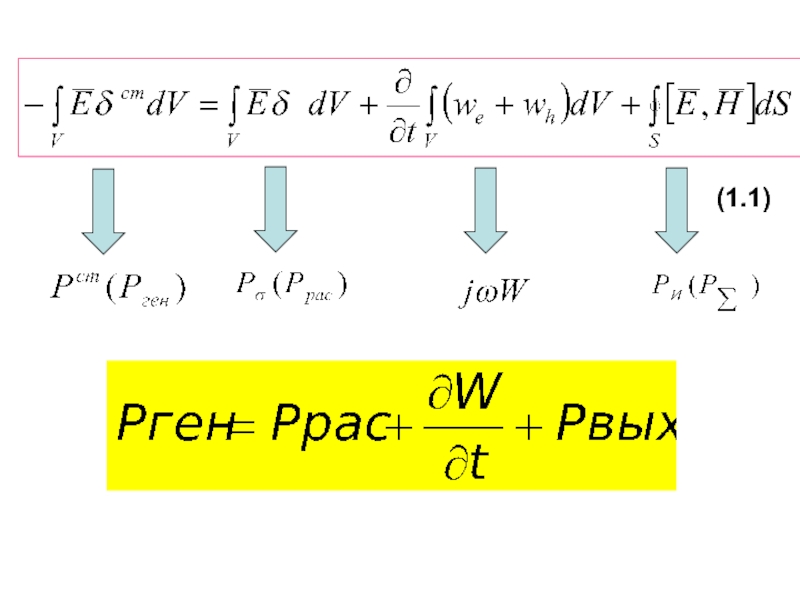
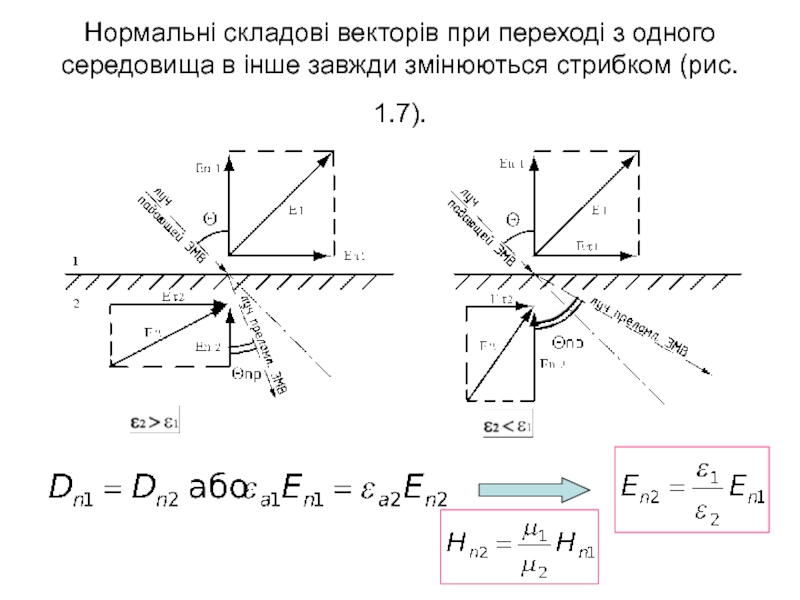
нормальних складових ЕМП;рівняння ЕМП у комплексній формі;
комплексна діелектрична проникність, її розрахунок.


![Додаткові рівняння ЕМП Самостійно законспектувати слідуючи питання [1, с. 23…28]; [2, с.25…47]; [4, с.18...29]: Самостійно законспектувати слідуючи питання [1, с. 23…28]; [2, с.25…47]; [4, с.18...29]: матеріальні рівняння та класифікація середовищ;граничні умови](/img/tmb/3/273765/2283a4ebbb3f65d7927944f2c5a8374b-800x.jpg)

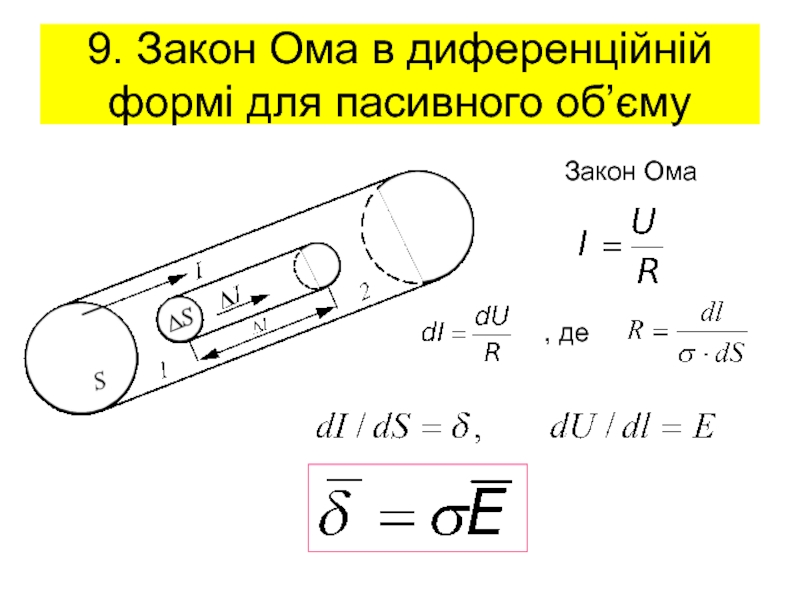










![Додаткові рівняння ЕМП Уточнення класифікації середовищ на НВЧДіелектрикНапівпровідне середовищеПровідникf[Гц] Уточнення класифікації середовищ на НВЧДіелектрикНапівпровідне середовищеПровідникf[Гц]](/img/tmb/3/273765/327e4eaf07c1a154fb160cf95f6da25e-800x.jpg)