Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение-это жизнь
Содержание
- 1. Движение-это жизнь
- 2. 22.04. 20Движение
- 3. ДвиженияСимметрияПараллельныйпереносПоворотОсеваясимметрияЦентральнаясимметрия
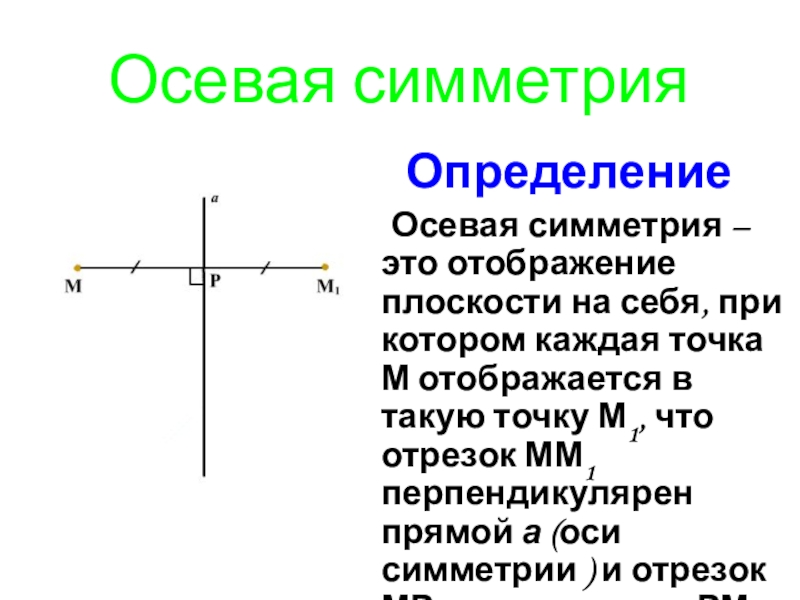
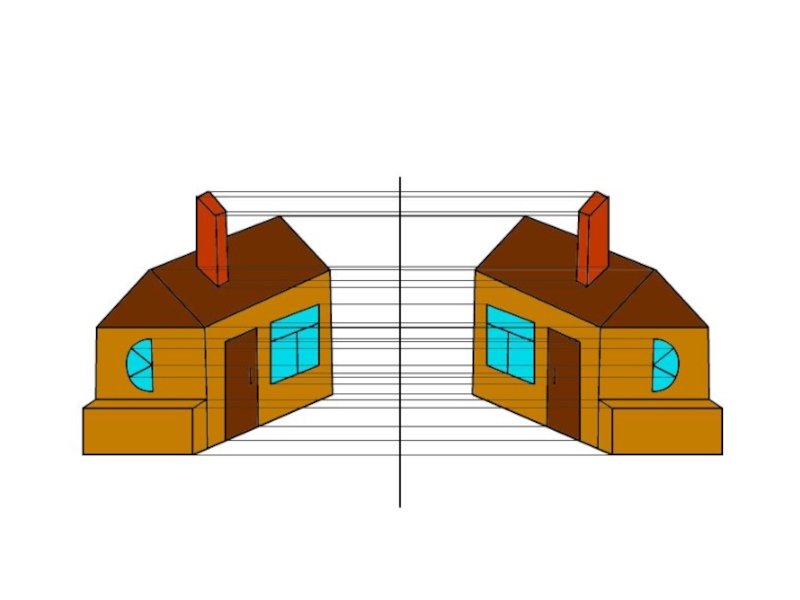
- 4. Осевая симметрия Определение Осевая
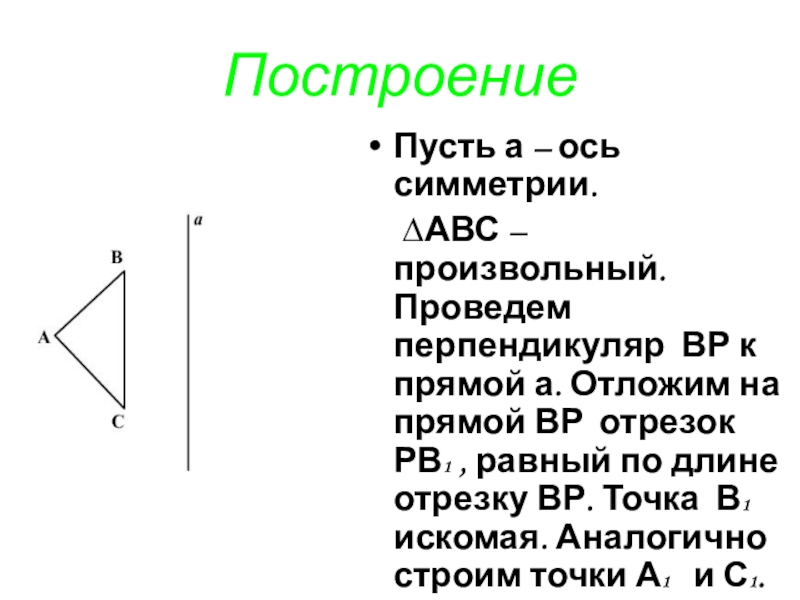
- 5. ПостроениеПусть а – ось симметрии.
- 6. Слайд 6
- 7. Слайд 7
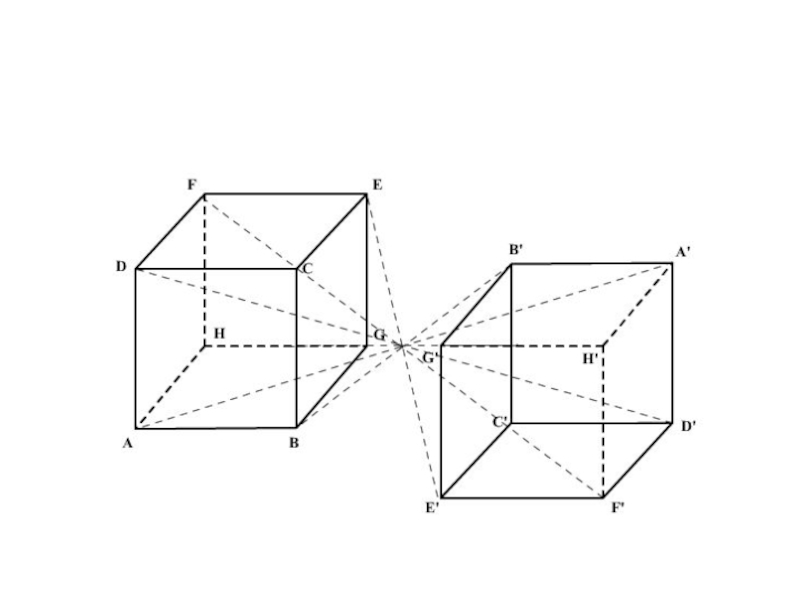
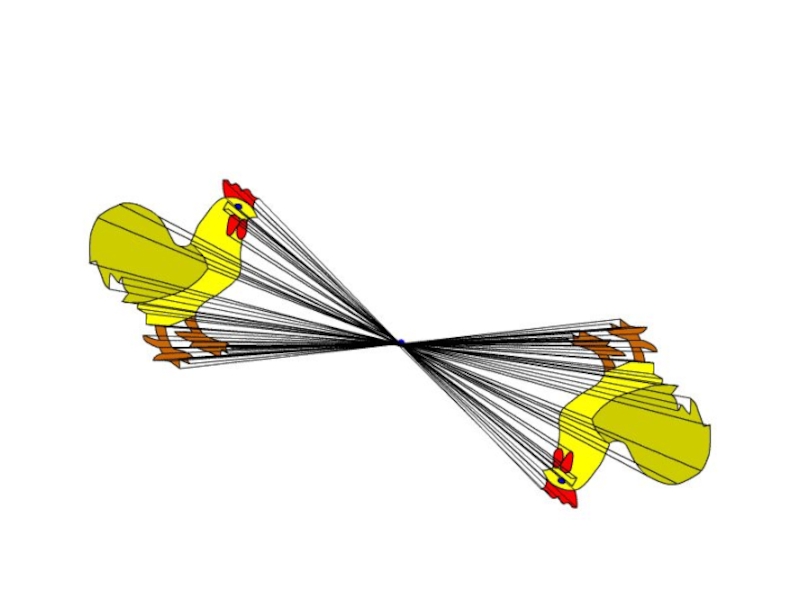
- 8. Центральная симметрияОпределение Центральная симметрия –это отображение
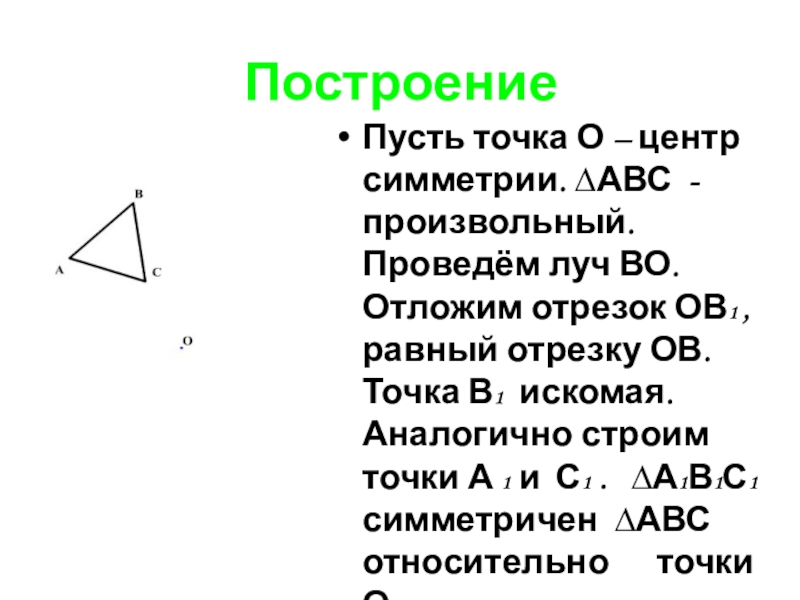
- 9. ПостроениеПусть точка О – центр симметрии. ∆АВС
- 10. Слайд 10
- 11. Слайд 11
- 12. Движение в архитектуре. Определить вид движения.
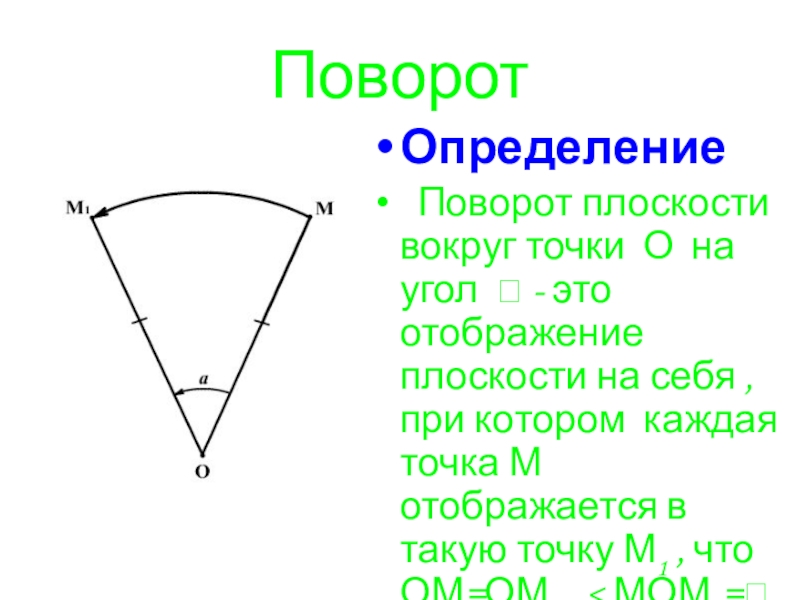
- 13. ПоворотОпределение Поворот плоскости вокруг точки
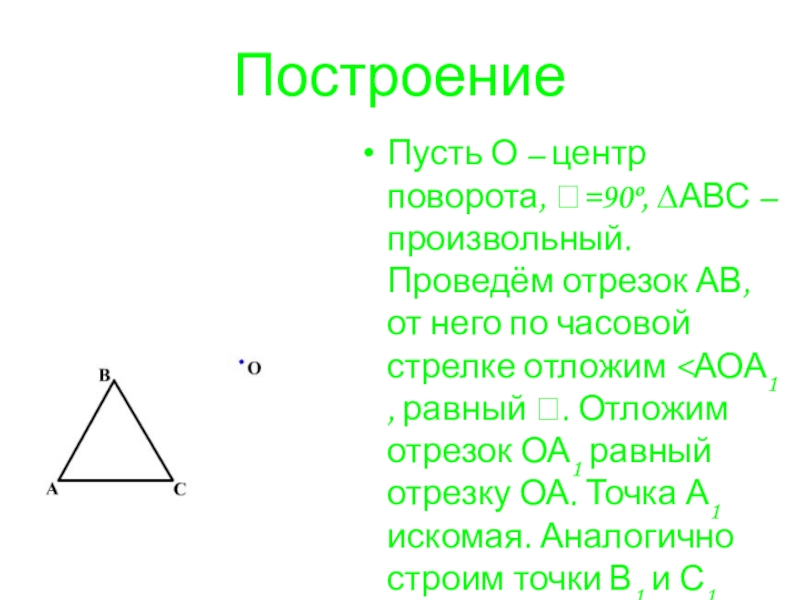
- 14. ПостроениеПусть О – центр поворота, =90º, ∆АВС
- 15. Точка О называется центром поворота,α – угол
- 16. OММ1М2Если поворот выполняется по часовой стрелке, то
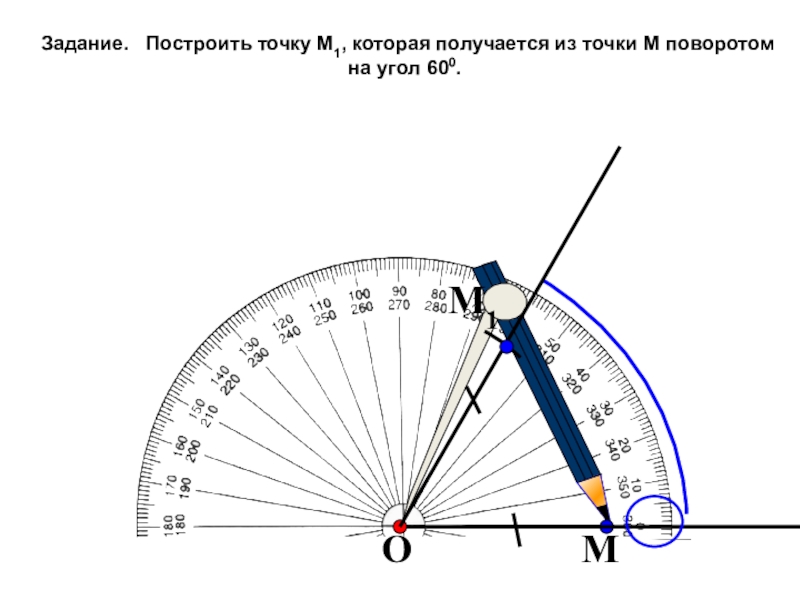
- 17. OMM1Задание. Построить точку M1, которая получается из точки M поворотом на угол 600.
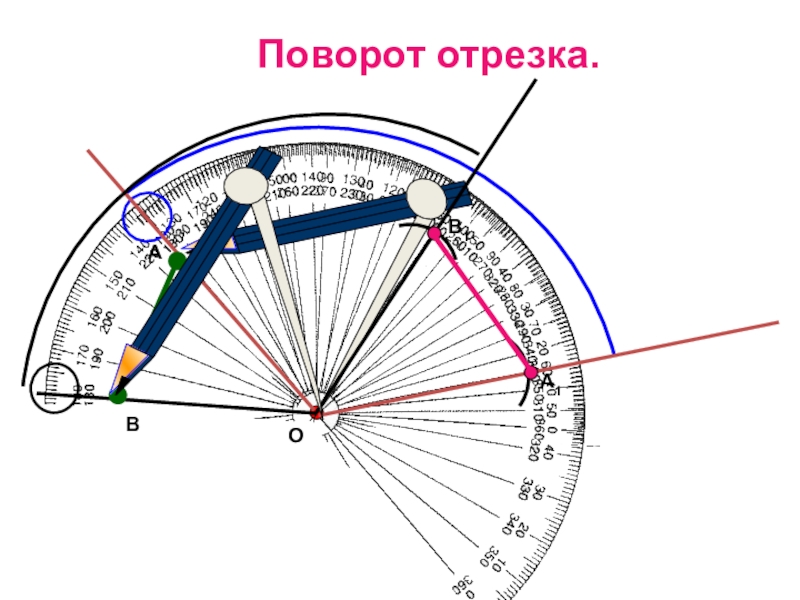
- 18. АВОА1В1Поворот отрезка.
- 19. Слайд 19
- 20. Слайд 20
- 21. а) поворот;б) параллельный перенос;в) симметрия относительно точки;г)
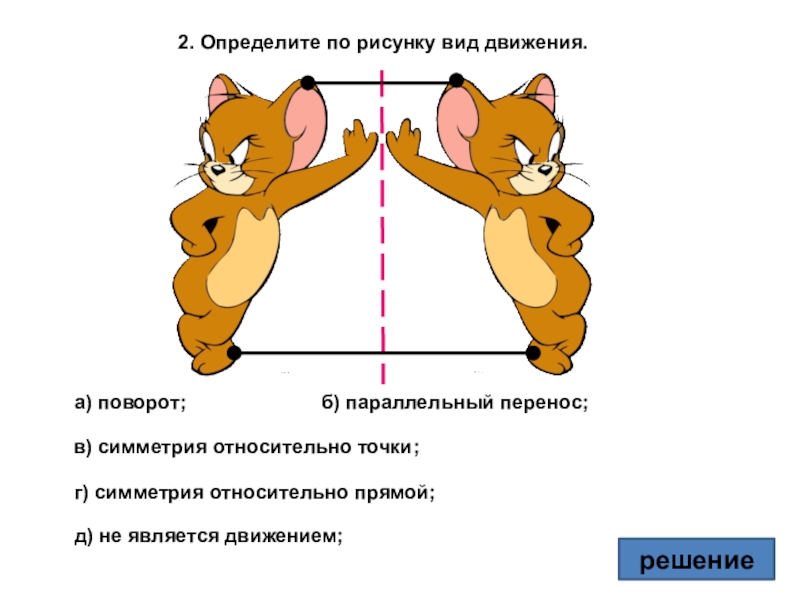
- 22. 2. Определите по рисунку вид движения.а) поворот;в)
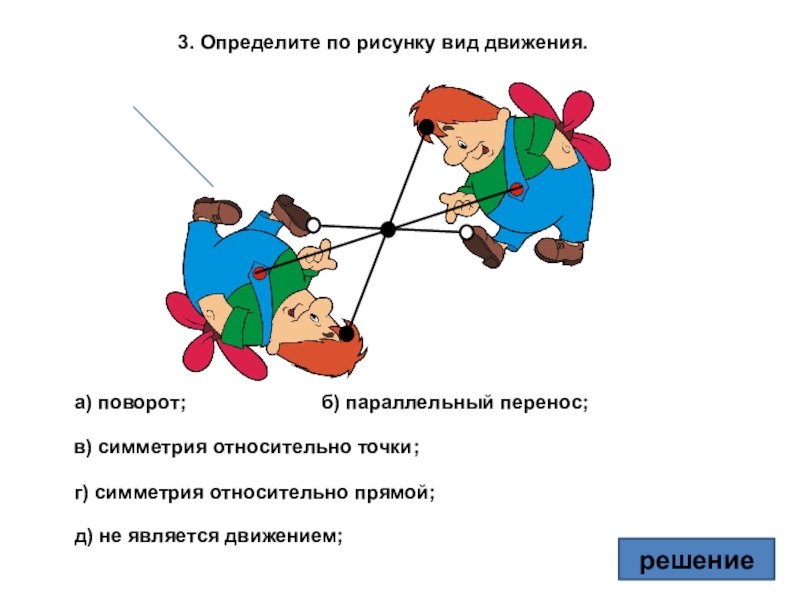
- 23. 3. Определите по рисунку вид движения.а) поворот;в)
- 24. 4. Определите по рисунку вид движения.а) поворот;б)
- 25. 5. Определите по рисунку вид движения.а) поворот;в)
- 26. ВопросыОпределить вид симметрии.Что вам приходилось встречать в природе из известных видов симметрии?
- 27. Симметрия в природе
- 28. Слайд 28
- 29. Слайд 29
- 30. Симметрия в архитектуре
- 31. Слайд 31
- 32. Что происходит в алгебре?
- 33. Какие из данных графиков можно отнести к
- 34. Успехов в выполнении домашнего задания!
- 35. СПАСИБО ЗА РАБОТУ!
- 36. Скачать презентанцию
22.04. 20Движение
Слайды и текст этой презентации
Слайд 5Построение
Пусть а – ось симметрии.
∆АВС – произвольный.
Проведем перпендикуляр ВР к прямой а. Отложим на прямой ВР
отрезок РВ1 , равный по длине отрезку ВР. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С 1 симметричен ∆АВС относительно прямой а.
Слайд 8Центральная симметрия
Определение
Центральная симметрия –это отображение плоскости на себя
, при котором каждая точка М отображается в такую точку
М1,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).
Слайд 9Построение
Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч
ВО. Отложим отрезок ОВ1 , равный отрезку ОВ. Точка В1
искомая. Аналогично строим точки А 1 и С1 . ∆А1В1С1 симметричен ∆АВС относительно точки О.
Слайд 13Поворот
Определение
Поворот плоскости вокруг точки О на угол
- это отображение плоскости на себя , при котором
каждая точка М отображается в такую точку М1 , что ОМ=ОМ1 , < МОМ1=.
Слайд 14Построение
Пусть О – центр поворота, =90º, ∆АВС – произвольный. Проведём
отрезок АВ, от него по часовой стрелке отложим
равный . Отложим отрезок ОА1 равный отрезку ОА. Точка А1 искомая. Аналогично строим точки В1 и С1
Слайд 16O
М
М1
М2
Если поворот выполняется по часовой стрелке, то угол поворота α
считается отрицательным.
Если поворот выполняется против часовой стрелки, то угол поворота
– положительный.
Слайд 21а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д)
не является движением;
1. Определите по рисунку вид движения.
Слайд 222. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г)
симметрия относительно прямой;
д) не является движением;
б) параллельный перенос;
Слайд 233. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г)
симметрия относительно прямой;
д) не является движением;
б) параллельный перенос;
Слайд 244. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия
относительно точки;
г) симметрия относительно прямой;
д) не является движением;
Слайд 255. Определите по рисунку вид движения.
а) поворот;
в) симметрия относительно точки;
г)
симметрия относительно прямой;
д) не является движением;
б) параллельный перенос;
Слайд 26Вопросы
Определить вид симметрии.
Что вам приходилось встречать в природе из известных
видов симметрии?
