Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двоичная система счисления
Содержание
- 1. Двоичная система счисления
- 2. Двоичная система счисленияСистема счисления (CC)— совокупность правил
- 3. Римская система счисленияНесколько чисел приняты за основные
- 4. Позиционные ССсистема счисления характеризуется основанием. Так, основание
- 5. Позиционные СС11,012 =1 · 21 +1 ·
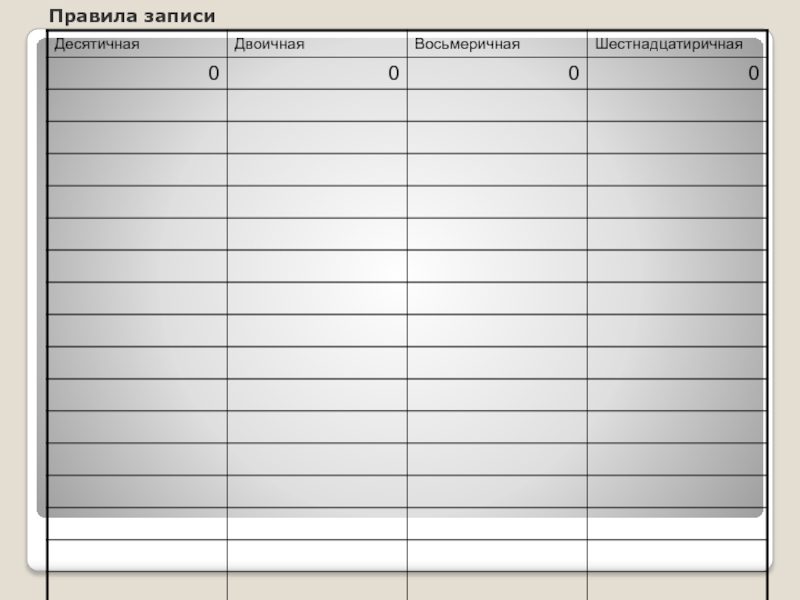
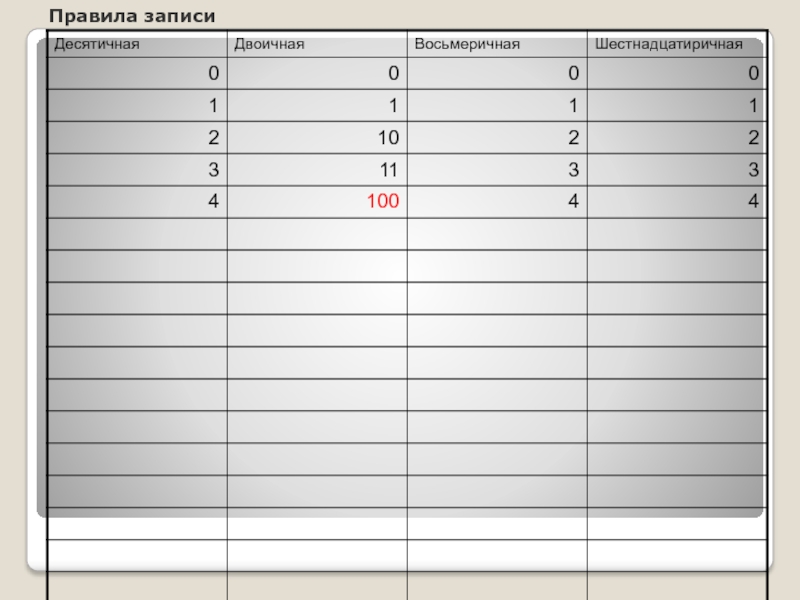
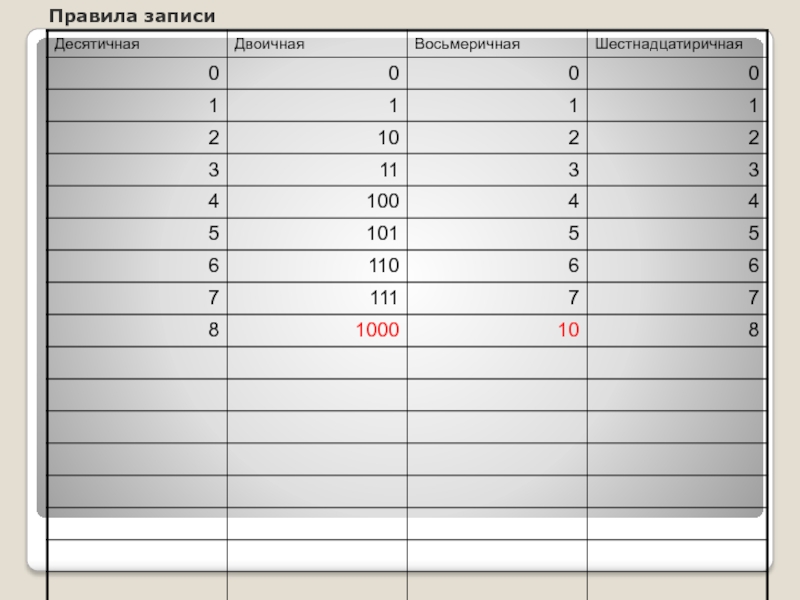
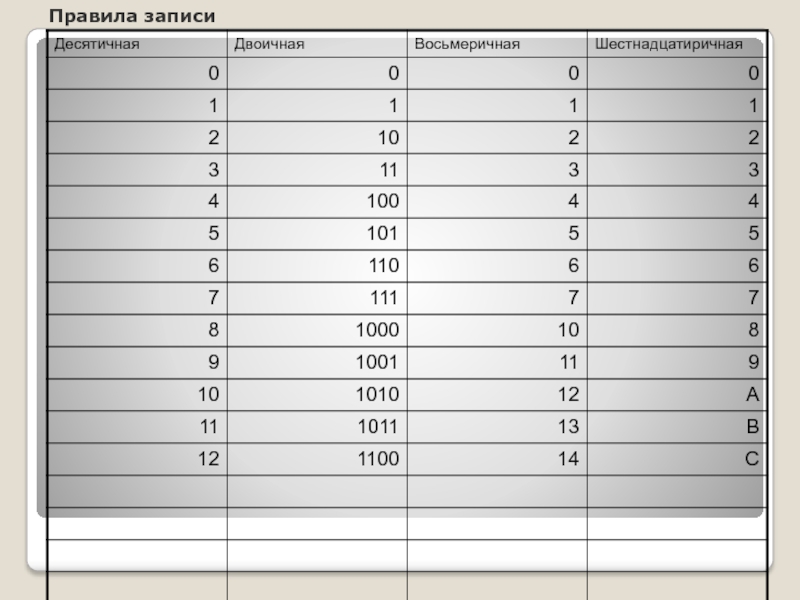
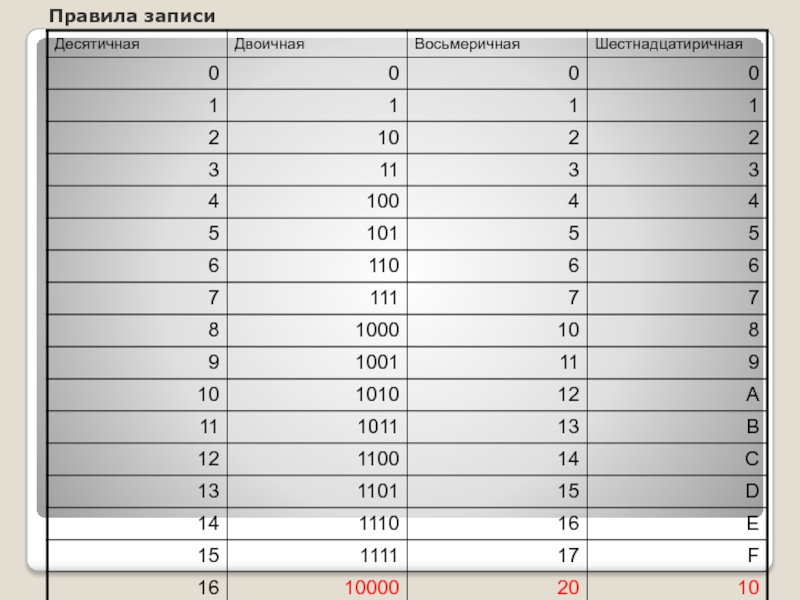
- 6. Правила записи
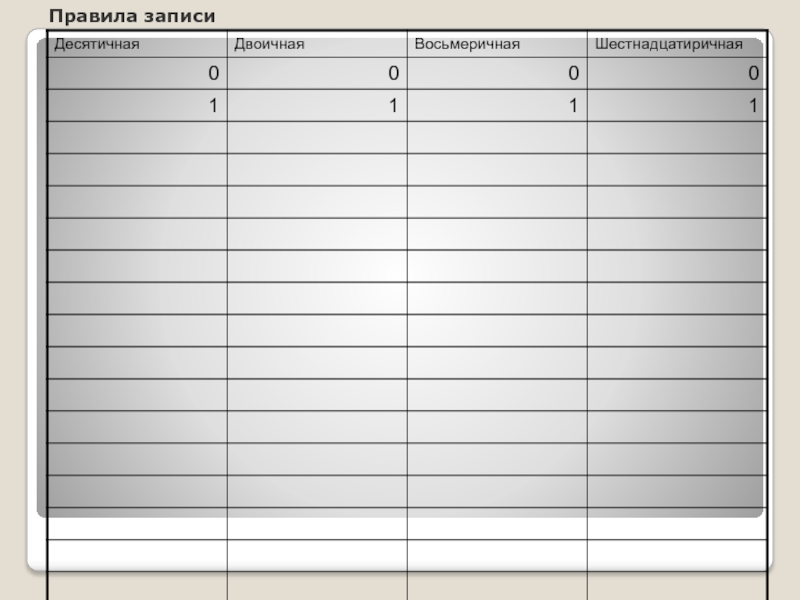
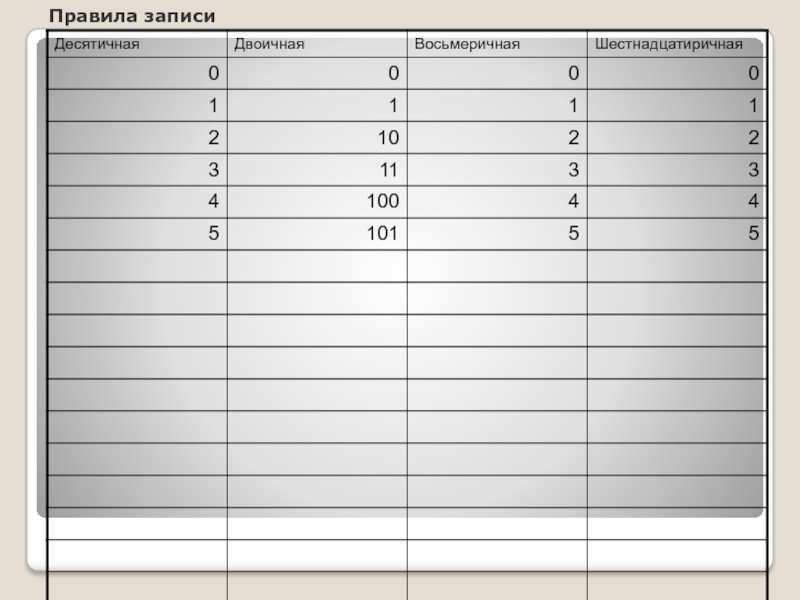
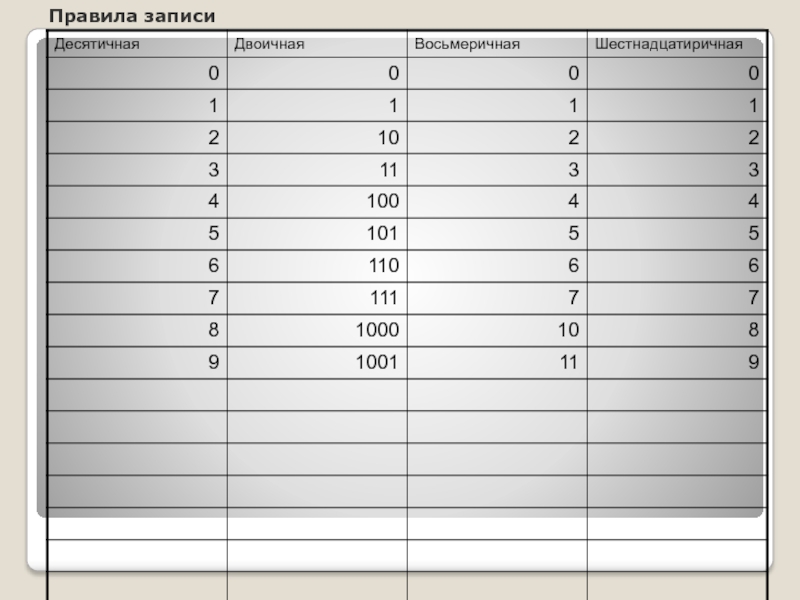
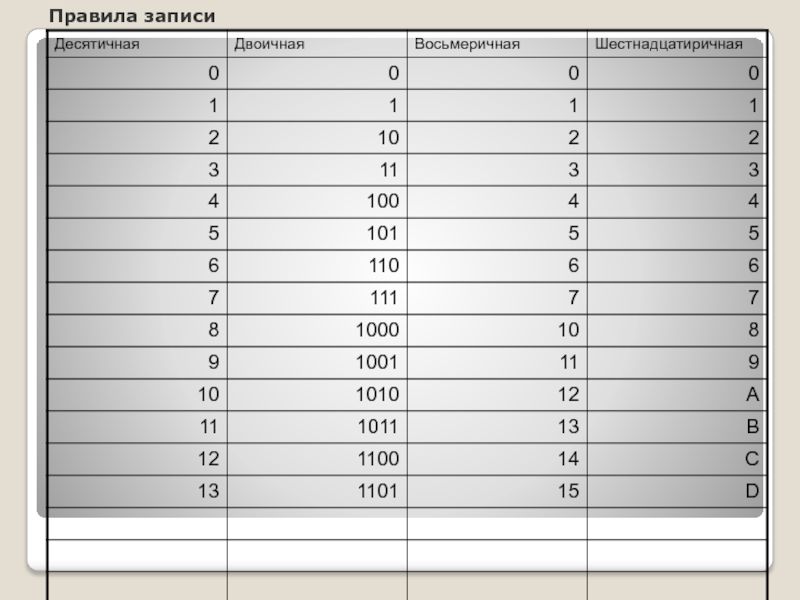
- 7. Правила записи
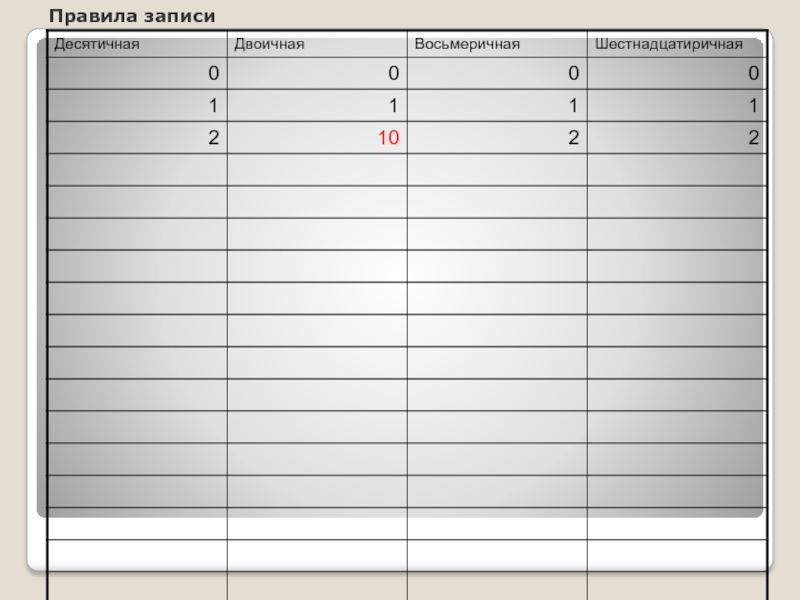
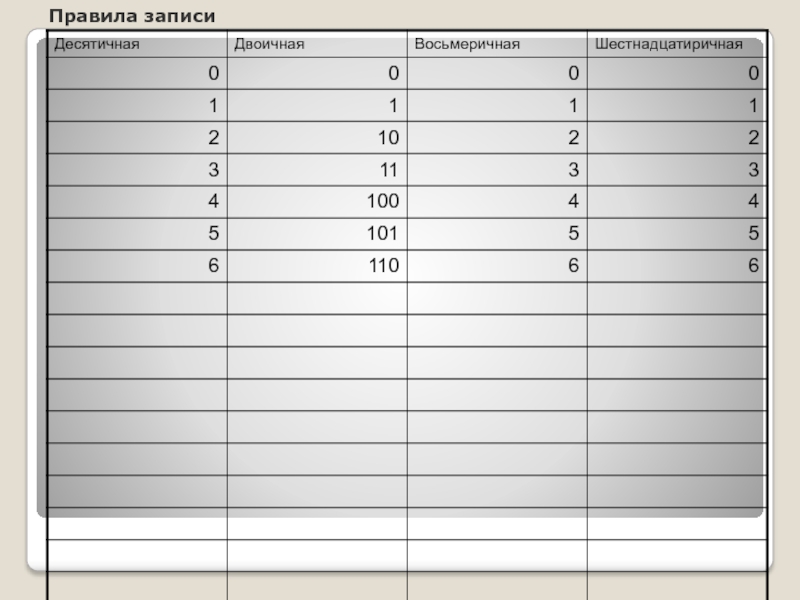
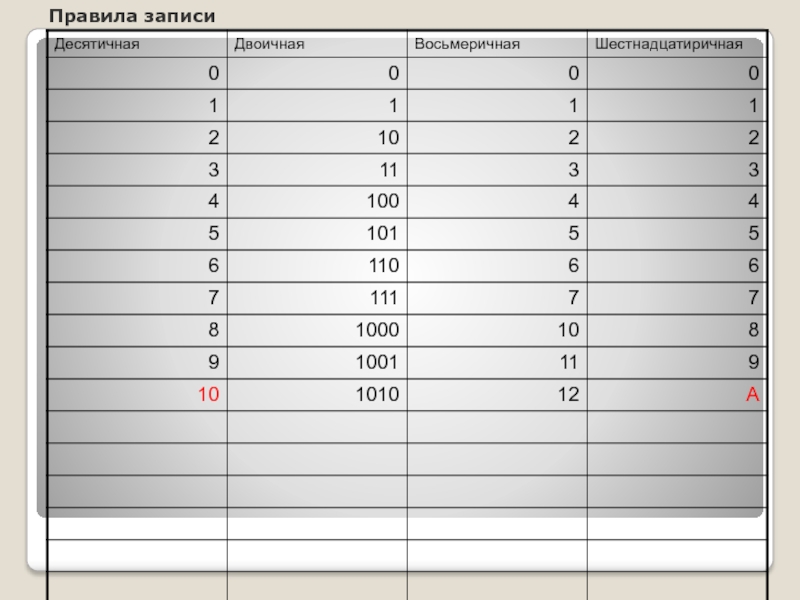
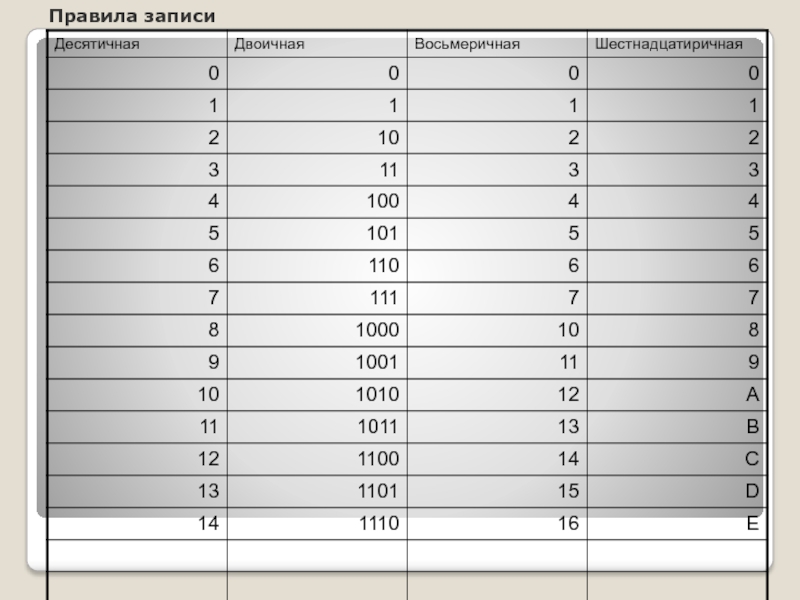
- 8. Правила записи
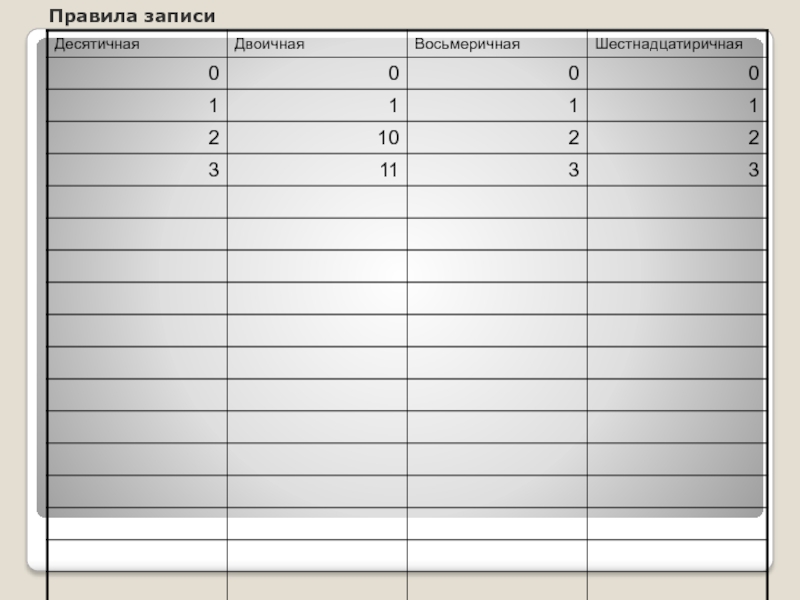
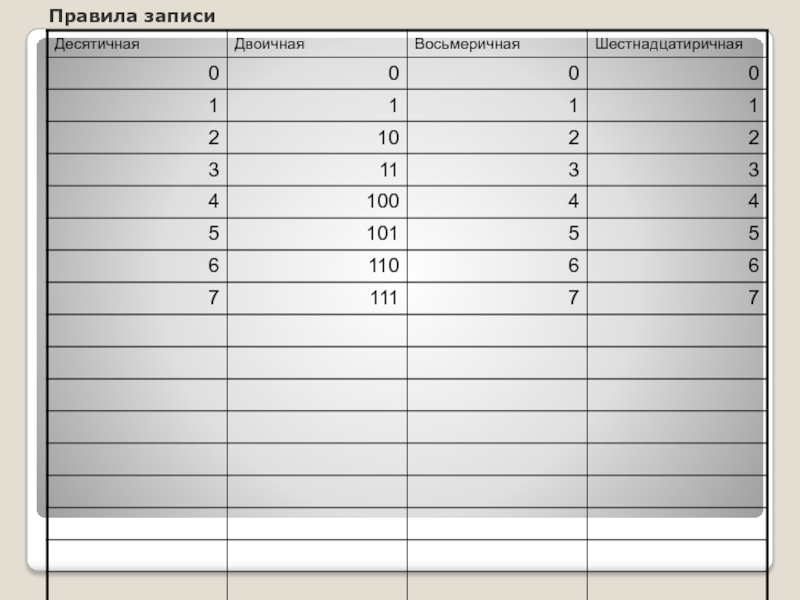
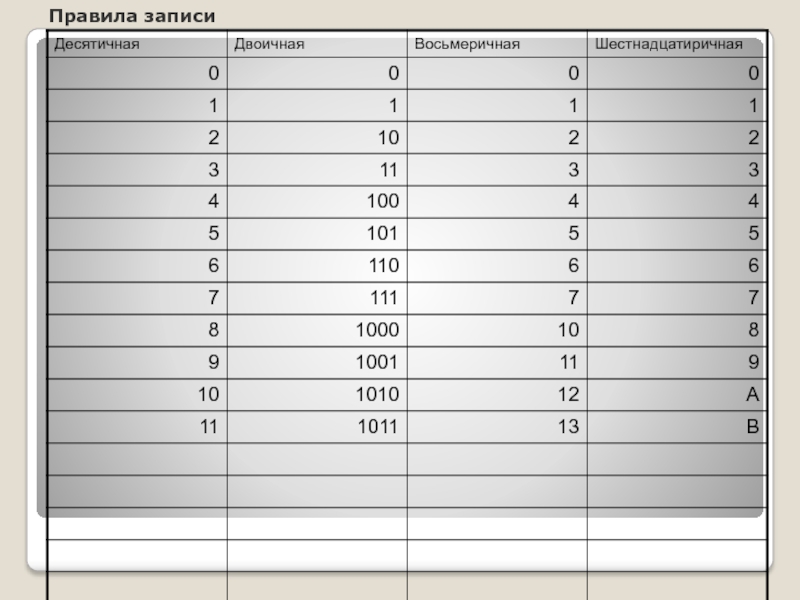
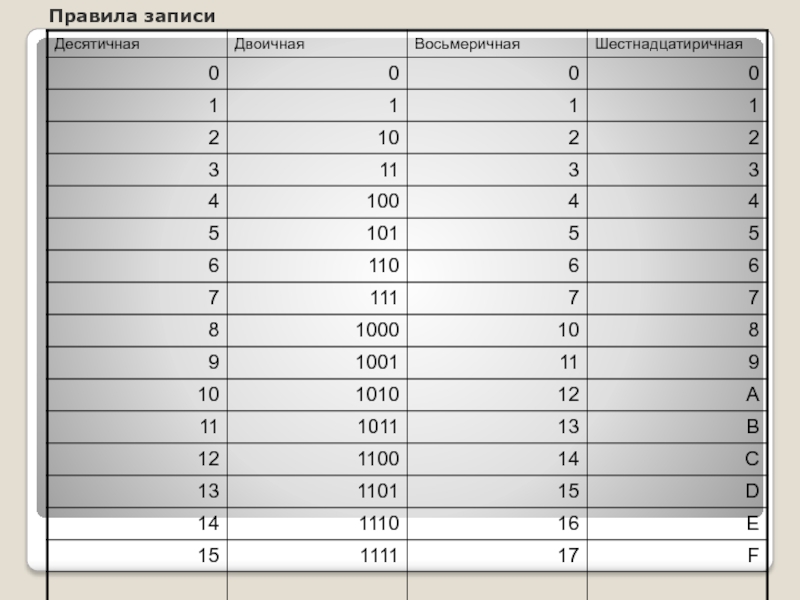
- 9. Правила записи
- 10. Правила записи
- 11. Правила записи
- 12. Правила записи
- 13. Правила записи
- 14. Правила записи
- 15. Правила записи
- 16. Правила записи
- 17. Правила записи
- 18. Правила записи
- 19. Правила записи
- 20. Правила записи
- 21. Правила записи
- 22. Правила записи
- 23. Веса восьми двоичных цифр 7
- 24. 1. Арифметические действия в двоичной системе счисления
- 25. 1. Арифметические действия в двоичной системе счисления
- 26. 1. Арифметические действия в двоичной системе счисления
- 27. 1.4. Деление в двоичной системе счисленияОсуществляется так
- 28. 2. Перевод числа из десятичной системы счисления
- 29. 2. Перевод числа из десятичной системы счисления
- 30. 2. Перевод числа из десятичной системы счисления
- 31. 3. Перевод числа из двоичной системы счисления
- 32. Преимущества и недостатки использования двоичной системы счисления
- 33. Скачать презентанцию
Двоичная система счисленияСистема счисления (CC)— совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами. Системы счисления делятся на позиционные и непозиционные.
Слайды и текст этой презентации
Слайд 2Двоичная система счисления
Система счисления (CC)— совокупность правил наименования и изображения
чисел с помощью набора символов, называемых цифрами.
на позиционные и непозиционные. 
Слайд 3Римская система счисления
Несколько чисел приняты за основные
I, V, X,
С-100, D-500, M-1000,
а остальные получаются использую следующие принципы:
Повторяемая буква
увеличивает значение в количество повторов.Одна или более букв, помещенных после другой буквы большего значения, увеличивают значение этой буквы на величину более мелкой (VI=6, LXX = 70, MCC = 1200).
Буква, помещенная перед другой буквой большего значения, уменьшает значение этой буквы на величину более мелкой (IV=4, XL = 40, XC=90, CM = 900, IMM=1999).
Горизонтальная черта, помещенная над буквой, повышает ее значение в тысячу раз ().
Слайд 4Позиционные СС
система счисления характеризуется основанием.
Так, основание (Q) десятичной СС
= 10, двоичной СС = 2, восьмеричной СС = 8
и т.д.где s - основание системы счисления;
i - номер разряда (позиции);
n,m - номера соответствующего старшего и младшего разрядов;
xi принадлежит {0,1, ... , (s-1)} - коэффициент, показывающий, сколько единиц i-го разряда содержится в числе.
Слайд 5Позиционные СС
11,012 =1 · 21 +1 · 20 +0 ·
2-1+1 · 2-2 = 3,2510
555,510 =5 ·102 +5 · 101
+5 · 100 +5 · 10-1;
Слайд 23 Веса восьми двоичных цифр
7
6 5
4 3 2 1 0 < позиция бита7 6 5 4 3 2 _1 1 1 1 1 1 1 1
128 64 32 16 8 4 2 1 <--- десятичное значение
Слайд 241. Арифметические действия в двоичной системе счисления
1.1. Сложение в двоичной
системе счисления
0 + 0 = 0;
1 + 0 =
1; 0 + 1 = 1;
1 + 1 = 10
Слайд 251. Арифметические действия в двоичной системе счисления
1.2.Вычитание в двоичной системе
счисления
0 – 0 = 0;
1 – 0 = 1;
1 – 1 = 0;
10 – 1 = 1.
Слайд 261. Арифметические действия в двоичной системе счисления
1.3. Умножение в двоичной
системе счисления
0 · 0 = 0;
1 · 0 =
0;0 · 1 = 0;
1 · 1 = 1.
10,1
х 11,1
101
101
101
1000,11
2,5
х 3,5
125
75
8,75
Слайд 271.4. Деление в двоичной системе счисления
Осуществляется так же, как и
в десятичной, с использованием умножения и вычитания.
Слайд 282. Перевод числа из десятичной системы счисления в двоичную
2.1.
1-й способ перевода числа из десятичной системы счисления в двоичную.
1210 —> X2
12 |_2_
12 6 |_2_
0 6 3 |_2_
0 2 1
1
1210 —> 11002
Слайд 292. Перевод числа из десятичной системы счисления в двоичную
2.1.
1-й способ перевода числа из десятичной системы счисления в двоичную.
Перевод десятичных дробей, меньших единицы
0,2510 —> X2
0__|_25_ х2
0 50
1 00
0,2510 —> 0,012
Перевод десятичных дробей, больше единицы
Слайд 302. Перевод числа из десятичной системы счисления в двоичную
2.2.
2-й способ перевода числа из десятичной системы счисления в двоичную.
Состоит в представлении числа в виде суммы степеней двойки и последующем выделении коэффициентов такого представления
12,2510 = (8 + 4 + 1/4) 10= (23 +22 +2-2) 10 =
= (1•23 + 1•22 + 0•21+0•2°+0•2-1+1•2-2)10=1100,012.
2-й способ перевода записи числа из десятичной системы счисления в двоичную, очевидно, требует меньших трудозатрат, но оба способа правильны и допустимы. Поэтому мы вправе выбрать его по своему усмотрению.
Слайд 313. Перевод числа из двоичной системы счисления в десятичную
1000001001,1012 =
(1 • 29 + 0 • 28 + 0 •
27 + 0 • 26 + 0 • 25 + +0•24+ 1•23+0•22+0•21+ 1•2°+ 1•2-1+0•2-2+ 1•2-з) 10 = (512+8+1+1/2+1/8) 10= (521+5/8) 10=
(521,625) 10
Слайд 32Преимущества и недостатки использования двоичной системы счисления по сравнению с
любой другой позиционной системой счисления.
Недостатки: длина записи, представляющей двоичное
число. Основные преимущества:
простота совершаемых операций, а также
возможность осуществлять автоматическую обработку информации, реализуя только два состояния элементов компьютера
