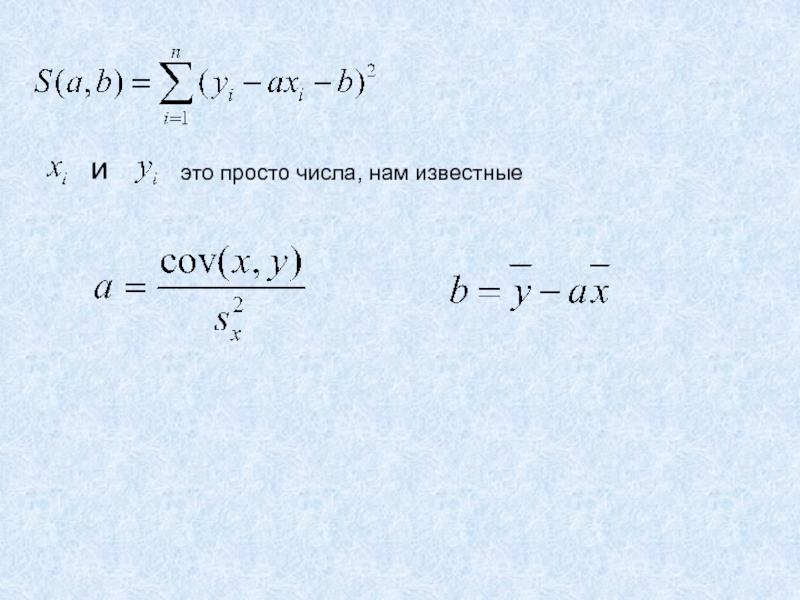Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЭКОНОМЕТРИКА ЛИТЕРАТУРА К КУРСУ:
Содержание
- 1. ЭКОНОМЕТРИКА ЛИТЕРАТУРА К КУРСУ:
- 2. ЧТО ТАКОЕ ЭКОНОМЕТРИКАЭкономическая теорияТеория Вероятностей и математическая статистикаЭкономическая статистикаМикроэкономикаМакроэкономикаЭконометрика
- 3. Эконометрика Формулирует экономические модели, основываясь на экономической
- 4. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая) переменнаях – независимая (объясняющая) переменная
- 5. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 6. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 7. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 8. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 9. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 10. ПАРНАЯ РЕГРЕССИЯКоэффициент корреляции близок к 1
- 11. Коэффициент корреляции близок к -1
- 12. Коэффициент корреляции близок к 0
- 13. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИy – зависимая (объясняемая)
- 14. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИПредположим, что необходимо получить
- 15. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
- 16. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИНанесем точки на график
- 17. Метод наименьших квадратовНанесем точки на графикТочки разбросаны вокруг некоторой прямой!Как ее найти?
- 18. Метод наименьших квадратовНанесем точки на графикРасстояние от каждой точки до прямой должно быть как можно меньше!
- 19. Метод наименьших квадратовНанесем точки на графикПлохая прямая!
- 20. Метод наименьших квадратовНанесем точки на графикХорошая прямая! Но может быть есть еще лучше?
- 21. Метод наименьших квадратовНанесем точки на графикУравнение прямой
- 22. Обозначим доход 1-го домохозяйстваспрос 1-го домохозяйства на продуктxyy=ax+b
- 23. Обозначим доход 1-го домохозяйстваспрос 1-го домохозяйства на продуктxyy=ax+bОтклонение точки от прямой. Должно бытькак можно меньше!
- 24. Обозначим доход 1-го домохозяйстваспрос 1-го домохозяйства на продуктxyy=ax+bОтклонение точки от прямой. Должно бытькак можно меньше!
- 25. А если точка лежит ниже прямой?Тогда отклонение xyy=ax+bОтклонение точки от прямой. Должно бытькак можно меньше!
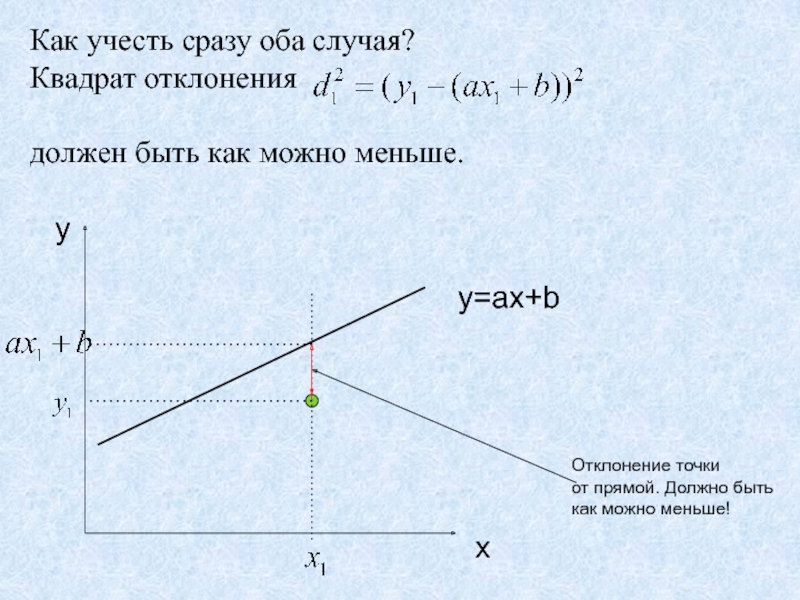
- 26. Как учесть сразу оба случая?Квадрат отклонения
- 27. Квадрат отклонения до второй точки тоже должен быть как можно меньше.
- 28. Квадрат отклонения до второй точки тоже должен быть как можно меньше.И для третьей точки
- 29. Предположим, что у нас n точек.Тогда и для последней точки
- 30. Как учесть все точки сразу?Сумма квадратов расстояний от точек до прямой должна быть как можно меньше.
- 31. Как учесть все точки сразу?Сумма квадратов расстояний от точек до прямой должна быть как можно меньше.обозначение
- 32. Как учесть все точки сразу?Получили функцию двух
- 33. это просто числа, нам известныеи
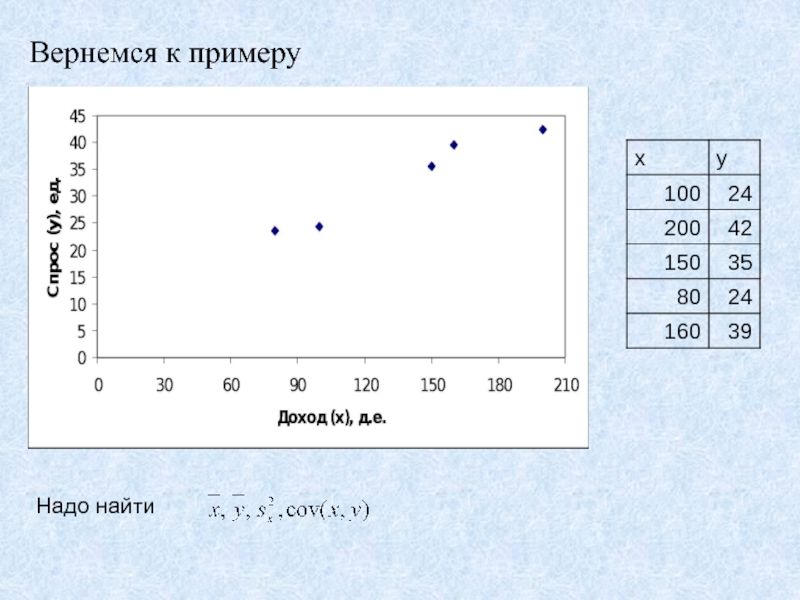
- 34. Вернемся к примеруНадо найти
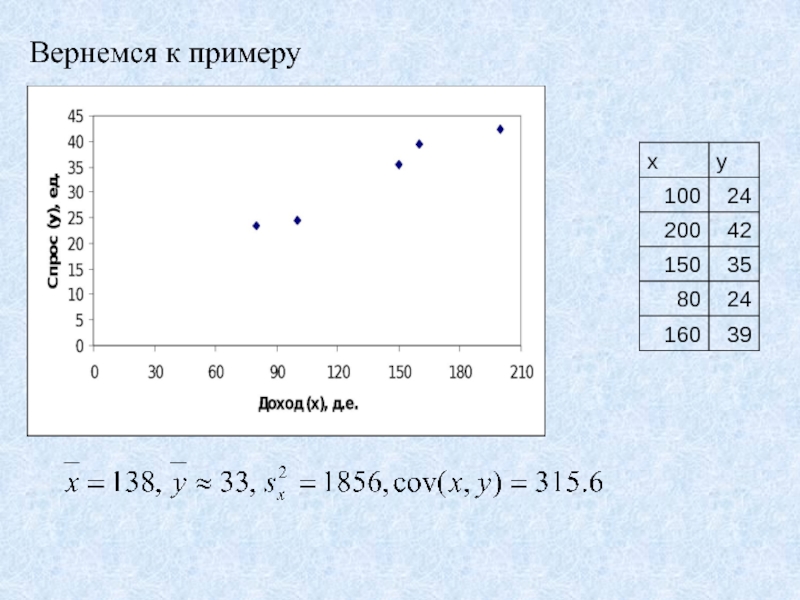
- 35. Вернемся к примеру
- 36. a=0,17, b=9,33y=0,17x+9,33 - уравнение прямой, которая проходит ближе всего к точкам.
- 37. y=0,17x+9,33 - функция спроса в зависимости от
- 38. y=0,17x+9,33 - функция спроса в зависимости от дохода.
- 39. y=0,17x+9,33 - функция спроса в зависимости от
- 40. Как оценить качество построенной модели?Построим прогноз по модели по формуле
- 41. Как оценить качество построенной модели?Вычисляем остатки
- 42. Как оценить качество построенной модели?Находим относительную ошибку аппроксимацииПроцентный формат
- 43. Как оценить качество построенной модели?Находим среднюю относительную
- 44. Как оценить качество построенной модели?Еще один показатель
- 45. Как оценить качество построенной модели?коэффициент детерминации
- 46. Как оценить качество построенной модели?коэффициент детерминациипоказывает долю
- 47. Как оценить качество построенной модели?94,9% вариации спроса
- 48. Как оценить качество построенной модели?
- 49. Проверка значимости коэффициентов модели регрессииПостроено уравнение Даже
- 50. Проверка значимости коэффициентов модели регрессииДля проверки значимости
- 51. Проверка значимости коэффициентов модели регрессии
- 52. Проверка значимости коэффициентов модели регрессииР-значение - это
- 53. y=0,17x+9,33 - функция спроса в зависимости от
- 54. y=0,17x+9,33 - функция спроса в зависимости от
- 55. Модели парной нелинейной регрессии
- 56. Слайд 56
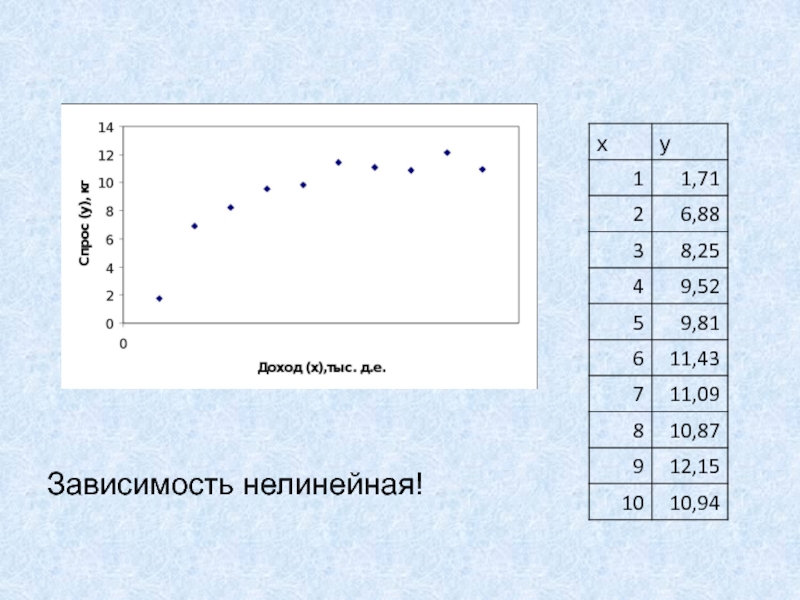
- 57. Зависимость нелинейная!
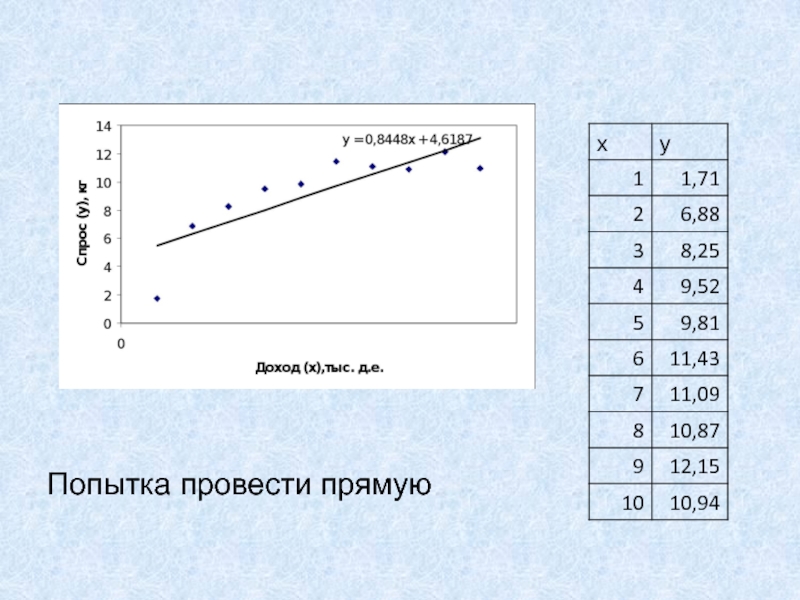
- 58. Попытка провести прямую
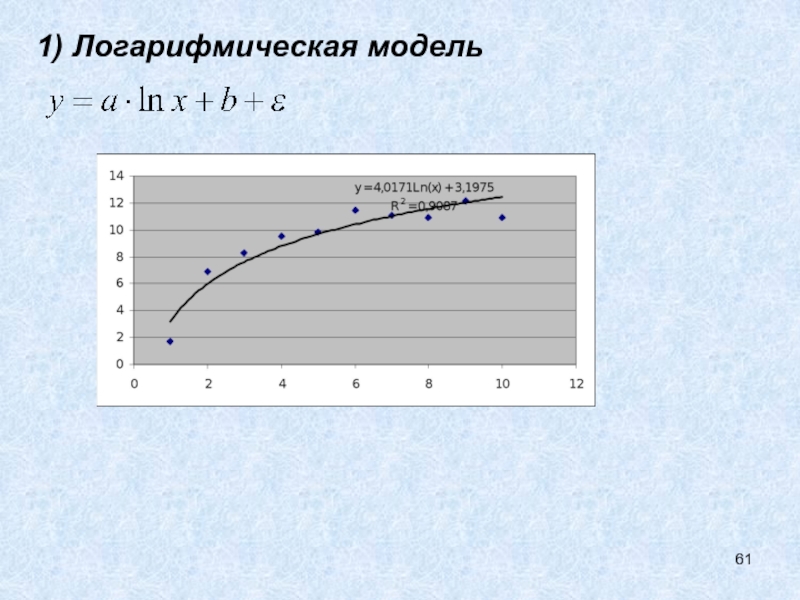
- 59. 1) Логарифмическая модельДля оценки такой зависимости создаем столбец с ln(x)
- 60. 1) Логарифмическая модельИспользуя сервис Анализ данных построим
- 61. 1) Логарифмическая модель
- 62. 1) Логарифмическая модельИнтерпретация коэффициента а: при увеличении
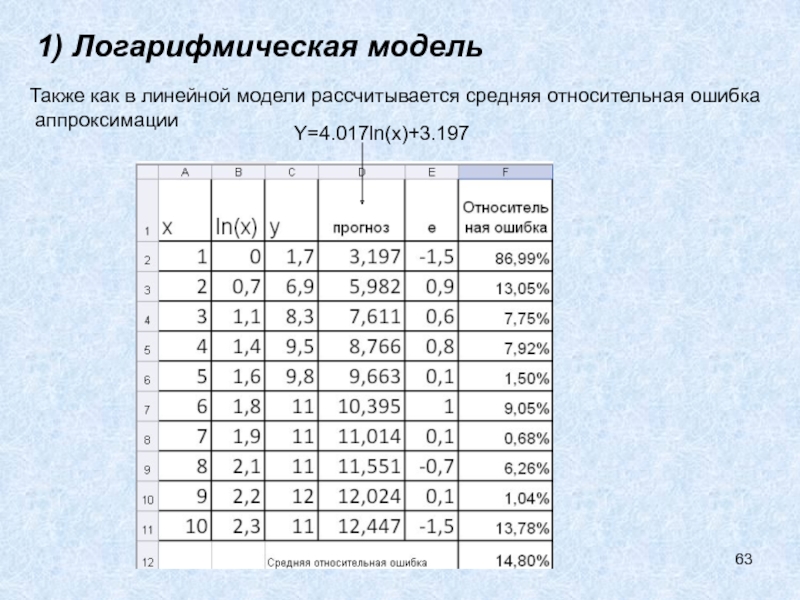
- 63. 1) Логарифмическая модельТакже как в линейной модели рассчитывается средняя относительная ошибка аппроксимацииY=4.017ln(x)+3.197
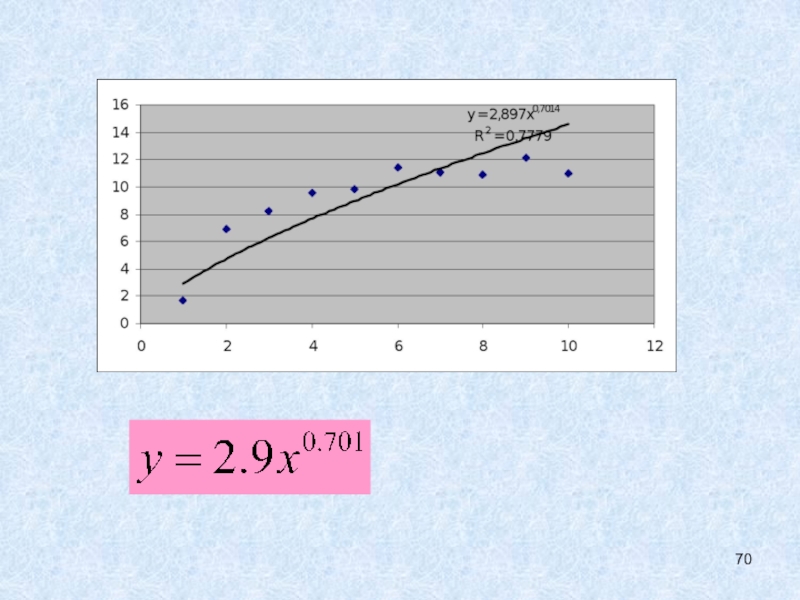
- 64. Степенная модельИнтерпретация коэффициента a – эластичность зависимой
- 65. Степенная модельСводится к линейной модели логарифмированием
- 66. Степенная модельСоздаем столбцы с логарифмами
- 67. Используя сервис Анализ данных построим модель линейной
- 68. Используя сервис Анализ данных построим модель линейной
- 69. Используя сервис Анализ данных построим модель линейной
- 70. Слайд 70
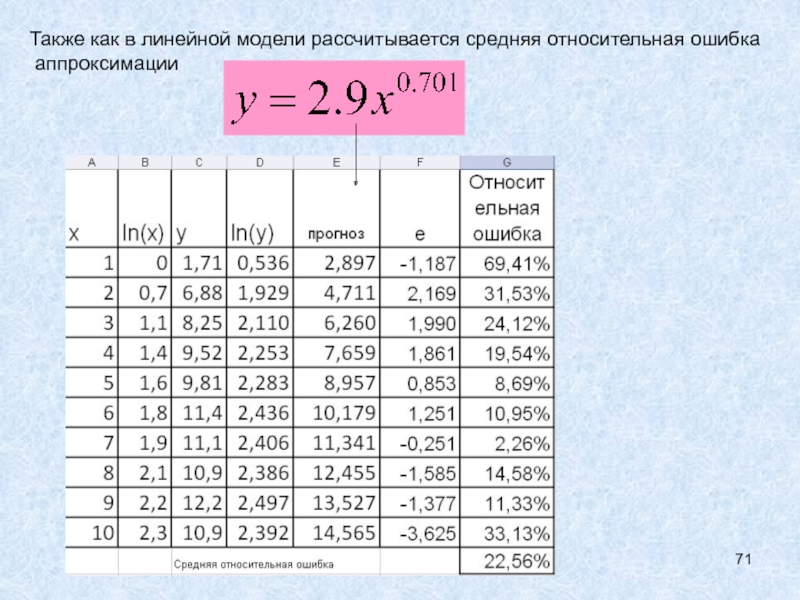
- 71. Также как в линейной модели рассчитывается средняя относительная ошибка аппроксимации
- 72. Скачать презентанцию
ЧТО ТАКОЕ ЭКОНОМЕТРИКАЭкономическая теорияТеория Вероятностей и математическая статистикаЭкономическая статистикаМикроэкономикаМакроэкономикаЭконометрика
Слайды и текст этой презентации
Слайд 1ЭКОНОМЕТРИКА
ЛИТЕРАТУРА К КУРСУ:
Основная
К.Доугерти
«Введение в эконометрику» , М.: Инфра-М
(пер. под
ред. Замкова)
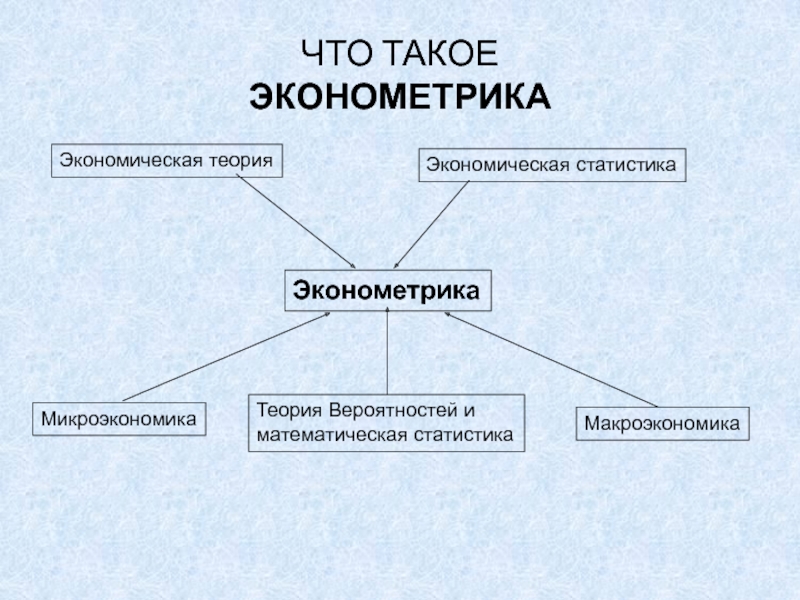
Слайд 2ЧТО ТАКОЕ
ЭКОНОМЕТРИКА
Экономическая теория
Теория Вероятностей и
математическая статистика
Экономическая статистика
Микроэкономика
Макроэкономика
Эконометрика
Слайд 3 Эконометрика
Формулирует экономические модели, основываясь на экономической теории (микро и
макроэкономике)
Оценивает неизвестные параметры модели на базе реальных статистических данных
Использует построенные
модели для объяснения поведения исследуемых экономических показателей, прогнозирования, а также для осмысленного проведения экономической политики.
Слайд 4МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
Слайд 5МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
1. Вычисляем средние значения
СРЗНАЧ(диапазон
данных)
Слайд 6МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
2. Вычисляем дисперсии
ДИСПР(диапазон данных)
Слайд 7МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
3. Вычисляем ковариацию
КОВАР(диапазон данных х,
диапазон данных y)
Слайд 8МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
4. Вычисляем корреляцию
КОРРЕЛ(диапазон данных х,
диапазон данных y)
Слайд 9МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
4. Анализируем коэффициент корреляции
Коэффициент корреляции
принимает значения от -1 до 1.Значения близкие к 1 – есть тесная прямая связь между х и у
Значения близкие к -1 – есть тесная обратная связь между х и у
Значения близкие к 0 – связь между х и у отсутствует
Слайд 13МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая
(объясняющая) переменная
6. Если коэффициент корреляции не
близок к 0 строим модель парной линейной регрессии
Слайд 14МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
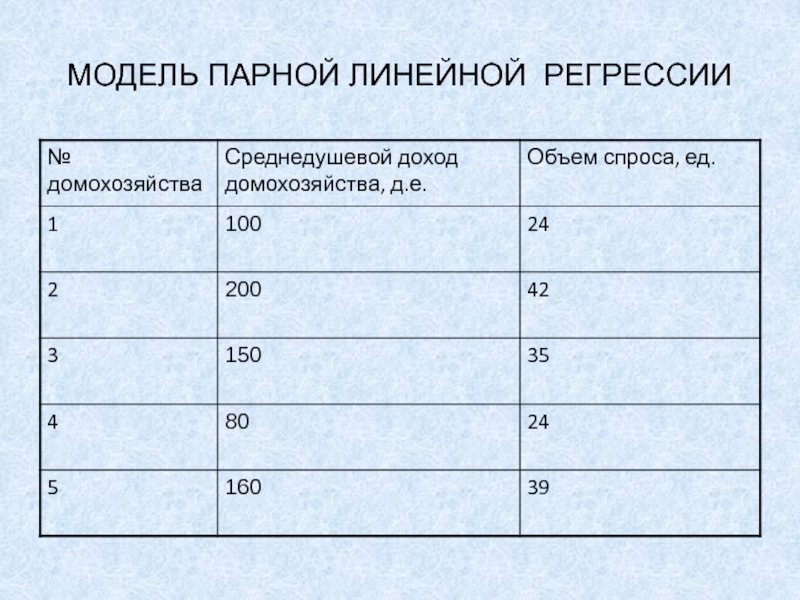
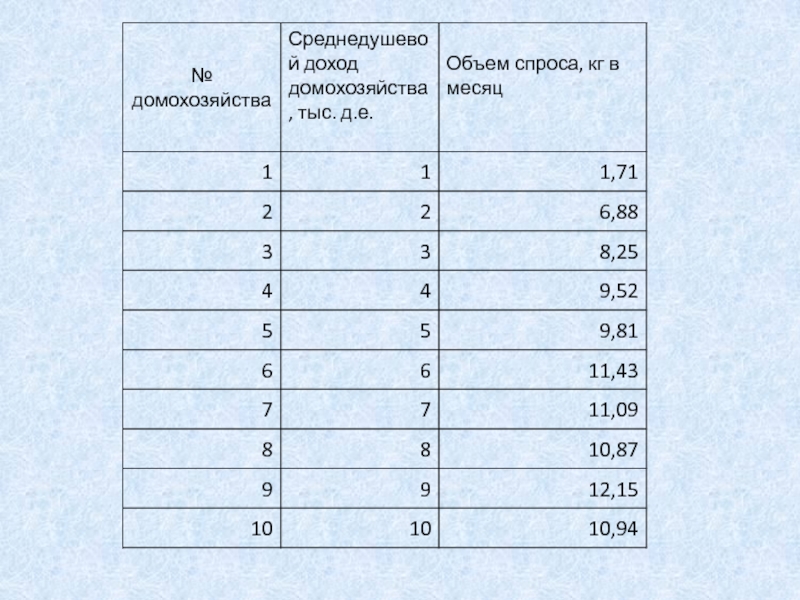
Предположим, что необходимо получить функцию
спроса на
некоторый товар в зависимости от дохода.
Проводится опрос домохозяйств.
1. Среднедушевой доход
домохозяйства?2. Сколько единиц товара приобрело домохозяйство за месяц?
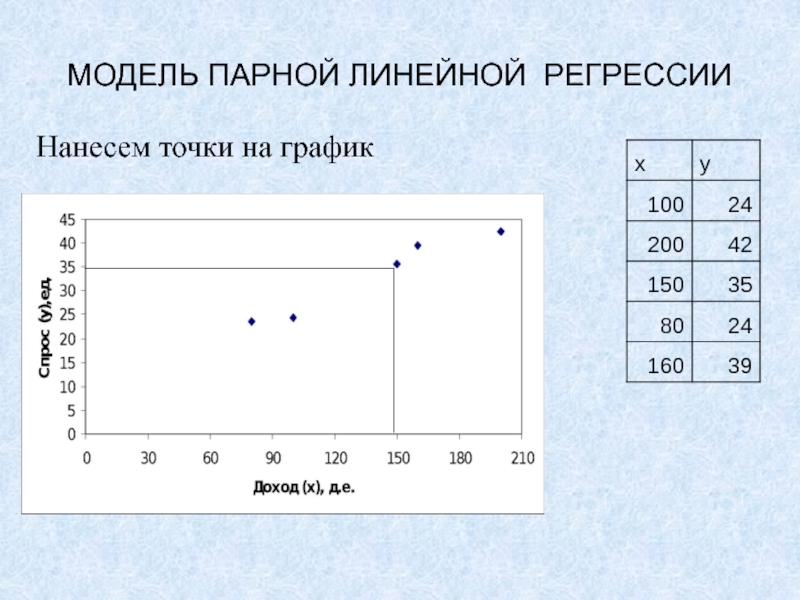
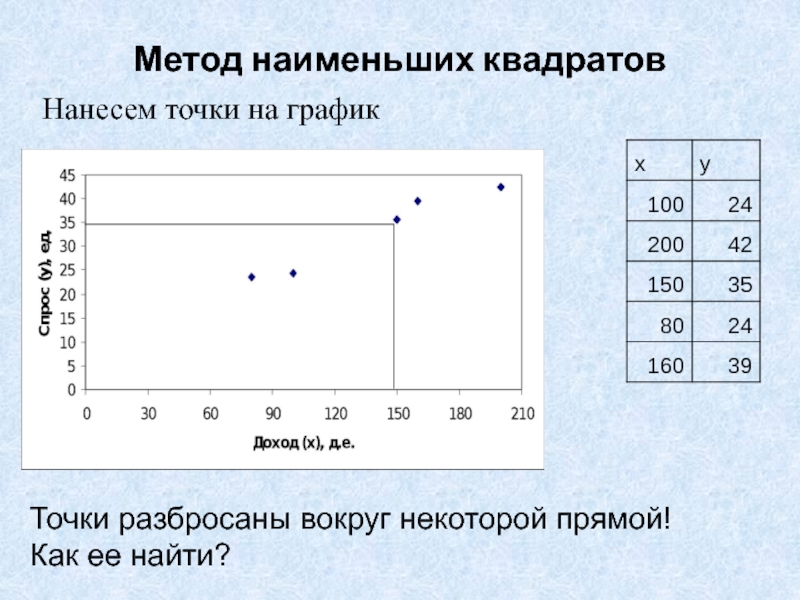
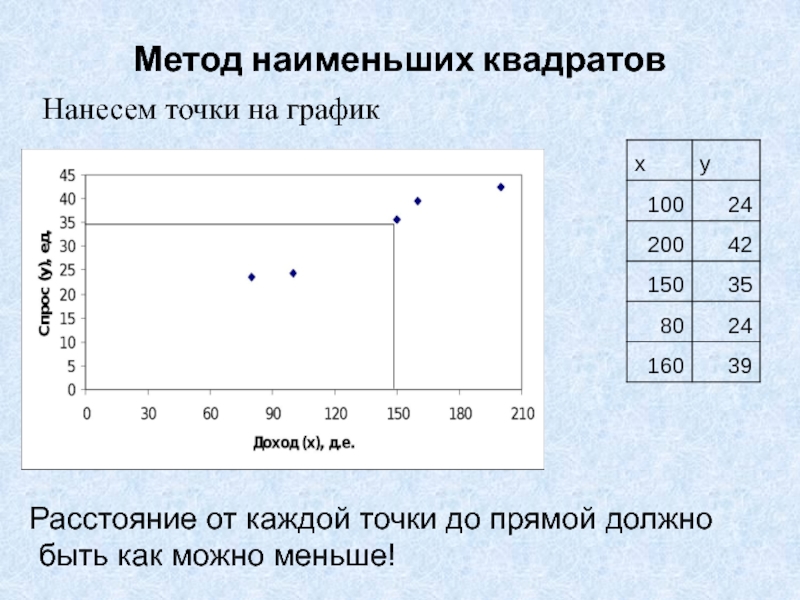
Слайд 17Метод наименьших квадратов
Нанесем точки на график
Точки разбросаны вокруг некоторой прямой!
Как
ее найти?
Слайд 18Метод наименьших квадратов
Нанесем точки на график
Расстояние от каждой точки до
прямой должно
быть как можно меньше!
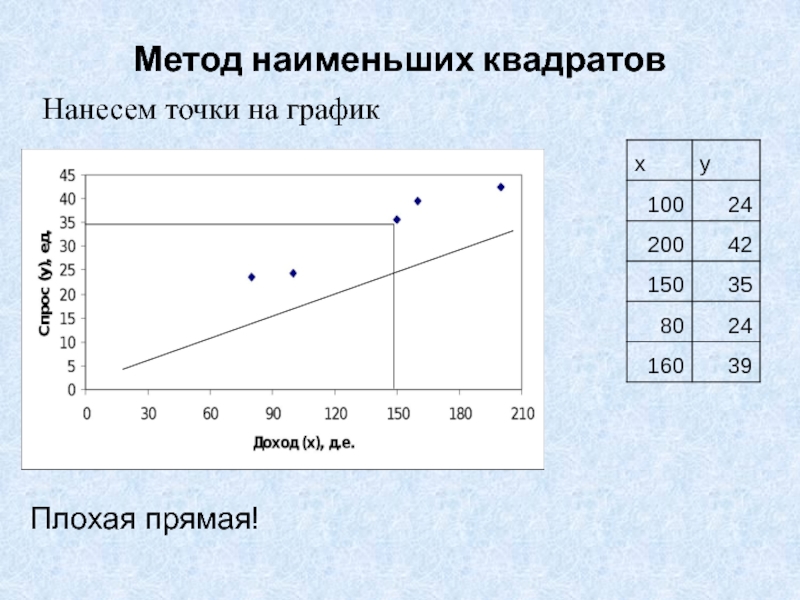
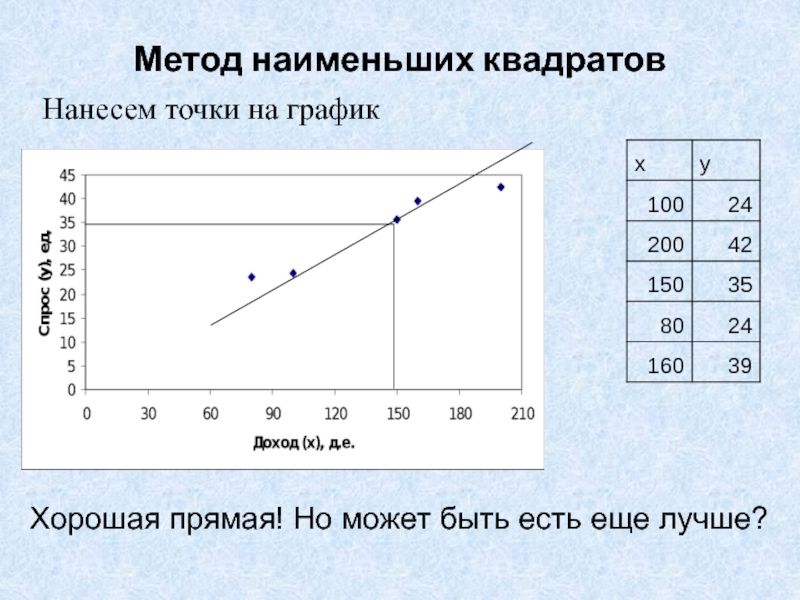
Слайд 20Метод наименьших квадратов
Нанесем точки на график
Хорошая прямая! Но может быть
есть еще лучше?
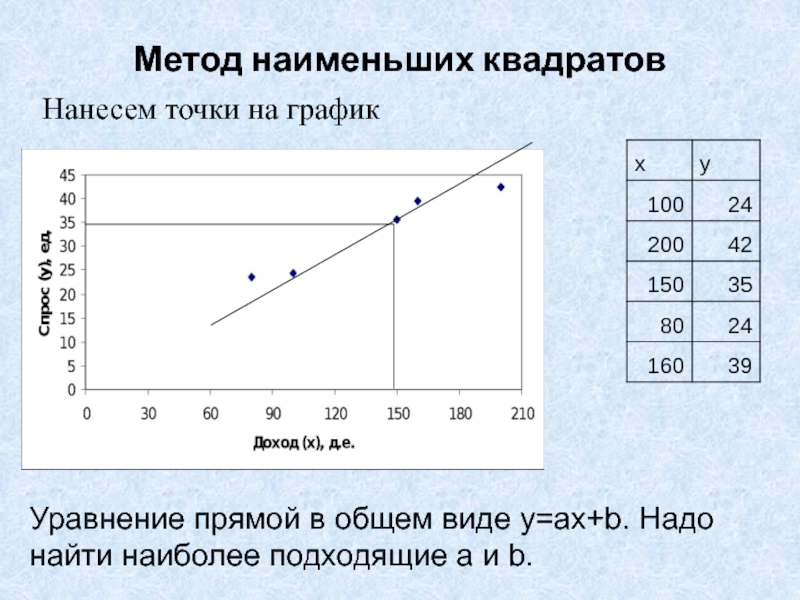
Слайд 21Метод наименьших квадратов
Нанесем точки на график
Уравнение прямой в общем виде
y=ax+b. Надо
найти наиболее подходящие a и b.
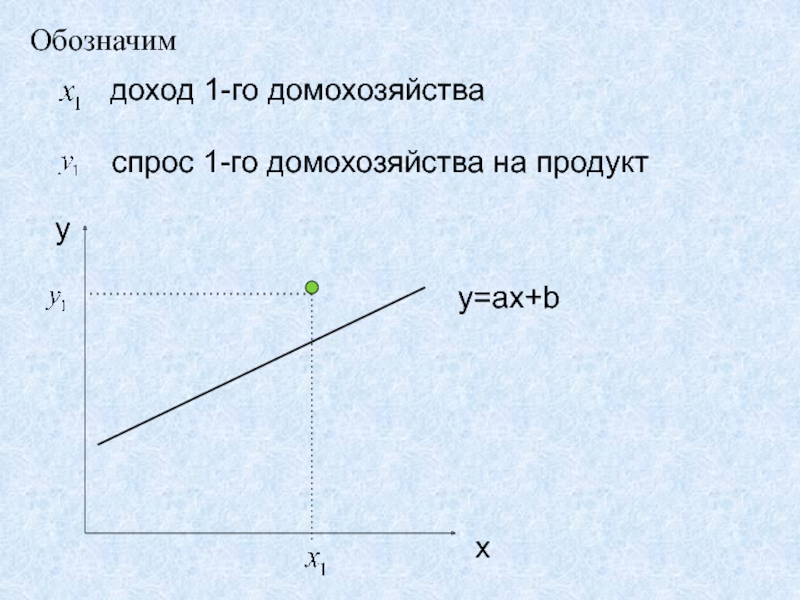
Слайд 23Обозначим
доход 1-го домохозяйства
спрос 1-го домохозяйства на продукт
x
y
y=ax+b
Отклонение точки
от
прямой. Должно быть
как можно меньше!
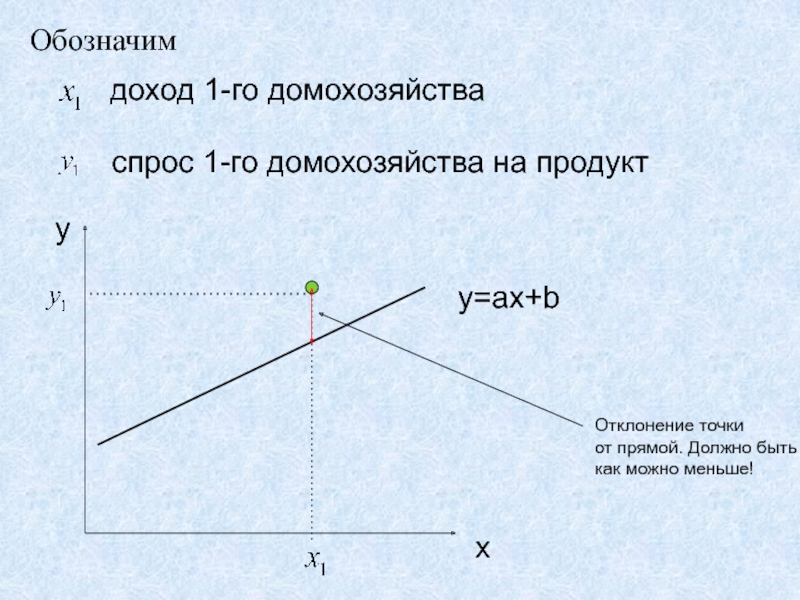
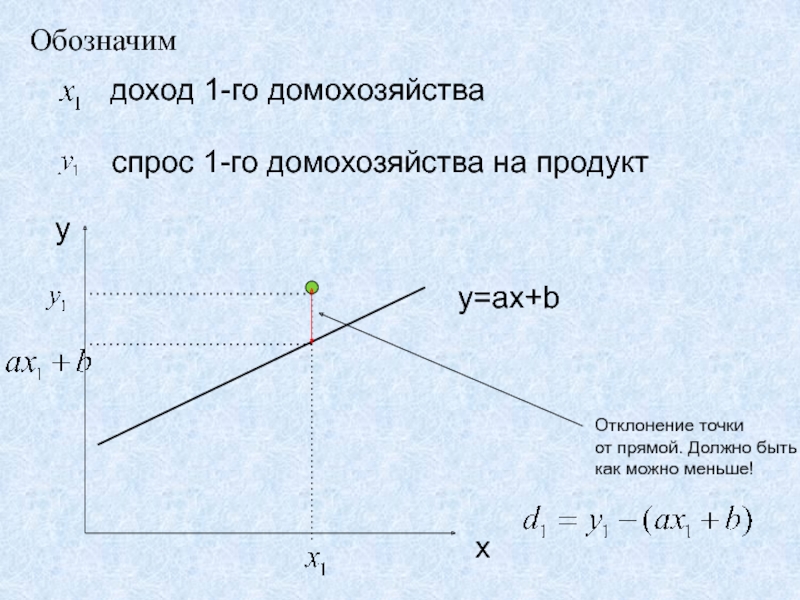
Слайд 24Обозначим
доход 1-го домохозяйства
спрос 1-го домохозяйства на продукт
x
y
y=ax+b
Отклонение точки
от
прямой. Должно быть
как можно меньше!
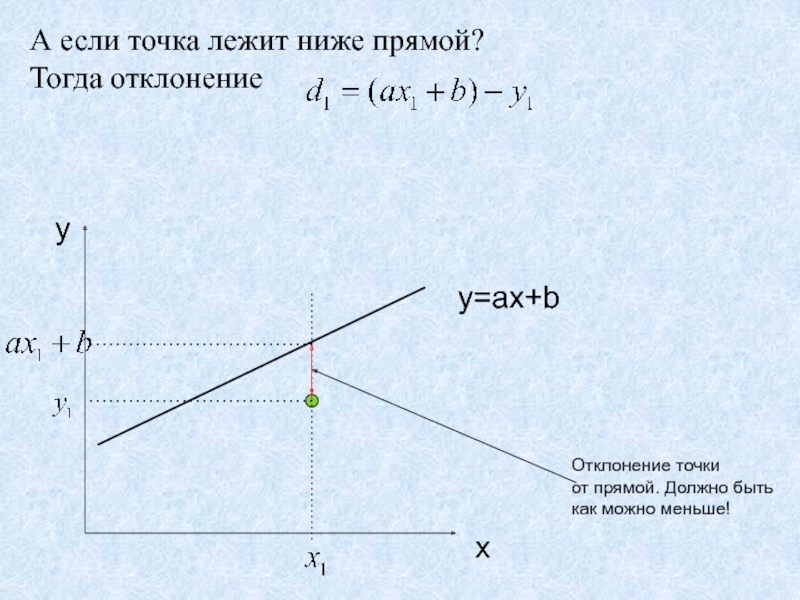
Слайд 25А если точка лежит ниже прямой?
Тогда отклонение
x
y
y=ax+b
Отклонение точки
от
прямой. Должно быть
как можно меньше!
Слайд 26Как учесть сразу оба случая?
Квадрат отклонения
должен быть как можно меньше.
x
y
y=ax+b
Отклонение точки
от прямой. Должно быть
как можно меньше!
Слайд 30Как учесть все точки сразу?
Сумма квадратов расстояний от точек до
прямой должна быть как можно меньше.
Слайд 31Как учесть все точки сразу?
Сумма квадратов расстояний от точек до
прямой должна быть как можно меньше.
обозначение
Слайд 32Как учесть все точки сразу?
Получили функцию двух переменных, для которой
надо найти минимум,
т.е. надо исследовать на экстремум.
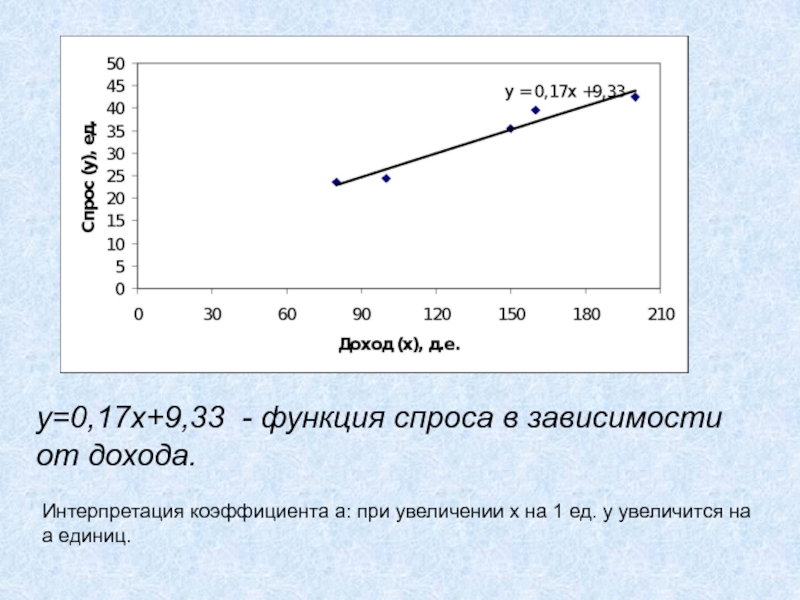
Слайд 37y=0,17x+9,33 - функция спроса в зависимости
от дохода.
Интерпретация коэффициента а:
при увеличении х на 1 ед. y увеличится на
а
единиц. 
Слайд 39y=0,17x+9,33 - функция спроса в зависимости
от дохода.
С ростом дохода
на 1 ден.ед. спрос на товар
растет на 0,17 ед.
Слайд 42Как оценить качество построенной модели?
Находим относительную ошибку аппроксимации
Процентный формат
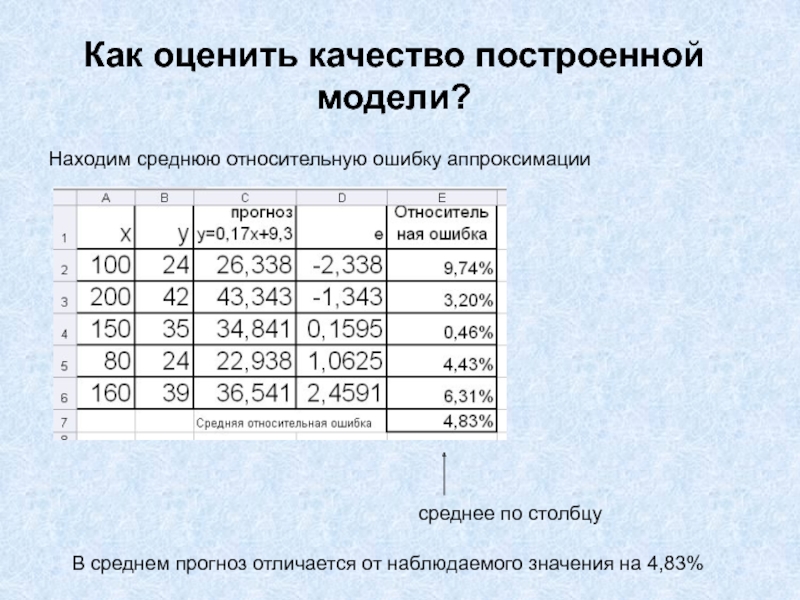
Слайд 43Как оценить качество построенной модели?
Находим среднюю относительную ошибку аппроксимации
среднее по
столбцу
В среднем прогноз отличается от наблюдаемого значения на 4,83%
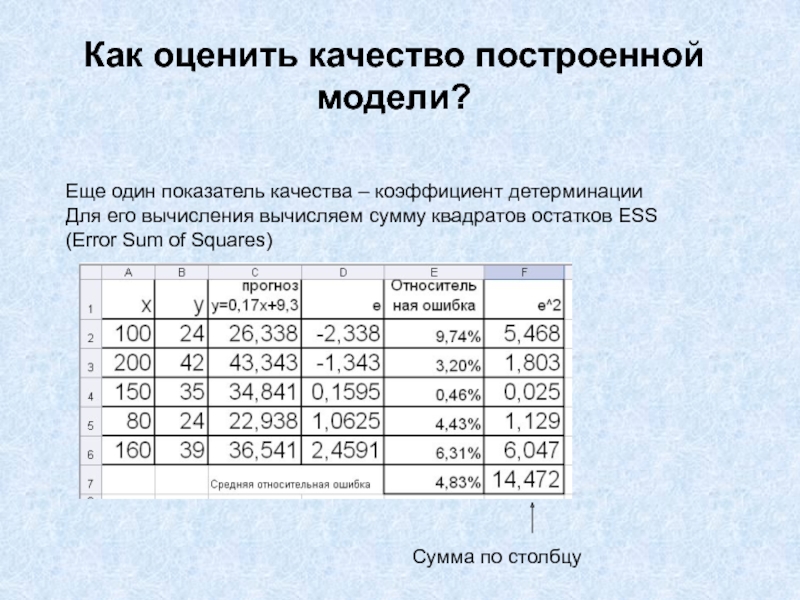
Слайд 44Как оценить качество построенной модели?
Еще один показатель качества – коэффициент
детерминации
Для его вычисления вычисляем сумму квадратов остатков ESS
(Error Sum of
Squares)Сумма по столбцу
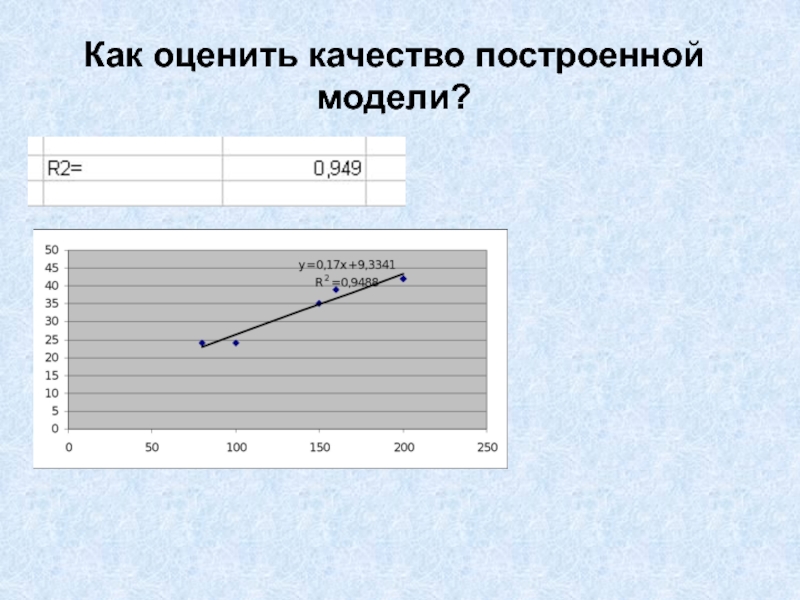
Слайд 46Как оценить качество построенной модели?
коэффициент детерминации
показывает долю вариации зависимой переменной,
объясненную
регрессией. Изменяется от 0 до 1
Чем ближе этот показатель
к 1, тем лучше качество регрессии
Слайд 47Как оценить качество построенной модели?
94,9% вариации спроса на продукт объясняется
доходом и остальные 5,1%
прочими факторами, не включенными в модель
Слайд 49Проверка значимости коэффициентов модели регрессии
Построено уравнение
Даже если в реальности
y не зависит от х, уравнение можно построить.
Но пользоваться им
для прогноза нельзя.В связи с этим проверяют значимость коэффициента a, т.е. насколько
существенно а отличается от 0. Если коэффициент незначим, то переменная
y не зависит от переменной х и моделью нельзя пользоваться
Слайд 50Проверка значимости коэффициентов модели регрессии
Для проверки значимости коэффициента a рассчитывается
величина
Построено уравнение
Даже если в реальности y не зависит
от х, уравнение можно построить.Но пользоваться им для прогноза нельзя.
В связи с этим проверяют значимость коэффициента a, т.е. насколько
существенно а отличается от 0. Если коэффициент незначим, то переменная
y не зависит от переменной х и моделью нельзя пользоваться
где, - стандартная ошибка коэффициента а.
Рассчитывается по специальным формулам
Слайд 52Проверка значимости коэффициентов модели регрессии
Р-значение - это вероятность того, что
переменная х не значима. При Р-значении меньще 0,05 обычно считают,
что соответствующая переменная значима, т.е. y зависит от хВ этом примере переменная х значима, т.е. влияет на переменную y
На основе t-статистики рассчитывают Р-значение
Слайд 53y=0,17x+9,33 - функция спроса в зависимости
от дохода.
Выполнить прогноз потребления
продукта
домохозяйством с доходом 200 д.е.
2) Найти среднюю эластичность спроса
по доходу
Слайд 54y=0,17x+9,33 - функция спроса в зависимости
от дохода.
Выполнить прогноз потребления
продукта
домохозяйством с доходом 200 д.е.
2) Найти среднюю эластичность спроса
по доходу
Слайд 601) Логарифмическая модель
Используя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной y, а в качестве независимой
ln(x). Y=4.017ln(x)+3.197
Слайд 621) Логарифмическая модель
Интерпретация коэффициента а: при увеличении х на 1%
y увеличится на
а/100 единиц.
Y=4.017ln(x)+3.197
При увеличении дохода на 1%
спрос на товар увеличится на 0,0417 единиц.
Слайд 631) Логарифмическая модель
Также как в линейной модели рассчитывается средняя относительная
ошибка
аппроксимации
Y=4.017ln(x)+3.197
Слайд 64Степенная модель
Интерпретация коэффициента a – эластичность зависимой переменной по объясняющей
переменной
a показывает, на сколько процентов возрастает y при возрастании
x на 1%. 
Слайд 67Используя сервис Анализ данных построим модель линейной регрессии,
используя в
качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
Слайд 68Используя сервис Анализ данных построим модель линейной регрессии,
используя в
качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
Слайд 69Используя сервис Анализ данных построим модель линейной регрессии,
используя в
качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
