Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономические показатели
Содержание
- 1. Экономические показатели
- 2. ОпределениеЭкономический показатель – это количественная характеристика экономического
- 3. Два блока показателей1. Обобщающие показатели – относительные
- 4. Два блока статистических показателей2. Конкретные показатели –
- 5. Четыре группы обобщающих показателейАбсолютные показателиОтносительные показателиСредние показателиПоказатели вариации
- 6. Абсолютные показатели– это показатели, отражающие уровень развития
- 7. Абсолютные показателиГлавная особенность – абсолютные показатели являются
- 8. Относительные показателиОтносительная величина (i) – это показатель,
- 9. Виды относительных показателей5 групп относительных показателей (ОП): ОП динамики ОП структуры ОП сравненияОП координации ОП плана
- 10. Относительные показатели динамикиОПД – это результат сравнения
- 11. Относительные показатели динамикиПример (условный): если в качестве
- 12. Относительные показатели структурыОПС – d – отношение
- 13. Относительные показатели структурыПример (условный): в текущем году
- 14. Относительные показатели сравненияДанный показатель используется для сравнения
- 15. Относительные показатели сравненияПример (условный): в Москве количество
- 16. Относительные показатели координацииОПК – ik – отношение
- 17. Относительные показатели координацииПример (условный): число принятых судами
- 18. Относительные показатели планаДва типа: Относительный показатель планового
- 19. Относительные показатели планаПример: прибыль от реализации в
- 20. Средние показателиСредняя – это то, что сглаживает
- 21. Степенные средние величиныДва вида: простые и взвешенные
- 22. Степенные средние величины2. Взвешенная средняя величина рассчитывается
- 23. Степенные средние величиныПояснения к задачам: на практическом
- 24. Средняя арифметическая величинаРасчеты следует вести по этим
- 25. Средняя арифметическая величинаРешение.Нельзя использовать простой метод, т.к.
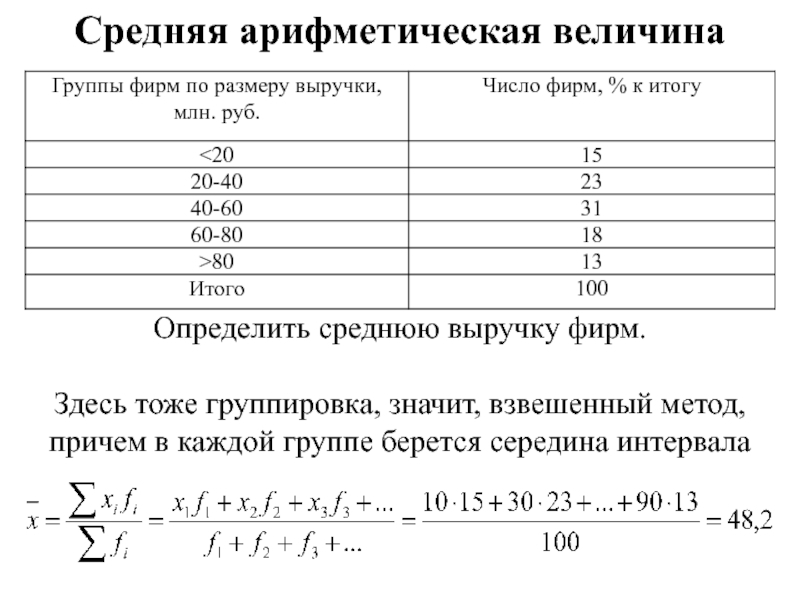
- 26. Средняя арифметическая величинаОпределить среднюю выручку фирм.Здесь тоже
- 27. Показатели вариацииВариация – это отклонения от средней
- 28. Показатели вариацииВыделяют 4 основных показатели вариации:1. Среднее
- 29. Показатели вариацииВсе показатели вариации (также как раньше
- 30. «Простые» показатели вариацииСреднее квадратическое отклонение:Коэффициент вариации:
- 31. «Взвешенные» показатели вариацииСреднее квадратическое отклонение:Коэффициент вариации:
- 32. Критерий типичности средней величиныV < 1/3 –
- 33. Пример 1У первой фирмы прибыль в 2015
- 34. Пример 1У первой фирмы прибыль в 2015
- 35. Пример 1У первой фирмы прибыль в 2015
- 36. Пример 2 Определить коэффициент вариации выручки.
- 37. Пример 2 1. Найдем среднюю выручку по формуле средней взвешенной (т.к. есть группировка):
- 38. Пример 22. Найдем среднее квадратическое отклонение по формуле взвешенной:
- 39. Пример 2 3. Найдем коэффициент вариации:
- 40. Скачать презентанцию
ОпределениеЭкономический показатель – это количественная характеристика экономического объекта или явления (например, есть показатели инфляции, показатели деятельности предприятия, демографические показатели и т.п.)
Слайды и текст этой презентации
Слайд 2Определение
Экономический показатель – это количественная характеристика экономического объекта или явления
Слайд 3Два блока показателей
1. Обобщающие показатели – относительные и средние величины,
дисперсия, темпы роста и т.п. – не зависят от конкретного
содержания явления (задачи на практическом занятии будут именно по этому блоку)Слайд 4Два блока статистических показателей
2. Конкретные показатели – коэффициент занятости, экспорт
и импорт, объем производства и т.п. – зависят от конкретного
содержания явления (изучаются разными разделами экономической науки)Слайд 5Четыре группы обобщающих показателей
Абсолютные показатели
Относительные показатели
Средние показатели
Показатели вариации
Слайд 6Абсолютные показатели
– это показатели, отражающие уровень развития или размеры объекта,
процесса или явления.
Примеры: заработная плата, число осужденных лиц, сумма ущерба,
прибыль и т.п. – очень много примеров можно найти, в том числе и из правовой сферыСлайд 7Абсолютные показатели
Главная особенность – абсолютные показатели являются именованными показателями, т.е.
показателями, которые измеряются либо в натуральных, либо в денежных единицах.
Слайд 8Относительные показатели
Относительная величина (i) – это показатель, характеризующий соотношение сопоставляемых
(сравниваемых) величин, т.е. это всегда частное от деления двух показателей.
Выражается одним из трех способов: коэффициентом, в процентах % или в промилле
Слайд 9Виды относительных показателей
5 групп относительных показателей (ОП):
ОП динамики
ОП
структуры
ОП сравнения
ОП координации
ОП плана
Слайд 10Относительные показатели динамики
ОПД – это результат сравнения двух уровней одного
признака, относящихся к разным периодам. Т.е. относительная величина динамики id
получается путем деления значения признака в текущем периоде (х1) к значению этого же признака в предыдущем или базисном периоде (х0):id > 1 означает рост признака, id < 1 – снижение признака, id = 1 – неизменность признака.
Слайд 11Относительные показатели динамики
Пример (условный): если в качестве признака взять число
рассмотренных административных дел в каком-либо городе, то сравнение их в
2012 г. по отношению к 2011 г. дастили 110,8%. Т.е. в этом городе число дел в 2012 г. по отношению к 2011 г. увеличилось в 1,108 раза или на 10,8%.
Слайд 12Относительные показатели структуры
ОПС – d – отношение индивидуального значения признака
х к суммарному значению х, т.е.
d = 1 (или
100%)Т.е. ОПС характеризуют доли или удельные веса показателей
Слайд 13Относительные показатели структуры
Пример (условный): в текущем году судами было осуждено
9179 тыс. чел., из которых 8942,2 тыс. чел. получили реальные
сроки, а 236,8 тыс. чел. – условные.Тогда доля реально осужденных в общем объеме осужденных лиц составит
или 97,4%.
Доля условно осужденных составит
или 2,6%.
Слайд 14Относительные показатели сравнения
Данный показатель используется для сравнения разных объектов по
одноименным признакам.
где хА – показатель, характеризующий объект А, хБ –
аналогичный показатель, характеризующий объект Б.Слайд 15Относительные показатели сравнения
Пример (условный): в Москве количество осужденных за год
составило 5229 чел., а в Санкт-Петербурге – 2675 чел. Следовательно,
или 195,5%.
Это означает, что в столице осужденных граждан почти в два раза больше, чем в Санкт-Петербурге.
Слайд 16Относительные показатели координации
ОПК – ik – отношение двух признаков (х1
и х2), характеризующих разные части одной совокупности:
Данный показатель используется для
анализа соотношений между частями одного целого.ОПК и ОПС очень похожи друг на друга.
Слайд 17Относительные показатели координации
Пример (условный): число принятых судами к рассмотрению дел
было равно 26605, из которых 14605 – это гражданские дела,
а 12000 – уголовные.Т.е. число рассмотренных гражданских дел превышает число уголовных дел в 1,217 раза или на 21,7%.
Слайд 18Относительные показатели плана
Два типа:
Относительный показатель планового задания – характеризует
относительный уровень того, что запланировано хпл
2. Относительный показатель выполнения планового
задания – характеризует степень перевыполнения (недовыполнения) планового значенияСлайд 19Относительные показатели плана
Пример: прибыль от реализации в 2015 г. составляла
25 тыс. руб. Фирма предполагает в 2016 г. сократить издержки
и довести эту прибыль до 30 тыс. руб. ТогдаТ.е. фирма планирует увеличить прибыль на 20%.
Если предположить, что фактически фирме в 2016 г. удалось получить прибыль в размере 28 тыс. руб., то
Это означает, что фирма недовыполнила план по прибыли на 6,7%.
Слайд 20Средние показатели
Средняя – это то, что сглаживает индивидуальные различия в
признаках (например, различия в зарплатах у разных людей или в
успеваемости разных студентов), и в конечном итоге дает некое одно число, характеризующее по этому признаку объект в целом.Примеры: средняя зарплата в компании, средняя цена на товары и т.п.
Слайд 21Степенные средние величины
Два вида: простые и взвешенные средние величины
Простая
средняя величина рассчитывается в тех случаях, когда данные расположены в
произвольном (несгруппированном) порядке, т.е. рассчитывается для несгруппированных данных.Слайд 22Степенные средние величины
2. Взвешенная средняя величина рассчитывается в тех случаях,
когда данные расположены в сгруппированном порядке, т.е. рассчитывается для сгруппированных
данных.Слайд 23Степенные средние величины
Пояснения к задачам: на практическом занятии в разных
подгруппах исходные данные могут быть как сгруппированы, так и нет.
Сначала нужно определить есть или нет группировка, а затем выбрать тот вид средней, которую нужно использовать – простую или взвешенную.Нельзя применять оба метода к одним и тем же данным.
Слайд 24Средняя арифметическая величина
Расчеты следует вести по этим формулам, но выбрав
одну из них, которая подходит к конкретной задаче.
Простая арифметическая величина
Взвешенная арифметическая величина
Пример: у троих менеджеров фирмы зарплата 50 тыс. руб., у пятерых – 20 тыс. руб., а у десятерых – 15 тыс. руб. Какова средняя зарплата?
Слайд 25Средняя арифметическая величина
Решение.
Нельзя использовать простой метод, т.к. менеджеры сгруппированы (есть
3 группы), т.е. неверно
Нужно использовать взвешенный метод, т.е. верно
Слайд 26Средняя арифметическая величина
Определить среднюю выручку фирм.
Здесь тоже группировка, значит, взвешенный
метод, причем в каждой группе берется середина интервала
Слайд 27Показатели вариации
Вариация – это отклонения от средней величины. С помощью
показателей вариации определяется типичность (адекватность) или нетипичность (неадекватность) средних величин.
Чем ближе показатели вариации к нулю, тем типичнее средняя величина.Слайд 28Показатели вариации
Выделяют 4 основных показатели вариации:
1. Среднее линейное отклонение.
2. Среднее
квадратическое отклонение.
3. Дисперсия.
4. Коэффициент вариации.
В задачах рассчитывать нужно будет 4-й
показатель.Слайд 29Показатели вариации
Все показатели вариации (также как раньше средние величины) можно
разделить на две группы:
Простые – применяются для несгруппированных данных.
Взвешенные –
применяются для сгруппированных данных.Также как и для средних в задачах нужно будет выбрать тот метод, который подходит.
Слайд 32Критерий типичности средней величины
V < 1/3 – средняя величина типична
(адекватна).
V > 1/3 – средняя величина нетипична (неадекватна).
Слайд 33Пример 1
У первой фирмы прибыль в 2015 г. составила 20
млн. руб., у второй – 25 млн. руб., у третьей
– 21 млн. руб.Определить коэффициент вариации прибыли.
Найдем сначала среднюю прибыль. Данные не сгруппированы, значит, используем простой метод
Слайд 34Пример 1
У первой фирмы прибыль в 2015 г. составила 20
млн. руб., у второй – 25 млн. руб., у третьей
– 21 млн. руб.Найдем затем дисперсию прибыли (тоже простым методом) и возьмем квадратный корень – получится среднее квадратическое отклонение
Слайд 35Пример 1
У первой фирмы прибыль в 2015 г. составила 20
млн. руб., у второй – 25 млн. руб., у третьей
– 21 млн. руб.Затем находим коэффициент вариации:
0,098 < 1/3, следовательно, средняя прибыль – адекватная величина, вариация прибыли незначительна.