Экспериментальные и теоретические основы квантовой теории

4, 5, 6.
Государственный университет «Дубна»
Инженерно-физический институт
Кафедра ядерной физики
Кафедра фундаментальных проблем

физики микромира

Специальный семинар по физике ядра и ядерным реакциям

2019

В.В.Самарин

тела, фотоэффект и эффект Комптона.
Спектры атомов водорода и щелочных

элементов.
Атом водорода по Бору.
Волновые и корпускулярные свойства материи.

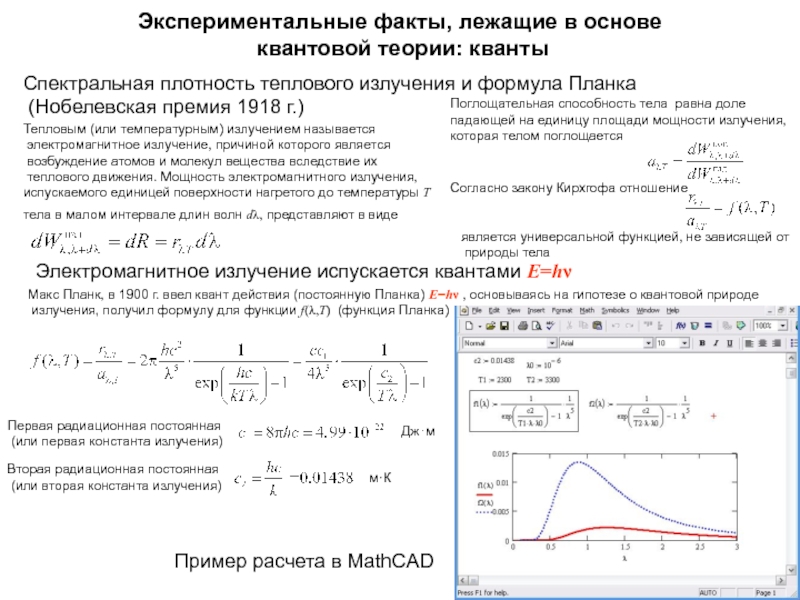
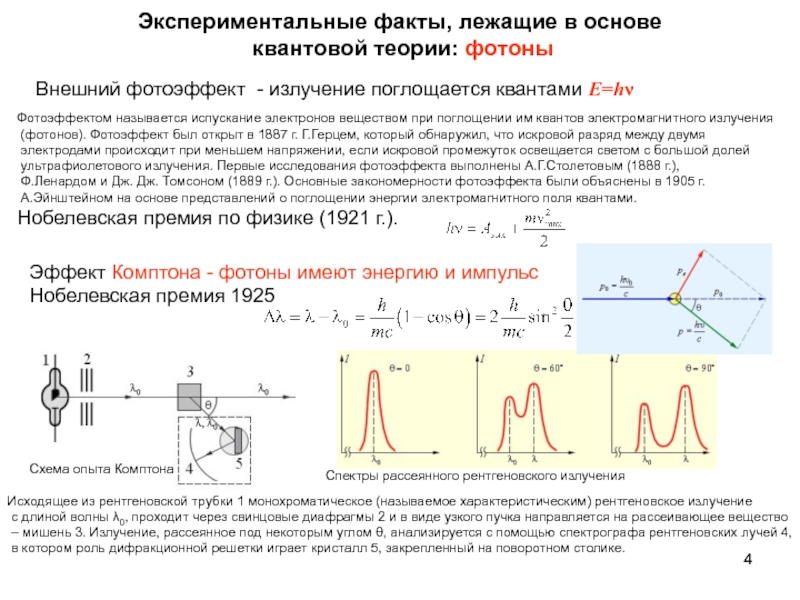
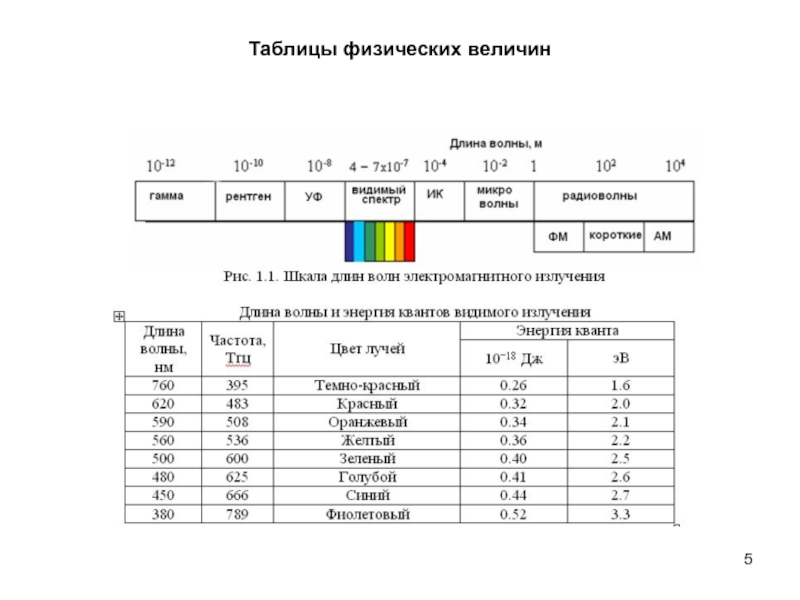
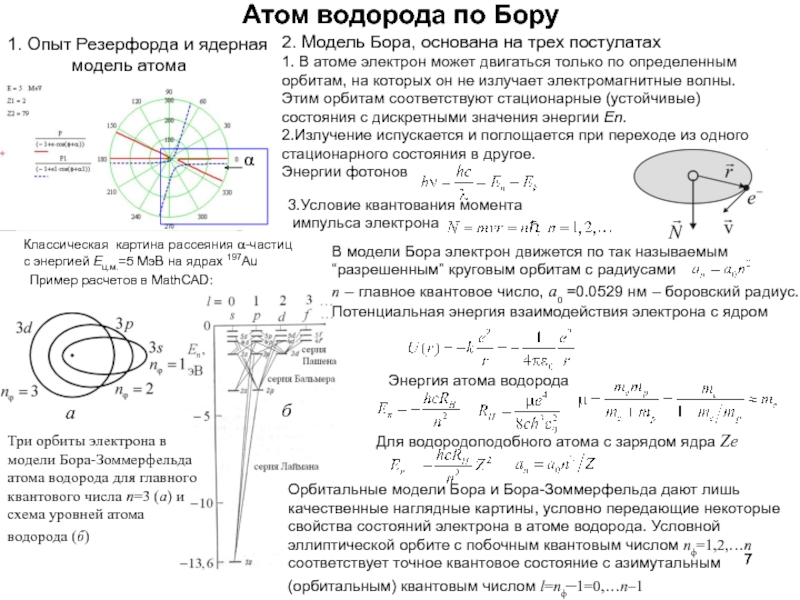
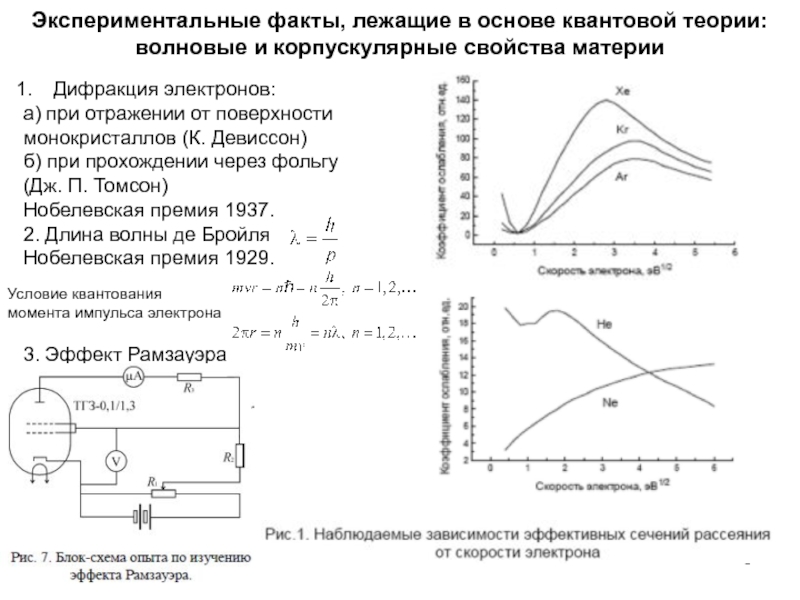
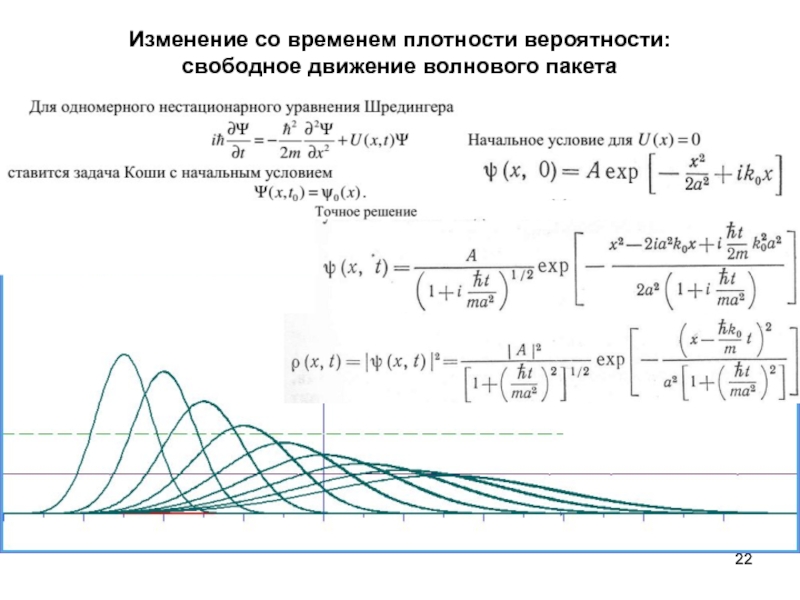
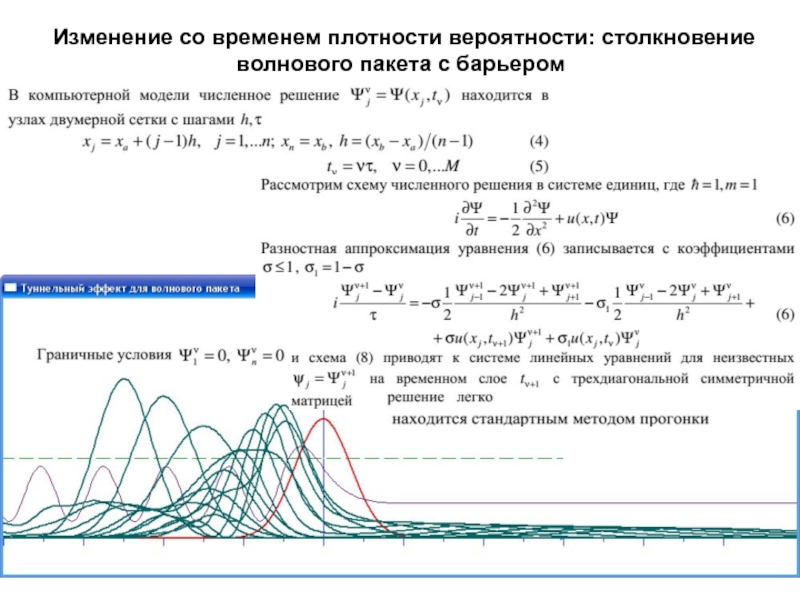
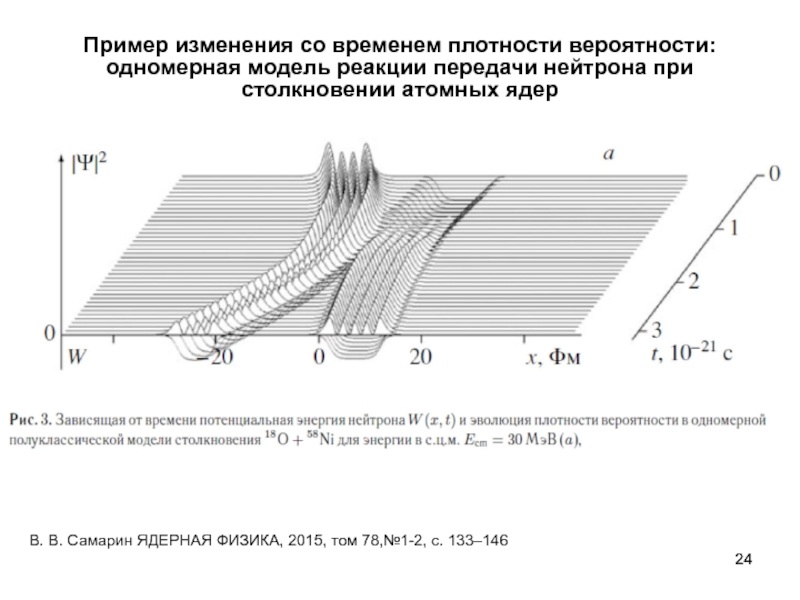
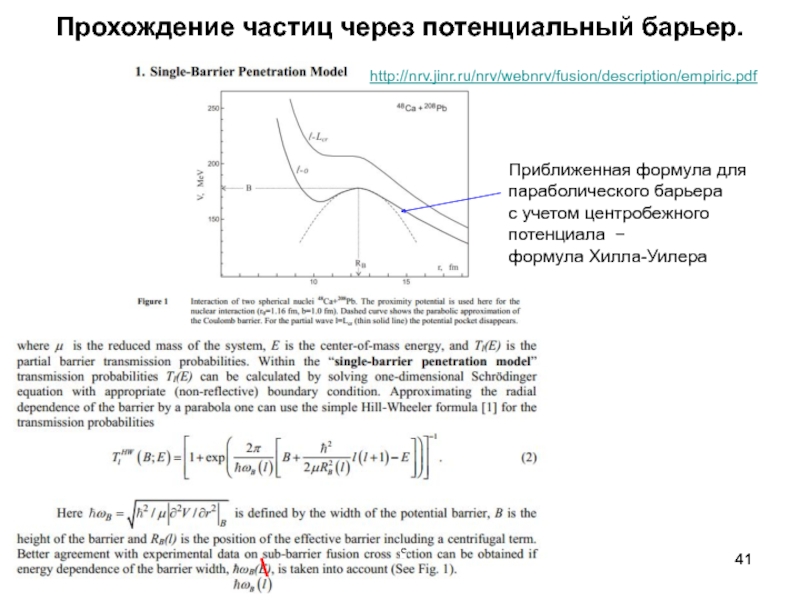
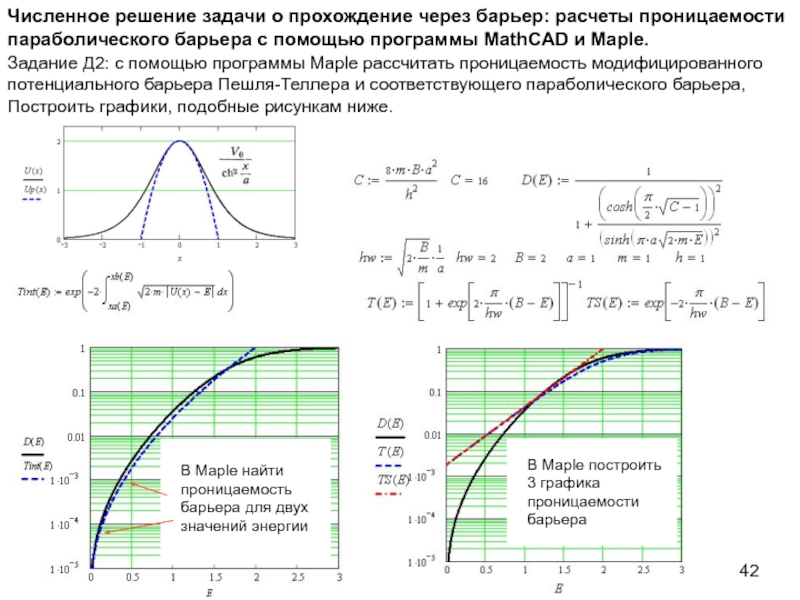
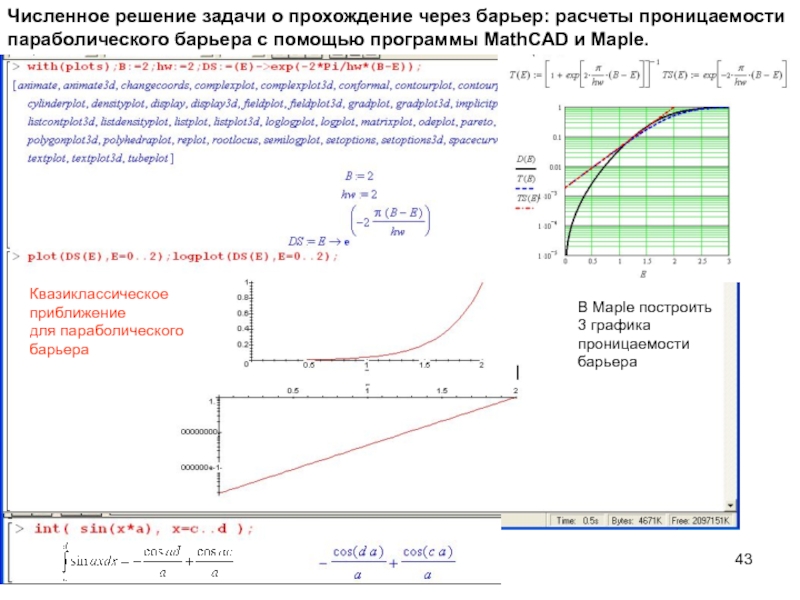
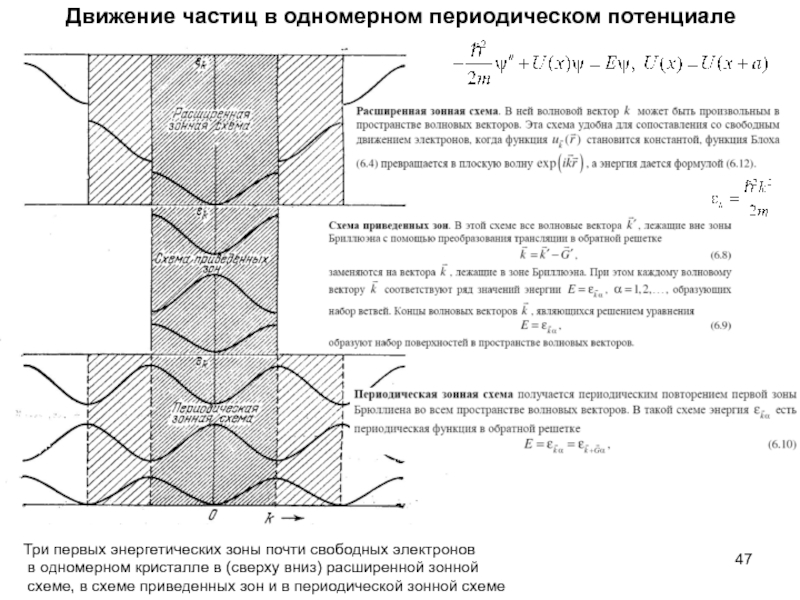
излучения и формула Планка
(Нобелевская премия 1918 г.)
Тепловым (или

температурным) излучением называется
электромагнитное излучение, причиной которого является
возбуждение атомов и молекул вещества вследствие их
теплового движения. Мощность электромагнитного излучения,
испускаемого единицей поверхности нагретого до температуры T
тела в малом интервале длин волн d, представляют в виде

Поглощательная способность тела равна доле
падающей на единицу площади мощности излучения,
которая телом поглощается

Согласно закону Кирхгофа отношение

является универсальной функцией, не зависящей от
природы тела

Макс Планк, в 1900 г. ввел квант действия (постоянную Планка) E=hn , основываясь на гипотезе о квантовой природе
излучения, получил формулу для функции f(,T) (функция Планка)

Вторая радиационная постоянная
(или вторая константа излучения)

Первая радиационная постоянная
(или первая константа излучения)

Джм

м·К

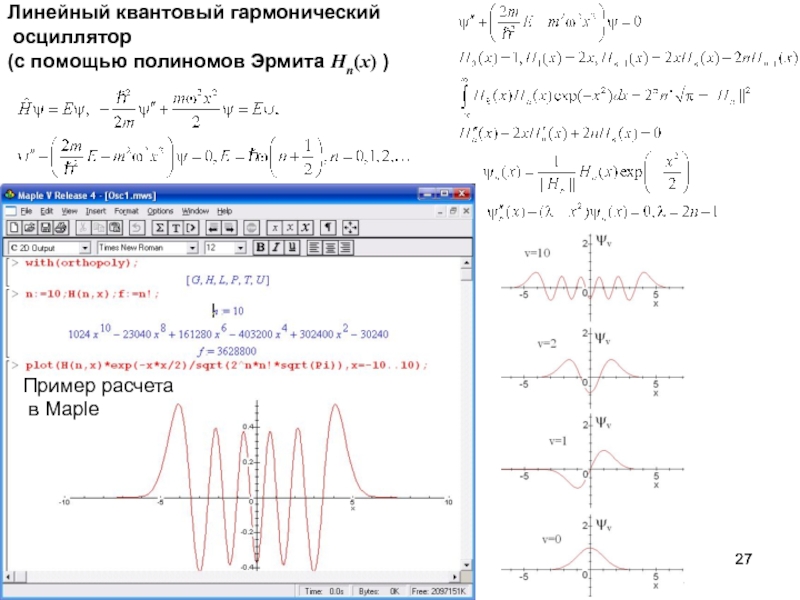
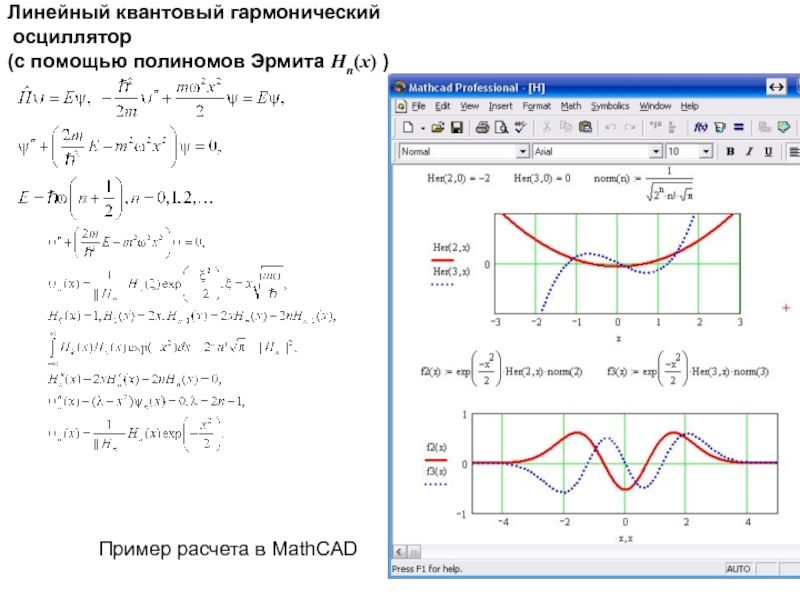
Пример расчета в MathCAD

Электромагнитное излучение испускается квантами E=hn

излучение поглощается квантами E=hn
Эффект Комптона - фотоны имеют энергию и

импульс
Нобелевская премия 1925

Фотоэффектом называется испускание электронов веществом при поглощении им квантов электромагнитного излучения
(фотонов). Фотоэффект был открыт в 1887 г. Г.Герцем, который обнаружил, что искровой разряд между двумя
электродами происходит при меньшем напряжении, если искровой промежуток освещается светом с большой долей
ультрафиолетового излучения. Первые исследования фотоэффекта выполнены А.Г.Столетовым (1888 г.),
Ф.Ленардом и Дж. Дж. Томсоном (1889 г.). Основные закономерности фотоэффекта были объяснены в 1905 г.
А.Эйнштейном на основе представлений о поглощении энергии электромагнитного поля квантами. Нобелевская премия по физике (1921 г.).

Схема опыта Комптона

Исходящее из рентгеновской трубки 1 монохроматическое (называемое характеристическим) рентгеновское излучение
с длиной волны λ0, проходит через свинцовые диафрагмы 2 и в виде узкого пучка направляется на рассеивающее вещество
– мишень 3. Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей 4,
в котором роль дифракционной решетки играет кристалл 5, закрепленный на поворотном столике.

Спектры рассеянного рентгеновского излучения

границы серий показаны штриховкой;
Спектр
излучения Na
Спектр
поглощения Na
Спектр Hg
Формула Бальмера для длин

волн в видимой и ближней ультрафиолетовой частях спектра, RH -постоянная Ридберга

Экспериментальные факты, лежащие в основе квантовой теории: спектры атомов водорода, щелочных элементов и ртути

Спектры излучения атомов H, Hg и молекулы Н2

l

Hg

Длины волн главной серии натрия

Ds , Dp – квантовые дефекты

Частоты линий равны разностям термов

1. Серия Бальмера в спектре атома Н.

на ядрах 197Au
Пример расчетов в MathCAD:
a
Три орбиты электрона в

модели Бора-Зоммерфельда атома водорода для главного квантового числа n=3 (а) и схема уровней атома водорода (б)

Орбитальные модели Бора и Бора-Зоммерфельда дают лишь качественные наглядные картины, условно передающие некоторые свойства состояний электрона в атоме водорода. Условной эллиптической орбите с побочным квантовым числом nj=1,2,…n соответствует точное квантовое состояние с азимутальным (орбитальным) квантовым числом l=nj–1=0,…n–1

В модели Бора электрон движется по так называемым “разрешенным” круговым орбитам с радиусами n – главное квантовое число, a0 =0.0529 нм – боровский радиус. Потенциальная энергия взаимодействия электрона с ядром

Для водородоподобного атома с зарядом ядра Ze

1. Опыт Резерфорда и ядерная модель атома

2. Модель Бора, основана на трех постулатах 1. В атоме электрон может двигаться только по определенным орбитам, на которых он не излучает электромагнитные волны.
Этим орбитам соответствуют стационарные (устойчивые) состояния с дискретными значения энергии En.
2.Излучение испускается и поглощается при переходе из одного стационарного состояния в другое. Энергии фотонов

3.Условие квантования момента импульса электрона

Энергия атома водорода

а

б

серий показаны штриховкой; б) схема уровней атома натрия переходы между

ними, приводящие к образованию серий; рядом с переходами указаны длины волн излучения в нм

Спектр
излучения Na

Спектр
поглощения Na

Спектр Hg

Экспериментальные факты, лежащие в основе квантовой теории: спектры атомов водорода и щелочных элементов

Спектры излучения атомов H, Hg и молекулы Н2

l

Hg

Ds , Dp – ридберговские поправки (или квантовые дефекты

1. Серия Бальмера в спектре атома Н.

Энергии фотонов

n1

n2

Dd <<1

13,6 эВ

через фольгу
(Дж. П. Томсон)
Нобелевская премия 1937.
2. Длина волны де Бройля
Нобелевская

премия 1929.



3. Эффект Рамзауэра

Экспериментальные факты, лежащие в основе квантовой теории: волновые и корпускулярные свойства материи

Условие квантования момента импульса электрона

системы. Волновая функция, матрица плотности.
Принцип неопределенности

Гамильтона (гамильтониан) Н.
Среднее значение физической величины f при измерении для

некоторого состояния системы равно интегралу где y – волновая функция системы. В стационарном состоянии с yn - собственной функцией оператора при измерении f получится собственное значение оператора fn. Стационарное уравнение Шредингера Плотность вероятности равна нормировка
Матрицы операторов
В квазиклассическом пределе h  0 y  aexp(iS/h), S − действие. В пределе малых длин волн де Бройля плотность вероятности соответствует классическим траекториям частицы.

Квантовая (верхняя половина) и классическая
(нижняя половина) картины столкновения ядер
16О + 208Pb: для энергии E=70 МэВ, упругое рассеяние, длина волн де Бройля мала по сравнению с размерами ядер.
Окружность - точки соприкосновения ядер.
Степень почернения пропорциональна плотности вероятности

траектории

плотность вероятности

Транспонированный оператор для оператора
Собственные и

средние значения физических величин вещественны

Сопряженный оператор для оператора

Операторы, соответствующие в математическом аппарате квантовой механики вещественным физическим величинам должны быть эрмитовыми (самосопряженными) .

чистыми состояниями. Они соответствуют максимально полным сведениям о квантовой системе.

В общем случае волновые функции могут быть представлены в виде суперпозиции собственных функций некоторых операторов, имеющих дискретный и непрерывный спектр собственных значений (принцип суперпозиции).

Состояния, которым нельзя сопоставить волновую функцию называют смешанными состояниями. Примерами могут быть состояния, задаваемые набором чисел , т.е. вероятностями состояний с определенными значениями соответствующих величин F. Смешанное состояние можно рассматривать как некогерентную смесь чистых состояний y(i) со статистическими весами W(i), удовлетворяющими соотношению При вычислении среднего значения какой-либо физической величины в смешанном состоянии необходимо определить значения этой величины в чистых состояниях y(i) и усреднить полученные величины со статистическими весами W(i):

Для вычисления средних значений и вероятностей различных значений физических величин в смешанных состояниях используется матрица плотности.

или других состояний для конечного числа собственных функций некоторого оператора. Для

произвольного чистого состояния

В более общем случае матрица плотности характеризует произвольное состояние подсистемы (с полным набором координат x), образующей вместе со второй подсистемой (с полным набором координат x) большую систему с волновой функцией y(x,x),

Если в квантовой системе возможно N независимых чистых состояний, то N2 комплексных элементов матрицы плотности r зависят от N21 действительных параметров.

где js(x)  полная ортонормированная система собственных функций некоторого оператора, действующего на координаты подсистемы x.

 матричные элементы матрицы плотности в s-представлении,

матрица плотности как функция координат подсистемы x:

ни в одном состоянии, если их операторы не коммутируют, пример:

Для

двух самосопряженных операторов с перестановочным соотношением (  также самосопряженный оператор)
соотношение неопределенности для величин F и К: Для координаты и проекции импульса на ту же ось получается соотношение неопределенности Гейзенберга

Соотношение неопределенности часто используют для оценки среднего значения кинетической энергии частицы, которая движется в некотором ограниченном объеме пространства с линейным размером а:
В силу малости постоянной Планка соотношение неопределенности существенно только для микросистем. Согласно Н.Бору каждая физическая величина вместе со своей канонически сопряженной (например, х и рх) образуют пару дополнительных величин. В любом состоянии квантовых систем определенное значение может иметь только одна из них, либо обе не имеют определенного значения. Согласно принципу дополнительности Бора два взаимно исключающих класса квантового описания состояний могли бы дать при классическом описании полное описание состояния системы, например, задать начальные условия для определения единственной траектории материальной точки.

состояния.

уравнение Шредингера выражает принцип причинности в квантовой механике
Пример: оператор производной

скорости по времени − оператор ускорения

Изменение со временем средних значений физических величин

Оно позволяет определить значение волновой функции Y(t) в любой момент времени t , если известно это значение в начальный момент t0.

уравнением Лиувилла, так как оно соответствует уравнению Лиувилла для классической

функции распределения в статистической физике

величин в представлениях Шредингера и Гейзенберга (Н)
Изменение со временем волновой функции

в представлении Шредингера

Уравнения для операторов в представлении Гейзенберга

Изменение со временем плотности вероятности в представлении Шредингера

Волновая функция в представлении Гейзенберга (Н) не зависит от времени

Операторы в представлении Гейзенберга зависят от времени t:

Изменение со временем средних значений физических величин в представлениях Шредингера и Гейзенберга (Н)

нейтрона при столкновении атомных ядер
В. В. Самарин ЯДЕРНАЯ ФИЗИКА, 2015,

том 78,№1-2, с. 133–146

называются стационарными состояниями системы.
Стационарное состояние с наименьшим из всех возможных

значением энергии называется нормальным или основным состоянием системы. Разложение произвольной волновой функции Y по волновым функциям стационарных состояний с вероятностями различных значений энергии системы:

Уровни энергии, которым соответствуют несколько различных стационарных состояний называются вырожденными.
Стационарное состояние дискретного спектра всегда соответствует финитному движению системы, т.е. движению, при котором система или какая-либо ее часть не уходит на бесконечность система находится в связанном состоянии). Стационарные состояния непрерывного спектра соответствуют инфинитному движению системы.

состояний.

расчета в Maple

расчета в MathCAD

и модель параболического барьера.
Математическая модель туннельного эффекта.

решение нестационарного уравнения Шредингера
Численное решение стационарного уравнения Шредингера для установившегося режима при непрерывном движении

частиц из - на потенциальный барьер

|y(x)|2

|y(x)|2

|Y(x,t)|2

U(x)

U(x)

E

E

Прохождение частиц через потенциальный барьер

Отражение

в стабилитроне

в туннельном диоде

формула
Квазиклассическое приближение
Условие применимости D

параболического барьера
Приближение Хилла-Уилера
Точная формула
Точная формула
Приближение Хилла-Уилера
Квазиклассическое

приближение для парабо- лического барьера

потенциального барьера Пешля-Теллера https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B8%D1%84%D0%B8%D1%86%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BF%D0%BE%D1%82%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB_%D0%9F%D1%91%D1%88%D0%BB%D1%8F_%E2%80%94_%D0%A2%D0%B5%D0%BB%D0%BB%D0%B5%D1%80%D0%B0

центробежного потенциала 
формула Хилла-Уилера
http://nrv.jinr.ru/nrv/webnrv/fusion/description/empiric.pdf
e

барьера с помощью программы MathCAD и Maple.
Задание Д2: с помощью

программы Maple рассчитать проницаемость модифицированного потенциального барьера Пешля-Теллера и соответствующего параболического барьера,
Построить графики, подобные рисункам ниже.

42

В Maple найти проницаемость барьера для двух значений энергии

В Maple построить 3 графика проницаемости барьера

барьера с помощью программы MathCAD и Maple.
Квазиклассическое приближение для параболического барьера
В Maple

построить 3 графика проницаемости барьера

Зонные схемы.

трансляции a, b, c вдоль векторов

примитивных трансляций пространственной решетки.
Согласно теореме Блоха собственные функции уравнения Шредингера с периодическим потенциалом имеют вид где функция является периодической функцией в пространственной решетке. Индексом функции Блоха и энергии является волновой вектор
Для анализа свойств функций Блоха в пространстве волновых векторов строят так называемую обратную решетку. Ее произвольный вектор задается формулами с помощью векторов примитивных трансляций обратной решетки

свободных электронов в одномерном кристалле в (сверху вниз) расширенной зонной

схеме, в схеме приведенных зон и в периодической зонной схеме

Шредингера для свободного движения частиц (электронов), соответствующее бегущим волнам,
В

частности, при k=±p/a имеются два приближенных решения в виде стоячих волн

Плотность вероятности нахождения электронов для первого решения максимальна на положительных ионах (см. рис.), для второго решения области с большой вероятностью нахождения электронов удалены от положительных ионов. Поэтому энергия первого состояния меньше, чем второго, а разница энергий равна ширине запрещенной зоны.

принципу Паули – состояние с определенным значением волнового числа k=nDk, n=0,±1,

±2,… , может быть занято двумя электронами с противоположными спинами. Различные случаи заполнения зонных структур могут привести к тому, что рассматриваемый одномерный кристалл будет иметь свойства диэлектрика или проводника (металла), см. рис.

Занятые состояния (заштрихованные области) в различных зонных структурах: а – диэлектрик, б – металл с перекрытием зон, в – металл с частичным заполнением верхней зоны

Схема заполнения электронами разрешенных энергетических зон в диэлектрике (а), проводниках (б, в) (в), (металле) и полупроводниках с электронной (г) и дырочной (д) проводимостью). Штриховкой показаны области разрешенных значений энергии, заполненные электронами.

Поверхность Ферми, определяемая из условия

в пространстве волновых векторов может иметь сложную форму.

а

б

в

а

б

в

образом, влияние взаимодействия электрона с атомами кристалла приводит к тому,

что во внешнем поле он движется как частица с эффективной массой m*. Использование известного значения m* позволяет в дальнейшем проводить расчеты без явного учета кристаллического поля. Аналогичным образом вводится и эффективная масса дырки

Дирака

Квантовая механика. − М. Наука. 1971.
Давыдов А.С. Квантовая механика. −

М. Наука. 1973.
Ситенко А.Г. Теория рассеяния. − Киев. “Вища школа”, 1975.
Фрауэнфельдер, Г. Субатомная физика. /Г. Фрауэнфельдер, Э. Хэнли. – М.: Мир. 1979.
Nuclear Reaction Video. База знаний по низкоэнергетическим ядерным реакциям. http://nrv.jinr.ru/nrv/.
Гольдман И. И., Кривченков В. Д. Сборник задач по квантовой механике. (ГИТТЛ, Москва, 1957).
Флюгге З. Задачи по квантовой механике. Т. 1. М.: Мир, 1974.