ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ В УСТАНОВИВШЕМСЯ РЕЖИМЕ

способы его описания
В электротехнике простейшим переменным сигналом является гармонический (ЭДС

- е(t), напряжение - (u(t), ток - i(t)). Аналитически гармонический сигнал (например, напряжение) записывается выражением:
u(t) = Umcos(ω0t+φ0) , (1.1)
где u(t) – мгновенное значение напряжения – напряжение в момент времени t.
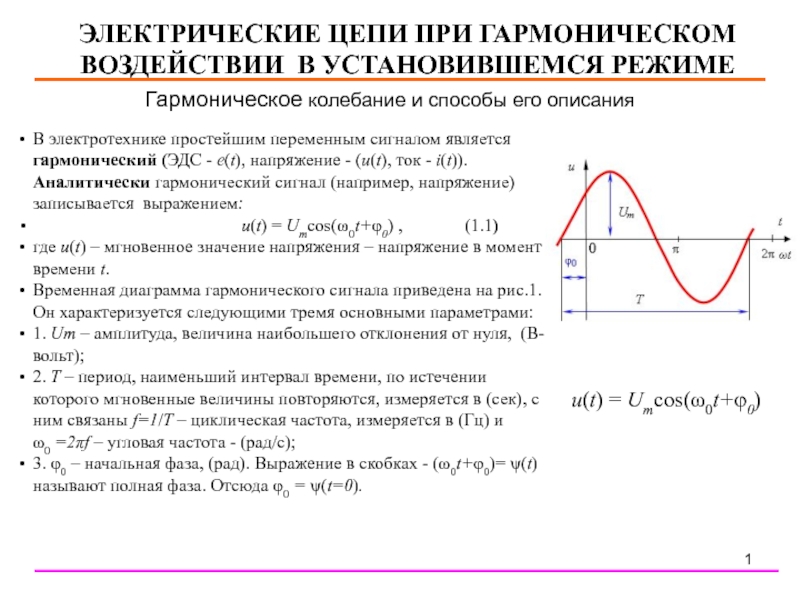
Временная диаграмма гармонического сигнала приведена на рис.1. Он характеризуется следующими тремя основными параметрами:
1. Um – амплитуда, величина наибольшего отклонения от нуля, (В- вольт);
2. Т – период, наименьший интервал времени, по истечении которого мгновенные величины повторяются, измеряется в (сек), с ним связаны f=1/Т – циклическая частота, измеряется в (Гц) и
ω0 =2πf – угловая частота - (рад/с);
3. φ0 – начальная фаза, (рад). Выражение в скобках - (ω0t+φ0)= ψ(t) называют полная фаза. Отсюда φ0 = ψ(t=0).

u(t) = Umcos(ω0t+φ0)

от долей герца до миллиардов герц. В наших промышленных энергосистемах

применяется частота f=50 Гц. В зависимости от частоты источниками синусоидальной э.д.с. являются генераторы того или иного типа:
Вращающиеся электрические машины генерируют э.д.с. промышленной частоты (50Гц); Ионные или полупроводниковые инверторы - промышленные и повышенные частоты. Рассмотрим принцип действия генератора – электромагнитной машины.
В обмотке (витке), по закону Фарадея (правило правой руки), наводится э.д.с.,:
,

где В – магнитная индукция поля, Вб; l – длина провода; v – линейная скорость перемещения проводника.

их среднеквадратичным (действующим) значениям за период, I, U, E –

Например, действующее значение периодического тока равно такому значению постоянного тока, который, проходя через сопротивление r, за период Т выделяет то же количество тепла, что и данный переменный ток i.
Связь между амплитудным и действующим значениями синусоидального тока равна
(1.3)

.
Иногда гармонические сигналы характеризуют средним значением.
Среднее значение синусоидальной величины за период равно нулю, поэтому за среднее значением гармонического тока принимают среднее значение за положительный полупериод:
. (1.4)

сигналов (рис.1.23) одной частоты разность их начальных фаз, называют сдвигом

фаз и обозначают φ ,


Если φ=0,то напряжение и ток совпадают по фазе,
если - в противофазе,

если - в квадратуре.

Если φ>0, то i(t) отстает от U(t) по фазе на угол φ,
если φ<0, то i(t) опережает U(t) по фазе на угол φ.

комплексное число Ím = Imejφ, где амплитуда тока Im – модуль,

а угол φ - начальная фаза, – аргумент комплексного тока.

Между ними при известной частоте ω существует взаимнооднозначное соответствие
i(t) = Im sin(ωt +  φ )↔ Ím = Imejφ,
т.е. зная одно можно записать другое.
Комплексную амплитуду можно записать в алгебраической, показательной и тригонометрической форме
Ím = Re[Ím ]+jIm[Ím ]= Imejφ = Imcos φ + jImsin φ,
где – мнимая единица;
Re[Ím ] = Imcos φ и Im[Ím ] =Imsin φ - реальная и мнимая части комплексного числа;
Ím =(( Re[Ím ]2 + (Im[Ím ]2)1/2 и φ =arctg Im/ Re - модуль и аргумент комплексной амплитуды.
и представить на комплексной плоскости (рис. 1.5) вектором с длиной Im и углом поворота ψ относительно вещественной оси Re.

Во многих случаях пользуются понятием комплексного действующего значения синусоидальной величины
Í = Iеj φ , (1.2)
т.е. комплексного числа с модулем в виде действующего значения Í =Ím/ синусоидальной величины и аргументом в виде начальной фазы.

Использование комплексной формы представления позволяет:
1. заменить операции над функциями времени на операциями над комплексными числами,
2. применять для анализу цепей переменного тока все методы анализа цепей постоянного тока.

(ток, напряжение, ЭДС) одной и той же частоты называют векторной

диаграммой.
и представить на комплексной плоскости (рис. 1.5) вектором с длиной Im и углом поворота ψ относительно вещественной оси Re

такой же вид, как и соответствующие уравнения для цепей постоянного

тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин: комплексных амплитуд и комплексных сопротивлений.
1. Закон Ома. Он устанавливает связь между комплексными амплитудами тока и напряжения на участке цепи. 1.8.
Закон Ома для участка цепи, не содержащего источника ЭДС (рис. 1.8):

Где и - комплексные амплитуды тока и напряжения на участке цепи; Z – комплексное сопротивление участка цепи, –комплексные амплитуды потенциалов на данном участке цепи.

2. Первый закон Кирхгофа: Алгебраическая сумма комплексных амплитуд (действующих значений) токов в узле равна нулю
. (1.5 а)
3. Второй закон Кирхгофа: В замкнутом контуре электрической цепи алгебраическая сумма комплексных амплитуд (действующих значений, ЭДС) равна алгебраической сумме комплексных падений напряжений в нём.
. (1.5 б)

отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:

R - активного сопротивления, Х– реактивному сопротивлению,
Z –модуль комплексного сопротивления: Z=(R2+X2)1/2
φ=ψu - ψi – начальная фаза или аргумент комплексного сопротивления:
φz(ω)=ψu-ψi =arctg(X/R).

Взаимосвязь между полным, активным и реактивным сопротивлением графически представляется векторной диаграммой в виде «треугольника сопротивления».

По виду записи комплексного сопротивления можно судить о характере участка цепи:
Z=R – активное (резистивное) сопротивление;
Z=R+jX — активно-индуктивное сопротивление;
Z=R – j X — активно-емкостное.

совершенно такой же вид, как и соответствующие уравнения для цепей

постоянного тока. Только все резистивные сопротивления заменены на комплексные сопротивления элементов.

синусоидального тока используются следующие понятия
Мгновенная мощность, характеризует скорость изменения

энергии в цепи в любой момент времени
p(t)=u(t)i(t)=UmSin (ωt+ψu) ImSin(ωt+ψ i)= UICos(ψu- ψi)- UICos(2ωt+ψu+ψi).
Мгновенная мощность содержит постоянную составляющую и переменную составляющую, меняющуюся с удвоенной частотой относительно частоты изменения напряжения и тока.
Активная мощность –средняя мощность за период «Т» : Р=UICosφ → [Вт].
Эта мощность характеризует энергию, рассеиваемую за период питающего напряжения в виде тепла в резистивных элементах цепи, и измеряется в Ваттах. Видно, что средняя или активная мощность всегда положительна и равна постоянной составляющей мгновенной мощности.
Реактивноая мощность Q, вычисляется по формуле: Q = UISinφ , → [ВАР].
Эта мощность не совершает полезной работы, а характеризует интенсивность обмена энергией между генератором и реактивными элементами цепи L и С. Протекание тока обмена приводит к дополнительным потерям энергии в проводах линий передач. Поэтому реактивная мощность должна быть по возможности минимальной.
Реактивная мощность может быть положительной, если φ >0 и отрицательной, если φ<0.
Полная или кажущаяся мощность S равна произведению действующих значений тока и напряжения на зажимах цепи, она измеряется в вольтамперах : S=Um.Im/2= UI →[ВА].
Между полной, активной и реактивной мощностью существует связь



Графически ее можно представить в виде «треугольника мощностей» (рис.1.6).
Коэффициент к=Р/S=cosφ называется «коэффициентом мощности» (К→1).

уравнение по второму закону Кирхгофа для мгновенных значений запишем в

виде:

(1.7)
Пусть ,тогда:

(1.8)
Вектор тока и векторная диаграмма напряжений приведены на рис. 1.10. Векторы напряжений на активном и реактивном элементах ортогональны, а векторы напряжений на L и C смещены на .
В комплексной форме уравнение (1.8) примет вид:

(1.9)
Здесь: Z=R+j(XL-XC)=Zejφ - комплексное сопротивление, - модуль комплексного сопротивления; - фаза комплексного сопротивления; X=(XL-XC) – реактивное сопротивление.
На комплексной плоскости сопротивления R, jXL, -jXC, Z - образуют треугольник сопротивления, рис. 1.11. Если сопротивления умножить на , получим диаграмму напряжений, рис. 2.12 – треугольник напряжений.

заменяется комплексной схемой замещения, в которой:
а) все пассивные элементы заменяют

их комплексными сопротивлениями, как показано на рис. 1.3.
б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е. х(t) = Xm cos(0t – x)  Xm = Xm e–jx и Ym cos(0t – y) .




Рис. 1.3. Замена пассивных элементов цепей их комплексными сопротивлениями
2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е. Ym = Ym e–jy. методами анализа линейных цепей по постоянному току
3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.
 y(t) = Ym cos(0t – y).
4) определить комплексную частотную характеристику по формуле (1).
На рис.1.4 приведены схемы замещения реактивных элементов, когда частота входного сигнала стремится к 0 или ∞. Ими удобно пользоваться при расчете входных и передаточных параметров цепи на этих частотах.

1.2. Расчет цепей при гармоническом воздействии методом комплексных амплитуд (МКА)

РИИТ
(кафедра Радиоэлектроники и информационно-измерительной техники)


Электротехника и электроника