Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электромагнитные волны. Интерференция и поляризация ЭМВ
Содержание
- 1. Электромагнитные волны. Интерференция и поляризация ЭМВ
- 2. 1. Понятие об электромагнитных волнахТеория электромагнитного поля была создана в 1864 г. Джеймсом Кларком Максвеллом (1831-1879).
- 3. Д.К. Максвелл проанализировал все известные к тому
- 4. Максвелл ввел в физику понятие вихревого электрического
- 5. Максвелл высказал гипотезу о существовании и обратного процесса:Всякое переменное электрическое поле порождает вихревое магнитное.
- 6. Слайд 6
- 7. Эта гипотеза была лишь теоретическим предположением, не
- 8. Из теории Максвелла вытекает ряд важных выводов:1. Единое электромагнитное поле распространяется в виде электромагнитных волн.
- 9. Электромагнитные волны представляют собой взаимосвязанные и взаимопорождающие
- 10. Слайд 10
- 11. ЭМВ поперечны – векторы и
- 12. Уравнения плоской ЭМВ имеют вид: E = Emcos
- 13. Как видно из уравнений, колебания электрической и магнитной составляющей электромагнитной волны происходят синфазно.
- 14. 2) Электромагнитные волны распространяются в веществе с конечной скоростью:где с - скорость света в вакууме.
- 15. Скорость распространения ЭМВ равна скорости света.Это послужило
- 16. Основные свойства ЭМВ – интерференция, дифракция, поляризация – наиболее наглядно проявляются при изучении света.
- 17. 2. Интерференция света. Практическое применение интерференции
- 18. Устойчивую во времени интерференционную картину можно получить
- 19. Обычные источники света представляет собой совокупность огромного
- 20. Поэтому картина взаимного усиления, возникшая в каком-либо
- 21. Единственный способ получения когерентных световых волн -
- 22. Зеркало Ллойда В зеркале Ллойда прямой пучок
- 23. Бизеркало Френеля Свет от точечного
- 24. Определим условия максимумов и минимумов интерференционной картины на примере двух монохроматических когерентных плоских волн.
- 25. Колебания вектора напряженности электрического поля Е этих
- 26. Сложение волн, распространяющихся в среде, определяется сложением
- 27. Слайд 27
- 28. Амплитуду результирующих колебаний вектора напряженности в точке
- 29. Очевидно, что амплитуда результирующего колебания будет максимальной
- 30. Амплитуда результирующего колебания будет минимальной (условие минимума),
- 31. Чему же равна разность фаз рассматриваемых волн?
- 32. Вспомним, что ω = 2π/Т.Отношение скорости света
- 33. Продолжая вывод формулы, получим:
- 34. Произведение геометрического пути волны x на абсолютный
- 35. Объединим условие интерференционного максимума: Δφ = 2kπ
- 36. Максимум интерференции наблюдается в тех точках, в
- 37. Интерференция в тонких пленках
- 38. Условие максимума интерференции в тонкой пленке:Условие минимума интерференции в тонкой пленке:
- 39. Здесь - толщина пленки; i -
- 40. Проанализируем формулы интерференционных минимумов и максимумов для
- 41. 2) При освещении пластинки белым светом условия
- 42. Предположим, что свет падает на пластину переменной
- 43. При освещении пластинки переменной толщины белым светом
- 44. Применение интерференции 1) Просветление оптикиСовременные оптические устройства
- 45. При падении света нормально поверхности от каждой
- 46. В результате этого освещенность изображения получается малой.
- 47. Для устранения этих неприятных последствий отражения света
- 48. На поверхность оптического стекла наносят тонкую пленку
- 49. Из условий интерференции в тонкой пленке следует,
- 50. Толщину пленки подбирают так, чтобы полное гашение
- 51. 2) Интерферометры -приборы для измерения с высокой
- 52. Интерферометр Жамена
- 53. 3) Интерференционный микроскоп - сочетание двухлучевого интерферометра
- 54. 3) Интерференционный микроскоп - сочетание двухлучевого интерферометра
- 55. 3. Естественный и поляризованный свет. Почти все
- 56. Естественный свет представляет собой совокупность световых волн,
- 57. Если в свете есть преимущественное направление колебаний
- 58. Плоскость, в которой колеблется электрический вектор Е, называется плоскостью поляризации света.
- 59. Слайд 59
- 60. Способы получения плоскополяризованного света1) Поляризация света при
- 61. Устройства для получения плоскополяризованного света из естественного
- 62. Поляризатор можно использовать для анализа плоскополяризованного света. В этом случае его называют анализатором.
- 63. Слайд 63
- 64. Пусть на анализатор П2 падает плоскополяризованная волна,
- 65. В результате этого через анализатор пройдет только
- 66. где IА – интенсивность поляризованного света, вышедшего
- 67. Как видно из закона Малюса, при повороте
- 68. 4. Вращение плоскости поляризации. Оптически активные
- 69. В зависимости от того, в каком направлении
- 70. Опыт показывает, что все оптически активные вещества
- 71. Для растворов угол поворота плоскости поляризации прямо
- 72. [α0] = 1 град·см3·г‑1·дм‑1 - физическая величина, численно равная стократному
- 73. Зная удельное вращение, угол вращения и длину
- 74. Скачать презентанцию
1. Понятие об электромагнитных волнахТеория электромагнитного поля была создана в 1864 г. Джеймсом Кларком Максвеллом (1831-1879).
Слайды и текст этой презентации
Слайд 1ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ
имени С.М. Кирова
Кафедра биологической и медицинской физики
ЛЕКЦИЯ № 6
по
дисциплине «Физика, математика»
курсантов и студентов I курса ФПВ, ФПиУГВ, спецфакультета
Слайд 21. Понятие об электромагнитных волнах
Теория электромагнитного поля была создана в
1864 г. Джеймсом Кларком Максвеллом (1831-1879).
Слайд 3
Д.К. Максвелл проанализировал все известные к тому времени законы электродинамики
и сделал попытку применить их к изменяющимся во времени электрическому
и магнитному полям.
Слайд 4
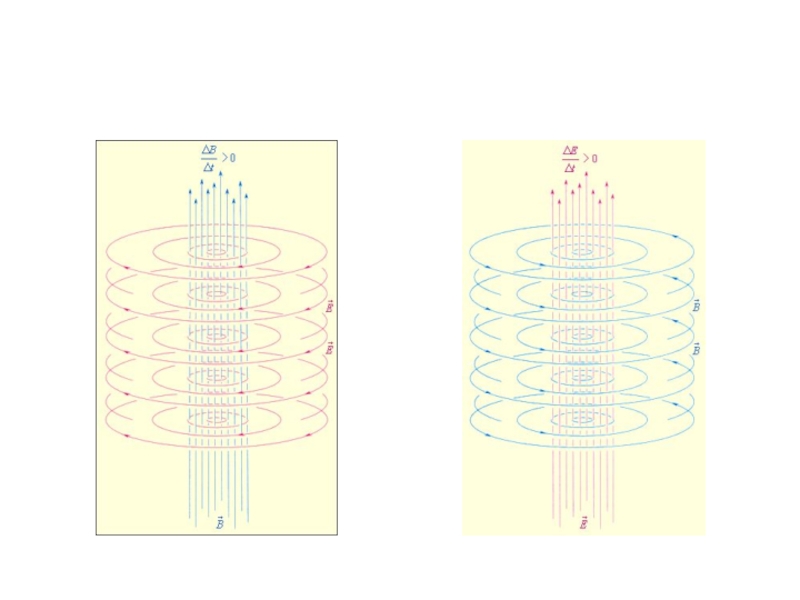
Максвелл ввел в физику понятие вихревого электрического поля и предложил
новую трактовку закона электромагнитной индукции, открытой Майклом Фарадеем в 1831 г.:
Всякое
переменное магнитное поле порождает вихревое электрическое поле.
Слайд 5
Максвелл высказал гипотезу о существовании и обратного процесса:
Всякое переменное электрическое
поле порождает вихревое магнитное.
Слайд 7
Эта гипотеза была лишь теоретическим предположением, не имеющим экспериментального подтверждения,
однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений,
описывающих взаимные превращения электрического и магнитного полей, т. е. систему уравнений единого электромагнитного поля (уравнений Максвелла).
Слайд 8
Из теории Максвелла вытекает ряд важных выводов:
1. Единое электромагнитное поле
распространяется в виде электромагнитных волн.
Слайд 9
Электромагнитные волны представляют собой взаимосвязанные и взаимопорождающие друг друга распространяющиеся
колебания электрических и магнитных полей, переносящие в пространстве энергию.
Слайд 11
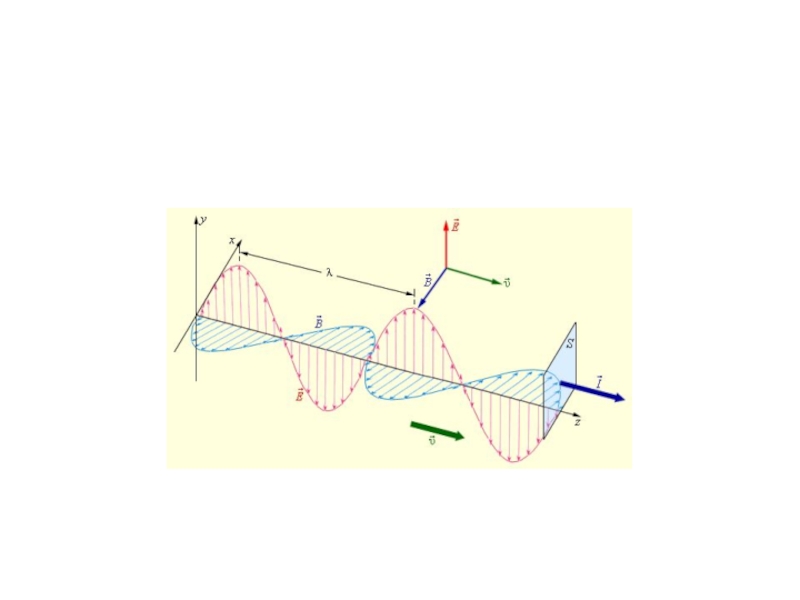
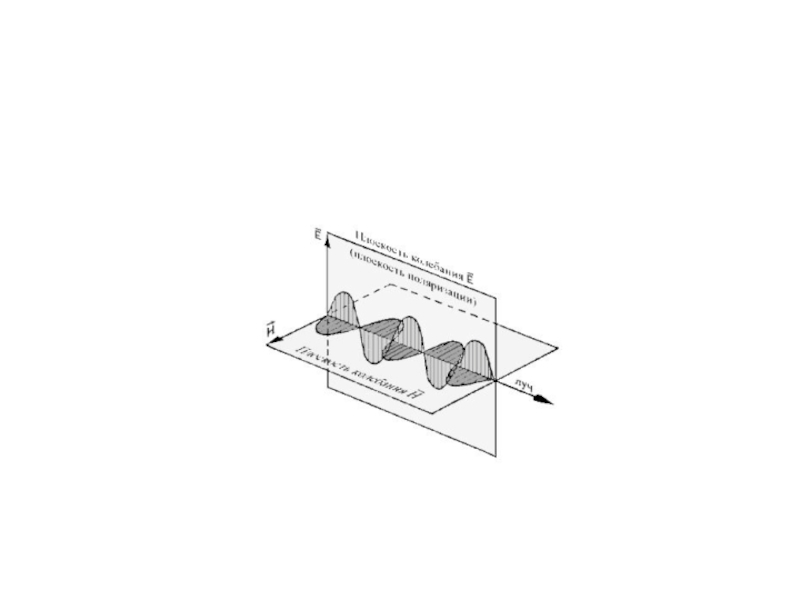
ЭМВ поперечны – векторы и перпендикулярны друг
другу и лежат в плоскости, перпендикулярной направлению распространения волны.
Слайд 12
Уравнения плоской ЭМВ имеют вид:
E = Emcos ω(t-x/v)
H = Hmcos
ω(t-x/v)
Здесь H = B/μ0μ – напряженность МП;
μ0 = 12,56.10-7 Гн/м
- магнитная постоянная.
Слайд 13
Как видно из уравнений, колебания электрической и магнитной составляющей электромагнитной
волны происходят синфазно.
Слайд 14
2) Электромагнитные волны распространяются в веществе с конечной скоростью:
где с
- скорость света в вакууме.
Слайд 15
Скорость распространения ЭМВ равна скорости света.
Это послужило основанием для создания
Д.К. Максвеллом электромагнитной теории света.
Видимый свет – это ЭМВ в
диапазоне длин волн от 380 до 760 нм.
Слайд 16
Основные свойства ЭМВ – интерференция, дифракция, поляризация – наиболее наглядно
проявляются при изучении света.
Слайд 17
2. Интерференция света. Практическое применение интерференции
Интерференцией света называют сложение световых
волн с образованием в пространстве устойчивой интерференционной картины, представляющей собой
чередование максимумов и минимумов интенсивностей света (максимумов и минимумов освещенности).
Слайд 18
Устойчивую во времени интерференционную картину можно получить только при сложении
когерентных волн.
Определение: Волны называют когерентными, если они имеют одинаковую частоту
и постоянную во времени разность фаз.
Слайд 19
Обычные источники света представляет собой совокупность огромного числа излучающих атомов
или молекул.
Эти атомы и молекулы излучают свет независимо друг
от друга, то есть излучаемые волны не согласованы по фазе, а кроме того, могут отличаться по частоте. 
Слайд 20
Поэтому картина взаимного усиления, возникшая в каком-либо участке пространства, уже
через миллиардные доли секунды сменяется картиной взаимного ослабления и т. д.
Смена таких мгновенных картин глазом не воспринимается, а создает ощущение ровного потока света, не изменяющегося во времени.
Слайд 21
Единственный способ получения когерентных световых волн - разделить один световой
пучок на два, провести их по разным путям, а затем
свести их вместе.В силу общности происхождения таких пучков света, они будут когерентными.
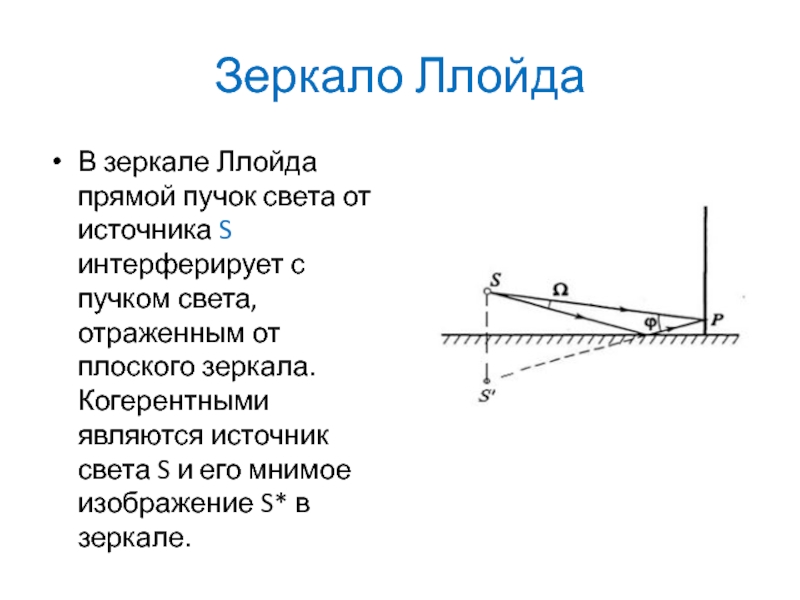
Слайд 22Зеркало Ллойда
В зеркале Ллойда прямой пучок света от источника
S интерферирует с пучком света, отраженным от плоского зеркала. Когерентными
являются источник света S и его мнимое изображение S* в зеркале.
Слайд 23
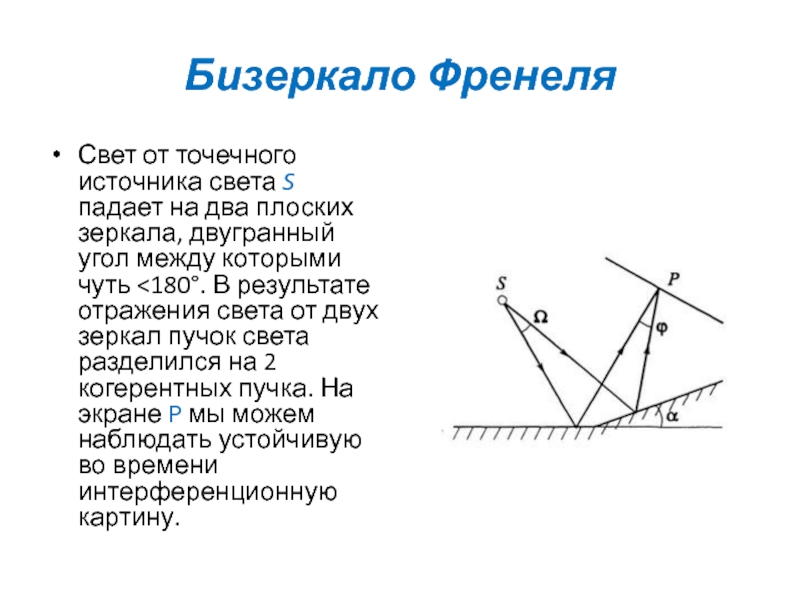
Бизеркало Френеля
Свет от точечного источника света S падает на
два плоских зеркала, двугранный угол между которыми чуть
результате отражения света от двух зеркал пучок света разделился на 2 когерентных пучка. На экране P мы можем наблюдать устойчивую во времени интерференционную картину.
Слайд 24
Определим условия максимумов и минимумов интерференционной картины на примере двух
монохроматических когерентных плоских волн.
Слайд 25
Колебания вектора напряженности электрического поля Е этих волн в некоторой
точке A, удаленной на расстояния x1 и x2 соответственно от
каждого источника, происходят по гармоническому закону:
Слайд 26
Сложение волн, распространяющихся в среде, определяется сложением соответствующих колебаний.
Наиболее
простой случай сложения электромагнитных волн наблюдается тогда, когда их частоты
одинаковы, а направления колебаний совпадают.
Слайд 28
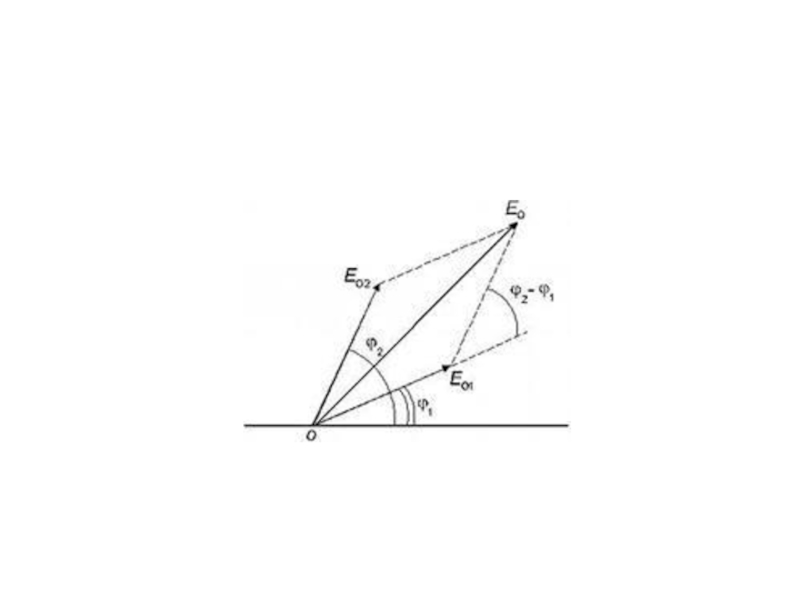
Амплитуду результирующих колебаний вектора напряженности в точке A находим по
теореме косинусов:
где Δφ - разность фаз между двумя волнами.
Слайд 29
Очевидно, что амплитуда результирующего колебания будет максимальной (условие максимума), если
соs Δφ = 1,
то есть Δφ =
2kπ (k = 0, ±1, ±2, …).Такие колебания называют синфазными.
Слайд 30
Амплитуда результирующего колебания будет минимальной (условие минимума), если соs Δφ
= -1,
то есть Δφ = (2k+1)π (k
= 0, ±1, ±2, …)..Такие колебания называют противофазными.
Слайд 32
Вспомним, что ω = 2π/Т.
Отношение скорости света в вакууме к
скорости света в среде называют показателем преломления среды:
Тогда
Слайд 34
Произведение геометрического пути волны x на абсолютный показатель преломления среды
n называется оптической длиной пути, а разность оптических путей –
оптической разностью хода двух волн.
Слайд 35
Объединим условие интерференционного максимума: Δφ = 2kπ (k = 0,
±1, ±2, …) и полученное нами выражение
.Получаем
Отсюда
Слайд 36
Максимум интерференции наблюдается в тех точках, в которых оптическая разность
хода равна целому числу длин волн (четному числу полуволн).
Аналогично можно
показать, что минимум интерференции наблюдается в тех точках, в которых δ равна нечетному числу длин полуволн.
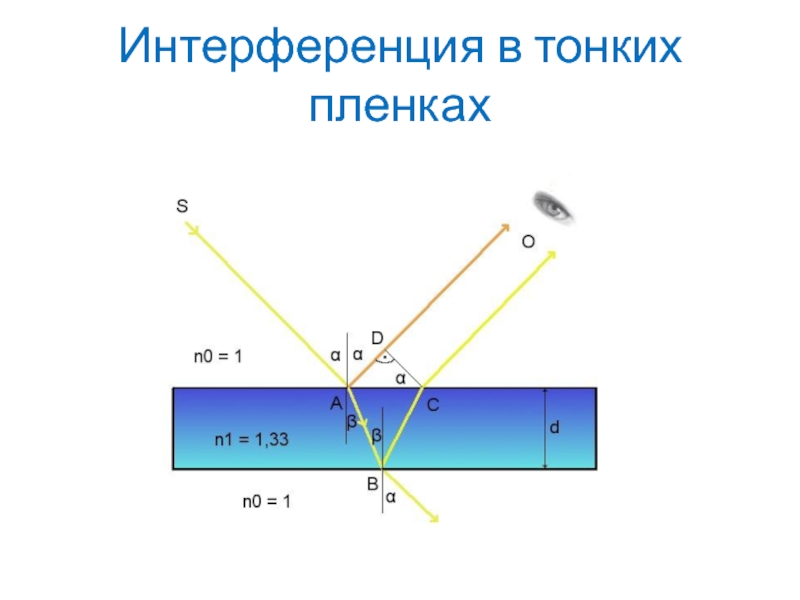
Слайд 38
Условие максимума интерференции в тонкой пленке:
Условие минимума интерференции в тонкой
пленке:
Слайд 39
Здесь - толщина пленки;
i - угол падения;
n –
показатель преломления пленки (полагаем, что луч света падает на пленку
из воздуха и nвозд.= 1).
Слайд 40
Проанализируем формулы интерференционных минимумов и максимумов для тонких пленок:
1) Если
на тонкую плоскопараллельную пластинку под некоторым углом падает параллельный пучок
монохроматического света, то пластинка в отраженном свете выглядит яркой или темной.
Слайд 41
2) При освещении пластинки белым светом условия минимумов и максимумов
будут выполняться для отдельных длин волн. Пластинка станет окрашенной, причем
цвета в отраженном и проходящем свете будут дополнять друг друга до белого.
Слайд 42
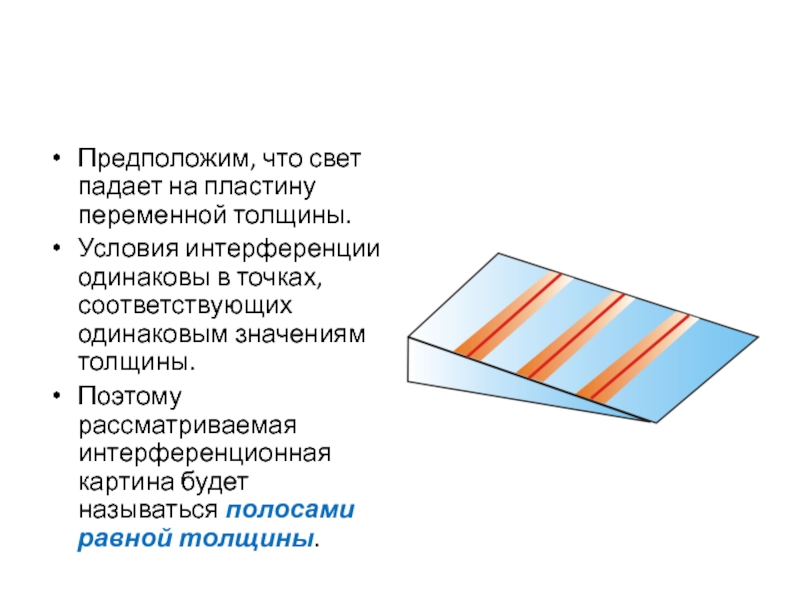
Предположим, что свет падает на пластину переменной толщины.
Условия интерференции
одинаковы в точках, соответствующих одинаковым значениям толщины.
Поэтому рассматриваемая интерференционная
картина будет называться полосами равной толщины.
Слайд 43
При освещении пластинки переменной толщины белым светом получаем разноцветные пятна
и линии: мыльные пузыри, CD-диски, переливчатые крылья насекомых и птиц.
Слайд 44Применение интерференции
1) Просветление оптики
Современные оптические устройства состоят из большого
количества оптических стекол (линз, призм и др.).
Проходя через такие
устройства, свет отражается от многих поверхностей.. 
Слайд 45
При падении света нормально поверхности от каждой поверхности отражается 5-9 %
всей энергии. А таких поверхностей может быть до 50 (в
частности, в перископах современных подводных лодок их до 40).Сквозь прибор часто проходит всего 10-20 % поступающего в него света.
Слайд 46
В результате этого освещенность изображения получается малой.
Многократное отражение от
преломляющих поверхностей приводит к появлению внутри приборов рассеянного света, что
ухудшает качество изображений.
Слайд 47
Для устранения этих неприятных последствий отражения света надо уменьшить долю
отраженной энергии света.
Для этого оптику просветляют.
Слайд 48
На поверхность оптического стекла наносят тонкую пленку (например, из оксидов
металлов) с показателем преломления
Толщину пленки подбирают таким образом, чтобы лучи,
отраженные от границ воздух-пленка и стекло-пленка при интерференции гасили друг друга.
Слайд 49
Из условий интерференции в тонкой пленке следует, что толщина слоя
просветления:
Выражение показывает, что требуемая толщина пленки зависит от длины волны.
Поэтому осуществить гашение отраженных волн всех частот невозможно.
Слайд 50
Толщину пленки подбирают так, чтобы полное гашение при нормальном падении
имело место для длин волн средней части спектра (зеленый цвет,
λ = 550 нм).Отражение света крайних участков спектра – красного и фиолетового – ослабляется незначительно. Поэтому объектив с просветленной оптикой в отраженном свете имеет пурпурный оттенок.
Слайд 51
2) Интерферометры -приборы для измерения с высокой точностью длин волн,
небольших линейных и угловых расстояний, малых разностей показателей преломления веществ,
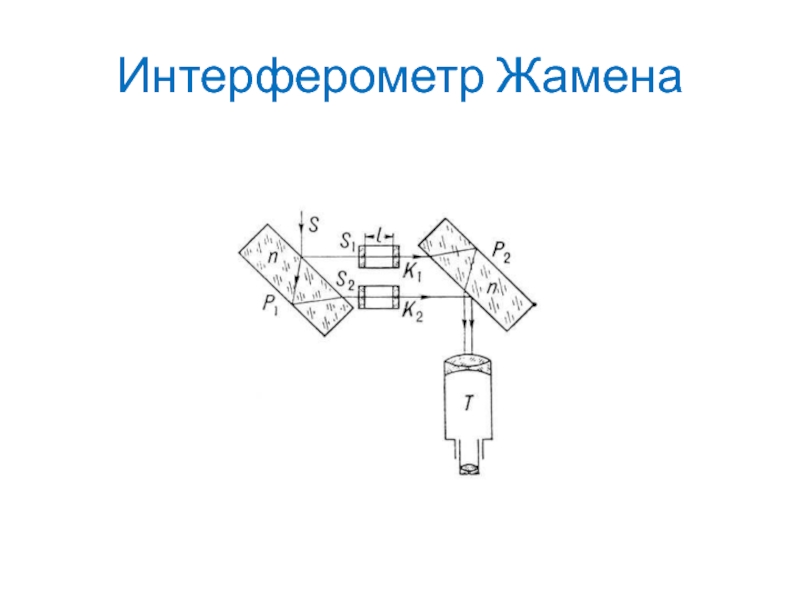
определения качества обработки оптических поверхностей, исследования структуры спектральных линий.
Слайд 53
3) Интерференционный микроскоп - сочетание двухлучевого интерферометра и микроскопа.
Используют в
биологии для измерения показателя преломления и толщины прозрачных микрообъектов.
Слайд 54
3) Интерференционный микроскоп - сочетание двухлучевого интерферометра и микроскопа.
Используют в
биологии для измерения показателя преломления и толщины прозрачных микрообъектов.
Слайд 553. Естественный и поляризованный свет.
Почти все источники света, представляющие
собой совокупность очень большого количества независимых друг от друга излучателей,
излучают так называемый естественный свет.
Слайд 56
Естественный свет представляет собой совокупность световых волн, в которых векторы
напряженности электрического поля Е колеблются вдоль всевозможных направлений, перпендикулярных лучу
(направлению распространения света).
Слайд 57
Если в свете есть преимущественное направление колебаний вектора , то
свет будет называться частично поляризованным.
Луч света, в котором колебания
электрического и магнитного векторов происходят во вполне определенных взаимно перпендикулярных плоскостях, положение которых не изменяется с течением времени, называется плоскополяризованным. Плоскополяризованную волну излучает отдельно взятый атом в единичном акте излучения.
Слайд 58
Плоскость, в которой колеблется электрический вектор Е, называется плоскостью поляризации
света.
Слайд 60Способы получения плоскополяризованного света
1) Поляризация света при отражении и преломлении
на границе раздела двух диэлектриков.
2) Поляризация света при двойном лучепреломлении.
3)
Дихроизм.
Слайд 61
Устройства для получения плоскополяризованного света из естественного называются поляризаторами.
Поляризатор,
при прохождении через него естественного света, пропускает только волны с
определенным направлением колебаний, лежащих в главной оптической плоскости поляризатора.
Слайд 62
Поляризатор можно использовать для анализа плоскополяризованного света.
В этом случае
его называют анализатором.
Слайд 64
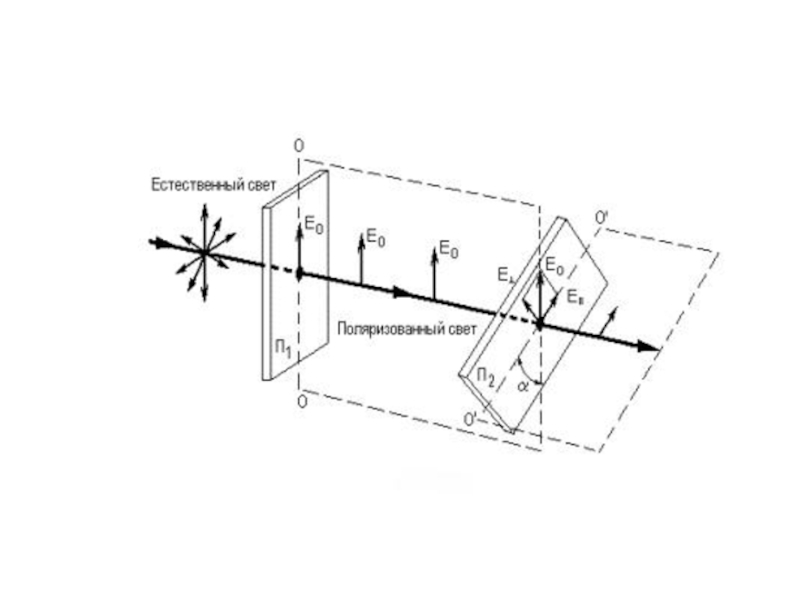
Пусть на анализатор П2 падает плоскополяризованная волна, прошедшая через поляризатор
П1.
Световой вектор этой волны пусть колеблется в плоскости ОО
(главная плоскость поляризатора). Пусть плоскость ОО составляет угол α с главной плоскостью О’О’ анализатора.
Слайд 65
В результате этого через анализатор пройдет только составляющая вектора Е0,
равная Е=Е0cosα.
Так как интенсивность света пропорциональна квадрату амплитуды колебаний, то
IА = IПcos2 α,
Слайд 66
где IА – интенсивность поляризованного света, вышедшего из анализатора;
IП
– интенсивность света, вышедшего из поляризатора (падающего на анализатор); α
– угол между главными плоскостями поляризатора и анализатора.Это закон Малюса.
Слайд 67
Как видно из закона Малюса, при повороте анализатора относительно луча
падающего поляризованного света, интенсивность вышедшего света изменяется от нуля до
IП.
Слайд 68
4. Вращение плоскости поляризации. Оптически активные вещества. Поляриметрия
Некоторые вещества обладают
способностью поворачивать плоскость поляризации луча, проходящего через них.
Такие вещества
называются оптически активными. Например, оптически активны некоторые кристаллы (кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы (растворы сахаров, аминокислот, винной кислоты).
Слайд 69
В зависимости от того, в каком направлении (со стороны наблюдателя)
происходит поворот плоскости поляризации в данном веществе, оно называется правовращающим
или левовращающим.Все ОА вещества существуют в двух разновидностях (право- и левовращающие, D- и L-изомеры).
Слайд 70
Опыт показывает, что все оптически активные вещества поворачивают плоскость поляризации
падающего на них света на угол
,где - толщина оптически активного слоя,
α – постоянная вращения.
Слайд 71
Для растворов угол поворота плоскости поляризации прямо пропорционален концентрации оптически
активного вещества:
где С – концентрация, выраженная в %,
– длина
пути в веществе, выраженная в дм, [α0] – удельное вращение.
Слайд 72
[α0] = 1 град·см3·г‑1·дм‑1 - физическая величина, численно равная стократному углу поворота плоскости
колебаний линейно поляризованного света 1%-ным раствором ОА вещества толщиной 1 дм.
Удельное вращение зависит от температуры вещества, длины волны плоскополяризованного света, давления, типа растворителя.
![[α0] = 1 град·см3·г‑1·дм‑1 - физическая величина, численно равная стократному углу поворота плоскости колебаний линейно поляризованного света 1%-ным раствором ОА](/img/thumbs/1d6bdb4a3f34d55fd95eec44279c0bb3-800x.jpg "Электромагнитные волны. Интерференция и поляризация ЭМВ [α0] = 1 град·см3·г‑1·дм‑1 - физическая величина, численно равная стократному углу поворота плоскости колебаний")
Слайд 73
Зная удельное вращение, угол вращения и длину пути в веществе,
можно найти концентрацию раствора ОАВ.
Метод определения концентрации ОАВ по
углу поворота плоскости поляризации называется поляриметрией (сахариметрией).Соответствующие приборы называют поляриметрами (сахариметрами).
