Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории вероятностей
Содержание
- 1. Элементы теории вероятностей
- 2. Тема: Предмет теории вероятностей. Статистическая вероятность. Алгебра событий. Аксиоматика. Вероятность, ее свойства.
- 3. Теория вероятностей -математическая наука, изучающая общие закономерности
- 4. Примеры случайных явленийдлительность произвольного телефонного разговора; выпадение
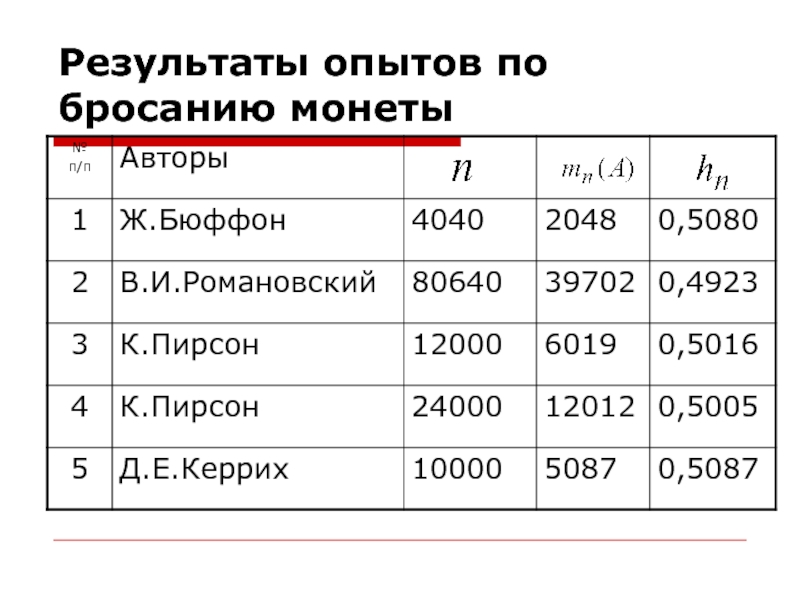
- 5. Результаты опытов по бросанию монеты
- 6. Результаты опытов по бросанию монетыПусть А- событие
- 7. Определение: Число P(A)- около которого группируются частоты
- 8. Слайд 8
- 9. Элементарный исход Возможный исход эксперимента (опыта) называется
- 10. Пространство элементарных исходовВозможный набор исходов эксперимента будем
- 11. Определение событияСобытием называется подмножество пространства элементарных исходов
- 12. Свершение событияПусть А (то есть А-событие)-произвольное подмножество
- 13. Операции над событиями (множествами)Объединение (сложение) событий А
- 14. Пример4Пример 4: Бросаем игральную кость и рассматриваем
- 15. Пересечение (произведение) событий А и В :
- 16. Вложенность событий A BБудем говорить, что событие
- 17. Пример 5,6Пример 5: Бросаем игральную кость один
- 18. Дополнение к событию Дополнением ( )
- 19. Разность событий A\BРазностью между событиями А и
- 20. Объединение или суммаСобытие, состоящее в наступлении хотя
- 21. Достоверное и невозможноеСобытие, отвечающее всему множеству элементарных
- 22. Свойства операций над событиями
- 23. Доказательство Отметим справедливость формул: Покажем справедливость
- 24. Законы двойственности Де МорганаПри доказательстве будут использоваться
- 25. Доказательство утверждения Пусть тогда Значит:
- 26. Доказательство утверждения
- 27. Алгебра событийПусть есть пространство
- 28. Ещё раз о множествахМножество событий {Ai} называется
- 29. Определение вероятностиПусть пространство элементарных
- 30. Вероятностное пространствоТройка объектов
- 31. Свойства вероятностей(1,2)Вероятность невозможного события равна нулюВероятность противоположного
- 32. Свойства вероятностей(3,4)3. Если
- 33. Свойства вероятностей(5,6)5. Для любого событияТак как
- 34. Свойство вероятностей 7Для произвольных событий А и
- 35. Классическая вероятностная модельПусть каждый элементарный исход эксперимента
- 36. Полная группа событийСобытия
- 37. Классическая схемаПусть пространство элементарных исходов
- 38. Скачать презентанцию
Тема: Предмет теории вероятностей. Статистическая вероятность. Алгебра событий. Аксиоматика. Вероятность, ее свойства.
Слайды и текст этой презентации
Слайд 1Элементы теории вероятностей
Лектор: Веричев Станислав Николаевич
К.т.н., доцент.
Телефон кафедры 346-07-33.
Корпус 1,
ком. 420.
Слайд 2Тема: Предмет теории вероятностей. Статистическая вероятность. Алгебра событий. Аксиоматика.
Вероятность, ее свойства.
Слайд 3Теория вероятностей -математическая наука, изучающая общие закономерности случайных явлений независимо
от их конкретной природы и дающая методы количественной оценки влияния
случайных факторов на различные процессы.Слайд 4Примеры случайных явлений
длительность произвольного телефонного разговора;
выпадение определенного количества очков
на игральной кости;
выигрышные номера в лотерее и т.д.
Слайд 6Результаты опытов по бросанию монеты
Пусть А- событие (наступает в опыте,
которое может быть повторено с соблюдением одних и тех же
условий неограниченное число раз), которое в данном случае заключается в выпадении герба при бросании монеты;кол-во появлений события А в “ ”-опытах;
-частота появления события А в “ ”-опытах.
Слайд 7Определение:
Число P(A)- около которого группируются частоты появления события А при
неограниченном увеличении числа испытаний называется статистической вероятностью, т.е.
Слайд 9Элементарный исход
Возможный исход эксперимента (опыта)
называется элементарным исходом
или
элементарным событием.
Обозначение элементарного исхода:
Пример 1: Самый простой эксперимент
имеет два исхода. Бросание монеты, где исходами являются выпадение “герба” или “решки”. Слайд 10Пространство элементарных исходов
Возможный набор исходов эксперимента будем называть пространством элементарных
исходов (событий). В примере 1: пространство элементарных событий состоит из
двух точек. ={0;1}. ={}.Слайд 11Определение события
Событием называется подмножество пространства элементарных исходов
Пример 2: Бросание
игральной кости один раз – пример эксперимента с большим числом
исходов: ={1;2;3;4;5;6}Пример 3: Бросание игральной кости один раз и выпадение более 4-х очков-состоит из двух элементарных событий А={5};В={6}.
Слайд 12Свершение события
Пусть А (то есть А-событие)-произвольное подмножество пространства элементарных исходов
для некоторого эксперимента. Проведение эксперимента сводится к наблюдению элементарного
исхода . Если А, то говорят, что произошло событие А. Если же это не так, то говорят, что событие А не произошло (то есть А).Слайд 13Операции над событиями (множествами)
Объединение (сложение) событий А и В :
АВ это А или В
(АВ)(А)(В)
Операция “”-“или”
Слайд 14Пример4
Пример 4: Бросаем игральную кость и рассматриваем два события :А={1;3}
(выпадение единицы или тройки); и В={1;3;4} (выпадение единицы, тройки, четвёрки).
Здесь:
АВ={1;3;4}.Слайд 15Пересечение (произведение) событий А и В : АВ
АВ это означает,
что произошли события “А и В” одновременно, т.е.
(АВ)(A)(B)
где символ
“” означает “и”Здесь: АВ={1;3} (из примера 4)
Слайд 16Вложенность событий A B
Будем говорить, что событие А содержится в
событии В (A B), если любое элементарное событие из А
входит и в В.Здесь АВ (из примера 4)
События А и В совпадают или равны (А=В) если АВ и ВА.
События А и В называются несовместными, если АВ=.
Слайд 17Пример 5,6
Пример 5: Бросаем игральную кость один раз и рассматриваем
события А={1;3}; В={3;5}; С={5;6}. Здесь: АВ={3}; AC=. AB={1;3;5}; AC={1;3;5;6}.
Пример
6: Из чисел 1,2,3….100 наудачу выбирается одно число. Рассмотрим события: А={выбранное число делится на 2}, В={выбранное число делится на 6}. Тогда событие А является следствием события В (так как числа, делящиеся на 6 делятся и на 2), т.е. B ).Слайд 18Дополнение к событию
Дополнением ( ) к событию А
(или противоположное к А) называется событие, состоящее из тех элементарных
событий, которые не входят в А.Здесь (из примера 5):
Слайд 19Разность событий A\B
Разностью между событиями А и В (А\В) будем
называть событие, состоящее из тех элементарных событий, которые входят в
А, но не входят в В.Здесь (из примера 5):
С\В={6}; C\A=C,
так как СА=.
Слайд 20Объединение или сумма
Событие, состоящее в наступлении хотя бы одного из
событий A или B, называется объединением или суммой событий и
обозначается АВ . Событие АВ состоит из элементарных исходов, входящих в A или B.Слайд 21Достоверное и невозможное
Событие, отвечающее всему множеству элементарных исходов, называется достоверным
событием (оно происходит всегда, когда происходит эксперимент, так как
).Событие, которое никогда не происходит, т.е. отвечающее пустому множеству , называется невозможным
Слайд 23Доказательство
Отметим справедливость формул:
Покажем справедливость последнего из них:
то
есть нужно показать, что и .Пусть
И обратно:
т.е. .
Слайд 24Законы двойственности Де Моргана
При доказательстве будут использоваться следующие утверждения:
Если
и
, тоАналогично, если
и ,то
Слайд 25Доказательство утверждения
Пусть тогда
Значит:
Покажем, что из условия
следует .
Пусть , тогда
Или
Это означает, что
Таким образом,
Слайд 26Доказательство утверждения
Пусть
И обратно, равенство
следует на основе таких
же рассуждений, как и в предыдущем случаеСлайд 27Алгебра событий
Пусть есть пространство элементарных исходов (произвольное
множество), -Некоторая система подмножеств множества
называется алгеброй, если
выполнены следующие аксиомы:А1.
А2.Если и
А3. Если
Слайд 28Ещё раз о множествах
Множество событий {Ai} называется счётным , если
элементы этого множества можно занумеровать в бесконечную последовательность
Для счётного множества
событий {Ai} операции пересечения и объединения событий определяются так же, как и для конечного числа событий: событие, заключающееся в осуществлении хотя бы одного из событий- событие, заключающееся в осуществлении хотя бы одного из событий
событие, заключающееся в осуществлении всех событий одновременно
Слайд 29Определение вероятности
Пусть пространство элементарных исходов,
алгебра событий.
Вероятностью события А называют числовую функцию Р(А),
определённую на алгебре событий . Эта функция отображает множество , состоящее из событий в множество действительных чисел из отрезка [0,1], т.е.и удовлетворяет следующим аксиомам:
Р1. Для любого события Р(А)≥0 ( )
Р2.Вероятность достоверного события
Р3.Для несовм. событий:
Тройка объектов , где - непустое пространство элементарных исходов, -алгебра событий, Р-вероятность, называется вероятностным пространством.
Слайд 30Вероятностное пространство
Тройка объектов
называется вероятностным пространством.
Вероятностное
пространство называется дискретным, если пространство элементарных исходов конечно или счётно.
Вероятность определена для каждого одноточечного подмножества :
при этом , где -элементарные исходы,
свершение которых означают свершение события А.
Слайд 31Свойства вероятностей(1,2)
Вероятность невозможного события равна нулю
Вероятность противоположного события
т.к.
Слайд 32Свойства вероятностей(3,4)
3. Если
, то
,Так как события и несовместны, то
, но тогда
4. Если , то
Это свойство следует из аксиомы Р1: и предыдущего свойства, т.к.
Слайд 33Свойства вероятностей(5,6)
5. Для любого события
Так как
, то по предыдущему свойству
И по аксиоме 1 имеем:
6. Для произвольных событий А и В:имеет место равенство:
Пусть . Тогда
так как и ;
, так как и .
Отсюда и . Далее получаем:
#
Слайд 34Свойство вероятностей 7
Для произвольных событий А и В:
имеет место
неравенство:
Это свойство следует из аксиомы 1 и предыдущего свойства
#Слайд 35Классическая вероятностная модель
Пусть каждый элементарный исход эксперимента имеет одинаковую возможность
осуществиться (исходы равновероятны). В таком случае этим исходам естественно поставить
в соответствие одинаковые вероятности. Рассмотрим пространство элементарных исходов , где. В силу того, что
из аксиом Р2, Р3 вытекает: ,
поэтому , где –число
элементарных исходов эксперимента.
Слайд 36Полная группа событий
События
образуют полную группу попарно несовместных
событий, если и .Например, при бросании монеты событиями являются: (выпадение «орла»), (выпадение «решки»). И
Аналогично, при бросании игральной кости, имеем: – выпадение нечётного числа очков, – выпадение чётного числа очков. При этом , то есть рассматриваемые события образуют полную группу:
Слайд 37Классическая схема
Пусть пространство элементарных исходов
, а каждый из исходов равновероятен, т.е. , свершение события А есть свершение элементарных исходов: , т.е. событие А состоит из элементарных исходов . Тогда, согласно классической схеме вероятность события А есть число .
Пример: В урне имеется « » белых и« » красных шаров. Извлекается из урны 1 шар. Какова вероятность того, что этот шар белый?
Все исходы равновероятны, их всего . Событию благоприятствуют из исходов, поэтому, на основании теоремы имеем