Энергия, переносимая электромагнитной волной. Вектор Умова-Пойнтинга

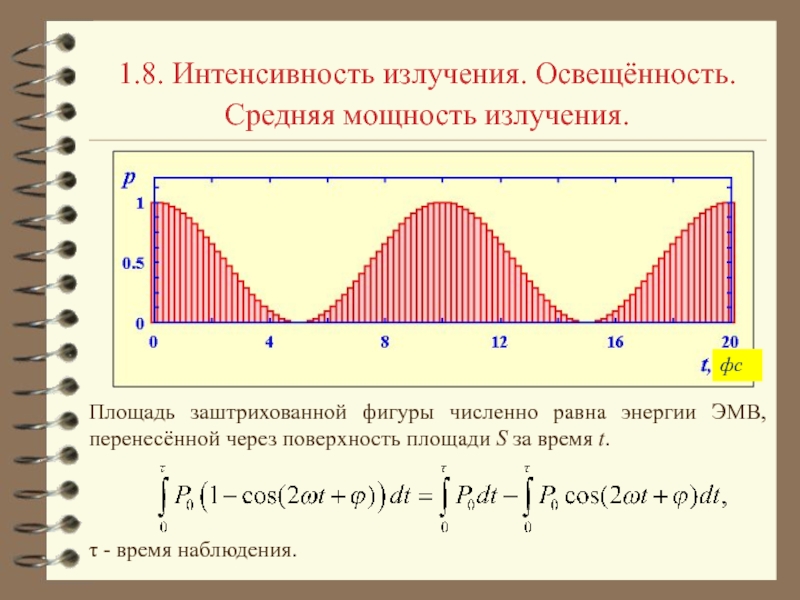
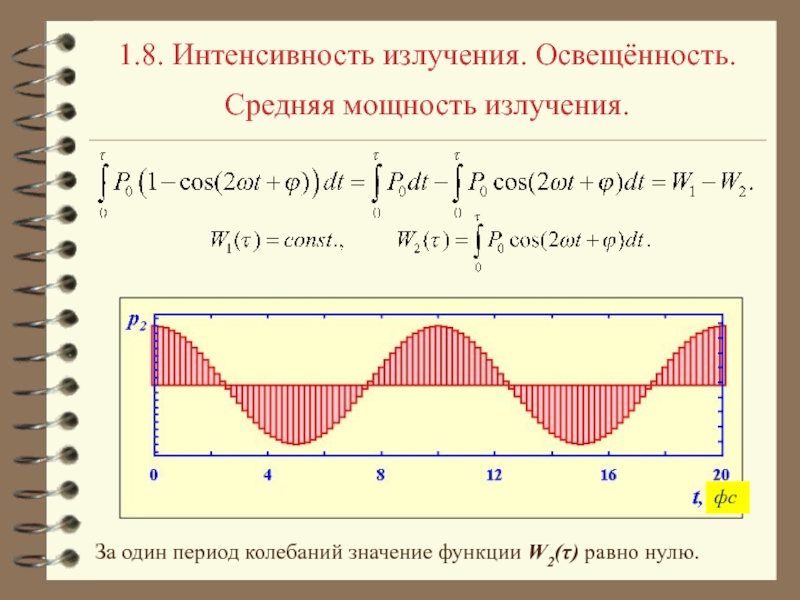
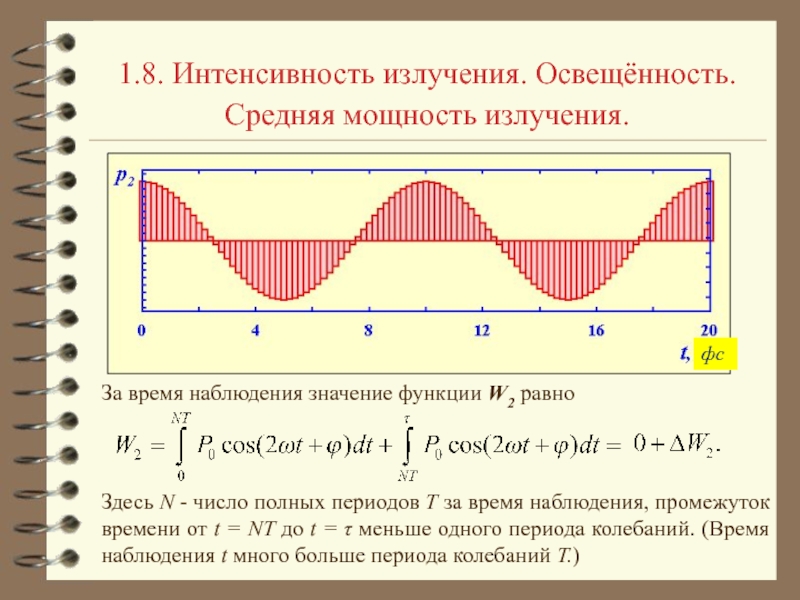
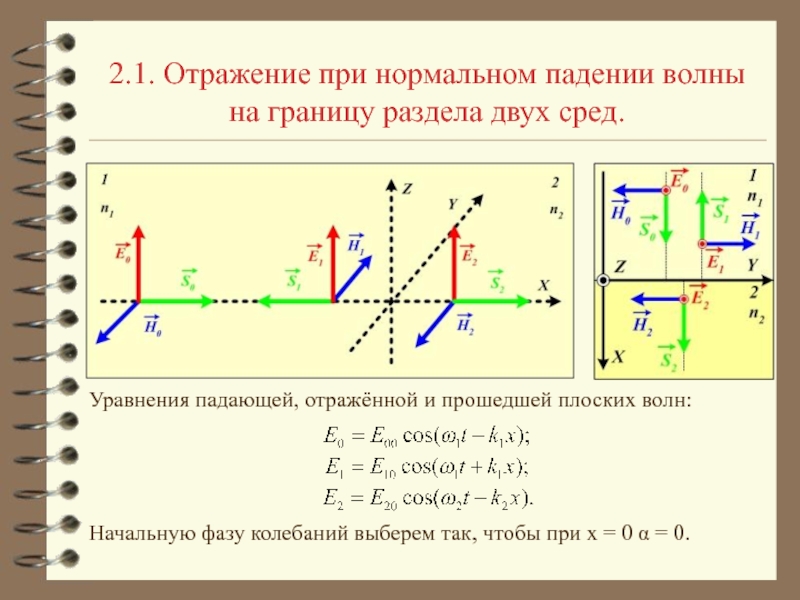
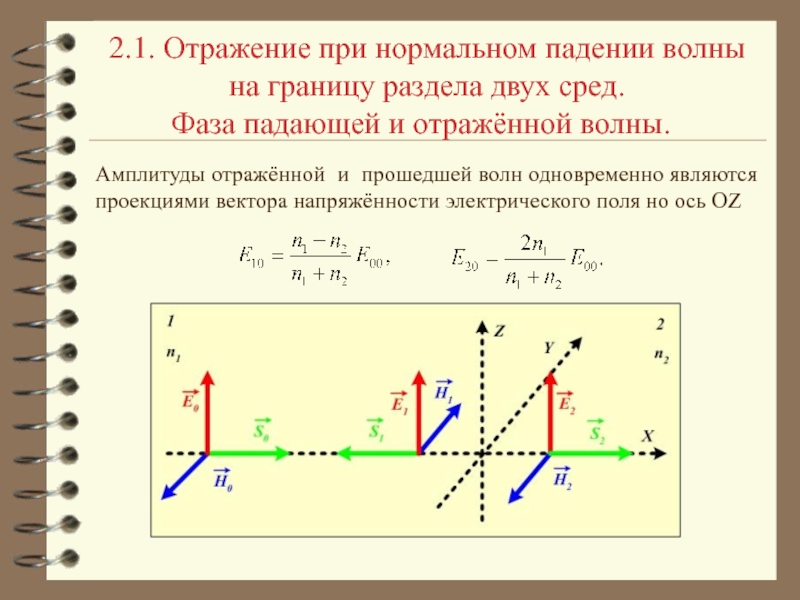
получить из уравнений Максвелла. Рассмотрим уравнения:
а плотность энергии магнитного

(1)

(2)

Умножим уравнение (1) на вектор H скалярно, а уравнение (2) умножим скалярно на вектор E.

переписать так:
Первое уравнение системы:

поэтому j = 0.
Итого, мы получили два уравнения:
Вычтем из второго

уравнения:
- плотность энергии электромагнитного поля.
- вектор Умова-Пойнтинга.
(1)

 - поверхность, окружающая объём V.
Чтобы равенство не нарушилось,

Здесь WЕМ - энергия электромагнитного поля в объёме V.

Итого, получилось:

(1)

поверхность равен убыли энергии электромагнитного поля в объёме, ограниченном этой

Согласно определению,

Таким образом,

Эти векторы образуют правую тройку.

Так как E и H лежат в плоскости, перпендикулярной направлению распространения волны, направление S совпадает с направлением распространения волны.

энергии электромагнитного поля
Если в пространстве распространяется электромагнитная волна, то в

Плотность энергии магнитного поля

В любой момент времени

волны в данной среде. В вакууме, когда v = c,
В

назовём её модулем плотности потока энергии. Эта величина будет равна

W – энергия,  - площадь, t – время.

Модуль плотности потока энергии (эта величина равна энергии, проходящей через единицу площади в единицу времени) равен модулю вектора Умова – Пойнтинга.

единицу площади в единицу времени, равна модулю вектора Умова –

электромагнитной волны, проходящую через единицу площади поверхности.
Мгновенное значение мощности
Для

перенесённая ЭМВ через поверхность площади S за время t равна
Рассматриваем

Средняя мощность за время наблюдения τ

ЭМВ, перенесённой через поверхность площади S за время t.
Средняя мощность

τ - время наблюдения.

колебаний значение функции W2(τ) равно нулю.

равно
Средняя мощность излучения.
Здесь N - число полных периодов T

время наблюдения τ:
так как интеграл ΔW2 вычисляется за очень

много меньше времени усреднения, то
Для подавляющего большинства диэлектриков μ =

где n – показатель преломления среды.

Краткие выводы:

Средняя мощность излучения.

с ней и интенсивность излучения
В оптике считается, что освещённость равна

двух сред.
2.
2.1.

сред.
Рассмотрим границу раздела двух однородных, изотропных, электрически нейтральных, непроводящих

Из среды 1 с ε = ε1 на границу раздела падает электромагнитная (световая) волна. Из опыта известно, что такая волна частично отражается от границы раздела, а частично проходит во вторую среду с ε = ε2 .
1. Изменяется ли скорость и частота волны пре переходе из одной среды в другую?
2. Как изменяется фаза волны при отражении?
3. Требуется также определить, как относятся интенсивности отражённой и падающей волн, а также прошедшей и падающей волн.

сред.
Уравнения падающей, отражённой и прошедшей плоских волн:
Начальную фазу

сред.
Амплитуды электрической и магнитной составляющих каждой из волн связаны

Можно считать, что точка x = 0 принадлежит как первой среде, так и второй. В первой среде существуют падающая волна и отражённая волна, во второй – прошедшая. Поэтому, согласно принципу суперпозиции электрических полей для проекций вектора напряжённости на ось OZ

сред.
Рассуждая аналогично, для проекций вектора напряжённости магнитного поля на

Итак, на границе раздела сред для векторов напряжённостей полей справедливы два уравнения:

Подставим в первое уравнение выражения для E0, E1, E2:

сред.
Мы рассматриваем точку x = 0, поэтому
Это равенство должно

При переходе через границу раздела, либо при отражении от границы раздела частота ЭМВ не изменяется.

Скорость ЭМВ при переходе через границу раздела изменяется,

сред.
Скорость ЭМВ при переходе через границу раздела изменяется,
Поэтому такие

Чтобы определить, как изменятся амплитуды отражённой и прошедшей волн, вернёмся к записанной ранее системе уравнений.

сред.
Подставим во второе уравнение выражения для H0, H1, H2:

сред.
Теперь систему уравнений можно переписать так:
Сложим два уравнения:
- амплитуда

сред.
Второе уравнение системы:
- амплитуда отражённой волны.
Подставим в него выражение

сред.
Итак, амплитуды отражённой и прошедшей волн равны
Относительная интенсивность отражённой

Относительная интенсивность прошедшей волны

сред.
Амплитуды отражённой и прошедшей волн одновременно являются проекциями вектора

Фаза падающей и отражённой волны.

сред.
Если
и
имеют одинаковые знаки (см. рисунок).
Это означает,

Среда с большим показателем преломления называется оптически более плотной, а среда с меньшим показателем преломления – оптически менее плотной.
При отражении от оптически менее плотной среды фаза отражённой волны не меняется.

Фаза падающей и отражённой волны.

сред.
Если
и
имеют разные знаки (см. рисунок).
Это означает,

При отражении от оптически более плотной среды фаза отражённой волны изменяется на π.

Фаза падающей и отражённой волны.

сред. Основные результаты.
1. При переходе через границу раздела, либо

2. Скорость ЭМВ при переходе через границу раздела изменяется,

3. Волновое число и длина волны также изменяются:

сред. Основные результаты
7. При отражении от оптически более плотной

6. При отражении от оптически менее плотной среды фаза отражённой волны не меняется.

4. Относительная интенсивность отражённой волны

5. Относительная интенсивность прошедшей волны

(n1 и n2 – показатели преломления сред)

сред. Задача №1.
Задача. Как изменяется интенсивность света, проходящего через

Решение. Относительная интенсивность волны, отражённой от границы раздела стекла и воздуха

Относительная интенсивность волны, прошедшей в стекло из воздуха

При выходе волны из стекла в воздух снова отражается 0,04 от интенсивности падающей на границу волны, следовательно

сред.
При прохождении второго стекла интенсивность света снова ослабляется:
Окончательно, на

Задание. Решить эту задачу в общем виде. Определить, при прохождении какого наименьшего числа стёкол (пренебрегая поглощением) свет ослабнет более, чем в 2 раза.