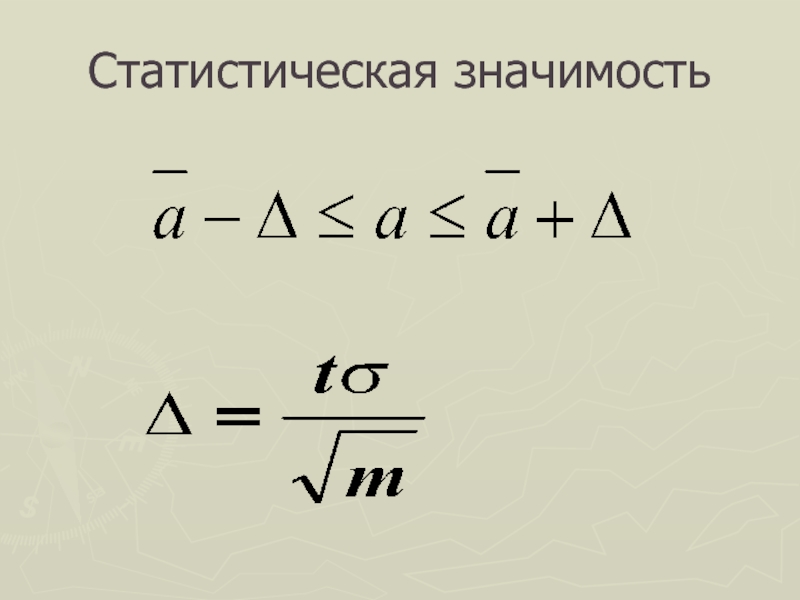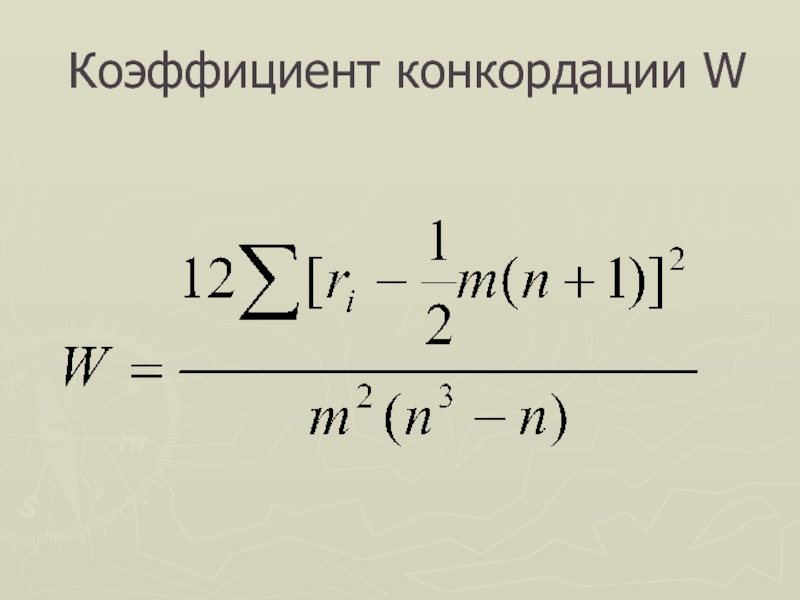Слайд 1Эвристические процедуры в ПР
Слайд 2Проблема объединения математических и неформальных методов анализа
Математика делает
однозначными,
строго обоснованными
любые следствия
из исходных посылок.
Но исходные посылки – аксиомы –
проистекают из гипотез, которые возникают как результат неформального мышления, как обобщение опыта и наблюдений.
Слайд 3Формальные и неформальные
процедуры
не нужно разделять,
рассматривая их как
элементы
целостного единого процесса исследования
Слайд 4 Традиционными процедурами использования коллективного опыта в ПР (выработать общий
подход к проблеме, направление дальнейших исследований и т.д.) являются различные
экспертизы, консилиумы, совещания, круглые столы...
Слайд 5Однако мнение большинства отражает некоторую среднюю точку зрения (референдум, голосование).
Неординарное
решение найти методом опроса нельзя
Слайд 6Анализ проблемы
начинается с построения модели:
- систематизация поступающей информации
- связывание различных
явлений в целостное внутреннее представление
Слайд 7Эвристическая модель
Невозможно указать или сформировать количественные показатели,
измерить их
или строго описать взаимосвязи
между ними
из-за слабой изученности или очень высокой сложности задачи
Слайд 8Эвристический анализ
Определение процедуры проведения Э
Проведение Э и получение оценок
Обработка
оценок
Интерпретация результатов
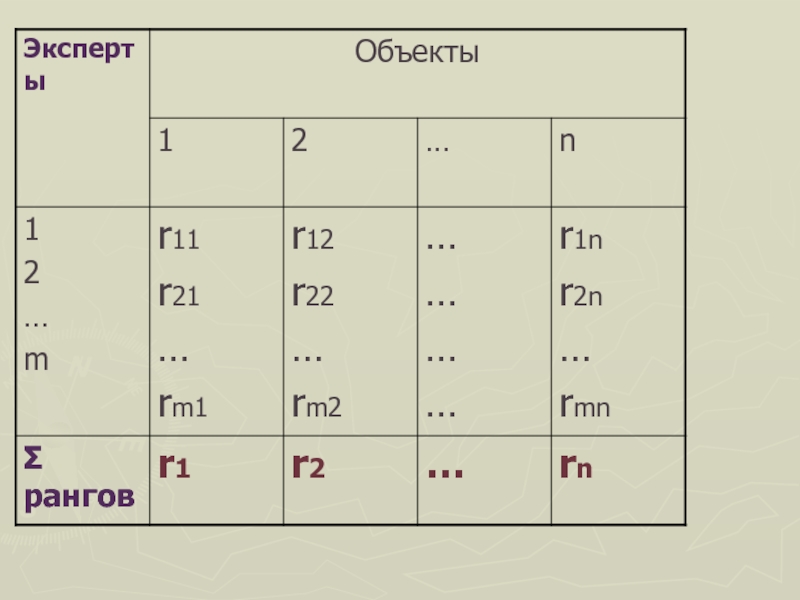
Слайд 9Экспертная информация
присутствует
в матрицах решений,
в оценках альтернатив по критериям,
в коэффициентах
относительной важности критериев,
в оценках последствий,
в выборе стратегий поведения,…
Слайд 10Экспертизы
Простые:
позволяет Э. легко ответить на поставленный
вопрос
Сложные:
с помощью принципа декомпозиции приводятся к простым
Слайд 11Этапы проведения экспертиз
Идентификация объектов Э.
Выбор критерия оценки объектов и
формулирование вопроса, раскрывающего этот критерий Эксперту
Разработка и описание шкалы оценок
Выбор
способа оценивания
Обработка экспертных оценок
Слайд 12Оценивать можно все:
Цели – по важности, ситуации – по вероятности,
факторы – по степени влияния,…
Анализ структуры рынка, конъюнктуры,…
Анализ качества: продукции,
знаний, проектов, решений, …
Оценка последствий применения упаковочных материалов, выпуска продукции …
Конкурсное распределение средств и работ, выделение кредитов, выбор инвестиционных проектов
Выработка политики (внешней, налоговой, строительной и т.д.)
Слайд 13Формулирование вопроса
Эксперт не видит всей подготовки Э
По форме:
открытые – ответ может быть дан в любой
форме
закрытые – в формулировке содержатся
варианты возможных
альтернативных ответов и надо
выбрать один из них
Слайд 14Прямые и косвенные
Косвенные
используются, чтобы замаскировать
цель Э, когда нет уверенности,
что Э. не
заинтересован в объективном освещении проблемы или
что он захочет дать информацию
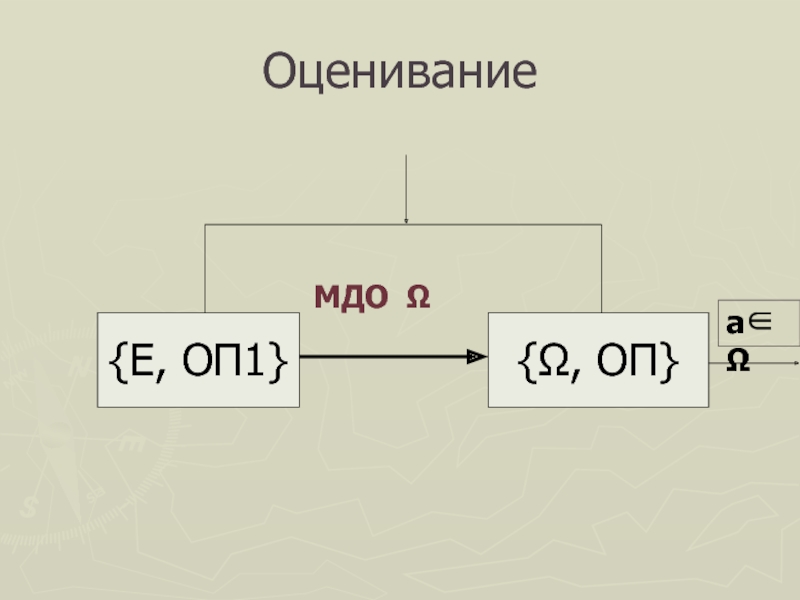
Слайд 15Оценивание
{E, ОП1}
{Ω, ОП}
МДО Ω
a∈Ω
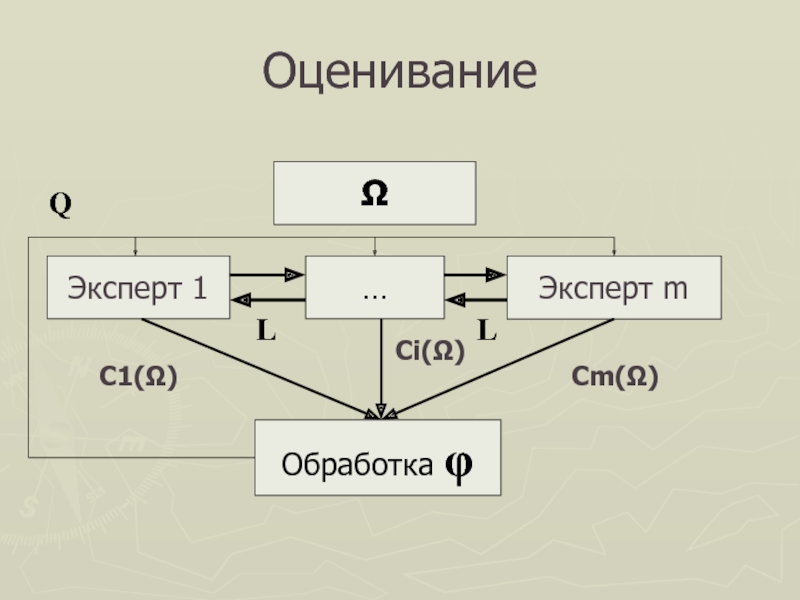
Слайд 16Оценивание
Ω
Эксперт 1
Эксперт m
…
Обработка φ
С1(Ω)
Сi(Ω)
Cm(Ω)
Q
L
L
Слайд 17Взаимодействие между Экспертами L
1) эксперты могут свободно обмениваться информацией
друг с другом;
2) обмен информацией между экспертами регламентирован;
3) эксперты изолированы
друг от друга;
Слайд 18Схема типа круглого стола
Взаимодействие между экспертами не регламентируется
Экспертная
группа собирается для определения общего мнения.
Такая обстановка способствует созданию
творческой атмосферы, так как эксперты будут обогащаться идеями друг друга.
Отрицательные стороны:
повышенные требования к экспертам: умение высказывать мнение, не зависящее от мнения большинства;
способность отказаться от своего мнения, если оно окажется неверным.
Слайд 19Метод мозговой атаки
Регламентация общения экспертов в схеме круглого стола:
в течение определенного промежутка времени любое высказанное мнение не
подлежит обсуждению и не может быть отвергнуто. За это время каждый из экспертов успевает хорошо обдумать высказанное другим мнение, и принятие или отклонение этого мнения имеет в этом случае большую обоснованность.
Слайд 20Эксперты изолированы
Каждый высказывает свое мнение независимо от других
(решает свою задачу выбора).
При этом используют статистические
методы обработки экспертной информации, поскольку оценки отдельных экспертов можно рассматривать как независимые реализации случайной величины
Слайд 21Обратная связь в экспертизе
Каждому Э предъявляют результирующую
оценку, возможно, вместе с другой информацией.
Эксперты уточняют
свои оценки, после чего процедура повторяется снова, до тех пор, пока не будет получена удовлетворяющая исследователя согласованность оценок
Слайд 22Метод Дельфы
Эксперты отвечают на ряд вопросов и свои ответы
аргументируют.
Исследователь изучает ответы Э и определяет их согласованность.
Если
мнения экспертов недостаточно согласованы, то он сообщает каждому из них дополнительные сведения о системе, а также ответы на поставленные вопросы и аргументацию других членов экспертной группы.
С учетом вновь полученной информации эксперты снова отвечают на поставленные вопросы.
Слайд 231 МДО - множество допустимых оценок
Ω
= {0,1}
Соответствующая задача попарного сравнения заключается в
выявлении лучшего из двух имеющихся объектов a и b.
При этом
C(Ω) =
Слайд 242 Ранжирование
Ω={1,2,…,n}
упорядочивание n
объектов по убыванию (возрастанию) значения некоторого признака
МДО экспертов
состоит из перестановок длины n
C(Ω)=,
где ij - номер j - го объекта при упорядочении
Слайд 253 Классификация
Ω={1,…,l}
отнесение заданного элемента x одному из l непересекающихся подмножеств
S1,…,Sl.
C (Ω) = i, если x∈Si
Слайд 264 Числовые оценки
Ω =Em
сопоставление системе
одного или нескольких чисел
С (Ω)=a,
если оценкой системы является
вектор а∈Em
Слайд 27Примеры сложных экспертиз
Метод дерева целей
Метод решающих матриц
Метод
анализа иерархий
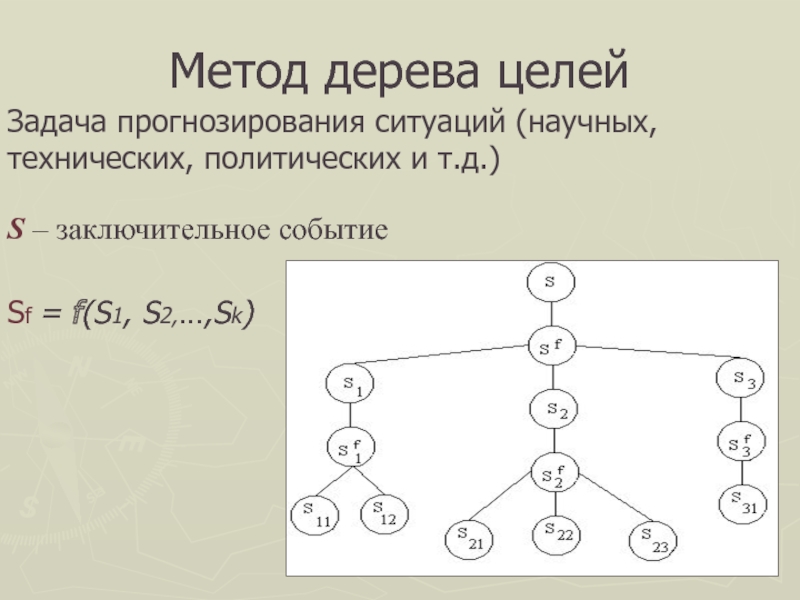
Слайд 28Метод дерева целей
Задача прогнозирования ситуаций (научных, технических, политических и т.д.)
Sf = f(S1, S2,…,Sk)
S – заключительное событие
Слайд 29Метод решающих матриц
Задача распределения ассигнований на фундаментальные
исследования:
как оценить существующее в стране распределение средств
на исследования фундаментального характера и свести к минимуму субъективный элемент.
Интересы общества должны быть представлены в форме некоторого
перечня целей,
который и является отправной точкой всей работы
Слайд 30Перечень научных целей
- это вектор
с компонентами
Слайд 31Разделение исследовательских работ
опытно-конструкторские разработки
прикладные и
фундаментальные исследования
Слайд 32Перечень опытно-конструкторских разработок
Задача - построение матрицы значимости
опытно-конструкторских работ
- вес опытно-конструкторской разработки
Слайд 33
отображение множества
научно-технических целей
на множество
опытно-конструкторских разработок
Слайд 34Перечень исследований прикладного характера
- матрица значимости прикладных
исследований для обеспечения
опытно-конструкторских разработок
γ
Слайд 35Направления фундаментальных исследований
- отображение множества
прикладных исследований на множество фундаментальных исследований,
Слайд 36Методы обработки экспертной информации
Статистические методы:
отклонение оценок экспертов от истинных происходит в силу случайных
причин;
задача в том, чтобы восстановить это истинное значение с наименьшей погрешностью
Алгебраические методы:
на множестве допустимых оценок Ω задается расстояние, и результирующая оценка определяется как оценка, сумма расстояний от которой до оценок экспертов минимальна
Слайд 37Статистические методы
Статистические методы позволяют определить согласованность мнений экспертов, значимость полученных
оценок и т.д.
Степень согласованности указывает на качество результирующей оценки.
Методы получения результирующих оценок различаются в зависимости от решаемой задачи оценивания.
Слайд 38Числовые оценки
Э1: Ω=E1;
L - эксперты изолированы;
Q -
обратная связь отсутствует;
Слайд 39Числовые оценки
Степенью согласованности мнений экспертов в экспертизе Э1
служит дисперсия:
Слайд 41Ранжирование
Задача состоит в сопоставлении оцениваемой системе одной перестановки
Э2:
Ω
- множество всех перестановок;
L – эксперты изолированы;
Q – обратная
связь отсутствует.
Слайд 44Задача попарного сравнения
А = (aij) – множество всех матриц, где
aij
∈ {0,1},
aij + aji = 1 (i≠j),
aii =
0 (i =1,n)
Слайд 45Алгебраический метод
Задача состоит в сопоставлении системе нестрогой ранжировки
Для ее решения используется экспертиза Э3:
Ω - множество всех
нестрогих ранжировок n объектов;
L – эксперты изолированы;
Q – обратная связь отсутствует
Слайд 47Матрица А
А = (aij), в которых
aij =
1 тогда и только тогда, когда i-ый объект предшествует j-му;
если объекты i и j равноценны, то aij = 0; кроме того,
aii = 0 (i=1,n);
aij = 1 => aji = -1.
Слайд 48Расстояние d между ранжировками
1) d(A,B) ≥ 0, причем d(A,B)
= 0 тогда и только тогда, когда A=B.
2) d(A,B) =
d(B,A).
3) d(A,B)+d(B,C) ≥ d(A,C), причем равенство достигается тогда и только тогда, когда В находится между А и С.
6) Минимальное положительное расстояние между ранжировками равно единице.
Слайд 50Пример
А = , B = , C = .
d(A,B)
= 0, d(A,C) = d (B,C) = 2.
А0=А и А0=В