Слайд 1Факультет прикладной информатики
Финансовые вычисления по сложным процентам
1. Сущность и формула
сложных процентов.
2. Соотношение роста по простым и сложным процентам.
3.
Начисление сложных процентов несколько раз в году.
4. Наращение по сложным процентам при дробном количестве периодов начисления.
5. Определение срока, формулы удвоения и правила приближенного счета.
Слайд 2
1. Сущность и формула наращения сложных
процентов.
В средне- и
долгосрочных финансово-кредитных операциях, если проценты не выплачиваются, а присоединяются к
сумме долга, для наращения применяют, сложные проценты.
База для начисления сложных процентов (в отличие от простых) не остается постоянной — она увеличивается с каждым шагом во времени, и процесс роста первоначальной суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простой процент на один период начисления.
Факультет прикладной информатики
Слайд 3 Найдём формулу для расчета наращенной суммы при условии, что проценты
начисляются и капитализируются один раз в году, т. е. применяется
сложная годовая ставка наращения. Очевидно, что в конце первого года проценты равны величине Pi, а наращенная сумма составит:
S1 =P (1+i),
К концу второго года составит:
S2 =S1 (1+i)=P (1+i)(1+i)=P (1+i)2
S3 =S2 (1+i)=P (1+i)2(1+i)=P (1+i)3 и т.д.
В конце n-го года наращенная сумма будет равна:
S=P (1+i)n ,
где: P – первоначальная сумма долга,
S – наращенная сумма,
n – срок, число лет наращения,
i – ставка наращения по сложным процентам,
Величину 1+i называют сложным декурсивным коэффициентом.
Величину q=(1+i)n называют множителем наращения по сложным процентам – он показывает конечную стоимость одной денежной единицы, вложенной под сложные проценты декурсивно. Значения этого множителя для различных значений i и целых чисел n приводятся в таблицах сложных процентов.
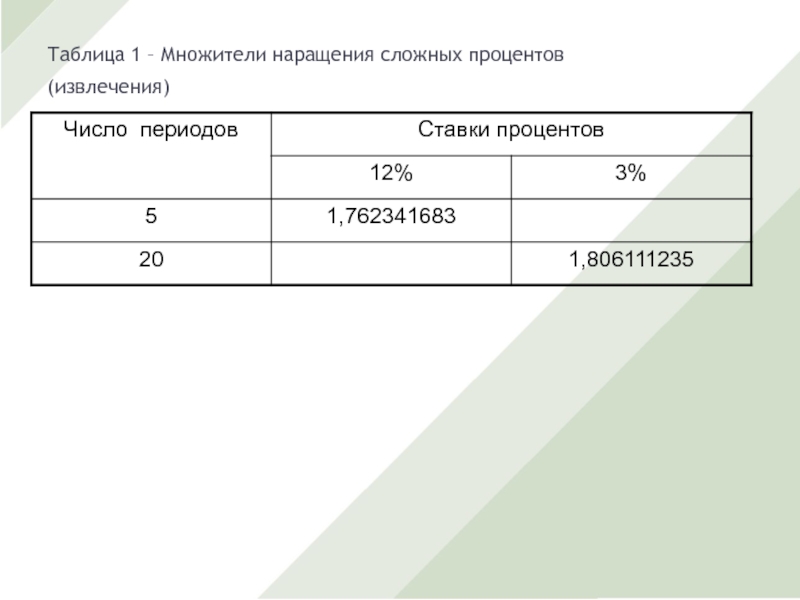
Слайд 4Таблица 1 – Множители наращения сложных процентов
(извлечения)
Слайд 5 Точность расчета множителя в практических вычислениях определяется допустимой степенью округления
наращенной суммы (до последней копейки, рубля, тысячи и т.д.), как правило,
до последней денежной единицы (обычно в таблицах – шесть знаков после запятой).
Пример:
Какой величины достигнет долг, равный 1 млн. руб. через пять лет при росте по сложной ставке 12% годовых (проценты капитализируются 1 раз в год).
S=1000000(1+0,12)5=1 000 0001,762341683=1 762 341,68 руб.
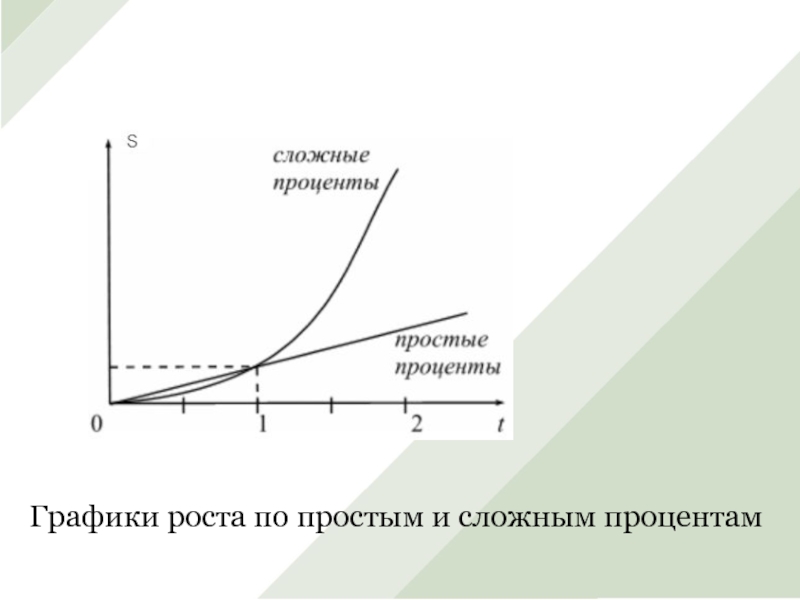
Слайд 62. Соотношение роста по простым и сложным годовым процентам.
Чтобы сопоставить результаты
наращения по разным процентным ставкам, достаточно сравнить соответствующие множители наращения.
Соотношение множителей наращения по простым и сложным годовым ставкам процентов при одинаковой абсолютной величине ставок зависит от срока ссуды:
- для срока меньше года (n<1):
(1+n i)>(1+i)n,
- для срока больше года (n>1):
(1+n i)<(1+i)n,
-для срока равного году (n=1):
(1+ni)=(1+i)n, если временная база 365(366) дней.
(1+ni)<(1+i)n если временная база 360 дней.
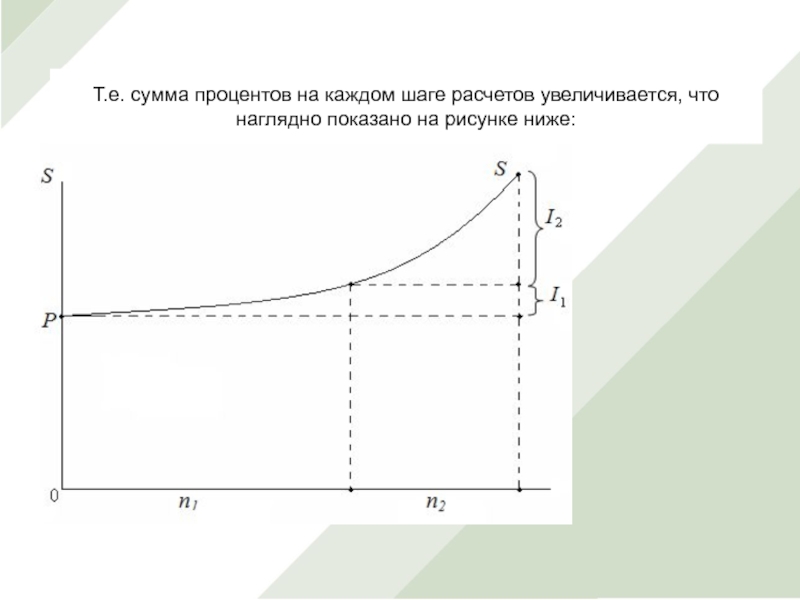
Слайд 8Т.е. сумма процентов на каждом шаге расчетов увеличивается, что наглядно
показано на рисунке ниже:
Слайд 9Графики роста по простым и сложным процентам
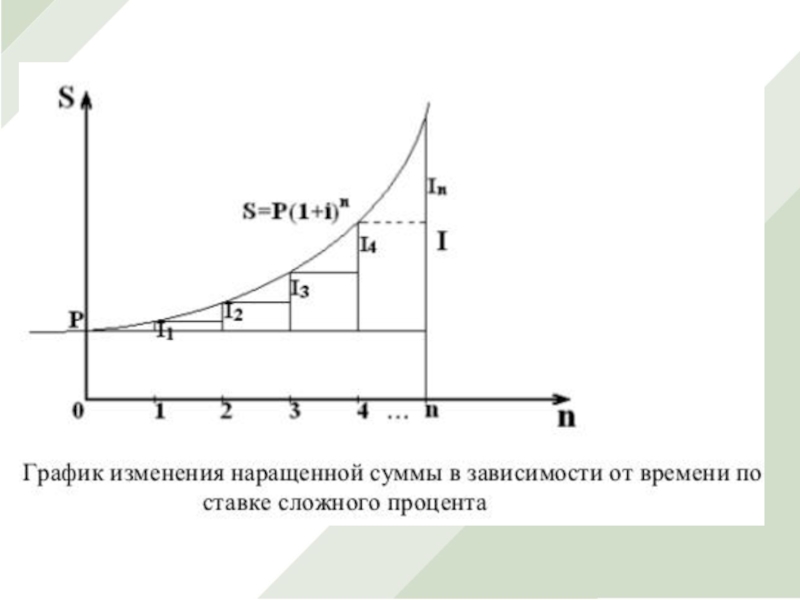
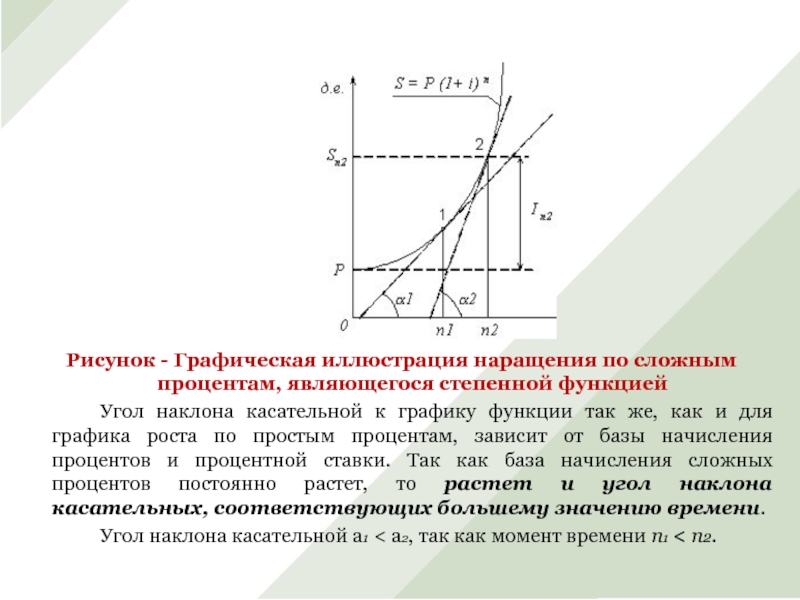
Слайд 11Рисунок - Графическая иллюстрация наращения по сложным процентам, являющегося степенной
функцией
Угол наклона касательной к графику функции так же, как и
для графика роста по простым процентам, зависит от базы начисления процентов и процентной ставки. Так как база начисления сложных процентов постоянно растет, то растет и угол наклона касательных, соответствующих большему значению времени.
Угол наклона касательной a1 < a2, так как момент времени n1 < n2.
Слайд 12Влияние уровня процентной ставки на результат наращения
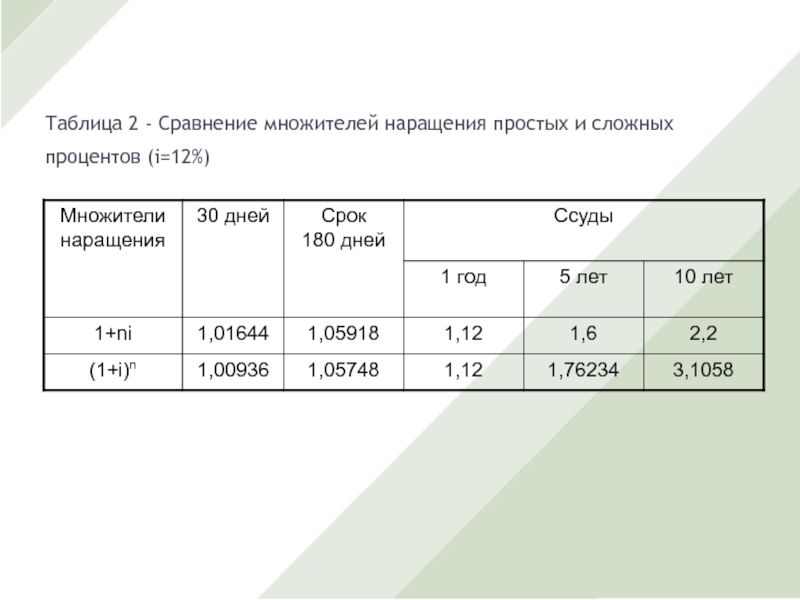
Слайд 13Таблица 2 - Сравнение множителей наращения простых и сложных процентов
(i=12%)
Слайд 14
3. Начисление сложных процентов несколько раз в году.
В современных
условиях проценты капитализируются обычно не один, а несколько раз в
году – по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневное начисление процентов.
Формула S=P(1+i)n получена для годовой процентной ставки и срока, измеряемого в годах. Однако, её можно применить и при других периодах начисления.
В этих случаях:
i - ставка за период начисления,
n - число таких периодов.
Если i-ставка за полугодие, то n-число полугодий,
Если i-ставка за квартал, то n-число кварталов и т.д.
Слайд 15Пример:
Какой величины достигнет долг, равный 1 млн. руб. через пять лет
при росте по сложной ставке 12% годовых (проценты капитализируются ежеквартально).
S=P(1+i)n,
где
i- ставка наращения за квартал,
n- число кварталов.
i=12:4=3%, т. е.0,03
n=54кв.=20 кварталов
S=1000000(1+0.03)20=10000001,806111235=1806111,24 руб.
Слайд 16 На практике, как правило, в контрактах фиксируется не ставка за
период, а годовая ставка, и одновременно указывается период начисления процентов,
как в предыдущем примере «12% годовых с поквартальным начислением процентов».
Пусть годовая ставка равна j, а число периодов начисления в году равно m.
Таким образом, каждый раз проценты начисляются по ставке j/m. Ставку j называют номинальной.
Формула наращения примет вид:
S=P (1+j/m)m·n,
где m – число периодов начисления в году,
j – номинальная годовая ставка процента,
Слайд 17Графики роста денежных сумм, вложенных под 6 % годовых
простые проценты
сложные
проценты с ежегодной капитализацией
сложные проценты с полугодовой капитализацией
сложные проценты с
ежеквартальной капитализацией
сложные проценты с ежемесячной капитализацией
Слайд 18Счеты А.П. Пелёнкина
В 1891 г. общественный деятель и автор книг
по бухгалтерскому учету Андрей Платонович Пелёнкин выпустил книгу «Новый прибор
«счеты сложных процентов», а через два года еще одну, «Применение «счетов сложных процентов» к определению логарифмов чисел и чисел по их логарифмам», на ту же тему.
Андрей Платонович Пелёнкин, черноморский казак, уроженец Азовского уезда, окончив Артиллерийскую Михайловскую академию работал техником на Сестрорецком заводе, позже "был призван к сооружению на Васильевском острове казенного патронного завода". После отставки поступил на службу в Дворянский банк, а позже "на Государственную службу по министерству финансов на должность фабричного инспектора в Петербурге". Опубликовал работы о закалке стали, а также книгу "Рациональная теория бухгалтерских счетов», состоя в отставке напечатал 2 работы: о неверности 2-го закона Киргофа и о вычислении сложных процентов и срочных уплат. Умер в 1907 г. Источник: histpol.pl.ua›pages/content.php…
Слайд 19
Пеленкин, Андрей Платонович , черноморский казак, уроженец Азовского уезда. Окончив
унтер-офицерский специальный класс Петровского Полтавского кадетского корпуса перешел в 3
специальный класс Михайловского артиллерийского училища [Константиновского военного училища], по окончании которого прямо перешел в Михайловскую артиллерийскую академию и окончил техническое ее отделение по 1 разряду. По окончании академии поступил на службу техником на Сестрорецкий оружейный завод, где показал себя талантливым и трудолюбивым работником. В это время напечатал в оружейном сборнике первые свои труды о закалке стали и о производительности работы новых автоматических станков при выделке ручного оружия. Через 2 года службы своей на Сестрорецком оружейном заводе, Андрей Платонович, как талантливый артиллерист, был призван к сооружению на Васильевском острове казенного патронного завода, который настолько хорошо устроил и организовал там все работы, что на этот завод были командированы из Франции молодые артиллеристы, для обучения патронному делу.
К этому времени относится напечатанная его работа — о цельнотянутых латунных патронных гильзах.

Слайд 20 В начале 70-х годов, по прискорбным причинам, Андрей Платонович вынужден
был оставить военную службу и несколько времени жил в Перми
и Варшаве, а затем, в конце 70-х годов, вновь возвратился в Петербург и поступил на службу в Дворянский банк, откуда вскоре вышел в отставку.
Состоя в отставке Андрей Платонович напечатал 2 работы: о неверности 2-го закона Киргофа и о вычислении сложных процентов и срочных уплат.
В 80-х годах Андрей Платонович снова поступил на Государственную службу по министерству финансов на должность фабричного инспектора в Петербурге, в каковой и оставался до самой смерти.
Во время службы фабричным инспектором он напечатал несколько статей по поводу расчетов страховых обществ с клиентами. Благодаря своим выдающимся способностям и наблюдательности, Андрей Платонович быстро ориентировался в каждом техническом вопросе и, анализируя условия его, находил те практические пути и приемы, которые всегда приводили его к верному успеху.
Его прямая и честная натура не терпела никаких сделок с совестью; единственным путем для приобретения средств к жизни неизменно служил ему честный труд, которому всецело преданный, Андрей Платонович оставался верным до гробовой доски.

Слайд 21 4. Наращение по сложным процентам при дробном количестве периодов начисления.
Для
случаев, когда n не является целым числом, множитель наращения определяется
двумя способами:
1. на основе общего метода:
(1+i)n=(1+i) na (1+i) nb (3)
2. на основе смешанного (комбинированного) метода:
(1+i)n=(1+i) na (1+nbi), (4)
т. е. за целое количество периодов начисления – по сложной ставке, за дробную часть – по простой процентной ставке.
Где n=na+nb
na- целое число периодов,
nb- дробная часть периода.
Слайд 22При выборе метода расчета множителя наращения следует иметь в виду,
что величина множителя наращения по второму способу больше, чем по
первому: (1+i) na (1+nbi (1+i) na (1+i) nb
В практике некоторых финансовых организаций предусматривается начисление процентов только за целые периоды начисления.
Пример:
Кредит в размере 30 тыс. руб. выдан на срок 3 года и 160 дней под 6,5% годовых, проценты начисляются 1 раз в год.
Если предусмотрен смешанный метод начисления процентов
S = 30000(1 + 0,065)3 (1 + 160:3650,065) = 37271,04 руб.
Если проценты начисляются только за целые периоды начисления, то
S=300001,0653=36234,49
Слайд 23 Общий метод, несмотря на свою формальную правомерность с математических позиций,
с точки зрения сущности начисления процентов является приблизительным. Погрешность вычислений
будет тем больше, чем больше значения входящих в формулу величин. Этот метод дает меньший, чем в действительности результат.
При внимательном рассмотрении можно увидеть, что на практике обычно используется смешанный метод, поскольку капитализация процентов до истечения срока реинвестирования производиться не может. Тем не менее, даже в солидных изданиях можно встретить изложение и того, и другого методов. Здесь уместно вспомнить слова великого Эйнштейна: «Математика – единственный совершенный метод, позволяющий провести самого себя за нос».
Слайд 245. Определение срока, формулы удвоения и правила приближенного счета («правило
69», «правило 70», «правило 71», «правило 72», )
Альберт Эйнштейн назвал
исчисление сложного процента роста доходов «величайшим математическим открытием в истории человечества».
Как определить, когда ваши деньги вырастут в 2 раза?
ПРАВИЛО 72.
Чтобы определить, за какое время количество ваших денег удвоится, можно воспользоваться так называемым «правилом 72». Просто разделите число 72 на процентную ставку. Например, если вы вложили деньги под 8% годовых, разделив 72 на восемь, вы получите число девять. Это значит, что вам понадобится девять лет, чтобы удвоить свой вклад при годовой ставке в 8%.
Кто-то подсчитал, что один доллар, вложенный под 3 % во времена Христа, сейчас стоил бы половину всех имеющихся в мире денег.
24 доллара, выплаченные голландцами местным индейцам за остров Манхэттен, если бы их положили в то время под 5 % годовых, сегодня стоили бы более 2,2 миллиарда долларов.
Слайд 25 Правило семидесяти (правило 70), правило 72, правило 69 — простой способ
(приближённой) оценки срока, в течение которого величина вырастет вдвое при
постоянном росте на некоторый процент.
Согласно «правилу семидесяти»
где — годовая ставка инфляции,
— срок (в годах) удвоения цен.
Слайд 26Из формулы наращения по сложным процентам
S=P (1+i)n выразим
срок n.
Разделим обе части уравнения на P:
S/P = (1+i)n
.
Пролагорифмируем обе части уравнения, получим:
n=log1+i (S/P).
При использовании натуральных логарифмов получим:
ln (S/P) = n ln(1+i)
n = ln (S/P) / ln(1+i)
При малых значениях i значение
ln(1+i) ≈ i
Поэтому n ≈ ln (S/P):i
При S/P = 2 имеем ln ≈ 0,7 (0,693147), поэтому
n ≈ 70:i
Слайд 27«Правило семидесяти» является аппроксимацией посредством гиперболы точной формулы
Поэтому наиболее
точным при использовании малых процентов среди целых чисел является числитель
69. Вместо 70 % также используются числа от 69 % до 72 %. Таким образом, упоминаются «правило 69», «правило 70», «правило 71», «правило 72».
Две кривые, задаваемые этими функциями, достаточно хорошо совпадают (см. рисунок).
Слайд 28 Множитель 72 имеет большое количество делителей, соответствующих малым процентам (1,
2, 3, 4, 6, 8, 9, 12) и потому более
удобен для использования в качестве делимого по сравнению с более точным значением 69 и более лёгким для запоминания значением 70. По этой причине правило используется как в виде «Правило 70», так и «Правило 72» (но и также «Правило 69»).
Первое упоминание о правиле содержится у Луки Пачоли в его математическом труде "Сумма арифметики, геометрии, дробей, пропорций и пропорциональности» (1494 г.). Пачоли не приводит расчёт и не объясняет данное правило, что позволяет сделать вывод о том, что оно было известно и ранее.
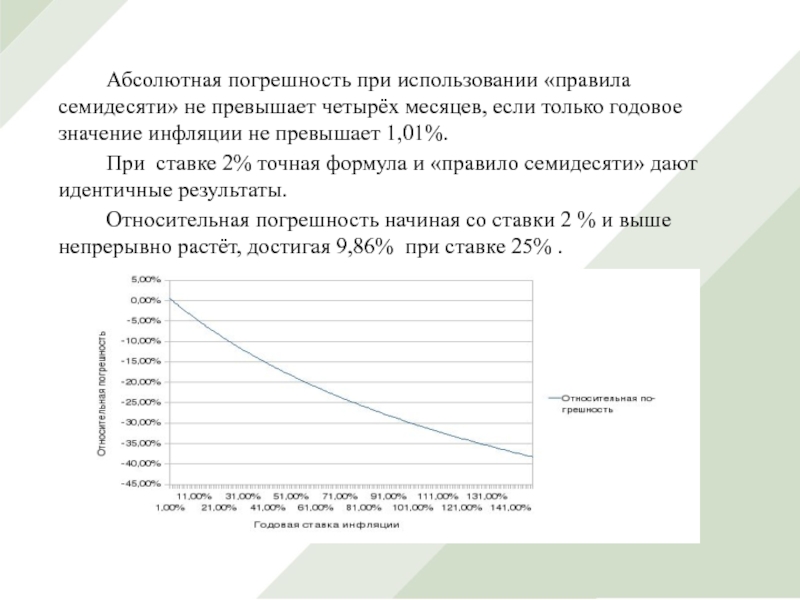
Слайд 29 Абсолютная погрешность при использовании «правила семидесяти» не превышает четырёх месяцев,
если только годовое значение инфляции не превышает 1,01%.
При ставке 2%
точная формула и «правило семидесяти» дают идентичные результаты.
Относительная погрешность начиная со ставки 2 % и выше непрерывно растёт, достигая 9,86% при ставке 25% .
Слайд 30Правило семидесяти может использоваться не только для оценки инфляции, но
также для любых других процессов.
Примеры использования :
Оценка срока, в течение
которого цены упадут вдвое в результате дефляции, если за год они падают на определенное значение процентов.
Оценка срока, в течение которого ВВП удвоится при заданном темпе экономического роста.
Оценка срока, в течение которого удвоится вклад в банке при заданной процентной ставке.
Закон радиоактивного распада: за тысячелетие количество радиоактивного материала в слитке падает на определенное значение процентов. Через какое время количество радиоактивного материала сократится вдвое?
Срок при этом не обязательно исчисляется в годах; нужно только, чтобы коэффициент говорил об изменении величины за ту же единицу времени, в каких измеряется период удвоения .
Кроме того, величина может уменьшаться на за единицу времени. Тогда, конечно, оценивается срок не удвоения величины, а уменьшения её вдвое.
Слайд 31Юридический факультет
Факультет прикладной информатики
Кафедра экономической кибернетики
Бурда Алексей Григорьевич
Спасибо за
внимание