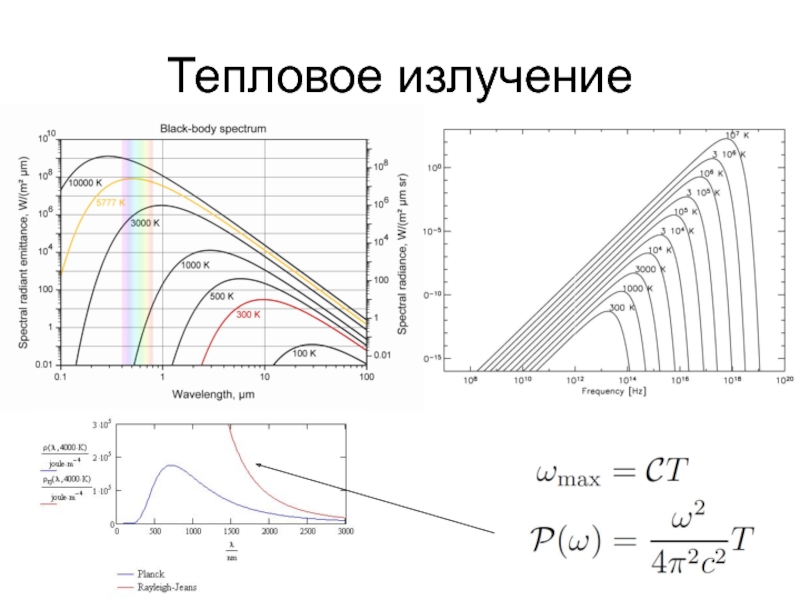
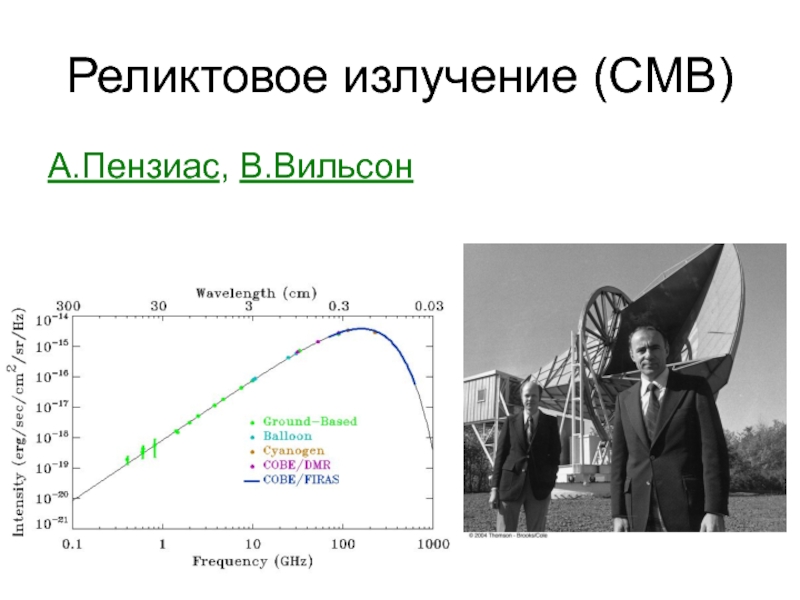
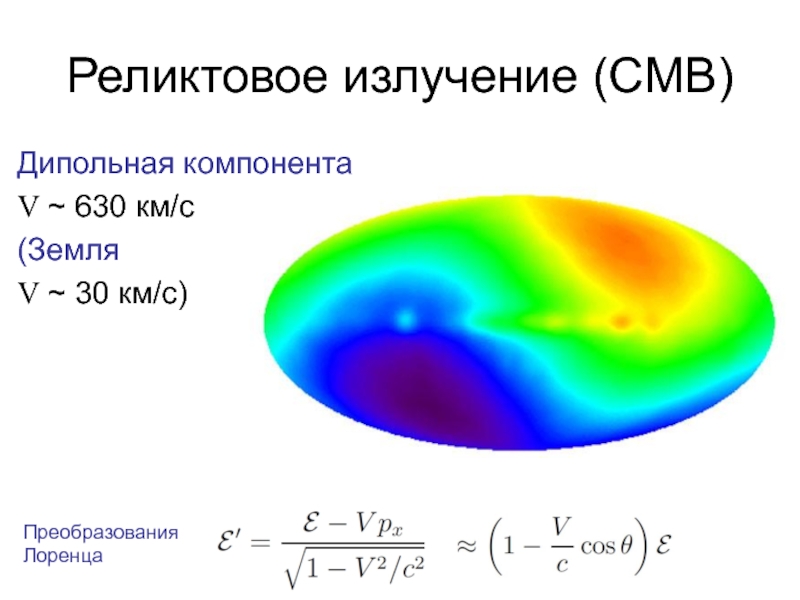
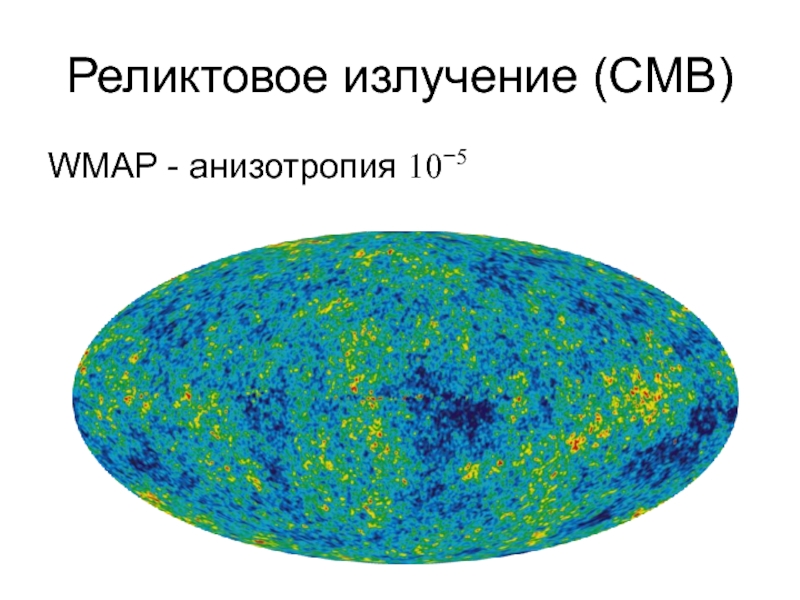
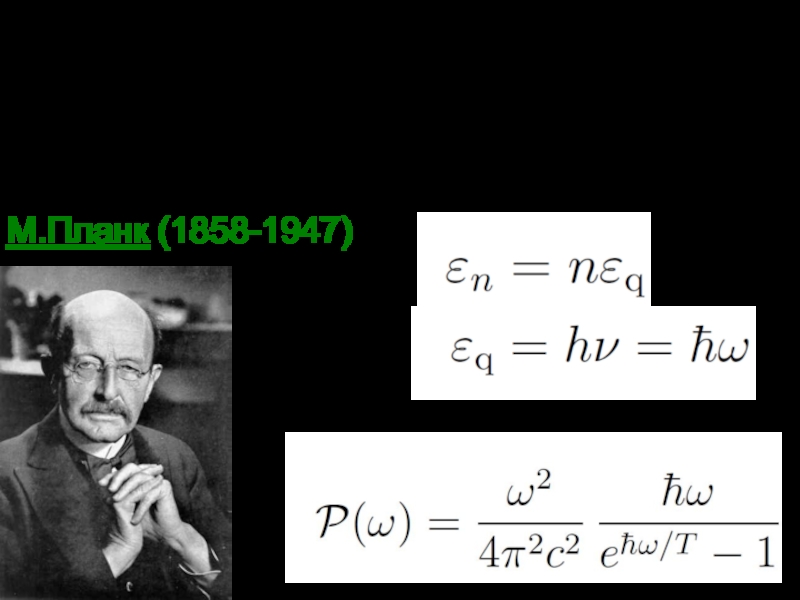Квазары, реликтовое излучение, мазерные источники, радиопульсары (НЗ)
1970
Рентгеновские пульсары, источники гамма-всплесков, PSR1913+161980
Сверхновая 1987а, COBE, гравитационные линзы, нейтринная астрофизика
1990
Микролинзирование, ускоренное разбегание галактик
2000
Гравитационные антенны
2010