Форму Бинома Ньютона

Содержание

1. Форму Бинома Ньютона
2. Формула Бинома Ньютона нужна, чтобы считать квадраты
3. Это – знак суммы. Это кажется
4. Пример, где используется знак суммы для пониманияy
5. Это знак, обозначающий количество сочетаний из нижнего
6. Например, эта формула используется в случае, когда
7. Теперь мы разобрали всё до сегодняшнего дня
8. С подробным доказательством формулы Бинома Ньютона вы
9. Скачать презентанцию

Формула Бинома Ньютона нужна, чтобы считать квадраты суммы следующего вида(a+b)^2 = aa + 2ab + bb(a+b)^3 = aaa + 3aab + 3abb + bbbНо чаще для куда более сложных случаев, например

Слайды и текст этой презентации

Слайд 1Форму Бинома Ньютона

Слайд 2Формула Бинома Ньютона нужна, чтобы
считать квадраты суммы следующего вида
(a+b)^2

= aa + 2ab + bb

(a+b)^3 = aaa + 3aab

+ 3abb + bbb

Но чаще для куда более сложных случаев, например с 6 степенью

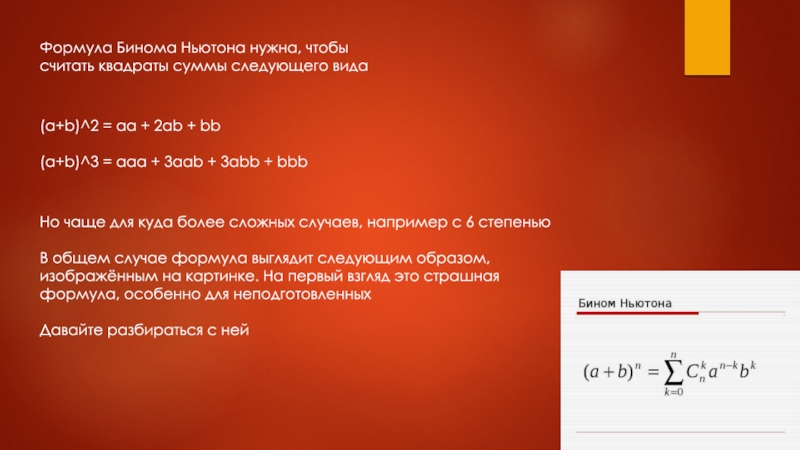
В общем случае формула выглядит следующим образом,
изображённым на картинке. На первый взгляд это страшная
формула, особенно для неподготовленных

Давайте разбираться с ней

Формула Бинома Ньютона нужна, чтобы считать квадраты суммы следующего вида(a+b)^2 = aa + 2ab + bb(a+b)^3 =

Слайд 3 Это – знак суммы. Это кажется сложным, но на

самом деле очень легко.
Его используют для краткой записи выражения.

Внизу знака суммы пишется число начиная с которого ведётся суммирование.
В нашем случае это 0

Вверху знака суммы пишется число, до которого включительно ведётся суммирование.
В нашем случае это n

Читается в данном случае « сумма от нуля до n ».

Это – знак суммы. Это кажется сложным, но на самом деле очень легко. Его используют для

Слайд 4Пример, где используется знак суммы для понимания

y – это сумма

таких икс, индекс которых от 1 до n

В случае с

формулой Бинома Ньютона мы будем
складывать целые выражения, где используется k

Пример, где используется знак суммы для пониманияy – это сумма таких икс, индекс которых от 1 до

Слайд 5Это знак, обозначающий количество сочетаний из нижнего числа (в нашем

случае n)
по верхнему числу (в нашем случае k)

Считается число

сочетаний по следующей формуле

Это знак, обозначающий количество сочетаний из нижнего числа (в нашем случае n)по верхнему числу (в нашем случае

Слайд 6Например, эта формула используется в случае, когда нам нужно сосчитать
количество

не упорядоченных вариаций элементов из набора, включающего
в себя 3 элемента

Например

из набора ЖЕЛТЫЙ СИНИЙ ЗЕЛЕНЫЙ

Можно выбрать такие наборы, включающие 2 элемента

ЖЕЛТЫЙ СИНИЙ
ЖЕЛТЫЙ ЗЕЛЕНЫЙ
СИНИЙ ЗЕЛЕНЫЙ

Таких наборов существует 3, и действительно: 3!/2!(3-2)! = 6/2 = 3

Например, эта формула используется в случае, когда нам нужно сосчитатьколичество не упорядоченных вариаций элементов из набора, включающегов

Слайд 7Теперь мы разобрали всё до сегодняшнего дня незнакомое
Вот пример использования

данной формулы для n, равного 1

Слайд 8С подробным доказательством формулы Бинома Ньютона вы можете
ознакомиться в

видео по ссылке https://youtu.be/24J8nXGGl5s

Если вы не понимаете что-то из данной

презентации или видео, вы всегда можете
задать свой вопрос в сообщения группы

https://vk.com/mathhubb
Мы всегда вам рады, наша цель помочь студентам технических вузов

С подробным доказательством формулы Бинома Ньютона вы можете ознакомиться в видео по ссылке https://youtu.be/24J8nXGGl5sЕсли вы не понимаете

Скачать презентацию

Разделы презентаций

Форму Бинома Ньютона

Содержание

Слайды и текст этой презентации

Слайд 1Форму Бинома Ньютона

Слайд 2Формула Бинома Ньютона нужна, чтобы
считать квадраты суммы следующего вида
(a+b)^2

= aa + 2ab + bb

(a+b)^3 = aaa + 3aab

Слайд 3 Это – знак суммы. Это кажется сложным, но на

самом деле очень легко.
Его используют для краткой записи выражения.

Слайд 4Пример, где используется знак суммы для понимания

y – это сумма

таких икс, индекс которых от 1 до n

В случае с

Слайд 5Это знак, обозначающий количество сочетаний из нижнего числа (в нашем

случае n)
по верхнему числу (в нашем случае k)

Считается число

Слайд 6Например, эта формула используется в случае, когда нам нужно сосчитать
количество

не упорядоченных вариаций элементов из набора, включающего
в себя 3 элемента

Например

Слайд 7Теперь мы разобрали всё до сегодняшнего дня незнакомое
Вот пример использования

данной формулы для n, равного 1

Слайд 8С подробным доказательством формулы Бинома Ньютона вы можете
ознакомиться в

видео по ссылке https://youtu.be/24J8nXGGl5s

Если вы не понимаете что-то из данной

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Форму Бинома Ньютона

Содержание

Слайды и текст этой презентации

Слайд 1Форму Бинома Ньютона

Слайд 2Формула Бинома Ньютона нужна, чтобы считать квадраты суммы следующего вида(a+b)^2

= aa + 2ab + bb(a+b)^3 = aaa + 3aab

Слайд 3 Это – знак суммы. Это кажется сложным, но на

самом деле очень легко. Его используют для краткой записи выражения.

Слайд 4Пример, где используется знак суммы для пониманияy – это сумма

таких икс, индекс которых от 1 до nВ случае с

Слайд 5Это знак, обозначающий количество сочетаний из нижнего числа (в нашем

случае n)по верхнему числу (в нашем случае k) Считается число

Слайд 6Например, эта формула используется в случае, когда нам нужно сосчитатьколичество

не упорядоченных вариаций элементов из набора, включающегов себя 3 элементаНапример

Слайд 7Теперь мы разобрали всё до сегодняшнего дня незнакомоеВот пример использования

данной формулы для n, равного 1

Слайд 8С подробным доказательством формулы Бинома Ньютона вы можете ознакомиться в

видео по ссылке https://youtu.be/24J8nXGGl5sЕсли вы не понимаете что-то из данной

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 2Формула Бинома Ньютона нужна, чтобы
считать квадраты суммы следующего вида
(a+b)^2

= aa + 2ab + bb

(a+b)^3 = aaa + 3aab

самом деле очень легко.
Его используют для краткой записи выражения.

Слайд 4Пример, где используется знак суммы для понимания

y – это сумма

таких икс, индекс которых от 1 до n

В случае с

случае n)
по верхнему числу (в нашем случае k)

Считается число

Слайд 6Например, эта формула используется в случае, когда нам нужно сосчитать
количество

не упорядоченных вариаций элементов из набора, включающего
в себя 3 элемента

Например

Слайд 7Теперь мы разобрали всё до сегодняшнего дня незнакомое
Вот пример использования

Слайд 8С подробным доказательством формулы Бинома Ньютона вы можете
ознакомиться в

видео по ссылке https://youtu.be/24J8nXGGl5s

Если вы не понимаете что-то из данной