Фотоэффект Фотоэффект – это испускание электронов веществом под действием

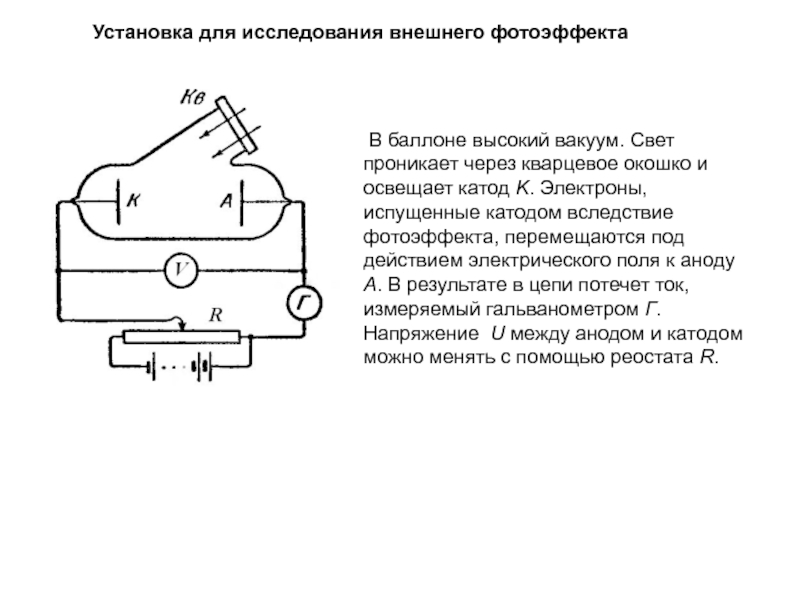
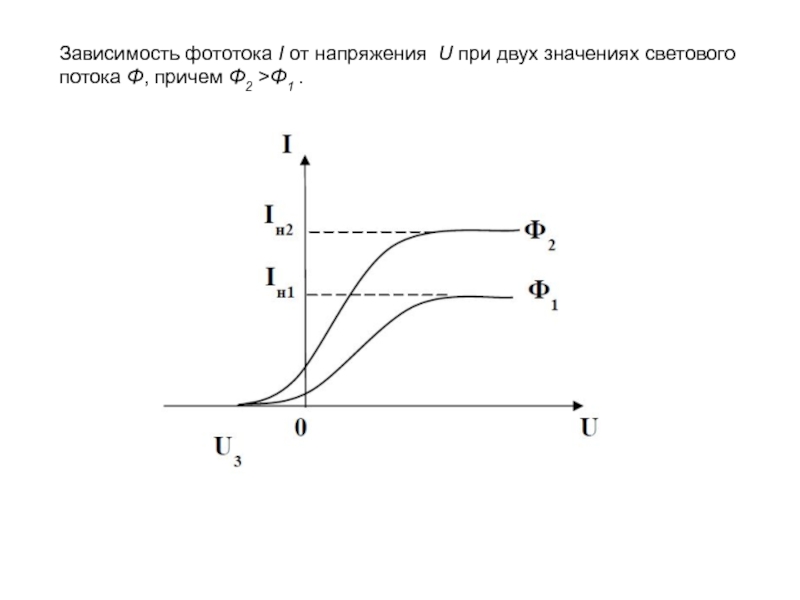
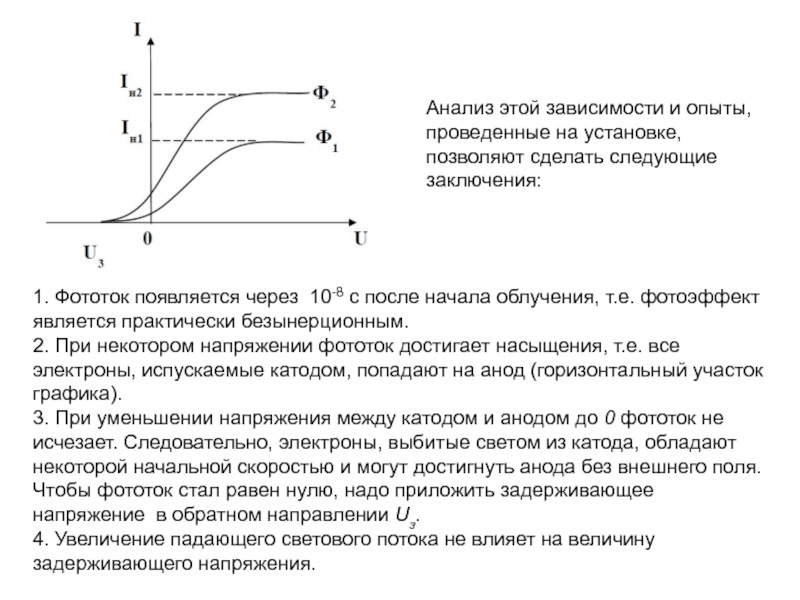
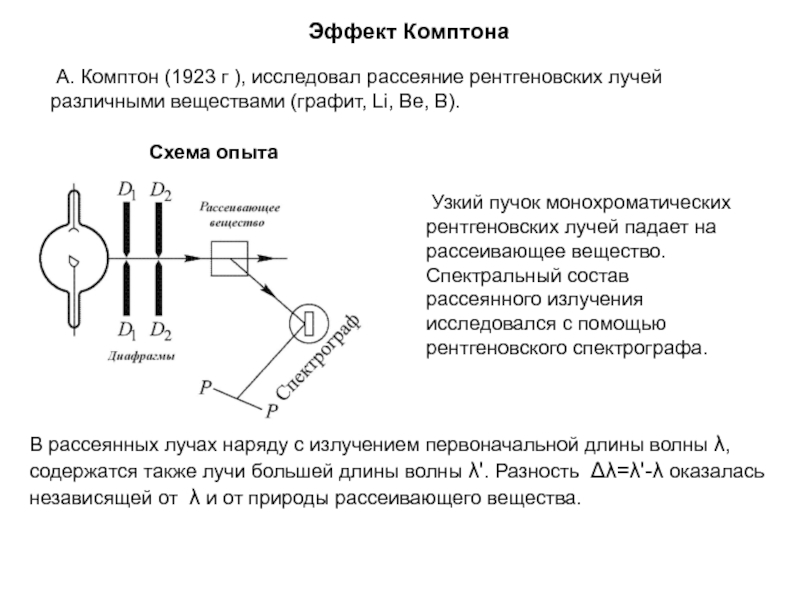
излучения (фотонов).
Фотоэффект был открыт Генрихом Герцем в 1887 году

Различают: внешний фотоэффект, при котором поглощение фотонов сопровождается вылетом электронов за пределы тела, и внутренний фотоэффект, при котором электроны, оставаясь в теле, перераспределяются по энергетическим уровням.

Внутренний фотоэффект проявляется в изменении электропроводности, диэлектрической проницаемости вещества или в возникновении на его границах электродвижущей силы, называемой фото ЭДС.

проникает через кварцевое окошко и освещает катод K. Электроны, испущенные

катодом вследствие фотоэффекта, перемещаются под действием электрического поля к аноду A. В результате в цепи потечет ток, измеряемый гальванометром Г. Напряжение U между анодом и катодом можно менять с помощью реостата R.

потока , причем 2 >1 .

следующие заключения:
1. Фототок появляется через 10-8 c после начала облучения,

т.е. фотоэффект является практически безынерционным.
2. При некотором напряжении фототок достигает насыщения, т.е. все электроны, испускаемые катодом, попадают на анод (горизонтальный участок графика).
3. При уменьшении напряжения между катодом и анодом до 0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью и могут достигнуть анода без внешнего поля. Чтобы фототок стал равен нулю, надо приложить задерживающее напряжение в обратном направлении Uз.
4. Увеличение падающего светового потока не влияет на величину задерживающего напряжения.

(1888-1889 гг.): при фиксированной частоте падающего света величина фототока насыщения

прямо пропорциональна падающему световому потоку.

2. Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности.

3. Для каждого вещества существует минимальная частота света, при которой ещё возможен внешний фотоэффект. Эта минимальная частота 0 (или максимальная длина волны 0) зависит от химической природы вещества, состояния его поверхности и называется красной границей фотоэффекта.

Второй и третий законы фотоэффекта находятся в противоречии с представлением классической физики о волновой природе света. Действительно, чем больше световой поток, тем больше энергия, переносимая световой волной, т.е. тем большую энергию должны были получать фотоэлектроны.

закономерности фотоэффекта объясняются, если предположить, что свет не только испускается,

но и поглощается порциями (квантами).

Согласно Эйнштейну, энергия фотона , полученная электроном, поглощается им целиком.

Рассмотрим с квантовой точки зрения фотоэффект в металлах

Для того чтобы покинуть металл, электрон должен совершить работу выхода Aвых,
против сил притяжения положительных ионов кристаллической решетки.

Если полученная электроном энергия

то он при вылете будет обладать кинетической энергией. Величина этой энергии максимальна, если электрон покидает металл с поверхности, а не из глубины.

В этом случае в соответствии с законом сохранения энергии выполняется соотношение, которое называется уравнением Эйнштейна для внешнего фотоэффекта:

при частотах, удовлетворяющих условию
Тогда красную границу фотоэффекта 0 можно

определить из уравнения

Следовательно

Выражение для максимальной длины волны

следует, что максимальная кинетическая энергия электрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов)

Объяснение II закона фотоэффекта

Объяснение III закона фотоэффекта

частоты 0, соответствующей красной границе можно найти работу выхода электронов

из металла

Уравнение Эйнштейна преобразованное к виду

может быть использовано для экспериментального определения постоянной Планка

и импульсом.
Массу фотона можно вывести из закона взаимосвязи массы

и энергии

следовательно

Фотон движется со скоростью света =с

Подстановка этого значения скорости в формулу

обращает знаменатель в ноль.

Вместе с тем, согласно формуле

масса фотона имеет конечное значение.

Это возможно лишь в том случае, если масса покоя m0 фотона равна нулю. Таким образом, фотон не имеет массы покоя и может существовать, только двигаясь со скоростью света c.

какое-то тело, должен оказывать на это тело давление, равное импульсу,

сообщаемому фотонами единице поверхности в единицу времени. Давление будет зависеть от того, поглощаются фотоны телом или отражаются от него

Каждый из поглощенных фотонов передает поверхности свой импульс pф. При отражении фотоны подобны абсолютно упругим шарикам. В этом случае, считая систему «фотон – поверхность» замкнутой и, применяя закон сохранения импульса, получим:

– импульсы фотона до и после взаимодействия с поверхностью

– импульс, передаваемый телу фотоном

Таким образом, каждый отраженный фотон передает телу импульс
каждый поглощенный

фотон -

Пусть N – общее число фотонов, падающих на тело.

– число фотонов, падающих на единицу поверхности тела в единицу времени.

времени отражается n фотонов, а поглощается (1-n) фотонов
По II

закону Ньютона, давление света на поверхность равно суммарному импульсу, который передают единице поверхности за одну секунду падающие фотоны. Следовательно, давление света на тело выражается формулой:

Энергию света можно выразить через число фотонов:

На поверхность S за время t падают фотоны, находящиеся в объеме

Тогда объемная плотность энергии:

Отсюда:

лучей различными веществами (графит, Li, Be, B).
Схема опыта

Узкий пучок монохроматических рентгеновских лучей падает на рассеивающее вещество. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа.

В рассеянных лучах наряду с излучением первоначальной длины волны , содержатся также лучи большей длины волны '. Разность ='- оказалась независящей от  и от природы рассеивающего вещества.

- комптоновская длина волны
Комптон показал, что данное явление можно

объяснить с квантовой точки зрения, как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами.

и импульсом
падает фотон с энергией
и импульсом
После столкновения

электрон будет обладать энергией

и импульсом

Энергия и импульс фотона также изменятся и станут равными
и .

энергии к виду
и возведем в квадрат
По теореме косинусов
или
(1)
(2)

сокращений получим
Так как
то можно записать
следовательно
Эта формула совпадает с

записанной ранее эмпирической формулой, так как

свидетельствуют о его волновых свойствах.
С другой стороны законы

теплового излучения, фотоэффект и эффект Комптона объясняются исходя из квантовых (корпускулярных) представлений о свойствах света.