Слайд 1Методы получения фрактальных структур в микро и нанотехнологии.
В принципе методы получения фрактальных структур ничем не отличаются от
обычных технологических методов микро и нанотехнологии. Более того, фрактальные структуры зачастую получаются не только без всяких особых ухищрений, но и самопроизвольно.
Поскольку эти структуры существенно отличаются от того, что рассчитывали получить технологи, то они всегда объявлялись браком и служили объектом борьбы и уничтожения, вместо того, чтобы служить предметом исследования и источником различных, в том числе и нобелевских премий. Но, безусловно, получение фрактальных структур имеет свои нюансы и тонкости.
Слайд 2 Фрактальные агрегаты металлов и получают при испарении металла
в атмосфере аргона при давлении 0,25 - 10 торр и
собирают образовавшийся конденсат металлических частиц в виде фрактальных образований.
Осадок имеет пористую структуру и основной объем его занимают поры.
Средний радиус частиц в этих образованиях возрастает с увеличением давления аргона.
Фрактальная размерность агрегатов лежит обычно в пределах 1,75 - 1,9 при давлении аргона в 0,9 - 8 торр, средний радиус частиц - менее 0,8 нм.
Слайд 3 Фрактальные агрегаты могут быть получены также путем сжигания
смеси в горящем пламени, если обеспечиваются условия конденсации и образования
твердых частиц.
Этот метод используется для получения фрактальных агрегатов Si02 путем сжигания в водородно-кислородном пламени SiH4.
Образующийся при сжигании порошок содержит фрактальные агрегаты, состоящие из частиц с радиусом в пределах 8 - 10 нм. Фрактальная размерность агрегатов D = 1,8 - 2,0.
Полученные путем конденсации в газовой среде фрактальные агрегаты имеют очень высокую степень пористости. Объемная доля твердого вещества обычно составляет 10-2 - 10-4.
Определение каких-либо свойств твердого тела становится при этом чрезвычайно затруднительным и в большинстве случаев даже невозможным. Поэтому актуальным является поиск способов и методов создания в твердых телах управляемой фрактальной структуры.
Слайд 4 Фрактальные агрегаты можно также получать путем изменения дислокационной
структуры в металле при возрастающих степенях деформации, приводящих к созданию
ячеистой структуры.
В начальной стадии пластической деформации образуется значительное количество дислокаций, равномерно распределенных по объему. При более высоких степенях деформации образуются скопления в виде клубков и рыхлых стенок ячеек.
В конце концов, образуется четко выраженная ячеистая структура. Считается, что скопления дислокаций, формирующие стенки ячеек, являются фракталами, размерность которых сначала увеличивается от D = 1 (равномерное распределение дислокаций) до 1 < D < 2 (рыхлые скопления), а затем достигает D = 2 (геометрические стенки ячейки).
Слайд 5 Все больший интерес привлекают пористые фрактальные структуры, относящиеся
к классу аэрогелей и представляющие собой макроскопическое твердое тело, состоящее
из связанных между собой микрочастиц, образующих жесткий каркас, который занимает лишь малую часть общего объема.
В названии "аэро" (воздух) отражен малый удельный вес вещества. Способ производства аэрогеля SiO2 был разработан в 30-х годах двадцатого столетия.
Слайд 6 Образование аэрогеля происходит следующим образом. На первой стадии
выделяется одно из веществ (SiO2) из раствора в твердую фазу
в виде микроскопических частичек на многих центрах конденсации.
Диаметр таких микрочастиц на порядок и более превышает диаметр входящих в ее состав молекул.
Растущая микрочастица должна приобретать заряд, который препятствует присоединению к ней молекул Si02, которые сами заряжены.
Такой процесс возможен всего лишь в небольшом интервале кислотности раствора.
Слайд 7 По своему строению аэрогель представляет собой систему связанных
между собой твердых частиц, причем объем, занимаемый частицами, составляет малую
часть объема аэрогеля.
Практически весь его объем приходится на пустоты — поры.
Характерный размер отдельных частиц, входящих в состав аэрогеля, обычно порядка нескольких нм.
Простейшая модель аэрогеля может быть построена из сферических частиц близкого радиуса, причем связь между ними осуществляется, когда частицы практически касаются друг друга.
В этом случае удельная площадь внутренней поверхности аэрогеля S выражается через радиус частиц r0.
В частности, для аэрогеля двуокиси кремния при ρ0 = 2,2 г/см3 при r0 = 2 нм имеем S = 700 м2/г.
Для большинства реальных образцов аэрогеля двуокиси кремния S находится в пределах 300—1000 м2/г.
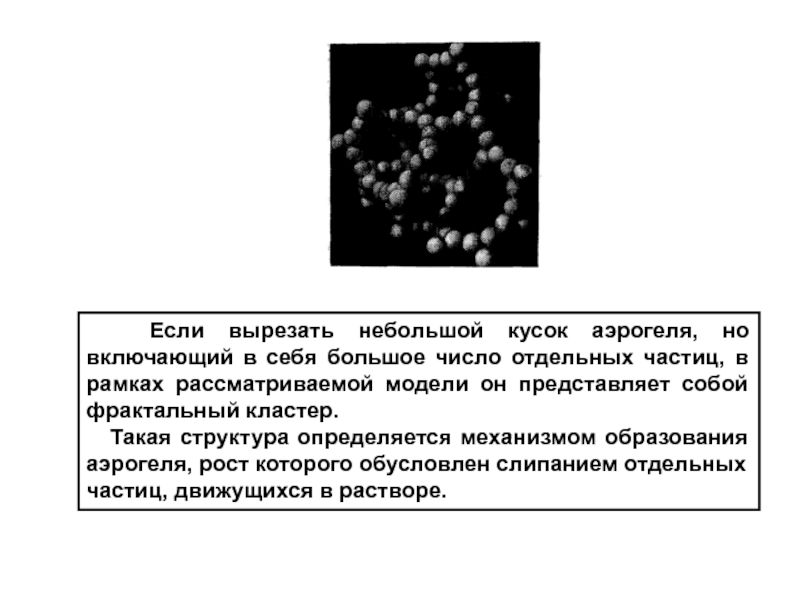
Слайд 8 Если вырезать небольшой кусок аэрогеля, но включающий в
себя большое число отдельных частиц, в рамках рассматриваемой модели он
представляет собой фрактальный кластер.
Такая структура определяется механизмом образования аэрогеля, рост которого обусловлен слипанием отдельных частиц, движущихся в растворе.
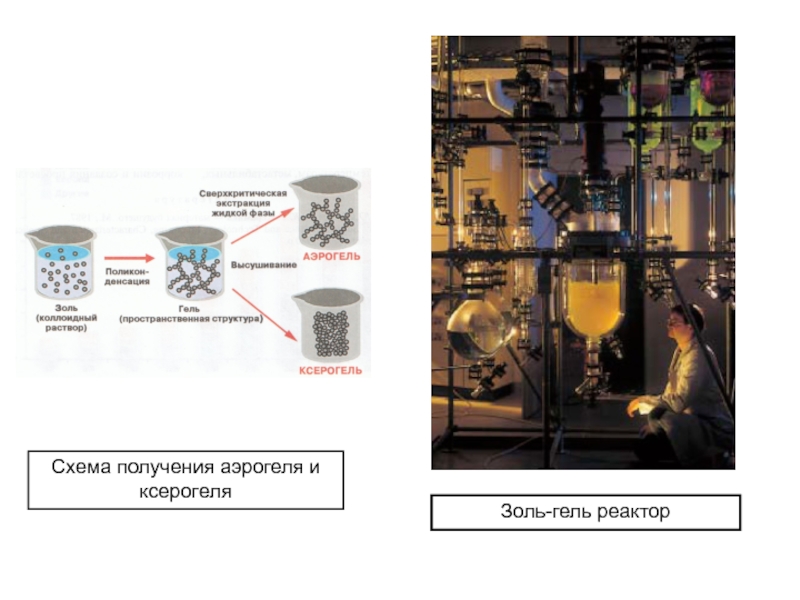
Слайд 9Схема получения аэрогеля и ксерогеля
Золь-гель реактор
Слайд 10Ксерогель оксида ванадия. Растровая электронная микроскопия
Слайд 11 По мере образования частиц в растворе начинается объединение
отдельных частиц, определяющее структуру аэрогеля. Оно идет достаточно медленно, ибо
зависит от диффузии микрочастиц в растворе. Очень важное значение имеет последняя стадия процесса формирования аэрогеля, связанная с удалением жидкости, находящейся в его порах.
Молекулы жидкости создают высокие давления в порах. Расчеты показывают, что в порах аэрогеля Si02 диаметром 2 нм молекулы воды создают давление порядка 20 кбар. Высушивание аэрогеля на воздухе или в вакууме создает большие внутренние напряжения в каркасе, приводящие к его разрушению. Высушенный таким образом аэрогель получил название ксерогеля.
Чтобы предотвратить разрушение структуры каркаса аэрогеля, воду в порах заменяют этиловым спиртом (какое варварство!), молекулы которого создают меньшее напряжение, а удаление спирта облегчается благодаря более низким, чем у воды, критическим точкам. После этого аэрогель высушивается в автоклаве.
Слайд 12 Фрактальная размерность аэрогеля Si02, определяемая по интенсивности рассеяния
рентгеновского излучения, оказалась равной D = 2,12 ± 0,05.
Радиус частиц находится в пределах 4 - 10 нм, а максимальный размер пор 35 - 120 нм.
Наиболее характерным свойством аэрогеля является гигантский объем внутренних пор. Поэтому аэрогель можно использовать для хранения различных веществ в виде так называемого наноконтейнера.
В частности, аэрогели Аl2О3 и SiO2 могут быть использованы для хранения компонент ракетного топлива: азотной кислоты, оксидов азота и диметилгидразина.
Аэрогель SiO2 является прозрачным веществом с низкой теплопроводностью, поэтому его можно использовать в качестве прозрачных теплоизолирующих стен и перегородок, например в космических кораблях.
Слайд 13 Другим объектом, состоящим из фрактальных кластеров и являющимся
в чем-то сходным с аэрогелем являются фрактальные нити, полученные при
лазерном облучении металлических поверхностей.
Фрактальные нити являются аналогами аэрогелей, но в отличие от аэрогелей фрактальные нити анизотропны, ибо образуются во внешнем поле (диаметр нити в эксперименте составляет 30 - 40 мкм, их длина - несколько сантиметров).
Слайд 14 Система связанных фрактальных нитей - фрактальный клубок -
является своеобразным состоянием вещества.
Это состояние по своему
удельному весу соответствует газам, а по поведению - жидкостям и твердым телам.
Фрактальный клубок в силу жесткости конструкции обладает поверхностным натяжением, однако из-за малого удельного веса поверхностное натяжение относительно невелико.
Поэтому вблизи отверстия сферическая форма поверхности фрактального клубка нарушается; из него вырывается цилиндрическая струя, с помощью которой все вещество перетекает по другую сторону отверстия.
Там вдали от отверстия под действием поверхностного натяжения восстанавливается сферическая форма системы.
Слайд 15Основные понятия нелинейной динамики
С точки зрения особенностей
взаимодействия с внешней средой все системы (от маленького забитого вируса
до наглой гигантской звездной Метагалактики) делятся на открытые и закрытые.
Открытая система обменивается с внешней средой веществом, энергией и информацией, вследствие чего в ней происходят различные процессы, изменяющие ее состояние во времени.
Такая система, во-первых, находится в положении далеком от равновесия, поскольку обмен веществом, энергией и информацией с внешней средой все время изменяет ее состояние и она просто не успевает должным образом отрелаксировать.
Во-вторых, она эволюционирует, и если процессы, в ней происходящие, необратимы во времени, то эволюция может протекать различным образом в зависимости от изменения начальных параметров системы.
Слайд 16
Биологические системы принципиально не могут быть
закрытыми, они эволюционируют с уменьшением энтропии до момента прекращения своего
существования и с ее увеличением после наступления этого во многом прискорбного факта (грубо говоря, начинают разлагаться после смерти - но это не изысканная формулировка).
Переход к изучению открытых систем означает также ломку сложившихся научных стереотипов и косных систем мышления, тесно связанных с их биологическими носителями и соответствующими материальными и социальными благами.
Слайд 17 Классическая физика в основном оперирует с закрытыми системами,
а если на такую систему и подается какое-то возмущение, то
интересуются только двумя состояниями - до возмущения и после него, когда система придет в равновесие.
Переходной процесс, эволюция системы даже в таком маленьком временном интервале внимания не заслуживали, что очень странно, т.к. пример истинной закрытой системы отыскать практически невозможно.
Слайд 18 Поскольку для открытых систем не пригоден принцип временной
инвариантности, то описание процессов, происходящих в открытых системах отличается от
такового для закрытых (изолированных).
Для описания закрытой системы используются уравнения, обратимые во времени и, соответственно, обратимы во времени все происходящие в ней процессы.
В открытых системах происходящие процессы не обратимы во времени, для них характерна так называемая стрела времени.
Представления о стреле времени, процессах самоорганизации и принципах науки синергетики были развиты нашим соотечественником, ныне покойным нобелевским лауреатом Ильей Романовичем Пригожиным.
Слайд 19 Особый интерес представляют динамические системы. Под динамической системой
понимают любой объект или процесс, для которого однозначно определено понятие
состояния как совокупности некоторых величин в данный момент времени и задан оператор, описывающий эволюцию начального состояния во времени.
Это система любой природы (физической, химической, биологической и даже социальной или экономической), состояние которой изменяется во времени, дискретно или непрерывно.
Описание динамических систем в смысле задания оператора эволюции также допускает большое разнообразие: оно осуществляется с помощью дифференциальных уравнений, дискретных отображений, с помощью теории графов, теории марковских цепей и т.д.
Выбор одного из способов описания задает конкретный вид математической модели соответствующей динамической системы.
Слайд 20 Все системы по способу своего описания делятся на
линейные и нелинейные.
Геометрическим образом линейной функции на
плоскости будет прямая линия, а геометрическим образом нелинейной функции - любая кривая.
Нелинейные функции изменчивы и неповторимы.
То, что точно описывает характерные особенности одного класса нелинейных функций может быть абсолютно неприменимо к другому их классу.
Слайд 21 При переходе в нелинейный мир навсегда утрачивается основной
краеугольный камень предыдущей, классической физики - принцип суперпозиции, позволявший конструировать
любую задачу как набор частных решений, к примеру всем известная кусочно-линейная аппроксимация.
Для забывших или не выучивших: принцип суперпозиции - это допущение, согласно которому в случае, если составляющие сложного процесса воздействия взаимно не влияют друг на друга результирующий эффект будет представлять собой сумму эффектов, вызываемых каждым воздействием в отдельности.
Слайд 22 Нелинейность в мировоззренческом смысле означает многовариантность путей развития,
наличие выбора из альтернатив путей и определенного темпа эволюции, а
также необратимость эволюционных процессов.
Нелинейность в математическом смысле означает определенный вид математических уравнений (нелинейные дифференциальные уравнения), содержащих искомые величины в степенях, больше единицы или коэффициенты, зависящие от свойств среды.
Слайд 23 В случае применения классических моделей (например, трендовых, регрессионных
и т. д.), будущее объекта однозначно детерминированное и его можно
предсказать, зная прошлое объекта (исходные данные для моделирования).
Фракталы применяются в том случае, когда объект имеет несколько вариантов развития и состояние системы определяется положением, в котором она находится на данный момент, что является попыткой смоделировать хаотичное развитие.
Слайд 24 Для описания нелинейного мира необходима не только новая
математика (она уже есть), но и не заскорузлое мышление и
способность воспринимать новое и непривычное.
Однако самое болезненное для большинства, так сказать пик формы - это соединение в "одном флаконе" нелинейных и открытых систем.
Речь идёт о системах, имеющих выход и вход, то есть обменивающихся с окружающей средой потоками энтропии (энергии, вещества, информации), благодаря этому система оказывается выведенной из состояния термодинамического равновесия, то есть оказывается неравновесной.
В таких системах происходят необратимые процессы, которые могут самопроизвольно протекать только в одном определённом направлении.
Нелинейность означает, что распространяющиеся через систему потоки энтропии изменяют её параметры тем в большей мере, чем интенсивней эти потоки.
Слайд 25 Поэтому динамику системы описывают нелинейные модели, например, нелинейные
дифференциальные равнения.
Они имеют не одно, а несколько
возможных решений, а это означает, что система может эволюционировать несколькими путями.
Изменение параметров системы способно вызывать ветвление пути эволюции.
Построением математических и компьютерных моделей процессов в системах любой природы, в том числе и нелинейных, занимается возникшая в прошлом веке наука синергетика.
А также изучением условий, механизмов, типов переходов структуры, выяснением свойств структуры и хаоса, их связи с процедурами обработки информации, возможности управления сложными системами посредством стимулирования оптимальных процессов самоорганизации и др.
Слайд 26 Если подводимый к системе поток, например, энергии, превышает
некоторое пороговое значение, при котором компенсируются потери энергии в системе,
в ней образуются пространственно-временные структуры, т.е. происходит самоорганизация.
Слайд 27 Так, в лазере, когда подводимая к лазерному веществу
энергия накачки мала, его атомы испускают свет несогласованно, создавая излучение,
характеристики которого изменяются хаотически.
Достижение порогового значения приводит - скачком - к возникновению упорядоченной структуры, то есть волны когерентного излучения, характеристики которой постоянны. Иначе говоря, имеет место переход хаос-структура.
Дальнейший рост подводимой к лазерному веществу энергии при условии сильных её потерь способен вызвать переход структура-хаос.
Существенно, что такой хаос, называемый динамическим или детерминированным, структурен, то есть обладает той или иной степенью упорядоченности.
Слайд 28 Математическая модель динамической системы считается заданной, если введены
параметры (координаты) системы, определяющие однозначно ее состояние, и указан эволюционный
оператор, позволяющий решать задачу определения изменения состояния во времени.
Слайд 29 Описывать эволюцию динамической системы во времени можно по
разному, в зависимости от того, какой аспект ее эволюции представляет
интерес для исследователя.
Если интерес представляет конфигурация системы, ее положение в эвклидовом пространстве или состав, то принято пользоваться конфигурационным пространством, в котором каждая точка описывает какую-то конфигурацию системы.
Но для описания эволюции системы во времени информации, содержащейся в конфигурационном пространстве, недостаточно.
Пространство, каждая точка которого соответствует состоянию динамической системы, называется фазовым пространством.
Слайд 30Q(x,y,z)
x
y
z
E
Вещество
Энергия
t=0
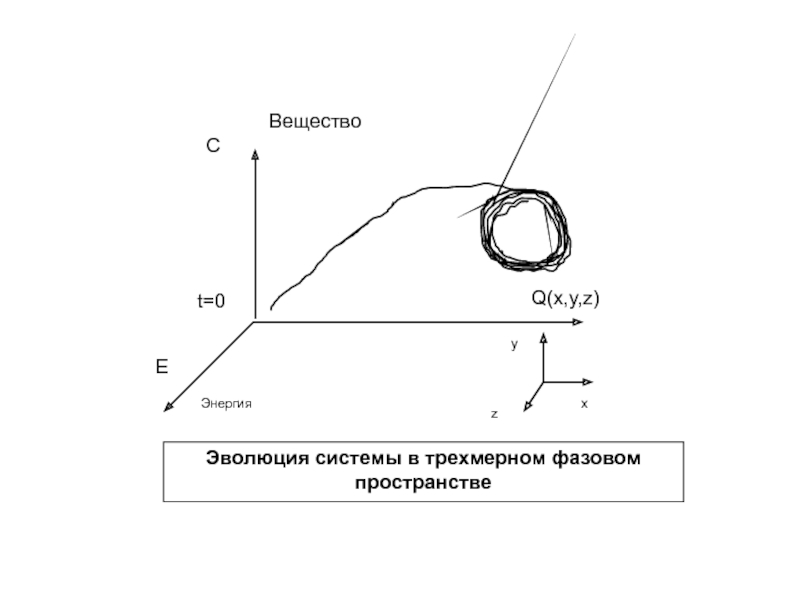
Эволюция системы в трехмерном фазовом пространстве
С
Слайд 31 По оси ординат в общем виде обозначим изменения
какой-либо другой характеристики системы - пусть количества вещества С, которым
система обменивается с окружающим миром.
По оси абсцисс положение системы в эвклидовом пространстве.
Тогда по оси у можем отложить либо изменения в энергии системы Е, что мы и сделали, или информации, что мы не сделали, так как не захотели, вернее, не смогли.
Потому, что для информации в трехмерном фазовом пространстве места не осталось.
Слайд 32Для любой нормальной системы игнорирование информационного обмена может быть катастрофичным
(это в жизни лучше не читать газет и не смотреть
в ящик для идиотов) - точно так же, как игнорирование обмена веществом или энергией.
Из этого следует весьма печальный вывод, что для описания системы даже в самом общем виде не хватает трехкоординатной эвклидовой сетки, а оперировать с большим числом координат в эвклидовом пространстве мы не умеем.
Поэтому реальную полноценную нелинейную открытую систему даже в самом общем виде наглядно описать невозможно, а только с помощью математических уравнений.
Слайд 33
Рассмотрим далее наш график.
Эволюция системы началась для нас с временной точки t=0, но
поскольку система уже располагалась в пространстве и имела в своем составе какое-то вещество, и обладала какой-то энергией и информацией, то развитие системы (эволюция) пойдет не из начала координат.
В каждый последующий момент времени за счет обмена с внешней средой веществом и энергией система будет перемещаться в фазовом пространстве (и в эвклидовом тоже, но лишь как составляющей фазового, т.е. каждая новая совокупность всех трех координат в эвклидовом пространстве в фазовом пространстве будет отображаться одной точкой, но учет эвклидова пространства автоматически делает фазовое пространство континууминальным, т.е. непрерывным).
Слайд 34 Эволюция во времени большинства систем приводит к тому,
что фазовая траектория начинает эволюционировать вокруг некоей области притяжения, называемой
аттрактором, как это и показано на графике.
Если траектория при t→∞ будет описывать такую фигуру ни разу не пересекаясь сама с собой, то такой аттрактор будет именоваться странным.
Река и мячик
Слайд 35 Реакция динамической системы на малое возмущение определяется ее
состоянием и в одних случаях возмущающие факторы влияют на режим
функционирования системы незначительно, а в других - приводят к резкому отличию характера возмущенного движения по сравнению с исходным.
В первом случае состояние системы устойчиво, во втором - нет.
Слайд 36 Большинство интересных (и не интересных) физических задач при
их математическом описании приводит к дифференциальным уравнениям, зависящим от параметров.
Изменение параметра может вызвать потерю устойчивости одним режимом движения и переход системы в другое состояние.
Это явление называется бифуркацией, а значение параметра, при котором оно происходит, - точкой бифуркации.
Особо интересны такие бифуркации, в результате которых при прохождении точки бифуркации в системе возникают новые устойчивые режимы движения.
Слайд 37 До работ А. Пуанкаре считалось, что все динамические
системы похожи друг на друга и могут анализироваться с помощью
математического аппарата интегрального и дифференциального исчисления (математического анализа).
Поэтому, когда Пуанкаре открыл неинтегрируемость целого класса систем, это было настоящим шоком.
Сам Пуанкаре называл их отвратительными и кошмарными. Оказалось, что таких систем множество (например, траектория броуновского движения частицы).
В этом случае аппарат дифференциальных уравнений становится непригодным, и необходимо переходить к вероятностным методам исследования.
В силу открытия свойства неинтегрируемости некоторые положения классической динамики, оказались несостоятельными.
Слайд 38 Согласно положениям классической термодинамики, равновесное состояние замкнутой системы, характеризующееся
возрастанием энтропии, — является конечным пунктом всякой эволюции.
Создавая неклассическую термодинамику И. Пригожин доказал, что существуют структуры, в которых возрастание энтропии может быть компенсировано ее оттоком в окружающую среду.
Такие структуры получили название "диссипативных".
На этой основе появилось новое научное направление - синергетика.
Слайд 39 Для того чтобы соответствующим образом отобразить случайный характер
перехода от беспорядка к порядку, теория диссипативных структур вводит понятие
бифуркации (bifurcus, лат. - двузубый).
Согласно теории бифуркации, прошлое состояние системы исчезает скачком в силу накопления в системе флуктуации (fluctus, лат. - бурлящий).
В любой системе имеют место флуктуации, связанные со сбоями в функционировании ее элементов, с поломками в структурных образованиях.
Флуктуации необходимы и присутствуют в любой системе, но вместе с тем их появления означают нарушения в способе существования системы: отклонения от статистически среднего.
Слайд 40 С физической точки зрения точка бифуркации это критическое
значение порога устойчивости термодинамической ветви.
Это точка ветвления путей
эволюции открытой нелинейной системы, как в общем виде это показано на рисунке, где по оси абсцисс отложены некоторые временные промежутки, а по оси ординат изменение какой-либо характеристики системы.
С точки зрения математики бифуркация означает ветвление решений нелинейного дифференциального уравнения.
Если есть бифуркация, то существует и вероятность. Следовательно, необратимость ведет к вероятности.
Таким образом, вероятность обнаруживается через бифуркацию, потому что изначально неизвестно, по какой ветви будет развиваться система.
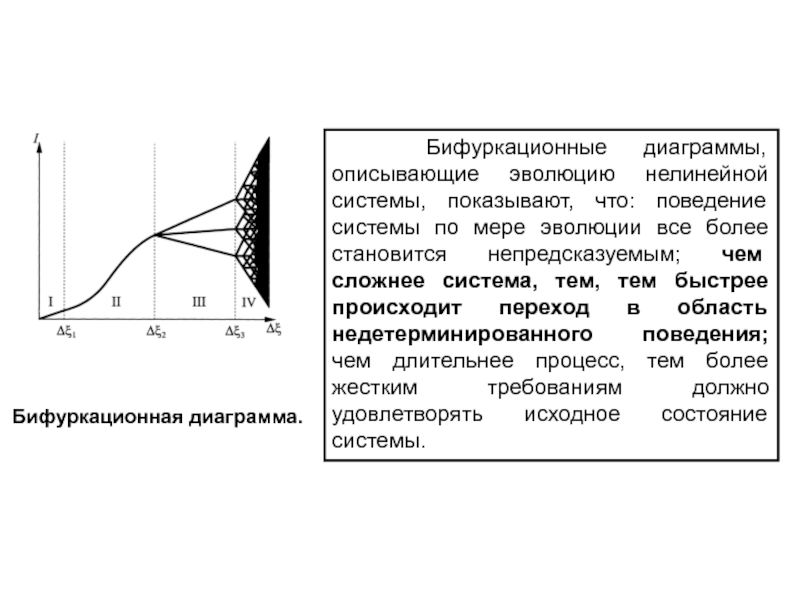
Слайд 41Бифуркационная диаграмма.
Бифуркационные диаграммы, описывающие эволюцию нелинейной системы,
показывают, что: поведение системы по мере эволюции все более становится
непредсказуемым; чем сложнее система, тем, тем быстрее происходит переход в область недетерминированного поведения; чем длительнее процесс, тем более жестким требованиям должно удовлетворять исходное состояние системы.
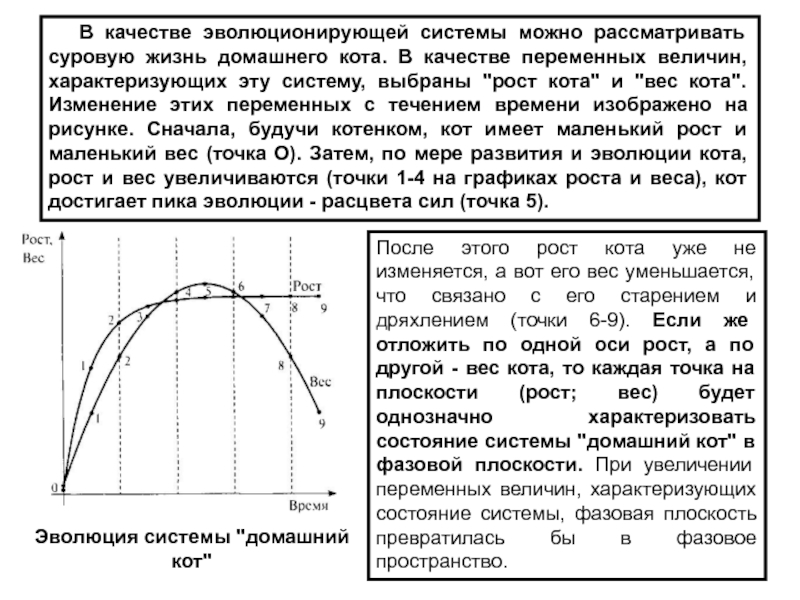
Слайд 42 В качестве эволюционирующей системы можно рассматривать суровую жизнь
домашнего кота. В качестве переменных величин, характеризующих эту систему, выбраны
"рост кота" и "вес кота". Изменение этих переменных с течением времени изображено на рисунке. Сначала, будучи котенком, кот имеет маленький рост и маленький вес (точка О). Затем, по мере развития и эволюции кота, рост и вес увеличиваются (точки 1-4 на графиках роста и веса), кот достигает пика эволюции - расцвета сил (точка 5).
После этого рост кота уже не изменяется, а вот его вес уменьшается, что связано с его старением и дряхлением (точки 6-9). Если же отложить по одной оси рост, а по другой - вес кота, то каждая точка на плоскости (рост; вес) будет однозначно характеризовать состояние системы "домашний кот" в фазовой плоскости. При увеличении переменных величин, характеризующих состояние системы, фазовая плоскость превратилась бы в фазовое пространство.
Эволюция системы "домашний кот"
Слайд 43 Для более углубленного знакомства с нелинейной динамикой, синергетикой,
теорией детерминированного хаоса потребуется несколько курсов лекций на последнем году
магистерской подготовки, чему не бывать.
Посему перейдем к очень краткому знакомству с элементной базой микроэлектроники.