Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
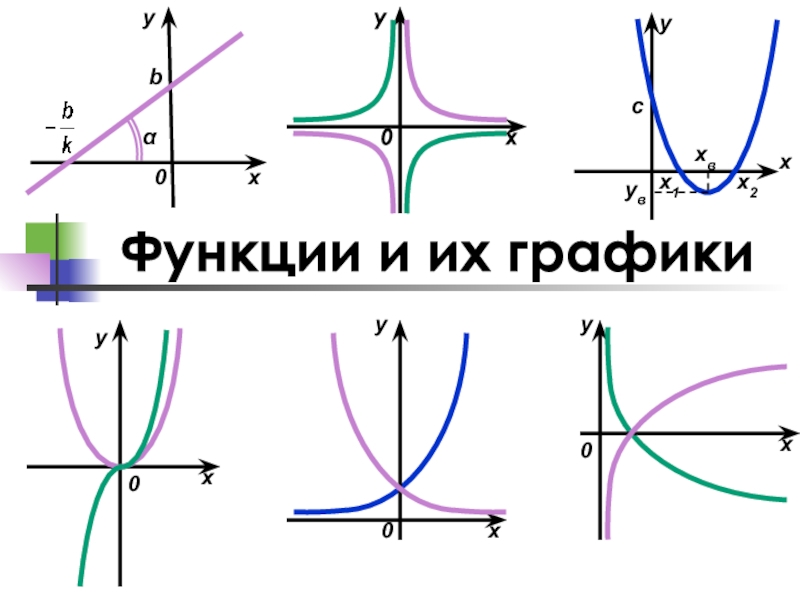
Функции и их графики
Содержание
- 1. Функции и их графики
- 2. Содержание Функции и их графики.Преобразование графиков функций.Свойства функций.
- 3. Функции.Линейная функцияКвадратичная функцияСтепенная функцияОбратная пропорциональностьПоказательная функцияЛогарифмическая функцияТригонометрические функции
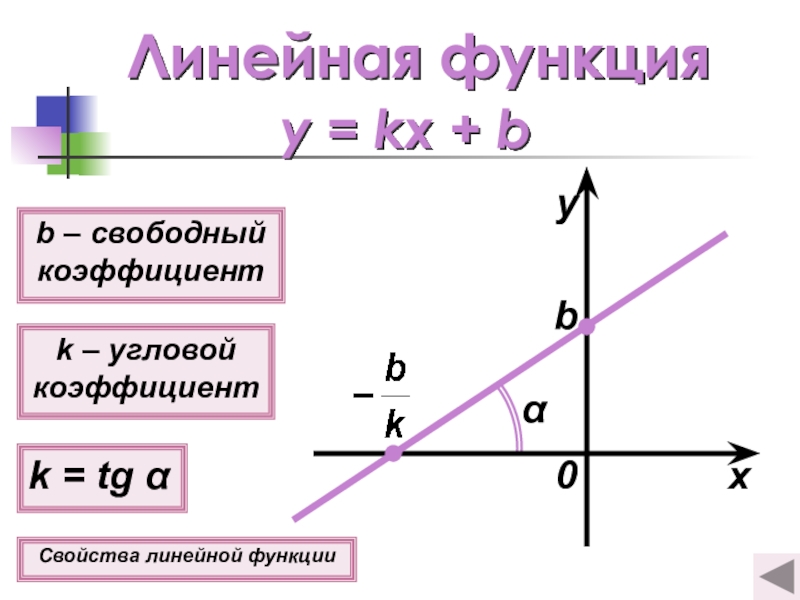
- 4. Линейная функцияy = kx + bk –
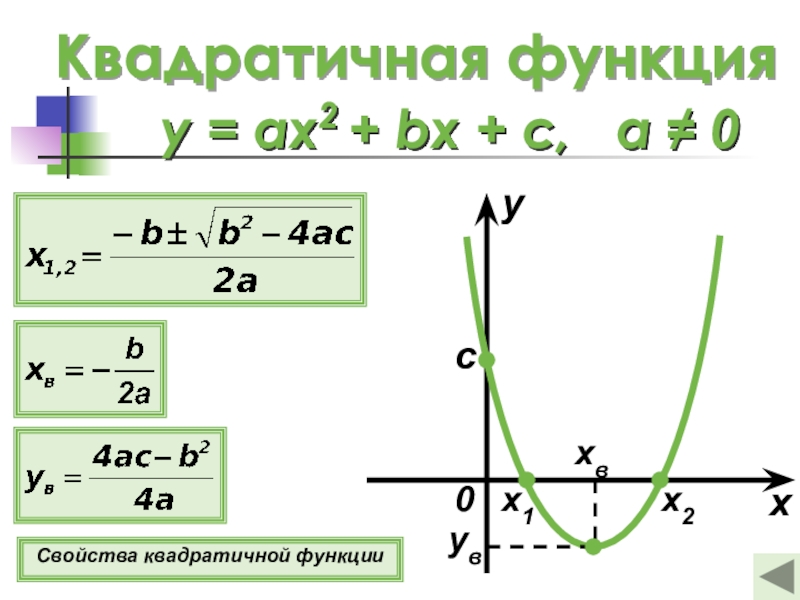
- 5. Квадратичная функцияy = ax2 + bx + c, а ≠ 0xy0cx1x2xвувСвойства квадратичной функции
- 6. Степенная функцияy = xnxy0y = xn, где
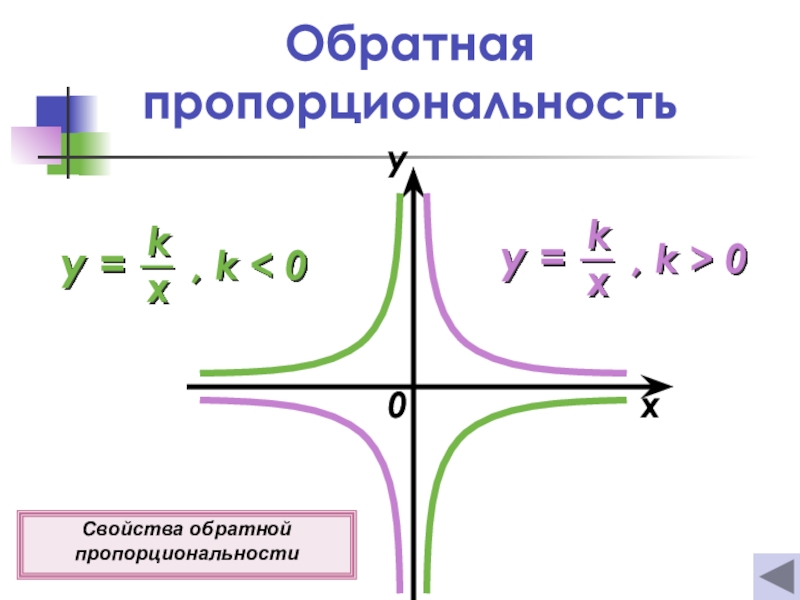
- 7. Обратная пропорциональность0xyСвойства обратной пропорциональности
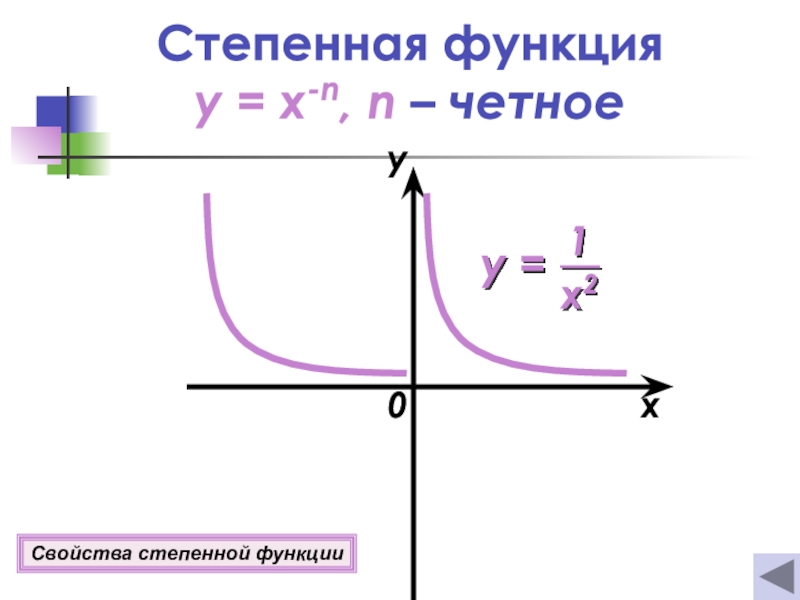
- 8. Степенная функция y = x-n, n – четное0xyСвойства степенной функции
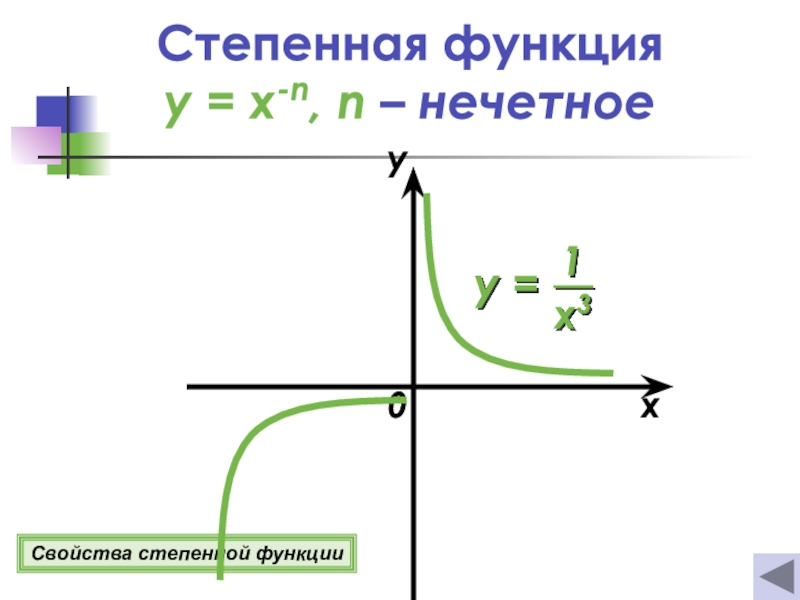
- 9. 0xyСвойства степенной функцииСтепенная функция y = x-n, n – нечетное
- 10. Геометрические преобразования графиковПреобразование вида y = f(x)+
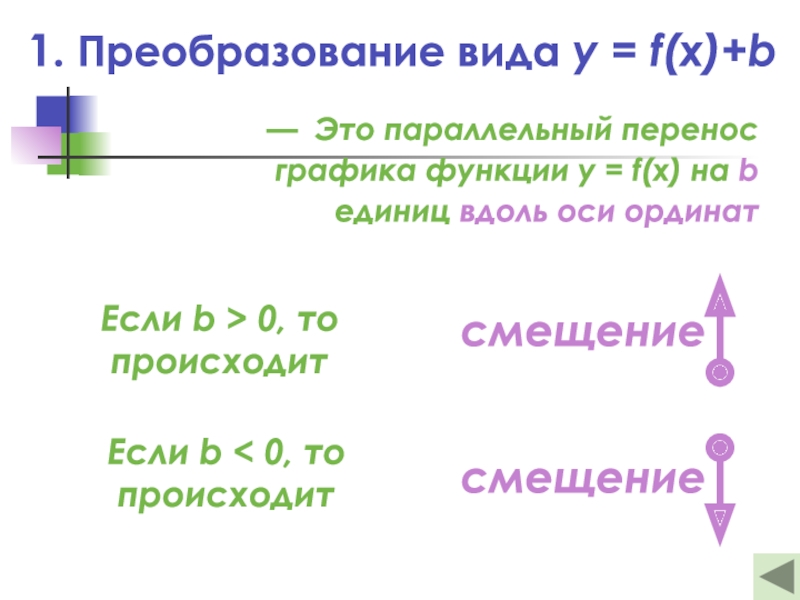
- 11. 1. Преобразование вида y = f(x)+b— Это
- 12. 1. Преобразование вида y = f(x)+bxy0by = x2y = x2 + b
- 13. 2. Преобразование вида y = f(x –
- 14. 2. Преобразование вида y = f(x – a)xy0y = (x – a)3y = x3a
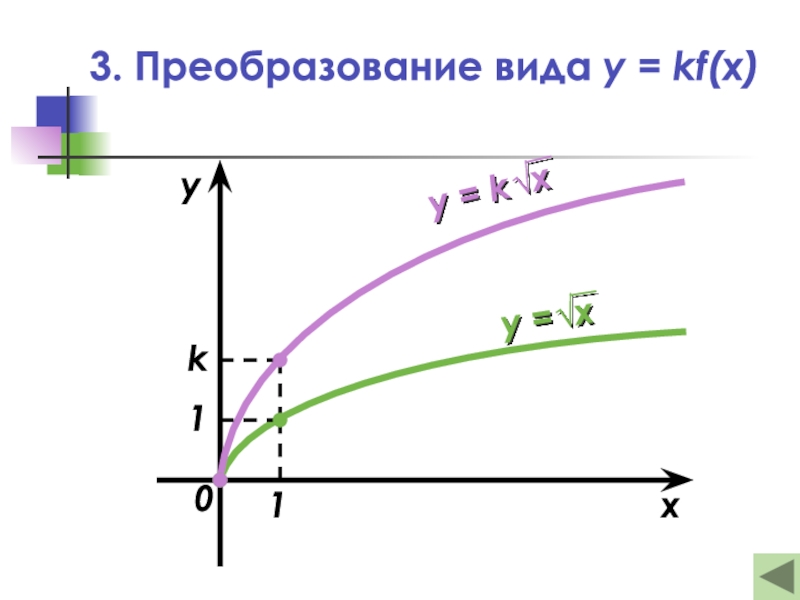
- 15. 3. Преобразование вида y = kf(x)— Это
- 16. 3. Преобразование вида y = kf(x)xy11k0
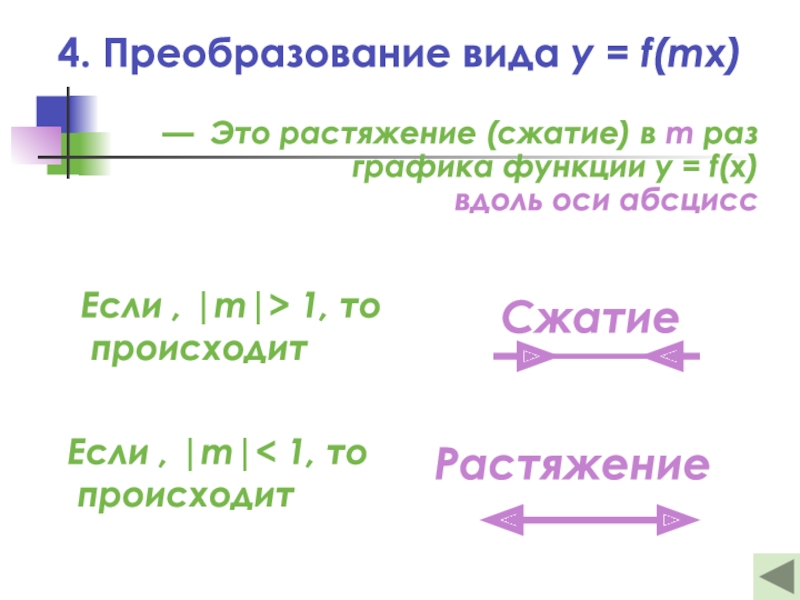
- 17. 4. Преобразование вида y = f(mx)— Это
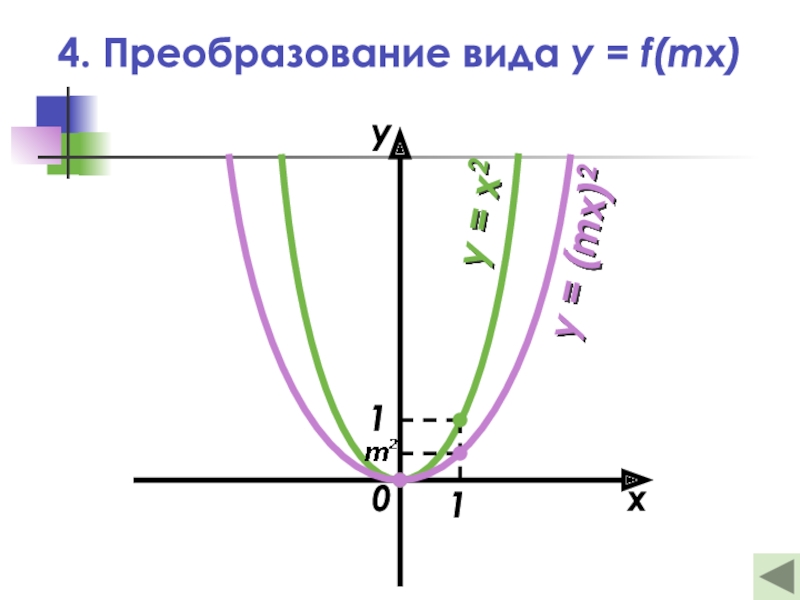
- 18. 4. Преобразование вида y = f(mx)0xy11y = x2y = (mx)2
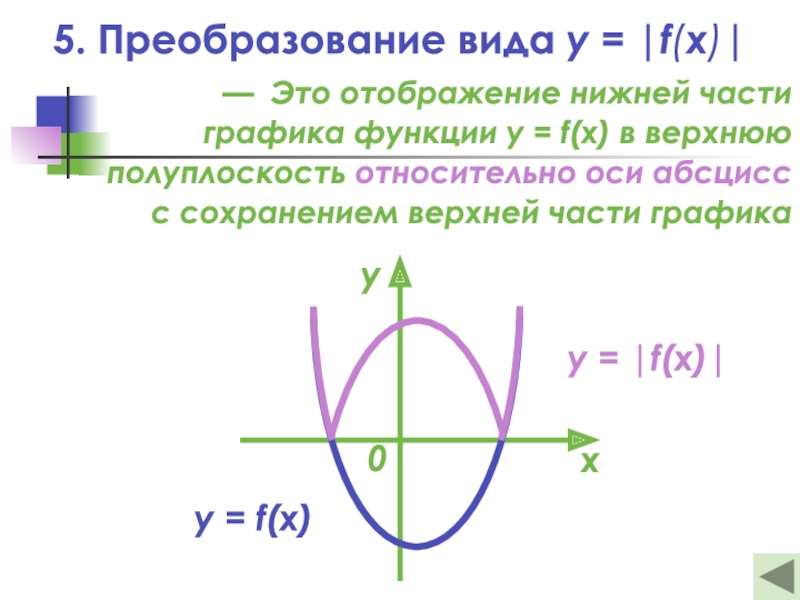
- 19. 5. Преобразование вида y = |f(x)|— Это
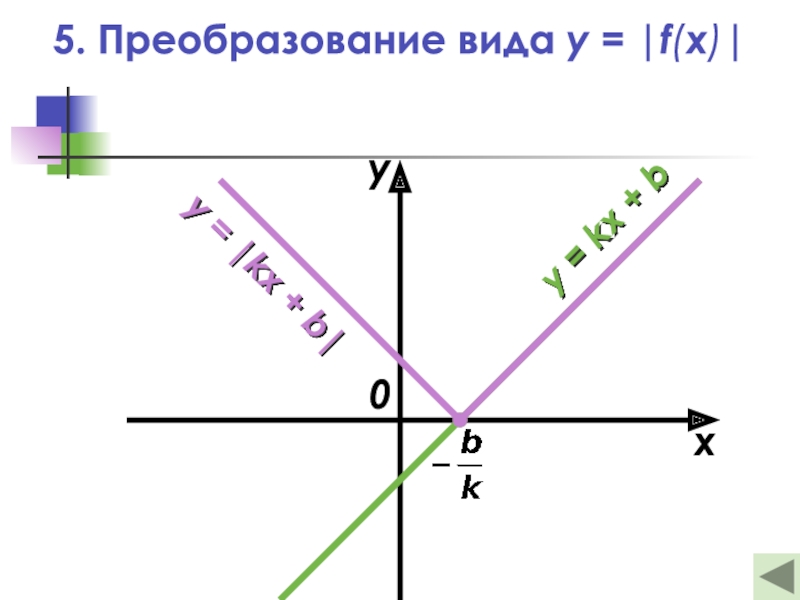
- 20. 5. Преобразование вида y = |f(x)|xy0y = kx + by = |kx + b|
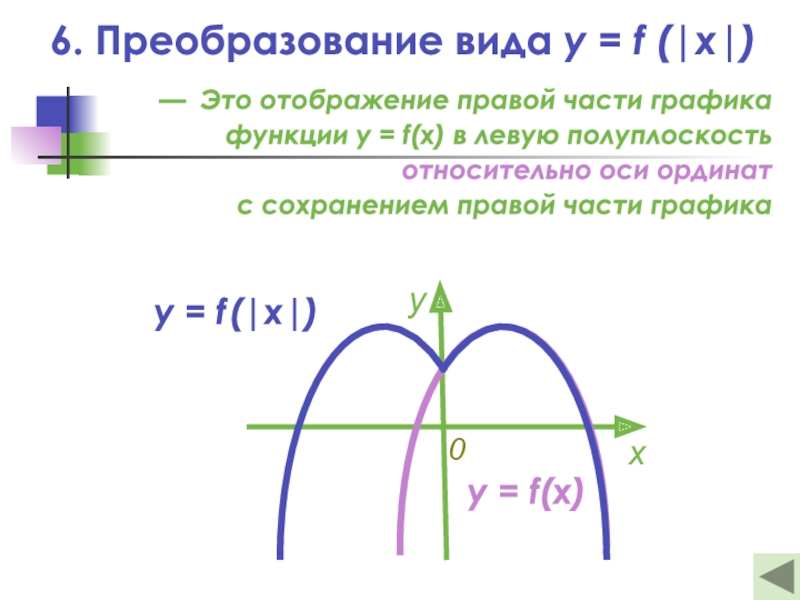
- 21. 6. Преобразование вида y = f (|x|)—
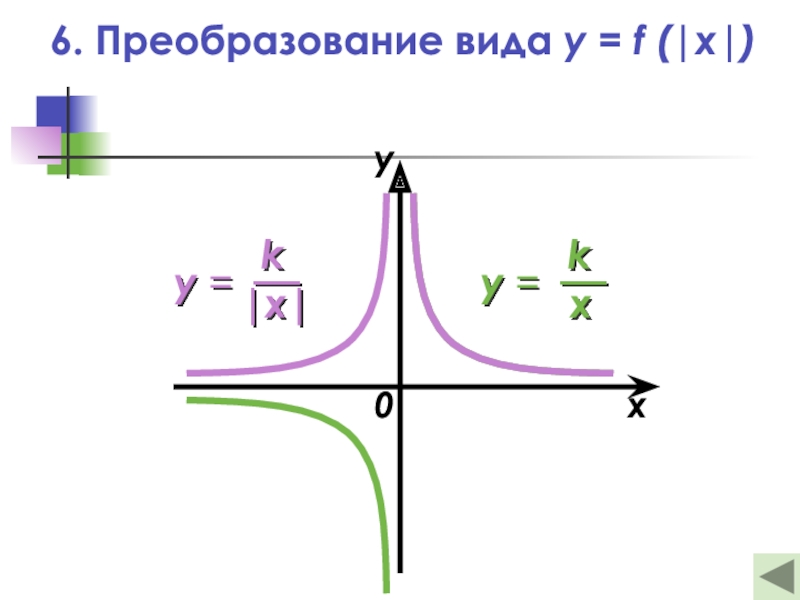
- 22. 6. Преобразование вида y = f (|x|)0xy
- 23. — Это отображение верхней части графика функции
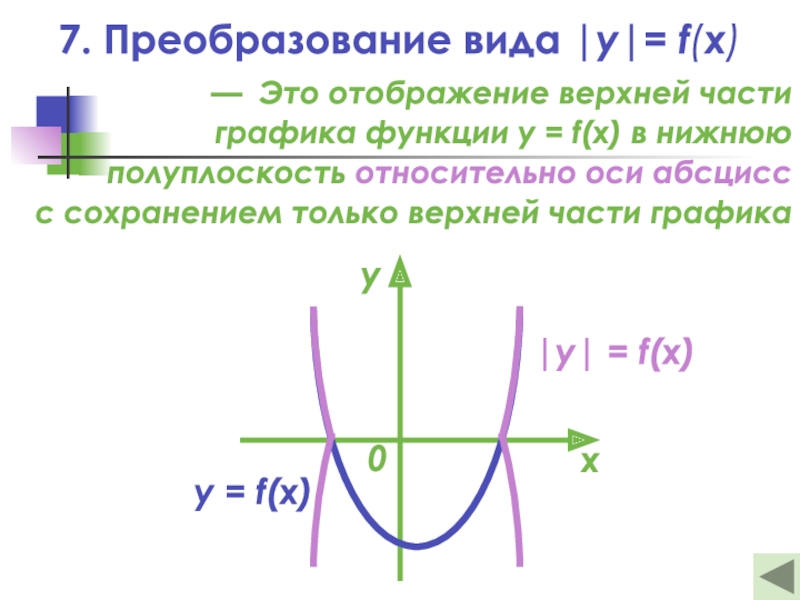
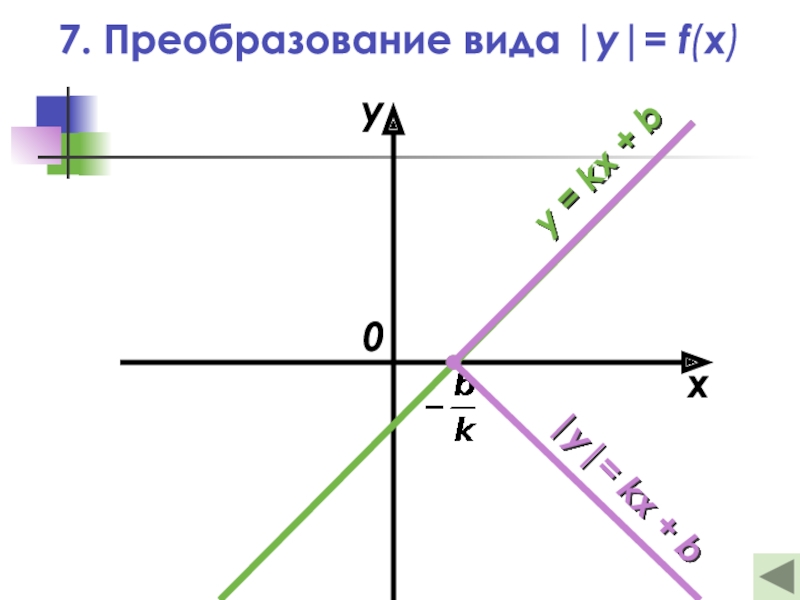
- 24. 7. Преобразование вида |y|= f(x)xy0y = kx + b|y|= kx + b
- 25. Свойства функцийСвойства линейной функцииСвойства квадратичной функцииСвойства степенной
- 26. Свойства линейной функции1о D(y) = (−∞; +∞);
- 27. Свойства квадратичной функции1о D(y) = (−∞; +∞).
- 28. Свойства степенной функцииy = xnЕсли n =
- 29. Свойства обратной пропорциональности1о D(y) = (−∞; 0)u(0;
- 30. Свойства степенной функцииy = x-nЕсли n =
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Функции.
Линейная функция
Квадратичная функция
Степенная функция
Обратная пропорциональность
Показательная функция
Логарифмическая функция
Тригонометрические функции
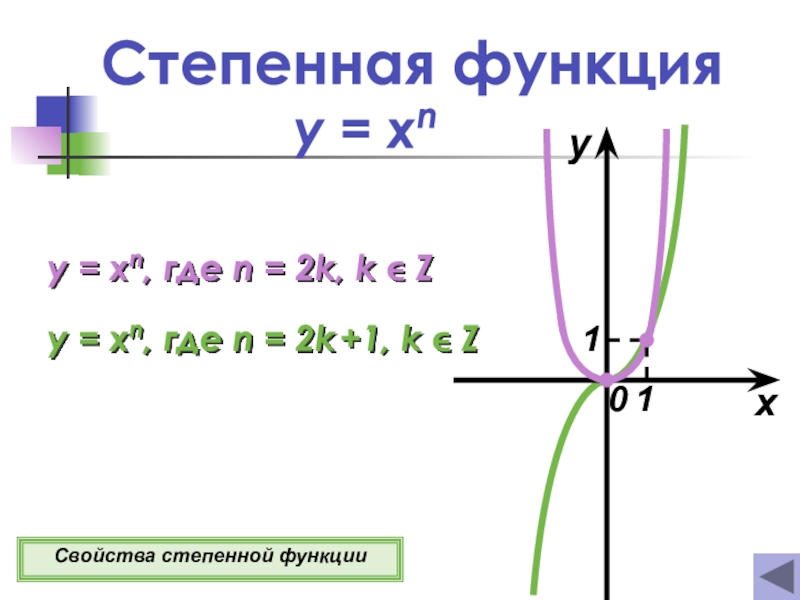
Слайд 6Степенная функция
y = xn
x
y
0
y = xn, где n = 2k,
k Z
y = xn, где n = 2k +1,
k ZСвойства степенной функции
1
1
Слайд 10Геометрические преобразования графиков
Преобразование вида y = f(x)+ b
Преобразование вида y
= f(x – a)
Преобразование вида y = kf(x)
Преобразование вида y
= f(mx)Преобразование вида y = |f(x)|
Преобразование вида y = f(|x|)
Преобразование вида |y|= f(x)
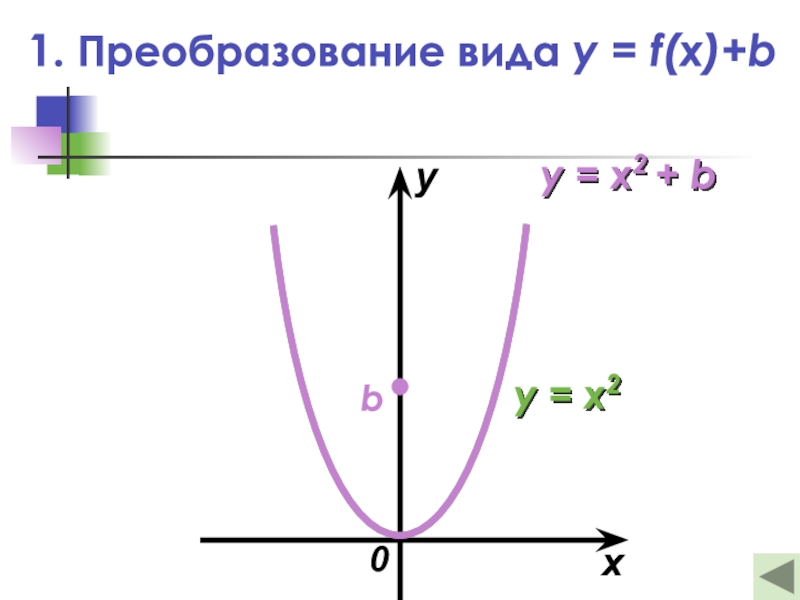
Слайд 111. Преобразование вида y = f(x)+b
— Это параллельный перенос графика
функции y = f(x) на b единиц вдоль оси ординат
Если
b > 0, топроисходит
Если b < 0, то
происходит
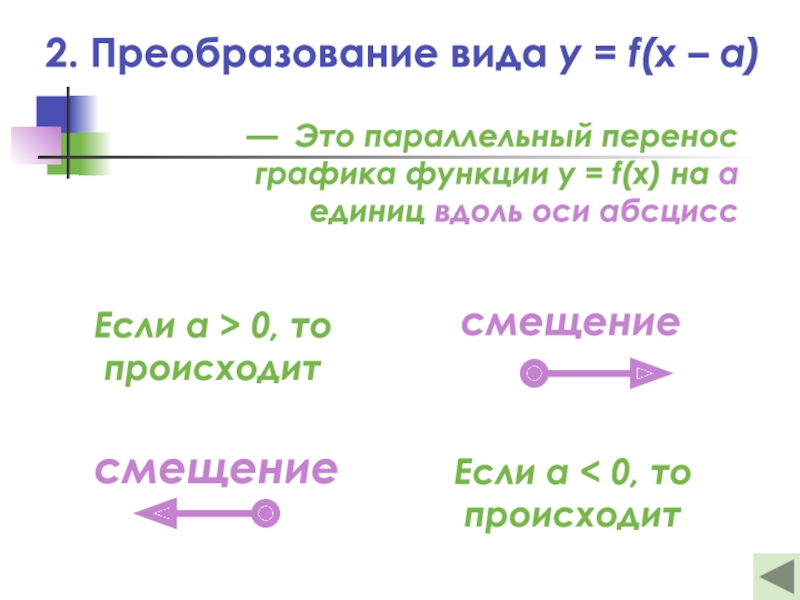
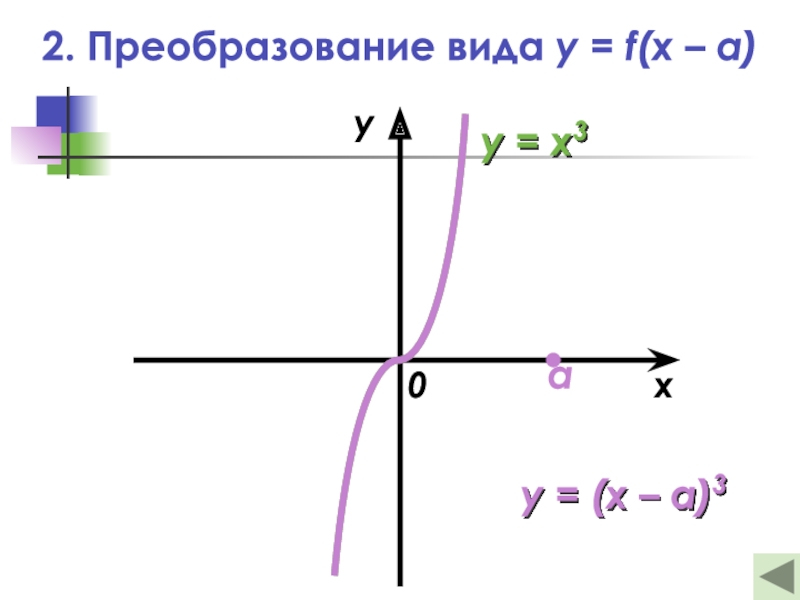
Слайд 132. Преобразование вида y = f(x – a)
— Это параллельный
перенос
графика функции y = f(x) на а единиц вдоль
оси абсциссЕсли а > 0, то
происходит
Если а < 0, то
происходит
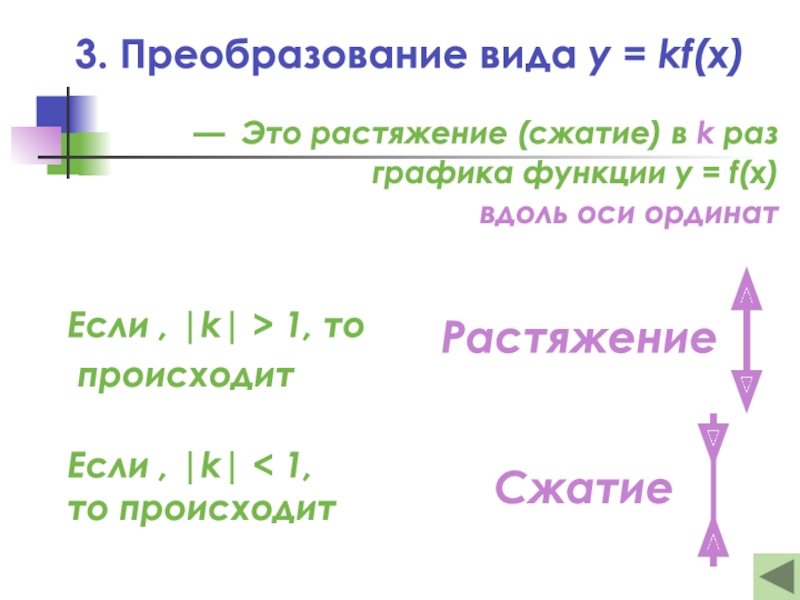
Слайд 153. Преобразование вида y = kf(x)
— Это растяжение (сжатие) в
k раз
графика функции y = f(x)
вдоль оси ординат
Если , |k|
> 1, топроисходит
Если , |k| < 1, то происходит
Слайд 174. Преобразование вида y = f(mx)
— Это растяжение (сжатие) в
m раз графика функции y = f(x)
вдоль оси абсциссЕсли , |m|> 1, то
происходит
Если , |m|< 1, то
происходит
Слайд 195. Преобразование вида y = |f(x)|
— Это отображение нижней части
графика функции y = f(x) в верхнюю
полуплоскость относительно оси
абсциссс сохранением верхней части графика
y = |f(x)|
Слайд 216. Преобразование вида y = f (|x|)
— Это отображение правой
части графика функции y = f(x) в левую полуплоскость
относительно оси ординат с сохранением правой части графикаy = f (|x|)
Слайд 23— Это отображение верхней части
графика функции y = f(x)
в нижнюю
полуплоскость относительно оси абсцисс
с сохранением только верхней
части графика|y| = f(x)
7. Преобразование вида |y|= f(x)
Слайд 25Свойства функций
Свойства линейной функции
Свойства квадратичной функции
Свойства степенной функции
Свойства обратной пропорциональности
Свойства
показательной функции
Свойства логарифмической функции
Свойства тригонометрических функций:
y = sin x
y = tg xy = cos x y = ctg x
Слайд 26Свойства линейной функции
1о D(y) = (−∞; +∞); E(y) =
(−∞; +∞).
2о Если b = 0, то функция нечетная.
Если b ≠ 0, то функция ни четная, ни нечетная.3о Если х = 0, то у = b, если у = 0, то х = − .
4о Если k > 0, то функция возрастает при х(−∞; +∞).
Если k < 0, то функция убывает при х(−∞; +∞).
y = kx + b
Слайд 27Свойства квадратичной функции
1о D(y) = (−∞; +∞).
2о Если a
> 0, то E(y) = [ув ; +∞);
Если
a < 0, то E(y) = (−∞; ув ].3о Если b = 0, то функция четная.
Если b ≠ 0, то функция ни четная, ни нечетная.
4о Если х = 0, то у = c, если у = 0, то х1,2 =
5о Если a > 0, то функция возрастает при х[xв ; +∞);
функция убывает при х(−∞; хв ].
Если a < 0, то функция возрастает при х(−∞; хв ];
функция убывает при х[xв ; +∞).
y = ax2 + bx + c, а ≠ 0
Подробнее
Слайд 28Свойства степенной функции
y = xn
Если n = 2k, где k
Z
1о D(y)=(−∞; +∞).
2о E(y)=[0 ; +∞).
3о
Функция четная.4о Если х = 0, то у = 0.
5о Функция возрастает
при х[0 ; +∞);
убывает при х(−∞; 0].
Если n = 2k +1, где k Z
1о D(y)=(−∞; +∞).
2о E(y)=(−∞; +∞).
3о Функция нечетная.
4о Если х = 0, то у = 0.
5о Функция возрастает
при х(−∞; +∞).
Слайд 29Свойства обратной пропорциональности
1о D(y) = (−∞; 0)u(0; +∞)
2о E(y)
= (−∞; 0)u(0 ; +∞)
3о Функция нечетная.
4о х ≠ 0,
у ≠ 0. 5о Если k > 0, то функция убывает
при х(−∞; 0)u(0; +∞).
Если k < 0, то функция возрастает
при х(−∞; 0)u(0; +∞).
Слайд 30Свойства степенной функции
y = x-n
Если n = 2k, где k
Z
1о D(y)=(−∞; 0)U(0; +∞).
2о E(y)=(0 ; +∞).
3о Функция четная.
4о Если х = 1, то у = 1.
5о Функция возрастает
при х(−∞; 0);
убывает при х(0 ; +∞).
6º функция ограничена
снизу прямой у = 0.
Если n = 2k +1, где k Z
1о D(y)=(−∞; 0)U(0; +∞).
2о E(y)=(−∞; 0)U(0; +∞).
3о Функция нечетная.
4о Если х = 1, то у = 1;
если х = -1, то у = -1.
5о Функция убывает
при х(−∞; 0);(0; +∞).
6º Функция не
ограничена