Периодическая кусочно-гладкая функция – определена и непрерывна на всей оси,
за исключением заданных точек, в которых она терпит разрыв первого рода, и удовлетворяет равенству:Пример 1. Построить график периодической функции с периодом T = 2





![Функциональные ряды. Продолжение Ортогональность системы тригонометрических функцийИнтеграл по отрезку [-, ] от произведения двух Ортогональность системы тригонометрических функцийИнтеграл по отрезку [-, ] от произведения двух любых функций, входящих в ряд Фурье](/img/thumbs/2bd2a646afe30438c27e5535d7ef8e99-800x.jpg)
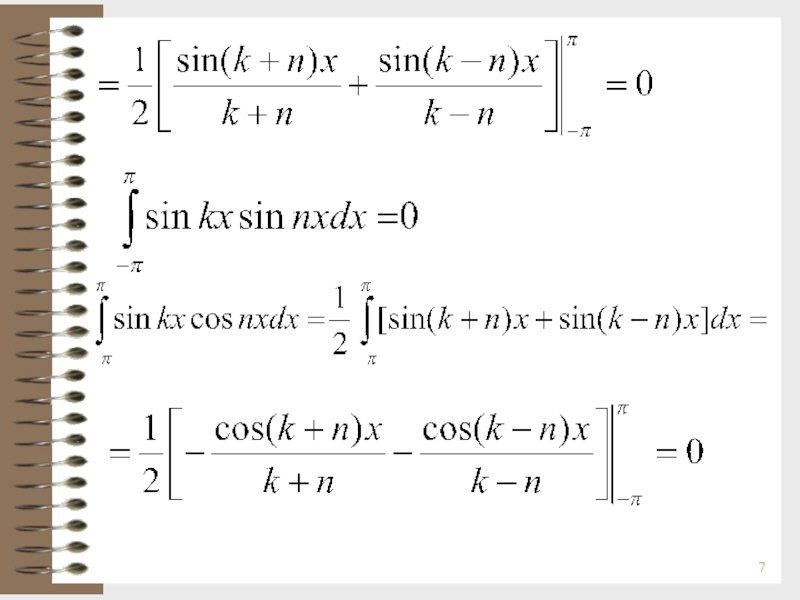
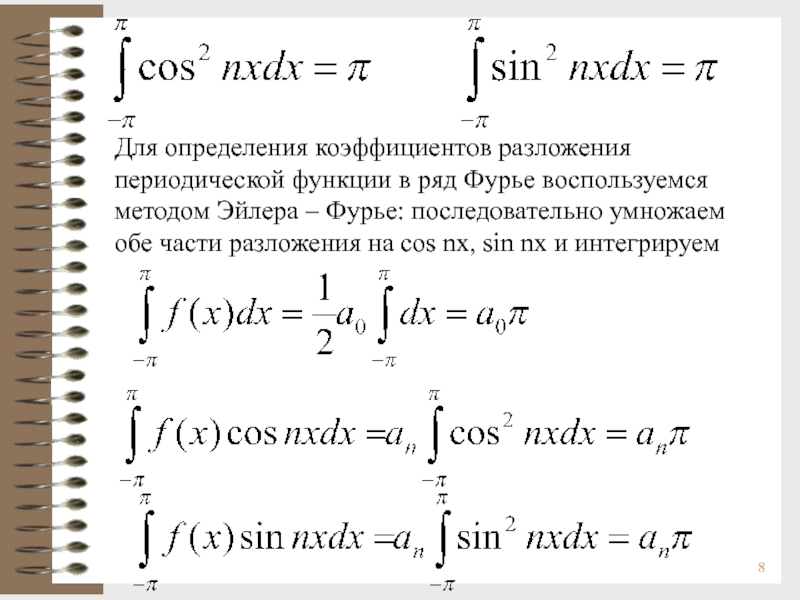

![Функциональные ряды. Продолжение Сходимость ряда ФурьеТеорема. Пусть функция непрерывна вместе со своей производной на Сходимость ряда ФурьеТеорема. Пусть функция непрерывна вместе со своей производной на отрезке [-p, p] или они имеют](/img/thumbs/51a0e0a2ca57883bef3f5c5acde4ffd6-800x.jpg)
![Функциональные ряды. Продолжение на концах отрезка [-p,p] сумма ряда равна для любой точки на концах отрезка [-p,p] сумма ряда равна для любой точки вне отрезка [-p,p] предыдущие утверждения справедливы](/img/thumbs/fcea47cd5a83871e07af44f3a110ec1e-800x.jpg)




















