Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Жазы?ты?та?ы т?зуді? те?деуі
Содержание
- 1. Жазы?ты?та?ы т?зуді? те?деуі
- 2. Сабақтың мақсаты:
- 3. Екі нүкте арқылы өтетін түзудің теңдеуіA(x1; y1)M(x; y)B(x2; y2)
- 4. МысалКоординаттары А(5; –8) және В(–3; 0) нүктелері арқылы өтетін түзудің теңдеуін жазыңдар
- 5. Берілген нүкте арқылы және бағыттауыш векторы бар түзудің теңдеуіA(x1; у1)M(x; y)
- 6. МысалКоординатасы А(5; 5) нүктесі арқылы өтетін және s = (9; 10)бағыттауыш векторы бар түзудің теңдеуін жазу
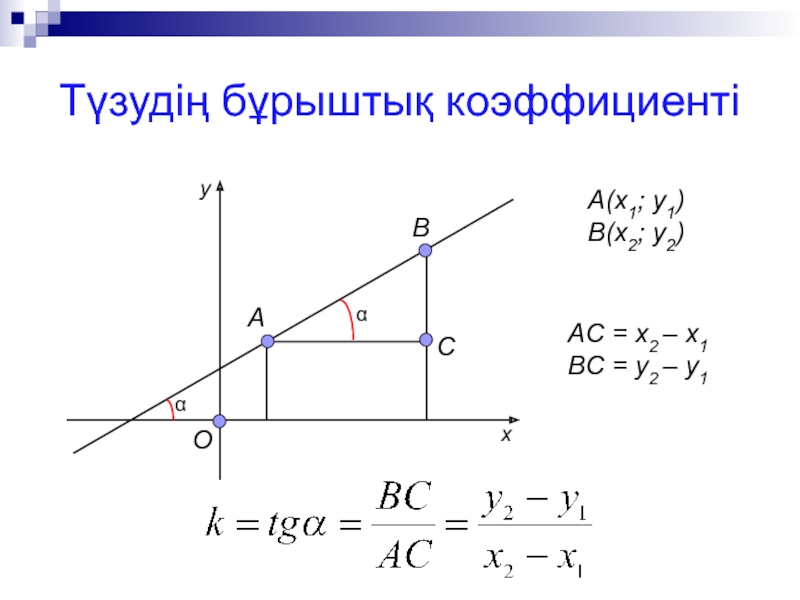
- 7. Түзудің бұрыштық коэффициентіОАВА(х1; у1)В(х2; у2)СααAC = x2 – x1BC = y2 – y1xy
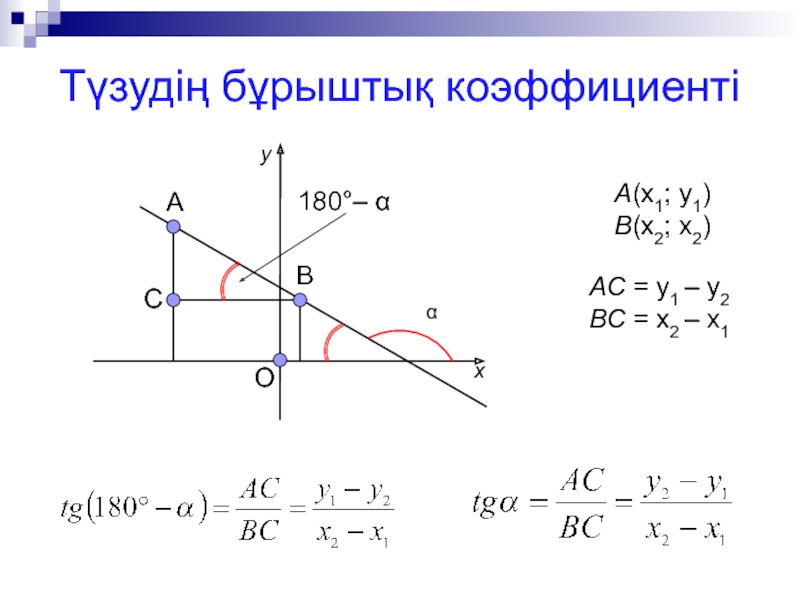
- 8. Түзудің бұрыштық коэффициентіA(x1; y1)B(x2; x2)OBACα180°– αAC = y1 – y2BC = x2 – x1xy
- 9. МысалA(-1; 4) және B(5; 8) нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табу
- 10. Берілген нүкте арқылы өтетін және берілген бұрыштық
- 11. Уравнение прямой, заданной угловым коэффициентом и начальной
- 12. Түзудің жалпы теңдеуіy = kx + b
- 13. Сызықтық теңдеу Ax + Bx +
- 14. Скачать презентанцию
Сабақтың мақсаты:
Слайды и текст этой презентации
Слайд 6Мысал
Координатасы А(5; 5) нүктесі арқылы өтетін және s = (9;
10)бағыттауыш векторы бар түзудің теңдеуін жазу
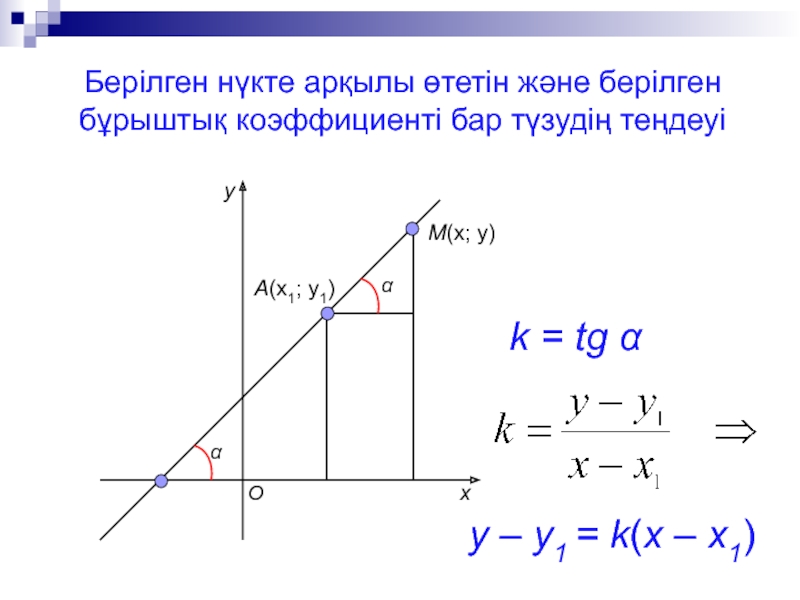
Слайд 10Берілген нүкте арқылы өтетін және берілген бұрыштық коэффициенті бар түзудің
теңдеуі
A(x1; y1)
M(x; y)
O
α
α
k = tg α
y – y1 = k(x
– x1)x
y
Слайд 11
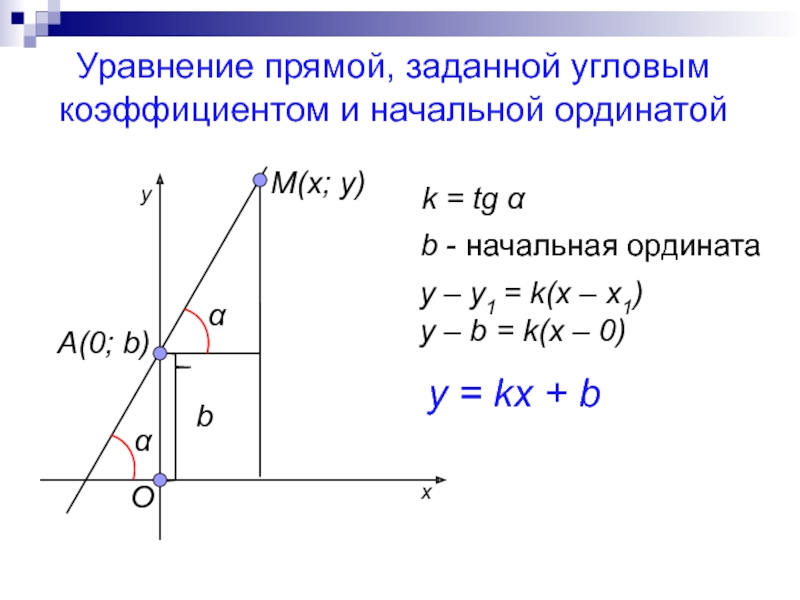
Уравнение прямой, заданной угловым коэффициентом и начальной ординатой
М(x; y)
A(0; b)
O
b
α
α
k
= tg α
b - начальная ордината
y – y1 = k(x
– x1)y – b = k(x – 0)
y = kx + b
x
y
Слайд 12Түзудің жалпы теңдеуі
y = kx + b ? 0 =
kx – y + b ?
kx – y +
b = 0A = k;
B = -1;
C = b
Ax + By + c = 0 где, А ≠ 0 или В ≠ 0
Слайд 13Сызықтық теңдеу
Ax + Bx + C = 0,
в котором хотя бы один из коэффициентов А или В
отличен от нуля, называется общим уравнением прямой
