Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ СТРОИТЕЛЬСТВЕ И ЭКСПЛУАТАЦИИ МОСТОВ
Содержание
- 1. ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ СТРОИТЕЛЬСТВЕ И ЭКСПЛУАТАЦИИ МОСТОВ
- 2. ЛитератураОсновнаяИнтернет- ресурс: Михелев Д.Ш. Инженерная геодезия: учебник
- 3. ВВЕДЕНИЕ Задачи геодезии в разных циклах строительного
- 4. 1. Изыскания дорог, мостовых переходов и транспортных тоннелейТребуемый масштаб составляемого плана
- 5. Методы изысканий дорог и мостов1. Геодезический методНазначение
- 6. Методы создания планово-высотного обоснования съемки местности Разомкнутый
- 7. Вычисление разомкнутого теодолитного ходаУравнивание углов: Фактическая угловая невязка Допустимая угловая невязка Поправки в измеренные углы Вычисление дирекционных углов линий
- 8. Вычисление разомкнутого теодолитного ходаУравнивание сторон:Линейные невязки по
- 9. Вычисление разомкнутого теодолитного ходаВычисление координатПоправки в приращения координатИсправленные приращения координатВычисление координат
- 10. Методы создания планово-высотного обоснования съемки местностиСвободная сеть полигонов
- 11. Методы создания планово-высотного обоснования съемки местностиА121(X, Y)А(X, Y)С34 (X, Y)5 (X, Y)67891011121314151654Несвободная сеть полигонов
- 12. Методы создания планово-высотного обоснования съемки местности123456781234Сеть треугольников (центральная система)Цепочка треугольниковГеодезический четырехугольник123456
- 13. Съемка местности электронным теодолитом Режим прямой геодезической
- 14. Съемка местности электронным теодолитом1. Угловая невязка::
- 15. Съемка местности электронным теодолитомРежим обратной геодезической засечкиАXYВXYDXYCγDγAγB
- 16. Преобразование цифровой в аналитическую модель местности 173,15271,29377,88477,981078,16РекаЦифровая модель местностиАналитическая модель местности
- 17. Спутниковые методы геодезических измерений ГЛОНАСС – ГЛОбальная
- 18. Космический сегментГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система24
- 19. Космический сегментNAVSTAR – GPS – NAVigation Sistem
- 20. Сегмент контроля и управленияГЛОНАСС – ГЛОбальная НАвигационная
- 21. Сегмент контроля и управленияСтанция слеженияКонтроль траектории движения
- 22. Сегмент пользователя Структурная схема приемникаЧастотное разделение сигналовКодовое разделение сигналов
- 23. Сегмент пользователя Структурная схема приемникаАнтена с
- 24. Сегмент пользователяКлассификация приемников по кодировке сигнала: C/A
- 25. Сегмент пользователяРежимы наблюдений:Статика;Быстрая статика;Кинематика;Кинематика “в полете”;Кинематика в
- 26. Теоретические основы уравнивания геодезических измерений 3 Количество измерений
- 27. Теоретические основы уравнивания геодезических измерений Теория способа
- 28. Теория способа наименьших квадратовВероятности появления оптимальных значений
- 29. Реализация способа наименьших квадратов Способ полигонов
- 30. Способ полигонов Уравнивание угловАВ21А(X, Y)На точку ВС345678910111213141516j=1j=21234j=3j=4j=5j=6j=7j=8
- 31. Способ полигонов Уравнивание углов Угловые невязки в
- 32. Способ полигонов Уравнивание угловВычисление весовых коэффициентов и поправок в углыVj(i) = Pj(i)Wi.
- 33. Способ полигонов Уравнивание приращений координатНевязки в полигонах
- 34. Способ полигонов Уравнивание приращений координатВычисление весовых коэффициентов и поправок в приращения координатVxij = PijfxiVyij = Pijfyi
- 35. Способ полигонов Уравнивание превышений, исходные данные
- 36. Способ полигонов Уравнивание превышенийВычисление невязок в полигонахПолигон
- 37. Способ полигонов Уравнивание превышенийВычисление весовых коэффициентов и поправок в превышенияVhij = Pijfhi
- 38. Способ полигонов Уравнивание превышений Практическая реализация
- 39. Особенности геодезических работ Изыскания мостовых переходовУрез воды
- 40. Особенности геодезических работ Изыскания мостовых переходовУрез
- 41. Особенности геодезических работ Изыскания мостовых переходовУрез
- 42. Особенности геодезических работ Изыскания мостовых переходовОтметка
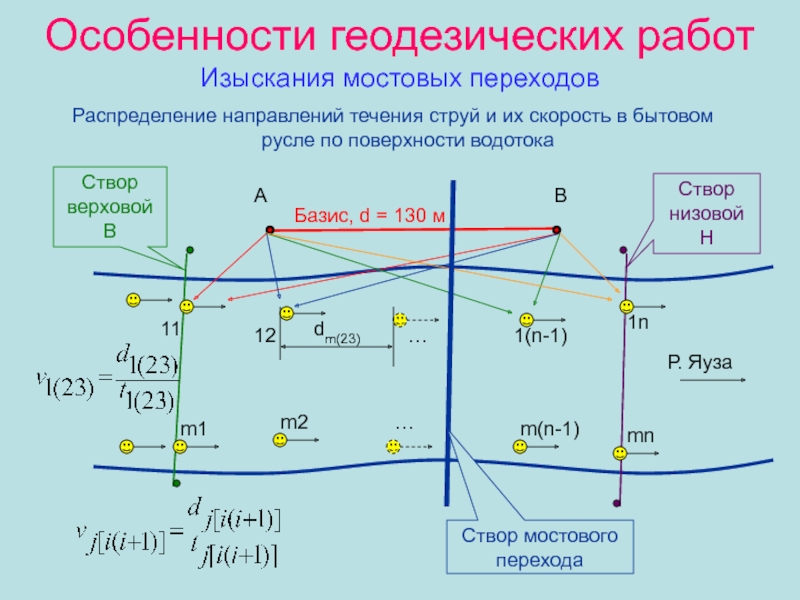
- 43. Особенности геодезических работ Изыскания мостовых переходовРаспределение
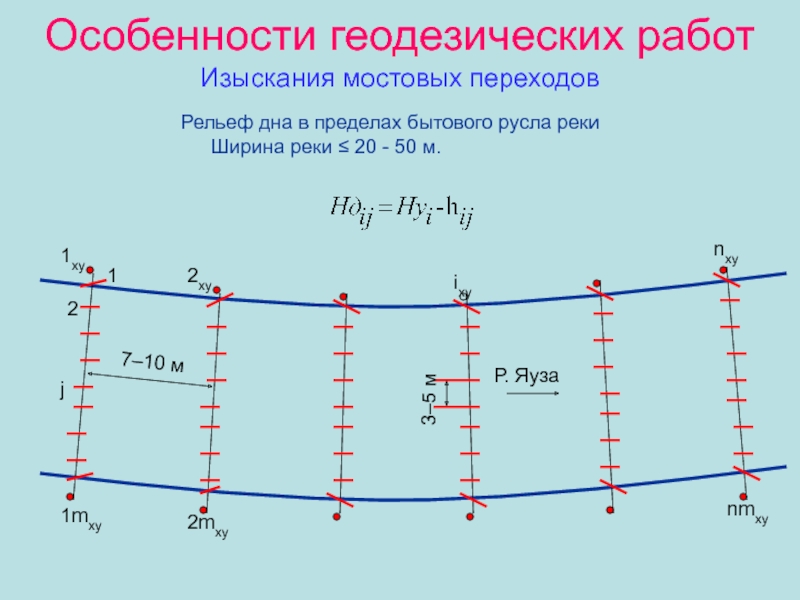
- 44. Особенности геодезических работ Изыскания мостовых переходовРельеф
- 45. Особенности геодезических работ Изыскания мостовых переходовРельеф
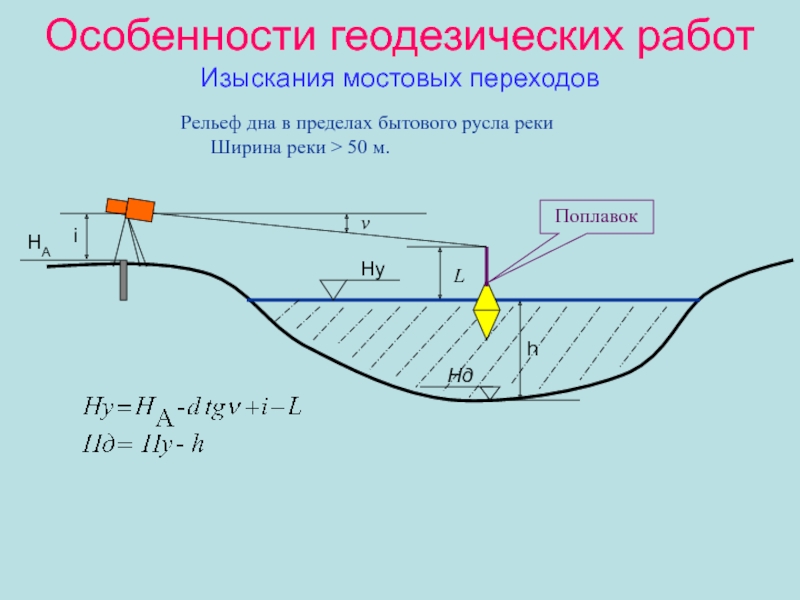
- 46. Особенности геодезических работ Изыскания мостовых переходовРельеф
- 47. Особенности геодезических работ. Изыскания тоннелей. Условия
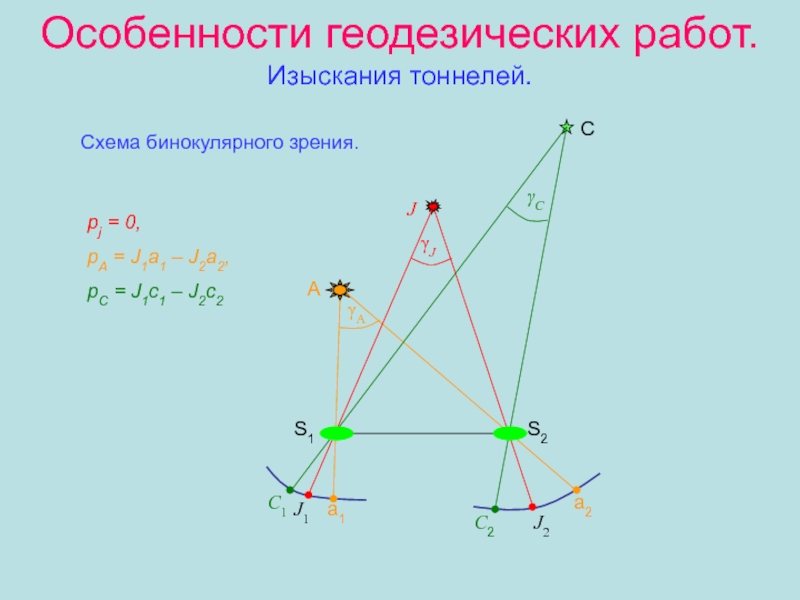
- 48. Особенности геодезических работ. Изыскания тоннелей. J1рj
- 49. Особенности геодезических работ. Изыскания тоннелей.
- 50. Особенности геодезических работ. Изыскания тоннелей. Элементы
- 51. Особенности геодезических работ. Изыскания тоннелей Координаты
- 52. Особенности геодезических работ. Изыскания тоннелей Случаи
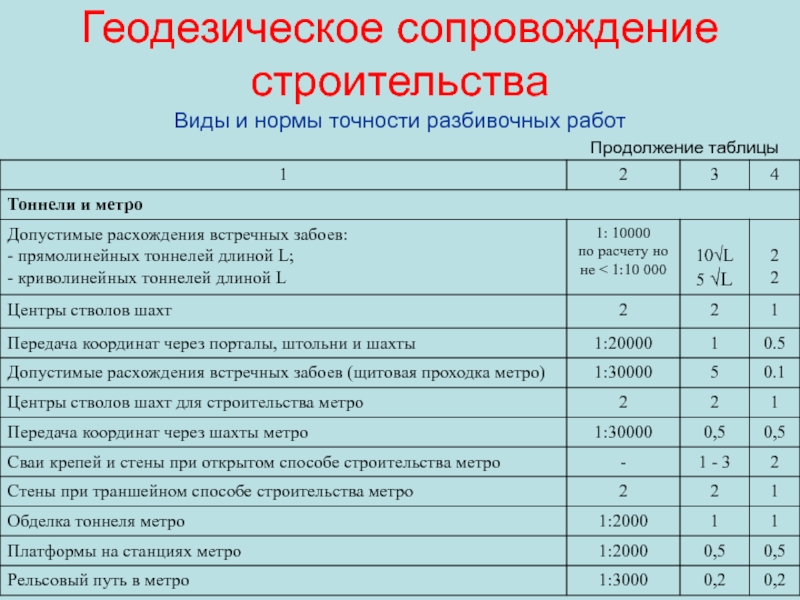
- 53. Геодезическое сопровождение строительства Виды и нормы точности
- 54. Геодезическое сопровождение строительства Виды и нормы точности разбивочных работТаблица
- 55. Геодезическое сопровождение строительства Виды и нормы точности разбивочных работПродолжение таблицы
- 56. Геодезическое сопровождение строительства Виды и нормы точности разбивочных работПродолжение таблицы
- 57. Геодезическое сопровождение строительства Опорная сеть для разбивки
- 58. Геодезическое сопровождение строительства Методы разбивки сооружений Метод
- 59. Геодезическое сопровождение строительства Методы разбивки сооружений (метод
- 60. Геодезическое сопровождение строительства Методы разбивки сооружений (метод координат)Погрешность метода координат
- 61. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод
- 62. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод
- 63. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод
- 64. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод
- 65. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод
- 66. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод засечек) Способ обратной засечки, гдеПогрешность положения точки С′, где
- 67. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод засечек) Способ створной засечки 12А341′2′D3′4′BXYDXYγBγDР. Соть
- 68. Геодезическое сопровождение строительства Методы разбивки сооружений (Метод засечек) Способ линейной засечки BAbaληMCC′cττ
- 69. Геодезическое сопровождение строительства Разбивка точек электронным теодолитомCXYX = +2,65 мY = +1,53 м+X+Y+X+YAXYAXYBXY-YβCXYXX+Y+Y-Y-XilC′
- 70. Геодезическое сопровождение строительства Типичное размещение опорных точек
- 71. Геодезическое сопровождение строительства Технологический островок под мостовой опорой
- 72. Типичное размещение опорных точек для разбивки опор мостовых переходов Первый случай1/3(MN)1/3(MN)1/3(MN)1/3(MN)MNM′N′123ADBEР. Хоперγγγ
- 73. Типичное размещение опорных точек для разбивки опор мостовых переходов Второй случай1/3(MN)1/3(MN)MNM′N′123ADР. Хопер½(MN)½(MN)BCEFγγγγγПойма
- 74. Типичное размещение опорных точек для разбивки опор мостовых переходов Третий случай1/3(MN)1/3(MN)MNM′N′123ABР. ХоперСγγγγγ
- 75. Типичное размещение опорных точек для разбивки опор мостовых переходов Четвертый случайMNM′N′123Р. ХоперBCγАDЕγγПойма
- 76. Разбивка тоннеля Схема тоннельной триангуляции и подходной полигонометрииIIIIIIIVVVIВходной порталВыходной порталТоннельная полигонометрияТоннельная триангуляция
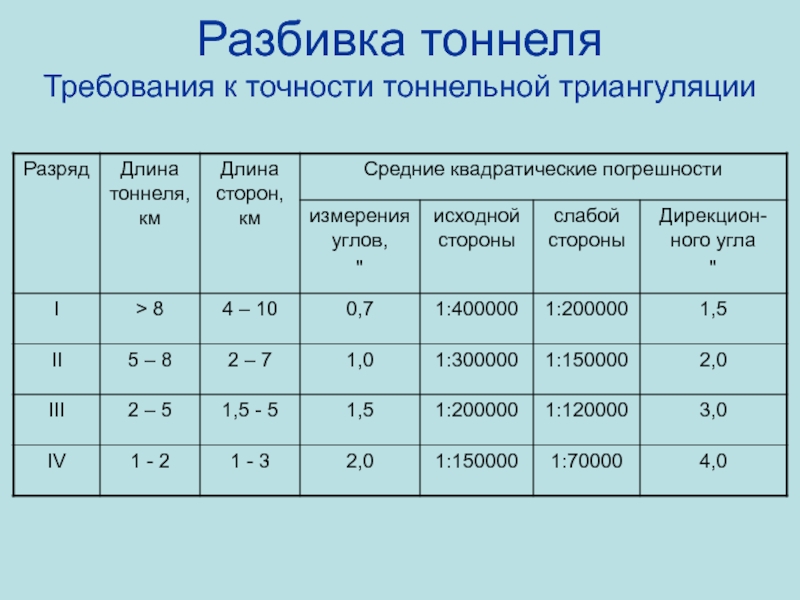
- 77. Разбивка тоннеля Требования к точности тоннельной триангуляции
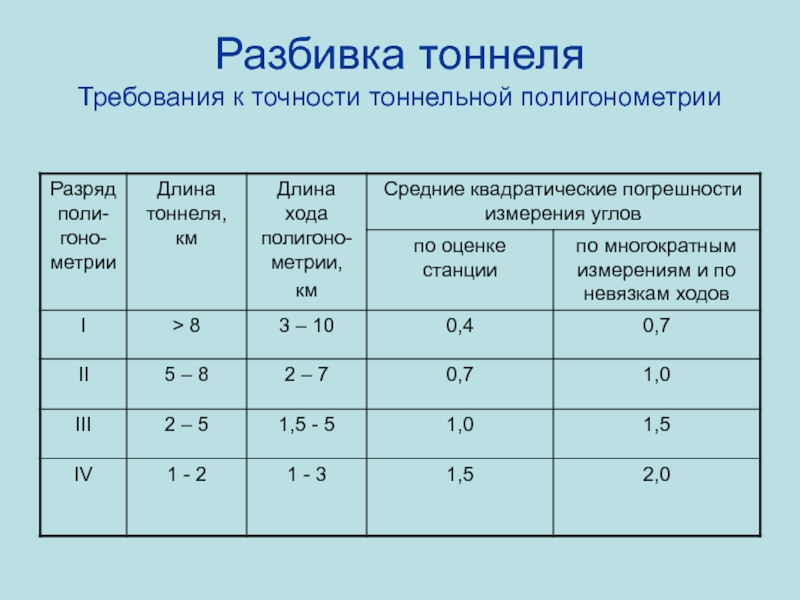
- 78. Разбивка тоннеля Требования к точности тоннельной полигонометрии
- 79. Разбивка тоннеля Передача координат и дирекционного угла
- 80. FED′Разбивка тоннеля Передача координат и дирекционного угла
- 81. Разбивка тоннеля Передача координат и дирекционного угла
- 82. Разбивка тоннеля Передача дирекционного угла через шахту
- 83. Разбивка тоннеля Передача отметки на дно шахтыЕмкость
- 84. Разбивка тоннеля Прямолинейный тоннель с постоянным уклоном
- 85. Разбивка тоннеля Прямолинейный тоннель с постоянным уклоном
- 86. Разбивка тоннеля Криволинейный тоннель с постоянным уклономНК(XYH)A(X,Y,H)B(X,Y,H)КК(X,Y,H)ВУ(X,Y,H)СК(X,Y,H)RОRRВходной порталВыходной порталdAНК, AНК, idККВ, ККВ, iТТК
- 87. Разбивка тоннеля Способы разбивки простых круговых
- 88. Разбивка тоннеля Способы разбивки простых круговых кривых Способ прямоугольных координатНКO
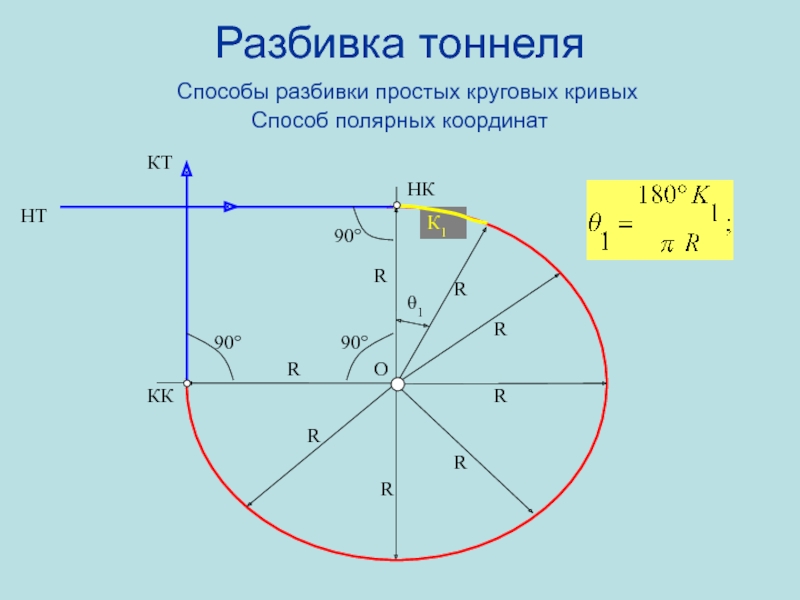
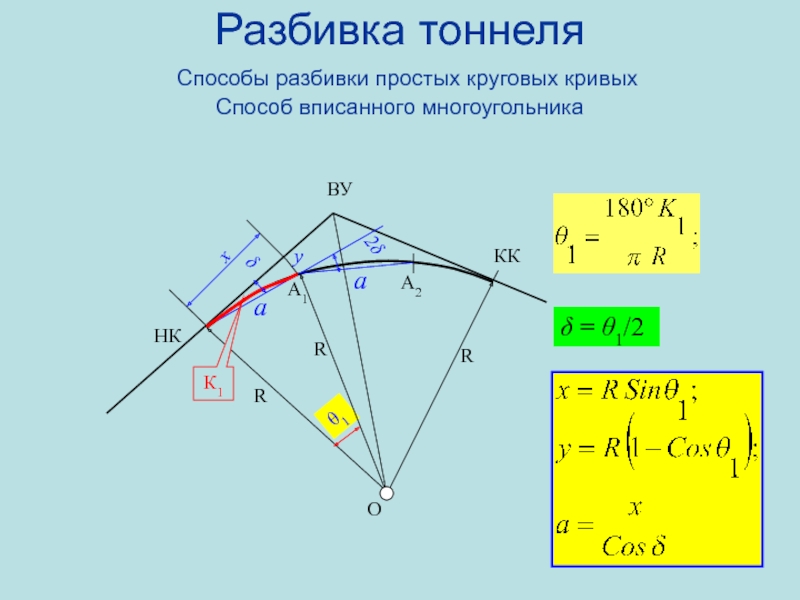
- 89. βaРазбивка тоннеля Способы разбивки простых круговых кривых Способ полярных координатНКА1А2ККRRRROВУθ1δδ = θ1/2 ТxyК1
- 90. Разбивка тоннеля Способы разбивки простых круговых кривых Способ полярных координатНКККRRRRRRRRНТКТOК1θ190°90°90°
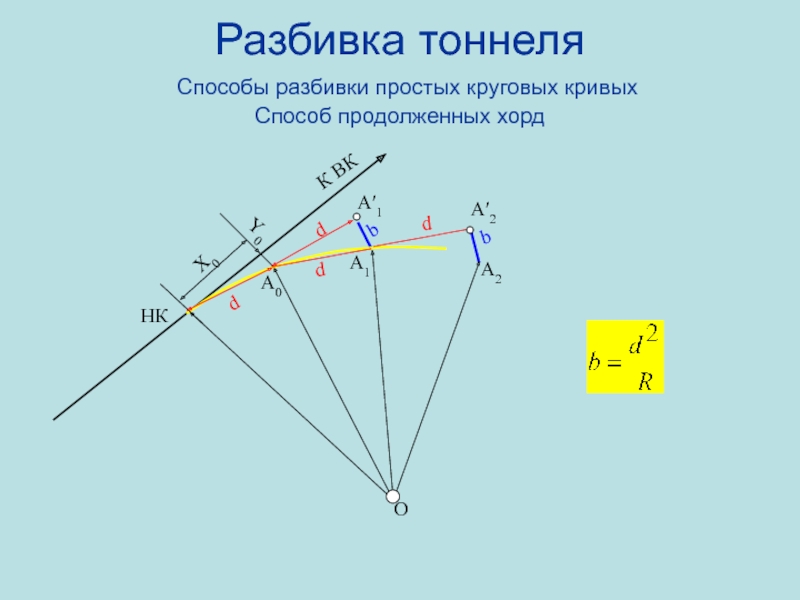
- 91. Разбивка тоннеля Способы разбивки простых круговых кривых Способ продолженных хордX0Y0bddНКА0А1bOddA2К ВКА′1А′2
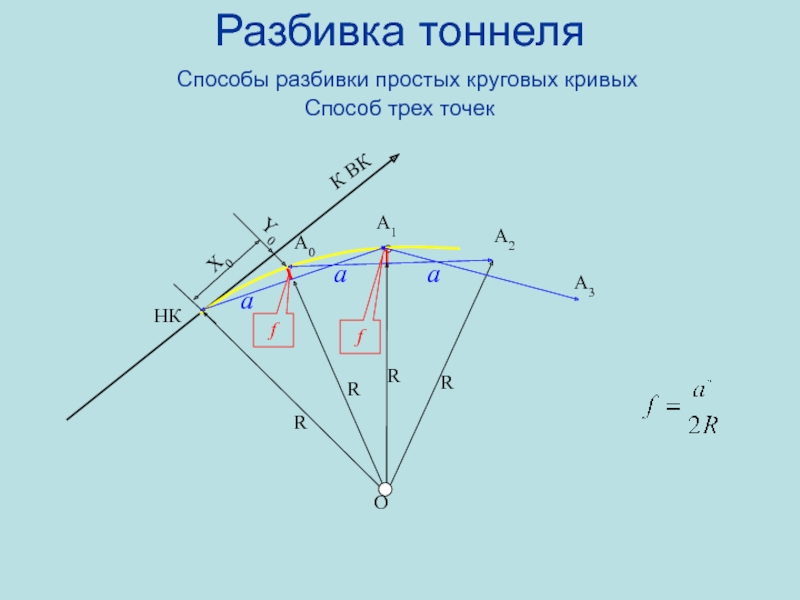
- 92. Разбивка тоннеля Способы разбивки простых круговых кривых Способ трех точек
- 93. Разбивка тоннеля Способы разбивки простых круговых
- 94. Разбивка тоннеля Способы разбивки простых круговых кривых Способ вписанного многоугольника НКА1ККRRВУθ1δxyК1А22δааδ = θ1/2 RO
- 95. Разбивка тоннеля Способ разбивки с учетом переходных кривыхθpНПК1φ1φ2xt1t2НККНПК2КПК1КККxt1t2RКПК2R1OyyВУll
- 96. Разбивка тоннеля Способ разбивки с учетом переходных
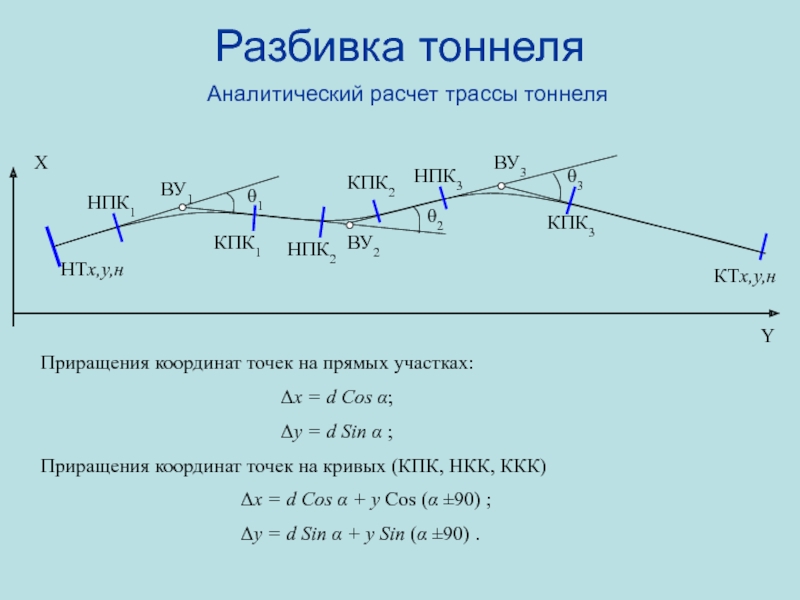
- 97. Разбивка тоннеля Аналитический расчет трассы тоннеляНТx,y,нНПК1НПК2НПК3КПК3КПК2КПК1КТx,y,нВУ1ВУ2ВУ3XYθ1θ2θ3Приращения
- 98. Разбивка тоннеля Аналитический расчет трассы тоннеля Ведомость прямых и кривых
- 99. Геодезические работы при эксплуатации мостовДеформация сооружений и их видыВертикальные: осадка, пучениеГоризонтальные - сдвигXY-δx-δyδδδzΔYZX
- 100. Определение деформаций CB α = r
- 101. Геодезические методы определения деформацийметод геометрического нивелирования I,
- 102. метод геометрического нивелирования. Классы нивелирования и
- 103. Конструкции деформационных реперов и марокГоловка репера7550150102030Выступающая часть репераНесущая опора МПРейка
- 104. Конструкции деформационных реперов и марок150Ø 30Скважина с
- 105. метод гидронивелирования Определение относительных смещений строительных конструкцийаbh = a - bМензурки с миллиметровыми делениямиСоединительный шлангПатрубокh
- 106. метод угловых измерений Определение смещений верхней части высотных сооруженийAпр021OAТ 2Т 1XYТ 2′Т 1′AпрAпрAлAлAл
- 107. метод угловых измерений Определение смещений верхней части
- 108. метод координат Схема мостовой триангуляции Наблюдение горизонтальных смещений опор мостового перехода564321C87DАB
- 109. метод координат Ведомость смещений верхнего строения опор
- 110. метод координатС4,65,23,85,34,11,84.92.3Векторная диаграмма смещений верхнего строения опор
- 111. фотограмметрический методZXBAНаправление оптической оси фотокамерыНаправление ориентирования
- 112. стереофотограмметрический методBXYZS1S2
- 113. Элементы внутреннего ориентирования - координаты главной
- 114. стереофотограмметрический метод Схема стереоприбора для наблюдения и измерения объема
- 115. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ СТРОИТЕЛЬСТВЕ И ЭКСПЛУАТАЦИИ МОСТОВ
Кафедра
Инженерные изыскания и
информационные технологии в строительстве
Слайд 2Литература
Основная
Интернет- ресурс: Михелев Д.Ш. Инженерная геодезия: учебник /Е.Б. Клюшин [и
др.]; под ред. Д.Ш.Михелева, - 9-е изд. стер. – Электронные
текстовые данные –М.: ИЦ «Академия», 2008.Инженерная геодезия: учебник для студ. высш. учеб. заведений / Е.Б. Клюшин, М.И. Киселев, Д.Ш. Михелев, В.Д. Фельдман; под ред. Д.Ш. Михелева. – 8-е изд., стер. – М.: Изд. Центр “Академия”, 2008. – 480 с.
Федотов Г.А. Инженерная геодезия: учебник / Г.А. Федотов. – 4-е изд. стер. – М.: Высш. шк., 2007. – 463 с.
Новиков В.И. Геодезические измерения в строительстве: учеб пособие / В.И.Новиков, А.Б.Рассада. Саратов: РИЦ, СГТУ, 2010, 187 с
Новиков В.И. Геодезические съемки: учеб пособие / В.И.Новиков, А.Б.Рассада. Саратов: РИЦ, СГТУ, 2011, 136 с.
Дополнительная
Брайт П.И. Геодезические методы измерения деформаций оснований и сооружений. М.: Недра, 1965. - 298 с.
Левчук. Г.П. Курс инженерной геодезии. Основные виды инженерно-геодезических работ. Геодезические работы при изысканиях и строительстве транспортных и промышленных сооружений. М.: Недра, 1970. - 408 с.
Трунин А.Ф., Финаревский И.И., Чистяков С.В. Фототеодолитная съемка в крупных масштабах. Изд. 2, испр. и доп. М.: Недра, 1978. - 207 с.
Федоров В.И. Инженерная геодезия: Учебник для вузов. М.: Недра, 1990. - 357 с.
Слайд 3ВВЕДЕНИЕ
Задачи геодезии в разных циклах строительного производства
В период проектирования:
сбор
исходной картографической информации для принципиального решения вопроса размещения объекта строительства;
съемочные
работы в крупном масштабе для детального проектирования элементов объекта строительства.В период строительства:
определение местоположения площадки строительства и пространственное размещение в плане и по высоте элементов запроектированного сооружения;
геодезическое сопровождение строительства объекта для контроля правильности возведения конструкции в целом и взаимного расположения его элементов.
В период эксплуатации:
исполнительная съемка для контроля правильности завершенного строительства и выявления отступлений от проекта;
геодезические работы по определению эксплуатационных сдвигов объекта в целом и смещений его элементов для контроля и прогноза устойчивости конструкции.
Слайд 41. Изыскания дорог, мостовых переходов и транспортных тоннелей
Требуемый масштаб составляемого
плана
Слайд 5Методы изысканий дорог и мостов
1. Геодезический метод
Назначение морфоствора по карте;
Трассирование автомобильной дороги непосредственно в полевых условиях – определение положения
ключевых точек;Полный комплекс нивелировочных работ по трассе;
Тахеометрическая съемка сложных мест трассы (переходы через овраги, пересечения с иными объектами и др.);
Привязка трассы к пунктам государственной сети;
Камеральная обработка материалов полевых работ.
2. Метод геоинформатки
Съемка местности в крупном масштабе;
Составление электронной версии плана для полосы варьирования трассы;
Камеральное назначение и выбор трассы подходов и морфоствора из множества вариантов;
Камеральное определение координат ключевых точек трассы;
Вынос на местность ключевых точек трассы по координатам;
Трассирование и нивелировочные работы по трассе.
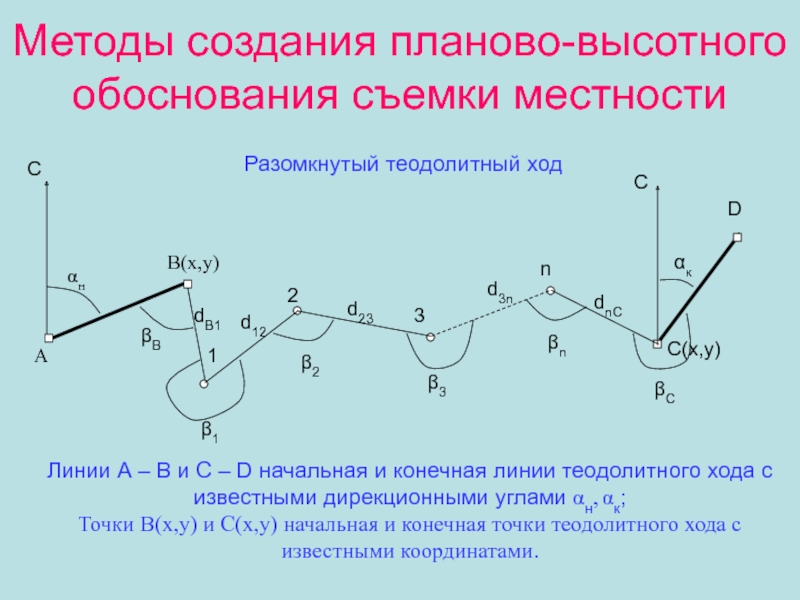
Слайд 6Методы создания планово-высотного обоснования съемки местности
Разомкнутый теодолитный ход
Линии А
– В и С – D начальная и конечная линии
теодолитного хода с известными дирекционными углами н, к;Точки В(x,y) и С(x,y) начальная и конечная точки теодолитного хода с известными координатами.
Слайд 7Вычисление разомкнутого теодолитного хода
Уравнивание углов:
Фактическая угловая невязка
Допустимая угловая невязка
Поправки в
измеренные углы
Вычисление дирекционных углов линий
Слайд 8Вычисление разомкнутого теодолитного хода
Уравнивание сторон:
Линейные невязки по осям координат:
Абсолютная погрешность
Относительная погрешность
Допустимая относительная погрешность
Слайд 9Вычисление разомкнутого теодолитного хода
Вычисление координат
Поправки в приращения координат
Исправленные приращения координат
Вычисление
координат
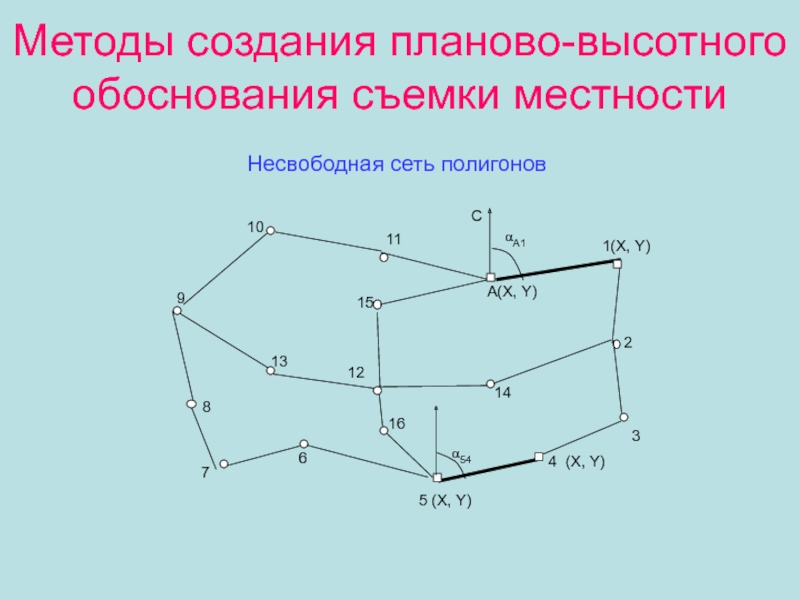
Слайд 11Методы создания планово-высотного обоснования съемки местности
А1
2
1(X, Y)
А(X, Y)
С
3
4 (X, Y)
5
(X, Y)
6
7
8
9
10
11
12
13
14
15
16
54
Несвободная сеть полигонов
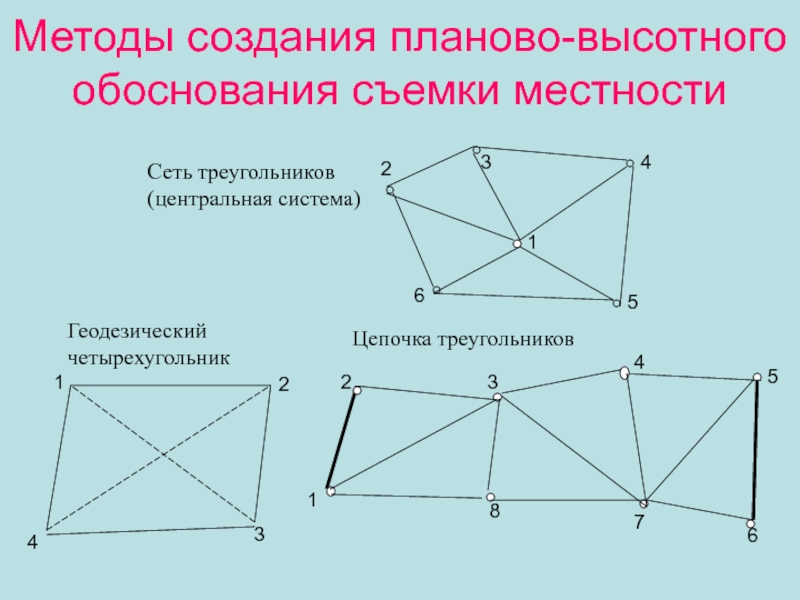
Слайд 12Методы создания планово-высотного обоснования съемки местности
1
2
3
4
5
6
7
8
1
2
3
4
Сеть треугольников
(центральная система)
Цепочка треугольников
Геодезический
четырехугольник
1
2
3
4
5
6
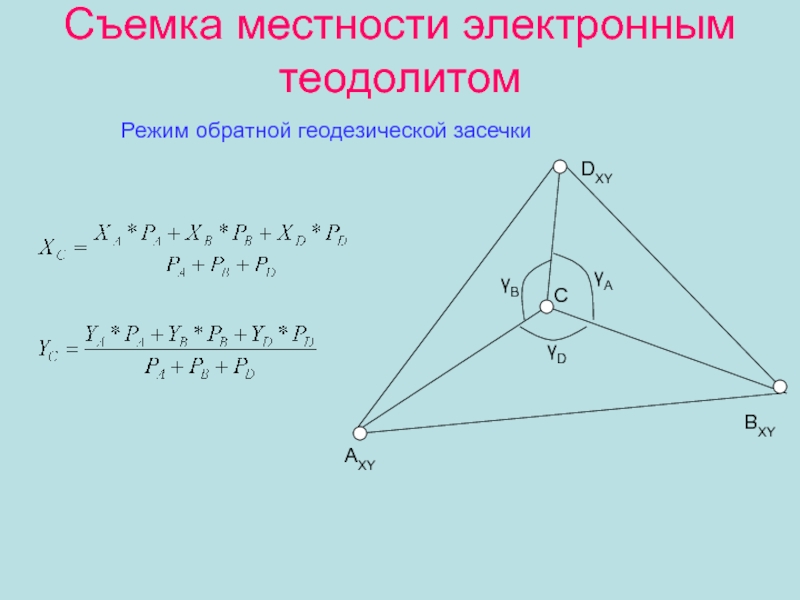
Слайд 13Съемка местности электронным теодолитом
Режим прямой геодезической задачи
di =
Di Cos νi; αi+1 = αi + βправ – 180°;
Xi+1
= Xi + di * Cos αi+1; Yi+1 = Yi + di * Sin αi+1; Hi+1 = Hi + Di*Sin νi + ii – li+1,
10
11
12
i
4
= αСD
Слайд 14Съемка местности электронным теодолитом
1. Угловая невязка:: fβ = αk
- αCD ,
если
, то “недопустимая угловая невязка”; если ,то βi = βi +(- fβ/n), αi+1 = αi + βi – 180°;
2. Линейная невязка: fx = Xk - XС, fy = Yk - YC , ;
если fабс/∑d ≥ 0.0005, то “недопустимая линейная невязка”
если fабс/∑d ≤ 0.0005, то
Xi+1 = Xi + di * Cos αi + ; Yi+1 = Xi + di * Sin αi +
3. Высотная невязка: fH = Hk - HC ;
если fH ≥ , то“недопустимая высотная невязка”
если fH ≤ , то Hi+1 = Hi + Di*Sin νi + ii – li +
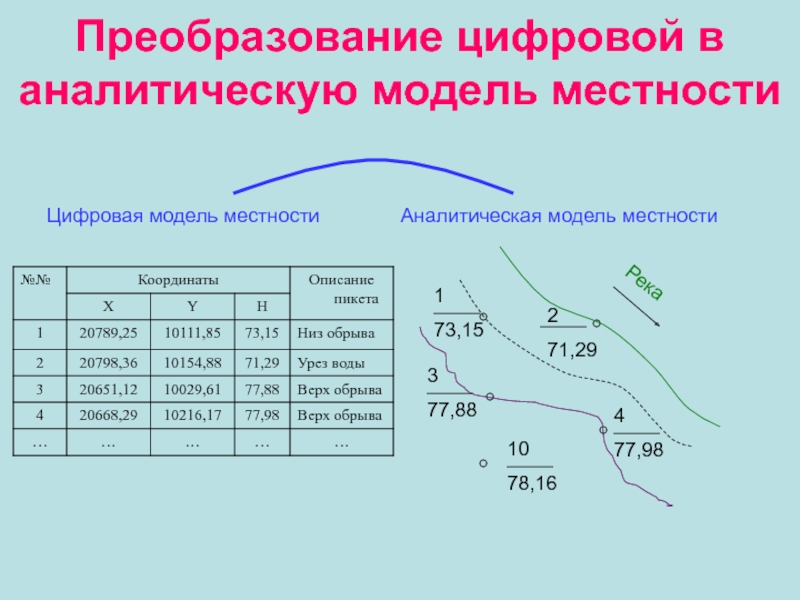
Слайд 16Преобразование цифровой в аналитическую модель местности
1
73,15
2
71,29
3
77,88
4
77,98
10
78,16
Река
Цифровая модель местности
Аналитическая модель
местности
Слайд 17Спутниковые методы геодезических измерений
ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система;
NAVSTAR
– GPS – NAVigation Sistem with Time And Rangiring –
Global Positioning System (Навигационная система определения расстояний и времени – глобальная позиционирования система).Состоят из трех сегментов:
космического, контроля и управления, сегмент пользователя
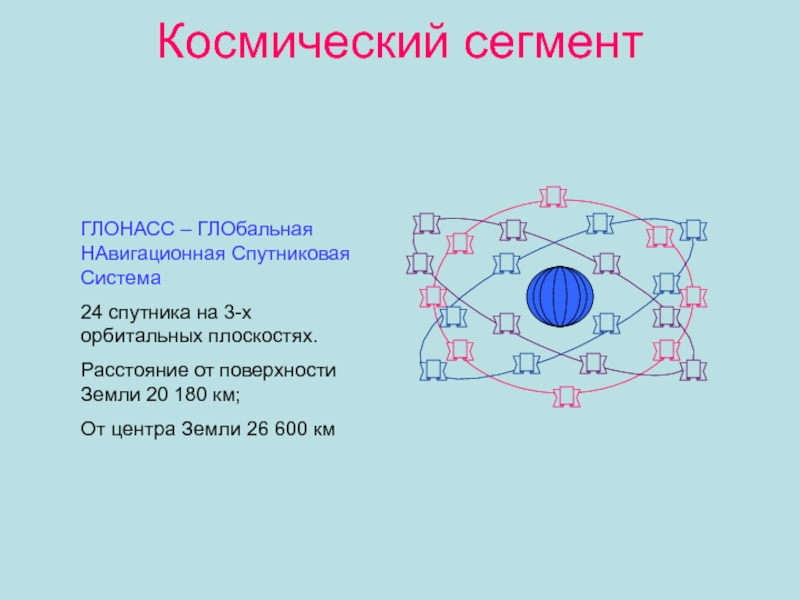
Слайд 18Космический сегмент
ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система
24 спутника на 3-х
орбитальных плоскостях.
Расстояние от поверхности Земли 20 180 км;
От центра Земли
26 600 кмСлайд 19Космический сегмент
NAVSTAR – GPS – NAVigation Sistem with Time And
Rangiring – Global Positioning System (Навигационная система определения расстояний и
времени – глобальная позиционирования система).21 рабочий и 3 запасных спутника на 6-и орбитальных плоскостях.
Расстояние от поверхности Земли 20 180 км;
От центра Земли 26 600 км
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Слайд 20Сегмент контроля и управления
ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система
ЦУС -
центр управления системой;
ЦС – центральный синхронизатор;
КС – контрольная станция;
СКФ –
система контроля фаз;КОС – квантово-оптическая станция;
АКП – аппаратура контроля параметров;
КСС – контрольная станция слежения.
NAVSTAR – GPS – NAVigation Sistem with Time And Rangiring – Global Positioning System
Станции слежения;
Главные станции контроля;
Наземные антены.
Слайд 21Сегмент контроля и управления
Станция слежения
Контроль траектории движения и часов спутника
Главная
станция контроля
Прогноз эфемерид и ухода часов спутника, формирование навигационного сообщения
Наземная
передающая антенаПередача навигационного сообщения на спутник
Слайд 22Сегмент пользователя
Структурная схема приемника
Частотное разделение сигналов
Кодовое разделение сигналов
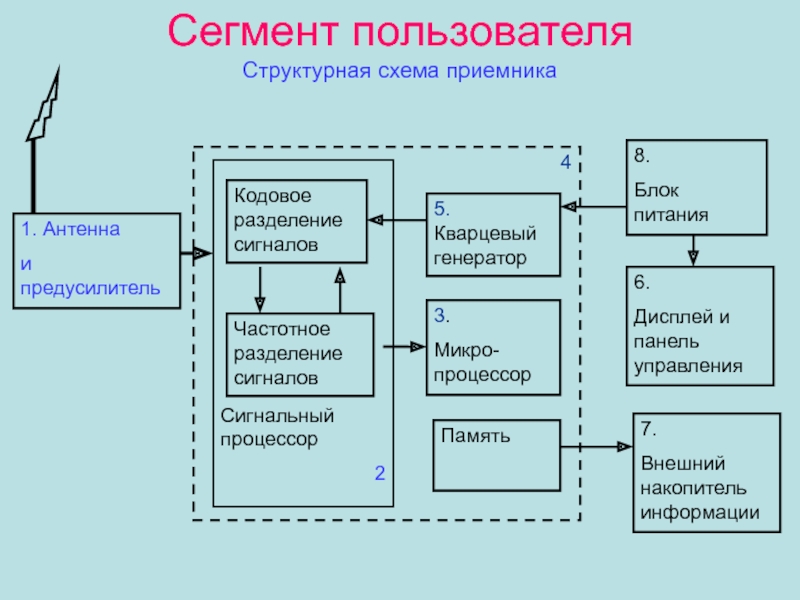
Слайд 23Сегмент пользователя
Структурная схема приемника
Антена с предусилителем;
Идентификатор сигралов и распределение
частот по каналам;
Микропроцессор для управления работой приемника;
Расшифровка принятой информации, вычисление
абсолютных координат и поправок в часы приемника, выполнение фазовых измерений;Стабильный кварцевый генератор;
Дисплей и панель управления;
Блок памяти для записи и хранения информации;
Блок питания.
Слайд 24Сегмент пользователя
Классификация приемников по кодировке сигнала:
C/A код;
C/A код
+ фазовые измерения на частоте L1;
C/A код + фазовые
измерения на частотах L1 и L2;C/A код + P-код + фазовые измерения на частотах L1 и L2;
Определение расстояний и координат приемника
Псевдодальность равна D' = (TП – ТС) v ;
Расстояние между спутником и приемником равно:
D + δtv = (TП – ТС) v;
ИЛИ
Слайд 25Сегмент пользователя
Режимы наблюдений:
Статика;
Быстрая статика;
Кинематика;
Кинематика “в полете”;
Кинематика в реальном времени.
Преобразование координат:
XR
= Xr(1+μ) – Zrωy + Yr ωz + ΔX0;
YR
= Yr(1+μ) – Zrωx + Xr ωz + ΔY0;ZR = Zr(1+μ) – Yrωx + Xr ωy + ΔZ0;
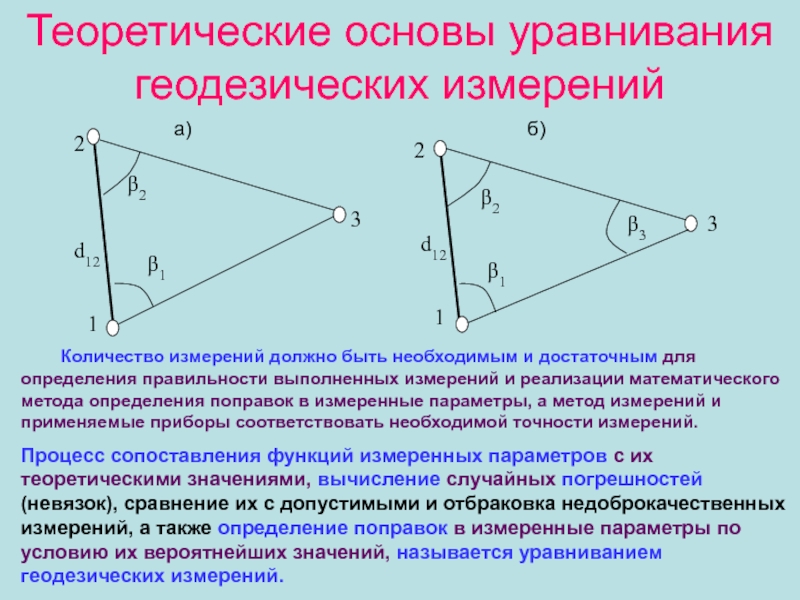
Слайд 26Теоретические основы уравнивания геодезических измерений
3
Количество измерений должно быть необходимым
и достаточным для определения правильности выполненных измерений и реализации математического
метода определения поправок в измеренные параметры, а метод измерений и применяемые приборы соответствовать необходимой точности измерений.Процесс сопоставления функций измеренных параметров с их теоретическими значениями, вычисление случайных погрешностей (невязок), сравнение их с допустимыми и отбраковка недоброкачественных измерений, а также определение поправок в измеренные параметры по условию их вероятнейших значений, называется уравниванием геодезических измерений.
Слайд 27Теоретические основы уравнивания геодезических измерений
Теория способа наименьших квадратов
Имеется серия
измеренных параметров, функции которых определяются следующей последовательностью чисел:
X1, X2,
X3, …, Xn. Каждой функции в этой последовательности соответствуют погрешности:
∆1, ∆2, ∆3, …, ∆n,
По теореме умножения вероятностей:
(1)
Слайд 28Теория способа наименьших квадратов
Вероятности появления оптимальных значений совокупности распределения погрешностей
в левой части уравнения (1) будет соответствовать условие:
Или для поправок
в измеренные параметрыВесовой коэффициент равен
(2)
(3). Подставим (3) в (2),
получим основное уравнение поправок →
PiVi2 min (4)
Установим вероятнейшее значение величины X при неравноточных измерениях. Так как Vi = Xср – Xi, то используя (4), имеем
f(x) = Pi(Xср – Xi)2 min. Отсюда XсрPi = Pi Xi, или
Слайд 29Реализация способа наименьших квадратов
Способ полигонов
Уравнивание углов;
Уравнивание приращений координат;
Уравнивание
превышений.
В основе уравнивания:
способ наименьших квадратов;
основное уравнение поправок
PV2 min
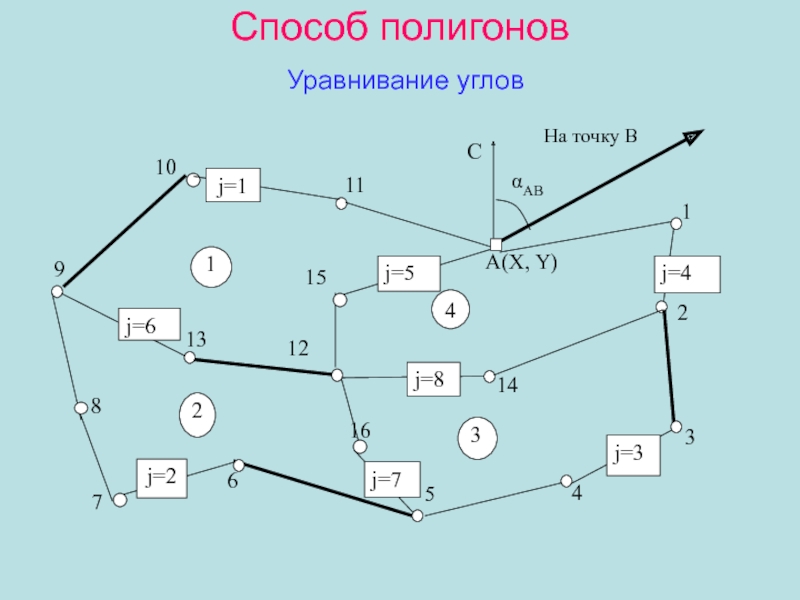
Слайд 30Способ полигонов
Уравнивание углов
АВ
2
1
А(X, Y)
На точку В
С
3
4
5
6
7
8
9
10
11
12
13
14
15
16
j=1
j=2
1
2
3
4
j=3
j=4
j=5
j=6
j=7
j=8
Слайд 31Способ полигонов
Уравнивание углов
Угловые невязки в полигонах
Полигон 1, W1 =
– 180(n1 – 2), n1 = 7.
Полигон 2, W2 =
– 180(n2 – 2), n2 = 8.Полигон 3, W3 = – 180(n3 – 2), n3 = 7.
Полигон 4, W4 = – 180(n4 – 2), n4 = 6.
W1 + W2 + W3 + W4 = W(1,2,3,4).
Слайд 32Способ полигонов
Уравнивание углов
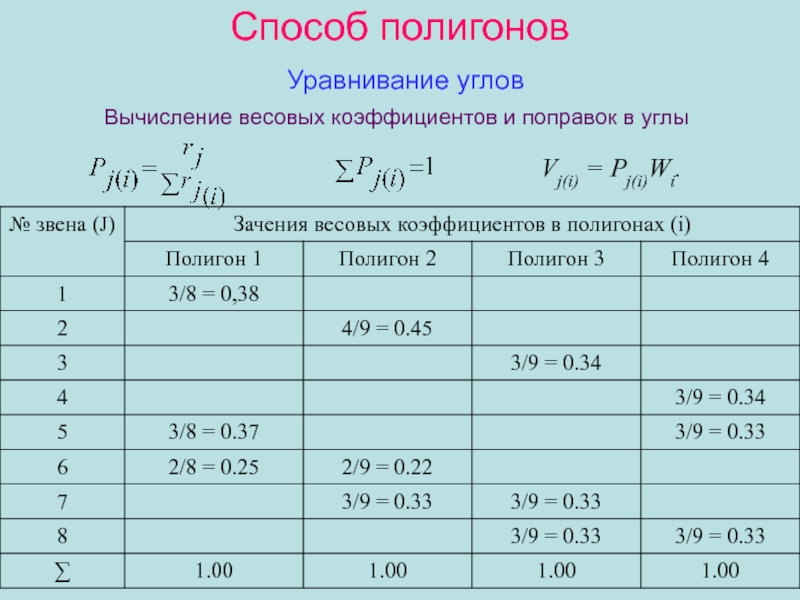
Вычисление весовых коэффициентов и поправок в углы
Vj(i)
= Pj(i)Wi.
Слайд 33Способ полигонов
Уравнивание приращений координат
Невязки в полигонах по координатам X, Y.
Полигон
1, fx1 = ΣΔx(1)выч – ΣΔxтеор.
fy1 = ΣΔy(1)выч – ΣΔyтеор.
Полигон
2, fx2 = ΣΔx(2)выч – ΣΔxтеор.fy2 = ΣΔy(2)выч – ΣΔyтеор.
Полигон 3, fx3 = ΣΔx(3)выч – ΣΔxтеор.
fy3 = ΣΔy(3)выч – ΣΔyтеор.
Полигон 4, fx4 = ΣΔx(4)выч – ΣΔxтеор.
fy4 = ΣΔy(4)выч – ΣΔyтеор.
fx1 + fx2 + fx3 + fx4 = fx(1,2,3,4).
fy1 + fy2 + fy3 + fy4 = fy(1,2,3,4).
ΣΔxтеор= 0
ΣΔyтеор = 0
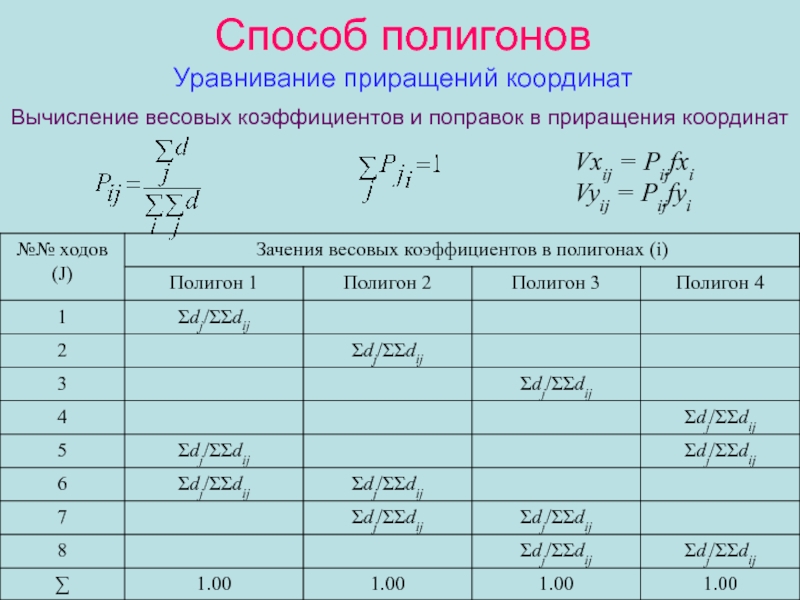
Слайд 34Способ полигонов
Уравнивание приращений координат
Вычисление весовых коэффициентов и поправок в приращения
координат
Vxij = Pijfxi
Vyij = Pijfyi
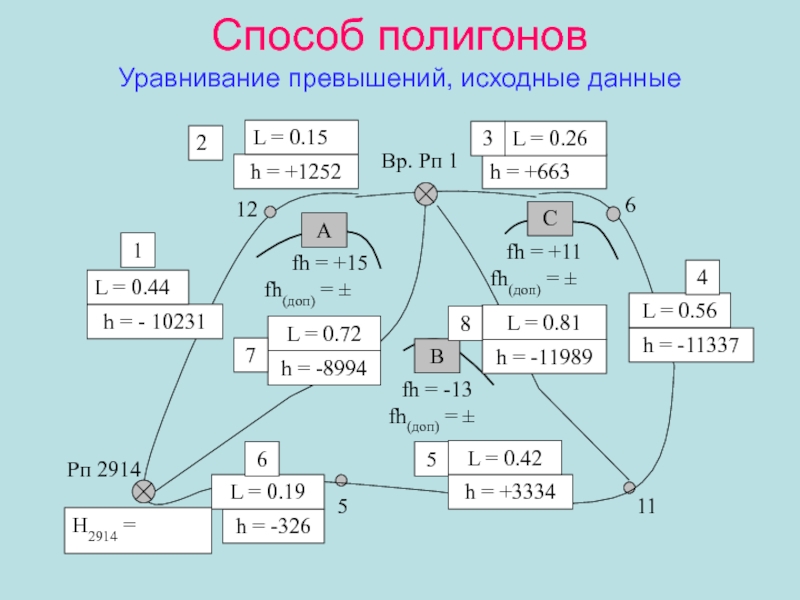
Слайд 36Способ полигонов
Уравнивание превышений
Вычисление невязок в полигонах
Полигон А, fhА = Σh(А)выч
– Σhтеор=
= (-10231 +1252 +8994) - (0) = +15 мм.
fhА(доп)
=Полигон В, fhВ = Σh(В)выч – Σhтеор =
= (-8994 +11989 -3334 +326) – (0) = -13 мм.
fhА(доп) =
Полигон С, fhС = Σh(С)выч – Σhтеор =
= (+663 + 11337 – 11989) – (0) = +11 мм.
fhА(доп) =
fhA + FhB + fhC = +15 – 13 + 11 = +13 мм.
fh(ABC)= -10231 + 1252 +663 + 11337 – 3334 + 326 = +13 мм
Слайд 37Способ полигонов
Уравнивание превышений
Вычисление весовых коэффициентов и поправок в превышения
Vhij =
Pijfhi
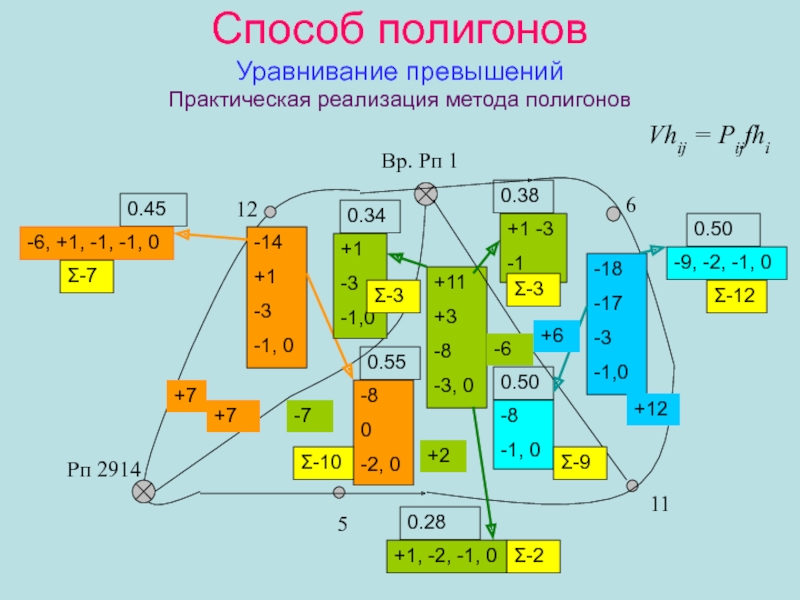
Слайд 38Способ полигонов
Уравнивание превышений
Практическая реализация метода полигонов
6
Рп 2914
Вр. Рп 1
12
11
5
-14
+1
-3
-1,
0
+11
+3
-8
-3, 0
-18
-17
-3
-1,0
Vhij = Pijfhi
0.45
0.55
0.34
0.38
0.28
0.50
0.50
-6, +1, -1, -1, 0
-8
0
-2, 0
+1
-3
-1,0
+1 -3
-1
+1,
-2, -1, 0-9, -2, -1, 0
-8
-1, 0
Σ-7
Σ-3
Σ-10
Σ-2
Σ-12
Σ-9
Σ-3
+7
+7
-7
-6
+2
+6
+12
Слайд 39Особенности геодезических работ Изыскания мостовых переходов
Урез воды в бытовом русле
по оси мостового перехода;
Изменение (превышение) горизонта воды в бытовом русле
по оси мостового перехода при зарегулированном стоке за заданный период;Отметку горизонта высокой воды (ГВВ) по оси мостового перехода;
Уклон водной поверхности бытового русла;
Распределение направлений течения струй и их скорость в бытовом русле по поверхности водотока;
Рельеф дна в пределах бытового русла реки.
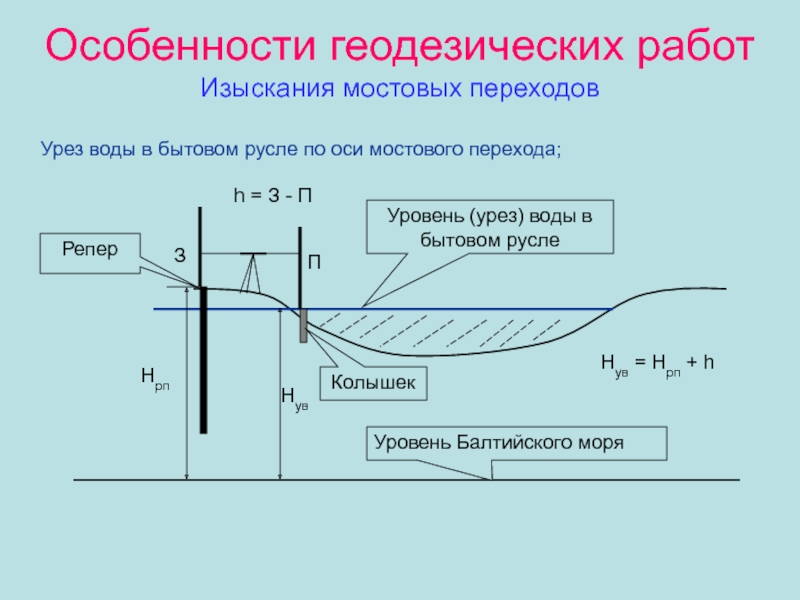
Слайд 40Особенности геодезических работ
Изыскания мостовых переходов
Урез воды в бытовом русле
по оси мостового перехода;
Репер
Колышек
Уровень (урез) воды в бытовом русле
З
П
h =
З - ПHрп
Hув
Hув = Hрп + h
Уровень Балтийского моря
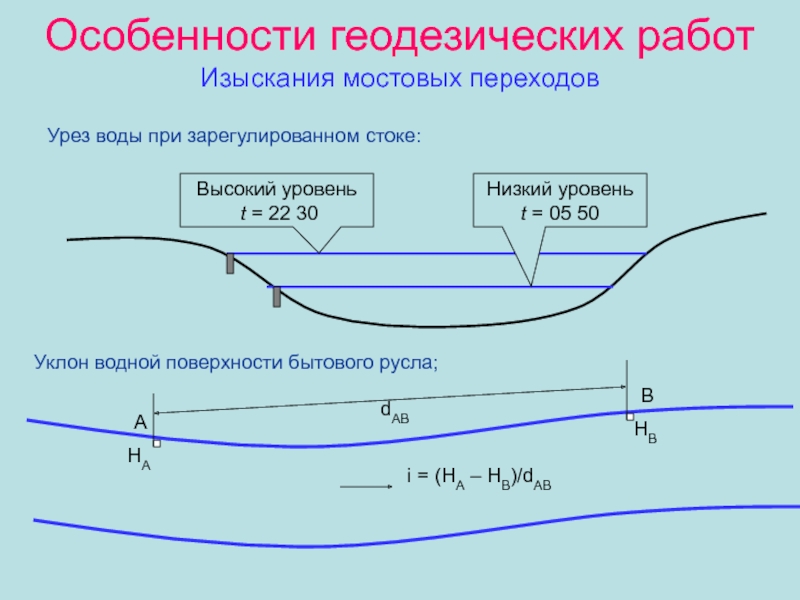
Слайд 41Особенности геодезических работ
Изыскания мостовых переходов
Урез воды при зарегулированном стоке:
Низкий
уровень t = 05 50
Высокий уровень
t = 22 30
Уклон
водной поверхности бытового русла;А
В
dАВ
HА
HВ
i = (HА – HВ)/dАВ
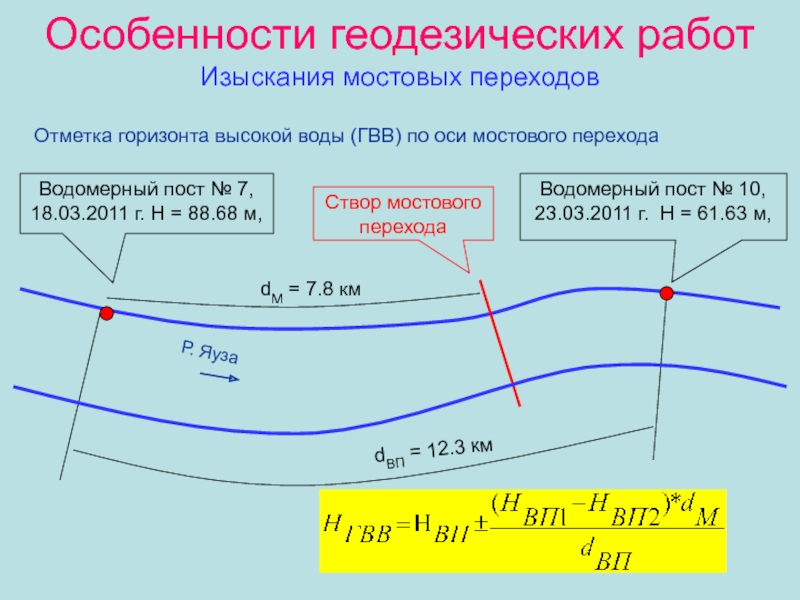
Слайд 42Особенности геодезических работ
Изыскания мостовых переходов
Отметка горизонта высокой воды (ГВВ)
по оси мостового перехода
Р. Яуза
Водомерный пост № 7, 18.03.2011 г.
H = 88.68 м, Водомерный пост № 10, 23.03.2011 г. H = 61.63 м,
dМ = 7.8 км
dВП = 12.3 км
Створ мостового перехода
Слайд 43Особенности геодезических работ
Изыскания мостовых переходов
Распределение направлений течения струй и
их скорость в бытовом русле по поверхности водотока
11
12
…
1(n-1)
1n
m1
m2
…
m(n-1)
mn
А
В
Базис, d =
130 мСтвор верховой В
Створ низовой Н
Створ мостового перехода
Р. Яуза
dm(23)
Слайд 44Особенности геодезических работ
Изыскания мостовых переходов
Рельеф дна в пределах бытового
русла реки Ширина реки ≤ 20 - 50 м.
1xy
2xy
ixy
nxy
2
1mxy
j
2mxy
nmxy
7–10 м
3–5
мР. Яуза
1
Слайд 45Особенности геодезических работ
Изыскания мостовых переходов
Рельеф дна в пределах бытового
русла реки Ширина реки > 50 м.
HА
i
L
v
h
Hд
Hу
Поплавок
Слайд 46Особенности геодезических работ
Изыскания мостовых переходов
Рельеф дна в пределах бытового
русла реки Ширина реки > 50 м.
Слайд 47Особенности геодезических работ. Изыскания тоннелей. Условия использования способов съемки в горных
условиях
Теодолитно-тахеометрическая съемка –
не применяется в связи с трудоемкостью передвижений
и переноской оборудования в условиях гор. применяется электронная техника для создания планово высотного обоснования.
2. Аэросъемка и аэрокосмическая съемка –
не применяется: появляются недопустимые погрешности планового и высотного положения крутых горных склонов.
3. Спутниковые методы –
не применяются в связи с трудоемкостью передвижений и переноской оборудования в условиях гор.
применяется для создания планово высотного обоснования.
4. Наземная стереофотограмметрическая (фототеодолитная) съемка –
применяется при готовом планово-высотном обосновании
Слайд 48Особенности геодезических работ.
Изыскания тоннелей.
J1
рj = 0,
рА = J1а1
– J2а2,
рС = J1c1 – J2c2
S1
S2
J2
А
С
J
а1
а2
γА
γJ
γC
C1
C2
Схема бинокулярного зрения.
Слайд 49
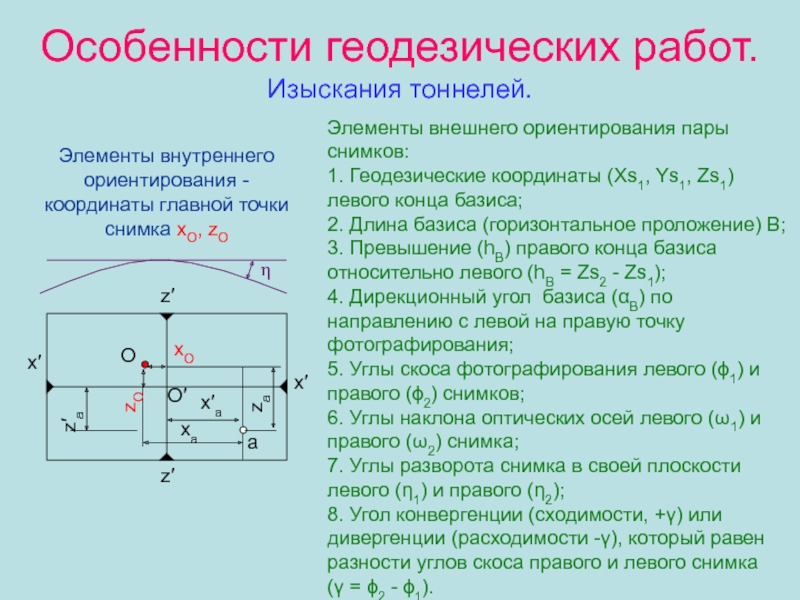
Особенности геодезических работ.
Изыскания тоннелей.
Элементы внутреннего ориентирования - координаты главной
точки снимка xO, zO
z′
z′
x′
x′
а
О
О′
xO
zO
x′a
z′a
xa
za
Элементы внешнего ориентирования пары снимков:
1. Геодезические координаты
(Xs1, Ys1, Zs1) левого конца базиса;2. Длина базиса (горизонтальное проложение) В;
3. Превышение (hВ) правого конца базиса относительно левого (hВ = Zs2 - Zs1);
4. Дирекционный угол базиса (В) по направлению с левой на правую точку фотографирования;
5. Углы скоса фотографирования левого (1) и правого (2) снимков;
6. Углы наклона оптических осей левого (1) и правого (2) снимка;
7. Углы разворота снимка в своей плоскости левого (1) и правого (2);
8. Угол конвергенции (сходимости, +) или дивергенции (расходимости -), который равен разности углов скоса правого и левого снимка
( = 2 - 1).
η
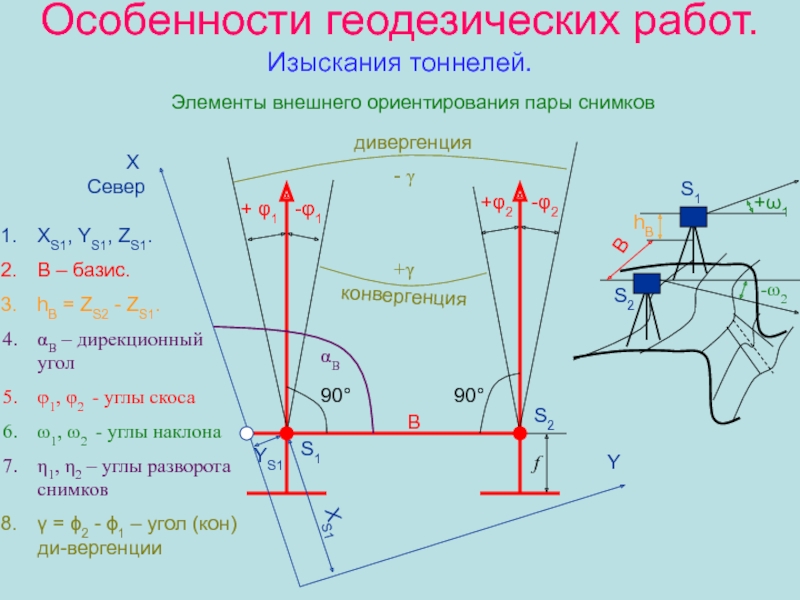
Слайд 50Особенности геодезических работ.
Изыскания тоннелей.
Элементы внешнего ориентирования пары снимков
+ φ1
-φ1
+φ2 -φ2
S1
S2
B
+γ
- γ
конвергенция
дивергенция
90°
90°
X
СеверY
f
αB
XS1
YS1
XS1, YS1, ZS1.
B – базис.
hВ = ZS2 - ZS1.
αВ – дирекционный угол
φ1, φ2 - углы скоса
ω1, ω2 - углы наклона
η1, η2 – углы разворота снимков
= 2 - 1 – угол (кон)ди-вергенции
-ω2
+ω1
В
S1
S2
hB
Слайд 51Особенности геодезических работ.
Изыскания тоннелей
Координаты снимка и координаты местности
X =
XS1 + NX1
Y = YS1 + NY1
Z =
ZS1 + NZ1 + Zгде
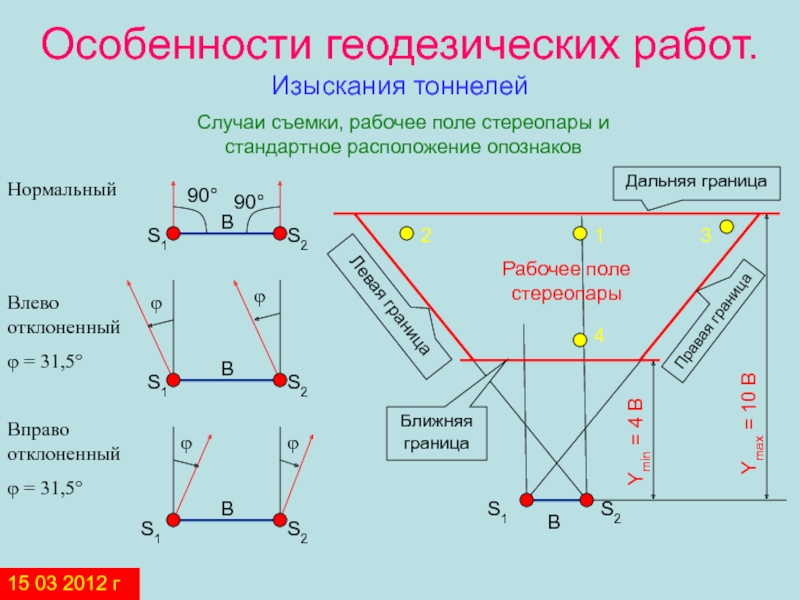
Слайд 52Особенности геодезических работ.
Изыскания тоннелей
Случаи съемки, рабочее поле стереопары и
стандартное расположение опознаков
Нормальный
Влево отклоненный
φ = 31,5°
Вправо отклоненный
φ = 31,5°
В
В
В
φ
φ
φ
φ
90°
90°
S1
S2
S1
S2
S1
S2
В
S1
S2
Ближняя
границаДальняя граница
Ymin = 4 В
Ymax = 10 B
1
2
3
4
Левая граница
Правая граница
Рабочее поле стереопары
15 03 2012 г
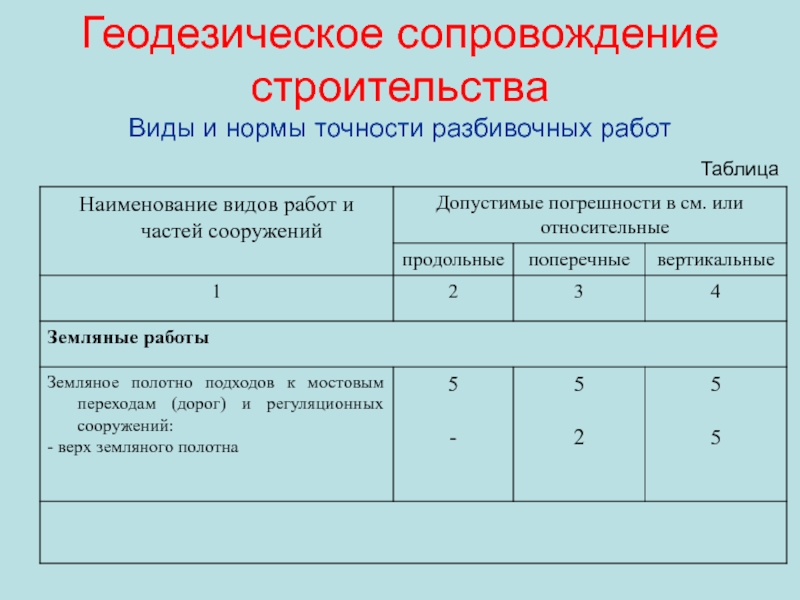
Слайд 53Геодезическое сопровождение строительства
Виды и нормы точности разбивочных работ
Разбивкой сооружения называют
обозначение и закрепление на местности с необходимой точностью осей и
ключевых точек объекта, которые определяют его местоположение и размеры.mП2 = mP2 + mТ2,
Геодезическое обоснование должно строиться в два раза точнее по отношению к требуемой точности разбивочных работ и в три раза точнее по отношению к точности приемки сооружения в эксплуатацию.
если mТ = mП, то
или
Слайд 55Геодезическое сопровождение строительства
Виды и нормы точности разбивочных работ
Продолжение таблицы
Слайд 56Геодезическое сопровождение строительства
Виды и нормы точности разбивочных работ
Продолжение таблицы
Слайд 57Геодезическое сопровождение строительства
Опорная сеть для разбивки сооружений (проект)
Принципиальная схема с
указанием альтернативных вариантов и методов разбивки ключевых точек мостового перехода
или транспортного тоннеля;Геометрическая схема построения опорных точек разбивки сооружения (геодезический четырехугольник, цепочка треугольников, центральная система и др.) с указанием схемы привязки этих точек к государственной геодезической сети;
Схема закрепления на местности точек опорной сети с указанием необходимого времени сохранности и способа обустройства закрепленных точек;
Схема наблюдения углов и расстояний;
Обоснование требуемой точности определения координат и отметок геодезического обоснования и предрасчет точности измерений;
Перечень приборов и геодезического оборудования;
Рекомендуемый метод уравнивания углов, расстояний и превышений.
Слайд 58Геодезическое сопровождение строительства
Методы разбивки сооружений
Метод координат:
способ прямоугольных координат (способ
перпендикуляров);
способ полярных координат.
Метод засечек:
способ угловых засечек;
способ микротриангуляции;
способ обратной засечки;
способ створных
засечек;способ линейных засечек (геометрический).
Слайд 59Геодезическое сопровождение строительства
Методы разбивки сооружений (метод координат)
отложить в направлении оси
координат OX расстояние dOA от начала координат О до точки
А;центрировать на точке А теодолит и отложить угол ;
отложить по направлению угла расстояние dAС от точки А до точки С;
фиксировать положение точки С на местности.
Y
X
А
С
С′
О
dOA
XC
YC
dAC
β
ΔY
ΔX
M
Слайд 60Геодезическое сопровождение строительства
Методы разбивки сооружений (метод координат)
Погрешность метода координат
Слайд 61Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Прямая угловая засечка
измерить расстояние
между точками А и В (базис);
установить на точках А и
В теодолиты и отложить углы и ;зафиксировать в пересечении направлений АС и ВС точку “С”.
Аxy
Вxy
С
ε ε
ε ε
α
β
γ
Поперечная погрешность, η
Продольная погрешность, λ
c
a
в
Поле существования точки С
Слайд 62Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Прямая угловая засечка
поперечном
Влияние
погрешности базиса в направлении:
продольном
Влияние погрешности отложения углов и
в направлении:поперечном
продольном
Суммарная погрешность:
поперечная
продольная
Слайд 63Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Способ микротриангуляции
Условия применения:
Для точек
А и В известны координаты;
Известно приближенное местоположение точки “С”
на местности; Место доступно для установки теодолита;
Аxy
Bxy
C′x′y′
Cxy
Север
αС′С
αС′В
γ1 = αС′В - αС′С
δ = С′С
Y
X
а
с
в
α
β
γ
Слайд 64Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Способ микротриангуляции
Действия:
В окрестностях точки
“С” фиксируют точку “С” и формируют треугольник АВС′, в котором
измеряют углы , и ;Уравнивают углы и вычисляют расстояния а и в;
Вычисляют координаты точки С′ (x′, y′) и сопоставляют их с проектными координатами точки С;
Решением обратной геодезической задачи устанавливают расстояние δ = СС′ и разбивочный угол γ1;
Откладывают угол γ1 и по заданному направлению откладывают расстояние δ. Фиксируют точку С.
Слайд 65Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Способ обратной засечки
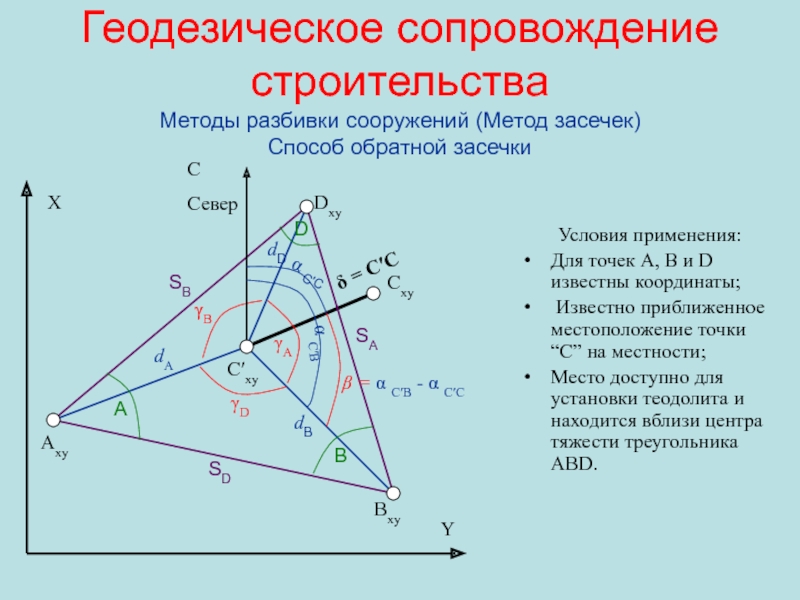
Условия применения:
Для
точек А, В и D известны координаты;
Известно приближенное местоположение
точки “С” на местности; Место доступно для установки теодолита и находится вблизи центра тяжести треугольника ABD.
Y
X
Axy
Bxy
Dxy
Cxy
C′xy
С
Север
γD
γB
γA
β = α C′B - α C′C
δ = C′C
α C′C
α C′B
A
B
D
SA
SD
SB
dA
dB
dD
Слайд 66Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Способ обратной засечки
, где
Погрешность
положения точки С′
, где
Слайд 67Геодезическое сопровождение строительства
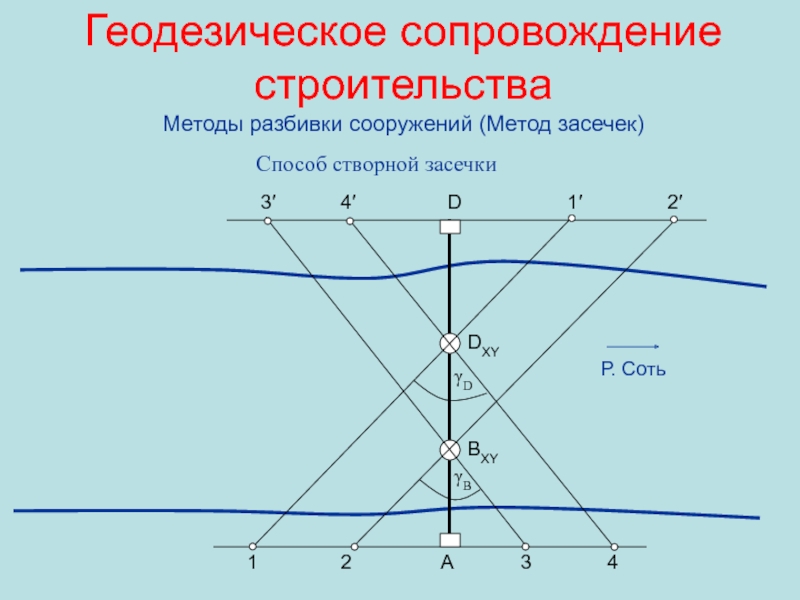
Методы разбивки сооружений (Метод засечек)
Способ створной засечки
1
2
А
3
4
1′
2′
D
3′
4′
BXY
DXY
γB
γD
Р.
Соть
Слайд 68Геодезическое сопровождение строительства
Методы разбивки сооружений (Метод засечек)
Способ линейной засечки
B
A
b
a
λ
η
M
C
C′
c
τ
τ
Слайд 69Геодезическое сопровождение строительства
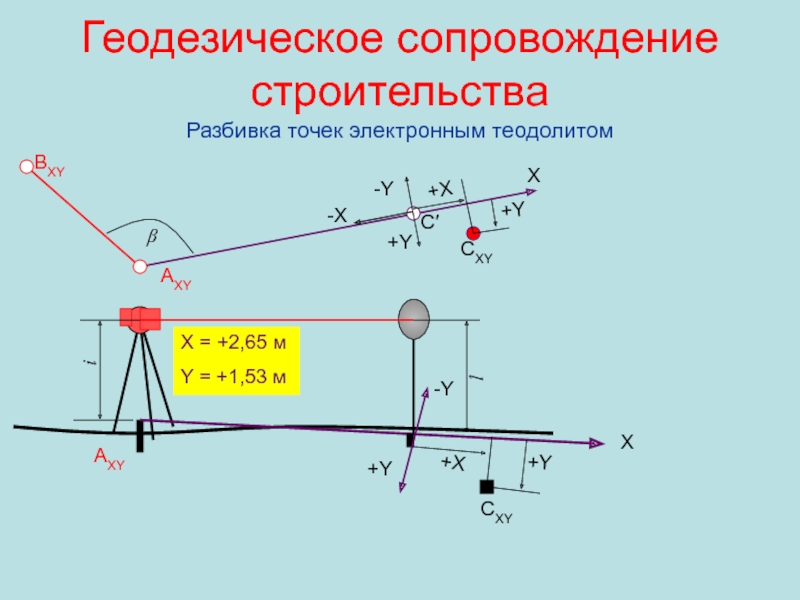
Разбивка точек электронным теодолитом
CXY
X = +2,65 м
Y =
+1,53 м
+X
+Y
+X
+Y
AXY
AXY
BXY
-Y
β
CXY
X
X
+Y
+Y
-Y
-X
i
l
C′
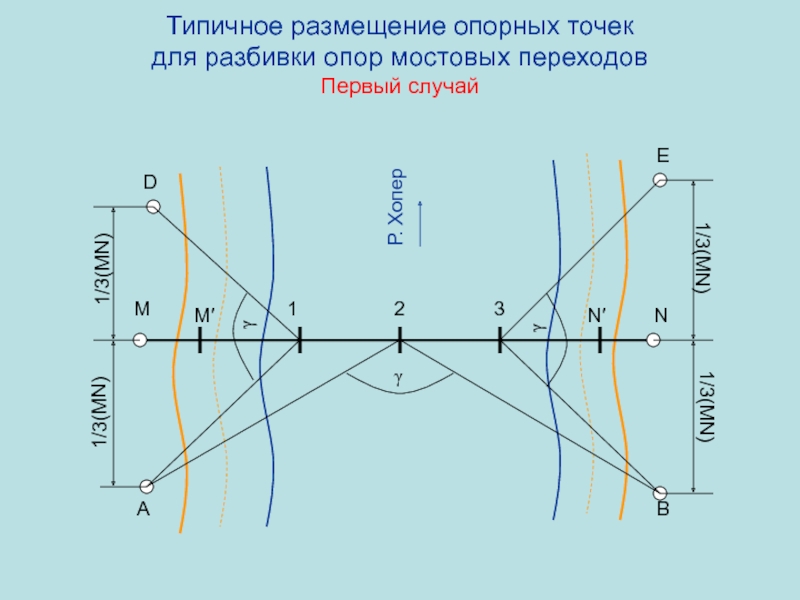
Слайд 70Геодезическое сопровождение строительства Типичное размещение опорных точек для разбивки опор мостовых
переходов
1. Оба берега реки крутые (не затопляемые) и их бровки
находятся высоко над уровнем воды;2. Один берег реки крутой (не затопляемый), а другой пологий с периодическим затоплением паводковой водой;
3. Оба берега реки крутые (не затопляемые) и их бровки находятся высоко над уровнем воды, при этом в средней части реки имеет место остров, который находится на некотором расстоянии от створа мостового перехода вверх или вниз по течению;
4. Один берег реки крутой (не затопляемый), а другой пологий с периодическим затоплением паводковой водой, но в середине реки имеет место остров, который находится в створе мостового перехода и имеет достаточную длину вдоль течения реки.
Слайд 72Типичное размещение опорных точек
для разбивки опор мостовых переходов
Первый случай
1/3(MN)
1/3(MN)
1/3(MN)
1/3(MN)
M
N
M′
N′
1
2
3
A
D
B
E
Р.
Хопер
γ
γ
γ
Слайд 73Типичное размещение опорных точек
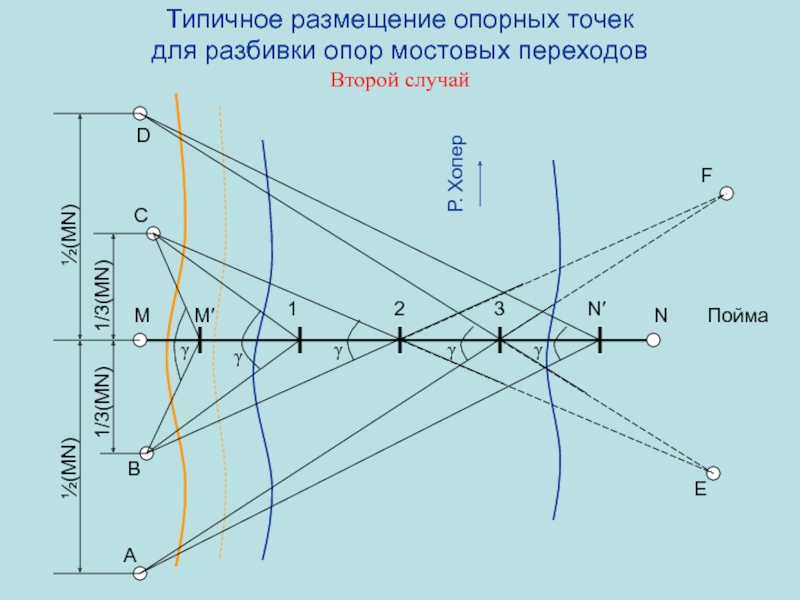
для разбивки опор мостовых переходов
Второй случай
1/3(MN)
1/3(MN)
M
N
M′
N′
1
2
3
A
D
Р.
Хопер
½(MN)
½(MN)
B
C
E
F
γ
γ
γ
γ
γ
Пойма
Слайд 74Типичное размещение опорных точек для разбивки опор мостовых переходов Третий
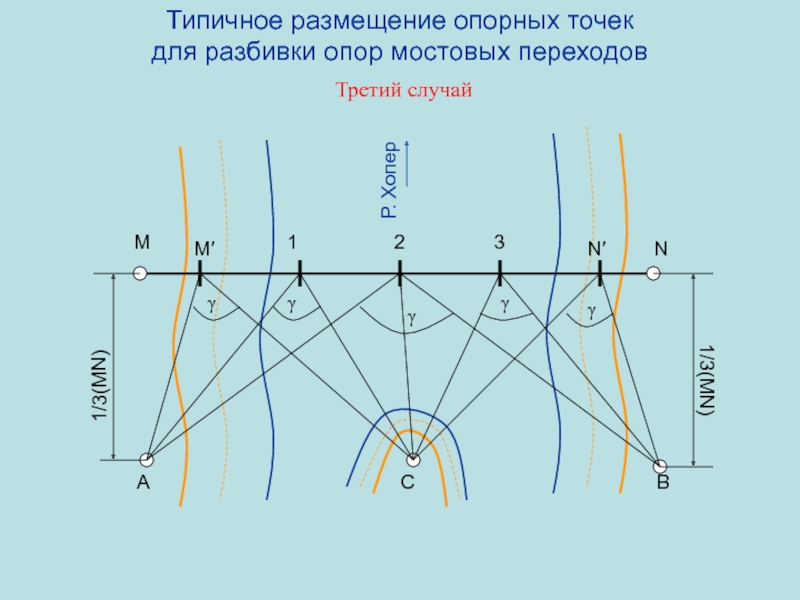
случай
1/3(MN)
1/3(MN)
M
N
M′
N′
1
2
3
A
B
Р. Хопер
С
γ
γ
γ
γ
γ
Слайд 75Типичное размещение опорных точек для разбивки опор мостовых переходов Четвертый
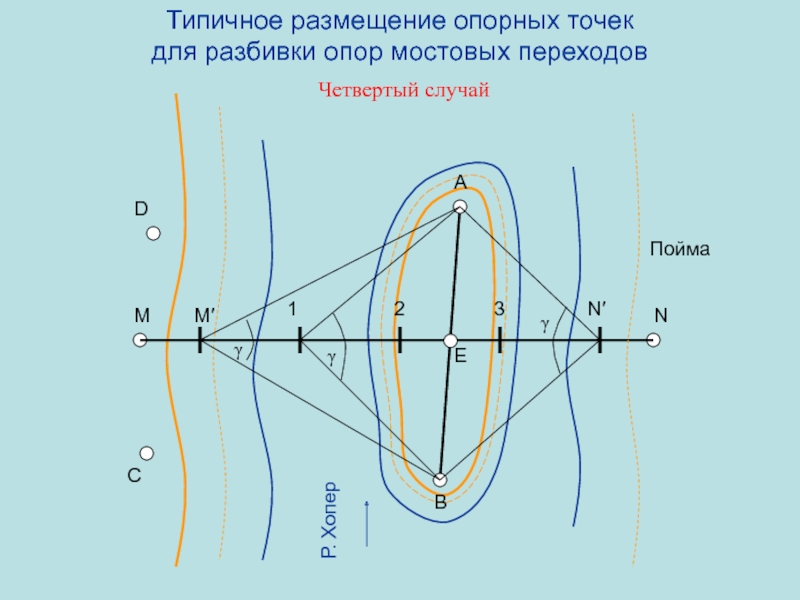
случай
M
N
M′
N′
1
2
3
Р. Хопер
B
C
γ
А
D
Е
γ
γ
Пойма
Слайд 76Разбивка тоннеля
Схема тоннельной триангуляции и подходной полигонометрии
I
II
III
IV
V
VI
Входной портал
Выходной портал
Тоннельная полигонометрия
Тоннельная
триангуляция
Слайд 79Разбивка тоннеля Передача координат и дирекционного угла через шахту в тоннель Способ
створа двух отвесов
А
В
С
D
C′
D′
E
F
d1
d2
d3
d4
u
u
τ
u
u
τ
На поверхности
В тоннеле
u
u
τ
u
u
τ
τ
Слайд 80F
E
D′
Разбивка тоннеля
Передача координат и дирекционного угла через шахту в тоннель
Способ
соединительного треугольника
α
β
γ
α1
β1
γ1
ψ1
A
B
D
C
ψ
C′
В тоннеле
На поверхности
в
а
с
в1
а1
с1
d
αC′D′ = αCD а1 = а
XC′ =
XCYC′ = YC
XD′ = XD
YD′ = YD
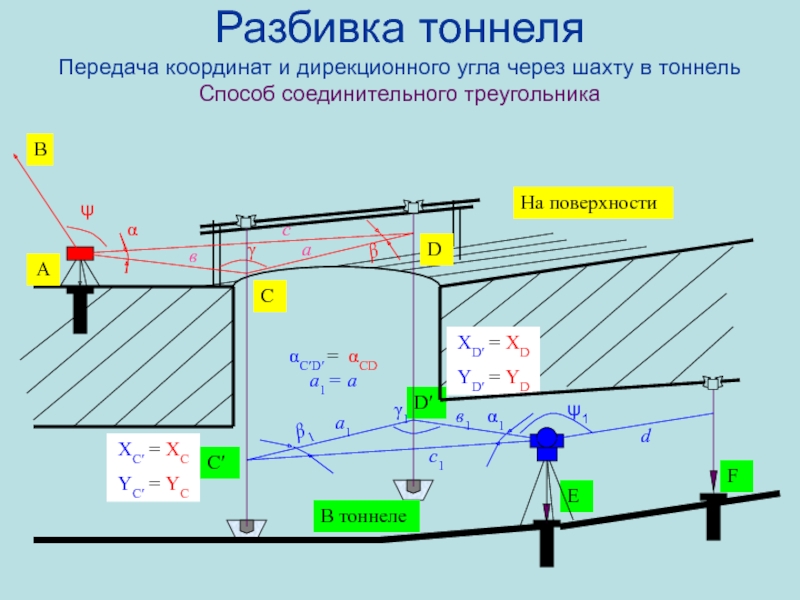
Слайд 81Разбивка тоннеля Передача координат и дирекционного угла через шахту в тоннель Способ
соединительного треугольника
Исходные данные: Координаты точки А: XA, YA; Дирекционный угол:
αВА.Измерения на поверхности: углы α, ψ, расстояния: а, в, с.
Измерения в тоннеле: углы α1, ψ1, расстояния: а1, в1, с1, d.
Вычисление элементов треугольника на поверхности:
Вычислить углы β, γ по формуле:
Определить: Координаты: XЕ, YЕ, XF, YF; Дирекционный угол: αEF.
Вычислить дирекционные углы линий на поверхности:
αAD = αBA + ψ − 180
αDC = αAD + (360-β) − 180
αCA = αDC + (360-γ) − 180
αAB = αCA + (360-α-ψ) − 180
Вычислить координаты точек D, C на поверхности:
XD = XA + c Cos αAD YD = YA + c Sin αAD
XC = XD + a Cos αDC YC = YD + a Sin αDC
XA = XC + в Cos αCА YА = YС + в Sin αCА
Слайд 82Разбивка тоннеля
Передача дирекционного угла через шахту в тоннель
Способ соединительного треугольника
Вычислить
углы β1, γ1 по формуле:
Принять: αC′D′ = αCD ;
XC′ = XC, YC′ = YC ; XD′ = XD, YD′ = YD.
Вычислить дирекционные углы линий в тоннеле:
αD′Е = αC′D′ + 180 − γ1; αC′Е = αD′C′ + β1 − 180;
αЕF = αD′E + 180 − (360 - ψ1);
Контроль αЕF = αC′E + (α1 + ψ1) − 180;
Вычисление элементов треугольника в тоннеле:
Вычислить координаты точек E, F в тоннеле:
XE = XD′ + в1 Cos αD′Е ; YE = YD′ + в1 Cos αD′Е
XF = XE + d Cos αЕF ; YF = YE + d Sin αЕF
Контроль
XE = XС′ + с1 Cos αС′Е ; YE = YС′ + с1 Cos αС′Е
XF = XE + d Cos αЕF ; YF = YE + d Sin αЕF
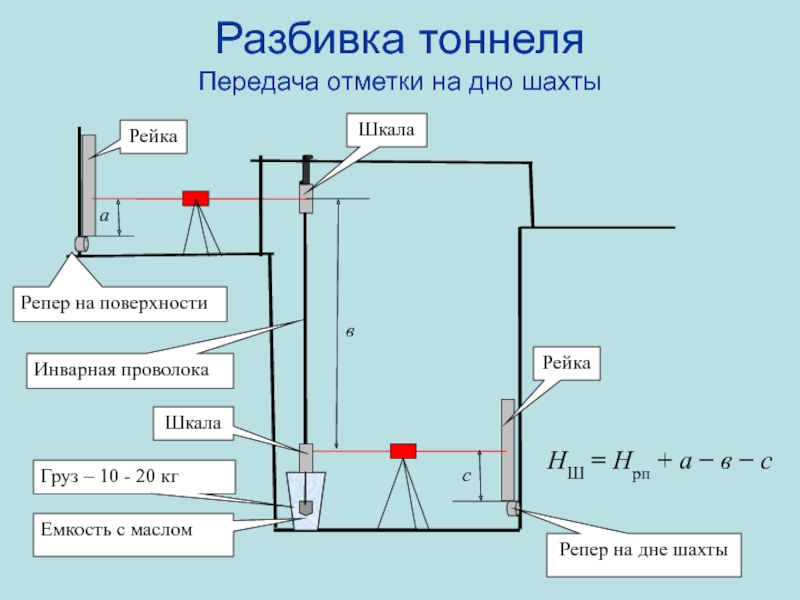
Слайд 83Разбивка тоннеля
Передача отметки на дно шахты
Емкость с маслом
Груз – 10
- 20 кг
Инварная проволока
НШ = Нрп + а − в
− са
в
с
Репер на дне шахты
Репер на поверхности
Шкала
Рейка
Рейка
Шкала
Слайд 84Разбивка тоннеля
Прямолинейный тоннель с постоянным уклоном
Частный случай
АXY
E
E′
ВXY
С
D
1
2
4
3
А′
В′
d, α, i ,
v
C
Ю
CB α = r
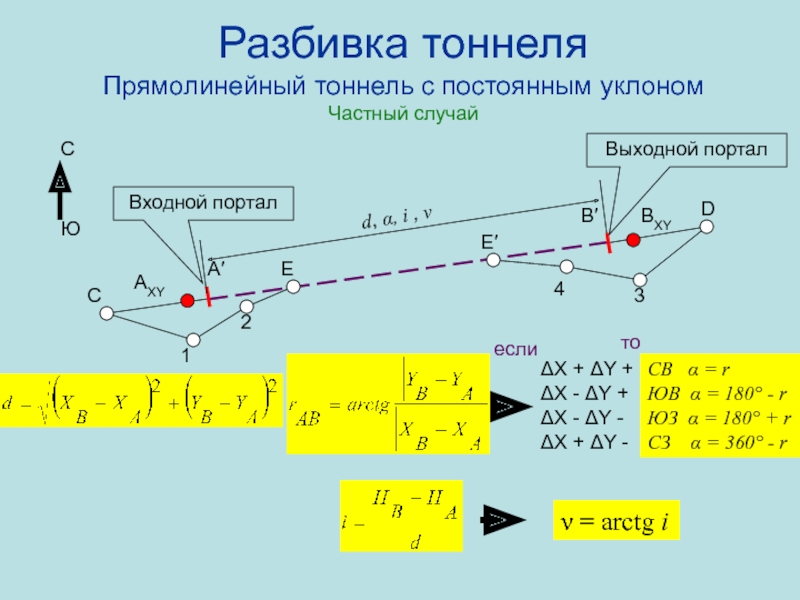
ЮВ α = 180° - r ЮЗ α = 180° + r СЗ α = 360° - r = arctg i
Входной портал
Выходной портал
ΔX + ΔY + ΔX - ΔY + ΔX - ΔY - ΔX + ΔY -
если
то
Слайд 85Разбивка тоннеля
Прямолинейный тоннель с постоянным уклоном
Общий случай
АXY
E
E′
ВXY
С
D
1
2
4
А′
В′
d, α, i ,
v
C
Ю
3
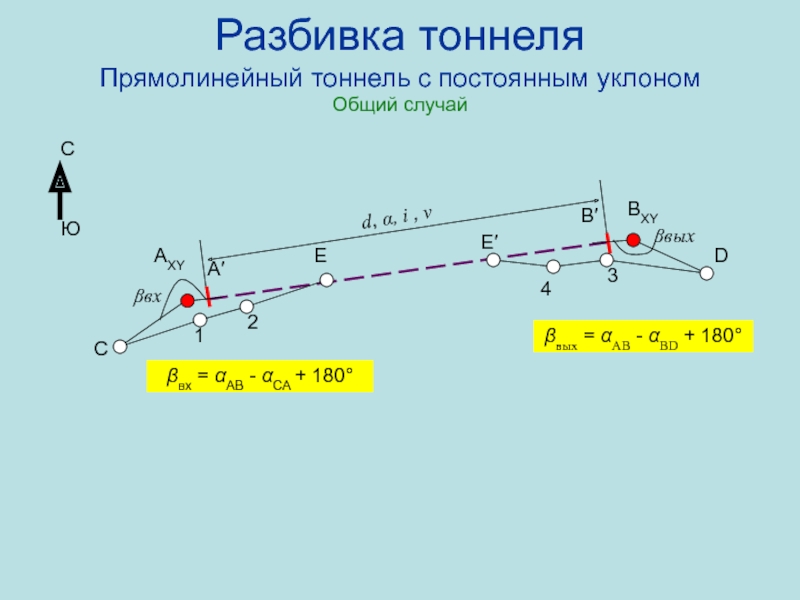
βвх
βвых
вх = АВ - СА + 180
вых = АВ -
BD + 180Слайд 86Разбивка тоннеля
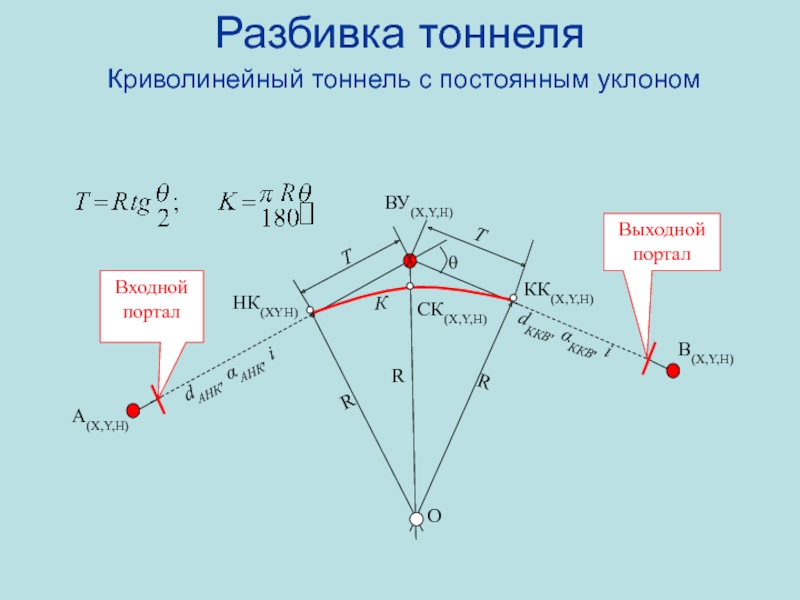
Криволинейный тоннель с постоянным уклоном
НК(XYH)
A(X,Y,H)
B(X,Y,H)
КК(X,Y,H)
ВУ(X,Y,H)
СК(X,Y,H)
R
О
R
R
Входной портал
Выходной портал
dAНК, AНК,
i
dККВ, ККВ, i
Т
Т
К
Слайд 87Разбивка тоннеля
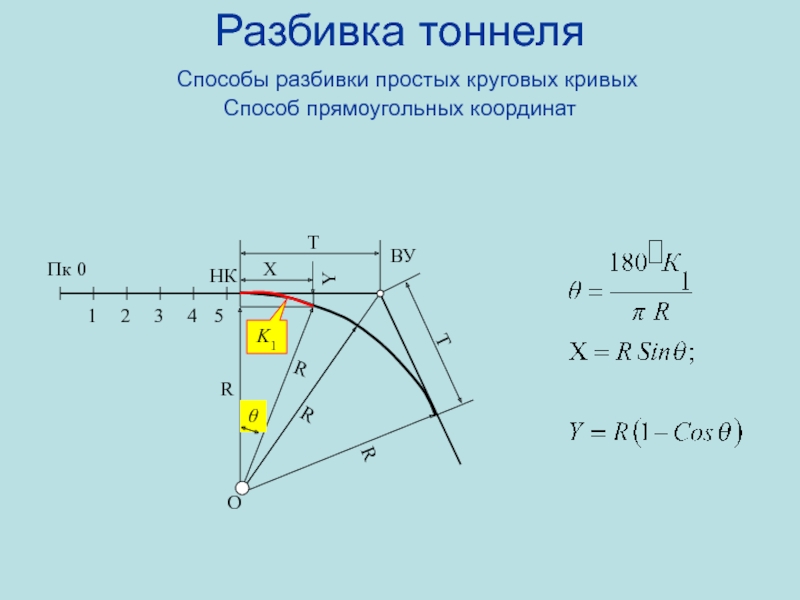
Способы разбивки простых круговых кривых
Прямоугольных координат.
Полярных
координат (способ углов).
Продолженных хорд.
Трех точек.
Описанного многоугольника.
Вписанного
многоугольника.Разбивка тоннеля с учетом переходных кривых
Слайд 89β
a
Разбивка тоннеля
Способы разбивки простых круговых кривых
Способ полярных координат
НК
А1
А2
КК
R
R
R
R
O
ВУ
θ1
δ
δ =
θ1/2
Т
x
y
К1
Слайд 90Разбивка тоннеля
Способы разбивки простых круговых кривых
Способ полярных координат
НК
КК
R
R
R
R
R
R
R
R
НТ
КТ
O
К1
θ1
90°
90°
90°
Слайд 91Разбивка тоннеля
Способы разбивки простых круговых кривых
Способ продолженных хорд
X0
Y0
b
d
d
НК
А0
А1
b
O
d
d
A2
К ВК
А′1
А′2
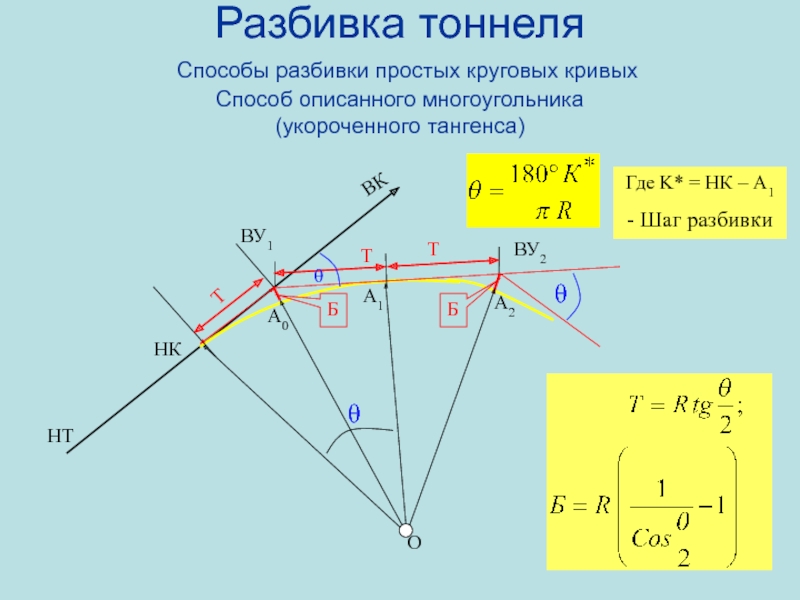
Слайд 93Разбивка тоннеля Способы разбивки простых круговых кривых Способ описанного многоугольника (укороченного
тангенса)
Т
НК
А0
А1
O
A2
ВК
ВУ1
ВУ2
Т
Т
θ
θ
НТ
θ
Б
Б
Где K* = НК – А1
- Шаг разбивки
Слайд 94Разбивка тоннеля
Способы разбивки простых круговых кривых
Способ вписанного многоугольника
НК
А1
КК
R
R
ВУ
θ1
δ
x
y
К1
А2
2δ
а
а
δ
= θ1/2
R
O
Слайд 95Разбивка тоннеля
Способ разбивки с учетом переходных кривых
θ
p
НПК1
φ1
φ2
x
t1
t2
НКК
НПК2
КПК1
ККК
x
t1
t2
R
КПК2
R1
O
y
y
ВУ
l
l
Слайд 96Разбивка тоннеля
Способ разбивки с учетом переходных кривых
x = t1 +
t2
Сдвижка круговой кривой:
Расстояния от начала (конца) круговой кривой до начала
(t1) и до конца (t2) переходной кривойR1 = R - p
Радиус сдвинутой круговой вставки
Координаты конца переходной кривой в системе координат трассы тоннеля
Контроль правильности вычисления координаты x
Угол поворота переходной кривой
Слайд 97Разбивка тоннеля
Аналитический расчет трассы тоннеля
НТx,y,н
НПК1
НПК2
НПК3
КПК3
КПК2
КПК1
КТx,y,н
ВУ1
ВУ2
ВУ3
X
Y
θ1
θ2
θ3
Приращения координат точек на прямых
участках:
Δx = d Cos α;
Δy = d
Sin α ;Приращения координат точек на кривых (КПК, НКК, ККК)
Δx = d Cos α + y Cos (α ±90) ;
Δy = d Sin α + y Sin (α ±90) .
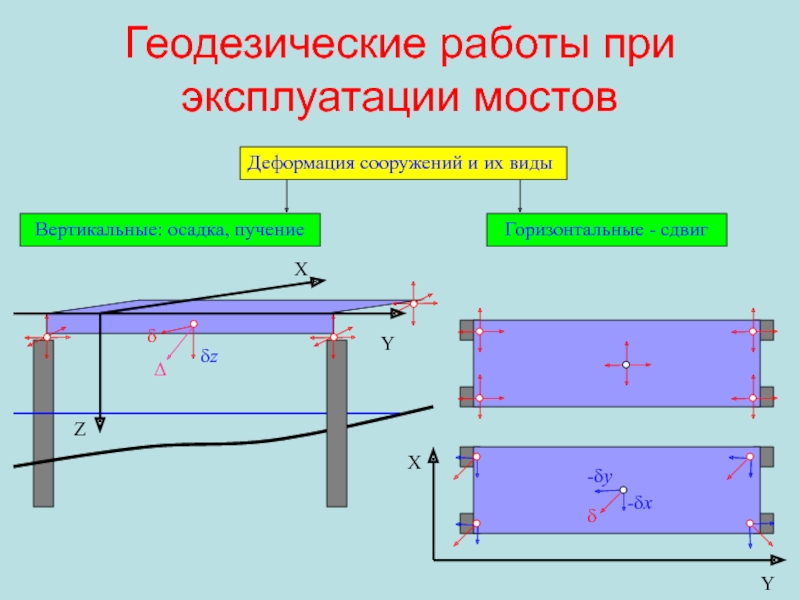
Слайд 99Геодезические работы при эксплуатации мостов
Деформация сооружений и их виды
Вертикальные: осадка,
пучение
Горизонтальные - сдвиг
X
Y
-δx
-δy
δ
δ
δz
Δ
Y
Z
X
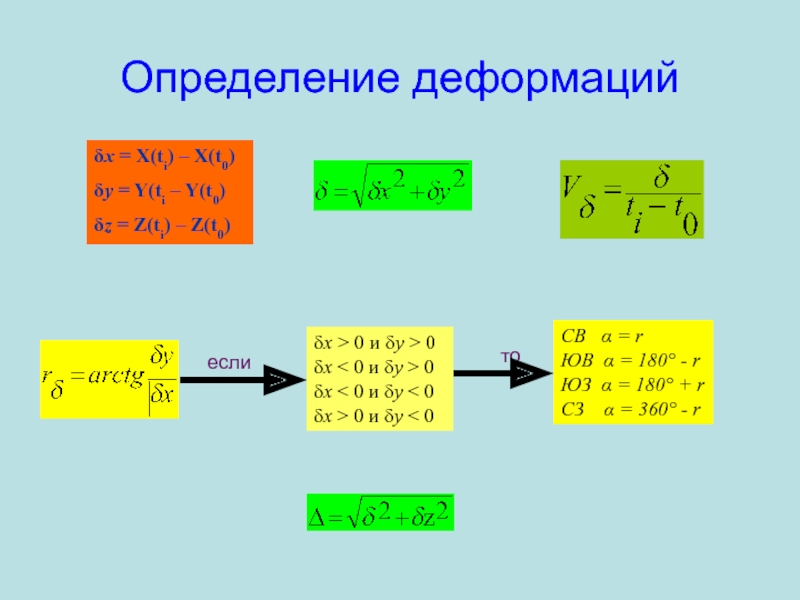
Слайд 100Определение деформаций
CB α = r
ЮВ α = 180°
- r ЮЗ α = 180° + r СЗ α = 360° - rδx > 0 и δy > 0 δx < 0 и δy > 0 δx < 0 и δy < 0 δx > 0 и δy < 0
если
то
δx = X(ti) – X(t0)
δy = Y(ti – Y(t0)
δz = Z(ti) – Z(t0)
Слайд 101Геодезические методы определения деформаций
метод геометрического нивелирования I, II и III
класса. Применяется для измерения осадок и пучения;
метод гидронивелирования. Применяется
для измерения относительных смещений деталей строительной конструкции, например, примыкающих друг к другу плит пролетных строений; метод угловых измерений. Применяется для определения горизонтальных смещений вертикальных (высотных) конструкций;
метод координат. Применяется для определения горизонтальных смещений строительных конструкций, имеющих в верхнем строении площадки (верхние части опор, пролетные строения мостовых переходов или путепроводов;
фотограмметрический метод. Применяется для определения горизонтальных и вертикальных смещений фасадов строительных конструкций сложной формы;
стереофотограмметрический метод. Применяется для определения горизонтальных и вертикальных смещений фасадов строительных конструкций сложной формы.
Слайд 102метод геометрического нивелирования.
Классы нивелирования и необходимая точность определения деформаций
I
класс, fh(доп) =
II класс, fh(доп) =
III класс, fh(доп) =
,
применяется в научных целях, при выяснении подвижек Земной коры и при ожидаемой осадке < 1 мм., применяется при ожидаемой осадке 1 – 5 мм.
, применяется при ожидаемой осадке > 5 мм.
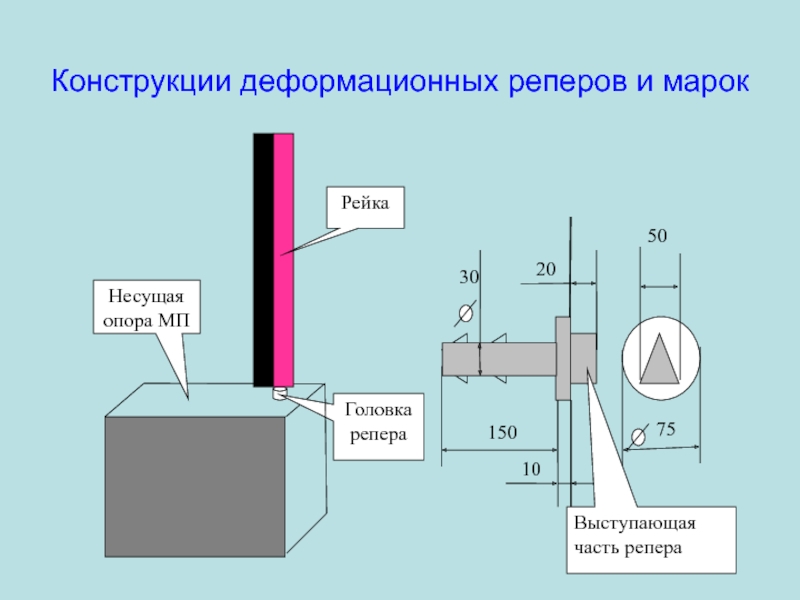
Слайд 103Конструкции деформационных реперов и марок
Головка репера
75
50
150
10
20
30
Выступающая часть репера
Несущая опора МП
Рейка
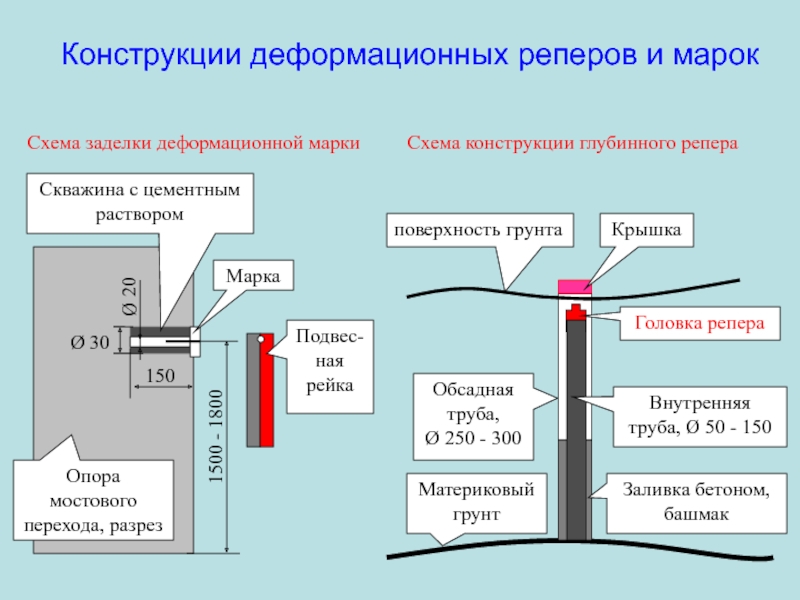
Слайд 104Конструкции деформационных реперов и марок
150
Ø 30
Скважина с цементным раствором
Марка
1500 -
1800
Ø 20
Опора мостового перехода, разрез
поверхность грунта
Материковый грунт
Головка репера
Обсадная
труба, Ø 250 - 300
Внутренняя труба, Ø 50 - 150
Заливка бетоном, башмак
Крышка
Подвес-ная рейка
Схема конструкции глубинного репера
Схема заделки деформационной марки
Слайд 105метод гидронивелирования
Определение относительных смещений строительных конструкций
а
b
h = a - b
Мензурки
с миллиметровыми делениями
Соединительный шланг
Патрубок
h
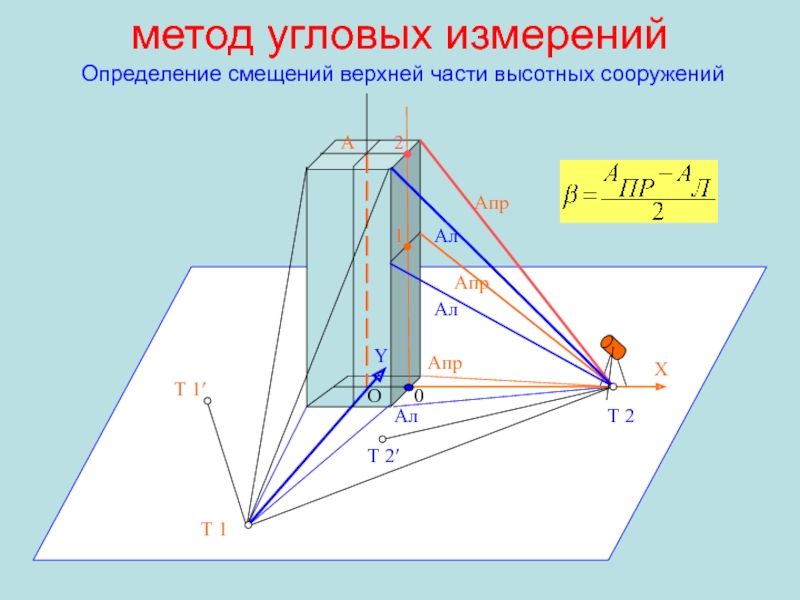
Слайд 106метод угловых измерений
Определение смещений верхней части высотных сооружений
Aпр
0
2
1
O
A
Т 2
Т
1
X
Y
Т 2′
Т 1′
Aпр
Aпр
Aл
Aл
Aл
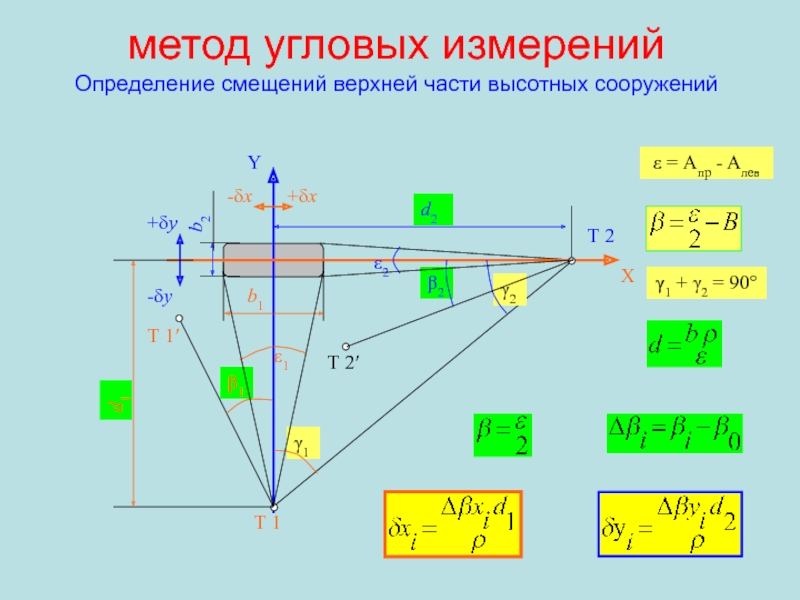
Слайд 107метод угловых измерений
Определение смещений верхней части высотных сооружений
Т 1
Т 2
Т
1′
Т 2′
Y
X
β1
γ1
γ2
β2
γ1 + γ2 = 90°
+δx
-δx
+δy
-δy
d1
d2
ε1
ε2
b1
b2
ε = Aпр - Aлев
Слайд 108метод координат
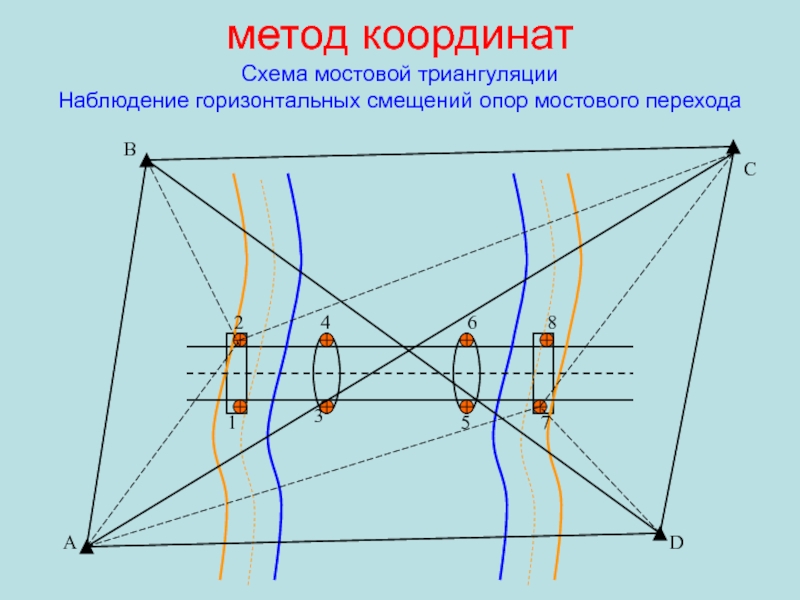
Схема мостовой триангуляции
Наблюдение горизонтальных смещений опор мостового перехода
5
6
4
3
2
1
C
8
7
D
А
B
Слайд 109метод координат Ведомость смещений верхнего строения опор мостового перехода Период наблюдений
с 15.05.2005 по 15.05.2006.
Автодорога Москва – Самара, км 459.
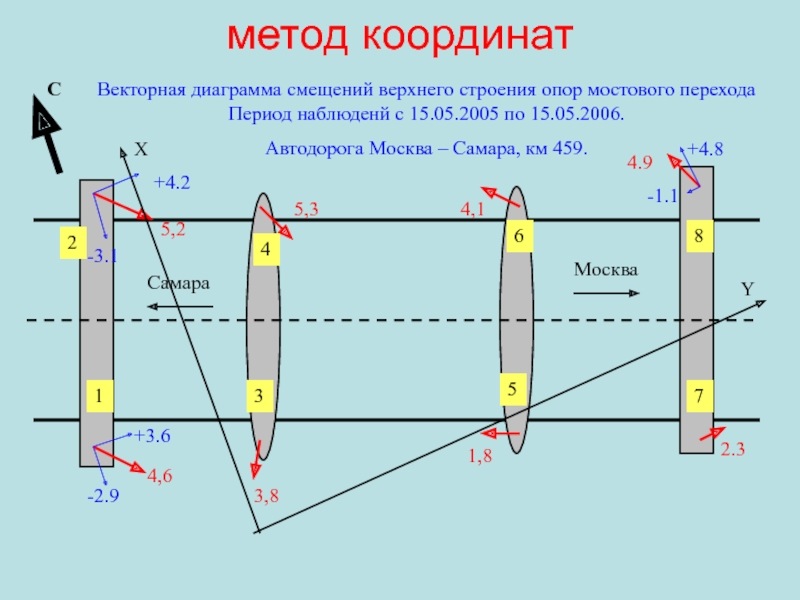
Слайд 110метод координат
С
4,6
5,2
3,8
5,3
4,1
1,8
4.9
2.3
Векторная диаграмма смещений верхнего строения опор мостового перехода Период
наблюденй с 15.05.2005 по 15.05.2006.
Автодорога Москва – Самара, км 459.
Москва
Самара
5
6
4
3
2
1
8
7
X
Y
-2.9
+3.6
-3.1
+4.2
-1.1
+4.8
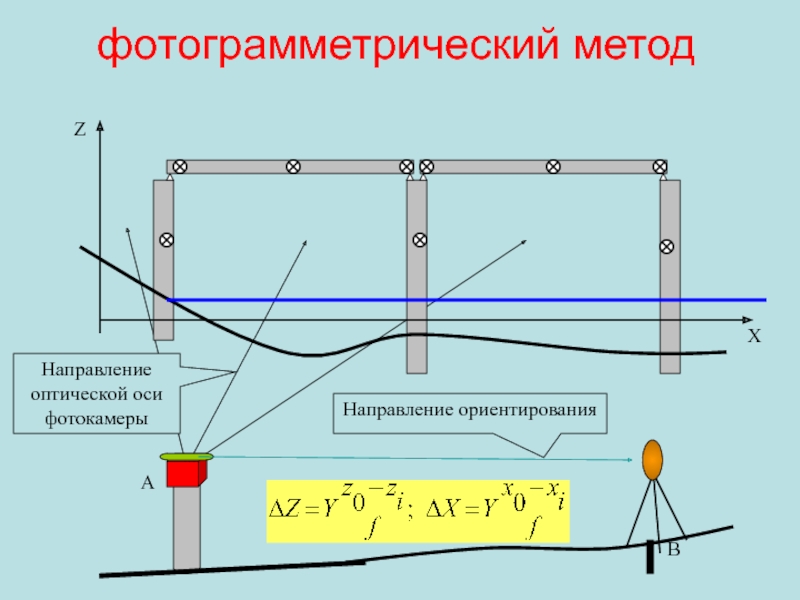
Слайд 111фотограмметрический метод
Z
X
B
A
Направление оптической оси фотокамеры
Направление ориентирования
Слайд 113
Элементы внутреннего ориентирования - координаты главной точки снимка xO, zO
z′
z′
x′
x′
а
О
О′
xO
zO
x′a
z′a
xa
za
Элементы
внешнего ориентирования пары снимков:
1. Геодезические координаты (Xs1, Ys1, Zs1) левого
конца базиса;2. Длина базиса (горизонтальное проложение) В;
3. Превышение (hВ) правого конца базиса относительно левого (hВ = Zs2 - Zs1);
4. Дирекционный угол базиса (В) по направлению с левой на правую точку фотографирования;
5. Углы скоса фотографирования левого (1) и правого (2) снимков;
6. Углы наклона оптических осей левого (1) и правого (2) снимка;
7. Углы разворота снимка в своей плоскости левого (1) и правого (2);
8. Угол конвергенции (сходимости, +) или дивергенции (расходимости -), который равен разности углов скоса правого и левого снимка
( = 2 - 1).
η
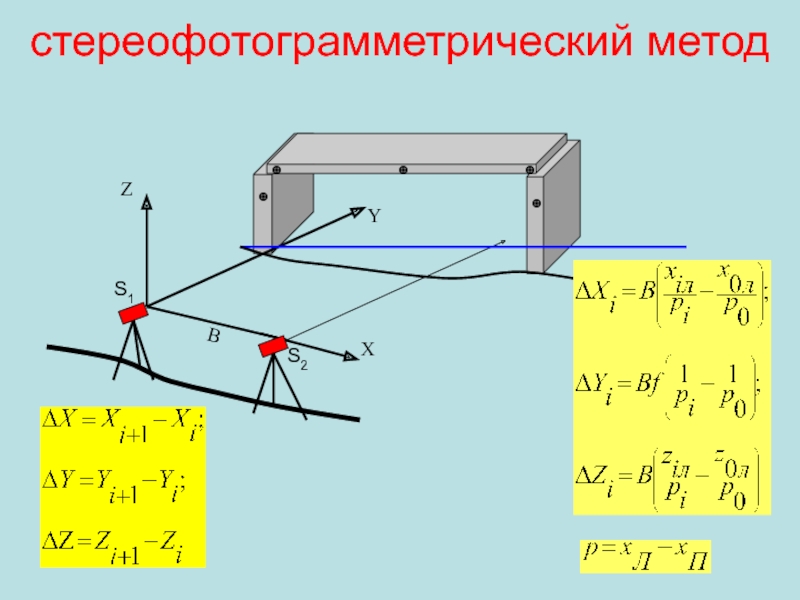
стереофотограмметрический метод
Элементы ориентирования пары снимков

![ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ СТРОИТЕЛЬСТВЕ И ЭКСПЛУАТАЦИИ МОСТОВ ЛитератураОсновнаяИнтернет- ресурс: Михелев Д.Ш. Инженерная геодезия: учебник /Е.Б. Клюшин [и др.]; ЛитератураОсновнаяИнтернет- ресурс: Михелев Д.Ш. Инженерная геодезия: учебник /Е.Б. Клюшин [и др.]; под ред. Д.Ш.Михелева, - 9-е изд.](/img/thumbs/bcda0bae80c29020e2e6e926294208f4-800x.jpg)