Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические тела
Содержание
- 1. Геометрические тела
- 2. Виртуальный справочник составили:Илюшкина Е,Л
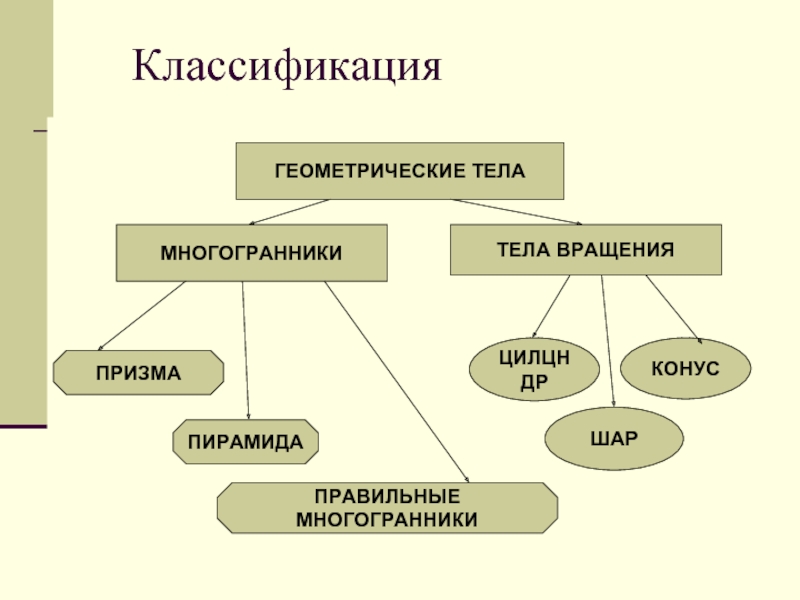
- 3. Классификация ГЕОМЕТРИЧЕСКИЕ ТЕЛАМНОГОГРАННИКИТЕЛА ВРАЩЕНИЯПРИЗМАПИРАМИДАПРАВИЛЬНЫЕ МНОГОГРАННИКИЦИЛЦНДРКОНУСШАР
- 4. Понятие многогранникаПоверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранником.Примеры многогранников
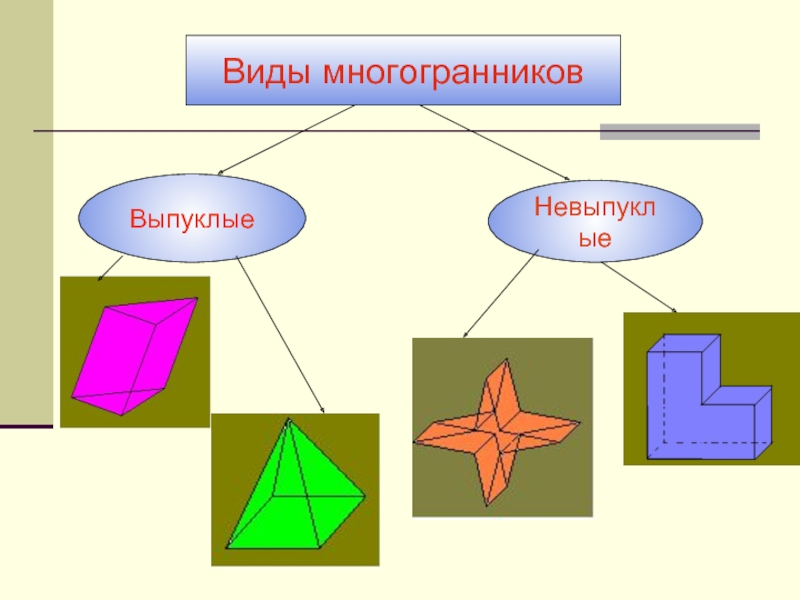
- 5. Виды многогранниковВыпуклыеНевыпуклые
- 6. Примеры многогранниковБольшой курносый икосододекаэдр
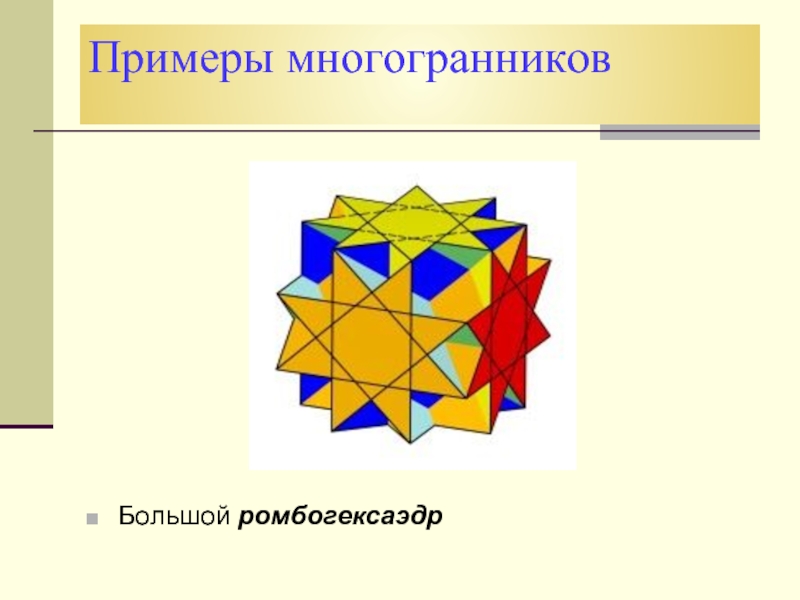
- 7. Примеры многогранниковБольшой ромбогексаэдр
- 8. Примеры многогранниковКвазиромбокубоктаэдр
- 9. Выпуклый многогранникМногогранник называется выпуклым, если он расположен
- 10. Элементы многогранникаМногоугольники, из которых составлен многогранник, называются
- 11. ПризмаПризмой называется многогранник, который состоит из двух
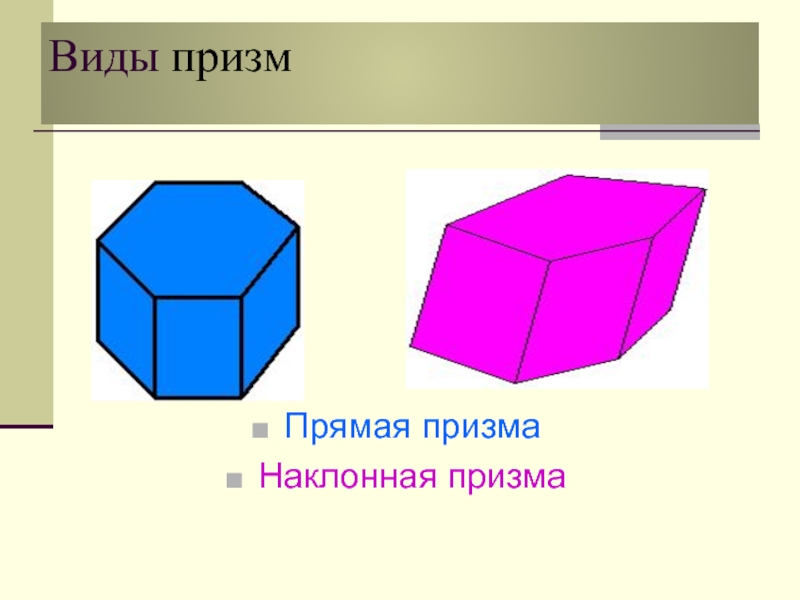
- 12. Виды призмПрямая призма Наклонная призма
- 13. определенияЕсли боковые рёбра призмы перпендикулярны к основаниям,
- 14. Формула нахождения S призмыПлощадью полнойповерхности призмы(Sполн)называется суммаплощадей
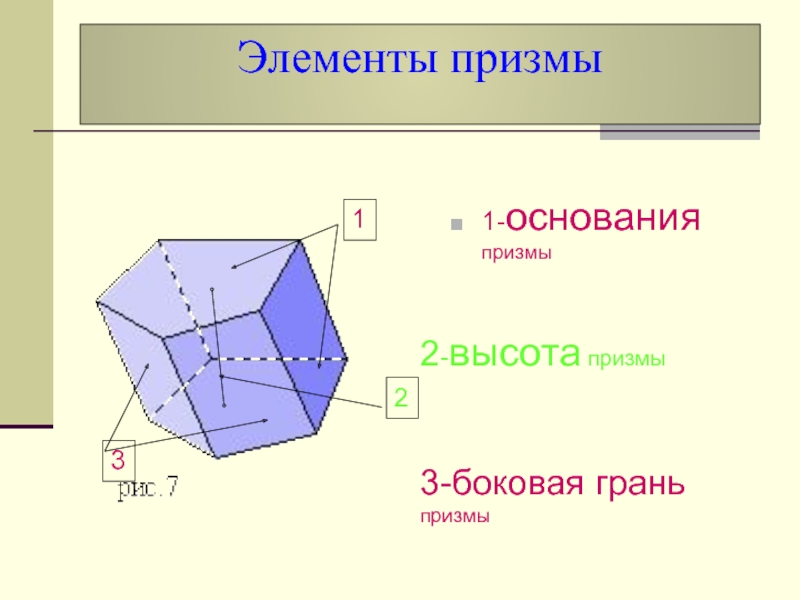
- 15. Элементы призмы1-основания призмы2-высота призмы3-боковая грань призмы
- 16. Определение элементов призмыА1А2А3В1В2В3Многоугогльники А1А2А3 и вВ1В2В3 называютсяоснованиямиПараллелограммы А1В1В2А2…А1В1В3А3 --боковые граниПерпендикуляр, проведенный изкакой-нибудь точки основания кплоскости
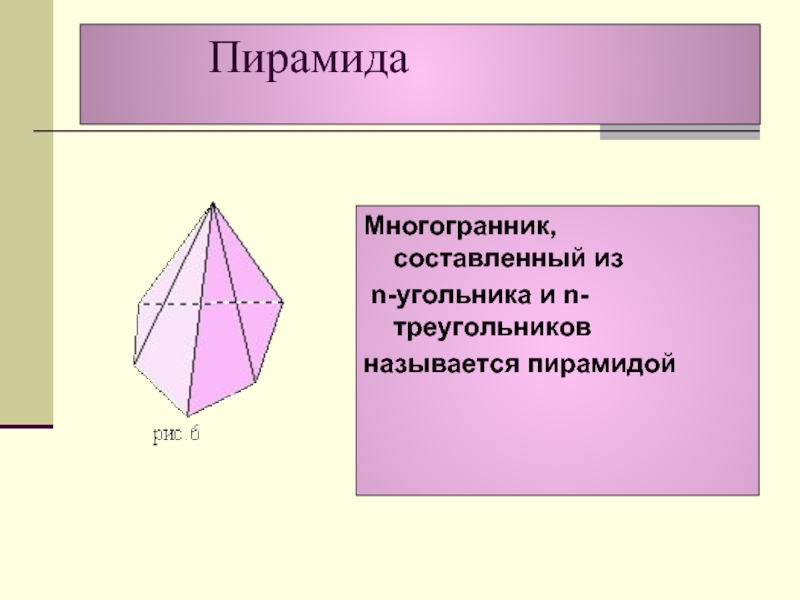
- 17. ПирамидаМногогранник, составленный из n-угольника и n-треугольников
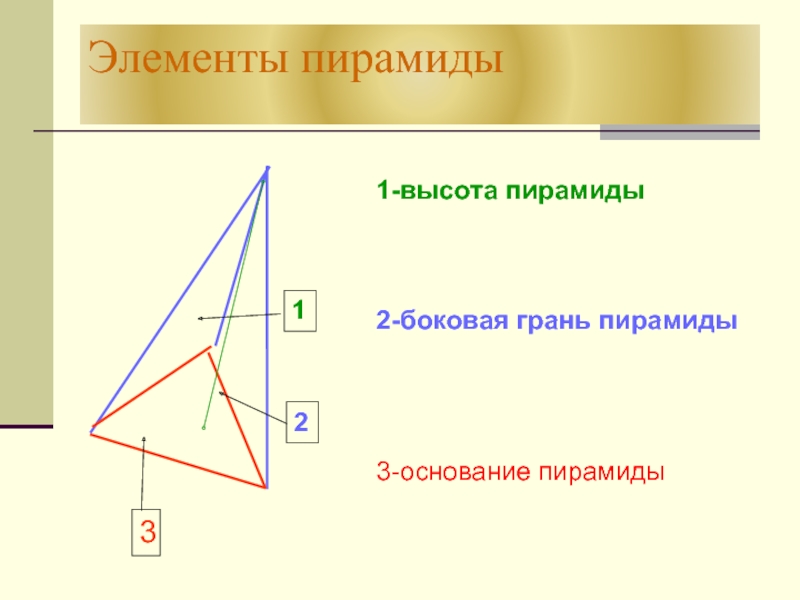
- 18. Элементы пирамиды1231-высота пирамиды2-боковая грань пирамиды3-основание пирамиды
- 19. Правильные многогранники Выпуклый многогранник называется правильным,
- 20. ГексаэдрКуб составлен из шести квадратов. Каждая его
- 21. Основные формулы для гексаэдраОбозначения: а – ребро,
- 22. ТетраэдрТетраэдр составлен из четырех равносторонних треугольников. Каждая
- 23. Основные формулы для тетраэдраОбозначения: а – ребро,
- 24. ОктаэдрОктаэдр составлен из восьми равносторонних треугольников. Каждая
- 25. Основные формулы для октаэдраОбозначения: а – ребро,
- 26. ДодекаэдрДодекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
- 27. Основные формулы для додекаэдраОбозначения: а – ребро,
- 28. ИкосаэдрИкосаэдр составлен из двадцати равносторонних треугольников. Каждая
- 29. Основные формулы для икосаэдраОбозначения: а – ребро,
- 30. Правильные многогранники
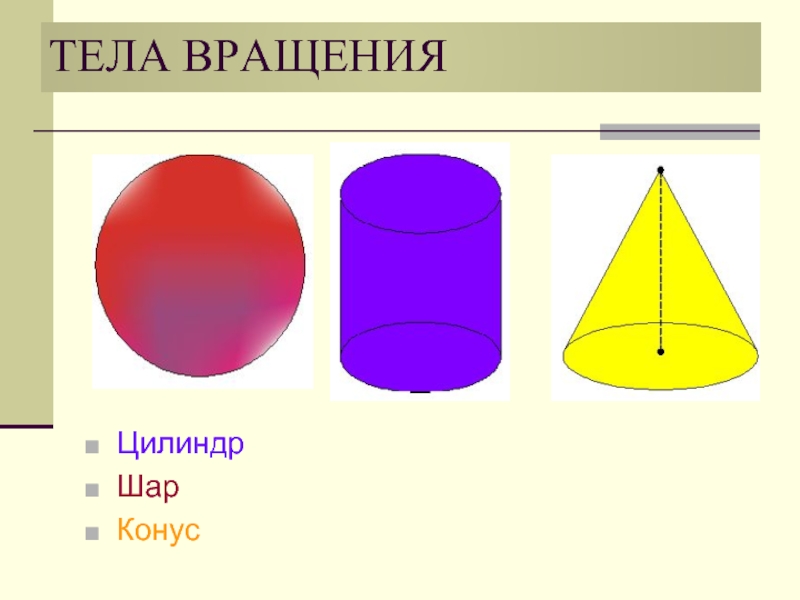
- 31. ТЕЛА ВРАЩЕНИЯЦилиндрШарКонус
- 32. ЦИЛИНДРЦилиндром называется тело, которое состоит из двух
- 33. ВИДЫ ЦИЛИНДРОВПрямой Наклонный
- 34. КОНУСКонусом называется тело, которое состоит из круга
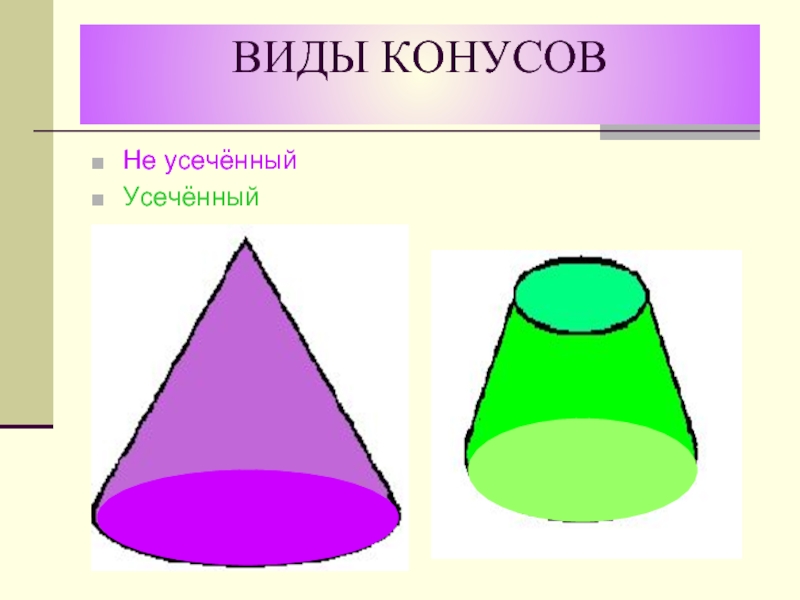
- 35. ВИДЫ КОНУСОВНе усечённый Усечённый
- 36. СФЕРА И ШАРСферой называется поверхность, состоящая из
- 37. ОСНОВНЫЕ ФОРМУЛЫ
- 38. Список литературы:Атанасян Л.С. Геометрия: Учеб. для 10-11кл.Крамор В.С. Повторяем и систематизируем школьный курс геометрии.
- 39. Скачать презентанцию
Виртуальный справочник составили:Илюшкина Е,Л
Слайды и текст этой презентации
Слайд 3 Классификация
ГЕОМЕТРИЧЕСКИЕ ТЕЛА
МНОГОГРАННИКИ
ТЕЛА ВРАЩЕНИЯ
ПРИЗМА
ПИРАМИДА
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
ЦИЛЦНДР
КОНУС
ШАР
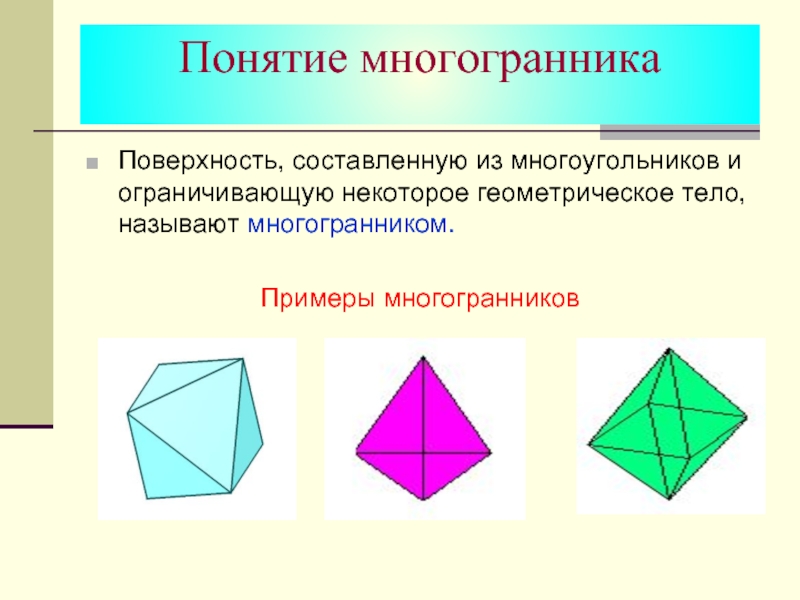
Слайд 4Понятие многогранника
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело,
называют многогранником.
Слайд 9Выпуклый многогранник
Многогранник называется выпуклым, если он расположен по одну сторону
от плоскости каждой его грани.
Все грани выпуклого многогранника являются выпуклыми
многоугольниками.В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360 градусов.
Слайд 10Элементы многогранника
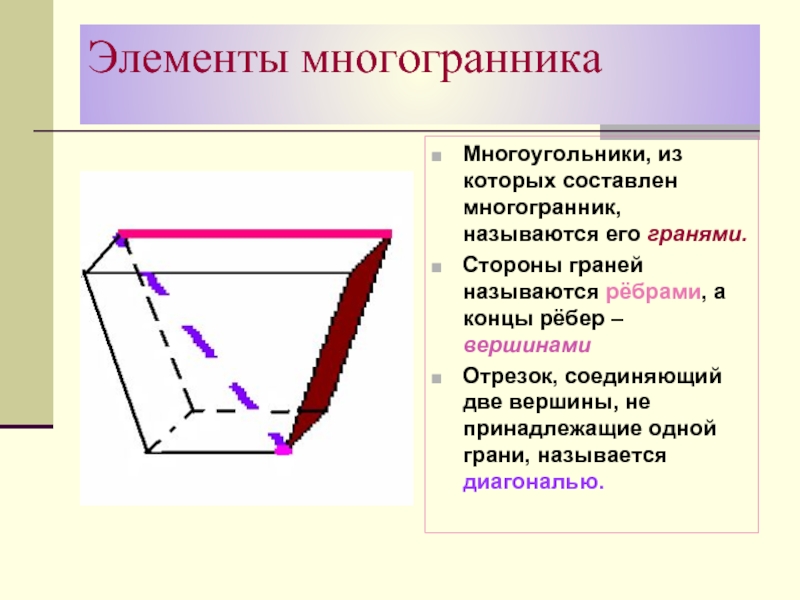
Многоугольники, из которых составлен многогранник, называются его гранями.
Стороны граней
называются рёбрами, а концы рёбер – вершинами
Отрезок, соединяющий две вершины,
не принадлежащие одной грани, называется диагональю. Слайд 11Призма
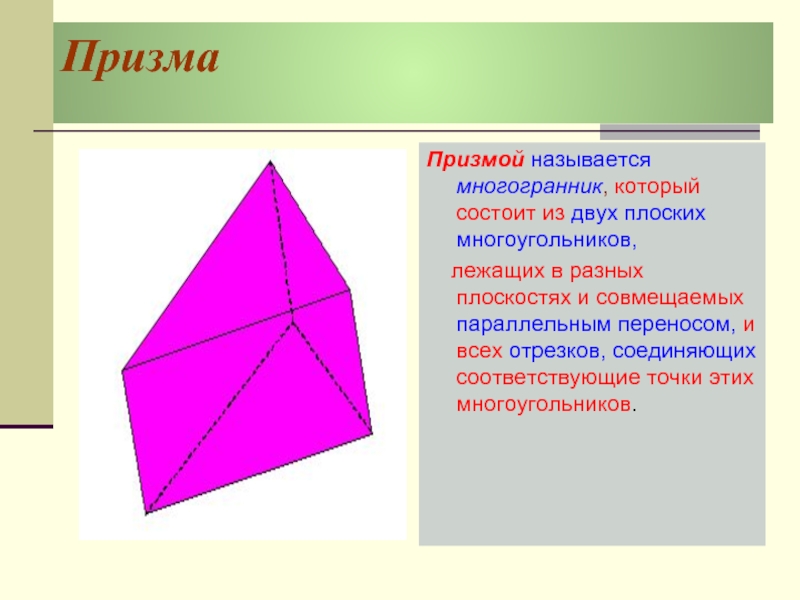
Призмой называется многогранник, который состоит из двух плоских многоугольников,
лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех
отрезков, соединяющих соответствующие точки этих многоугольников.Слайд 13определения
Если боковые рёбра призмы перпендикулярны к основаниям, то призма
называется прямой, в противном случае – наклонной.
Высота прямой
призмы равна её боковому ребру. Слайд 14Формула нахождения S призмы
Площадью полной
поверхности призмы(Sполн)
называется сумма
площадей всех её граней,
а
площадью боковой поверхности призмы (Sбок)-сумма площадей боковых её граней.
Sпол=Sбок+2Sосн
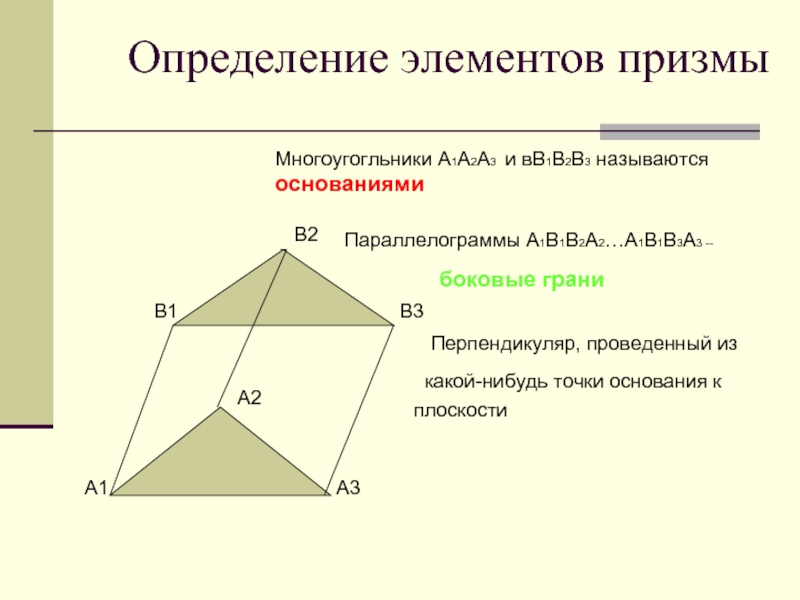
Слайд 16Определение элементов призмы
А1
А2
А3
В1
В2
В3
Многоугогльники А1А2А3 и вВ1В2В3 называются
основаниями
Параллелограммы А1В1В2А2…А1В1В3А3 --
боковые грани
Перпендикуляр,
проведенный из
какой-нибудь точки основания к
плоскости
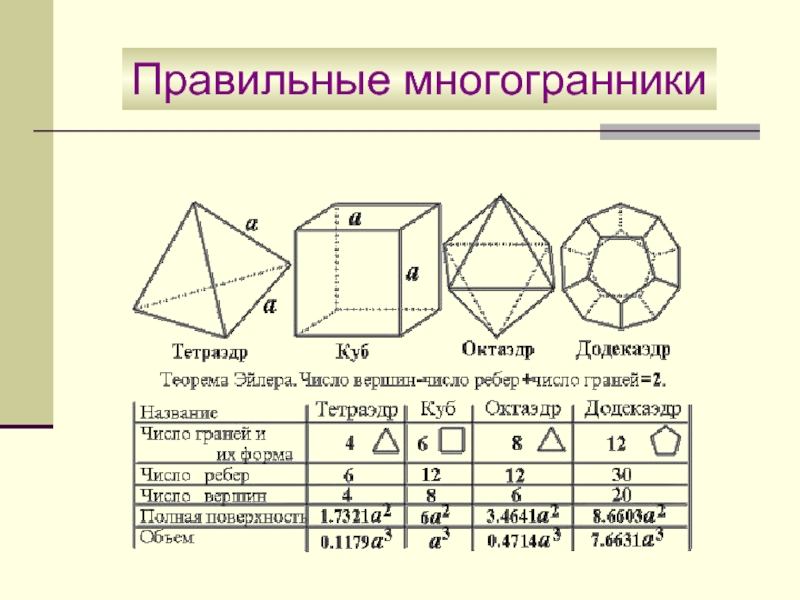
Слайд 19Правильные многогранники
Выпуклый многогранник называется
правильным, если все его
грани – равные
правильные многоугольники и в каждой его
вершине сходится одно и то же число рёбер.
Слайд 20Гексаэдр
Куб составлен из шести квадратов. Каждая его вершина является вершиной
трех квадратов.
Сумма плоских углов при каждой вершине равна 270
градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер Слайд 21Основные формулы для гексаэдра
Обозначения: а – ребро,
V-объём,
S-площадь боковой поверхности,R-радиус описанной сферы,
r- радиус вписанной сферы,
H- высота.
Слайд 22Тетраэдр
Тетраэдр составлен из четырех равносторонних треугольников.
Каждая его вершина является
вершиной трех треугольников.
Сумма плоских углов при каждой вершине равна
180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Слайд 23Основные формулы для тетраэдра
Обозначения: а – ребро,
V-объём,
S-площадь боковой поверхности,R-радиус описанной сферы,
r- радиус вписанной сферы,
H- высота.
Слайд 24Октаэдр
Октаэдр составлен из восьми равносторонних треугольников.
Каждая его вершина является
вершиной четырех треугольников.
Сумма углов при плоских каждой вершине равна
240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Слайд 25Основные формулы для октаэдра
Обозначения: а – ребро,
V-объём,
S-площадь боковой поверхности,R-радиус описанной сферы,
r- радиус вписанной сферы,
H- высота.
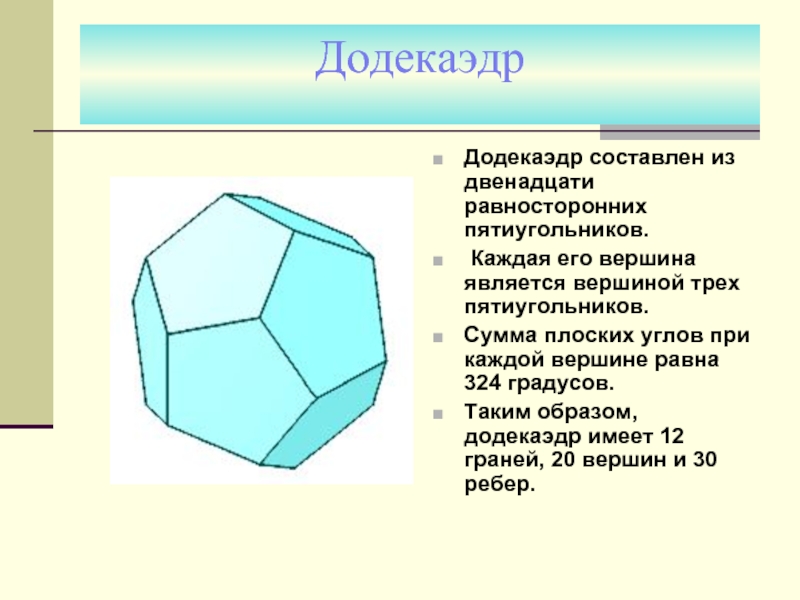
Слайд 26Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Каждая его вершина является
вершиной трех пятиугольников.
Сумма плоских углов при каждой вершине равна
324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Слайд 27Основные формулы для додекаэдра
Обозначения: а – ребро,
V-объём,
S-площадь боковой поверхности,R-радиус описанной сферы,
r- радиус вписанной сферы,
H- высота.
Слайд 28Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников.
Каждая его вершина является
вершиной пяти треугольников.
Сумма плоских углов при каждой вершине равна
300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Слайд 29Основные формулы для икосаэдра
Обозначения: а – ребро,
V-объём,
S-площадь боковой поверхности,R-радиус описанной сферы,
r- радиус вписанной сферы,
H- высота.
Слайд 32ЦИЛИНДР
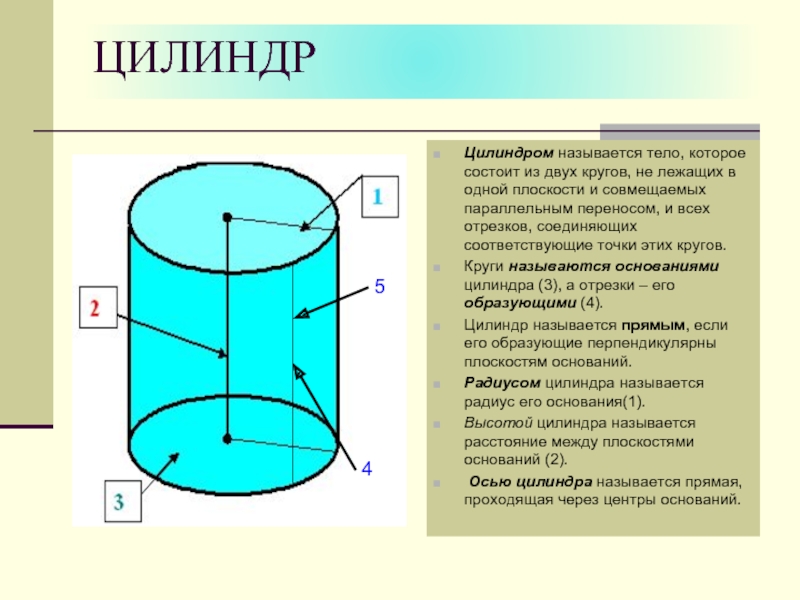
Цилиндром называется тело, которое состоит из двух кругов, не лежащих
в одной плоскости и совмещаемых параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих кругов.Круги называются основаниями цилиндра (3), а отрезки – его образующими (4).
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Радиусом цилиндра называется радиус его основания(1).
Высотой цилиндра называется расстояние между плоскостями оснований (2).
Осью цилиндра называется прямая, проходящая через центры оснований.
4
5
Слайд 34КОНУС
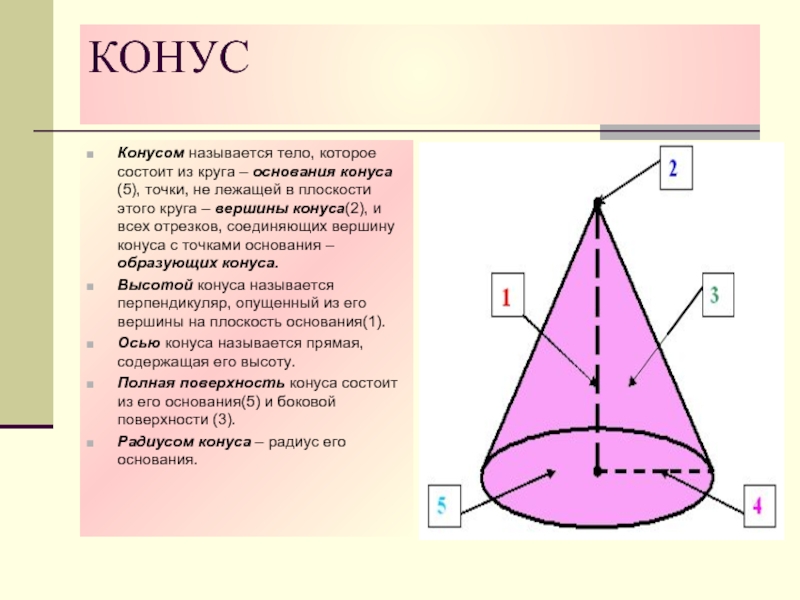
Конусом называется тело, которое состоит из круга – основания конуса(5),
точки, не лежащей в плоскости этого круга – вершины конуса(2),
и всех отрезков, соединяющих вершину конуса с точками основания – образующих конуса.Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания(1).
Осью конуса называется прямая, содержащая его высоту.
Полная поверхность конуса состоит из его основания(5) и боковой поверхности (3).
Радиусом конуса – радиус его основания.
Слайд 36СФЕРА И ШАР
Сферой называется поверхность, состоящая из всех точек пространства,
расположенных на данном расстоянии от данной точки (3).
Данная точка называется
центром сферы, а данное расстояние- радиусом сферы (1).Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
Плоскость, проходящая через центр шара , называется диаметральной плоскостью (2).
Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью.
3
Слайд 38Список литературы:
Атанасян Л.С. Геометрия: Учеб. для 10-11кл.
Крамор В.С. Повторяем и
систематизируем школьный курс геометрии.
Теги