Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия до Евклида
Содержание
- 1. Геометрия до Евклида
- 2. БиографияРодился в Греции. Был математиком, учеником Евдокса Книдского. Являлся также членом Платоновской Академии.Рафаэль, «Афинская школа»
- 3. Решение задачи о квадратуре круга с помощью
- 4. Слайд 4
- 5. Конические сеченияКонические сечения — плоские кривые, которые
- 6. Виды конических сечений Эллипс; гипербола; парабола.
- 7. Геометрическое обоснование первого замечательного пределаПлощадь треугольника AOB
- 8. Список литературы Решение задачи о квадратуре круга
- 9. Скачать презентанцию
БиографияРодился в Греции. Был математиком, учеником Евдокса Книдского. Являлся также членом Платоновской Академии.Рафаэль, «Афинская школа»
Слайды и текст этой презентации
Слайд 2Биография
Родился в Греции. Был математиком, учеником Евдокса Книдского. Являлся также
членом Платоновской Академии.
Рафаэль, «Афинская школа»
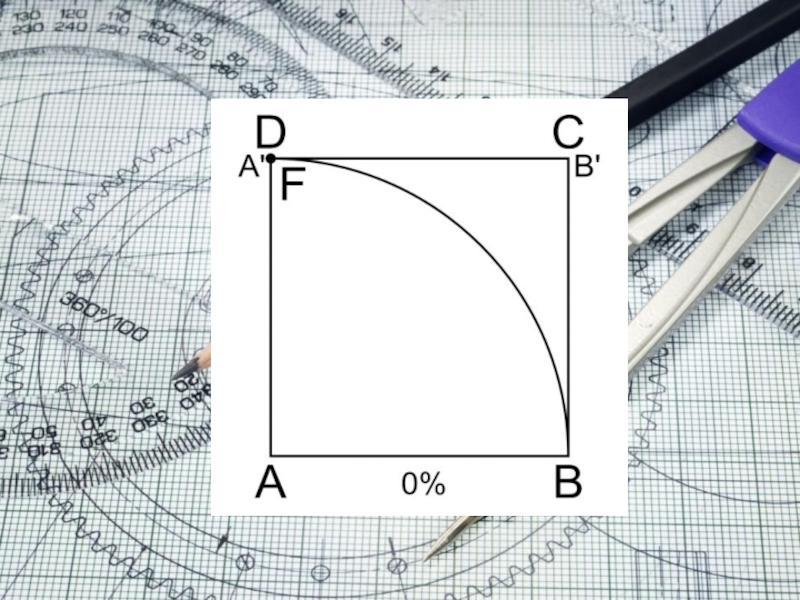
Слайд 3Решение задачи о квадратуре круга с помощью квадратрисы
Пусть ANB —
четверть окружности, расположенной в квадранте AOB, а AMC — квадратриса
этого квадранта.Динострат доказывает, что отрезок, отсекаемый квадратрисой на нижней стороне квадрата, так относится к стороне квадрата, как радиус окружности относится к длине дуги, составляющей четверть этой окружности.
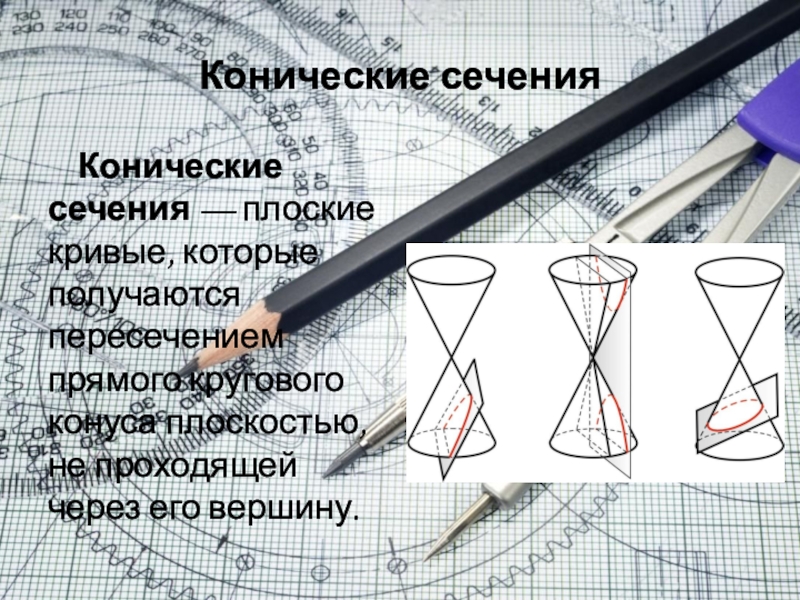
Слайд 5Конические сечения
Конические сечения — плоские кривые, которые получаются пересечением прямого
кругового конуса плоскостью, не проходящей через его вершину.
Слайд 7Геометрическое обоснование первого замечательного предела
Площадь треугольника AOB меньше площади сектора
AOB, которая меньше площади прямоугольного треугольника AOC.
Далее можно составить неравенство,
из которого получим 
Слайд 8Список литературы
Решение задачи о квадратуре круга при помощи вспомогательных
средств. [http://mathemlib.ru/] – URL: http://mathemlib.ru/books/item/f00/s00/z0000047/st022.shtml (Дата обращения: 15.09.2020.)
Конические сечения.
[https://graph.power.nstu.ru/] – URL: https://graph.power.nstu.ru/wolchin/umm/eskd/glosar/ru/K/con_sechenie.htm (Дата обращения: 15.09.2020.)Н.Ш. Крамер. Высшая математика для экономистов. – 2 – е изд., перераб. И доп. – М.: ЮНИТИ, 2003 – 471 с.
![Список литературы Решение задачи о квадратуре круга при помощи вспомогательных средств. [http://mathemlib.ru/] – URL: http://mathemlib.ru/books/item/f00/s00/z0000047/st022.shtml (Дата обращения:](/img/tmb/7/636977/45cfbd04433c64ce06ddb2b7f9d5aaba-800x.jpg "Геометрия до Евклида Список литературы Решение задачи о квадратуре круга при помощи вспомогательных средств.")
