TheSlide.ru

Геометрия Теоремы Менелая

Содержание

1. Геометрия Теоремы Менелая
2. Теорема Менелая:Пусть точка А1 лежит на
3. АВ1ВСА1С1 Эта теорема Входит в золотой
4. Задача 1. В треугольнике АВС на
5. РешениеПо условию задачи МА = АС, NC
6. Задача 2.Пусть AD – медиана треугольника
7. Скачать презентанцию

Теорема Менелая:Пусть точка А1 лежит на стороне ВС треугольника АВС, точка С1 – на стороне АВ, точка В1 – на продолжении стороны АС за точку С. Точки А1,В1 иС1 лежат

Главная
Разное
Геометрия Теоремы Менелая

Слайды и текст этой презентации

Слайд 1Геометрия
Теоремы Менелая

ГеометрияТеоремы Менелая

Слайд 2 Теорема Менелая:
Пусть точка А1 лежит на стороне ВС треугольника

АВС, точка С1 – на стороне АВ, точка В1 –

на продолжении стороны АС за точку С. Точки А1,В1 иС1 лежат на одной прямой тогда и только тогда, когда выполняется равенство

Теорема Менелая:Пусть точка А1 лежит на стороне ВС треугольника АВС, точка С1 – на стороне АВ,

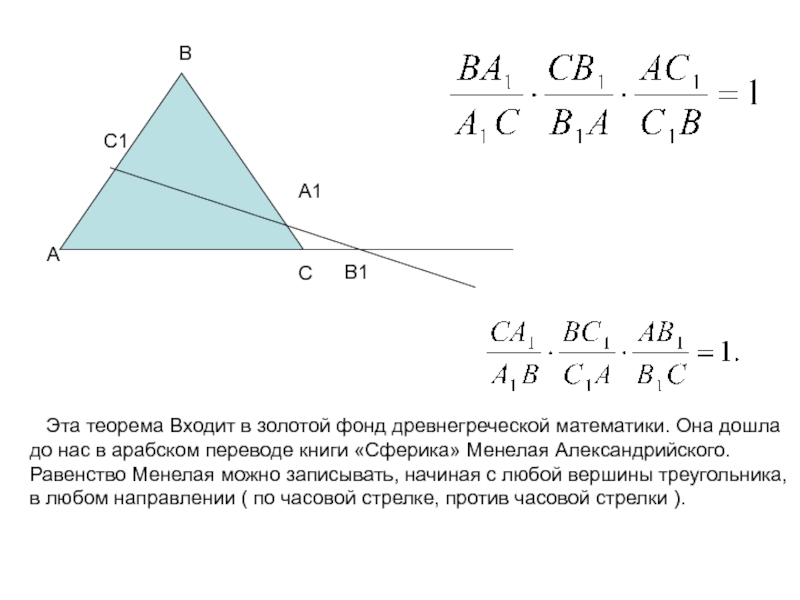
Слайд 3А
В1
В
С
А1
С1
Эта теорема Входит в золотой фонд древнегреческой математики.

Она дошла до нас в арабском переводе книги «Сферика» Менелая

Александрийского. Равенство Менелая можно записывать, начиная с любой вершины треугольника, в любом направлении ( по часовой стрелке, против часовой стрелки ).

АВ1ВСА1С1 Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе

Слайд 4 Задача 1. В треугольнике АВС на стороне ВС взята точка

N так, что NC = 3BN; на продолжении стороны АС

за точку А взята точка М так, что МА=АС. Прямая MN пересекает сторону АВ в точке F. Найдите: отношение

Задача 1. В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN;

Слайд 5Решение
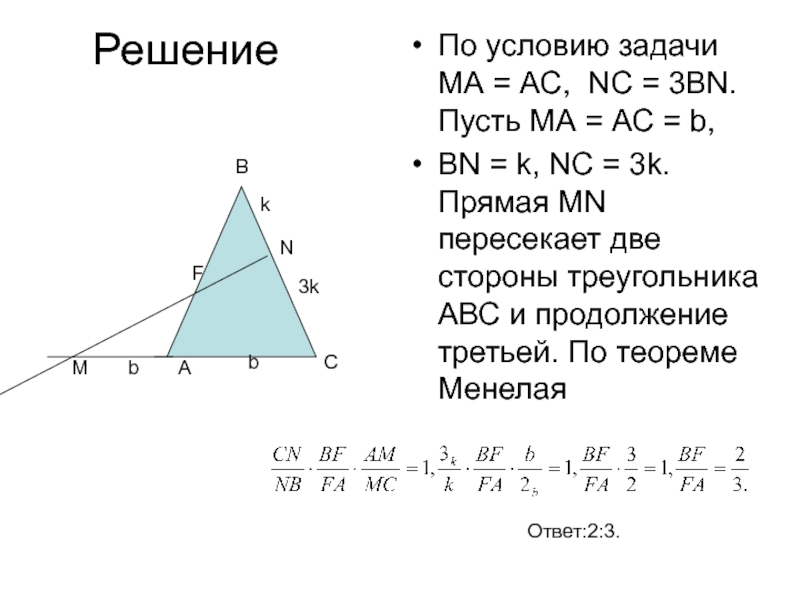
По условию задачи МА = АС, NC = 3BN. Пусть

МА = АС = b,
BN = k, NC = 3k.

Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая

В

F

C

А

M

N

k

3k

b

b

Ответ:2:3.

РешениеПо условию задачи МА = АС, NC = 3BN. Пусть МА = АС = b,BN = k,

Слайд 6 Задача 2.
Пусть AD – медиана треугольника АВС. На стороне

AD взята точка K так, что AK:KD=3:1. Прямая ВК разбивает

треугольник АВС на два. Найдите отношение площадей этих треугольников.

Задача 2.Пусть AD – медиана треугольника АВС. На стороне AD взята точка K так, что AK:KD=3:1.

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей