Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Градусная и радианная меры угла. Вращательное движение
Содержание
- 1. Градусная и радианная меры угла. Вращательное движение
- 2. Для чего нужны синусы и косинусы в
- 3. Слайд 3
- 4. Детская школа Гауди в Барселоне
- 5. Ресторан в Лос-Манантиалесе в Аргентине
- 6. Мост в Сингапуре
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Немного из истории…1. Древние вавилоняне и египтяне
- 11. Немного из истории…4. Насир ад-Дин Мухаммад ат-Туси
- 12. Тригонометрияраздел математики, изучающий соотношение сторон и углов
- 13. Чему равен угол квадрата?
- 14. На какой угол поворачивается солдат по команде «кругом»?
- 15. Чему равен угол между минутной и часовой стрелками на часах, когда они показывают 2ч?
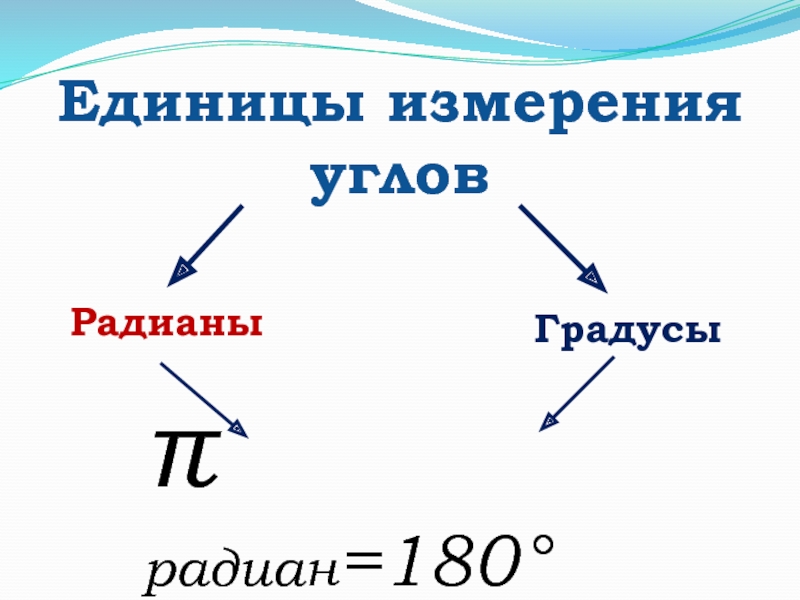
- 16. Единицы измерения угловГрадусыРадианы
- 17. Градусная мера угла1 – цена одного деления окружности, разделенной на 360 частей=1
- 18. Углом в 10 (один градус) называют центральный угол
- 19. Радианная мера угла1 радиан – это величина центрального угла, длина дуги которого равна радиусу1рад.R=1R=1l=R
- 20. Единицы измерения угловГрадусыРадианы радиан=180
- 21. радиан=180Перевод из градусной меры в радианную:
- 22. Пример:1.2.3.
- 23. Пример:4.5.6.
- 24. Пример:1.2.3.
- 25. Пример:4.5.6.
- 26. радиан=180Перевод из радианной меры в градусную:
- 27. Пример:1.2.3.
- 28. Пример:1.2.3.
- 29. №1: Переведите в радианную меру углы:1) 45
- 30. №2: Переведите в градусную меру углы:1) 2) 3) 4) 5) 6)
- 31. Перевод из градусной меры в радианную:Перевод из радианной меры в градусную:
- 32. Самостоятельная работа1. Переведите в радианную меру углы:1)
- 33. Ответы1. 1)2)3)I вариант II вариант 1) 2) 3)2. 1) 722) 4801) 4052) 150
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла.Гипотенуза
- 39. Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла.Синус
- 40. Синус, косинус, тангенс и котангенс как отношения
- 41. Для треугольника ABCABCABC, изображенного ниже на рисунке, найдем sin α, cos α, tg α, ctg αsin α=4/5=0,8cos α=3/5=0,6tg α=4/3ctg α=3/4=0,75Попробуйте посчитай то же самое для угла β.Ответы: sin β=0,6; cos β=0,8; tg β=0,75; ctg β=43.
- 42. Окружность с радиусом, равным 1называется единичной. Данная окружность построена
- 43. xyOПоложительное направление поворота:против часовой стрелки.Отрицательное направление поворота:по часовой стрелке.
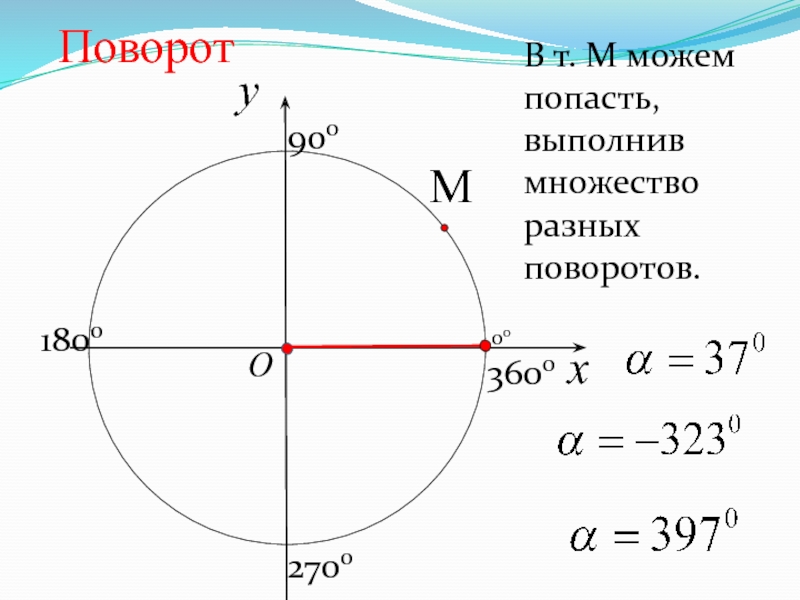
- 44. xyOПоворотВ т. М можем попасть, выполнив множество разных поворотов.90018002700360000
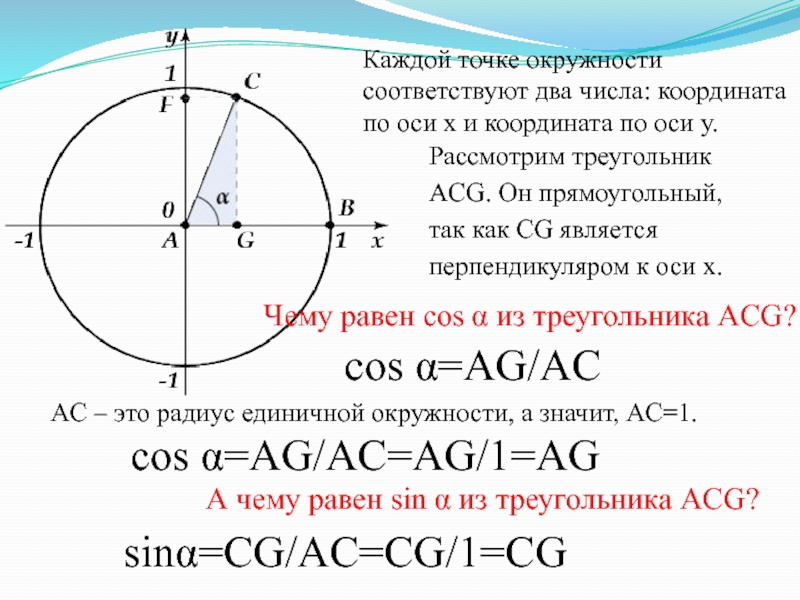
- 45. Каждой точке окружности соответствуют два числа: координата
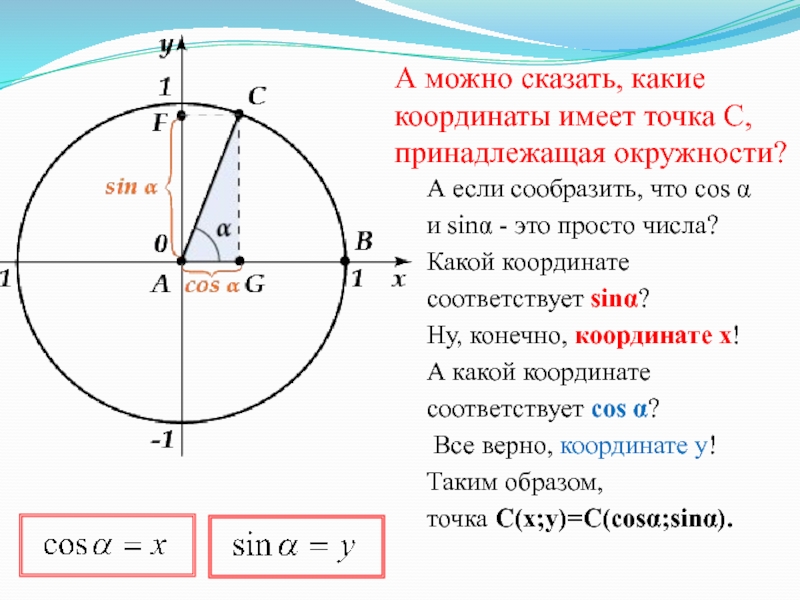
- 46. А можно сказать, какие координаты имеет точка C,
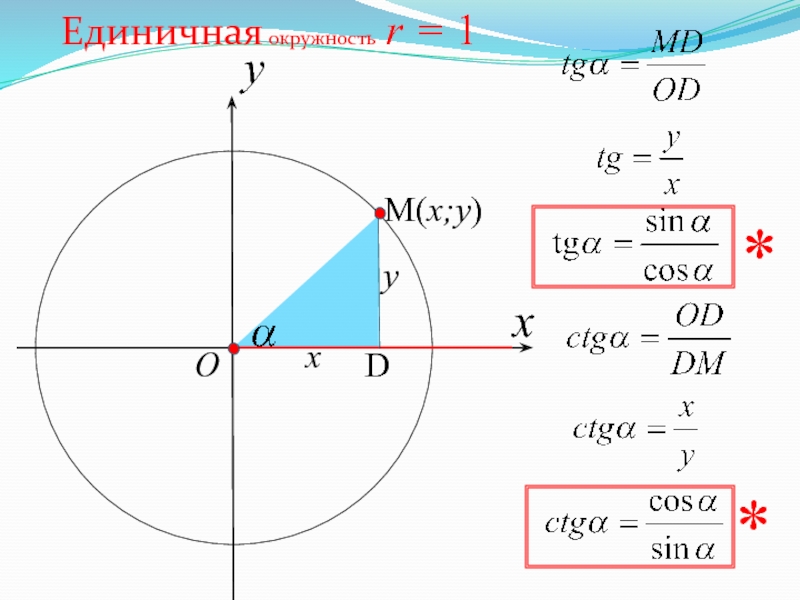
- 47. xЕдиничная окружность r = 1yOxy
- 48. Слайд 48
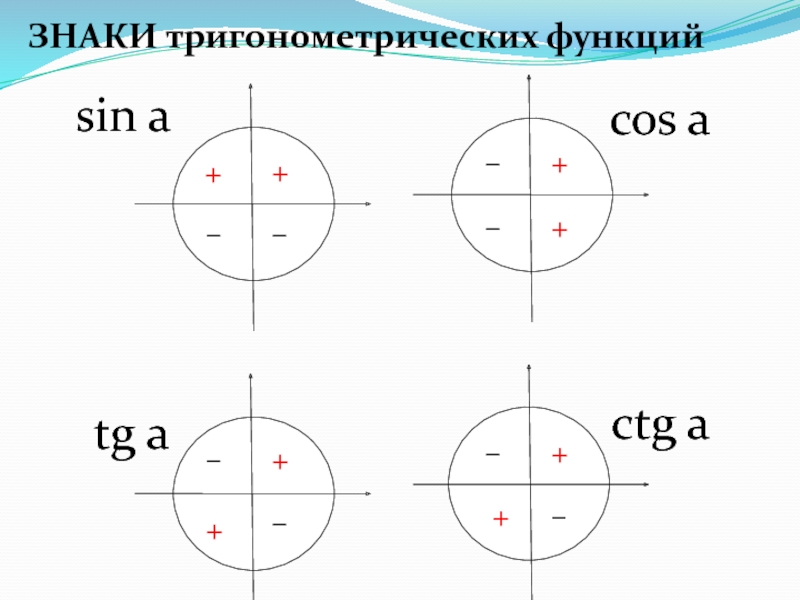
- 49. ЗНАКИ тригонометрических функцийsin acos a tg a ctg a
- 50. Домашнее заданиеВыучить формулы перевода из градусной меры
- 51. Ответьте на вопросы:1) Что означает «тригонометрия»?2) Разделом
- 52. Скачать презентанцию
Для чего нужны синусы и косинусы в обычной жизни?На практике синусы и косинусы применяются во всех инженерных специальностях, особенно в строительных. Их используют моряки и летчики в расчетах курса движения. Не
Слайды и текст этой презентации
Слайд 1
Градусная и радианная меры угла. Вращательное движение.
Синус, косинус,
тангенс
и котангенс.
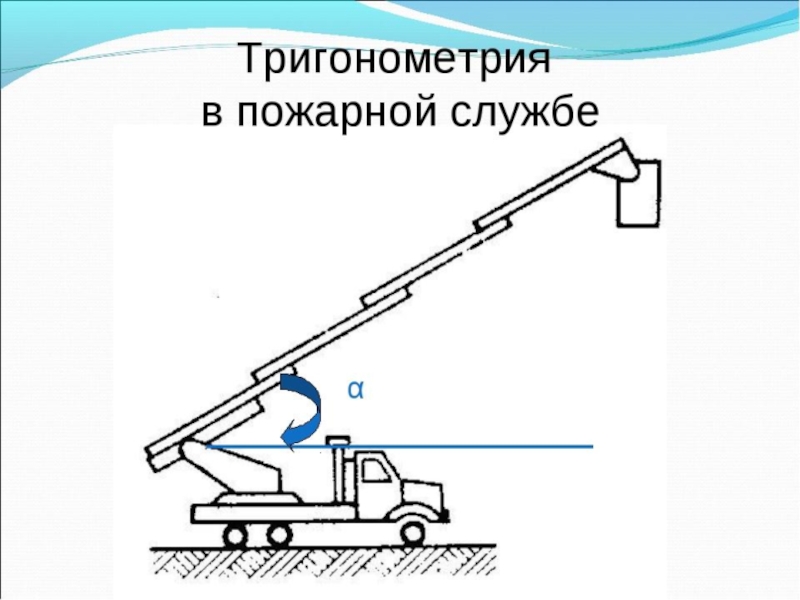
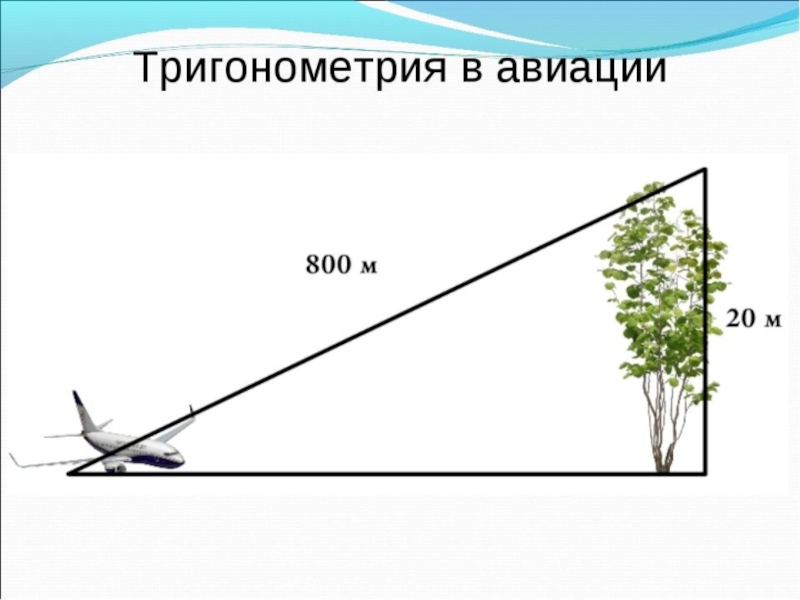
Слайд 2Для чего нужны синусы и косинусы в обычной жизни?
На практике
синусы и косинусы применяются во всех инженерных специальностях, особенно в
строительных. Их используют моряки и летчики в расчетах курса движения. Не обходятся без синусов и косинусов геодезисты, и даже путешественники. В географии применяют для измерения расстояний между объектами, а также в спутниковых навигационных системах.
Слайд 10Немного из истории…
1. Древние вавилоняне и египтяне изучали тригонометрию как
часть астрономии; разделили окружность на 360
2. Древние индийцы: ввели
названия «синус», «косинус», составили таблицы синусов, косинусов3. IX-XVвв – Средний и Ближний восток: составляли таблицы котангенса, тангенса, косеканса; ввели понятие единичной окружности
Слайд 11Немного из истории…
4. Насир ад-Дин Мухаммад ат-Туси (1201-1274) выделил раздел
тригонометрии из астрономии.
5. Лев Герсонид (1288-1344) – открыл теорему синусов.
6.
XVII-XIXвв: применение тригонометрии в механике, физике, технике, как часть математического анализа (Виетт, Бернулли) – тригонометрические символы, графики – синусоиды.7. Л.Эйлер: придал тригонометрии современный вид.
Слайд 12Тригонометрия
раздел математики, изучающий соотношение сторон и углов в треугольнике
(«три» -
три, «гониа» - угол, «метриа» - измеряю)
Слайд 18Углом в 10 (один градус) называют центральный угол в окружности, опирающийся
на круговую дугу, равную 1/360 части окружности.
Вся окружность состоит из 360 «кусочков»
круговых дуг, или угол, описываемый окружностью, равен 3600.На рисунке изображен угол β, равный 500 то есть этот угол опирается на круговую дугу размером 50/360 длины окружности.
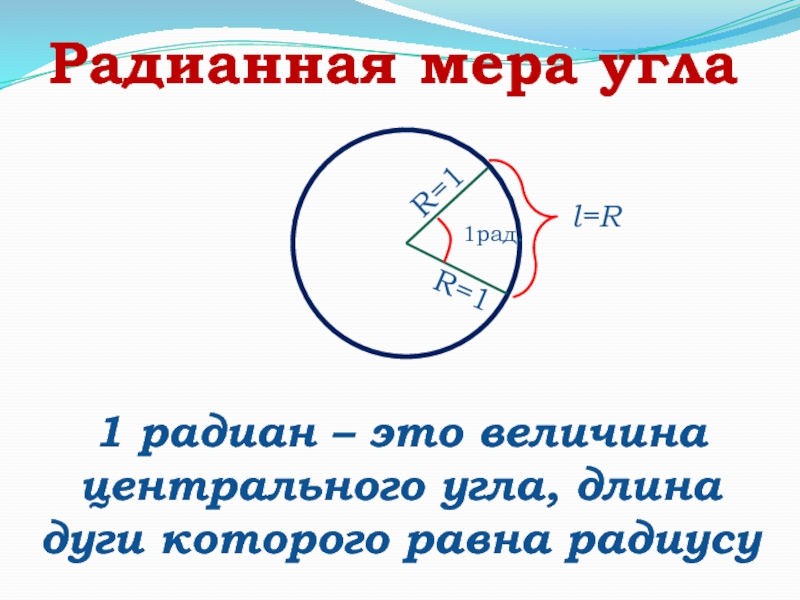
Слайд 19Радианная мера угла
1 радиан – это величина центрального угла, длина
дуги которого равна радиусу
1рад.
R=1
R=1
l=R
Слайд 29№1: Переведите в радианную меру углы:
1) 45
2) 15
3)
72
4) 100
5) 200
6) 360
7) 215
8)
150 9) 330
Слайд 32Самостоятельная работа
1. Переведите в радианную меру углы:
1) 60
2) 145
3) 240
I вариант
II вариант
1) 320
2) 105
3) 40
2. Переведите в градусную меру углы:
1)
2)
1)
2)
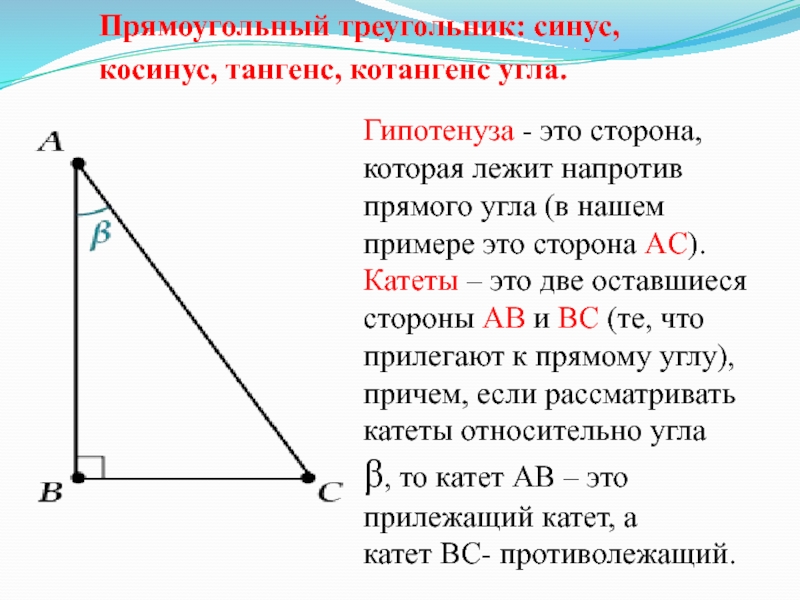
Слайд 38Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла.
Гипотенуза - это сторона,
которая лежит напротив прямого угла (в нашем примере это сторона AC).
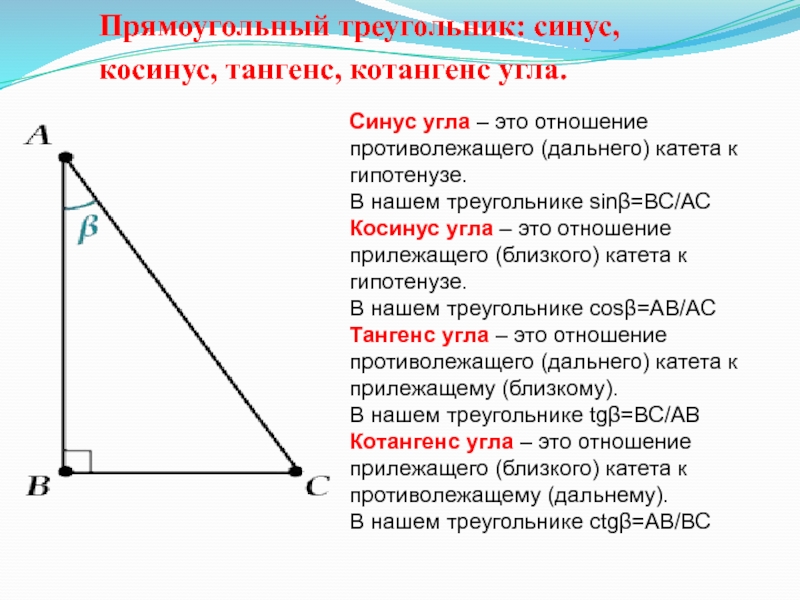
Катеты – это две оставшиеся стороны AB и BC (те, что прилегают к прямому углу), причем, если рассматривать катеты относительно угла β, то катет AB – это прилежащий катет, а катет BC- противолежащий.
Слайд 39Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла.
Синус угла – это отношение
противолежащего (дальнего) катета к гипотенузе.
В нашем треугольнике sinβ=BC/AC
Косинус угла – это отношение
прилежащего (близкого) катета к гипотенузе.В нашем треугольнике cosβ=AB/AC
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
В нашем треугольнике tgβ=BC/AB
Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).
В нашем треугольнике ctgβ=AB/BC
Слайд 40Синус, косинус, тангенс и котангенс как отношения сторон треугольника не
зависят от длин этих сторон (при одном угле).
Рассмотрим, к
примеру, косинус угла β. По определению, из треугольника ABC: cosβ=AB/AC=4/6=2/3, но ведь мы можем вычислить косинус угла β и из треугольника AHI: cosβ=AH/AI=6/9=2/3. Видите, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.
Слайд 41Для треугольника ABCABCABC, изображенного ниже на рисунке, найдем sin α, cos α, tg α, ctg α
sin α=4/5=0,8
cos α=3/5=0,6
tg α=4/3
ctg α=3/4=0,75
Попробуйте посчитай то же
самое для угла β.
Ответы: sin β=0,6; cos β=0,8; tg β=0,75; ctg β=43.
Слайд 42Окружность с радиусом, равным 1называется единичной.
Данная окружность построена в декартовой системе
координат. Радиус окружности равен единице, при этом центр окружности лежит
в начале координат, начальное положение радиуса-вектора зафиксировано вдоль положительного направления оси x (в нашем примере, это радиус AB).Единичная окружность r = 1
Слайд 43x
y
O
Положительное направление поворота:
против часовой стрелки.
Отрицательное направление поворота:
по часовой стрелке.
Слайд 45Каждой точке окружности соответствуют два числа: координата по оси x и координата
по оси y.
Рассмотрим треугольник ACG. Он прямоугольный, так как CG является
перпендикуляром к оси x.Чему равен cos α из треугольника ACG?
cos α=AG/AC
AC – это радиус единичной окружности, а значит, AC=1.
cos α=AG/AC=AG/1=AG
А чему равен sin α из треугольника ACG?
sinα=CG/AC=CG/1=CG
Слайд 46А можно сказать, какие координаты имеет точка C, принадлежащая окружности?
А
если сообразить, что cos α и sinα - это просто числа? Какой координате
соответствует sinα?Ну, конечно, координате x! А какой координате соответствует cos α?
Все верно, координате y! Таким образом, точка C(x;y)=C(cosα;sinα).
Слайд 50Домашнее задание
Выучить формулы перевода из градусной меры угла в радианную
и обратно.
Выучить определения sin, cos, tg, ctg
3) Переведите в
радианную меру углы: 75, 15, 130, 220, 3404) Переведите в градусную меру углы:
, , , ,
Слайд 51Ответьте на вопросы:
1) Что означает «тригонометрия»?
2) Разделом какой науки являлась
тригонометрия в начале развития?
3)Какие единицы измерения углов Вы знаете?
4) Чему
равно радиан?5) Как перевести из градусной меры в радианную и обратно?
6) Было ли интересно на уроке?
