Слайд 3Простая VAR(1) для двух рядов (k = 2, p =
1)
Вычисляя эти изменения последовательно для значений s = 0,
1, … , получаем функции откликов на шоки инноваций.
На сколько изменяются значения при изменении инновации
или на одно стандартное отклонение?
Слайд 4Однако:
Из-за того, что общем случае
, возникают затруднения с интерпретацией этих функций.
Из-за перекрестной коррелированности инноваций в приведенной форме, невозможно полностью изолировать шок для u1t от шока для u2t , т.е.,
Нельзя произвольно изменять значение u1t , сохраняя при этом значения неизменными.
Слайд 5“Фундаментальные” инновации
Для преодоления указанного затруднения предполагают, что система изменяется
благодаря воздействию некоррелированных между собой “фундаментальных” инноваций
.
Обычно предполагается, что все они имеют единичные дисперсии, так что – одинаково расределены с нулевым математическим ожиданием и единичной ковариационной матрицей Ik .
При этом предполагается, что инновации являются линейными комбинациями фундаментальных инноваций, так что
Слайд 6 В примере с двумерной VAR(1):
Поскольку
, то
,
Изменение u1t на одно стандартное отклонение складывается из изменений и , которые, в свою очередь, вызывают одновременное изменение u2t .
Слайд 7 Функция импульсных откликов
(impulse response function – IRF
)
С экономической точки зрения, первоочередной интерес представляют реакции значений
на единичные импульсные изменения отдельных фундаментальных инноваций при фиксированных значениях всех остальных фундаментальных инноваций во все моменты времени.
Именно на построение таких функций импульсных откликов нацелены алгоритмы, реализуемые в пакетах статистических программ.
Слайд 8Проблема отыскания матрицы D
Если матрица
известна, то как найти матрицу D
?
Слайд 9Отсюда:
Для нахождения четырех неизвестных d1 , d2 ,
d3 , d4 имеется всего три уравнения.
Следовательно, матрицу D
идентифицировать невозможно,
если не накладывать априорных ограничений на ее структуру.
Слайд 10упорядочивание инноваций в системе.
Пусть фундаментальная инновация
воздействует только на y2t , а фундаментальная инновация
воздействует и на y1t и на y2t .
Тогда фундаментальная инновация воздействует только на u2t , а фундаментальная инновация воздействует и на u1t и на u2t .
Предложение Симса:
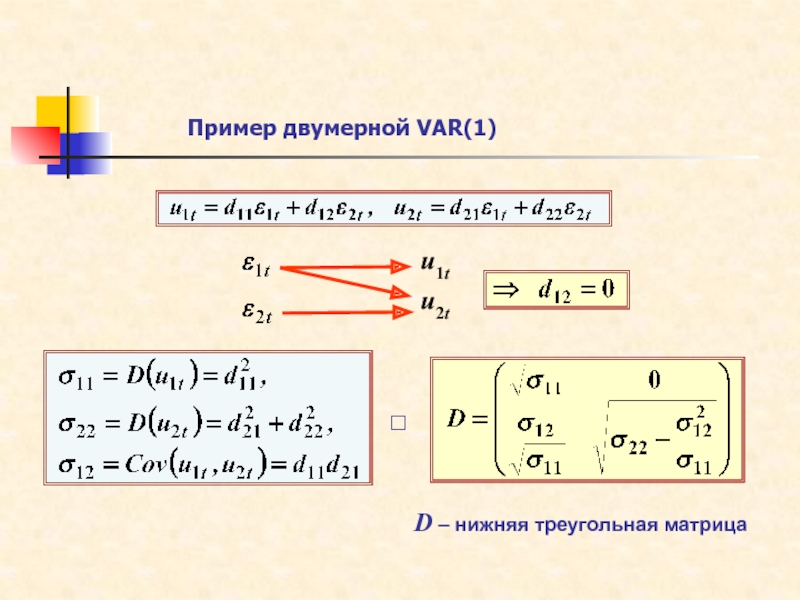
Пример двумерной VAR(1)
Слайд 11 Пример двумерной VAR(1)
u1t
u2t
D – нижняя треугольная матрица
Слайд 12Тогда
Обозначим
Умножим обе части VAR(1) на матрицу A :
Получаем структурную модель
в
которой
Представим:
B – диагональная матрица
Слайд 13Пусть в приведенной VAR(1) ковариационная матрица ошибок имеет вид
так что
Тогда структурная VAR имеет вид :
Слайд 14Изменим теперь упорядочение инноваций
Пусть
Тогда:
,
,
.
Слайд 15Структурная VAR имеет вид:
Представляем:
Слайд 16Резюме:
При первом упорядочении инноваций:
При втором упорядочении инноваций:
В обоих случаях
выбранная форма матрицы A приводит к рекурсивной системе .
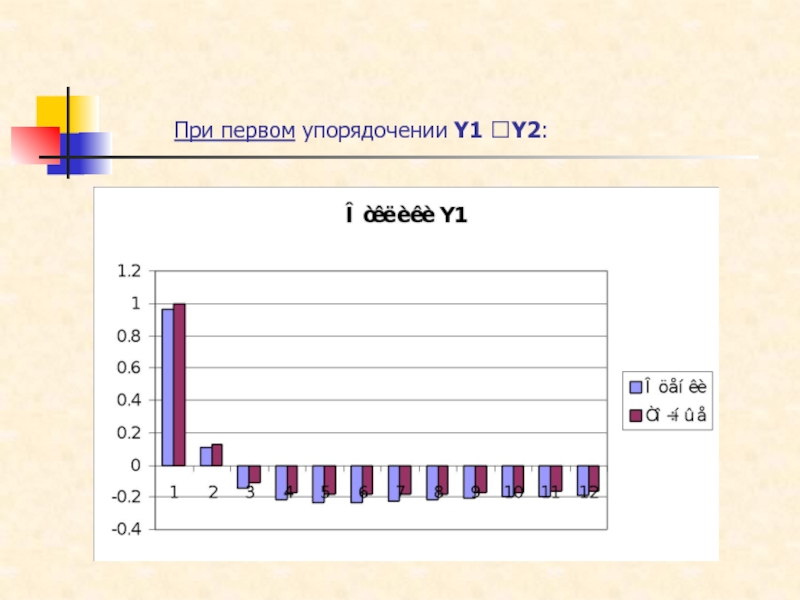
Слайд 17 Рекурсивная система
(первое упорядочение: Y1
Y2 )
В первое уравнение с текущим значением входит только одна
переменная y1t , т.е.,
y1t объясняется только запаздывающими значениями переменных y1t , y2t , . . . , ykt .
Во второе уравнение с текущими значениями входят обе переменные y1t и y2t , т.е. ,
y2t объясняется с помощью y1t и yt – 1 , yt – 2 , . . . ,
Такой порядок вхождения переменных интерпретируется как последовательное включение переменных в порядке возрастания их эндогенности, так что последней в систему включается наиболее эндогенная переменная.
Слайд 18Сравним функции отклика переменных y1t и y2t на импульсный шок
фундаментальной инновации .
При первом
упорядочении:
Пусть в момент t = 1 имеет место шок фундаментальной инновации для переменной y1t (в первом уравнении рекурсивной системы), так что
а не изменяется ни при каком t
Вернемся к двумерной VAR(1)
Слайд 19При этом мы получаем измененную реализацию
для которой
и
Для простоты, пусть . Тогда при t =1
а при t =2
Слайд 20Таким образом, мы получили следующие значения функций импульсного отклика на
единичный шок инновации :
Слайд 21При втором упорядочении
Получаются следующие значения функций импульсного отклика
на единичный
шок инновации :
Принимая различный
порядок последовательного вхождения
переменных, мы получили и различное поведение функций
импульсного отклика.
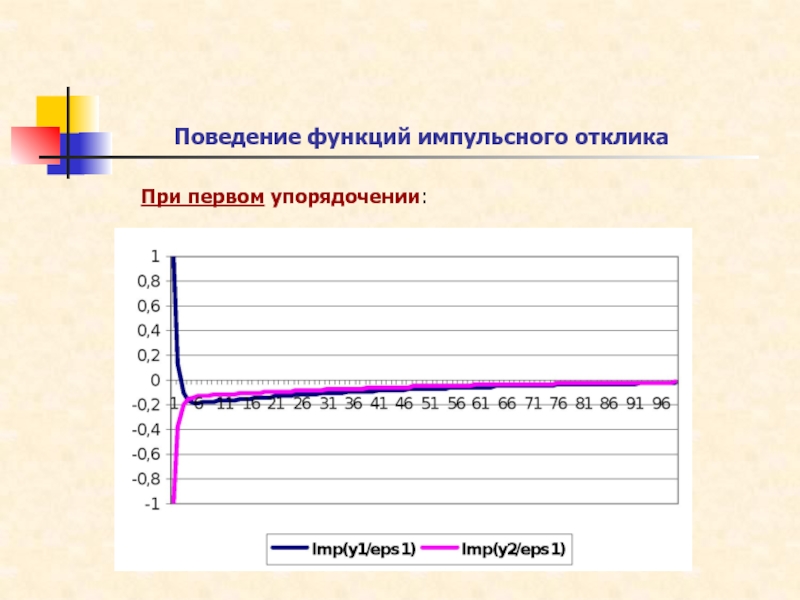
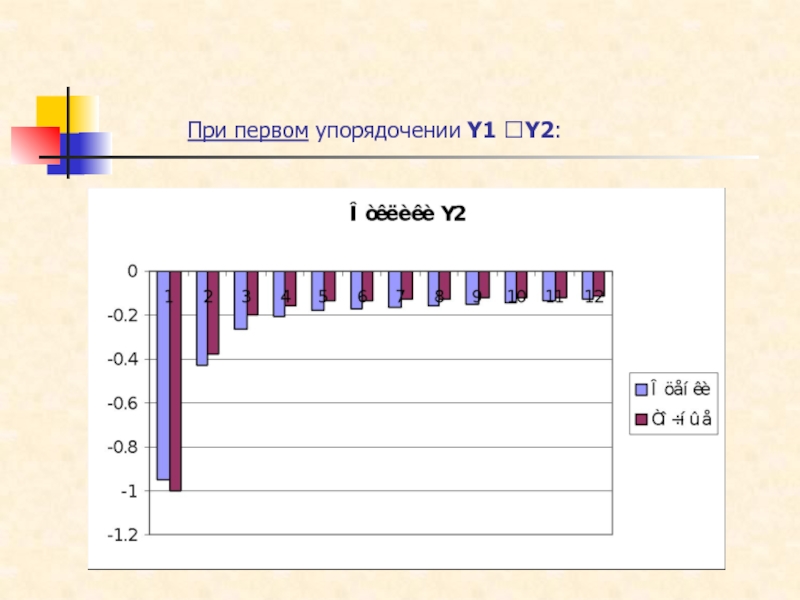
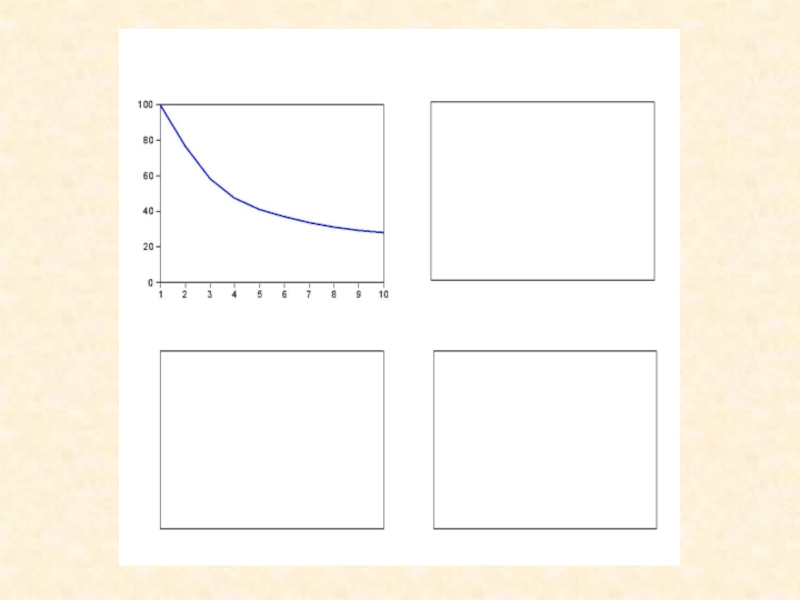
Слайд 22Поведение функций импульсного отклика
При первом упорядочении:
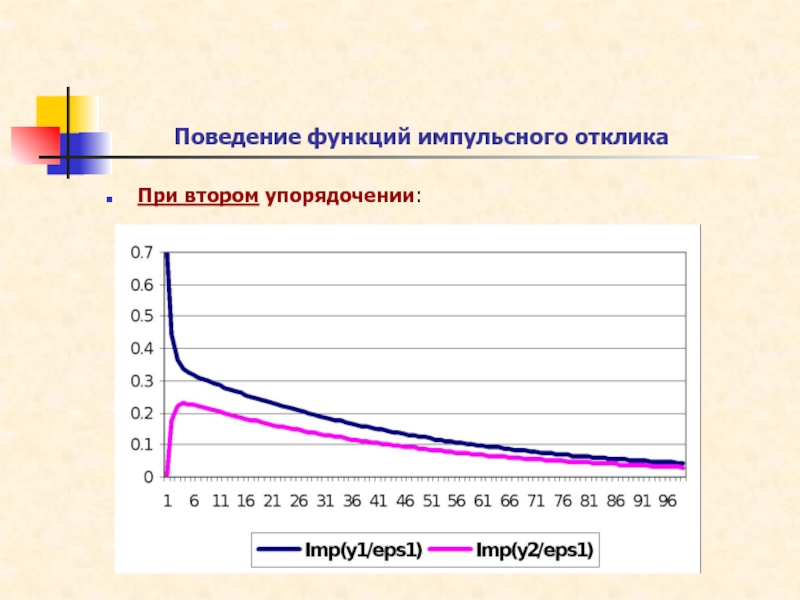
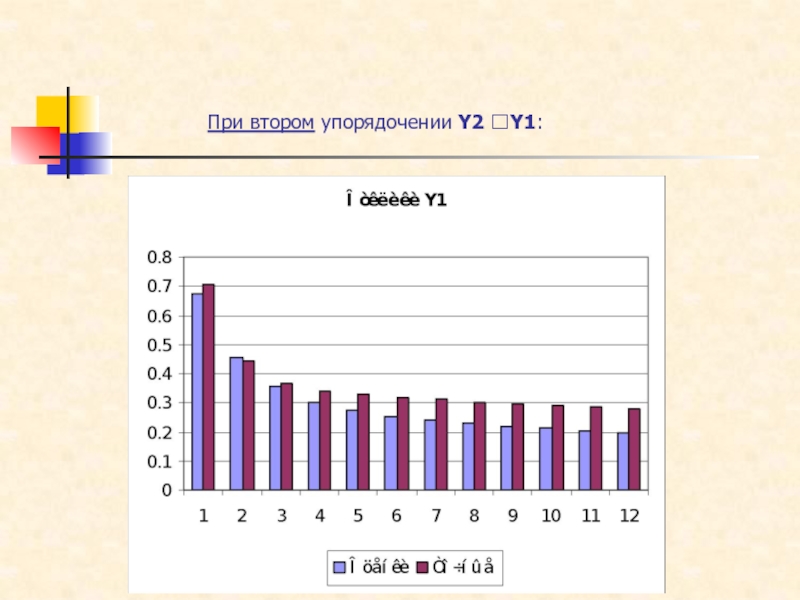
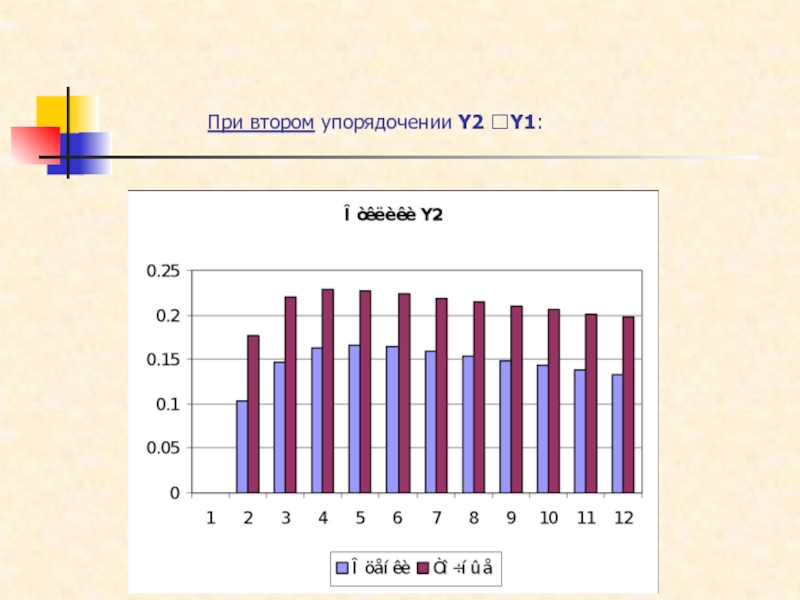
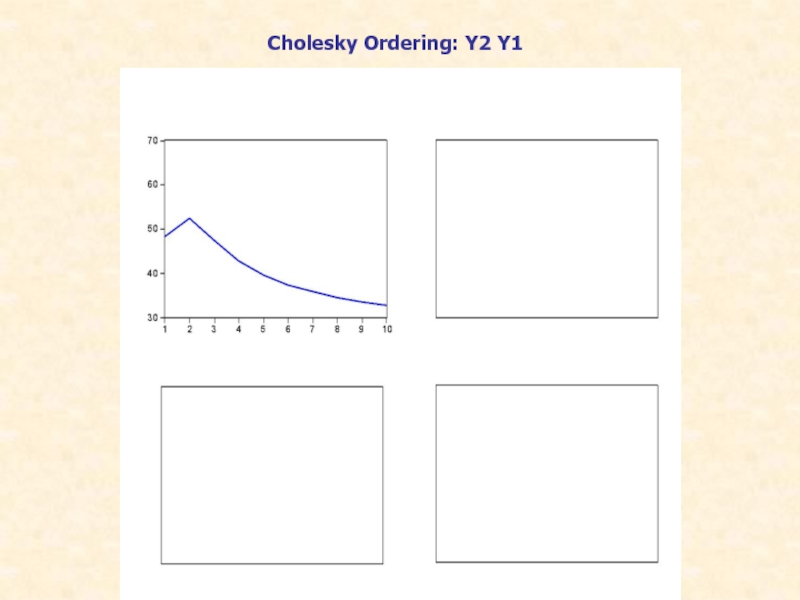
Слайд 23При втором упорядочении:
Поведение функций импульсного отклика
Слайд 24Проблема:
В примере функции импульсного
отклика были построены, опираясь на известные коэффициенты приведенной формы и
на известную ковариационную матрицу вектора инноваций в приведенной форме.
Будем считать теперь эти параметры неизвестными и использовать для построения функций отклика их оценки, построенные по смоделированным реализациям длины 100.
Слайд 25В нашем примере:
(impulse_new.wf1)
(impulse_new_reord.wf1)
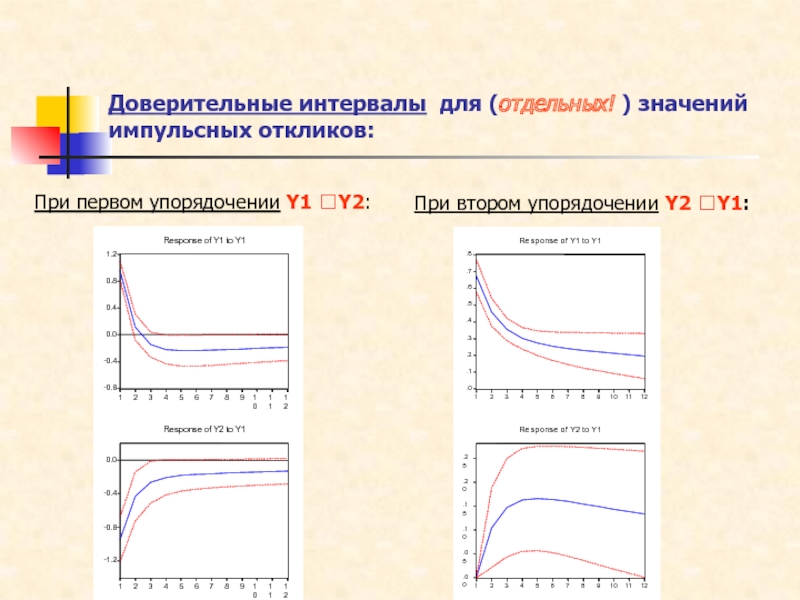
Слайд 30Доверительные интервалы для (отдельных! ) значений импульсных откликов:
При первом упорядочении
Y1 Y2:
При втором упорядочении Y2 Y1:
Слайд 31Замечание
Столь существенное различие в поведении функций импульсного отклика при альтернативных
упорядочениях связано с существенной перекрестной коррелированностью инноваций в приведенной форме
VAR.
В сгенерированных данных эта корреляция равна -0.628, а для остатков от оцененной VAR она равна -0.634.
Слайд 33В общем случае предполагают, что структурная модель VAR имеет вид
т.е.
где
– одинаково распределены с нулевым математическим ожиданием и единичной ковариационной матрицей Ik , так что инновации в структуре являются линейными комбинациями "ортогонализованных" (“фундаментальных”) инноваций.
Соответственно, в приведенной форме
k -мерная VAR(p)
Слайд 34Приведенная форма:
Структурная форма:
Здесь
.
Приведенную форму оцениваем OLS, получаем оценки матриц
. Но по этим оценкам не всегда удается восстановить структурную форму, т.к. не известны матрицы A и B.
Слайд 35Проблема идентификации структурных уравнений по приведенной форме
В рассматриваемой ситуации
Оценив приведенную VAR, мы можем получить и оценку
ковариационной матрицы .
Замена на приводит к оценочному уравнению для A и B:
Слайд 36Матрица симметрична, и поэтому достаточно оценить
ее элементов.
Общее количество неизвестных элементов в матрицах
и равно .
Поэтому идентификация возможна лишь при наложении на матрицы и достаточного количества ограничений.
Слайд 37Разложение Холецкого (Cholesky factorization)
Методология Симса, которую мы применили выше, фактически
основана на следующем результате (разложение Холецкого).
Всякую положительно полуопределенную матрицу
можно представить в виде произведения , где – верхняя треугольная матрица с положительными диагональными элементами, причем такая матрица единственна.
Обозначая , запишем указанное представление в виде:
Здесь D – нижняя треугольная матрица с положительными диагональными элементами.
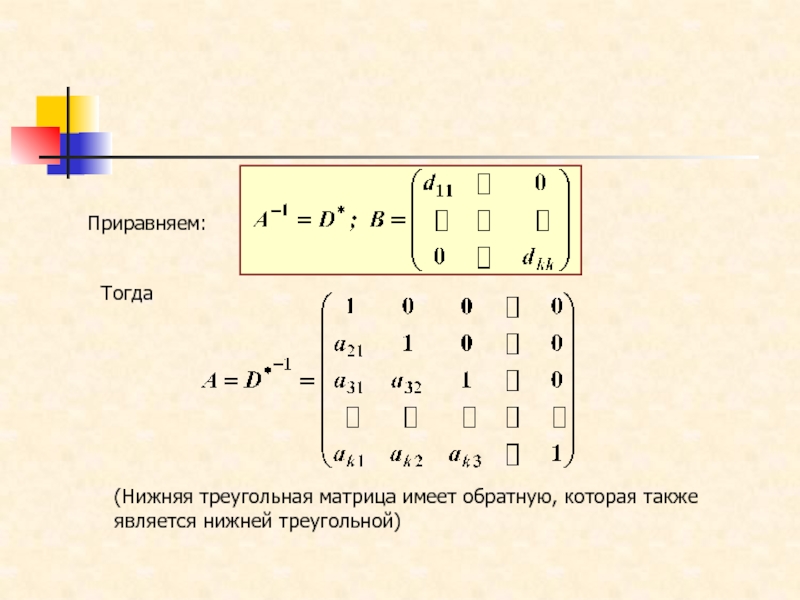
Слайд 39Приравняем:
Тогда
(Нижняя треугольная матрица имеет обратную, которая также является нижней
треугольной)
Слайд 40Резюме
Если наложить на матрицы A и B ограничения:
A – нижняя
треугольная матрица с единицами на диагонали;
B – диагональная матрица с
положительными диагональными элементами,
то уравнение
имеет единственное решение, т.е. имеет место точная идентифицируемость матриц A и B .
Диагональные элементы bjj матрицы B можно рассматривать как с.к.о. инновации в i-м уравнении структуры, а форма матрицы A соответствует рекурсивной системе .
Слайд 41Рекурсивная система
В первое уравнение с текущим значением входит только
одна переменная y1t , т.е.,
y1t объясняется только запаздывающими
значениями переменных y1t , y2t , . . . , ykt .
Во второе уравнение с текущими значениями входят только переменные y1t и y2t , т.е. ,
y2t объясняется с помощью y1t и yt – 1 , yt – 2 , . . . ,
. . .
В последнее, k-е уравнение с текущими значениями входят все переменные y1t , y2t , . . . , ykt , т.е.,
ykt объясняется с помощью y2t , . . . , yk-1,t и yt – 1 , yt – 2 , . . .
Такой порядок вхождения переменных интерпретируется как последовательное включение переменных в порядке возрастания их эндогенности, так что последней в систему включается наиболее эндогенная переменная.
При выбранной нормализации (единицы на диагонали матрицы ),
y1t – “наименее эндогенная” переменная,
ykt – “наиболее эндогенная” переменная
Слайд 42Вернемся к k -мерной VAR(p)
Приведенная форма:
Запишем ее в виде:
Если все
корни уравнения
лежат за пределами единичного круга, то VAR стабильна, и
можно записать:
Слайд 43k -мерная VAR(p)
Это есть векторное MA-представление k -мерного ряда
y1t ,
основанное на инновационной последовательности ut
.
Если для некоторого k-мерного случайного вектора выполнено соотношение
то
, то
так что матрица D является
корнем из матрицы и имеет левую нижне-треугольную форму:
Ее элементы легко вычисляются рекуррентным образом
по элементам ковариационной матрицы .
Слайд 45Матрицу D можно представить в виде
При этом, представление
называют
разложением Холецкого матрицы .
Слайд 46 Разложение Холецкого (Cholesky factorization)
P* – левая нижне-треугольная матрица с единицами на диагонали,
B – диагональная матрица.
Мы уже фактически использовали такую факторизацию ранее для матрицы
где
Слайд 47 Функция импульсных
откликов
Теперь мы можем возвратиться к векторному MA-представлению ряда yt
, основанному на инновационной последовательности ut :
и произвести подстановку .
В результате получаем разложение
основанное на инновационной последовательности
Элемент матрицы с индексом ij равен изменению i-ой переменной в момент времени t+h в ответ на единичное изменение шока j-ой переменной в момент времени t при сохранении неизменными всех остальных шоков во все моменты времени.
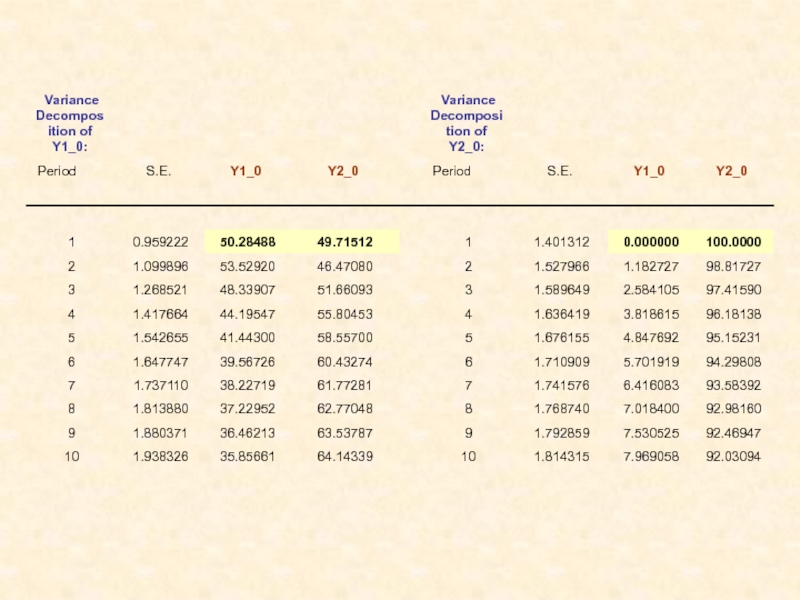
Слайд 48Декомпозиция (разложение) дисперсии ошибок прогнозов (variance decomposition)
Прогноз по VAR
на один шаг вперед:
Ошибка прогноза по VAR на один шаг
вперед:
Слайд 49Ошибка прогноза по VAR на один шаг вперед:
Рассмотрим матрицу
Ee математическое
ожидание есть матрица
на диагонали которой находятся значения дисперсий ошибок
прогнозов на
один шаг вперед рядов y1 и y2 .
Слайд 51Дисперсия ошибки прогноза на один шаг вперед ряда y1
Дисперсия ошибки
прогноза на один шаг вперед ряда y2
Слайд 52Дисперсия ошибки прогноза на один шаг вперед ряда y1
Дисперсия ошибки
прогноза на один шаг вперед ряда y2
Получили декомпозиции дисперсий ошибок
прогноза
– разложение каждой из них на две компоненты.
Что представляют собой эти компоненты?
Слайд 53 – составляющая ошибки прогноза на один шаг вперед ряда
y1,
обусловленная фундаментальной инновацией
– составляющая ошибки прогноза на один
шаг вперед ряда y1,
обусловленная фундаментальной инновацией
– дисперсия ошибки прогноза на один шаг вперед ряда y1
Слайд 54 – составляющая ошибки прогноза на один шаг вперед ряда
y1,
обусловленная фундаментальной инновацией
– составляющая ошибки прогноза на один
шаг вперед ряда y1,
обусловленная фундаментальной инновацией
– дисперсия ошибки прогноза на один шаг вперед ряда y1
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
Слайд 55 – дисперсия ошибки прогноза на один шаг вперед ряда
y1
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда
y1, обусловленная фундаментальной инновацией
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
Слайд 56 – дисперсия ошибки прогноза на один шаг вперед ряда
y2
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда
y2, обусловленная фундаментальной инновацией
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
Слайд 57Вернемся к двумерной VAR(1)
При упорядочении Y1 Y2
Слайд 58– доля дисперсии ошибки прогноза на один шаг вперед
ряда
y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на
один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
Слайд 59Ошибка прогноза по VAR на h шагов вперед вычисляется по
формуле:
где dj – j-й столбец матрицы D.
В скобках – вклад
j-ой фундаментальной инновации.
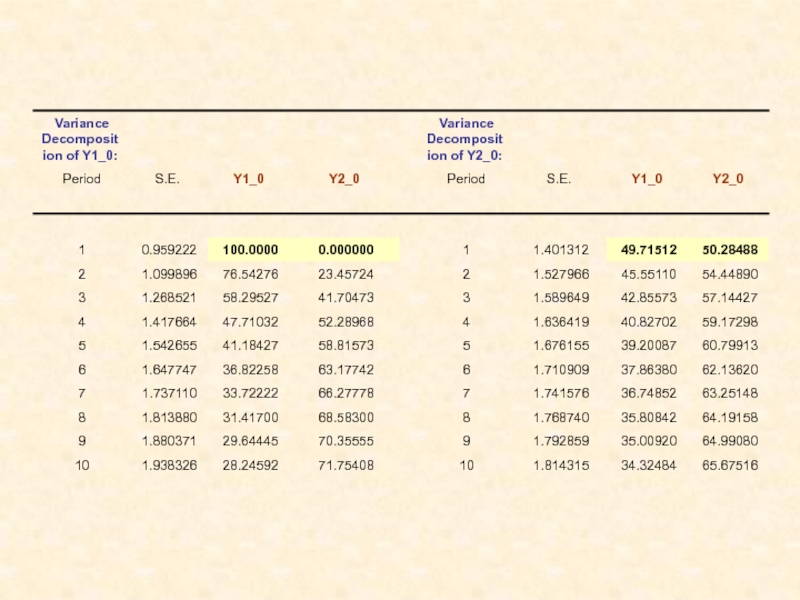
Декомпозиция дисперсии ошибок прогнозов
Слайд 60 Декомпозиция дисперсии ошибок прогнозов
Обычно результат такой декомпозиции представляется
как перечень долей каждого из слагаемых в общей сумме.
В
пакетах программ статистического анализа предлагаются также графики, показывающие динамику изменений каждой такой доли с изменением h, h =1, 2, . . .
Слайд 65Оценивание SVAR в EViews 6
При первом упорядочении
или
И, так как
и А – нижняя треугольная матрица с единицами на диагонали,
а B – диагональная матрица, то
Слайд 66Таким образом, при первом упорядочении SVAR (структурная VAR) принимает вид:
Слайд 67В рекурсивной структуре, полученной с использованием изложенного метода, случайные ошибки
в разных уравнениях являются взаимно некоррелированными случайными величинами. Это означает,
что соответствующую систему одновременных уравнений можно оценивать, используя обычный метод наименьших квадратов (OLS).
Статистическая модель:
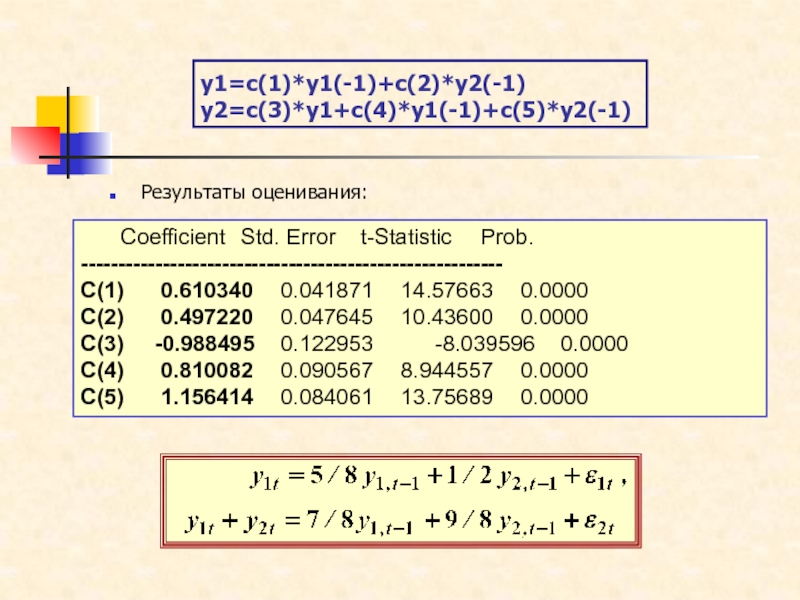
Слайд 68y1=c(1)*y1(-1)+c(2)*y2(-1)
y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1)
Результаты оценивания:
Coefficient Std. Error t-Statistic Prob. ---------------------------------------------------------
C(1) 0.610340 0.041871 14.57663 0.0000
C(2) 0.497220 0.047645 10.43600 0.0000
C(3) -0.988495 0.122953
-8.039596 0.0000
C(4) 0.810082 0.090567 8.944557 0.0000
C(5) 1.156414 0.084061 13.75689 0.0000
Слайд 69EViews 6:
Оценивание матриц A и B структурной формы
Создав объект
VAR и оценив коэффициенты приведенной VAR,
можно получить
в рамках этого объекта и оценки указанных матриц.
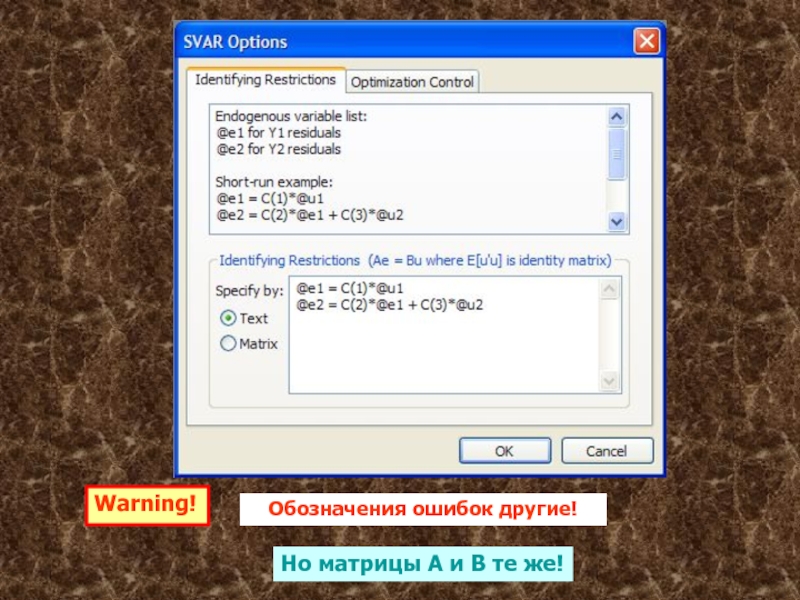
Для этого заказываем: Proc Estimate Structural Factorization
В открывшемся окне указываем форму связи между ошибками в приведенной VAR и фундаментальными инновациями, соответствующую выбранному упорядочению в схеме Холецкого.
Слайд 70Warning!
Обозначения ошибок другие!
Но матрицы A и B те же!
Слайд 71
Model: Ae = Bu where E[uu']=I
Restriction Type: short-run text form
@e1
= C(1)*@u1
@e2 = C(2)*@e1 + C(3)*@u2
where
@e1 represents Y1 residual
@e2 represents
Y2 residuals
Coefficient
C(2) -0.997582
C(1) 0.962944
C(3) 1.143882
Estimated A matrix:
1.000000 0.000000
0.997582 1.000000
Estimated B matrix:
0.962944 0.000000
0.000000 1.143882
Результаты оценивания матриц A и B
Слайд 72Замечания
Принимая различные порядки последовательного вхождения переменных, мы получаем и различное
поведение импульсных функций отклика, что дает возможность сравнивать альтернативные теории.
В
рекурсивной структуре, полученной с использованием изложенного метода, случайные ошибки в разных уравнениях являются взаимно некоррелированными случайными величинами. Это означает, что соответствующую систему одновременных уравнений можно оценивать, используя обычный метод наименьших квадратов (OLS).
Слайд 73Пример.
В модели двумерной VAR переменная y1t может представлять объем производства
(output), а переменная y2t – “деньги” (money).
Упорядочение y1t
y2t соответствует схеме
В этой схеме шоки в объеме производства оказывают немедленное воздействие и на объем производства и на деньги, тогда как шоки в деньгах оказывают немедленное воздействие только на деньги.
Такое упорядочение соответствует представлению, согласно которому денежная политика имеет только запаздывающее влияние на объем производства.
u1t
u2t
Слайд 74Пример (продолжение)
Упорядочение y2t y1t соответствует схеме
В этой схеме
шоки в объеме производства оказывают немедленное воздействие только на объем
производства, тогда как шоки в деньгах оказывают немедленное воздействие и на деньги и на объем производства.
Это соответствует представлению о том, что деньги поставляются центральным банком, а объем производства становится известным центральному банку лишь с опозданием. Поэтому деньги не могут немедленно реагировать на шоки в объеме производства.
u2t
u1t























































![Эконометрика- II Model: Ae = Bu where E[uu']=I Restriction Type: short-run text form @e1 = Model: Ae = Bu where E[uu']=I Restriction Type: short-run text form @e1 = C(1)*@u1 @e2 = C(2)*@e1 + C(3)*@u2 where @e1 represents](/img/thumbs/ba6594e8b04de87bc2b71bc92669be6b-800x.jpg)






















