Граф вычислений ДПФ

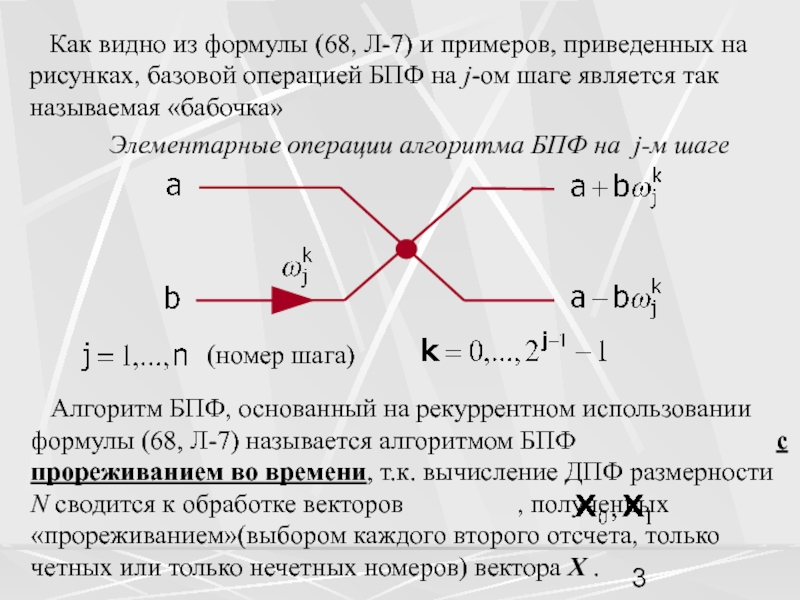
приведенных на рисунках, базовой операцией БПФ на j-ом шаге является

(номер шага)

Элементарные операции алгоритма БПФ на j-м шаге

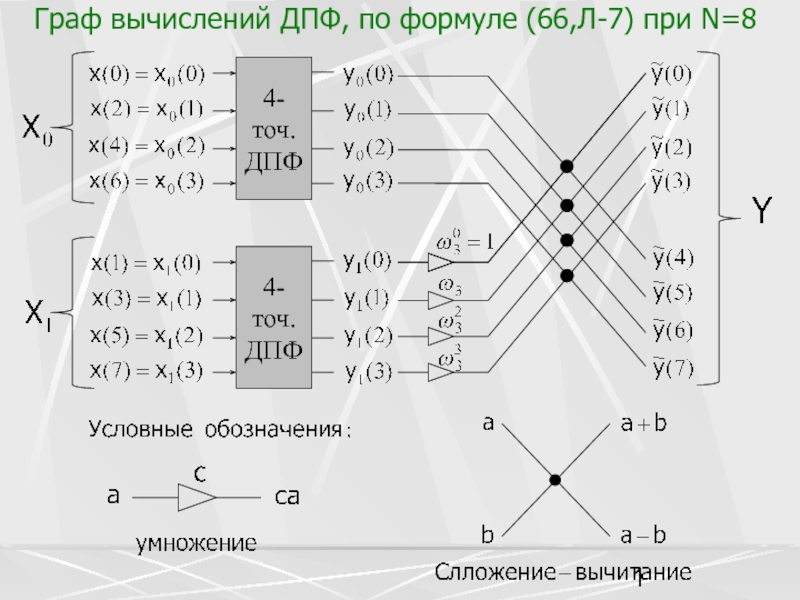
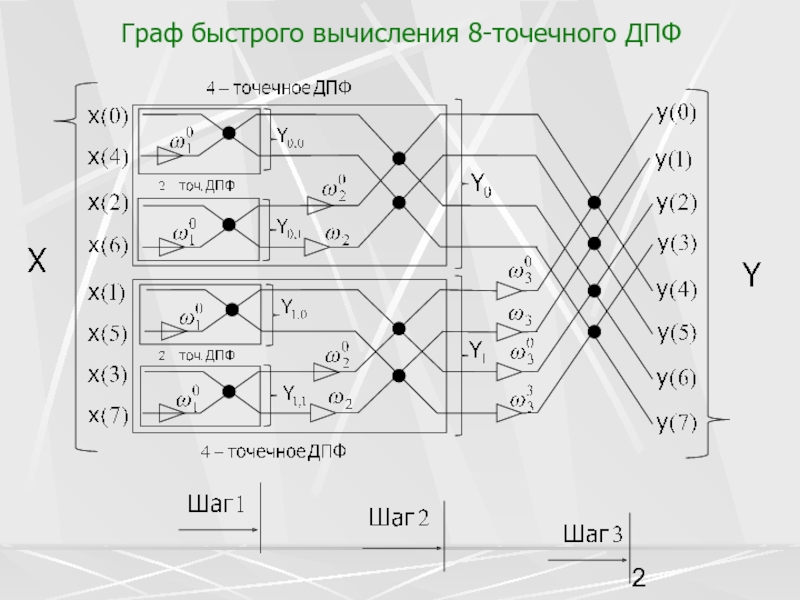
Алгоритм БПФ, основанный на рекуррентном использовании формулы (68, Л-7) называется алгоритмом БПФ с прореживанием во времени, т.к. вычисление ДПФ размерности N сводится к обработке векторов , полученных «прореживанием»(выбором каждого второго отсчета, только четных или только нечетных номеров) вектора X .

проектирования дискретных фильтров лежат методы проектирования аналоговых фильтров. Поэтому квалифицированное

Систему обработки сигнала представим в виде схемы

самые разные физические свойства. Важнейшим свойством системы является линейность или

(1)

нелинейной системой.
Например, для системы с квадратичной нелинейностью, преобразование

(2)

Доказать самостоятельно соотношение (2).

во времени характеристик системы.
Если произвольная задержка по времени

(3)

системой с переменными параметрами. В дальнейшем мы будем рассматривать линейные

Характеристики линейных систем

Мы рассматриваем ЛПП системы. Для таких систем справедливы принципы суперпозиции и стационарности.
Это сильно упрощает анализ прохождения сигналов через такие системы.

найти реакцию системы на любой входной сигнал, зная всего лишь

(4)

y(t) связаны линейным соотношением (4) , то рассматриваемая система, очевидно,

(5)

Если система стационарна, то на выходе должен появится сдвинутый сигнал

(6)

сигналом (6).
Подадим на вход системы сигнал в виде дельта-функции.

Подставим (5) в формулу (4) и получим сигнал на выходе системы

(7)

(8)

импульсной характеристикой h(t). Поэтому импульсную характеристику называют так же реакцией

Сделаем в формуле (4) замену переменной интегрирования.

В результате получим:

(9)

Формула (9) определяет свертку двух функций. Другим словами, выходной сигнал в ЛПП системе является сверткой входного сигнала и импульсной характеристики.

должна удовлетворять свойству причинности – выходная реакция не может возникнуть

Тогда используя формулу (9) получаем.

(10)

выходной сигнал был бы равен нулю y(t) = 0. Поэтому

(11)

Обозначим аргумент импульсной характеристики . Сложим два неравенства.

аргумента.
Таким образом, для любой физически реализуемой системы

(12)

показано выше (9), представляет собой свертку входного сигнала и импульсной

(13)

для Фурье образов.

(14)
Здесь

(15)

Эта функция называется комплексным коэффициентом передачи системы. Для математического удобства мы здесь вместо частоты f используем циклическую частоту ω.

изображать в виде схемы.


Модуль и фазу комплексного коэффициента

(16)

следующие соотношения.

(17)
Соотношения (17) означают следующее. Для

На рисунках показаны сигнал на входе ЛПП системы и на выходе.

Гц. АЧХ и ФЧХ системы на этой частоте оказались равными

линейной системой различают два вида задержки.
Фазовая задержка (phase delay)

(18)

На приведенном выше рисунке для гармонического сигнала с частотой f = 2 Гц, время фазовой задержки равно.

огибающей узкополосного сигнала со средней частотой ω, проходящего через систему.

(19)

На рисунках показано прохождение узкополосного сигнала через ЛПП систему.

из рисунка, оказалась равной

с постоянными параметрами (ЛПП) реализуют в виде линейной цепи с

(20)

В этом дифференциальном уравнении , - постоянные коэффициенты. Кроме того, должно выполняться условие m ≤ n . Значение n называют порядком цепи.

преобразование Лапласа

(21)
Здесь s – комплексное число, а

производной оригинала.

Изображение первой производной оригинала определяется следующим выражением

(22)
Изображение n

(23)

условиями.

(24)
Тогда применение преобразования Лапласа к обеим частям уравнения

(25)

H(s) называется функцией передачи и определяется формулой.

(27)

передачи путем замены аргумента.

(28)
Здесь i - мнимая единица.
Доказать

Таким образом, для ЛПП системы комплексный коэффициент передачи вычисляется по формуле.

(29)

знаменатель функции передачи (27) на элементарные множители, мы получаем функцию

(30)

Здесь - коэффициент усиления (gain). – нули функции передачи (zero), - полюсы функции передачи (pole). В точках нулей , а в точках полюсов .

передачи H(s) надо использовать обратное преобразование Лапласа. Для нахождения обратного

система (ЛДС) – это произвольная система обработки дискретного сигнала, обладающая

Систему обработки сигнала представим в виде схемы

ЛДФ

x(n)

y(n)

линейной, если для нее выполняется принцип суперпозиции. Реакция системы на

(31)

Если произвольная задержка «по времени» (по индексу) во входном сигнале приводит лишь к такой же задержки в выходном сигнале, не меняя его формы, то система называется стационарной, или системой с постоянными параметрами.

(32)

легко найти реакцию системы на любую входящую последовательность, зная всего

(33)

сигнал y(n) связаны линейным соотношением (4) , то рассматриваемая система,

(34)

Если система стационарна, то на выходе должен появится сдвинутый сигнал

(35)

системы

(36)
Таким образом, сигнал на выходе совпадает со сдвинутым

(37)

импульсной характеристикой h(n). Поэтому импульсную характеристику называют так же реакцией

В результате получим.

(38)

Мы видим, что формула (38) определяет дискретную свертку двух последовательностей. Другим словами, выходной сигнал в ЛДФ является дискретной сверткой входного сигнала и импульсной характеристики.

система должна удовлетворять свойству причинности – выходная реакция не может

Тогда используя формулу (40) получаем.

(39)

выходной сигнал был бы равен нулю

(40)

Обозначим аргумент импульсной характеристики n – m = k. Сложим два неравенства.

значений аргумента.
Таким образом, для любой физически

(41)

Линейный дискретный фильтр часто обозначают в виде схемы

На этой схеме обозначены входящий сигнал, импульсная характеристика и выходящий сигнал.

любого ограниченного входящего сигнала, выходящий сигнал также ограничен.

Здесь

условия.

(42)
Здесь - некоторая константа

Доказательство. Достаточность устойчивости ЛДФ.

(43)

(44)
Тогда для фиксированного n бесконечный ряд (43) заменяется суммой.

(45)

Возьмем модуль от уравнения (45).

(46)

теоремы (44) окончательно получаем

(48)
Соотношение (48) означает, что выходящий сигнал

условия (42).
Доказывать будем от противного. Допустим,

(49)

Фиксируем число n. Рассмотрим ограниченный входящий сигнал равный ±1 и заданный по следующему правилу.

(50)

модуль от уравнения (45). Учтем условие (51). Теперь в отличии

(52)

Здесь мы учли, что модуль входящего сигнала равен единице.

к бесконечности, то благодаря условию (45) выходной сигнал тоже будет

Это противоречит предположению об устойчивости выходного сигнала. Необходимость доказана
Таким образом, устойчивость ЛДФ определяется условием, накладываемым на его импульсную характеристику.

(53)

На рисунках приведены импульсные характеристики устойчивого и неустойчивого фильтров.

системы с постоянными параметрами (ЛПП) основным уравнением является дифференциальное уравнение

(54)

В этом разностном уравнении , - постоянные коэффициенты.
Отметим, что в отличие о аналогового случая, здесь нет ограничений на величину чисел N и M.

, и уравнение (54) перепишем в виде.

(55)

В зависимости от структуры разностного уравнения (55) различают два больших класса фильтров: рекурсивные и нерекурсивные фильтры.
Если в уравнении (55) все коэффициенты в первой сумме равны нулю

вид.

(56)
Уравнение (56) показывает, что для нерекурсивного фильтра

значение выходного сигнала y(k) зависит не только от текущего x(k)

Пример 1. Рассмотрим рекурсивный фильтр, который описывается следующим разностным уравнением.

(57)

Если теперь вспомнить, что отклик ЛДФ на единичный

(60)

сумму

(61)
Сумма (61) является суммой геометрической прогрессии, результат

(62)

Если теперь устремить n к бесконечности, то сумма (63) будет

уравнения (20) является преобразование Лапласа. Точно так же для решения

Определение. Z – преобразованием числовой последовательности

является функция комплексной переменно X(z). Эта функция определяется следующим образом.

Символически связь между Z – преобразованием и числовой последовательностью обозначим,

случаем ряда Лорана, который в общем случае представляет собой следующий

(66)

где - точка комплексной плоскости, - комплексные числа.

Вспомним теорему из теории рядов Лорана.

таковы что имеют место соотношения.

(67)
то областью сходимости ряда Лорана

Это кольцо изображено в комплексной плоскости с центром в точке .

является аналитической функцией. Коэффициенты ряда (66) выражаются с помощью контурных

(68)

замкнутый контур (обход контура – в положительном направлении), целиком лежащий

Применим теорему 2 к нашему ряду (64)

(69)

соответствие

Поэтому для нашего ряда (69) мы имеем

(70)

(71)

собой аналитическую функцию. Аналитичность функции подразумевает, что в этой области

Пример 2. Найти Z – преобразование следующей последовательности.

(72)

равен единице

(74)
Таким образом, ряд Z – преобразования в области

(75)

в выражении (75) является бесконечной суммой геометрической прогрессии со знаменателем

(76)

Хотя формула (77) была получена для области |z| > 1

(78)

справедлива и для области |z| ≤ 1, благодаря аналитическому продолжению формулы (77) в эту область.