Разделы презентаций

Графы поиск в глубину ( DFS) Хранение графа в программе

Содержание

ОпределениеГраф – это набор вершин, некоторые пары из которых соединены между собой рёбрами.Связный граф – это граф, из любой вершины которого по рёбрам можно попасть в любую другую.Направленный граф – это

Слайды и текст этой презентации

Слайд 1Графы поиск в глубину (DFS) Хранение графа в программе
Школа::Кода
Олимпиадное программирование

2020-2021 Таганрог

Графы поиск в глубину (DFS) Хранение графа в программеШкола::КодаОлимпиадное программирование2020-2021 Таганрог

Слайд 2Определение
Граф – это набор вершин, некоторые пары из которых соединены

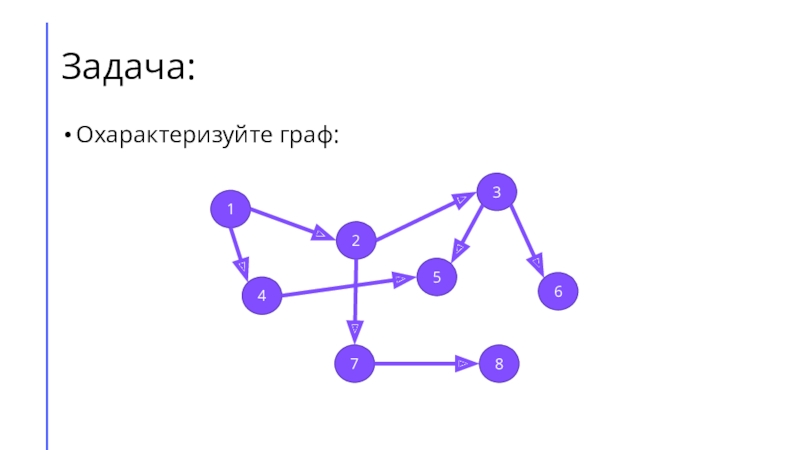
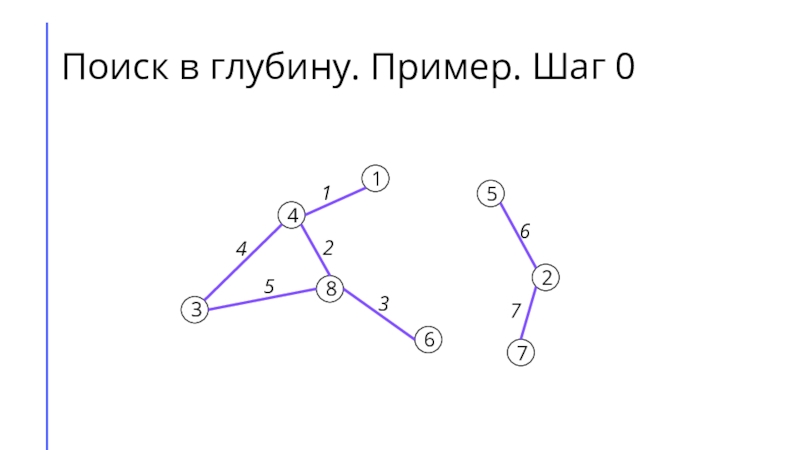
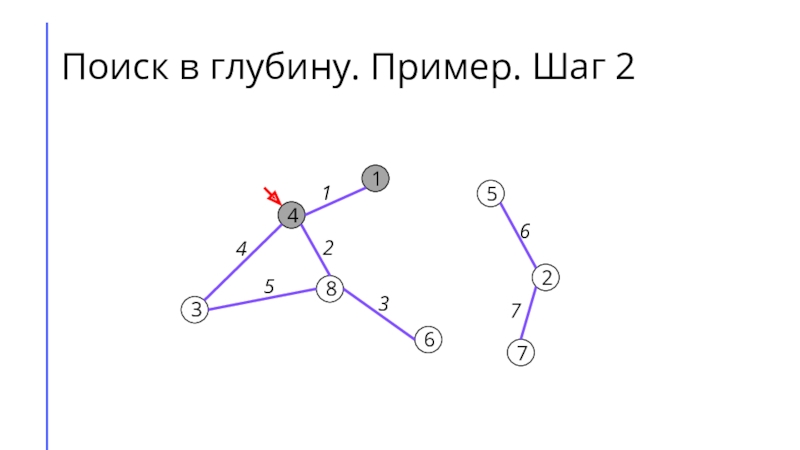
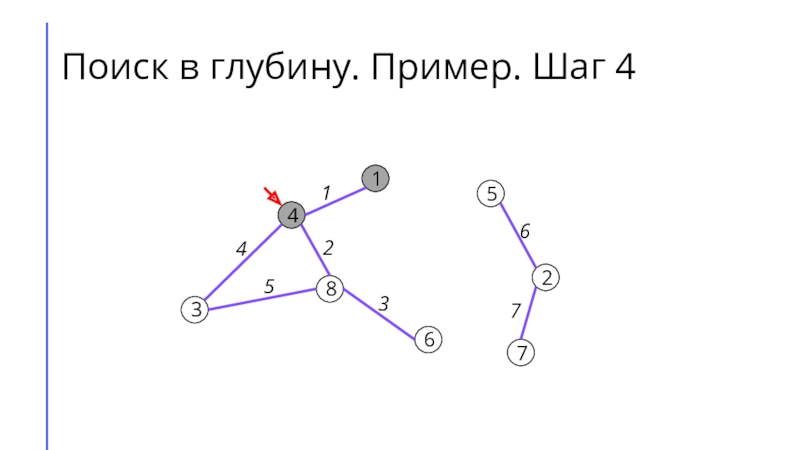
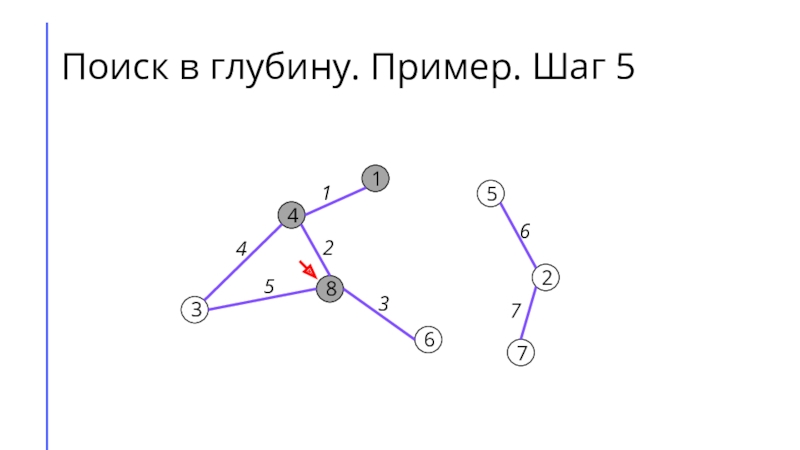
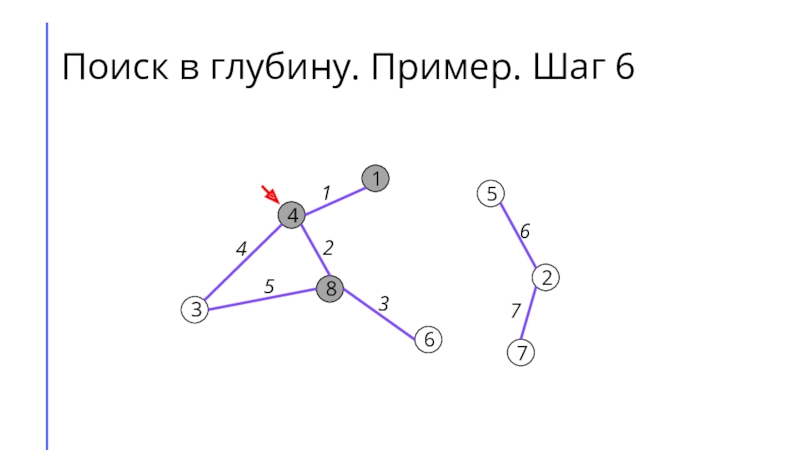
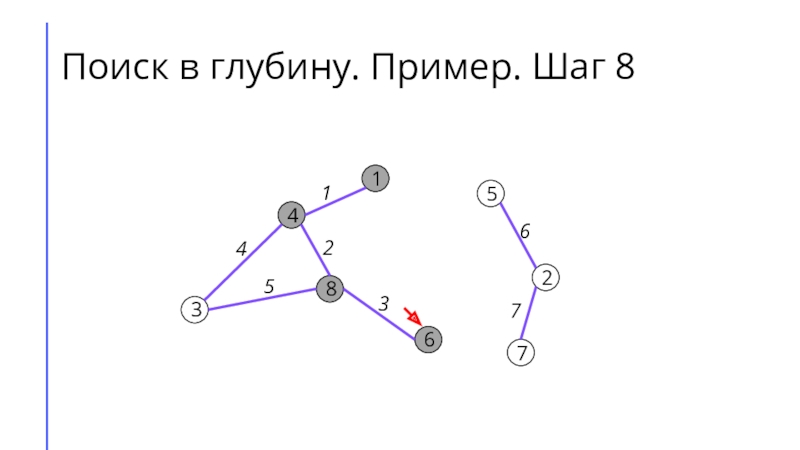
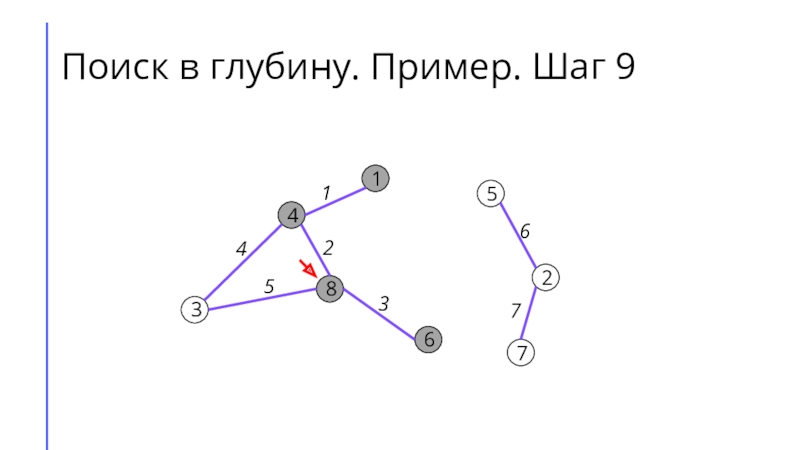
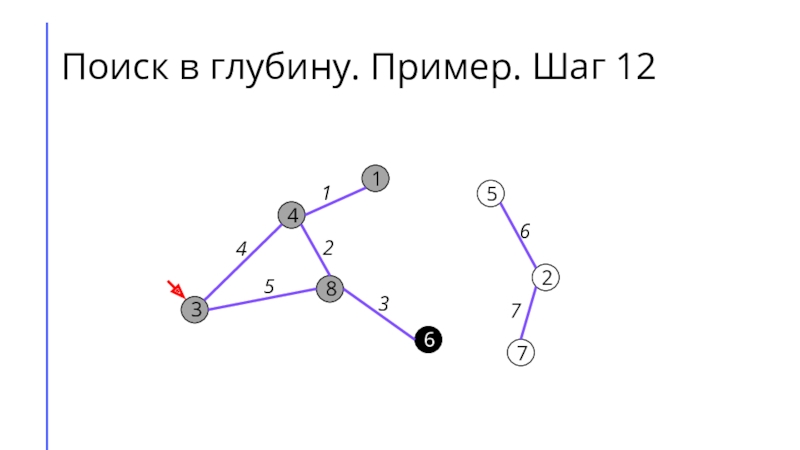
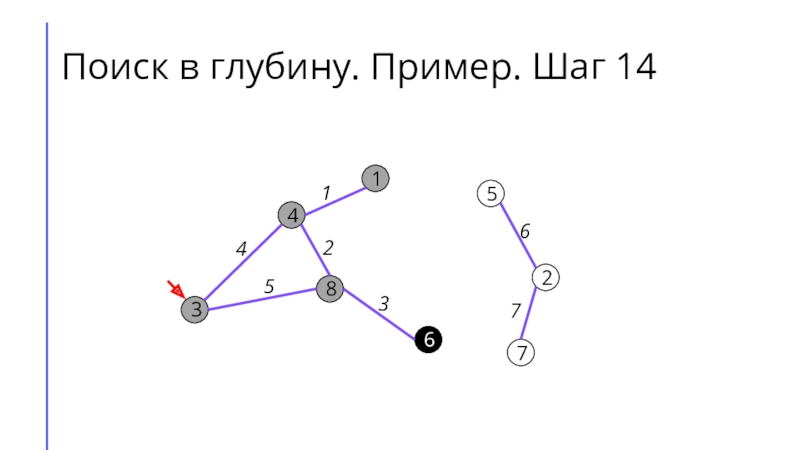
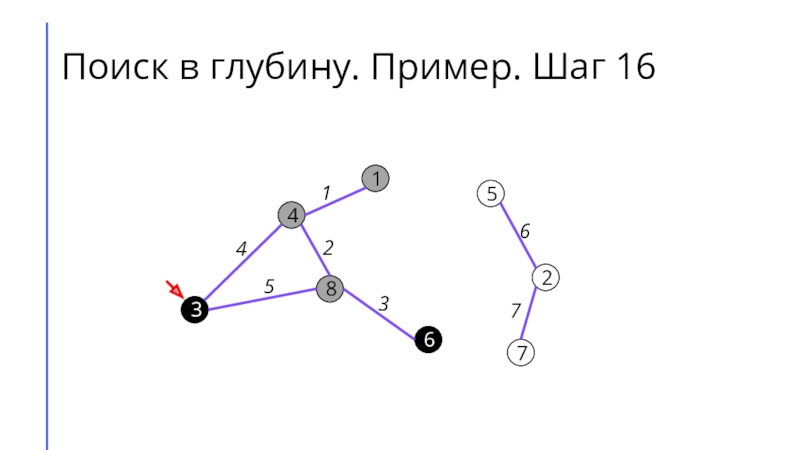
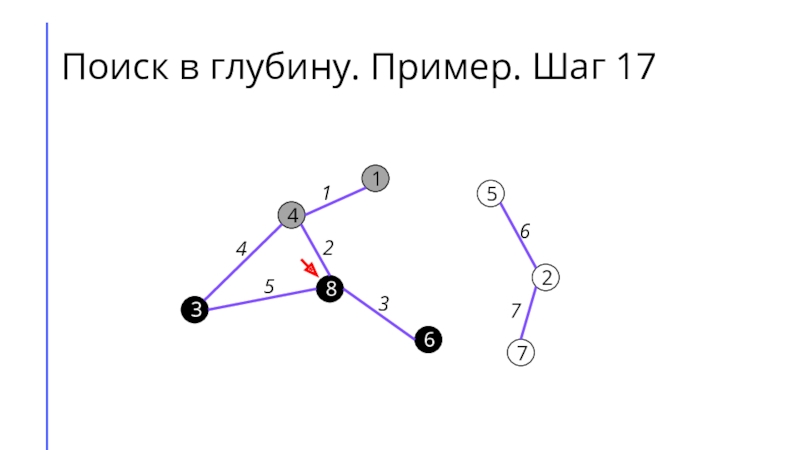
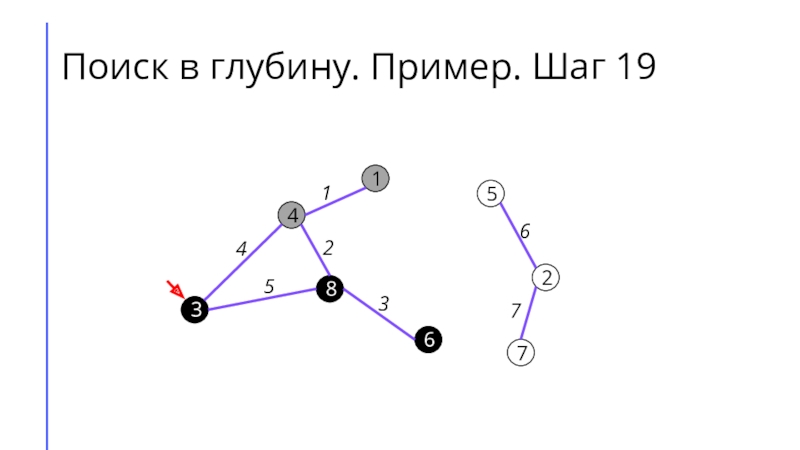
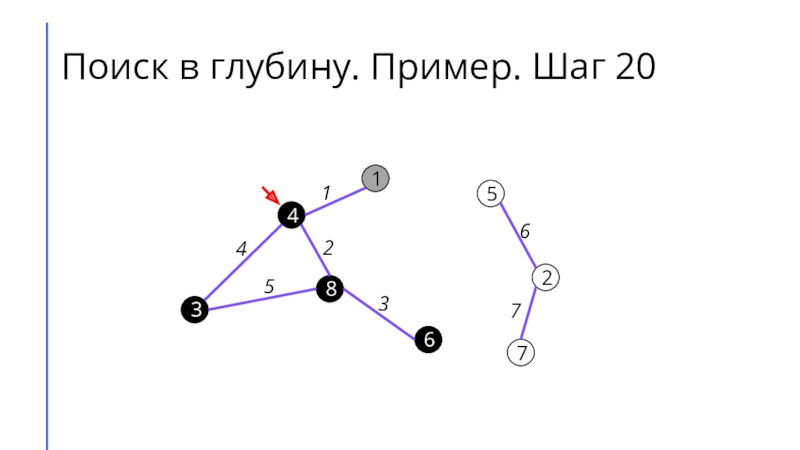
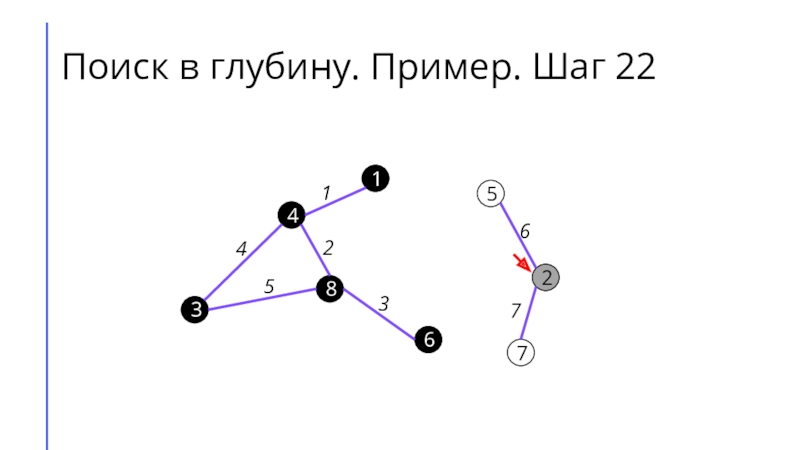
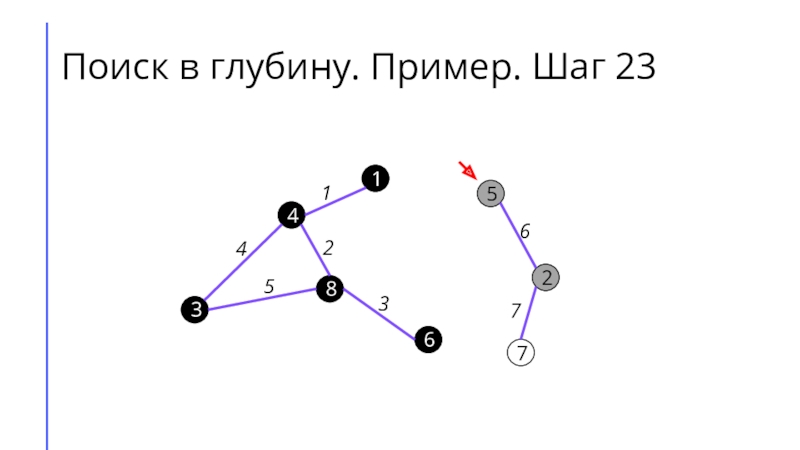
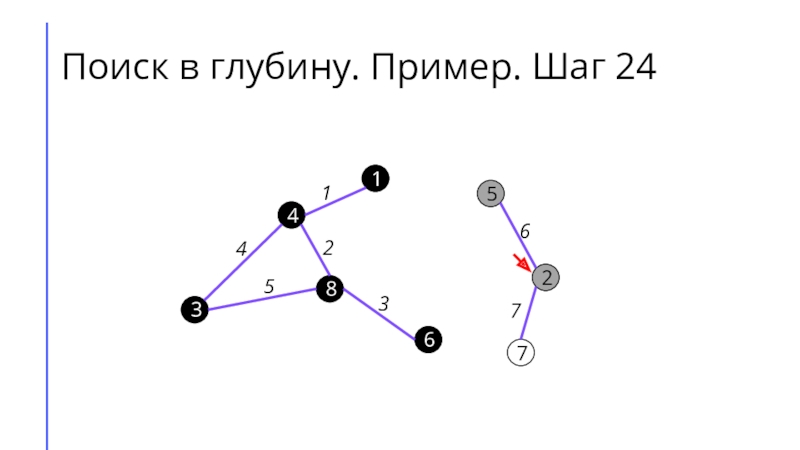
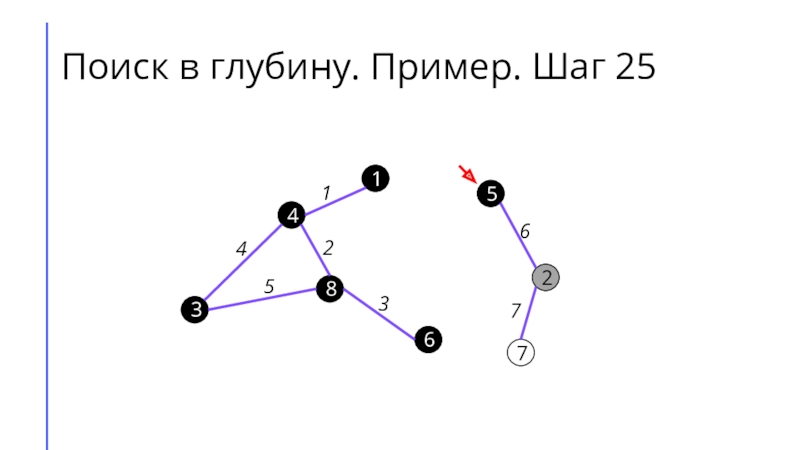
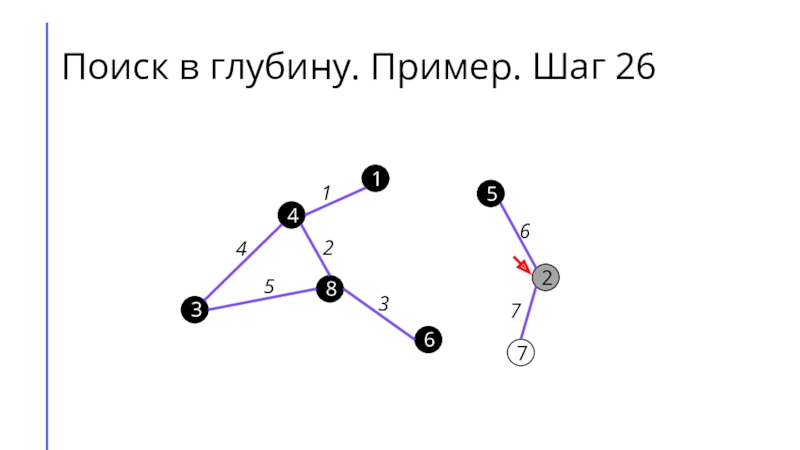
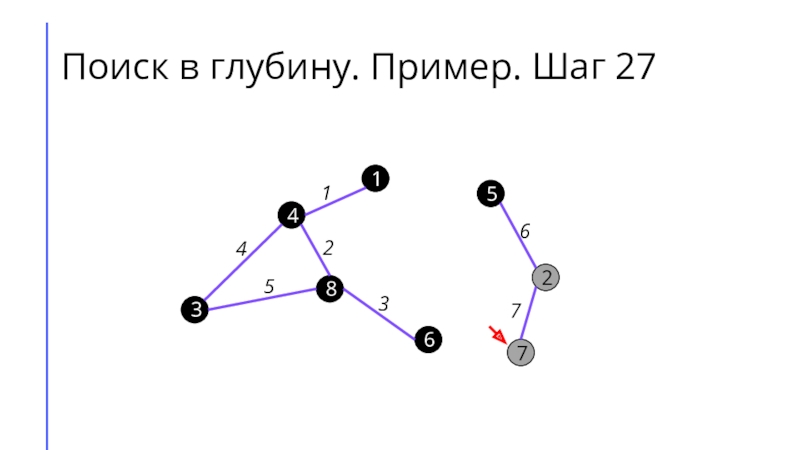
между собой рёбрами.
Связный граф – это граф, из любой вершины

которого по рёбрам можно попасть в любую другую.
Направленный граф – это граф, по рёбрам которого можно передвигаться только в одном заданном направлении.
Ациклический граф – это граф, не содержащий циклов.
Дерево – это связный граф, имеющий N вершин и N-1 ребро.
Взвешенный граф – это граф, в котором каждое ребро имеет свой вес (обычно длину).
Компонента связности – максимальный по включению связный подграф.
ОпределениеГраф – это набор вершин, некоторые пары из которых соединены между собой рёбрами.Связный граф – это граф,

Слайд 3Задача:
Охарактеризуйте граф:
1
2
3
4
5
6
7
8

Задача:Охарактеризуйте граф:12345678

Слайд 4Задача:
Охарактеризуйте граф:
1
2
3
4
5
6
7
8
3
2
4
1
5
2
1

Задача:Охарактеризуйте граф:123456783241521

Слайд 5Задача:
Охарактеризуйте граф:
1
2
3
4
5
6
8
7

Задача:Охарактеризуйте граф:12345687

Слайд 6Поиск (обход) в глубину (DFS)
Для каждой вершины графа будем хранить

её цвет. Пусть изначально вершины будут белыми, когда мы в

них входим, они будут становиться серыми, а когда выходим – чёрными.
Будем перебирать вершины графа. Если встречаем белую вершину – запускаем из неё поиск в глубину.
Во время поиска в глубину перебираем все вершины, смежные той, в которой сейчас находится алгоритм, и по очереди запускаем из них поиск в глубину.
Если поиск запущен не из белой вершины, то дальше его продолжать не следует.
Поиск (обход) в глубину (DFS)Для каждой вершины графа будем хранить её цвет. Пусть изначально вершины будут белыми,

Слайд 7Поиск в глубину. Пример. Шаг 0
7
2
6
5
8
3
4
1
1
3
2
5
4
6
7

Поиск в глубину. Пример. Шаг 0726583411325467

Слайд 8Поиск в глубину. Пример. Шаг 1
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 1726583411326754

Слайд 9Поиск в глубину. Пример. Шаг 2
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 2726583411326754

Слайд 10Поиск в глубину. Пример. Шаг 3
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 3726583411326754

Слайд 11Поиск в глубину. Пример. Шаг 4
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 4726583411326754

Слайд 12Поиск в глубину. Пример. Шаг 5
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 5726583411326754

Слайд 13Поиск в глубину. Пример. Шаг 6
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 6726583411326754

Слайд 14Поиск в глубину. Пример. Шаг 7
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 7726583411326754

Слайд 15Поиск в глубину. Пример. Шаг 8
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 8726583411326754

Слайд 16Поиск в глубину. Пример. Шаг 9
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 9726583411326754

Слайд 17Поиск в глубину. Пример. Шаг 10
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 10726583411326754

Слайд 18Поиск в глубину. Пример. Шаг 11
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 11726583411326754

Слайд 19Поиск в глубину. Пример. Шаг 12
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 12726583411326754

Слайд 20Поиск в глубину. Пример. Шаг 13
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 13726583411326754

Слайд 21Поиск в глубину. Пример. Шаг 14
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 14726583411326754

Слайд 22Поиск в глубину. Пример. Шаг 15
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 15726583411326754

Слайд 23Поиск в глубину. Пример. Шаг 16
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 16726583411326754

Слайд 24Поиск в глубину. Пример. Шаг 17
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 17726583411326754

Слайд 25Поиск в глубину. Пример. Шаг 18
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 18726583411326754

Слайд 26Поиск в глубину. Пример. Шаг 19
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 19726583411326754

Слайд 27Поиск в глубину. Пример. Шаг 20
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 20726583411326754

Слайд 28Поиск в глубину. Пример. Шаг 21
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 21726583411326754

Слайд 29Поиск в глубину. Пример. Шаг 22
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 22726583411326754

Слайд 30Поиск в глубину. Пример. Шаг 23
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 23726583411326754

Слайд 31Поиск в глубину. Пример. Шаг 24
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 24726583411326754

Слайд 32Поиск в глубину. Пример. Шаг 25
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 25726583411326754

Слайд 33Поиск в глубину. Пример. Шаг 26
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 26726583411326754

Слайд 34Поиск в глубину. Пример. Шаг 27
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 27726583411326754

Слайд 35Поиск в глубину. Пример. Шаг 28
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 28726583411326754

Слайд 36Поиск в глубину. Пример. Шаг 29
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 29726583411326754

Слайд 37Поиск в глубину. Пример. Шаг 30
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4

Поиск в глубину. Пример. Шаг 30726583411326754

Слайд 38Хранение графа в программе
Создадим собственную структуру Node для хранения информации

о вершине графа.
В Node будем хранить цвет самой вершины и

перечень смежных вершин.
Граф будем хранить в виде массива (вектора) вершин.
Хранение графа в программеСоздадим собственную структуру Node для хранения информации о вершине графа.В Node будем хранить цвет

Слайд 39Реализация поиска в глубину
Поиск в глубину реализуется в виде рекурсивной

функции, критерием остановки которой является повторное посещение вершины.

Реализация поиска в глубинуПоиск в глубину реализуется в виде рекурсивной функции, критерием остановки которой является повторное посещение

Слайд 40Ввод графа и запуск поиска в глубину
Пусть дан граф из

N вершин и M рёбер. Во входных данных сначала даются

числа N и M, а затем M пар чисел U и V – номера вершин графа, между которыми есть ребро. (1 ≤ U, V ≤ N)
Ввод графа и запуск поиска в глубинуПусть дан граф из N вершин и M рёбер. Во входных

Похожие презентации

Кровь как часть внутренней среды.ppt Кровь как часть внутренней среды.ppt 270
Наполеон I Бонапарт Наполеон I Бонапарт 181
ЖОСПАР ЖОСПАР 540
АЛГЕБРА + АҒЫЛШЫН ТІЛІ + ГЕОМЕТРИЯ = ? АЛГЕБРА + АҒЫЛШЫН ТІЛІ + ГЕОМЕТРИЯ = ? 221
Deep Learning Club Deep Learning Club 194
М.Ю. Лермонтов М.Ю. Лермонтов 386
АТЕРОСКЛЕРОЗ АТЕРОСКЛЕРОЗ 306
Те, кто не написал зачет, получают задание. Посмотреть проверенные работы можно Те, кто не написал зачет, получают задание. Посмотреть проверенные работы можно 172
БЕЗОПАСНОСТЬ В СОЦСРЕДЕ.ppt БЕЗОПАСНОСТЬ В СОЦСРЕДЕ.ppt 308
Нейротрансплантация. Возможности и перспективы Нейротрансплантация. Возможности и перспективы 363
Web-сервисы release Web-сервисы release 258
Викторина Викторина "Лесная газета" О зверях О птицах О растениях Загадки: 129
До свидания, детский сад! 2020 год Группа № 6 Непоседы До свидания, детский сад! 2020 год Группа № 6 Непоседы 151
Масленица для 3 класса Масленица для 3 класса 153
Психофизиологические основы деятельности водителя Психофизиологические основы деятельности водителя 308
Особенности рациона детей раннего возраста Особенности рациона детей раннего возраста 236
Учет посещений групп в социальных сетях Учет посещений групп в социальных сетях 167
Какой биоматериал можно использовать для исследования? Венозную кровь. Как Какой биоматериал можно использовать для исследования? Венозную кровь. Как 203
МЕТАЛЛУРГИЯ ЦВЕТНЫХ МЕТАЛЛОВ МЦМ-1 МЕТАЛЛУРГИЯ ЦВЕТНЫХ МЕТАЛЛОВ МЦМ-1 234
ДРЕВНИЙ КИТАЙ ДРЕВНИЙ КИТАЙ 226

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика