Слайд 1Гравитационное поле Земли
Cила тяжести, действующая на тело в данной системе
координат, равна величине реакции опоры, поддерживающей данное тело.
При этом
и тело и опора предполагаются неподвижными в рассматриваемой системе координат.
Сила тяжести, действующая на массу, лежащую на поверхности Земли, есть равнодействующая двух главных сил –гравитационного притяжения со стороны Земли и центробежной силы от вращения Земли вокруг своей оси.
Слайд 2Если бы Земля не вращалась,
была бы сферически симметричным телом
и имела бы сферически симметричное распределение плотностей,
то ускорение силы
тяжести g было бы одним и тем же во всех точках сферической поверхности радиуса r:
g= M / r2 (r R) и g = M(r) / r2 (r < R) (1)
R – радиус Земли, М – её масса, M(r) – масса пород внутри сферы радиуса r и - гравитационная постоянная ( = 6.67310-11 м3/кгс2).
Вращение Земли, а также отклонение фигуры Земли от сферы, связанное с этим вращением, обуславливают широтную зависимость g.
Слайд 3Локальный рельеф земной поверхности и горизонтальные неоднородности в распределении плотностей
ответственны за вариации в значениях g в разных точках поверхности
Земного шара.
Ньютон: из-за вращения Земли её фигура должна быть не сферой, а эллипсоидом вращения со сжатием:
(2)
Он получил для него значение 1/230. С современными значениями Re = 6378.139 км и Rp = 6356.75 (экваториальный и полярный радиусы Земли) это значение равно: = 1 / 298.256. Французский математик Клеро показал, что ускорение силы тяжести на поверхности такого вращающегося сфероида изменяется с широтой места по закону:
g = ge[1 + sin2()] (3)
где ge – ускорение силы тяжести на экваторе,
= (5 / 2)q - (4)
и q = 2Re / ge – отношение центробежной силы к силе тяжести на экваторе, - угловая скорость вращения Земли, Re – радиус Земли на экваторе.
Слайд 4ПОТЕНЦИАЛ ГРАВИТАЦИОННОГО ПОЛЯ
Гравитационное поле Земли (без вклада центробежных сил от
её вращения) является потенциальным, т.е. таким, в котором работа по
перемещению массы не зависит от формы пути, а определяется лишь координатами начальной и конечной точек перемещения массы.
Ускорение силы тяжести получается как градиент потенциала:
(5)
Если бы Земля представляла точную сферу, и распределение плотностей было сферически-симметричным, то внешний гравитационный потенциал Земли V и ускорение g имели бы вид:
V = M / r g = M / r2 (6)
Слайд 5Реальная форма Земли близка к сфере. Поэтому потенциал внешнего гравитационного
поля Земли отличается от ньютонового потенциала (6) на одну трёхсотую.
До запуска спутников с помощью наземных геодезических измерений был определён первый поправочный член к ньютоновской части поля (6) и в результате потенциал внешнего гравитационного поля Земли стал выражаться формулой :
(7)
где Re–экваториальный радиус Земли,
(8) - гравитационный момент
Земли и Р2 -- второй полином Лежандра:
(9)
А и С – моменты инерции Земли относительно экваториальной и полярной осей, соответственно, = (/2) - .
Слайд 6Современное значение гравитационного момента Земли J2 = 1.0826510-3 (Жарков, 1983).
Относительно простой вид потенциала (7) обязан тому, что он содержит
лишь начальные члены разложения по сферическим функциям, а также тому что он записан в системе координат, в которой оси координат совмещены с главными осями инерции. В общем случае разложение потенциала внешнего гравитационного поля Земли по сферическим функциям имеет вид :
r, , - сферические координаты в точке наблюдения, Pn – полином Лежандра n-того порядка относительно cos, Pnm – присоединённые полиномы Лежандра относительно cos, sin.
Слайд 7Гравитационные моменты Jn, Anm, Bnm в (10) определяются экспериментально по
траекториям искусственных спутников. До запуска спутников в (10) был известен
лишь один коэффициент J2 и потенциал записывался в виде (7). Сейчас определены коэффициенты для всех гармоник 2 n 30. Минимальная длина разрешения при этом составляет:
n 2R / n (23.146.3103 / 30) 1.3103 км
Если бы Земля находилась в состоянии гидростатического равновесия, то в разложении (10) остались бы лишь члены с чётными зональными элементами J2, J4, J6. Отклонение формы Земли от гидростатически равновесной имеет порядок квадрата сжатия: h 2R 70 м.
Слайд 8Геоид
Геоид (геофизическая форма Земли) - определяется как эквипотенциальная поверхность внешнего
потенциала силы тяжести (геопотенциала) W.
W = V + V
= Ко (11)
где Ко – значение внешнего потенциала силы тяжести (геопотенциала) W на поверхности Земли (например, на поверхности невозмущённого океана).
Геопотенциал W - это сумма потенциала внешнего гравитацион-ного поля Земли, V (слайд 4) и центробежного потенциала определяемого вращением Земли:
V=2r2/2,
Три четверти поверхности Земли покрыто океанами и невозмущённая ветровыми течениями поверхность океана в точности совпадает с поверхностью геоида. На континентах поверхность геоида располагается под поверхностью континентов.
Слайд 9Референц-эллипсоид
Высоту поверхности геоида, т.е. эквипотенциальной поверхности (11), определяют обычно относительно
другой эквипотенциальной поверхности – референц-эллипсоида:
Wref = V2
+ V = Ko (12),
где Wref – потенциал нормального поля, равного сумме центробежного потенциала V=2r2/2
и поля V2, определяемого формулой (7)
где
- гравитационный потенциал
Слайд 10Геоид строится в два приема аналогично тому, как внешнее поле
тяготения разделяется на нормальное и возмущенное.
Вначале определяют основную фигуру
отсчета – нормальную фигуру,
а затем определяют высоты геоида (малые по величине) – расстояния геоида от нормальной фигуры.
На первый взгляд можно получить хорошее приближение, если за нормальную фигуру выбрать ньютоновскую сферу со средним радиусом R0 и средней плотностью. Так как отклонение внешнего потенциала от ньютоновского (MG/r) порядка сжатия a, то средние высоты геоида над сферой будут порядка aR0 21 км. Эта величина мала по сравнению с размерами Земли, но велика по сравнению с характерными высотами рельефа.
Слайд 11Поэтому за нормальную фигуру выбирают эллипсоид вращения, который является эквипотенциальной
поверхностью для нормального потенциала. Этот эллипсоид иногда называют референц-эллипсоидом; значения
определяющих его параметров J2, Re, M известны с достаточно высокой точностью.
Референц эллипсоид является весьма хорошим приближением для геоида. Действительно, внешний потенциал отклоняется от нормального на величину порядка a2. Следовательно, отклонение геоида от нормального эллипсоида (высоты геоида) порядка a2 R0 70 м.
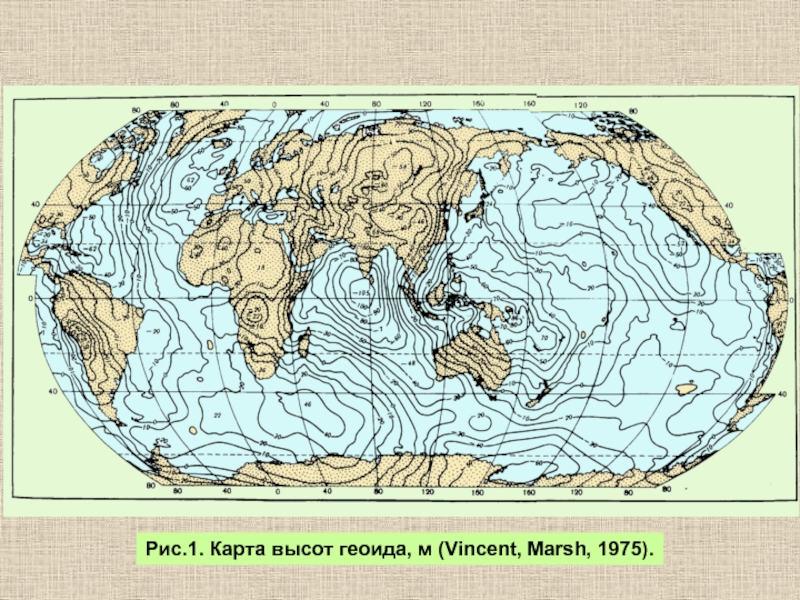
Слайд 12Рис.1. Карта высот геоида, м (Vincent, Marsh, 1975).
Слайд 13Высоту геоида определяют относительно референц-эллипсоида (12) и поэтому она качественно
характеризует отклонение гравитационного поля Земли от нормального значения и имеет
порядок квадрата сжатия:
(R 2 )
Можно было бы ожидать, что в горных местах гравитационное поле будет сильнее за счёт притяжения масс горы, и наоборот, во впадинах дефицит масс должен бы приводить к ослаблению гравитационного эффекта.
Однако, в действительности отклонения от нормального поля (высоты геоида) не связаны с главными топографическими особенностями Земли (континентами и океанами). Отсюда вывод: континентальные области изостатически скомпенси-рованы – материки плавают в подкоровом субстрате подобно гиганским айсбергам.
Слайд 15 Небольшие отклонения гравитационного поля Земли от нормального поля (7)
вызваны флюктуациями плотности в коре и мантии.
Согласно принципу изостазии,
лёгкая кора, состоящая из гранита и базальта, изостатически уравновешена на более тяжёлой мантии. Земная кора как бы плавает в подстилающих породах мантии.
Мантия (литосферы) пропускает поперечные волны и вроде бы должна быть твёрдой, а не течь. На самом деле для сейсмических деформаций с характерным временем порядка секунд она твёрдая, а для для движений с характерными временами порядка десятков и сотен тысяч лет – она ведёт себя как высоковязкое тело (Жарков, 1983).
Поверхность геоида принята за поверхность сравнения и сопоставления гравиметрических наблюдений и отсчёта высот рельефа (от уровня моря).
Слайд 16 Редукция Фая или
в свободном воздухе
учитывает разницу (Н) высот точки измерения аномалии g
и её проекции на поверхность геоида:
g(geoid) = g(measur) + g(free air
g(free air) = М/R2 - М/(R+H)2 2g0H/R
так как H << R. Принимая g0 = 979.77 гал (см/сек2) и R = 6371 км, получим g(free air) 0.3086 Н, где Н - высота точки наблюдения над (под) геоидом – в км.
Измерения g, проведён-ные в разных пунктах земной поверхности, срав-ниваются между собой после того, как они приве-дены к соответствующим точкам на поверхности геоида с помощью процедуры редукции Фая и Буге.
Редукция Буге
Поправки Буге основаны на формуле Буге,
выражающей аномалии силы тяжести, создаваемые притяжением бесконечного плоско-параллельного слоя толщины Н и распределением плотности с глубиной (z):
Если высота поднятия (над геоидом – уровнем моря) равна Н и плотность пород поднятия , то поправка Буге к измеренным значениям g определяется по формуле:
g(Bouger)=g(free air) - 2Н
= g(free air) - 0.0419Н
Слайд 18
Обычно выбирают = 2.67 г/см3, и поправку берут
отрицательной для измерений на суше и положительной – на дне
моря. Тогда формула показывает, что на каждый километр поднятия рельефа g(Bouger) = 0.307 – 0.112 = 0.195 гал. Эта формула позволяет эффективно исключать влияние местных особенностей рельефа, но только в том случае, если правильно определена плотность пород земной коры и рельеф поверхности не слишком крут. Для больших перепадов высот необходимо вносить дополнительную поправку за рельеф местности.
Слайд 19Главной причиной поверхностных аномалий силы тяжести являются неоднородности в распределении
плотностей, рельефа поверхности и Мохо.
Притяжение бесконечного цилиндра с осью
на глубине h радиусом R и контрастом плотности :
Притяжение шара с центром на глубине h радиуса R и контрастом плотности :
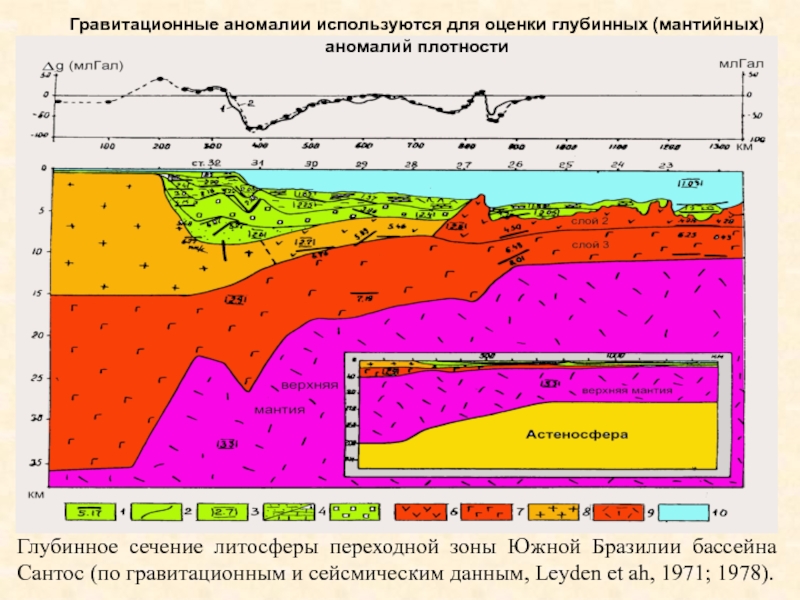
Слайд 20Глубинное сечение литосферы переходной зоны Южной Бразилии бассейна Сантос (по
гравитационным и сейсмическим данным, Leyden et ah, 1971; 1978).
Гравитационные
аномалии используются для оценки глубинных (мантийных) аномалий плотности