Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ii BÖLÜM. LoGIKanYŇ ESaSLarY. KomPÝUTErIŇ LoGIKI ESaSLarY
Содержание
- 1. Ii BÖLÜM. LoGIKanYŇ ESaSLarY. KomPÝUTErIŇ LoGIKI ESaSLarY
- 2. § 12. PIKIR ÝÖRETMÄNIŇ GÖRNÜŞLERILogika pikir ýöretmäniň
- 3. Düşünje. Düşünje obýekti beýleki obýektlerden tapawutlandyrýar we
- 4. Düşünje mazmundan we möçberden ybaratdyr. Mazmun obýektiň
- 5. Pikir aýtma. Adam gurşap alan dünýäni pikir
- 6. Pikir aýtmadaky düşünjeler hakyky bar bolan zatlaryň
- 7. Pikir aýtma – bu pikir ýöretmäniň formasy
- 8. Netije çykarma. Netije çykarma pikir aýtma görnüşinde
- 9. Formal logikanyň düzgünlerine laýyklykda netije çykarma diňe
- 10. SORAGLAR: 1. Pikir aýtma näme? 2. Nähili
- 11. GÖNÜKMELER: 1. Sözlemleriň haýsylarynyň logiki pikir aýtma
- 12. § 13. PIKIR AÝTMALAR ALGEBRASY Pikir aýtmalar algebrasy
- 13. Pikir aýtmalar algebrasynda pikir aýtmalaryň üstünde kesgitli
- 14. logiki köpeltmek (konýunksiýa) Iki (ýa-da birnäçe) pikir
- 15. Слайд 15
- 16. Pikir aýtmalar algebrasynyň nukdaý nazaryndan argumentleri «çyn»
- 17. Mysal üçin, çynlyk tablisany peýdalanyp kesgitläliň: «2.2=4
- 18. Logiki goşmak (dizýunksiýa) «Ýa-da» baglaýjynyñ kömegi bilen
- 19. Слайд 19
- 20. Logiki funksiýanyň bahasyny berlen funksiýanyň çynlyk tablisasynyň
- 21. Çynlyk tablisasynyň kömegi bilen logiki goşmagy ulanmak
- 22. Logiki inkär etme (inwersiýa) Pikir aýtma «däl»
- 23. Logiki pikir aýtmany inkär etme funksiýasynyň çynlyk
- 24. SORAGLAR: 1. Pikir aýtmalar algebrasy nämä niýetlenen?
- 25. GÖNÜKMELER 1. Konýunksiýanyň, dizýunksiýanyň, inwersiýanyň çynlyk tablisasyny
- 26. § 14. LOGIKI AŇLATMALAR WE ÇYNLYK TABLISALARY Logiki
- 27. Слайд 27
- 28. Слайд 28
- 29. 2. Çynlyk tablisasynda sütünleriň mukdaryny kesgitlemeli. Sütünleriň
- 30. Слайд 30
- 31. Слайд 31
- 32. Görşümiz ýaly çynlyk tablisalarynyň soňky sütünleriniň bahalary gabat gelýär, ýagny logiki aňlatmalar deňgüýçlüdir.
- 33. Слайд 33
- 34. 3. Aňlatmalaryň çynlyk tablisalaryny düzmeli:
- 35. § 15. LOGIKI FUNKSIÝALAR
- 36. logiki implikasiýa (gelip çykma) Logiki implikasiýa (gelip
- 37. Logiki implikasiýa amalynyň kömegi bilen emele getirilen
- 38. Çynlyk tablisasy gabat gelýär, diýmek aňlatma subut edildi.
- 39. logiki ekwiwalentlik (deňlik) Logiki ekwiwalentlik «... şonda
- 40. Iki pikir aýtma hem bir wagtda ýalan
- 41. Слайд 41
- 42. 3. X, Y, Z argumentleri bolan F
- 43. § 16. LOGIKI KANUNLAR WE LOGIKI AŇLATMALARY
- 44. Слайд 44
- 45. Слайд 45
- 46. Kommutatiwlik kanuny. Adaty algebrada goşulyjylaryň we köpeldijileriň
- 47. Distributiwlik kanuny. Adaty algebrada ýaýlaryň daşyna diňe
- 48. SORAGLAR: 1. Toždestwo kanuny näme? 2. Gapma-garşy
- 49. Слайд 49
- 50. §17. Logiki meseleleri çözmek Logiki meseleler adaty ýagdaýda
- 51. 1-nji mesele. «Logikany siziň okuwçylaryňyzdan kimler öwrendi?»
- 52. Слайд 52
- 53. § 18. KOMPÝUTERIŇ GURLUŞYNYŇ LOGIKI ESASLARYEsasy (baza)
- 54. «WE» logiki element. Logiki elementiň A we
- 55. «ÝA-DA» logiki element. Logiki elementiň A we
- 56. «DÄL» logiki element. Logiki elementiň A girişinde
- 57. Mysal Girişdäki signalyň bahasy belli bolanda çykyşdaky signalyň bahasyny hasaplamaly we çynlyk tablisasyny düzmeli
- 58. Çözülişi.
- 59. Ikilik sanlary jemlegiç (summator) Kompýuteriň işini has
- 60. Goşulyjylary A, B, geçirişi P we jemi
- 61. Слайд 61
- 62. Şeýlelikde, alnan logiki aňlatmanyň esasynda esasy logiki
- 63. Слайд 63
- 64. Berlen shema ýarym jemlegiç diýilýär, sebäbi onda
- 65. Trigger Trigger kompýuteriň operatiw ýadynyň wajyp gurluşlarynyň
- 66. Informasiýany aýryp, täzesini kabul etmäge taýýarlanmak üçin
- 67. SORAGLAR: 1. Kompýuteriň informasiýany işläp taýýarlaýan, saklaýan
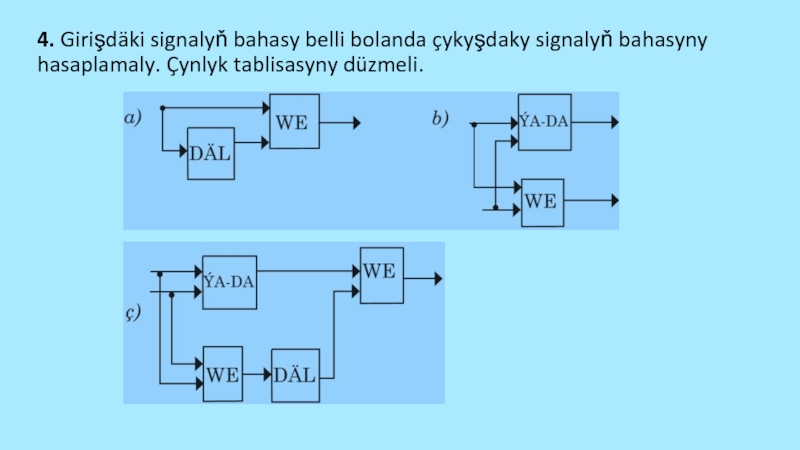
- 68. 4. Girişdäki signalyň bahasy belli bolanda çykyşdaky signalyň bahasyny hasaplamaly. Çynlyk tablisasyny düzmeli.
- 69. Слайд 69
- 70. SOŇY
- 71. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2§ 12. PIKIR ÝÖRETMÄNIŇ GÖRNÜŞLERI
Logika pikir ýöretmäniň formasy we usuly
baradaky ylymdyr.
Logikanyň kanunlary adamyň aňynda gurşap alýan dünýäniň obýektleriniň baglanyşyklaryny,
häsiýetlerini we gatnaşyklaryny şöhlelendirýär. Logika gurşap alýan dünýäniň formal modelini, onuň mazmunyndan aýratynlykda gurmaga mümkinçilik berýär. Pikir ýöretme mydama haýsy bolsa-da bir görnüşde amala aşyrylýar. Pikir ýöretmäniň esasy formasy düşünje, pikir aýtma, netije çykarma bolup durýar.Слайд 3Düşünje. Düşünje obýekti beýleki obýektlerden tapawutlandyrýar we onuň wajyp nyşanlaryny
özünde jemleýär. Meselem, «kompýuter» diýlende bu düşünje informasiýalary işläp taýýarlamak
üçin birleşdirilen elektron gurluşlary, monitory, klawiaturany we syçany özünde jemleýär. Kompýuteri şeýle gysga beýan etsek-de, ony beýleki obýektlerden aňsatlyk bilen (mysal üçin, awtoulagdan) tapawutlandyrmak bolar.Düşünje obýektiň esasy, wajyp nyşanlaryny özünde jemleýän pikir ýöretme formasydyr.
Слайд 4 Düşünje mazmundan we möçberden ybaratdyr. Mazmun obýektiň wajyp nyşanlarynyň jeminden
durýar. Düşünjäniň mazmunyny açmak üçin berlen obýekti beýleki obýektleriň köplüginiň
içinden tapawutlandyrýan zerur we ýeterlik nyşanlaryny tapmaly bolýar. Meselem, «şahsy kompýuter» düşünjäniň mazmunyny şeýle görnüşde açmak bolar: «Şahsy kompýuter – bu bir ulanyja niýetlenen, informasiýalary awtomatik işläp taýýarlamak üçin uniwersal elektron gurluşdyr». Düşünjäniň möçberi onuň saklanýan predmetleriniň jemi bilen kesgitlenýär. «Şahsy kompýuter» düşünjesiniň möçberi häzirki wagtda dünýäde bar bolan ähli şahsy kompýuterleriň jemini (ýüzlerçe million) aňladýar.Слайд 5 Pikir aýtma. Adam gurşap alan dünýäni pikir aýtmalar (pikir ýöretmeler,
tassyklamalar) görnüşinde kesgitleýär (formulirleýär). Pikir aýtma düşünjeler esasynda gurnalyp habar
sözlemi görnüşinde bolýar.Pikir aýtma diňe bir tebigy dillerde däl-de, eýsem formal dillerde hem aňladylyp bilner. Meselem, pikir ýöretme tebigy dilde şeýle görnüşde bolup biler: «Iki köpeltmeli iki deňdir dört». Formal, matematiki dilde bolsa «2· 2=4».
Слайд 6 Pikir aýtmadaky düşünjeler hakyky bar bolan zatlaryň häsiýetlerini we gatnaşyklaryny
dogry şöhlelendirýän ýagdaýynda şol pikir aýtma çyn bolup biler.
Obýekt baradaky
pikir dogry ýa-da nädogry, ýagny pikir aýtma çyn ýa-da ýalan bolup biler. «Prosessor informasiýalary işläp taýýarlamak üçin gurluşdyr» pikir aýtma çyn pikir aýtmadyr.Pikir aýtma hakykata laýyk gelmedik ýagdaýynda ýalan bolar, meselem, «Prosessor çap ediji gurluşdyr».
Слайд 7 Pikir aýtma – bu pikir ýöretmäniň formasy bolup, onda hakyky
bar bolan predmetleriň häsiýetleri we olaryň özara gatnaşyklary tassyklanýar ýa-da
inkär edilýär. Ýönekeý we düzme pikir aýtmalar bolup biler. Ýönekeý pikir aýtmalar esasynda düzme pikir aýtmalar gurulýar. Meselem, «Prosessor informasiýalary işläp taýýarlaýan gurluş we printer çap ediji gurluş» pikir aýtma düzme piker aýtma bolup, iki sany ýönekeý pikir aýtma «we» baglaýjy arkaly birikdirilýär. Ýönekeý pikir aýtmalaryň çynlygy ýa-da ýalanlygy kesgitlenen bolsa, onda düzme pikir aýtmanyň çynlygy ýa-da ýalanlygy pikir aýtmalar algebrasynyň kömegi bilen hasaplanýar.Ýokarda aýdylan düzme pikir aýtma çyn, sebäbi oňa girýän pikir aýtmalar çyndyr.
Слайд 8 Netije çykarma. Netije çykarma pikir aýtma görnüşinde aňladylan belli faktlaryň
esasynda netije (bilim) almakdyr. Geometrik subutnamalary muňa mysal getirmek bolar. Eger
«Üçburçlugyň hemme burçlary deň» fakta esaslansak: onda «Bu üçburçluk deňtaraply» pikir aýtma dogrudyr. Netije çykarma – bu pikir aýtmanyň görnüşi bolup, onuň kömegi bilen bir ýa-da birnäçe pikir aýtmadan täze pikir aýtma (netije) alynýar.Слайд 9Formal logikanyň düzgünlerine laýyklykda netije çykarma diňe çyn pikir aýtmalar
(pikir ýöretmeler) esas bolup biler. Eger netije çykarma formal logikanyň
düzgünlerine laýyklykda geçirilse, onda ol çyn bolar. Garşylykly ýagdaýda ýalan netije çykarma gelmek mümkin.Слайд 10 SORAGLAR: 1. Pikir aýtma näme? 2. Nähili pikir aýtmalar bolup biler? 3. Düşünjäniň
mazmuny bilen möçberiniň arasynda nähili tapawut bar? 4. Pikir aýtma sorag
sözlemi görnüşinde aňladylyp bilermi? 5. Düzme pikir aýtmanyň çynlygy ýa-da ýalanlygy nähili kesgitlenýär?Слайд 11 GÖNÜKMELER: 1. Sözlemleriň haýsylarynyň logiki pikir aýtma bolup bilýändigini, haýsylarynyň bolup
bilmeýändigini düşündiriň. a) «Gün Ýeriň hemrasydyr»; b) «2+3=6»; ç) «şu gün howa örän
gowy»; d) «Türkmenbaşy şäheri Hazar deňziniň kenarynda ýerleşýär»; e) Nury Halmämmedowyň sazlary örän ýakymly we täsirli; ä) «Türkmenistanyň iň beýik nokady Köýtendagda (3139metr) ýerleşýär»; f) «Eger üçburçlugyň iki tarapynyň kwadratlarynyň jemi beýleki tarapynyň kwadratyna deň bolsa, onda bu üçburçluk gönüburçludyr».Слайд 12§ 13. PIKIR AÝTMALAR ALGEBRASY
Pikir aýtmalar algebrasy düzme pikir aýtmalaryň
çynlygyny ýa-da ýalanlygyny olaryň mazmunyna içgin aralaşmazdan kesgitlemek üçin niýetlenendir. Pikir
aýtmalar algebrasynda ýönekeý pikir aýtmalar logiki üýtgeýän ululyklar (latyn baş harplary) bilen belgilenýär. A= «Iki köpeltmeli iki dörde deň». B= «Iki köpeltmeli iki bäşe deň». Çyn pikir aýtma logiki üýtgeýän ululygyň 1 (bir) bahasy, ýalan pikir aýtma bolsa 0 (nol) bahasy degişlidir. Biziň mysalymyzda birinji pikir aýtma (A=1), ikinji pikir aýtma (B=0). Pikir aýtmalar algebrasynda pikir aýtmalar logiki üýtgeýän ululyklar bilen belgilenýär, olar diňe iki: «çyn» (1) we «ýalan» (0) bahalary alyp bilýärler.Слайд 13 Pikir aýtmalar algebrasynda pikir aýtmalaryň üstünde kesgitli logiki amallary ýerine
ýetirmek mümkin, netijede täze düzme pikir aýtma alnar. Täze pikir aýtmalary
emele getirmek üçin, köplenç, «we», «ýa-da», «däl» logiki baglaýjylaryň kömegi bilen aňladylýan esasy logiki amallar ulanylýar.Слайд 14 logiki köpeltmek (konýunksiýa) Iki (ýa-da birnäçe) pikir aýtmalaryň «we» baglaýjynyň kömegi
bilen bir pikir aýtma birikdirilmegine logiki köpeltmek ýa-da konýunksiýa diýilýär. Logiki
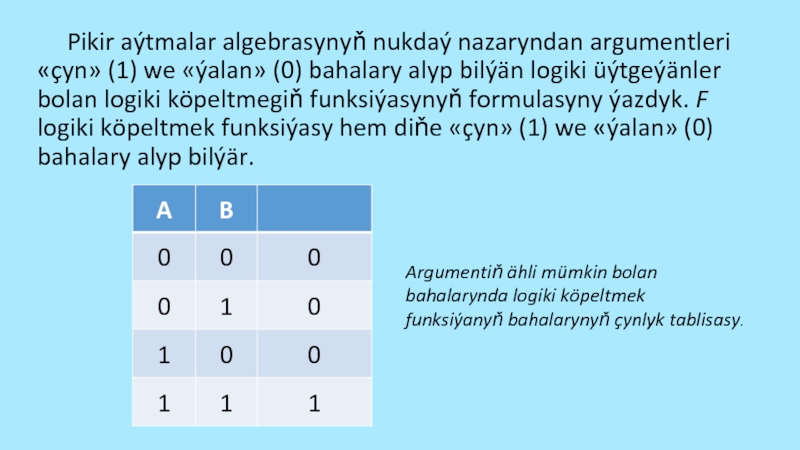
köpeltmegiň (konýunksiýanyň) kömegi bilen emele getirilen düzme pikir aýtma, oňa girýän hemme ýönekeý pikir aýtmalar çyn bolanda we diňe şonda çyndyr. Aşakdaky getirilen dört aňlatmanyň diňe dördünjisi çyndyr, sebäbi ilki üçüsindäki düzme pikir aýtmalarda iň bolmanda bir ýönekeý pikir aýtma ýalandyr: 1) «2.2=5 we 3.3=10»; 2) «2.2=5 we 3.3=9»; 3) «2.2=4 we 3.3=10»; 4) «2.2=4 we 3.3=9».Слайд 16 Pikir aýtmalar algebrasynyň nukdaý nazaryndan argumentleri «çyn» (1) we «ýalan»
(0) bahalary alyp bilýän logiki üýtgeýänler bolan logiki köpeltmegiň funksiýasynyň
formulasyny ýazdyk. F logiki köpeltmek funksiýasy hem diňe «çyn» (1) we «ýalan» (0) bahalary alyp bilýär.Argumentiň ähli mümkin bolan bahalarynda logiki köpeltmek funksiýanyň bahalarynyň çynlyk tablisasy.
Слайд 17 Mysal üçin, çynlyk tablisany peýdalanyp kesgitläliň: «2.2=4 we 3.3=10» düzme
pikir aýtmada birinji pikir aýtma çyn (A=1), ikinji pikir aýtma
bolsa ýalandyr (B=0), diýmek berlen düzme pikir aýtma ýalandyr (F=0).Слайд 18Logiki goşmak (dizýunksiýa) «Ýa-da» baglaýjynyñ kömegi bilen bir ýa-da birnäçe pikir
aýtmanyň birikmesine logiki goşmak ýa-da dizýunksiýa diýilýär. Logiki goşmagyň (dizýunksiýanyň) netijesinde
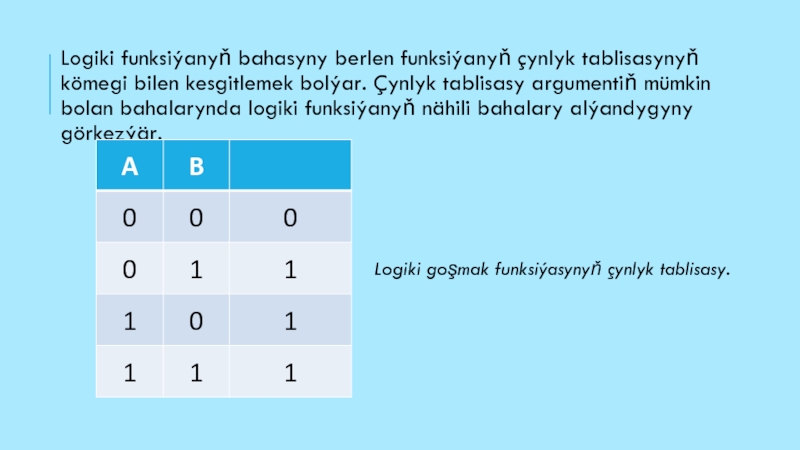
alnan düzme pikir aýtma oňa girýän ýönekeý pikir aýtmalaryň iň bolmanda biri çyn bolanda çyndyr. Aşakda getirilen dört sany düzme pikir aýtmalaryň diňe birinjisi ýalandyr, sebäbi soňky üç ýönekeý pikir aýtmalaryň iň bolmanda biri çyndyr. 1) «2.2 = 5 ýa-da 3.3 = 10»; 2) «2.2 = 5 ýa-da 3.3 = 9»; 3) «2.2 = 4 ýa-da 3.3 = 10»; 4) «2.2 = 4 ýa-da 3.3 = 9».Слайд 20Logiki funksiýanyň bahasyny berlen funksiýanyň çynlyk tablisasynyň kömegi bilen kesgitlemek
bolýar. Çynlyk tablisasy argumentiň mümkin bolan bahalarynda logiki funksiýanyň nähili
bahalary alýandygyny görkezýär.Logiki goşmak funksiýasynyň çynlyk tablisasy.
Слайд 21 Çynlyk tablisasynyň kömegi bilen logiki goşmagy ulanmak arkaly alnan düzme
pikir aýtmanyň çynlygyny kesgitlemek kyn däldir. «2 · 2=4 ýa-da
3 · 3=10» düzme pikir aýtmada birinji ýönekeý pikir aýtma çyn (A=1), ikinji ýönekeý pikir aýtma bolsa ýalandyr (B=0). Tablisa boýunça logiki funksiýanyň çyn bahany (F=1) alýandygyny kesgitleýäris. Diýmek, berlen düzme pikir aýtma çyndyr.Слайд 22 Logiki inkär etme (inwersiýa) Pikir aýtma «däl» sözüň birikdirilmegine logiki inkär
etme ýa-da inwersiýa diýilýär. Logiki inkär etmede çyn pikir aýtma, ýalana,
ýalan pikir aýtma bolsa, çyn pikir aýtma öwrülýär. Goý, A= «iki köpeltmeli iki deňdir dört» çyn pikir aýtma, bu çyn pikir aýtma logiki inkär etmäni ulanyp, F=«iki köpeltmeli iki deňdir dört däl» ýalan pikir aýtmany alarys. A logiki pikir aýtmalaryň üstünde geçirilýän logiki inkär etme logika algebrasynda Ā görnüşde belgilemek kabul edilendir. A pikir aýtmanyň logiki inkär etmesi aşakdaky görnüşde ýazylýar:F = Ā.
Слайд 23Logiki pikir aýtmany inkär etme funksiýasynyň çynlyk tablisasy
Şu çynlyk tablisasy
arkaly logiki inkär etme amaly bilen alnan pikir aýtmanyň çynlygyny
aňsat kesgitlemek bolýar. «Iki köpeltmeli iki deňdir dört däl» şu pikir aýtma ýalan (A=0). Bu pikir aýtmany logiki inkär etmek bilen «Iki köpeltmeli iki deňdir dört» çyn pikir aýtma alarys (F=1).Слайд 24 SORAGLAR: 1. Pikir aýtmalar algebrasy nämä niýetlenen? 2. Konýunksiýa näme? 3. Dizýunksiýa näme? 4.
Logiki inkär etme (inwersiýa) näme?
Слайд 25 GÖNÜKMELER 1. Konýunksiýanyň, dizýunksiýanyň, inwersiýanyň çynlyk tablisasyny düşündiriň. 2. Pikir aýtmalaryň jübütleriniň
haýsylary biri-biriniň inkär etmesi bolýandygyny düşündiriň. a) «510»; b) «10>9», «10
«Maşyn iki swetoforyň her biriniň ýanynda durdy», «Maşyn iki swetoforyň her biriniň ýanynda durmady»; 3. «A nokadyň a göni çyzykda ýatmaýandygy nädogry», «A nokat a göni çyzykda ýatýar». 4. Iki sany a we b pikir aýtmalaryň kömegi bilen düzme pikir aýtmany düzmeli: a) çyn we diňe şonda çyndyr, berlen iki pikir aýtma hem ýalan bolanda; b) ýalan we diňe şonda ýalandyr, berlen iki pikir aýtma hem çyn bolanda. 5. Özünde logiki köpeltmegi, goşmagy we inkär etmäni saklaýan düzme pikir aýtmany düzmeli. Onuň çynlygyny kesgitlemeli.Слайд 26§ 14. LOGIKI AŇLATMALAR WE ÇYNLYK TABLISALARY
Logiki aňlatmalar. Her bir
düzme pikir aýtmalary formula görnüşinde aňlatmak bolar. Formulanyň düzümine pikir
aýtmalary aňladýan logiki üýtgeýänler, logiki funksiýalary aňladýan logiki amallaryň belgileri girýärler. Düzme pikir aýtmany formal dilde (logiki algebranyň dilinde) ýazmak üçin ony düzýän ýönekeý pikir aýtmalary we olaryň arasyndaky baglanyşygy kesgitlemeli.Слайд 29 2. Çynlyk tablisasynda sütünleriň mukdaryny kesgitlemeli. Sütünleriň mukdary logiki üýtgeýänleriň
sanyna logiki amallaryň sanynyň goşulmagyna deňdir. Biziň seredýän ýagdaýymyzda üýtgeýänleriň sany
ikä deň, logiki amallaryň sany bolsa 5-e deň, ýagny çynlyk tablisasynyň sütünleriniň sany 7-ä deň.3. Setirleriň we sütünleriň görkezilen mukdarynda çynlyk tablisasyny gurmaly. Sütünleri belgiläp başdaky logiki üýtgeýänleriň mümkin bolan bahalaryny girizmeli.
4. Çynlyk tablisasyny sütünler boýunça logiki amallary zerur yzygiderlikde we dogry ýerine ýetirmek bilen doldurmaly.
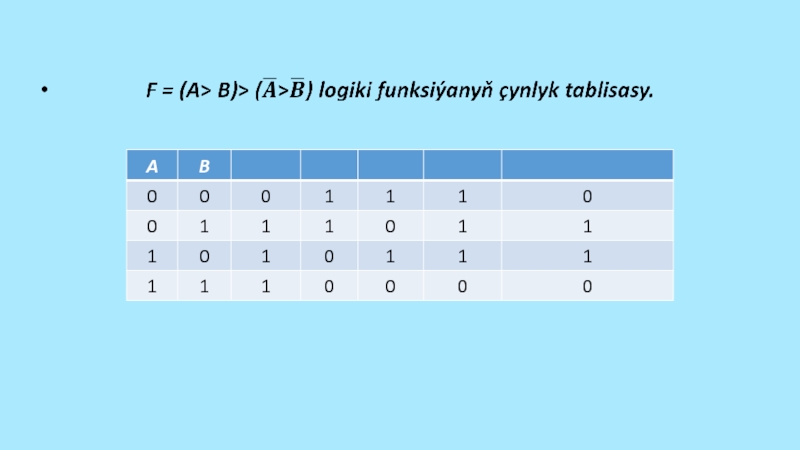
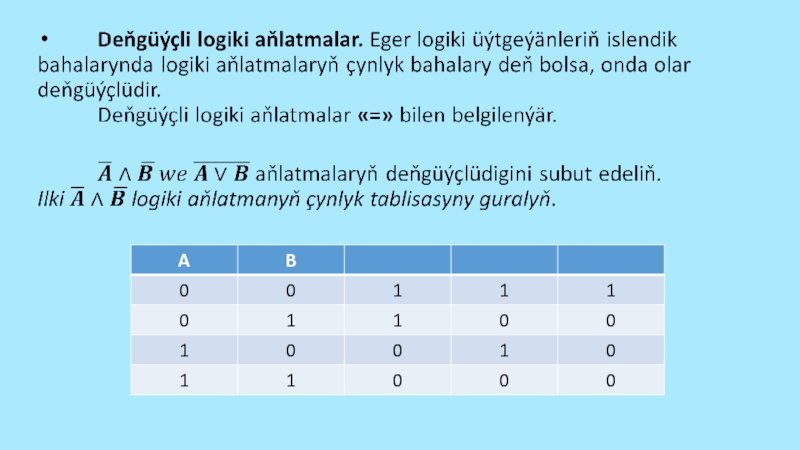
Слайд 32 Görşümiz ýaly çynlyk tablisalarynyň soňky sütünleriniň bahalary gabat gelýär, ýagny
logiki aňlatmalar deňgüýçlüdir.
Слайд 36logiki implikasiýa (gelip çykma) Logiki implikasiýa (gelip çykma) iki pikir aýtmanyň
«eger ..., onda ...» sözleriň kömegi bilen bir pikir aýtma
birikdirilmegi netijesinde emele gelýär. Logiki implikasiýa «eger A, onda B» amaly А→В görnüşde belgilenip, F logiki funksiýa arkaly aňladylýar. «Implikasiýa» logiki funksiýanyň çynlyk tablisasyСлайд 37Logiki implikasiýa amalynyň kömegi bilen emele getirilen düzme pikir aýtma,
birinji çyn pikir aýtmadan ýalan netije (ikinji pikir aýtma) gelip
çykanda we diňe şonda ýalandyr. Mysal üçin: «Eger san 10-a bölünýän bolsa, onda ol san 5-e bölünýändir» pikir aýtma çyndyr, sebäbi birinji (şert) we ikinji (netije) pikir aýtmalar çyndyr. «Eger san 10-a bölünýän bolsa, onda ol san 3-e bölünýändir» pikir aýtma ýalandyr, sebäbi birinji (şert) çyn pikir aýtmadan ikinji (netije) ýalan pikir aýtma gelip çykýar. Şeýle bolsa-da, logiki implikasiýa adaty gelip çykmadan tapawutlanýandyr, sebäbi eger birinji pikir aýtma ýalan bolsa, onda ikinji pikir aýtmanyň (netijäniň) çynlygyna ýalanlygyna garamazdan düzme pikir aýtma çyndyr.Слайд 39 logiki ekwiwalentlik (deňlik) Logiki ekwiwalentlik «... şonda we diňe şonda, haçan-da
...» sözleriň kömegi bilen iki pikir aýtmanyň bir pikir aýtma
birleşmesinden emele getirilýär. «A şonda we diňe şonda, haçan-da B bolanda» logiki ekwiwalentlik amaly. Ol А↔В görnüşde belgilenýär we F logiki funksiýanyň kömegi bilen aňladylýar hem-de degişli çynlyk tablisasy bilen berilýär. Logiki funksiýanyň ekwiwalentliginiň çynlyk tablisasy:Слайд 40 Iki pikir aýtma hem bir wagtda ýalan ýa-da çyn bolanda
we diňe şonda logiki ekwiwalentlik amaly bilen emele getirilen düzme
pikir aýtma çyndyr. Meselem, iki pikir aýtma: A= «Kompýuter hasaplamany ýerine ýetirip biler» we B= «Kompýuter işe taýýar». Ekwiwalentlik amaly bilen alnan düzme pikir aýtma çyn, iki pikir aýtma hem çyn ýa-da ýalan bolanda. «Kompýuter hasaplamany ýerine ýetirip biler, şonda we diňe şonda, kompýuter işe taýýar bolanda». «Kompýuter hasaplamany ýerine ýetirip bilmez, şonda we diňe şonda, kompýuter işe taýýar däl bolanda», diýmek, Logiki ekwiwalentlik amaly bilen emele getirilen düzme pikir aýtma ýalan, bir pikir aýtma çyn we beýlekisi ýalan bolanda.Слайд 423. X, Y, Z argumentleri bolan F funksiýanyň çynlyk tablisasy
berlen.
Aňlatmalaryň haýsylarynyň F funksiýa degişlüdigini anyklaň.
4. X, Y, Z argumentleri
bolan F funksiýanyň çynlyk tablisasy berlen.
Aňlatmalaryň haýsylarynyň F funksiýa degişlidigini anyklaň.
Слайд 43§ 16. LOGIKI KANUNLAR WE LOGIKI AŇLATMALARY ÖZGERTMEGIŇ DÜZGÜNLERI
Logikanyň kanunlary
logiki pikir aýtmalaryň iň bir wajyp kanunalaýyklaryny şöhlelendirýär. Pikir aýtmalar
algebrasynda logikanyň kanunlary formulalar görnüşinde ýazylýar, olar logiki aňlatmalary ekwiwalent özgertmeklige mümkinçilik berýär. Toždestwo kanuny. Her bir pikir aýtma öz-özüne deňdir (toždestwolaýyndyr).A=A
Слайд 46 Kommutatiwlik kanuny. Adaty algebrada goşulyjylaryň we köpeldijileriň ornuny çalşyryp bolýandygyny
bilýäris. Pikir aýtmalar algebrasynda logiki köpeltmek we logiki goşmak amallarynda
logiki üýtgeýänleriň orunlaryny çalşyrmak bolýar. Assosiatiwlik kanuny. Eger logiki aňlatmada diňe logiki köpeltmek amaly ýa-da diňe logiki goşmak amaly ulanylýan bolsa, onda ýaýlary hasaba alman ýa-da olary erkin ýagdaýda goýuşdyrmak bolar.
Слайд 47 Distributiwlik kanuny. Adaty algebrada ýaýlaryň daşyna diňe umumy köpeldijini çykarmak
bolýar, emma pikir aýtmalar algebrasynda ondan tapawutlylykda ýaýlaryň daşyna umumy
köpeldijini, şeýle hem umumy goşulyjyny çykarmak bolar.Слайд 48 SORAGLAR: 1. Toždestwo kanuny näme? 2. Gapma-garşy dällik kanuny nähili ýazylýar? 3. Üçünji
ýagdaýyň bolmazlyk kanuny näme? 4. Goşa inkär etmek kanunyna nähili düşünýärsiňiz? 5.
De Morganyň kanunlary nähili ýazylýar? 6. Kommutatiwlik, assosiatiwlik we distributiwlik kanunlary matematikada haýsy kanunlara meňzeş?Слайд 50§17. Logiki meseleleri çözmek
Logiki meseleler adaty ýagdaýda tebigy dilde goýulýar
(formulirlenýär). Ilkinji nobatda olar pikir aýtmalar algebrasynyň dilinde beýan edilýär.
Alnan logiki aňlatmany ýönekeýleşdirmek we seljermek zerurdyr. Käwagtlar bolsa logiki aňlatma üçin çynlyk tablisasyny gurmaly bolýar.Слайд 51 1-nji mesele. «Logikany siziň okuwçylaryňyzdan kimler öwrendi?» diýen soraga mugallym
şeýle jogap berdi: «Eger logikany Yhlas öwrenen bolsa, onda Ysmaýyl
hem öwrenendir. Şeýle-de logikany Daýanç öwrenen bolsa, Ysmaýyl hem öwrenendir diýmek nädogrudyr». Logikany kim öwrenipdir? Pikir aýtmalary üýtgeýänler bilen belläliň: «A– Logikany Yhlas öwrendi»; B – «Logikany Ysmaýyl öwrendi»; «C – Logikany Daýanç öwrendi». Pikir aýtmalaryň ikisini hem implikasiýa görnüşinde ýazmak bolar: «Eger logikany Yhlas öwrenen bolsa, onda Ysmaýyl hem öwrenendir». A→B=1. «Logikany Daýanç öwrenen bolsa, Ysmaýyl hem öwrenendir diýmek nädogrydyr». C→B=0. Meseläniň çözülişi: Diňe birinji pikir aýtmanyň çyn, ikinjiniň bolsa ýalan bolan ýagdaýynda implikasiýanyň ýalan bolýandygyny ýatlalyň. Şonuň üçin C→B=0 şertden B=0 we C=1 gelip çykýar. Onda alarys A→B=A→0=1, bu ýerden A=0: Diýmek, logikany diňe Daýanç öwrenipdir.Слайд 53§ 18. KOMPÝUTERIŇ GURLUŞYNYŇ LOGIKI ESASLARY
Esasy (baza) logiki elementler
Esasy logiki
elementler: • «WE» logiki element – logiki köpeltmek; • «ÝA-DA» logiki element
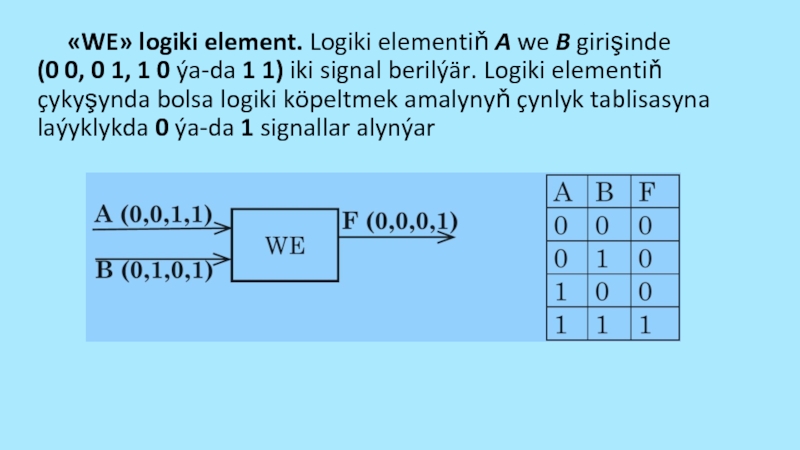
– logiki goşmak; • «DÄL» logiki element – logiki inkär etmek. Kompýuteriň informasiýany işläp taýýarlaýan, saklaýan islendik gurluşy ýokardaky esasy logiki elementlerden durýar. Kompýuteriň logiki elementleri elektrik impulslary görnüşindäki signallaryň üstünde amallary ýerine ýetirýär. Signal bar bolsa, signalyň logiki manysy – 1, signal ýok bolsa, signalyň logiki manysy – 0. Logiki elementiň girişindäki signal – argumentiň bahasy (kabul edilýär), logiki çykyşdaky signal bolsa funksiýanyň bahasy bolýar. Signalyň logiki element arkaly özgertmesi ýagdaý tablisasy bilen berilýär, ol logiki funksiýa laýyk gelýän çynlyk tablisasydyr.Слайд 54 «WE» logiki element. Logiki elementiň A we B girişinde (0 0,
0 1, 1 0 ýa-da 1 1) iki signal berilýär.
Logiki elementiň çykyşynda bolsa logiki köpeltmek amalynyň çynlyk tablisasyna laýyklykda 0 ýa-da 1 signallar alynýarСлайд 55 «ÝA-DA» logiki element. Logiki elementiň A we B girişinde
(0 0, 0 1, 1
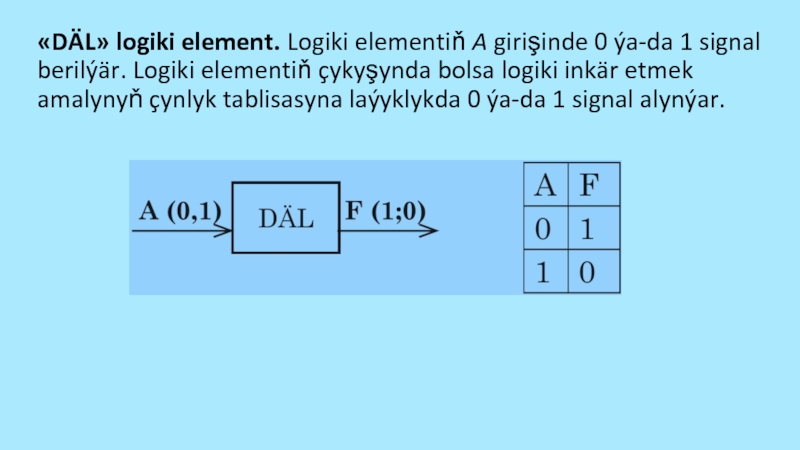
0 ýa-da 1 1) iki signal berilýär. Logiki elementiň çykyşynda bolsa, logiki goşmak amalynyň çynlyk tablisasyna laýyklykda 0 ýa-da 1 signallar alynýar.Слайд 56«DÄL» logiki element. Logiki elementiň A girişinde 0 ýa-da 1
signal berilýär. Logiki elementiň çykyşynda bolsa logiki inkär etmek amalynyň
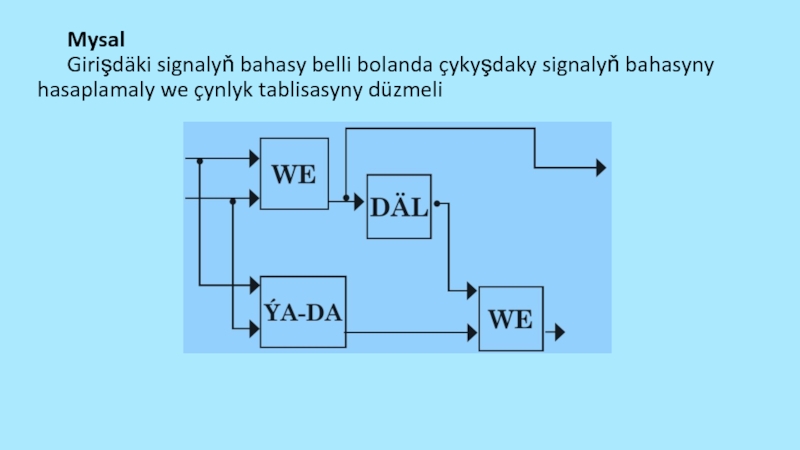
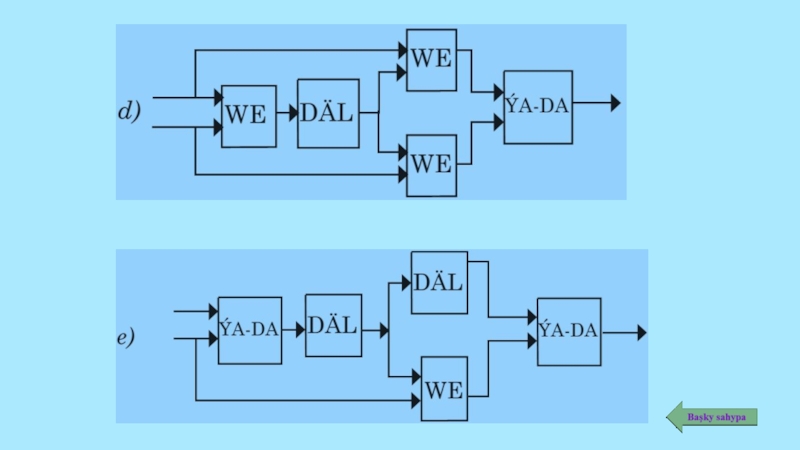
çynlyk tablisasyna laýyklykda 0 ýa-da 1 signal alynýar.Слайд 57 Mysal Girişdäki signalyň bahasy belli bolanda çykyşdaky signalyň bahasyny hasaplamaly we
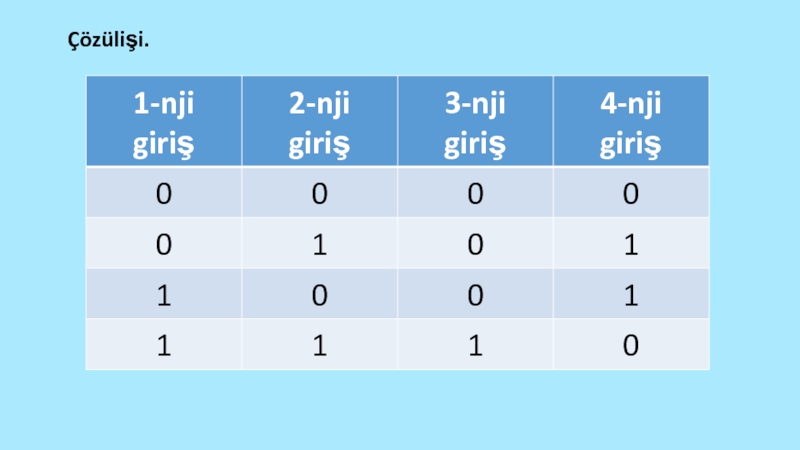
çynlyk tablisasyny düzmeli
Слайд 59 Ikilik sanlary jemlegiç (summator) Kompýuteriň işini has ýönekeýleşdirmek üçin matematiki amallaryň
dürli görnüşliligi ikilik sanlary goşmaklyga syrykdyrylýar. Şonuň üçin kompýuteriň prosessorynyň
esasy bölegini şeýle jemlemegi ýerine ýetirýän jemlegiçler tutýarlar.Ýarym jemlegiç (polusummator). Ikilik sanlar goşulanda her bir razrýadda jem emele getirilýär we şonda ýokarky razrýada geçiriş ýüze çykmagy mümkindir.
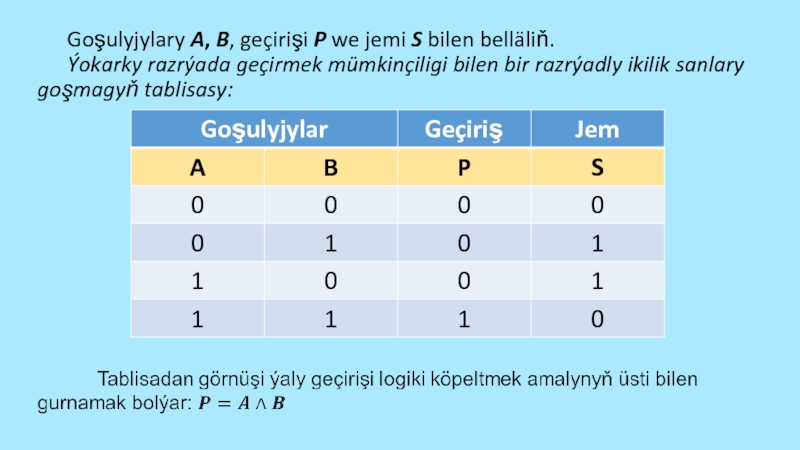
Слайд 60 Goşulyjylary A, B, geçirişi P we jemi S bilen belläliň. Ýokarky
razrýada geçirmek mümkinçiligi bilen bir razrýadly ikilik sanlary goşmagyň tablisasy:
Слайд 62 Şeýlelikde, alnan logiki aňlatmanyň esasynda esasy logiki elementlerden bir razrýadly
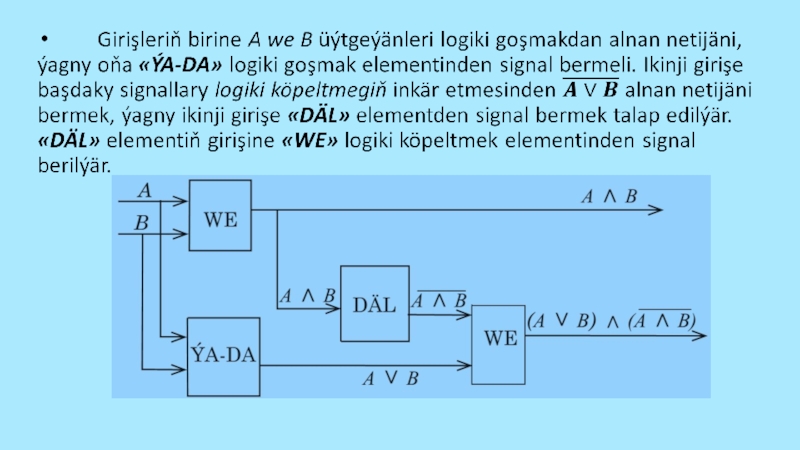
ikilik sanlary goşmagyň shemasyny düzmek bolar. Geçirişi almak üçin, «WE» logiki
elementi ulanmagyň zerurdygyna, geçirişiň logiki formulasy esasynda göz ýetirmek kyn däldir. Jem üçin logiki formulanyň seljermesi çykyşda (iki girişi bolan) logiki köpeltmek «WE» elementiniň durmalydygyny görkezýär.Слайд 64 Berlen shema ýarym jemlegiç diýilýär, sebäbi onda bir razrýadly ikilik
sanlar kiçi razrýaddan uly razrýada geçiriş hasaba almazdan jemlenýär. Doly bir
razrýadly we köp razrýadly jemlegiçleriň gurluşlary ýarym jemlegijiňkä meňzeşdir.Слайд 65 Trigger Trigger kompýuteriň operatiw ýadynyň wajyp gurluşlarynyň biridir, şeýle hem prosessoryň
içki registrleri triggerdir. Bu gurluş informasiýany ýatda saklamaga (her bir
trigger 1 bit informasiýany saklap bilýär) we okamaga mümkinçilik berýär. Triggeri iki «ÝA-DA» we iki «DÄL» logiki elementden gurmak bolýar. Adaty ýagdaýda triggeriň girişlerine 0 signal berlen, trigger 0-y saklaýar. S-iň girişine 1-i ýazmak üçin (gurnama) 1 signal berilýär. Shema boýunça signalyň geçişine yzygiderli seredip, onda bu ýagdaýyň S girişde signal ýitenden soň hem durnukly saklanýandygyny göreris. Trigger 1-i ýadynda saklaýar, ýagny triggeriň Q çykyşyndan 1-i okamak bolýar.
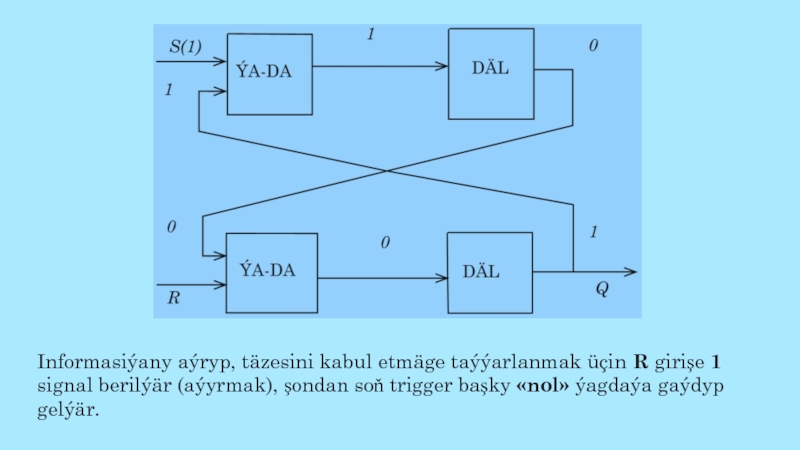
Слайд 66Informasiýany aýryp, täzesini kabul etmäge taýýarlanmak üçin R girişe 1
signal berilýär (aýyrmak), şondan soň trigger başky «nol» ýagdaýa gaýdyp
gelýär.Слайд 67 SORAGLAR: 1. Kompýuteriň informasiýany işläp taýýarlaýan, saklaýan islendik gurluşy nämelerden durýar? 2.
Ýarym jemlegiç näme? 3. Doly bir razrýadly jemlegiç nähili işleýär? 4. Köp
razrýadly jemlegiç nämelerden düzülýär? 5. Trigger näme?GÖNÜKMELER: 1. R (aýyrmak-taşlamak) girişe 1 signal gelenden soňky ýagdaýy, triggeriň logiki shemasy boýunça yzarlaň. 2. Özbaşdak logiki shemalary düzüň, girişdäki bahalary beriň, çykyşdaky bahalary tapyň we çynlyk tablisasyny düzüň. 3. Excel elektron tablisasyndan peýdalanyp, logiki shemalaryň çynlyk tablisalaryny dolduryň.