Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Имитационное моделирование
Содержание
- 1. Имитационное моделирование
- 2. Сведения о курсеПродолжительность – 36 часов;Форма итогового
- 3. Раздел I. «Теория массового обслуживания»Тема «Случайные процессы» Лекция №1
- 4. Случайные процессыОпределение: Случайный процесс (вероятностный, стохастический) –
- 5. Случайные процессыОпределение: Марковский процесс (случайный процесс без
- 6. Случайные процессыОпределение: Граф состояний – графическая схема
- 7. Случайные процессыГраф состояний:S0S2S3S1
- 8. Случайные процессыПотоки событийОпределение: Поток событий - это
- 9. Случайные процессыОпределение: Поток событий называется потоком без
- 10. Случайные процессыПростейший поток событий называется простейшим (стационарным
- 11. Случайные процессыРассмотрим простейший поток событий как неограниченную
- 12. Случайные процессыМатематическое ожидание равно дисперсии:a=σ2=λτВероятность того, что
- 13. Случайные процессыВероятность того, что на участке времени
- 14. Случайные процессыРаспределение, задаваемое функцией распределения (4) или
- 15. Случайные процессыВажнейшее свойство показательного распределения: Если
- 16. Раздел I. «Теория массового обслуживания» (продолжение)Тема «Случайные процессы» Лекция №2
- 17. Случайные процессыУравнения Колмогорова Рассмотрим пример из Лекции
- 18. Случайные процессыРассмотрим систему в момент t и
- 19. Случайные процессыПо теореме умножения вероятностей: p0(t)(1-(λ01+λ02)Δt) -
- 20. Случайные процессыПо теореме умножения вероятностей: p1(t)λ10Δt -
- 21. Случайные процессыПри Δt→0 получаем дифференциальное уравнение 1го
- 22. Случайные процессыПравило составления уравнений Колмогорова:В левой части
- 23. Случайные процессыЗададим начальные условия для системы дифференциальных
- 24. Случайные процессыПредельная вероятность состояния Sj. системы S
- 25. Случайные процессыПроцесс гибели и размноженияКласс случайных процессов
- 26. Случайные процессыСЛАУ для предельных вероятностей:Нормировочное условие: p0+p1+…+pn=1
- 27. Случайные процессыРешение СЛАУ:Числители в коэффициентах при p0
- 28. Случайные процессыПример:Задан граф состояний системы S:Решение: Таким
- 29. Раздел I. «Теория массового обслуживания» (продолжение)Тема «Системы массового обслуживания» Лекция №3
- 30. Системы массового обслуживанияОпределение: Система массового обслуживания (СМО)
- 31. Системы массового обслуживанияСхема работы СМОзаявказаявказаявкаСМООбработанные заявкизаявказаявказаявказаявказаявка
- 32. Системы массового обслуживанияПредмет теории массового обслуживания:построение математических
- 33. Системы массового обслуживанияПоказатели эффективности СМО:среднее число заявок,
- 34. Системы массового обслуживанияКлассификация СМО производится по различным признакам:Число каналов обслуживанияодноканальныемногоканальныеСМОСМО
- 35. Системы массового обслуживанияС отказамиС ожиданиемСМОСМОХарактер поступления заявок
- 36. Системы массового обслуживанияС приоритетомБез приоритетаСМОСМОДисциплина обслуживанияабсолютнымотносительным
- 37. Системы массового обслуживанияограниченнаянеограниченнаяСМОСМООрганизация очереди
- 38. Системы массового обслуживанияограниченноенеограниченноеСМОСМОВремя ожидания заявки в очереди
- 39. Раздел I. «Теория массового обслуживания» (продолжение)Тема «Системы массового обслуживания» Лекция №4
- 40. Системы массового обслуживанияСМО с отказами В качестве
- 41. Системы массового обслуживанияОдноканальная СМО с отказами Имеет
- 42. Системы массового обслуживанияИсследуем предельные вероятности состояний: Учитывая
- 43. Системы массового обслуживанияПример: Заявки на телефонные переговоры
- 44. Системы массового обслуживанияМногоканальная СМО с отказамиРассмотрим классическую
- 45. Системы массового обслуживанияПо формулам для процесса гибели
- 46. Системы массового обслуживанияВероятность отказа СМО есть предельная
- 47. Системы массового обслуживанияПример: В условиях предыдущей задачи
- 48. Системы массового обслуживанияНапример, при n=2:По условию оптимальности Q≥0.90 ⇒ необходимо установить 5 телефонных номеров.
- 49. Системы массового обслуживанияПример: В вычислительный центр коллективного
- 50. Системы массового обслуживанияРассчитаем предельные вероятности: Вывод: В
- 51. Системы массового обслуживанияQ=1-0.033=0.067 ⇒ из каждых 100
- 52. Раздел I. «Теория массового обслуживания» (продолжение)Тема «Системы массового обслуживания» Лекция №5
- 53. Системы массового обслуживанияСМО с ожиданием (очередью)Помимо показателей
- 54. Случайные процессыОдноканальная СМО с неограниченной очередьюИмеется 1
- 55. Системы массового обслуживанияВопрос: Существуют ли предельные вероятности?
- 56. Системы массового обслуживанияНайдем показатели эффективности СМО:
- 57. Системы массового обслуживанияПример: В порту имеется один
- 58. Системы массового обслуживанияВероятность того, что причал свободен
- 59. Системы массового обслуживанияМногоканальная СМО с неограниченной очередьюИмеется
- 60. Системы массового обслуживанияДоказано:при
- 61. Системы массового обслуживанияЗамечание: При
- 62. Системы массового обслуживанияпребыванием в очереди покупателей (задаваемая,
- 63. Системы массового обслуживанияНайдем характеристики обслуживания СМО при
- 64. Системы массового обслуживанияСреднее число покупателей в кассах
- 65. Системы массового обслуживанияб) При n=3:
- 66. Системы массового обслуживанияТ.о. min Cотн = 4,14
- 67. Системы массового обслуживанияв) Вероятность того, что в
- 68. Системы массового обслуживанияПример: Железнодорожная касса с двумя
- 69. Системы массового обслуживанияНеобходимо: а) Сравнить два
- 70. Системы массового обслуживанияРешение: а) 1 ВАРИАНТ –
- 71. Системы массового обслуживанияПо формулам Литтла: 2 ВАРИАНТ
- 72. Системы массового обслуживанияб) При среднем времени обслуживания
- 73. Раздел I. «Теория массового обслуживания» (продолжение)Тема «Системы массового обслуживания» Лекция №6
- 74. Системы массового обслуживанияСМО с ограниченной очередью Пусть
- 75. Системы массового обслуживанияОдноканальная СМО с ограниченной очередью
- 76. Системы массового обслуживанияМногоканальная СМО с ограниченной очередью
- 77. Системы массового обслуживанияПример: В условиях задачи про
- 78. Системы массового обслуживанияРешение: По условию m=3
- 79. Раздел I. «Теория массового обслуживания» (продолжение)Тема «Законы распределения случайных величин при имитации процессов» Лекция №7
- 80. Законы распределения случайных величинНормальное распределение (гауссово)Является одним
- 81. Законы распределения случайных величинТеорема (Одна из форм
- 82. Законы распределения случайных величинДля приближенной оценки среднего
- 83. Законы распределения случайных величинРавномерное распределениеПрименяется в случае,
- 84. Законы распределения случайных величинЭкспоненциальное распределение Также занимает
- 85. Законы распределения случайных величинДля экспоненциального распределения математическое
- 86. Законы распределения случайных величинСпроектируем моменты всех событий
- 87. Законы распределения случайных величинОбобщенное распределение Эрланга Используется
- 88. Законы распределения случайных величинТреугольное распределениеЛинейное изменение функции
- 89. Раздел II. «Инструментальные средства имитационного моделирования»Тема «Введение в имитационное моделирование»Лекция №8
- 90. Введение в имитационное моделированиеОпределение: Имитационное моделирование (simulation
- 91. Введение в имитационное моделированиеПримеры типовых задач, решаемых
- 92. Введение в имитационное моделированиеоценка параметров надежности и
- 93. Введение в имитационное моделированиеСовременные программные комплексы имитационного
- 94. Введение в имитационное моделированиеДостоинства программного пакета «Pilgrim-5»
- 95. Введение в имитационное моделированиеСредством построения моделей в
- 96. Введение в имитационное моделированиеЭтапы построения имитационной модели
- 97. Введение в имитационное моделированиеТранзакты Основной динамической единицей
- 98. Введение в имитационное моделированиеТранзакт может выполнять следующие
- 99. Введение в имитационное моделированиеОсновные параметры транзактов:уникальный идентификатор
- 100. Введение в имитационное моделированиеПримеры транзактов: требование на
- 101. Введение в имитационное моделированиеУзлы Узлы графа имитационной
- 102. Введение в имитационное моделированиеОпределение: Событием называется факт
- 103. Введение в имитационное моделированиеОпределение: Относительный масштаб времени
- 104. Введение в имитационное моделирование3) Пропорционально ускоренный. Вводится
- 105. Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)Тема «Структурирование имитационной модели»Лекция №9
- 106. Структура имитационной моделиМодель состоит из двух характерных частей: секции инициализации и блока описания стохастической сети.
- 107. Структура имитационной моделиВставляется в секцию Блок описания узловмодели (стохастическая многоуровневая сеть) Всегда необходим
- 108. Структура имитационной моделиМакрооперация #include подключает моделирующую среду
- 109. Структура имитационной моделиp3 - модельное время, в
- 110. Структура имитационной моделиp5 – признак режима пространственной
- 111. Структура имитационной моделиp6 – номер (int) одной
- 112. Структура имитационной моделиp8 – номер (int) терминатора
- 113. Структура имитационной моделиNETWORK (p1,p2) - координатор сети
- 114. Структура имитационной моделиMODEND (p1,p2,p3,p4) - оператор завершения
- 115. Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)Тема «Функциональные узлы имитационной модели »Лекция №10
- 116. Функциональные узлы имитационной моделиУзлы имитационной модели характеризуются
- 117. Функциональные узлы имитационной моделиАргументы функции AG (p1,p2,p3,p4,p5,p6,p7,p8):p1
- 118. Функциональные узлы имитационной модели3) expo – экспоненциальное
- 119. Функциональные узлы имитационной моделиp6 - величина, зависимая
- 120. Функциональные узлы имитационной моделиp7 – величина, зависимая
- 121. Функциональные узлы имитационной модели
- 122. Функциональные узлы имитационной моделиАргументы функции SERV (p1,p2,p3,p4,p5,p6,p7,p8):p1
- 123. Функциональные узлы имитационной моделиp4 – тип функции
- 124. Функциональные узлы имитационной моделиp5 – величина, зависимая
- 125. Функциональные узлы имитационной моделиp7 – величина, зависимая
- 126. Функциональные узлы имитационной модели - Узел
- 127. Функциональные узлы имитационной модели
- 128. Функциональные узлы имитационной модели
- 129. Функциональные узлы имитационной моделиСреднее время задержки -
- 130. Функциональные узлы имитационной модели
- 131. Функциональные узлы имитационной моделиp2 – идентификатор (int)
- 132. Функциональные узлы имитационной моделиЛогика функционирования узла CREAT:1)
- 133. Функциональные узлы имитационной модели
- 134. Функциональные узлы имитационной моделиp3 – конец (int)
- 135. Функциональные узлы имитационной моделиЛогика функционирования узла DELET:
- 136. Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)Тема «Функциональные узлы имитационной модели »Лекция №11
- 137. Функциональные узлы имитационной модели
- 138. Функциональные узлы имитационной моделиДля описания узла-счета с
- 139. Функциональные узлы имитационной моделиВнутри приоритетной группы транзакты
- 140. Функциональные узлы имитационной моделиsaldo - внутренний атрибут
- 141. Функциональные узлы имитационной моделиp3 – размер денежной
- 142. Функциональные узлы имитационной модели
- 143. Функциональные узлы имитационной модели При посещении транзактом узла
- 144. Функциональные узлы имитационной модели В случае отсутствия необходимого
- 145. Функциональные узлы имитационной модели Узел MANAGE проверяет наличие
- 146. Функциональные узлы имитационной модели Для изменения объема ресурса,
- 147. Функциональные узлы имитационной модели Остаток ресурса и дефицит
- 148. Функциональные узлы имитационной модели
- 149. Функциональные узлы имитационной моделиИнтервал требуемого обслуживания транзакта
- 150. Функциональные узлы имитационной моделиp2 - возможность подключения
- 151. Функциональные узлы имитационной моделиnorm – нормальное распределение;
- 152. Функциональные узлы имитационной моделиp5 – величина (float),
- 153. Функциональные узлы имитационной моделиp6 – параметр (float)
- 154. Функциональные узлы имитационной моделиp7 – величина (float),
- 155. Функциональные узлы имитационной модели
- 156. Функциональные узлы имитационной моделиУзел DYNAM - очередь
- 157. Функциональные узлы имитационной моделиУправление переходами в многослойных
- 158. Функциональные узлы имитационной модели
- 159. Функциональные узлы имитационной модели
- 160. Функциональные узлы имитационной модели
- 161. Функциональные узлы имитационной модели
- 162. Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)Тема «Сигнальные управляющие функции. Параметры транзактов и узлов»Лекция №12
- 163. Сигнальные управляющие функции
- 164. Сигнальные управляющие функцииCHEG (p2,p3,p4,p5,p6,p7,p8) – перенастроить генератор
- 165. Сигнальные управляющие функцииACTIV (i) – перевести процесс
- 166. Сигнальные управляющие функцииSUPPLY (p1,p2,p3) - изменить объем
- 167. Сигнальные управляющие функцииASSIGN (p1,p2,p3) – ассигновать на
- 168. Сигнальные управляющие функцииFREED (i) – изгнать уничтожающий
- 169. Сигнальные управляющие функцииSEWT (x) – поместить текущий
- 170. Сигнальные управляющие функцииGEOWAY (latA, lonA, latB, lonB)
- 171. Сигнальные управляющие функцииCLCODE – включить блок операторов
- 172. Параметры транзактовПараметры транзактов Для повышения эффективности создаваемых
- 173. Параметры транзактовt→ga – признак обслуживания транзакта вновь,
- 174. Параметры состояния узловПараметры состояния узлов Некоторые параметры
- 175. Параметры состояния узловaddr[n]→op – признак состояния узла
- 176. Датчики случайных величинДатчики случайных величин Часто в
- 177. Датчики случайных величинerlang(e,z) - обобщенный закон Эрланга;triplex(a,b,c)
- 178. Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)Тема «Создание моделей с помощью графического конструктора GEM»Лекция №13
- 179. Создание моделей с помощью графического конструктора GEMКонструктор
- 180. Создание моделей с помощью графического конструктора GEMОсновное
- 181. Создание моделей с помощью графического конструктора GEMРабочая
- 182. Создание моделей с помощью графического конструктора GEMРедактирование
- 183. Создание моделей с помощью графического конструктора GEMРедактирование
- 184. Создание моделей с помощью графического конструктора GEMСозданные
- 185. Создание моделей с помощью графического конструктора GEMОпределение
- 186. Создание моделей с помощью графического конструктора GEMДля
- 187. Создание моделей с помощью графического конструктора GEM Окно определения параметров узла
- 188. Создание моделей с помощью графического конструктора GEMПоле
- 189. Создание моделей с помощью графического конструктора GEMПанель
- 190. Создание моделей с помощью графического конструктора GEMУзел
- 191. Создание моделей с помощью графического конструктора GEMНеобходимым
- 192. Создание моделей с помощью графического конструктора GEMОпределение
- 193. Создание моделей с помощью графического конструктора GEM
- 194. Создание моделей с помощью графического конструктора GEMВ
- 195. Создание моделей с помощью графического конструктора GEMРедактирование переменных функции MODEND осуществляется через диалоговое окно:
- 196. Создание моделей с помощью графического конструктора GEMРабота
- 197. Создание моделей с помощью графического конструктора GEMВозможны
- 198. Создание моделей с помощью графического конструктора GEMДля
- 199. Создание моделей с помощью графического конструктора GEMЧтобы
- 200. Создание моделей с помощью графического конструктора GEMДля
- 201. Создание моделей с помощью графического конструктора GEMОпределение
- 202. Создание моделей с помощью графического конструктора GEMДополнительные
- 203. Создание моделей с помощью графического конструктора GEMПользователь-разработчик
- 204. Создание моделей с помощью графического конструктора GEMПроверка
- 205. Создание моделей с помощью графического конструктора GEMПроцедура
- 206. Создание моделей с помощью графического конструктора GEMПлан
- 207. Создание моделей с помощью графического конструктора GEMПоиск
- 208. Создание моделей с помощью графического конструктора GEMОкно поиска узла
- 209. Создание моделей с помощью графического конструктора GEMКопирование/вставка
- 210. Создание моделей с помощью графического конструктора GEMОчистить
- 211. Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)Тема «Обработка имитационной модели в системе Pilgrim »Лекция №14
- 212. Обработка имитационной модели в системе Pilgrim Формирование
- 213. Обработка имитационной модели в системе PilgrimПосле появления
- 214. Обработка имитационной модели в системе Pilgrim5. Выбрать
- 215. Обработка имитационной модели в системе PilgrimТрактовка результатов
- 216. Обработка имитационной модели в системе Pilgrim4) Точка.
- 217. Обработка имитационной модели в системе Pilgrim7) M
- 218. Обработка имитационной модели в системе Pilgrimдля TERM
- 219. Обработка имитационной модели в системе Pilgrim8) C2 [t]
- 220. Обработка имитационной модели в системе Pilgrim10) Количество
- 221. Обработка имитационной модели в системе PilgrimВ узле
- 222. Обработка имитационной модели в системе PilgrimТрассировка моделиСуществуют
- 223. Раздел III. «Имитационное моделирование экономических процессов»Тема «Моделирование обслуживания с разными приоритетами»Лекция №15
- 224. Открытая модель обслуживания с разными приоритетамиОписание моделируемого
- 225. Открытая модель обслуживания с разными приоритетамиВ этом
- 226. Открытая модель обслуживания с разными приоритетамиПараметры модели
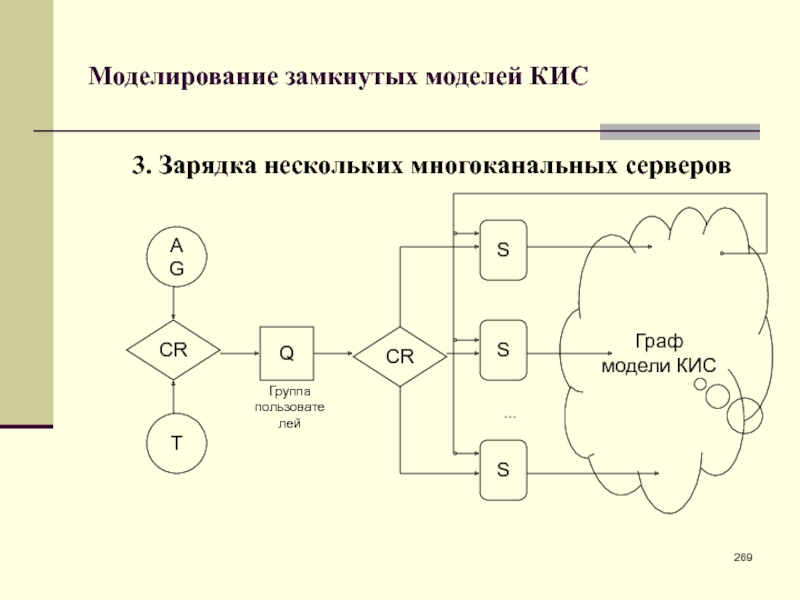
- 227. Открытая модель обслуживания с разными приоритетамиСхема моделиAGAGQSAGAGДокументыНеисправностиКомпьютерЖурнал учета неисправностей
- 228. Открытая модель обслуживания с разными приоритетамиТекст модели#include
- 229. Открытая модель обслуживания с разными приоритетамиnetwork(dummy, dummy)
- 230. Открытая модель обслуживания с разными приоритетами Serv ("АРМ
- 231. Открытая модель обслуживания с разными приоритетами Результаты моделирования
- 232. Замкнутая модель обслуживания с клапаном Замкнутая модель
- 233. Замкнутая модель обслуживания с клапаномПараметры модели
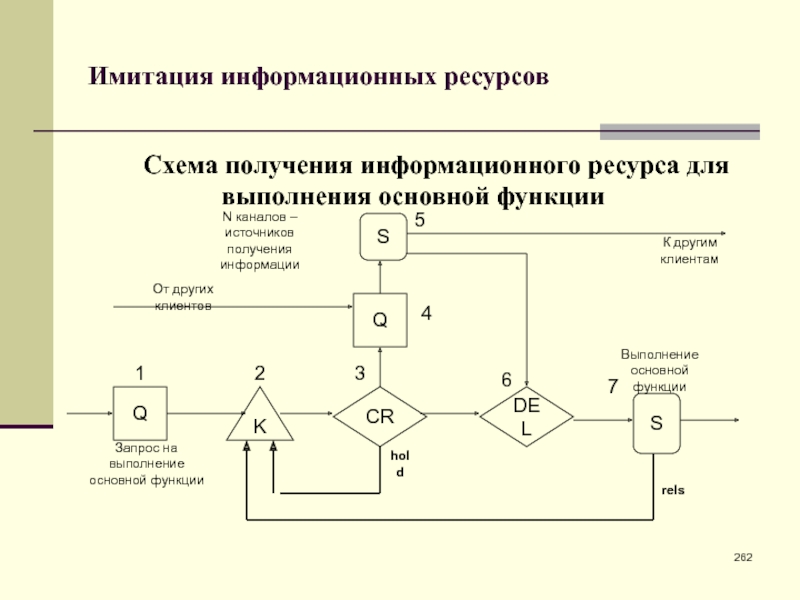
- 234. Замкнутая модель обслуживания с клапаномСхема моделиAGAGCRTSQKQS123456789Заселение поселкаСхема зарядкиПоселокПродавецОчередь перед магазиномВходная дверьОчередь перед продавцомholdrels
- 235. Замкнутая модель обслуживания с клапаномТекст модели#include int
- 236. Замкнутая модель обслуживания с клапаномforward /*
- 237. Замкнутая модель обслуживания с клапаном else /* генерация
- 238. Замкнутая модель обслуживания с клапаномtop(5): serv("Поселок", N1+N2,
- 239. Замкнутая модель обслуживания с клапаномtop(9): serv("Продавец", 1,
- 240. Раздел III. «Имитационное моделирование экономических процессов» (продолжение)Тема «Моделирование условного прерывания обслуживания»Лекция №16
- 241. Моделирование условного прерывания обслуживанияПример использования узла delet:
- 242. Моделирование условного прерывания обслуживанияПараметры модели
- 243. Моделирование условного прерывания обслуживанияСхема моделиAGAGTQKQ673183524ТаксиПассажирыТакси уехалоKDELholdrelsholdrels
- 244. Моделирование условного прерывания обслуживанияТекст модели#include float Pas=1.0;
- 245. Моделирование условного прерывания обслуживания clcode
- 246. Моделирование условного прерывания обслуживания top(7): queue("Такси", none, 4);
- 247. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Сведения о курсе
Продолжительность – 36 часов;
Форма итогового контроля – экзамен;
Состоит
из разделов:
моделирование экономических процессов»Слайд 4Случайные процессы
Определение: Случайный процесс (вероятностный, стохастический) – это процесс изменения
во времени
состояния какой-либо системы в соответствии с вероятностными закономерностями.
Определение:
Процесс с дискретными состояниями – это процесс, возможные состояния которого можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно.Определение: Процесс с непрерывным временем – это процесс, при котором моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны.
Слайд 5Случайные процессы
Определение: Марковский процесс (случайный процесс без последствий) – это
процесс, при котором для любого момента времени t0 вероятностные характериcтики
процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.Пример марковского процесса - показания счетчика в такси.
Слайд 6Случайные процессы
Определение: Граф состояний – графическая схема случайного процесса с
дискретными состояниями;
Пример: Устройство S состоит из двух узлов.
Состояния:
S0 –
оба узла исправны:S1 – первый узел ремонтируется, второй исправен;
S2 - второй узел ремонтируется, первый исправен;
S3 - оба узла ремонтируются;
Слайд 8Случайные процессы
Потоки событий
Определение: Поток событий - это последовательность однородных событий,
следующих одно за другим в случайныe моменты времени
Интенсивность λ
– частота появления событий в единицу времениОпределение: Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени.
Определение: Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.
Слайд 9Случайные процессы
Определение: Поток событий называется потоком без последействия, если для
любых двух непересекающихся участков времени τ1 и τ2 число событий,
попадающих на один из них, не зависит от числа событий, попадающих на другие.Определение: Поток событий называется ординарным, если вероятность попадания на малый участок времени t0 двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Слайд 10Случайные процессы
Простейший поток событий называется простейшим (стационарным пуассоновским), если он:
Стационарен;
Ординарен;
Не
имеет последействия;
Теорема: При наложении (суперпозиции) достаточно большого числа n независимых,
стационарных и ординарных потоков с интенсивностями λi (i=1,2..n) получается поток, близкий к простейшему с интенсивностью: Слайд 11Случайные процессы
Рассмотрим простейший поток событий как неограниченную последовательность случайных точек:
Число m событий, попадающих на отрезок τ, распределено по закону Пуассона:
Слайд 12Случайные процессы
Математическое ожидание равно дисперсии:
a=σ2=λτ
Вероятность того, что за время τ
не произойдет ни одного события (m=0):
Найдем распределение интервала времени Т
между произвольными двумя соседними событиями простейшего потока.Слайд 13Случайные процессы
Вероятность того, что на участке времени длиной t не
появится ни одного из последующих событий, равна:
Вероятность противоположного события,
т.е. функция распределения случайной величины T:Плотность вероятности случайной величины есть производная ее функции распределения:
Слайд 14Случайные процессы
Распределение, задаваемое функцией распределения (4) или плотностью вероятности (5)
называется показательным (или экспоненциальным)
Таким образом, интервал времени между двумя
соседними произвольными событиями имеет показательное распределение, для которого математическое ожидание равно среднему квадратическому отклонению случайной величины:a=σ=1/λ
Слайд 15Случайные процессы
Важнейшее свойство показательного распределения:
Если промежуток времени, распределенный
по показательному закону, уже длился некоторое время τ то это
никак не влияет на закон распределения оставшейся части промежутка (T- τ). Он будет таким же, как и закон распределения всего промежутка Т.Для простейшего потока с интенсивностью λ вероятность попадания на элементарный отрезок времени Δt хотя бы одного события:
Слайд 17Случайные процессы
Уравнения Колмогорова
Рассмотрим пример из Лекции №2.
Пусть λij –
интенсивность простейшего потока событий, под воздействием которых происходит переход системы
из состояния Si в состояние Sj.Вероятностью i-го состояния называется вероятность pi(t) того, что в момент t система будет находиться в состоянии Si.
Слайд 18Случайные процессы
Рассмотрим систему в момент t и зададим малый промежуток
времени Δt.
Найдем вероятность p0(t+Δt) того, что система в момент
(t+ Δt) будет находиться в состоянии S0.Это достигается разными способами:
1) Система в момент t с вероятностью po(t) находилась в состоянии S0 , и за время Δt не вышла из него.
(λ01+λ02) – интенсивность суммарного простейшего потока, выводящего систему из состояния S0.
PΔt≈ (λ01+λ02)Δt вероятность выхода системы из состояния S0.
Слайд 19Случайные процессы
По теореме умножения вероятностей:
p0(t)(1-(λ01+λ02)Δt) - вероятность того, что
система находилась в состоянии S0 и за время Δt не
вышла из него.2) Система в момент t с вероятностью p1(t) (или p2(t)) находилась в состоянии S1 (или S2) и за время Δt перешла в состояние S0.
λ10Δt – вероятность перехода системы из состояния S1 в состояние S0.
λ20Δt – вероятность перехода системы из состояния S2 в состояние S0.
Слайд 20Случайные процессы
По теореме умножения вероятностей:
p1(t)λ10Δt - вероятность того, что
система находилась в состоянии S1 и за время Δt перешла
в состояние S0.p2(t)λ20Δt - вероятность того, что система находилась в состоянии S2 и за время Δt перешла в состояние S0.
По теореме сложения вероятностей:
p0(t+ λ20Δt)= p1(t)λ10Δt+p2(t)λ20Δt+p0(t)(1-(λ01+λ02)Δt).
Отсюда,
Слайд 21Случайные процессы
При Δt→0 получаем дифференциальное уравнение 1го порядка:
Рассуждая аналогично для
других состояний системы S получаем систему дифференциальных уравнений Колмогорова для
вероятностей системы:Слайд 22Случайные процессы
Правило составления уравнений Колмогорова:
В левой части каждого уравнения стоит
производная вероятности i-го состояния. В правой части - сумма произведений
вероятностей всех состояний (из которых есть дуги в i-е состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i-го состояния.Для решения системы (7) необходимо добавить условие:
Слайд 23Случайные процессы
Зададим начальные условия для системы дифференциальных уравнений (7):
При
t=0 p0(0)=1,
p1(0)=p2(0)=p3(0)=0
(предположим, что при t=0
система была исправна, т.е. находилась в состоянии S0.).Решение уравнений Колмогорова позволяют найти все вероятности состояний системы как функции времени.
Особый интерес – предельные (финальные) вероятности системы (при Δt→∞).
Слайд 24Случайные процессы
Предельная вероятность состояния Sj. системы S показывает среднее время
пребывания системы в этом состоянии (в долевом отношении).
Предельные вероятности постоянны
⇒ в системе (7) p'0(t)= p'1(t)= p'2(t)=p'3(t)=0.Получаем СЛАУ, описывающих стационарный режим:
Слайд 25Случайные процессы
Процесс гибели и размножения
Класс случайных процессов с графом состояний:
Переходы
осуществляются только в соседние состояния!
Предположение: Все потоки событий случайного процесса
являются простейшими. S2
Sn
S1
Sk
S0
Слайд 27Случайные процессы
Решение СЛАУ:
Числители в коэффициентах при p0 представляют произведение всех
интенсивностей потоков слева направо до состояния Sk (k=I, 2, ...,
п), а знаменатели- произведение всех интенсивностей потоков справа налево до состояния Sk (k=I, 2, ..., п).Слайд 28Случайные процессы
Пример:
Задан граф состояний системы S:
Решение:
Таким образом, в стационарном
режиме система S находится в состоянии S0 – 70,6% времени;
в состоянии S1 – 17,6% времени; в состоянии S2 – 11,8% времени.S2
S1
S0
Найти предельные вероятности системы S.
Слайд 29Раздел I. «Теория массового обслуживания» (продолжение)
Тема «Системы массового обслуживания»
Лекция
№3
Слайд 30Системы массового обслуживания
Определение: Система массового обслуживания (СМО) – это совокупность
приборов, каналов, станков, линий обслуживания, на которые в случайные или
детерминированные моменты времени поступают заявки на обслуживание.Примеры СМО:
вычислительные комплексы,
банковские системы
торговые терминалы
коммутаторы телефонных станций
информационные службы
комбинаты бытового обслуживания и т.д.
Слайд 31Системы массового обслуживания
Схема работы СМО
заявка
заявка
заявка
СМО
Обработанные заявки
заявка
заявка
заявка
заявка
заявка
Слайд 32Системы массового обслуживания
Предмет теории массового обслуживания:
построение математических моделей, связывающих заданные
условия работы СМО (число заявок, каналов, характер потока заявок и
т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоком заявокСлайд 33Системы массового обслуживания
Показатели эффективности СМО:
среднее число заявок, обслуживаемых в единицу
времени;
среднее время ожидания обслуживания;
среднее число заявок в очереди;
вероятность отказа
в обслуживании без ожидания;вероятность превышения числа заявок в очереди определенного значения и др.
Слайд 34Системы массового обслуживания
Классификация СМО производится
по различным признакам:
Число каналов обслуживания
одноканальные
многоканальные
СМО
СМО
Слайд 36Системы массового обслуживания
С приоритетом
Без приоритета
СМО
СМО
Дисциплина
обслуживания
абсолютным
относительным
Слайд 38Системы массового обслуживания
ограниченное
неограниченное
СМО
СМО
Время ожидания
заявки в очереди
Слайд 39Раздел I. «Теория массового обслуживания» (продолжение)
Тема «Системы массового обслуживания»
Лекция
№4
Слайд 40Системы массового обслуживания
СМО с отказами
В качестве показателей эффективности СМО
с отказами будем рассматривать:
А - абсолютную пропускную способность СМО, т.е.
среднее число заявок, обслуживаемых в единицу времени;Q - относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;
Ротк - вероятность отказа, т.е. того, что заявка покинет СМО не обслуженной;
- среднее число занятых каналов (для многоканальной системы)
Слайд 41Системы массового обслуживания
Одноканальная СМО с отказами
Имеет 1 канал на
который поступает поток заявок с интенсивностью λ.
μ, - интенсивность
потока обслуживания- среднее время обслуживания;
Граф состояний:
Состояние S0 – канал свободен;
Состояние S1 – канал занят;
S0
S1
Слайд 42Системы массового обслуживания
Исследуем предельные вероятности состояний:
Учитывая p0+p1=1 ⇒
Таким образом,
⇒
Слайд 43Системы массового обслуживания
Пример: Заявки на телефонные переговоры поступают диспетчеру с
интенсивностью λ=90 заявок в час (l/ч). Средняя продолжительность разговора по
телефону= 2 мин. Определить показатели эффективности работы СМО при наличии одного телефонного номера.
Решение:
Тогда, , т.е. в среднем диспетчер
ответит только на 25% звонков
Вывод: Одного номера недостаточно
- среднее число
обслуженных заявок
Слайд 44Системы массового обслуживания
Многоканальная СМО с отказами
Рассмотрим классическую задачу Эрланга:
Имеется п
каналов, на которые поступает поток заявок ,с интенсивностью λ. Поток
обслуживаний имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.Граф состояний СМО соответствует процессу гибели и размножения:
Состояние Sk – когда в СМО заняты k каналов.
S2
Sn
S1
S0
Слайд 45Системы массового обслуживания
По формулам для процесса гибели и размножения:
Обозначим
– приведенная интенсивность потока
заявок;
Тогда,
………..
………
⇐ Формулы Эрланга
Слайд 46Системы массового обслуживания
Вероятность отказа СМО есть предельная вероятность того, что
все п каналов системы будут заняты:
Относительная пропускная способность:
Абсолютная пропускная
способность:Среднее число занятых каналов
Слайд 47Системы массового обслуживания
Пример: В условиях предыдущей задачи определить оптимальное число
телефонных номеров, если условием оптимальности считать удовлетворение в среднем из
каждых 100 заявок не менее 90 заявок на переговоры.Решение: Рассчитаем интенсивность нагрузки канала:
, т.е. за время среднего (по
продолжительности) телефонного разговора поступает в среднем 3 заявки на переговоры.
Будем постепенно увеличивать число каналов (телефонных номеров) п=2,3,4,… и определять характеристики СМО.
Слайд 48Системы массового обслуживания
Например, при n=2:
По условию оптимальности Q≥0.90 ⇒ необходимо
установить 5 телефонных номеров.
Слайд 49Системы массового обслуживания
Пример: В вычислительный центр коллективного пользования с 3
рабочими станциями поступают заказы на вычислительные работы. При загрузке всех
ЭВМ вновь поступивший заказ не принимается. Среднее время работы с одним заказом – 3 часа. Интенсивность потока заявок 0.25 (1/ч). Найти предельные вероятности состояний и показатели эффективности.Решение: По условию n=3 λ=0.25(1/ч) = 3 часа
Отсюда,
Интенсивность нагрузки: (1/ч)
Слайд 50Системы массового обслуживания
Рассчитаем предельные вероятности:
Вывод: В стационарном режиме в
среднем 47% времени нет ни одной заявки; 35,7 % времени
– обрабатывается 1 заявка; 13,4% времени – обрабатываются 2 заявки; 3,3% времени – обрабатываются 3 заявки;⇒
Слайд 51Системы массового обслуживания
Q=1-0.033=0.067 ⇒ из каждых 100 заявок в среднем
будет обслужено 96,7;
A=0.25*0.967=0.242 ⇒ в час будет обслужено в среднем
0.242 заявки⇒ каждая из трех ЭВМ будет занята обслуживанием заявок в среднем на = 29,2%
Замечание: При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоев ЭВМ. Что важнее – высокая пропускная способность СМО или значительный простой оборудования?
Слайд 52Раздел I. «Теория массового обслуживания» (продолжение)
Тема «Системы массового обслуживания»
Лекция
№5
Слайд 53Системы массового обслуживания
СМО с ожиданием (очередью)
Помимо показателей эффективности A, Q,
и Pотк рассмотрим следующие:
Lсист – среднее число заявок
в системе;Tсист – среднее время пребывания заявки в системе;
Lоч – среднее число заявок в очереди (длина очереди);
Tоч – среднее время пребывания заявки в очереди;
Pзан – вероятность того, что канал занят (степень загрузки канала)
Слайд 54Случайные процессы
Одноканальная СМО с неограниченной очередью
Имеется 1 канал, на которые
поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность
μ. Найти предельные вероятности состояний системы и показатели ее эффективности.…….
Состояние S0 – канал свободен;
Состояние S1 – канал занят, очереди нет;
Состояние S2 – канал занят, в очереди 1 заявка;
…………..
Состояние Sk – канал занят, в очереди (k-1) заявка;
…………..
S2
Sk
S1
S0
Слайд 55Системы массового обслуживания
Вопрос: Существуют ли предельные вероятности? Ведь при t→∞
очередь может неограниченно возрастать.
Доказано!
При предельные
вероятности существуют.При очередь растет до бесконечности.
Т.к. , то геометрический ряд сходится к сумме
Отсюда, ⇒ … …
Предельные вероятности образуют убывающую геометрическую прогрессию со знаменателем
Слайд 56Системы массового обслуживания
Найдем показатели эффективности СМО:
, где
- среднее число заявок, находящихся под обслуживанием;По формуле матожидания
⇒
Теорема. При любом характере потока заявок распределении времени обслуживания и дисциплине обслуживания выполняется:
⇐ Формулы Литтла
Слайд 57Системы массового обслуживания
Пример: В порту имеется один причал для разгрузки
судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее
время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.Решение: n=1
Т.к. ,то очередь не может бесконечно возрастать и предельные вероятности существуют.
Слайд 58Системы массового обслуживания
Вероятность того, что причал свободен p0=1-0.8
Вероятность того, что
причал занят pзан=1-0.2=0.8
По формуле предельных вероятностей:
p1=0.8(1-0.8)=0.16 - вероятность, что у
причала 1 судно;p2=0.82(1-0.8)=0.128 - вероятность, что у причала 2 судна
(т.е. 1 находится в очереди);
p3=0.83(1-0.8)=0.1024 - вероятность, что у причала 3 судна (т.е. 2 находятся в очереди);
Вероятность того, что разгрузку ожидают не более, чем 2
судна: p= p1 +p2+ p3=0.3904
Эффективность разгрузки низкая. Нужно ↓ или ↑ n.
Слайд 59Системы массового обслуживания
Многоканальная СМО с неограниченной очередью
Имеется n каналов с
неограниченной очередью и потоком заявок с интенсивностью λ. Поток обслуживания
имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.….. …..
….. ….. …..
S0- все каналы свободны ………….
Sn – заняты все каналы, очередь пустая…………
Sn+r – заняты все каналы, в очереди r заявок………….
S2
Sk
S1
S0
Sn
Sn+1
Sn+r
Слайд 60Системы массового обслуживания
Доказано:
при предельные вероятности
существуют.
При очередь растет до бесконечности.
… … … …- вероятность, что заявка окажется в очереди
- среднее число
занятых каналов
- среднее число
заявок в очереди
среднее число
заявок в СМО
Слайд 61Системы массового обслуживания
Замечание: При для СМО с
неограниченной очередью любая заявка будет обслужена, т.е. Pотк=0, Q=1, A=λ
.Пример: В универсаме к кассе поступает поток покупателей с интенсивностью λ = 81 чел. в час. Средняя продолжительность обслуживания кассиром одного покупателя tоб=2 мин. Определить:
a) Минимальное количество кассиров пmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при п=пmin.
б) Оптимальное количество nопт контролеров-кассиров, при котором относительная величина затрат Сотн, связанная с издержками на содержание кассиров и с
Слайд 62Системы массового обслуживания
пребыванием в очереди покупателей (задаваемая, например, по формуле
будет минимальна, и сравнить характеристики обслуживания при п=пmin и n=nопт.
в) Вероятность того, что в очереди будет не более трех покупателей.
Решение: а) По условию λ=81 (1/ч)=1.35(1/мин).
Очередь не будет ↑ до ∞ при ⇒ при n<ρ .
Таким образом, nmin=3 – минимальное число кассиров.
Слайд 63Системы массового обслуживания
Найдем характеристики обслуживания СМО при п = 3.
Т.о.
2.5% рабочего времени кассиры простаивают.
Вероятность того, что будет очередь:
Среднее число
покупателей в очереди к кассе:Среднее время ожидания в очереди:
Слайд 64Системы массового обслуживания
Среднее число покупателей в кассах (с учетом очереди):
Среднее время нахождения в кассах (с учетом очереди):
Среднее число занятых обслуживанием кассиров:
Доля занятых обслуживанием кассиров:
Итак, при n=3 узел кассового обслуживания перегружен!
Слайд 66Системы массового обслуживания
Т.о. min Cотн = 4,14 при n=5
⇒ nопт=5
Рассчитаем остальные характеристики для n=5:
Pоч=0.091
Lоч=0.198 Tоч=0.146 (мин)Lсист=2.9 Tсист=2.15 (мин)
Вывод: Среднее число занятых кассиров не изменилось, но остальные показатели улучшились!
Слайд 67Системы массового обслуживания
в) Вероятность того, что в очереди будет не
более трех покупателей:
При n=5:
Для сравнения при n=3
Слайд 68Системы массового обслуживания
Пример: Железнодорожная касса с двумя окошками продает билеты
в два пункта А и В. Интенсивность потока пассажиров, желающих
купить билеты, для обоих пунктов одинакова: λA=λВ = 0,45 (пассажиров в минуту). На обслуживание пассажиров кассир тратит в среднем 2 мин. Рассматриваются два варианта продажи билетов:1 ВАРИАНТ: Билеты продаются в одной кассе с двумя окошками одновременно в оба пункта А и В;
2 ВАРИАНТ: Билеты продаются в двух специали-зированных кассах (по одному окошку в каждой), одна только в пункт А, другая - только в пункт В.
Слайд 69Системы массового обслуживания
Необходимо:
а) Сравнить два варианта продажи билетов
по основным характеристикам обслуживания.
б) Определить, как надо изменить среднее
время обслуживания одного пассажира, чтобы по второму варианту продажи пассажиры затрачивали на приобретение билетов в среднем меньше времени, чем по первому варианту.Слайд 70Системы массового обслуживания
Решение:
а) 1 ВАРИАНТ – это двухканальная СМО
с неограни-ченной очередью.
λ=0.45+0.45=0.9
Т.к.
,то предельные вероятности ∃.Вероятность простоя
двух кассиров
Слайд 71Системы массового обслуживания
По формулам Литтла:
2 ВАРИАНТ – это две
одноканальные СМО с неограни-ченной очередью.
Для каждой СМО λ=0.45
Вывод: По 2му варианту длина очереди и среднее время ожидания больше, чем по 1му варианту.
Слайд 72Системы массового обслуживания
б) При среднем времени обслуживания
T1сист=10.5 (мин) –
по 1му варианту очереди;
T2сист=20 (мин) – по 2му варианту очереди.
Требуется
найти , чтобы T2сист < T1систТ.к. ⇒ ⇒
Вывод: При уменьшении среднего времени обслуживания до 1,83 мин. 2й вариант очереди более эффективный.
⇒
⇒
Слайд 73Раздел I. «Теория массового обслуживания» (продолжение)
Тема «Системы массового обслуживания»
Лекция
№6
Слайд 74Системы массового обслуживания
СМО с ограниченной очередью
Пусть число заявок в
очереди ограничено и не превышает некоторого заданного числа m. Если
в очереди все места заняты, заявка покидает СМО необслуженной.Для вычисления предельных вероятностей состояний и показателей эффективности таких СМО используется прежний подход, только суммируется не бесконечная прогрессия, а конечная.
Среднее время пребывания в очереди и СМО определяются по формулам Литтла.
Слайд 75Системы массового обслуживания
Одноканальная СМО с ограниченной очередью
…..
Lоб=1-p0 – среднее число заявок под обслуживанием
Lcист= Lоч+Lоб
Слайд 77Системы массового обслуживания
Пример: В условиях задачи про причал и разгрузку
судов найти показатели эффективности работы причала, если известно, что приходящее
судно покидает причал (без разгрузки), если в очереди на разгрузку стоит более 3 судов.Слайд 78Системы массового обслуживания
Решение: По условию m=3 ρ=0.8
- вероятность того, что причал свободен
вероятность того, что судно покинет
причал без разгрузки
Слайд 79Раздел I. «Теория массового обслуживания» (продолжение)
Тема «Законы распределения случайных величин
при имитации процессов»
Лекция №7
Слайд 80Законы распределения случайных величин
Нормальное распределение (гауссово)
Является одним из наиболее важных
и часто используемых видов непрерывных распределений.
Определение: Непрерывная случайная величина t
имеет нормальное распределение с параметрами m и σ, если плотность распределения вероятности p(t) имеет вид:где m – математическое ожидание;
σ – среднее квадратическое отклонение.
Слайд 81Законы распределения случайных величин
Теорема (Одна из форм центральной предельной теоремы):
Пусть - случайная величина, явля-ющаяся
суммой n независимых случайных величин, распределенных по неизвестному закону и имеющих конечный третий абсолютный момент. Тогда при n→∞ распределение случайной величины стремится к нормальному с математическим ожиданием M(t) и дисперсией D(t), определяемыми из следующих соотношений:где mi – математическое ожидание, - дисперсия случайной величины ti.
Слайд 82Законы распределения случайных величин
Для приближенной оценки среднего квадратического отклонения σ
можно использовать правило «трех сигм», согласно которому отклонение по абсолютной
величине нормально распределенной случайной величины от ее математического ожидания практически не превышает утроенного среднего квадратического отклонения (с вероятностью 0,9973). Таким образом, если в результате наблюдений над случайной величиной получены a - ее минимальное значение и b - максимальное значение, то можно полагать, что .Слайд 83Законы распределения случайных величин
Равномерное распределение
Применяется в случае, когда известно, что
случайная величина может принять значение в определенных границах с одинаковой
вероятностью.Плотность вероятностей равномерного распределения на интервале (m-s,m+s) имеет следующий вид:
Дисперсия
m-математическое
ожидание
Слайд 84Законы распределения случайных величин
Экспоненциальное распределение
Также занимает важное место при
проведении системного анализа экономической деятельности. Этому закону подчиняются многие явления,
например, срок безотказной работы различных технических устройств, частота поступлений заказов на предприятие, посещение покупателями магазина-супермаркета и др.Функция плотности вероятностей экспоненциального распределения с параметром λ задается выражением:
Слайд 85Законы распределения случайных величин
Для экспоненциального распределения математическое ожидание
и дисперсия .
Таким образом, характерно, что среднее квадратическое отклонение численно равно математическому ожиданию.Рассмотрим предельную теорему о суперпозиции потоков. Предположим, что наблюдается k независимых потоков событий. В свою очередь в каждом потоке наблюдается элементарных событий. Интерва-лы времени между событиями – независимые случайные величины, распределенные по неизвестному закону с математическим ожиданием .
Слайд 86Законы распределения случайных величин
Спроектируем моменты всех событий на общую ось
времени и рассмотрим случайный интервал времени t=T{k} между двумя событиями
полученного суммарного потока, состоящего из n событий, гдеТеорема: При n→∞ распределение случайной величины интервала t=T{k} в суммарном потоке событий, состоящем из k независимых потоков, стремится к экспоненциальному с математическим ожиданием
Слайд 87Законы распределения случайных величин
Обобщенное распределение Эрланга
Используется в случаях, когда
длительность какого-либо процесса можно представить как сумму k элементарных последовательных
составляющих, распределенных по экспоненциальному закону.Пусть математическое ожидание длительно-сти всего процесса при средней длительности элементарной составляющей ,тогда
При k=1 получаем
экспоненциальное
распределение
Слайд 88Законы распределения случайных величин
Треугольное распределение
Линейное изменение функции плотности вероятностей. Пусть
a - минимальное, b - максимальное и m-наиболее вероятное значение
случайной величины. ТогдаПри получаем
экспоненциальное
распределение
Слайд 89Раздел II. «Инструментальные средства имитационного моделирования»
Тема «Введение в имитационное моделирование»
Лекция
№8
Слайд 90Введение в имитационное моделирование
Определение: Имитационное моделирование (simulation modelling) - разновидность
аналогового моделирования, реализуемого с помощью набора математических инструментальных средств, специальных
имитирующих компьютерных программ и технологий программирования, позволяющих посредством процессов-аналогов провести целенаправленное исследование структуры и функций реального сложного процесса в памяти компьютера в режиме «имитации», выполнить оптимизацию некоторых его параметров.Определение: Имитационная модель – специальный программный комплекс, позволяющий имитировать деятельность какого-либо сложного объекта.
Слайд 91Введение в имитационное моделирование
Примеры типовых задач, решаемых средствами имитационного моделирования
при управлении экономическими объектами:
моделирование процессов логистики для определения временных и
стоимостных параметров;управление инвестиционными проектами на различных этапах его жизненного цикла с учетом возможных рисков;
прогнозирование финансовой деятельности предприятий на конкретный период времени;
анализ адаптивных свойств, расчет параметров надежности и задержек обработки информации в банковских информационных системах;
Слайд 92Введение в имитационное моделирование
оценка параметров надежности и задержек в централизованных
информационных системах с коллективным доступом (кассы продаж ж/д и авиабилетов,
системы бронирования и т.д.;анализ эксплуатационных параметров корпоративных информационных систем предприятий, пропускной способности информационных каналов и узлов обработки информации;
моделирование действий курьерской службы в регионе;
анализ пропускной способности обслуживания населения (торговые комплексы, комбинаты бытового обслуживания, государственные структуры и т.д.).
Слайд 93Введение в имитационное моделирование
Современные программные комплексы имитационного моделирования:
«Process Charter»
(разработчик - фирма «Scitor», США);
«Powersim» (фирма «Modell Data», Норвегия);
«Ithink» (фирма «High Performance Systems», США);«Extend+BPR» (фирма «Imagine That!», США);
«ReThink» (фирма «Gensym», США);
«Pilgrim» (разработчики системы – Московский институт статистики и информатики; фирма «МегаТрон», Россия; фирма «Keisy», Нидерланды; фирма «Enit», Эстония).
Слайд 94Введение в имитационное моделирование
Достоинства программного пакета «Pilgrim-5»
ориентация на совместное
моделирование материальных, информационных и финансовых процессов;
наличие развитой CASE-оболочки, позволяющей
конструировать многоуровневые модели;возможность непосредственного анализа результатов моделирования благодаря технологии создания функциональных окон наблюдения за моделью с помощью Visual C++, Delphy или других средств;
возможность управления моделями непосредственно в процессе их выполнения с помощью специальных диалоговых окон.
Слайд 95Введение в имитационное моделирование
Средством построения моделей в системе PILGRIM является
графический конструктор «Gem» (от «Generator models»).
Схема имитационной модели - ориентированный
граф, вершины которого представляют собой компоненты элементарных процессов, а дуги определяют направление потоков заявок и управляющих воздействий в моделируемой системе.Конструктор Gem генерирует программу на языке С++, которая в дальнейшем должна быть скомпилирована в составе проекта в среде MS Developer Studio, где предварительно должен быть установлен Visual C++ с библиотеками Pilgrim.
Слайд 96Введение в имитационное моделирование
Этапы построения имитационной модели
Анализ структуры моделируемого
процесса;
Определение входных и выходных параметров модели;
Построение графа модели
с помощью конструктора GEM (либо прямое создание программного файла);Описание узлов графа (определение значений параметров узлов модели).
Определение условий выбора узла, если в модели имеются ветвления;
Компиляция модели.
Слайд 97Введение в имитационное моделирование
Транзакты
Основной динамической единицей любой модели, работающей
под управлением имитатора, является транзакт.
Определение: Транзакт - это формальный запрос
на какое-либо обслуживание. Имеют набор динамически изменяющихся особых свойств и параметров. Пути миграции транзактов по графу модели определяются логикой функционирования компонентов модели в узлах сети.
Слайд 98Введение в имитационное моделирование
Транзакт может выполнять следующие действия:
порождать группы (семейства)
других транзактов;
поглощать другие транзакты конкретного семейства;
захватывать ресурсы, использовать их на
некоторое время и затем освобождать;определять время обслуживания, накапливать информацию о пройденном пути и иметь информацию о своем дальнейшем маршруте.
Слайд 99Введение в имитационное моделирование
Основные параметры транзактов:
уникальный идентификатор транзакта;
идентификатор семейства, к
которому принадлежит транзакт
наборы различных ресурсов, захватываемые и используемые транзактом;
время жизни
транзакта;приоритет транзакта;
параметры обслуживания транзакта в узлах, включая вероятностные характеристики.
Слайд 100Введение в имитационное моделирование
Примеры транзактов:
требование на перечисление денежных средств;
заказ на выполнение работы на предприятии;
телеграмма, поступающая на коммутатор
сообщений;покупатель в магазине;
проба загрязненной почвы, ожидающая химического анализа и др.
и другие…
Слайд 101Введение в имитационное моделирование
Узлы
Узлы графа имитационной модели – это
центры обслуживания транзактов. В узлах транзакты могут задерживаться, обслуживаться, порождать
семейства новых транзактов, уничтожать другие транзакты. Вид обслуживания транзакта определяется типом узла. Нумерация и присвоение имен узлам графа производится разработчиком модели.Примеры узлов:
счет бухгалтерского учета;
производственный или ремонтный участок;
транспортное средство, перемещающее ресурсы;
информационный центр и др.
Слайд 102Введение в имитационное моделирование
Определение: Событием называется факт выхода из узла
одного транзакта. Интервалы между событиями являются, как правило, случайными величинами.
События модели происходят в некотором модельном времени.Определение: Модельное время – это виртуальное время, в котором автоматически упорядочиваются все события, причем не обязательно пропорционально реальному времени, в котором развивается моделируемый процесс.
Определение: Масштаб времени – это число, которое задает длительность моделирования одной единицы модельного времени, пересчитанной в секунды, в секундах астрономического реального времени при выполнении модели.
Слайд 103Введение в имитационное моделирование
Определение: Относительный масштаб времени – это отношение,
показывающее, сколько единиц модельного времени содержится в одной единице процессорного
времени.Выделяют четыре разновидности масштаба времени:
1) Реальный. Вводится значение выбранной единицы измерения модельного времени, выраженное в секундах. Например, если 1 ед.мод.вр.=1 час, то вводится значение 3600. Относительный масштаб = 1.
2) Максимально ускоренный. Вводится значение 0. Время моделирования определяется процессорным временем выполнения модели. Позволяет достигнуть максимального быстродействия.
Слайд 104Введение в имитационное моделирование
3) Пропорционально ускоренный. Вводится значение, меньшее по
сравнению с выбранной единицей модельного времени, выраженной в секундах. Например,
если 1 ед.мод.вр.=1 час и введено значение 0.1, то 1 час реального процесса будет моделироваться за 0.1 секунды. При этом относительный масштаб = 1/36000.4) Замедленный. Вводится значение, большее по сравнению с выбранной единицей модельного времени, выраженной в секундах. Например, если 1 ед.мод.вр.=1 час и введено значение 7200, то модель будет выполняться в 2 раза медленнее реального процесса. При этом относительный масштаб = 2.
Слайд 105Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)
Тема «Структурирование имитационной модели»
Лекция
№9
Слайд 106Структура имитационной модели
Модель состоит из двух характерных частей: секции инициализации
и блока описания стохастической сети.
Слайд 107Структура имитационной модели
Вставляется
в секцию
Блок описания узлов
модели (стохастическая
многоуровневая
сеть)
Всегда
необходим
Слайд 108Структура имитационной модели
Макрооперация #include подключает моделирующую среду имитатора к
модели.
MODBEG (p1,p2,p3,p4,p5,p6,p7,p8,p9) - оператор перво-начальной настройки осуществляет первоначальную настройку
моделирующих программ и инициализацию в памяти ЭВМ графа модели.Аргументы этой функции имеют следующий смысл:
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – максимальный номер узла модели (int), причем 2≤p2≤mmax, где mmax – некоторое граничное значение, задаваемое при установке имитатора на ЭВМ (обычно mmax =1024);
Слайд 109Структура имитационной модели
p3 - модельное время, в течение которого необходимо
производить моделирование (float);
p4 - произвольное целое число, используемое для настройки
датчиков псевдослучайных величин ( long). В каждом узле есть свой независимый датчик. В качестве этого числа полезно использовать значение таймера ЭВМ, обращение к которому имеет следующий вид p4=(long)time(NULL). В этом случае результаты разных прогонов модели будут разными, имеющими случайные отклонения. При отладке лучше использовать постоянную комбинацию цифр, например, p4=(long)2013456789.Слайд 110Структура имитационной модели
p5 – признак режима пространственной имитации (int):
∙
earth – поверхность Земли (сферические географические координаты широта и долгота);
∙
plane – декартова плоскость (прямоугольная система координат);∙ cosmos – произвольное пространство (ответ-ственность за правильность его представления возлагается на разработчика модели)
∙ none – если пространственная имитация в моде-ли не используется.
Слайд 111Структура имитационной модели
p6 – номер (int) одной из очередей (узел
типа QUEUE, ATTACH или SEND), которую необходимо контролировать во времени
для анализа динамики задержек в этой очереди с графическим отображением результатов.p7 – номер (int) одного из процессов (узла типа PROC), который необходимо контролировать как в пространстве, так и во времени с графическим отображением результатов. Если нет необходимости в графической интерпретации, то указывается none.
Слайд 112Структура имитационной модели
p8 – номер (int) терминатора (узел типа TERM),
на входе которого необходимо наблюдать интенсивность потока транзактов во время
моделирования. Если такой необходимости нет, то указывается none.p9 – точность:
если p9=1..6, то имитатор будет использовать от 1 до 6 знаков после запятой при выводе результатов;
если p9=none, то результаты будут округляться до целых значений.
Слайд 113Структура имитационной модели
NETWORK (p1,p2) - координатор сети процессов. Осуществляет диспетчеризацию
транзактов в узлах модели, планирует события в едином модельном времени
и активизирует дискретные или непрерывные компоненты модели, имитирующие внешнюю среду.Аргументы p1 и p2 - это имена (адреса) соответствующих программных функций моделирования внешней среды, производящих интегрирование, решение разностных уравнений, вычисление по формулам и т.д.
Функции float p1(d) и float p2(d), если они необходимы, пишутся пользователем.
Если процессы p1(d) и p2(d) не моделируются, то в качестве p1 и p2 указывается слово dummy.
Слайд 114Структура имитационной модели
MODEND (p1,p2,p3,p4) - оператор завершения моделирования. Выполняется по
истечении времени моделирования, указанного в операторе MODBEG. Позволяет просмотреть на
экране монитора графические результаты и выводит итоговые результаты в файл-отчет.Аргументы функции следующие:
p1 – символическое имя файла-отчета (сhar);
p2 – номер первой страницы отчета (int);
p3 - число строк на каждой странице (int);
p4 - имеет два значения:
∙ page, если в файле-отчете необходимо проставить символ перевода страницы;
∙ none, если символ перевода страницы не ставится.
Слайд 115Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)
Тема «Функциональные узлы имитационной
модели »
Лекция №10
Слайд 116Функциональные узлы имитационной модели
Узлы имитационной модели характеризуются параметрами, задаваемыми пользователем
при написании моделирующей программы. Параметры узлов могут иметь как постоянное,
так и переменное значение.- узел AG - генератор транзактов
Узел AG представляет собой генератор транзактов с бесконечной емкостью. Предназначен для создания транзактов имитационной модели. Транзакты генерируются по одному через определенные поль-зователем промежутки времени.
Слайд 117Функциональные узлы имитационной модели
Аргументы функции AG (p1,p2,p3,p4,p5,p6,p7,p8):
p1 – символическое имя
узла: строка длиной до 14 символов (char);
p2 - номер
узла-генератора (int);p3 - приоритет (int), назначаемый каждому сгене-рированному транзакту, число в диапазоне 1- 32767; при отсутствии приоритета p3=none;
p4 – тип функции распределения интервала времени между двумя последовательно сгенерированными транзактами, имеющий значения:
1) norm – нормальное распределение;
2) unif – равномерное распределение;
Слайд 118Функциональные узлы имитационной модели
3) expo – экспоненциальное распределение;
4) erln –
обобщенное распределение Эрланга;
5) beta – треугольное распределение
6) none – если
интервал между транзактами является детерминированной величиной.p5 – величина, зависимая от типа функции распределения (float):
∙ математическое ожидание интервала времени (float) между двумя последовательно сгенерированными транзактами (p4 = norm, unif, expo);
∙ математическое ожидание одного слагаемого этого интервала (p4 = erln);
∙ минимальное значение интервала (p4= beta);
∙ постоянная величина этого интервала (p4 = none).
Слайд 119Функциональные узлы имитационной модели
p6 - величина, зависимая от типа функции
распределения (float):
среднеквадратичное отклонение (p4 = norm);
максимальное отклонение от среднего (p4
= unif);значение zero (p4 = expo, none);
число слагаемых, входящих в случайный интервал и распределенных по экспоненциальному закону (p4 = erln);
наиболее вероятное значение интервала времени между двумя последовательно сгенери-рованными транзактами (p4 = beta).
Слайд 120Функциональные узлы имитационной модели
p7 – величина, зависимая от типа функции
распределения (float):
максимальное значение интервала времени между двумя последовательно сгенерированными транзактами
(p4 = beta);значение zero (p4=norm, unif, expo, erln, none).
p8 - номер узла (int), в который передается сгенерированный транзакт (узел-приемник).
Параметры генератора могут быть изменены во время работы модели с помощью команды cheg (change generator).
Слайд 121Функциональные узлы имитационной модели
- Узел SERV – обслуживающий многоканаль-
ный прибор
Осуществляет какое-либо обслуживание транзактов в течение модельного времени, отличного от нуля. С точки зрения имитационной модели обслуживание заключается в задержке транзакта на заданный промежуток времени. Сервер - это одно- или многоканальный обслуживающий прибор, работающий по правилам абсолютных приоритетов или без них и имеющий стек для "прерванных" транзактов (правило относительных приоритетов реализуется в узле типа QUEUE - очередь).
Слайд 122Функциональные узлы имитационной модели
Аргументы функции SERV (p1,p2,p3,p4,p5,p6,p7,p8):
p1 – символическое имя
узла: строка длиной до 14 символов (char);
p2 - число
обслуживающих каналов (int), при этом ;p3 - дисциплина обслуживания:
∙ abs - приоритетная, с прерыванием обслуживания менее приоритетного транзакта более приоритетным;
∙ none – бесприоритетная.
Слайд 123Функциональные узлы имитационной модели
p4 – тип функции распределения интервала времени
обслуживания транзакта в узле SERV:
1) norm – нормальное распределение;
2) unif
– равномерное распределение;3) expo – экспоненциальное распределение;
4) erln – обобщенное распределение Эрланга;
5) beta – треугольное распределение
6) none – если интервал между транзактами является детерминированной величиной.
Слайд 124Функциональные узлы имитационной модели
p5 – величина, зависимая от типа функции
распределения (float):
∙ математическое ожидание интервала времени обслуживания транзакта (p4 =
norm, unif, expo);∙ математическое ожидание одного слагаемого этого интервала (p4 = erln);
∙ минимальное значение интервала (p4= beta);
∙ постоянная величина этого интервала (p4 = none).
Слайд 125Функциональные узлы имитационной модели
p7 – величина, зависимая от типа функции
распределения (float):
∙ максимальное значение интервала времени обслу-живания транзакта (p4 =
beta);∙ значение zero (p4=norm, unif, expo, erln, none).
p8 - номер узла (int), в который передается обслуженный транзакт.
Если задана приоритетная дисциплина обслуживания (p3 = abs), то имеются две возможности для работы с прерванными неприоритетными транзактами:
1) дообслуживание после ухода приоритетного транзакта;
2) возобновление обслуживания заново.
Слайд 126Функциональные узлы имитационной модели
- Узел QUEUE - очередь
транзактов (с
приоритетами или без приоритетов) Узел QUEUE моделирует очередь транзактов. Строится по одному из двух правил: либо транзакты упорядочены в порядке поступления, либо вновь поступающие транзакты поступают в конец своей приоритетной группы.
Аргументы функции QUEUE (p1,p2,p3):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 - тип организации очереди (int):
prty, если очередь с приоритетами;
none, если очередь без приоритетов.
p3 – номер узла-приемника (int).
Слайд 127Функциональные узлы имитационной модели
Узел TERM - безусловный терминатор
транзактовУзел TERM удаляет из модели входящий в него транзакт и фиксирует время его существования, начиная с момента выхода этого транзакта из генератора.
Аргумент функции TERM (p1):
p1 – символическое имя узла: строка длиной до 14 символов (char);
Слайд 128Функциональные узлы имитационной модели
Узел KEY - клапан на пути транзактов
Узел KEY - клапан или ключ - работает в модели по принципу “шлагбаума”. Когда клапан закрыт, транзакт не может в него войти из предшествующего узла. Если же клапан открыт, то транзакт проходит через него в следующий узел без задержки. Среднее время пребывания такого узла в закрытом состоянии подсчитывается автоматически. Для управления этим клапаном или ключом существуют вспомогательные функции hold и rels.
Слайд 129Функциональные узлы имитационной модели
Среднее время задержки - это среднее время
пребывания ключа в закрытом состоянии. Число обслуженных транзактов - это
число переключений ключа из закрытого состояния в открытое.Аргументы функции KEY (p1. p2):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – номер узла-приемника (int).
Слайд 130Функциональные узлы имитационной модели
Узел CREAT - управляемый генератор
транзактов (мультипликатор)
Узел CREAT предназначен для создания нового семейства транзактов. Все транзакты в модели принадлежат какому-то семейству. Транзакты, выходящие из обычного генератора AG, принадлежат к семейству с номером 0. Узел CREAT, в отличие от AG - это управляемый генератор. Назначение его самое различное. В замкнутых моделях он применяется для схемы зарядки.
Аргументы функции CREAT (p1,p2,p3,p4,p5,p6):
p1 – символическое имя узла: строка длиной до 14 символов (char);
Слайд 131Функциональные узлы имитационной модели
p2 – идентификатор (int) порождаемого семейства транзактов;
p3
– число порождаемых транзактов (int);
p4 – имеет следующие значения:
copy –
для тиражирования параметров порождающего транзакта каждому порожденному (включая время жизни);none - для присвоения каждому порожденному транзакту в качестве параметров нулевых значений.
p5 – номер узла (int), в который направляются порожденные транзакты.
p6 – номер узла (int), в который направляется порождающий транзакт.
Слайд 132Функциональные узлы имитационной модели
Логика функционирования узла CREAT:
1) через узел проходит
порождающий транзакт, который принадлежит семейству f1, и поступает в узел
p6;2) одновременно с этим в узле генерируются p3 новых транзактов, принадлежащих семейству с номером f2= p2, которые будут направлены в узел p5. В общем случае p5 и p6 - любые узлы (кроме ag), в частности - это может быть один и тот же узел. Номера семейств f1 и f2 в общем случае могут совпадать.
Слайд 133Функциональные узлы имитационной модели
Узел DELET – управляемый терминатор
транзактов (демультипликатор) Узел DELET предназначен для уничтожения группы транзактов, принадлежащих семействам из диапазона, задаваемому параметрами p2 и p3. В отличие от терминатора TERM данный узел управляется специальным поглощающим транзактом.
Аргументы функции DELET (p1,p2,p3,p4,p5,p6):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – начало (int) диапазона номеров семейств уничтожаемых транзактов;
Слайд 134Функциональные узлы имитационной модели
p3 – конец (int) диапазона номеров семейств
уничтожаемых транзактов;
p4 – идентификатор (int) семейства, к которому принадлежит поглощающий
транзакт;p5 – число уничтожаемых транзактов (int);
p6 – номер узла (int), в который направляется поглощающий транзакт.
Слайд 135Функциональные узлы имитационной модели
Логика функционирования узла DELET:
1) в узел
входит поглощающий транзакт семейства p4 и находится там до тех
пор, пока в него не поступят p5 транзактов семейства из диапазона [p2;p3]. После поступления требуемого количества транзактов они мгновенно уничтожаются, а поглощающий транзакт переходит в узел p6.2) если в узел DELET так и не поступят p5 транзактов, то поглощающий транзакт будет все время находиться в нем, блокируя его для поступления других поглощающих транзактов. Для принудительного изгнания такого транзакта из узла используется функция FREED(i).
Слайд 136Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)
Тема «Функциональные узлы имитационной
модели »
Лекция №11
Слайд 137Функциональные узлы имитационной модели
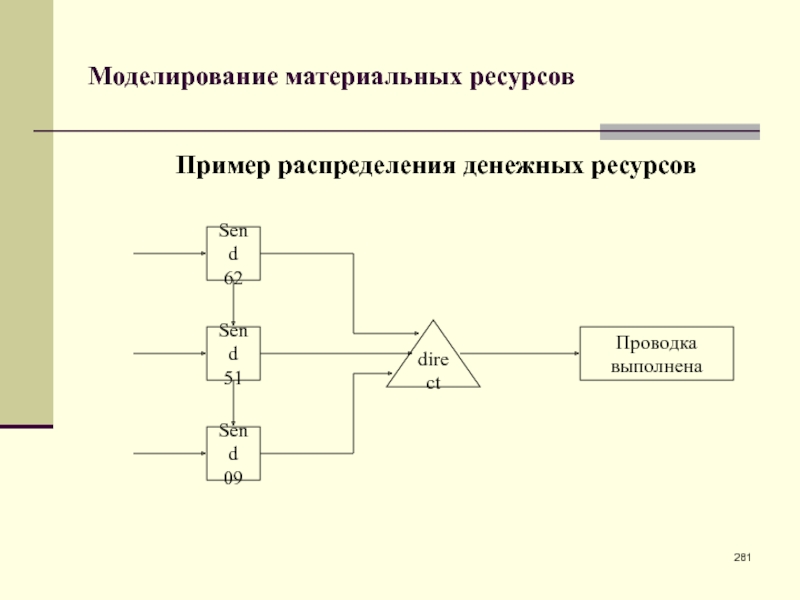
Узлы SEND и DIRECT - операции
с денежными ресурсами
Предназначены для моделирования финансовой динамики на счетах бухгалтерского учета предприятия (фирмы). Узлом считается счет (субсчет) бухгалтерского учета.
Пусть i - номер этого узла. Транзакт, вошедший в узел i, - это запрос на проводку со счета i определенной суммы на какой-то другой счет. При отсутствии требуемой суммы транзакт ожидает момент поступления на счет i достаточных средств. Таким образом, узел с номером i, который формирует запрос на бухгалтерскую проводку, - это специальная очередь транзактов.
Слайд 138Функциональные узлы имитационной модели
Для описания узла-счета с номером i предназначен
узел SEND (p1,p2,p3,p4,p5) с аргументами:
p1 – символическое имя узла: строка
длиной до 14 символов (char);p2 – узел-счет, на который требуется перевести заданную сумму (int).
p3 – размер заданной суммы (double). В обязательном порядке определяется до второго знака после запятой.
p4 – возможность работы с приоритетами:
∙ prty, если требования на перечисление денег удовлетворяются с учетом приоритетов. В случае отсутствия необходимой суммы на счете i транзакты образуют очередь в узле SEND, причем ближе к голове очереди находится более приоритетная группа транзактов.
Слайд 139Функциональные узлы имитационной модели
Внутри приоритетной группы транзакты расположены по возрастанию
требуемой суммы. Если запрашиваемые суммы одинаковы, то транзакты расположены в
хронологическом порядке (правило FIFO – «First In First Out»).∙ none, если требования на перечисление не имеют приоритетов. Тогда организация транзактов в очереди осуществляется по правилу FIFO.
p5 – номер узла типа DIRECT, играющего роль «финансового директора» и выполняющего проводки по мере необходимости.
Событием в узле типа SEND является факт выполнения проводки со счета i на счет p2. Момент времени этого события - это момент времени проводки, определяемый выводом транзакта из узла SEND.
Слайд 140Функциональные узлы имитационной модели
saldo - внутренний атрибут узла SEND, отражающий
остаток средств на счете i.
defic - дефицит средств на
счете i. Если атрибут saldo=0, и в этом узле имеются транзакты запросившие проводки, то суммарный дефицит затребованных этими транзактами сумм автоматически отражается в атрибуте defic.
Для управления узлом SEND используется функция ASSIGN (p1,p2,p3) со следующим параметрами:
p1 – номер узла-счета SEND (int);
p2 – признак:
add, если требуется добавить средства на счет в размере p3 ;
none, если требуется установить сальдо
Слайд 141Функциональные узлы имитационной модели
p3 – размер денежной суммы (double).
Узел DIRECT
является своеобразным клапаном, через который могут пройти только те транзакты,
проводки по которым можно выполнить. Обслуживание всех узлов SEND, имеющихся в модели может выполняться как одним, так и несколькими узлами типа DIRECT.Аргументы функции DIRECT (p1,p2):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – узел-приемник транзакта, выполнившего проводку Этот узел может быть любого типа, кроме DIRECT.
Слайд 142Функциональные узлы имитационной модели
Узлы ATTACH и MANAGE -
операции с материальными
ресурсами
Предназначены для моделирования динамики использования материальных ресурсов, необходимых для работы в моделируемых процессах. Под ресурсом могут пониматься любые объекты окружающего мира (сырье, оборудование, персонал и т.д.). Объем ресурса в модели измеряется в целых числах.
В модели все виды используемых процессами ресурсов хранятся в специальных узлах-«складах». Узел-«склад» имеет название ATTACH.
Man
Слайд 143Функциональные узлы имитационной модели
При посещении транзактом узла ATTACH ему выдается
некоторое количество единиц хранящегося там ресурса.
Узел ATTACH - очередь
запросов на получение ресурса. Аргументы функции ATTACH (p1,p2,p3,p4):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – требуемое количество элементов ресурса (long);
p3 – возможность работы с приоритетами:
∙ prty, если требования на ресурсы удовлетворяются с учетом приоритетов.
Слайд 144Функциональные узлы имитационной модели
В случае отсутствия необходимого объема ресурсов транзакты
образуют очередь в узле ATTACH, причем ближе к голове очереди
находится более приоритетная группа транзактов. Внутри приоритетной группы транзакты расположены по возрастанию требуемого объема ресурсов. Если требования одинаковы, то транзакты расположены в хронологическом порядке (правило FIFO – «First In First Out»).∙ none, если требования на перечисление не имеют приоритетов. Тогда организация транзактов в очереди осуществляется по правилу FIFO.
p4 – номер узла-приемника типа MANAGE. (int), выполняющего функцию «управляющего складом».
Слайд 145Функциональные узлы имитационной модели
Узел MANAGE проверяет наличие требуемого количества ресурса
для каждого транзакта, пришедшего в ATTACH. Если ресурса достаточно, транзакт
проходит через узел MANAGE и «путешествует» с захваченными единицами по графу модели. Если ресурсов недостаточно, транзакт остается в очереди в узле ATTACH. Таким образом, узел MANAGE - это своеобразный клапан.Узел MANAGE имеет параметры (p1,p2):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – узел-приемник транзакта. Таким узлом может быть любой узел модели, кроме MANAGE.
Слайд 146Функциональные узлы имитационной модели
Для изменения объема ресурса, имеющегося на складе
ATTACH используется функция SUPPLY (p1,p2,p3) с параметрами:
p1 – номер узла
ATTACH (int);p2 – признак:
add, если требуется добавить ресурс на склад в объеме p3 единиц;
none, если требуется заменить складской запас на объем p3 единиц;
p3 – количество единиц ресурса (long).
Слайд 147Функциональные узлы имитационной модели
Остаток ресурса и дефицит фиксируется в атрибутах
узла rsal и rdef. Дефицит равен суммарному объему запросов всех
стоящих в очереди в узле ATTACH транзактов.Полученный на складе ресурс транзакт может вернуть обратно на склад из любого узла модели с помощью команды DETACH (p1,p2), где
p1 – номер узла-склада ATTACH (int);
p2 – число возвращаемых единиц ресурса.
Слайд 148Функциональные узлы имитационной модели
Узел PROC – транзактно-управляемый
процесс Специальная функция моделирования транзактно-управляемого непрерывного процесса.
Объединяет в себе возможности имитации:
1) обслуживание в узле подобно SERV с одним каналом;
2) перемещение узла по общему полю данных на координатной сетке;
3) запуск на время активности функции типа float p2(d), где d - элементарный интервал активности, который определяется системой PILGRIM в процессе моделирования и зависит от параметров p3,p4,p5,p6.
Слайд 149Функциональные узлы имитационной модели
Интервал требуемого обслуживания транзакта может быть меньше
времени пребывания транзакта в этом узле, так как процесс может
быть переведен в состояние "пассивен" или "активен" каким-то транзактом из другого узла с помощью функций ACTIV и PASSIV.Если процесс пассивен, то обслуживание транзакта приостанавливается, а выполнение функции p2 прерывается до тех пор, пока процесс не будет переведен в активное состояние.
Аргументы функции PROC (p1,p2,p3,p4,p5,p6,p7,p8):
p1 – символическое имя узла: строка длиной до 14 символов (char);
Слайд 150Функциональные узлы имитационной модели
p2 - возможность подключения внешней программы:
∙ имя (адрес)
программы, написанной пользователем, и моделирующей процесс с помощью формул, дифференциальных
уравнений и т.д.;∙ dummy, если внешняя программа отсутствует.
p3 - номер исходной точки, в которую устанавливается узел PROC перед началом моделирования (int);
p4 - тип функции распределения интервала активности процесса, либо тип координатного пространства. Если это тип функции распределения, то используются условные обозначения:
Слайд 151Функциональные узлы имитационной модели
norm – нормальное распределение;
unif – равномерное
распределение;
expo – экспоненциальное распределение;
erln – обобщенное распределение Эрланга;
beta – треугольное распределение
none – если интервал является детерминированной величиной.
Обозначения для задания типа пространства:
earth – поверхность Земли (географические координаты широта и долгота);
plane – декартова плоскость (прямоугольная система координат);
cosmos – произвольное пространство;
none – если режим пространственной имитации в данном узле не нужен.
Слайд 152Функциональные узлы имитационной модели
p5 – величина (float), зависимая от параметра
p4, определяющего тип функции распределения интервала активности процесса, либо тип
координатного пространства:математическое ожидание интервала времени активности (p4 = norm, unif, expo);
математическое ожидание одного слагаемого этого интервала (p4 = erln);
минимальное значение интервала (p4= beta);
постоянная величина этого интервала (p4 = none);
интервал "непрерывного" нахождения этого узла на координатной сетке (p4= earth, plane, cosmos).
Слайд 153Функциональные узлы имитационной модели
p6 – параметр (float) интервала активности обслуживания,
зависимый от параметра p4:
среднеквадратичное отклонение времени обслуживания (p4 = norm);
максимальное
отклонение от среднего времени обслуживания (p4 = unif);значение zero (p4 = expo, none);
число слагаемых, входящих в случайный интервал и распределенных по экспоненциальному закону (p4 = erln);
наиболее вероятное значение интервала времени обслуживания транзакта (p4 = beta);
скорость перемещения узла от одной точки пространства к другой (p4= earth, plane, cosmos).
Слайд 154Функциональные узлы имитационной модели
p7 – величина (float), зависимая от параметра
p4:
значение zero (p4=norm, unif, expo, erln, none).
максимальное значение интервала времени
обслуживания транзакта (p4 = beta);p8 – номер узла-приемника (int).
Слайд 155Функциональные узлы имитационной модели
Узел DINAM -
очередь к процессу сдинамическими пространственно-
зависимыми приоритетами
Предназначен для моделирования обслуживания транзактов в очереди с динамическими пространственно-зависимыми приоритетами. Эта функция моделирует оптимально-управляемую очередь, которая находится на входе узла типа PROC.
Аргументы функции DYNAM (p1,p2):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 - номер узла-приемника, в который передается транзакт. Узел PROC обязательно должен использовать свой параметр p4= earth, plane или cosmos.
Слайд 156Функциональные узлы имитационной модели
Узел DYNAM - очередь транзактов, направляющихся на
обслуживание в узел PROC. Порядок обслуживания в этой очереди пересматривается
каждый раз при поступлении в хвост очереди нового транзакта и при переходе первого транзакта в узел PROC.Функция DYNAM всегда "заглядывает" в узел PROC и анализирует, не следует ли прервать обслуживание находящегося в нем транзакта. Если да, то вычисляется местонахождение текущей точки пространства, в которой находится узел PROC, извлекается из этого узла транзакт обратно в свою очередь и посылается в него более "выгодный" с точки зрения оптимизации транзакт.
Используется оригинальный алгоритм оптимизации динамического расписания, обладающий высоким быстродействием и имеющий практическое применение.
Слайд 157Функциональные узлы имитационной модели
Управление переходами в многослойных моделях
Декомпозиция в
имитационной модели – это детализация одного узла с помощью совокупности
других узлов.Существуют четыре вида декомпозиции процессов:
общий случай декомпозиции сложного процесса с помощью узлов типа DOWN;
декомпозиция процессов перечисления денежных средств с помощью узлов типа PAY;
декомпозиция процессов выделения ресурсов с помощью узлов типа RENT;
абстрактное объединение группы процессов в один псевдопроцесс с помощью виртуального узла PARENT без образования нового узла.
Слайд 158Функциональные узлы имитационной модели
Узел DOWN - переход на
нижерасположенный слой Предназначен для объединения большой группы узлов в один общий узел, который находится на одном из слоев модели. Этот узел подвергается декомпозиции на слоях модели, которые расположены ниже.
Аргументы функции DOWN (p1,p2,p3):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 - номер узла-приемника на нижнем слое модели (int);
p3 - номер узла возврата на данном слое, где расположен узел DOWN.
Слайд 159Функциональные узлы имитационной модели
Узел PAY -
имитация перечисленияденежной суммы
Подлежит детализации на более низком уровне с помощью узлов SEND и DIRECT.
Аргументы функции PAY (p1,p2,p3,p4,p5,p6,p7):
p1 – символическое имя узла (char);
p2 – номер узла-счета типа SEND, на который переводится денежная сумма (int);
p3 – значение денежной суммы (double);
p4 – номер узла-счета типа SEND, c которого переводится денежная сумма (int);
p5 – признак работы с приоритетами (prty или none);
p6 – номер узла-приемника на нижнем слое (int);
p7 – номер узла возврата на данном слое модели, где расположен узел PAY (int).
Слайд 160Функциональные узлы имитационной модели
Узел RENT
- имитация полученияресурса со склада
Подлежит декомпозиции на более низком уровне с помощью узлов ATTACH и MANAGE.
Аргументы функции RENT (p1,p2,p3,p4,p5,p6):
p1 – символическое имя узла: строка длиной до 14 символов (char);
p2 – требование на число элементов ресурса (long);
p3 – номер узла-склада ресурсов ATTACH, с которого необходимо получить ресурсы (int);
p4 – признак работы с приоритетами (prty или none);
p5 – номер узла-приемника на нижнем слое (int);
p6 – номер узла возврата на данном слое модели, где расположен узел RENT (int).
Слайд 161Функциональные узлы имитационной модели
Узел PARENT -
объединение группыпроцессов
Является особым типом узла, использующимся исключительно как средство создания наглядных многоуровневых моделей в графическом конструкторе GEM. Виртуальный узел типа PARENT содержит ссылку на плоскость, его детализирующую, т.е. используется для описания процессов, которые можно рассмотреть не отдельной плоскости. При этом он не выполняет никаких действий по обработке транзакта. При генерации программного кода заменяется своей декомпозицией.
Слайд 162Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)
Тема «Сигнальные управляющие функции.
Параметры транзактов и узлов»
Лекция №12
Слайд 163Сигнальные управляющие функции
Сигнальные управляющие функции
Могут использоваться в любом узле (кроме узла-генератора
AG), где необходима специальная логика или должны использоваться функциональные уточнения особенностей узла. Описание функций
INTERRUPT () – выполнить прерывание модели. После выполнения этой функции в каком-либо узле работа модели прекращается, а экспериментатор может исследовать полученные результаты.
Слайд 164Сигнальные управляющие функции
CHEG (p2,p3,p4,p5,p6,p7,p8) – перенастроить генератор транзактов AG(p1,p2,p3,p4,p5,p6,p7,p8) на
новые значения параметров. Номер перенастраиваемого генератора содержится в параметре p2.
Аргументы p3…p8 содержат новые значения параметров и имеют тот же смысл, что и при настройке генератора AG.RELS (i) – открыть узел-клапан KEY с номером i. После выполнения RELS клапан принимает состояние «открыт», если до этого он был закрыт.
HOLD (i) – закрыть узел-клапан KEY с номером i. После выполнения HOLD клапан принимает состояние «закрыт», если до этого он был в открытом состоянии.
Слайд 165Сигнальные управляющие функции
ACTIV (i) – перевести процесс (узел типа PROC)
в активное состояние, если он был пассивен. При этом возобновляется
обслуживание транзакта (т.е. отсчет активного времени) и выполнение модели процесса (программы с именем p2). Функция ACTIV может выполняться из любого узла, номер которого не равен i.PASSIV (i) – перевести процесс (узел типа PROC) в пассивное состояние, если он был активен. При этом транзакт переводится в стек прерванных транзактов. Прекращается выполнение модели процесса (программы с именем p2). Функция PASSIV может выполняться из любого узла, номер которого не равен i.
Слайд 166Сигнальные управляющие функции
SUPPLY (p1,p2,p3) - изменить объем ресурса, имеющегося на
складе ATTACH, где
p1 – номер узла ATTACH;
p2 – признак: add, если требуется добавить ресурс на склад в объеме p3 единиц; none, если требуется заменить складской запас на объем p3 единиц; p3 – количество единиц ресурса.
DETACH (p1,p2) - вернуть ресурс обратно на склад, где
p1 – номер узла-склада ATTACH;
p2 – число возвращаемых единиц ресурса.
Слайд 167Сигнальные управляющие функции
ASSIGN (p1,p2,p3) – ассигновать на счет SEND денежные
средства, где
p1 – номер узла-счета SEND;
p2
– признак: add, если требуется добавить средства на счет в размере p3 ; none, если требуется установить сальдо счета в размере p3 единиц; p3 – размер денежной суммы.
CHANGE (p1,p2) – заменить узел обслуживания очереди. Если состав или количество транзактов в узле-очереди (узлы типа QUEUE, SEND, ATTACH) с номером p1 перестают удовлетворять каким-то требованиям, то с помощью данной функции можно перенаправить все транзакты из узла p1 в узел p2, разгрузив тем самым очередь в узле p1.
Слайд 168Сигнальные управляющие функции
FREED (i) – изгнать уничтожающий транзакт из узла
DELET. При непоступлении в узел DELET заданного количества уничтожаемых транзактов
(параметр p5), в данном узле все время находится поглощающий транзакт, блокируя тем самым узел DELET для поступления других поглощающих транзактов. При прохождении транзакта через функцию FREED (i) в каком-либо другом узле, с ее помощью генерируется вспомогательный транзакт, который направляется в узел DELET с номером i, выталкивает из этого узла застрявший поглощающий транзакт, приводит DELET в нормальное состояние и сам погибает. Застрявший транзакт направляется в узел p6 в соответствии с заданными параметрами узла DELET.Слайд 169Сигнальные управляющие функции
SEWT (x) – поместить текущий транзакт в точку
пространства с номером x. Функция приписывает транзакту координаты этой точки
путем занесения значения x в параметр транзакта t→tx.SEWK (x,i) – поместить узел с номером i в точку пространства с номером x. Функция приписывает узлу координаты этой точки путем занесения значения x в параметр узла k→kx.
Слайд 170Сигнальные управляющие функции
GEOWAY (latA, lonA, latB, lonB) – определить расстояние
между точками A и B по их географическим координатам, измеряемым
в радианах, причем latA, lonA – широта и долгота точки A, latB, lon B – широта и долгота точки B. Для определения расстояния функция использует основные формулы сферической тригонометрии. Радиусы Земли для разных широт вычисляются по эллипсоиду Красовского.DEKART (xA, yA, xB, yB) – определить расстояние между точками A и B на декартовой плоскости в прямоугольной системе координат. Расстояние вычисляется по формуле: .
Слайд 171Сигнальные управляющие функции
CLCODE – включить блок операторов языка C++. Позволяет
разработчику помещать в модель свои программные блоки. При этом нельзя
использовать операцию goto не только внутри одного узла, но и для перехода в другой узел. Для принудительного завершения моделирования вместо goto можно использовать только функцию interrupt.После узлового оператора можно записать блок любых операторов языка C++ в формате:
clcode
{
Группа операторов языка C++
}
Слайд 172Параметры транзактов
Параметры транзактов
Для повышения эффективности создаваемых моделей разработчику доступны
следующие параметры транзактов:
t→iu0, t→iu1, t→iu2, t→iu3 – произвольные целочисленные параметры,
которые могут использоваться для различных целей, например, для помечивания транзакта;t→ru0, t→ru1, t→ru2, t→ru3 – произвольные параметры, имеющие вид переменной с плавающей точкой;
Слайд 173Параметры транзактов
t→ga – признак обслуживания транзакта вновь, который устанавливается операцией
присваивания ему глобальной константы again. Если перед узлом SERV транзакт
пройдет через оператор присваивания t→ga= again, то он при прохождении через SERV получает признак обслуживания заново. После выхода из SERV этот признак теряется;t→pr – приоритет транзакта;
t→ft – номер семейства, к которому принадлежит транзакт;
t→tx – индекс точки пространства. Позволяет определить координаты lat и lon в массиве space.
Слайд 174Параметры состояния узлов
Параметры состояния узлов
Некоторые параметры узлов доступны разработчику
для анализа (но не для их изменения). Параметры содержатся в
системном массиве addr.Пусть n – номер узла в модели, тогда:
addr[n]→nc – число каналов в узле;
addr[n]→na – число транзактов, прошедших через узел на данный момент модельного времени;
addr[n]→tn – число транзактов, находящихся в узле в данный момент;
addr[n]→ts – среднее время обслуживания, подсчитанное на данный момент;
Слайд 175Параметры состояния узлов
addr[n]→op – признак состояния узла типа KEY. Целочисленная
переменная, принимающая значение true, если клапан открыт, или false, если
он закрыт.addr[n]→se – признак состояния узла типа DELET. Целочисленная переменная, принимающая значение nil, если в узле нет уничтожающего транзакта.
addr[n]→kx – индекс точки, в которой находится узел типа CREAT, DELET или PROC. Позволяет определить координаты lat и lon.
Параметры узлов можно наблюдать в процессе выполнения имитационной модели.
Слайд 176Датчики случайных величин
Датчики случайных величин
Часто в процессе моделирования возникает
необходимость получить случайную величину в формате float, распределенную по какому-либо
закону. В системе PILGRIM есть стандартные 32-разрядные датчики псевдослучайных величин. В каждом узле есть свой датчик, независимый от датчиков других узлов. Связь с этими датчиками осуществляется с помощью следующих функций:normal(m,s) - нормальный закон распределения;
expont(m) - экспоненциальный закон;
unifrm(m,r) - равномерный закон на отрезке [m-r,m+r];
rundum() - равномерный закон на отрезке [0,1];
Слайд 177Датчики случайных величин
erlang(e,z) - обобщенный закон Эрланга;
triplex(a,b,c) – треугольный закон
распределения, где
m- математическое ожидание (в случаях normal, expont, unifrm);
s - cpeднeквадратичное
отклонение (в случае normal);e - математическое ожидание величины одного элемента (в случае erlang);
r - мaкcимальное oтклoнeниe (в случае unifrm);
z - количество отрезков (в случае erlang), z > 0;
a - минимальное значение (в случае triplex);
b - наиболее вероятное значение (в случае triplex);
с - максимальное значение (в случае triplex).
Слайд 178Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)
Тема «Создание моделей с
помощью графического конструктора GEM»
Лекция №13
Слайд 179Создание моделей с помощью графического конструктора GEM
Конструктор моделей GEM («Generator
Models») позволяет:
автоматизировать процесс создания графа модели;
автоматически генерировать программный код на
языке C++ предупреждает разработчика о возможных ошибках и не позволяет выполнять заведомо неверные действия.
Тем самым снимается ряд проблем, возникающих при ручном кодировании модели в виде программного файла.
Слайд 180Создание моделей с помощью графического конструктора GEM
Основное окно конструктора GEM
с пустой областью построения графа (при запуске файла gem.exe)
Слайд 181Создание моделей с помощью графического конструктора GEM
Рабочая область пуста, для
редактирования необходимо создать либо новую модель, либо загрузить ранее сохраненную.
Всю информацию о модели конструктор сохраняет в файле с расширением «pgf» (Pilgrim graf file). При создании законченной версии модели, разработчик может сгенерировать соответствующий модели программный файл с расширением «cpp», который подлежит дальнейшей компиляции в среде Visual C++ с подключением необходимых библиотек и ресурсов Pilgrim.
Слайд 182Создание моделей с помощью графического конструктора GEM
Редактирование графа модели
Выделим
типовые действия редактирования графа модели:
− добавление новых узлов;
− перемещение узлов в области
построения;− удаление существующих узлов;
− определение маршрутов переходов транзактов, или ссылок.
В конструкторе все перечисленные действия выполняются «перетягиванием» объекта, обозначающего тип требуемого узла или действия, из панели инструментов в область построения графа. Панель инструментов в левой части окна редактора содержит значки, обозначающие узлы системы.
Слайд 183Создание моделей с помощью графического конструктора GEM
Редактирование графа модели
Для
удаления узла в панели инструментов необходимо захватить значок удаления узла
и пере-тащить его на узел, который требуется удалить. Узел будет удален вместе со всеми входящими и исходящими ссылками.Для создания ссылок или путей переходов транзактов необходимо в панели инструментов захватить значок ⊕ и переместить на узел-источник транзакта. При отпускании кнопки мыши за курсором потянется стрелка, обозначающая ссылку с невыбранным узлом-приемником транзакта. Для выбора узла-приемника необходимо щелкнуть по нему мышью, в результате чего создастся новая ссылка.
Χ
Слайд 184Создание моделей с помощью графического конструктора GEM
Созданные ссылки отображаются на
экране в виде дуг, имеющих три звена, служащих для удобства
отображения графа на плоскости. Две промежуточные точки между звеньями выделены небольшими кругами, захватывая и перемещая которые можно придать стрелке нужную форму.Следует помнить, что некоторые типы узлов не могут иметь входящие или, напротив, исходящие ссылки. Конструктором GEM постоянно выполняется проверка корректности действий пользователя, запрещающая заведомо недопустимые преобразования графа модели, в частности создание неправильных ссылок.
Слайд 185Создание моделей с помощью графического конструктора GEM
Определение параметров узла
Каждый узел
модели характеризуется множеством параметров:
типом,
порядковым номером,
именем,
принадлежностью к
плоскости, ссылками,
условиями переходов,
встроенным программным текстом,
параметрами, определяемыми спецификой типа узла, такими, как закон распределения для узла типа SERV, приоритет для QUEUE и т.п.
Слайд 186Создание моделей с помощью графического конструктора GEM
Для просмотра или редактирования
параметров узла необходимо дважды щелкнуть по нему левой кнопкой мыши
либо один раз щелкнуть по узлу правой кнопкой, в результате чего отобразится всплывающее меню, и выбрать в нем пункт «параметры узла». Появится диалоговое окно, определяющее параметры.Номер узла присваивается конструктором при его создании. Обычно первые 100 номеров зарезервированы для узлов SEND - бухгалтерских счетов. Нумерация создаваемых узлов осуществляется последовательно, с номера 101. Смена номера узла возможна с помощью соседнего с номером диалогового поля, но не рекомендуется для узлов, созданных ранее.
Слайд 188Создание моделей с помощью графического конструктора GEM
Поле «Имя» содержит имя
узла, отображаемое на схеме и при выполнении модели. Поле доступно
для редактирования. Не рекомендуется использовать имена, не умещающиеся в поле редактирования.Поле «Класс узла» может быть выбран из списка. В списке приводятся только те типы узлов, которые имеют одинаковое обозначение. Например, узел типа SEND можно сменить на ATTACH (при этом изменяется набор и смысл параметров узла).
Поле «Плоскость» показывает, к какой плоскости принадлежит узел, и доступно только для просмотра.
Слайд 189Создание моделей с помощью графического конструктора GEM
Панель «Общий С++ текст»
позволяет пользователю включить в процедуру обработки узла произвольный текст на
языке С++. Текст делится на две части: одна выполняется до вызова функции узла, другая - после нее. Смысл такого разбиения заключается в том, что программный текст, выполняющийся до вызова функции узла, может подготавливать какие-либо переменные, которые функцией будут использованы. Так, например, может быть подсчитано время обслуживания транзакта перед выполнением функции узла типа SERV. Программный текст, следующий после вызова функции узла, на ее выполнение уже никак не влияет и может использоваться для обработки параметров выполненной функции или подготовки параметров для других функций модели.Слайд 190Создание моделей с помощью графического конструктора GEM
Узел может содержать несколько
исходящих ссылок, по которым способен переместиться транзакт. Выбор маршрута должен
осуществляться по условиям. Поэтому в правой нижней части окна определения параметров транзакта имеется поле «Условие перехода», определяющее эти условия, а также выполнение соответствующих им индивидуальных фрагментов программного кода. Выбор исходящей ссылки осуществляется щелчком мыши в диалоговом поле «Выходы». Любой вход и выход можно удалить, нажав кнопку внизу списка.Слайд 191Создание моделей с помощью графического конструктора GEM
Необходимым компонентом является кнопка
«Определить параметры», нажатие на которую вызывает окно определения параметров самой
функции обработки узла.Слайд 192Создание моделей с помощью графического конструктора GEM
Определение параметров инициализации и
завершения модели
Модель имеет параметры инициализации и завершения, задаваемые функциями
MODBEG и MODEND. Определение этих параметров производится через диалоговые окна, вызываемые нажатием кнопок «Modbeg» и «Modend» в основном окне редактора, либо выбором подпунктов основного меню в разделе «Модель».Слайд 194Создание моделей с помощью графического конструктора GEM
В правой верхней части
окна записывается начальный текст на С++, если он необходим. Программный
текст делится на две части: начальный С++ текст используется для подключения внешних библиотек и настройки глобальных параметров; текст инициализации ресурсов подготавливает параметры конкретных узлов типов ATTACH и SEND. Другие поля окна позволяют редактировать переменные, стандартные для функции MODBEG.Слайд 195Создание моделей с помощью графического конструктора GEM
Редактирование переменных функции MODEND
осуществляется через диалоговое окно:
Слайд 196Создание моделей с помощью графического конструктора GEM
Работа в плоскостях модели
При работе с большой моделью удобно пользоваться набором плоскостей построения.
Для этого конструктор предлагает набор плоскостей с номерами 1 - 9, фрагменты графов которых не пересекаются на уровне маршрутов транзактов. В каждой из плоскостей могут находиться узлы типа PARENT, РАY, RENT, или DOWN, в свою очередь порождающие новые плоскости. Порождаемые плоскости имеют номера, начинающиеся с 10.Слайд 197Создание моделей с помощью графического конструктора GEM
Возможны следующие операции перехода
с уровня на уровень:
переход на детализирующую плоскость,
подъем на
плоскость узла-родителяпереключение между корневыми плоскостями.
Для каждой открытой плоскости конструктор предоставляет собственное окно построения.
Переключение между корневыми плоскостями осуществляется через верхнюю панель управления. В правой части панели расположено специальное выпадающее меню, позволяющее выбирать номер корневой плоскости. При этом в информационной строке появится надпись «Корень» и номер плоскости.
Слайд 198Создание моделей с помощью графического конструктора GEM
Для перехода на плоскость,
детализирующую узел, необходимо дважды щелкнуть мышью по узлу-родителю. При этом
в рабочей области экрана будет активизирована детализирующая плоскость, в информационной строке на панели «имя плоскости» появятся имя узла-родителя, а также номер текущей плоскости. Для плоскости необходимо задать вход и выход, как номера узлов, в которые попадает транзакт при переходе на плоскость из порождающего узла и из которого происходит возврат на верхнюю плоскость.Слайд 199Создание моделей с помощью графического конструктора GEM
Чтобы назначить вход и
выход, необходимо на левой панели нажать кнопку «Слой». При этом
будет выведено диалоговое окно:Слайд 200Создание моделей с помощью графического конструктора GEM
Для удобства навигации в
многослойной модели предусмотрено диалоговое окно, отображающее иерархическую зависимость между плоскостями:
или узлами модели:Слайд 201Создание моделей с помощью графического конструктора GEM
Определение переменных модели
Блоком
диалога позволяет задавать имя, тип и начальное значение переменных.
При вводе
новой переменной обязательными параметрами являются имя и тип, значение пользователь может указывать по своему усмотрению. Слайд 202Создание моделей с помощью графического конструктора GEM
Дополнительные функции
Изменение настроек
экрана
Изменение настроек экрана выполняется через диалоговое окно (основное меню, пункт
«Настройки»): Слайд 203Создание моделей с помощью графического конструктора GEM
Пользователь-разработчик модели может по
своему усмотрению изменять масштаб, цвет фигур и фона, показать или
скрыть панель инструментов и установить признак прямых стрелок.Если признак прямых стрелок выключен, то при перемещении узла внутри плоскости промежуточные звеньевые точки стрелок, привязанных к нему, будут оставаться на месте, а при включенном признаке стрелки будут постоянно иметь прямой вид.
Слайд 204Создание моделей с помощью графического конструктора GEM
Проверка корректности модели
Конструктор
проводит проверку двумя независимыми способами:
не позволяет осуществлять заведомо ложные действия
при редактировании пользователем модели;имеет возможность проверки графа в целом.
Результат проверки графа выдается в окне, как список ошибок возможных и ошибок явных, не позволяющих генерировать программный Рilgrim-файл. К явным ошибкам относятся отсутствие выходов или входов узла и неопределенные вход/выход плоскости.
Слайд 205Создание моделей с помощью графического конструктора GEM
Процедура проверки корректности графа
вызывается автоматически при запросе пользователя сгенерировать программный Рilgrim-файл, а также
в любой момент времени из пункта «Выполнить» основного меню.Слайд 206Создание моделей с помощью графического конструктора GEM
План бухгалтерских счетов
При
моделировании бухгалтерских проводок необходимо знать номер счета-приемника. Поскольку номер любого
счета - это номер узла, его моделирующего, то для того, чтобы проще ориентироваться в их нумерации, существует информационное окно, отображающее номера и названия счетов. Это окно может быть вызвано выбором подпункта «План счетов» пункта «Модель» основного меню программы.Слайд 207Создание моделей с помощью графического конструктора GEM
Поиск узла
Функция вызывается
через меню «Узел» либо через «горячую кнопку» на верхней панели.
Поиск может осуществляться по номеру или по параметрам узла, таким, как имя или тип.Результаты поиска выводятся в виде списка, откуда можно перейти на любой узел, редактировать его параметры или скопировать узел в буфер.
Слайд 209Создание моделей с помощью графического конструктора GEM
Копирование/вставка узла
Для упрощения
создания набора узлов с рядом совпадающих параметров в конструкторе предусмотрена
функция копирования/вставки узла. Чтобы скопировать узел в буфер, необходимо выделить его щелчком мыши и выбрать пункт «Копировать» из меню «Узел». Вставка в текущую плоскость осуществляется выбором пункта «Вставить» меню «Узел». При этом будет создан узел того же типа, что и прототип, с аналогичными параметрами.Слайд 210Создание моделей с помощью графического конструктора GEM
Очистить плоскость
Функция удаляет все
узлы текущей плоскости. Вызывается через меню «плоскость». Операция недопустима и
выдаст сообщение об ошибке в случае, если хотя бы один из узлов плоскости содержит декомпозицию.Слайд 211Раздел II. «Инструментальные средства имитационного моделирования» (продолжение)
Тема «Обработка имитационной модели
в системе Pilgrim »
Лекция №14
Слайд 212Обработка имитационной модели в системе Pilgrim
Формирование программного файла модели
Рассмотрим процесс запуска модели на примере построенной модели PRODUCT:
1. Запустить
приложение Microsoft Visual C++.2. В меню файл выбрать New, далее вкладку Projects и Win32 Application.
В строке Project name указать название проекта (например, «Production»), а в строке Location указать путь к проекту, например, C:\Pilgrim-5-60\Pilgrim5\Samples. Нажать OK.
Слайд 213Обработка имитационной модели в системе Pilgrim
После появления окна с запросом
«Какой вид приложения вы хотите создать?» выбрать An empty project.
Нажать Finish и еще раз OK. Таким образом, создана рабочая область Production.dsw для проекта.3. Скопировать из папки C:\Pilgrim-5-60\Pilgrim5\Projects в папку C:\Pilgrim-5-60\Pilgrim5\Samples\Production следующие четыре файла: Palette.bmp, Pilgrim.ico, UserHid.h, UserRes.rc.
4. В меню выбрать Project -> Add To Project ->Files и добавить в проект эти четыре файла и файл Product.cpp, сгенерированный конструктором GEM. Таким же образом добавить файлы Comctl32.lib, Pilgrim.lib из папки C:\Visual Studio\VC98\Lib.
Слайд 214Обработка имитационной модели в системе Pilgrim
5. Выбрать в меню Build
->Build Production.exe. После этого, в случае отсутствия ошибок, в папке
C:\Pilgrim-5-60\Pilgrim5\Samples\ Production \Debug cформируется файл Production.exe.6. Запустить полученную модель Production.exe.
После запуска имитационной модели в папке C:\Pilgrim-5-60\Pilgrim5\Samples\ Production \Debug сформируется текстовый файл результатов с именем, указанным в тексте модели. В нашем примере это файл «Pilgrim.rep». Для просмотра файла результатов можно использовать любой текстовый редактор.
Слайд 215Обработка имитационной модели в системе Pilgrim
Трактовка результатов моделирования
Файл результатов представляет
собой таблицу, содержащую в зависимости от параметров модели до 12
столбцов:1) № узла. Указаны номера узлов модели;
2) Наименование узла. Смысловое название узла в модели, присвоенное разработчиком;
3) Тип узла. Указан тип узла: AG, SERV, KEY, QUEUE, TERM, CREAT, DELET, PROC, DYNAM, SEND, DIRECT, ATTACH, MANAGE, PAY, RENT, DOWN или PARENT;
Слайд 216Обработка имитационной модели в системе Pilgrim
4) Точка. Номер последней точки
пространства, в которой находится узел типа CREAT, DELET или PROC
в момент окончания моделирования;5) Загрузка (%=). Коэффициент использования транзактами узлов типа SERV или PROC в процентах. Для узла типа KEY – доля времени пребывания в закрытом состоянии;
6) Путь (км). Если производятся пространственные перемещения узлов типа PROC, CREAT или DELET, то подсчитывается пройденный путь. Для пространства типа GEO путь считается в километрах;
Слайд 217Обработка имитационной модели в системе Pilgrim
7) M [t] среднее время.
Среднее значение времени задержки транзакта в узле или иной интервал
времени, зависящий от типа узла:для SERV - это среднее время пребывания в узле (оно может быть больше времени обслуживания у неприоритетных транзактов при рз=аbs, т.е. при наличии приоритетных транзактов и правила абсолютных приоритетов);
для QUEUE - среднее время задержки в очереди;
для AG - среднее время между двумя сгенерированными транзактами;
Слайд 218Обработка имитационной модели в системе Pilgrim
для TERM или DELET -
среднее время существования транзакта;
для KEY - среднее время пребывания
в закрытом состоянии;для CREAT и DYNAM - всегда нулевое значение;
для PROC при p4=none, p4=поrm, p4=ехро или p4=unif - среднее время пребывания в узле (оно может быть больше времени обслуживания транзакта при переводе узла в пассивное состояние);
для PROC при p4=earth, p4=plane или p4=cosmos -суммарное время пребывания транзакта в узлах DYNAM и PROC с учетом возможных возвратов транзактов из PROC в DYNAM.
Слайд 219Обработка имитационной модели в системе Pilgrim
8) C2 [t] квадрат коэффициента вариации
– отношение дисперсии временного интервала к квадрату его среднего значения;
9) Счетчик входов и hold. Число транзактов:
прошедших через узел;
сгенерированных транзактов (для AG или CREAT);
уничтоженных (для TERM или DELET);
выполнивших операцию HOLD из другого узла в отношении узла KEY;
Слайд 220Обработка имитационной модели в системе Pilgrim
10) Количество каналов. Число каналов
в узле;
11) Осталось транзактов. Количество транзактов, которые остались в узле на
момент завершения моделирования;12) Состояние узла в этот момент. Состояние узла в момент окончания прогона модели:
узел может быть открыт (свободен), закрыт для входа очередного транзакта, активен или пассивен (узел PROC);
В узле типа SEND может быть положительное сальдо на момент завершения модели (денежная сумма с буквой S) и отрицательное сальдо (сумма с буквой D).
Слайд 221Обработка имитационной модели в системе Pilgrim
В узле типа ATTACH может
быть остаток ресурса на момент завершения модели (денежная сумма с
буквой S) и дефицит (сумма с буквой D).В узлах типа PAY и RENT указывается количество переходов транзактов на нижние уровни - слои модели (на момент завершения модели).
Слайд 222Обработка имитационной модели в системе Pilgrim
Трассировка модели
Существуют следующие режимы трассировки,
позволяющие ускорить процесс отладки:
выйти в режим трассировки после конкретного события;
перейти
в трассировку, если какой-то транзакт входит в определенный узел или выходит из него;отслеживать путь конкретного транзакта по сложному графу модели;
выйти в режим трассировки по показанию модельного таймера.
Управление трассировкой осуществляется из общего меню модельного окна.
Слайд 223Раздел III. «Имитационное моделирование экономических процессов»
Тема «Моделирование обслуживания с разными
приоритетами»
Лекция №15
Слайд 224Открытая модель обслуживания с разными приоритетами
Описание моделируемого процесса
В бухгалтерии
некоторой фирмы работает один бухгалтер. Он имеет персональный компьютер, на
котором установлен АРМ бухгалтера. Курьер приносит в бухгалтерию документы, которые бухгалтер обрабатывает на компьютере. Документы обрабатываются в порядке поступления в бухгалтерию. Обработанные документы подшиваются в специальную папку.В работе компьютера периодически возникают неполадки (неисправность в аппаратной части, сбой в программе, нарушение питания и т.п.).
Слайд 225Открытая модель обслуживания с разными приоритетами
В этом случае обработка документов
прекращается, и вызывают специалиста, который устраняет неисправность, после чего бухгалтер
продолжает свою работу. Считается, что устранение неполадки начинается мгновенно после ее возникновения. После устранения неполадка учитывается в специальном журнале. Курьер продолжает приносить документы и во время ремонта компьютера.Требуется построить модель, имитирующую обработку потоков документов и неполадок в работе компьютера.
Слайд 227Открытая модель обслуживания с разными приоритетами
Схема модели
AG
AG
Q
S
AG
AG
Документы
Неисправности
Компьютер
Журнал учета
неисправностей
Слайд 228Открытая модель обслуживания с разными приоритетами
Текст модели
#include
int Forw;
/* Номер следующего узла */
int Dist; /* Закон распределения
времени обслуживания */ float Tobs; /* Среднее время обслуживания */ float Pogr; /* Среднеквадратическое отклонение */
/* Время измеряется в часах */
forward
{
modbeg("Компьютер", 6, 1200.0, (long)time (NULL), none, 1, none, 3, 2); ag("Бухгалтерия", 5, none, norm, 0.1, 0.1/3, zero, 1);
ag("Неисправности", 6, 1, expo, 24.0, zero, zero, 1);
Слайд 229Открытая модель обслуживания с разными приоритетами
network(dummy, dummy)
{
top(1): queue("Столик-очередь",
prty, 2);
place;
top(2): if (t->pr == 1) /* Неполадка
*/ {
Forw=4; Dist=unif; Tobs=1.0; Pogr=0.5;
}
else /* Документ */
{
Forw=3; Dist=norm; Tobs=0.08; Pogr=0.08/3;
}
Слайд 230Открытая модель обслуживания с разными приоритетами
Serv ("АРМ бухгалтерии", 1, abs,
Dist, Tobs, Pogr, zero, Forw);
place;
top(3): term("Архивные папки");
place;
top(4): term("Неиспр. устр-на");
place;
fault(123);
}
modend("pilgrim.rep", 1, 12, page);
return 0;
Слайд 232Замкнутая модель обслуживания с клапаном
Замкнутая модель обслуживания с клапаном
В
небольшом поселке имеется магазин, где работает один продавец. Когда у
жителей поселка заканчиваются запасы продуктов, они приходят в магазин и после покупки возвращаются домой. Пенсионеры обслуживаются в магазине без очереди. Так как магазин небольшой, задано максимальное количество людей, которые могут выстроиться в очередь к продавцу. Если очередь достигла предела, дверь в магазин закрывается, и остальные покупатели выстраиваются в очередь перед магазином.Требуется построить модель, имитирующую поток покупателей в магазине.
Слайд 234Замкнутая модель обслуживания с клапаном
Схема модели
AG
AG
CR
T
S
Q
K
Q
S
1
2
3
4
5
6
7
8
9
Заселение
поселка
Схема
зарядки
Поселок
Продавец
Очередь
перед магазином
Входная
дверь
Очередь
перед продавцом
hold
rels
Слайд 235Замкнутая модель обслуживания с клапаном
Текст модели
#include
int Q_max=20; /* Максимальное
число людей в магазине/
float Mod_time=7*600.0; /* Время моделирования */
int N1=800;
/* Число обычных покупателей */int N2=200; /* Число пенсионеров */
int Ng; /* Номер генератора */
float T1=480.0; /* Время расхода продуктов у обычных покупателей */
float T2=240.0;/* Время расхода продуктов у пенсионеров*/
float T3=3.0; /* Время работы продавца */
Слайд 236Замкнутая модель обслуживания с клапаном
forward /* Время измеряется в
минутах */
{ modbeg("Магазин", 9, Mod_time, (long)time (NULL), none, 6, none,
4, 2); ag("Обычные люди", 1, none, none, 0.0, zero, zero, 3); ag("Пенсионеры", 2, 1, none, 0.0, zero, zero, 3); network(dummy, dummy)
{
top(3): if (t->pr == 0) /* генерация обычных покупателей */
{ t->iu0=N1;
t->ru0=T1;
}
Слайд 237Замкнутая модель обслуживания с клапаном
else /* генерация пенсионеров */
{
t->iu0=N2;
t->ru0=T2;
}
creat(" Заселение домов", none, t->iu0, copy, 5, 4); place;
top(4): if (t->pr = = 0) /* выключение генераторов */ Ng=1;
else Ng=2;
cheg (Ng, none, none, Mod_time, zero, zero, 3); term("Порождающие");
place;
Слайд 238Замкнутая модель обслуживания с клапаном
top(5): serv("Поселок", N1+N2, none, norm, t->ru0,
t->ru0/3, zero, 6);
place;
top(6): queue("Очередь перед магазином", prty, 7);
place;
top(7): key("Бабушка на входе", 9);
place;
top(8): queue("Очередь к продавцу", prty, 9);
clcode /* Если число покупателей в очереди */
if (addr[8]->tn == Q_max) /* достигло предела*/ hold(7); /* закрыть дверь */
place;
Слайд 239Замкнутая модель обслуживания с клапаном
top(9): serv("Продавец", 1, none, norm, T3,
T3/3, zero, 5);
clcode /* Покупатель покинул очередь */
rels(7);
/* открыть дверь для нового */ place;
fault(123);
}
modend("pilgrim.rep", 1, 12, page);
return 0;
Слайд 240Раздел III. «Имитационное моделирование экономических процессов» (продолжение)
Тема «Моделирование условного прерывания
обслуживания»
Лекция №16
Слайд 241Моделирование условного прерывания обслуживания
Пример использования узла delet: принцип «тележки»
Имеется остановка
маршрутного такси. С определенными интервалами времени на остановку приходят пассажиры
и подъезжают такси. Такси уезжает, когда в него сядет 10 пассажиров. Если пришедший пассажир не обнаруживает стоящего такси, он встает в очередь на посадку. Если такси подъехало на пустую остановку, оно ждет пассажиров. Если такси подъехало, а на остановке уже стоит такси, оно встает в очередь такси.Требуется построить модель, имитирующую пассажирский и транспортный потоки.
Слайд 243Моделирование условного прерывания обслуживания
Схема модели
AG
AG
T
Q
K
Q
6
7
3
1
8
3
5
2
4
Такси
Пассажиры
Такси уехало
K
DEL
hold
rels
hold
rels
Слайд 244Моделирование условного прерывания обслуживания
Текст модели
#include
float Pas=1.0; /* интервал прихода
пассажиров */
float Tax=10.0; /* интервал прихода такси */
float Mod_time=360.0;
forward
{ modbeg("Маршрутное такси", 5, Mod_time, (long)time(NULL), none, 2, none, 5, 2);
ag("Пассажиры", 1, none, expo, Pas, zero, zero, 2);
ag("Такси", 6, none, norm, Tax, Tax/3, zero, 2);
network(dummy, dummy)
{
top(2): queue("Пассажиры", none, 3);
Слайд 245Моделирование условного прерывания обслуживания
clcode
if (addr[2]->na == 1)
hold(3); /* начальное размыкание ключа */ place;
top(3): key("Есть такси?", 4);
place;
top(4): delet("Посадка в такси", 0, 10, 5); rels(3);
hold(8);
place;
top(5): term("Такси уехало");
hold(3);
rels(8);
place;
Слайд 246Моделирование условного прерывания обслуживания
top(7): queue("Такси", none, 4);
place;
top(8): key("Остановка свободна?", 4);
place;
fault(123);
}
modend("pilgrim.rep", 1, 12, page);
return 0;}
Слайд 247Моделирование клапана с таймером
Моделирование клапана с таймером
На платформу станции метро
приходят пассажиры. Если поезда нет, они ждут на перроне. Когда
поезд приходит, начинается посадка. Когда время посадки заканчивается, поезд уезжает. Рассматривается посадка в поезда только в одном направлении. Поездка пассажира в поезде не включается в моделируемый процесс.Требуется построить модель, имитирующую пассажирский поток и движение поездов.
Слайд 249Моделирование клапана с таймером
Схема модели
AG
AG
T
Q
5
6
1
7
3
2
4
Поезда
Пассажиры
Пассажир сел
в поезд
K
hold
rels
Перрон
Двери поезда
S
Поезд стоит
на перроне
T
Поезд ушел
Слайд 250Моделирование клапана с таймером
Текст модели
/* Модель работы станции метрополитена */
/* Единица измерения времени - 1 секунда */
/* Время
моделирования - 8 часов */ #include
#define T_PASS 15.0 /* Интервал прихода пассажиров */ #define T_POEZD 90.0 /* Интервал прихода поездов */ #define T_POEZD_STAND 30.0 /*Время стоянки поезда*
forward
{ modbeg("Станция метро", 7, 60.0*60*8,
(long)time(NULL), none, 2,none,4,2);
ag("Пассажиры",1,none,expo,T_PASS,zero,zero,2); ag("Поезда",5,none,none,T_POEZD,T_POEZD/3,
zero,6);
Слайд 251Моделирование клапана с таймером
network(dummy,dummy)
{ top(2): queue("Перрон",none,3);
clcode
if (addr[2]->na= =1)
hold(3);
place;
top(3): key("Двери поезда",4);
place;
top(4): term("Пассажир сел в поезд");
place;
top(6): serv("Поезд стоит",
1, none, none, T_POEZD_STAND, T_POEZD_STAND/3,
zero, 17);
rels(3);
place;
Слайд 252Моделирование клапана с таймером
top(7): term("Поезд ушел");
hold(3);
place;
fault(123);
}
modend ("Metro.rep",1,12,page);
return 0;
}
Слайд 253Управление маршрутом транзакта
Пример управления маршрутом транзакта
Имеется автобусный парк, который обслуживает
два маршрута. На каждом маршруте одновременно должно находиться определенное число
автобусов. Вначале диспетчер отправляет на оба маршрута необходимое число автобусов. После рейса автобус возвращается в парк. Когда на каком-либо маршруте автобусов становится меньше, чем нужно, диспетчер отправляет туда автобусы, оставшиеся в парке. Чтобы возвращающиеся из рейса автобусы имели передышку, в парке есть некоторое резервное количество автобусов.Требуется построить модель, имитирующую движение автобусов по маршруту и в парке.
Слайд 255Управление маршрутом транзакта
Схема модели
Схема зарядки
модели
3
2
S
Парк
Диспетчер
Q
S
S
4
Маршрут 1
Маршрут 2
Слайд 256Управление маршрутом транзакта
Текст модели
#include
float T1; /* Время рейса
по маршруту 1 */
float T2; /* Время рейса по
маршруту 2 */ float T3; /* Время обслуживания автобуса диспетчером */ int N1; /* Требуемое число автобусов на маршруте 1 */
int N2; /* Требуемое число автобусов нв маршруте 2 */
int N; /* Общее число автобусов в парке */
int Q; /* Число диспетчеров */
int Forw; /*Стандартное начало модели и схема зарядки */
...
Слайд 257Управление маршрутом транзакта
Текст модели
top(1): queue("Парк", prty, 2);
place;
top(2): if
addr[3]->tn < N1
Forw=3; /* на маршрут 1 */
else
if addr[4]->tn < N2 Forw=4; /* на маршрут 2 */
else /* оставить в парке */
{ t->pr=1; /* в начало очереди */
Forw=1; /* оставить в парке */
}
serv("Диспетчер", Q, none, norm, T3, T3/3,
zero,Forw);
place;
Слайд 258Управление маршрутом транзакта
top(3): t->pr=0; /* сброс приоритета */
serv ("Маршрут
1", N1, none, norm, T1, T1/3, zero, 1);
place;
top(4):
t->pr=0; serv("Маршрут 2", N2, none, norm, T2, T2/3, zero, 1);
place;
/* Стандартный конец модели */
...
Слайд 259Управление маршрутом транзакта
Текст модели
top(1): queue("Парк", prty, 2);
place;
top(2): if
addr[3]->tn < N1
Forw=3; /* на маршрут 1 */
else
if addr[4]->tn < N2 Forw=4; /* на маршрут 2 */
else /* оставить в парке */
{ t->pr=1; /* в начало очереди */
Forw=1; /* оставить в парке */
}
serv("Диспетчер", Q, none, norm, T3, T3/3,
zero,Forw);
place;
Слайд 260Раздел III. «Имитационное моделирование экономических процессов» (продолжение)
Тема «Моделирование информационных ресурсов»
Лекция
№17
Слайд 261Имитация информационных ресурсов
Информационные ресурсы – это необходимые сведения, оперативная информация,
временно предоставляемые права на что-либо, документация и иные нематериальные ценности,
без которых невозможно выполнение важной функции.Эти ресурсы подразделяются на две разновидности:
Стартовый информационный ресурс, без которого нельзя начинать выполнение функции;
Оперативный информационный ресурс, постоянно необходимый при выполнении функции.
Слайд 262Имитация информационных ресурсов
Схема получения информационного ресурса для выполнения основной функции
S
N
каналов – источников
получения информации
Q
S
Выполнение основной
функции
Q
K
CR
DEL
От других клиентов
Запрос на
выполнение основной функции
К другим клиентам
rels
hold
1
2
3
4
6
5
7
Слайд 263Имитация информационных ресурсов
Схема выполнения функции
основным транзактом при наличии доступа
к информации
S
Получение и прекращение
доступа к ресурсу
Q
Основной транзакт
Транзакт управления
доступом
к информацииpassiv
1
2
3
4
5
Q
Q
PR
Основная функция
транзактом выполнена
active
passiv
Слайд 264Моделирование замкнутых моделей КИС
Моделирование замкнутых моделей корпоративных информационных систем (КИС)
Замкнутая
модель КИС – это модель системы, работающей в режиме «запрос-ответ».
Транзакты, единожды сгенерированные, циркулируют в пределах графа модели.Транзакт – это запрос пользователя. Выйдя из генератора, транзакт проходит по графу модели, по мере работы КИС превращается в ответ и возвращается к пользователю. После этого вновь начинает играть роль запроса того же пользователя.
Слайд 265Моделирование замкнутых моделей КИС
Моделирование замкнутых моделей корпоративных информационных систем (КИС)
Замкнутая
модель КИС – это модель системы, работающей в режиме «запрос-ответ».
Транзакты, единожды сгенерированные, циркулируют в пределах графа модели.Транзакт – это запрос пользователя. Выйдя из генератора, транзакт проходит по графу модели, по мере работы КИС превращается в ответ и возвращается к пользователю. После этого вновь начинает играть роль запроса того же пользователя.
Слайд 266Моделирование замкнутых моделей КИС
Модель может быть построена следующим образом:
Пользователи представляются
одно- или многоканальными узлами типа serv;
число каналов сервера соответствует числу
пользователей, время обработки транзакта сервером соответствует времени подготовки пользователем запроса;Приписываемая транзакту роль запроса или ответа обозначается в одном из его параметров;
Для зарядки транзактами серверов пользователей, принадлежащих к одному классу, используется единственный генератор, порождающий всего один транзакт. Далее транзакты размножаются с помощью узлов типа creat.
Слайд 267Моделирование замкнутых моделей КИС
Варианты зарядки моделей транзактами:
1. Зарядка одного многоканального
сервера
S
Группа пользователей
AG
T
CR
Граф модели КИС
Слайд 268Моделирование замкнутых моделей КИС
2. Зарядка нескольких одноканальных серверов
S
Группа пользователей
AG
T
CR
Граф
модели КИС
Q
S
S
…
Слайд 269Моделирование замкнутых моделей КИС
3. Зарядка нескольких многоканальных серверов
S
Группа пользователей
AG
T
CR
Граф
модели КИС
Q
S
S
…
CR
Слайд 270Раздел III. «Имитационное моделирование экономических процессов» (продолжение)
Тема «Моделирование материальных и
финансовых ресурсов»
Лекция №18
Слайд 271Моделирование материальных ресурсов
Материальные ресурсы
перемещаемые
неперемещаемые
Перемещаемый ресурс – выделяется клиенту,
после чего
клиент использует его в других местах и
возвращает при отсутствии
необходимости дальнейшегоиспользования.
Неперемещаемый ресурс – представляет собой «базу»,
к которой приписаны ресурсные единицы. Их можно
использовать только на базе.
Слайд 272Моделирование материальных ресурсов
Мощность ресурса – максимальное число ресурсных единиц, которое
можно использовать для различных целей.
Остаток ресурса – число незанятых
на данный момент единиц, которые можно использовать для различных целей.Дефицит ресурса – количество единиц ресурса в суммарном запросе транзактов, стоящих в очереди к данному ресурсу.
ресурсы
пополняемые
непополняемые
Слайд 273Моделирование материальных ресурсов
Пример моделирования
непополняемого возвращаемого ресурса
Рассматривается пункт проката видеодисков.
Ресурсом являются видеодиски, выдаваемые клиенту. По прошествии определенного времени клиент
возвращает взятое в пункт проката.Слайд 274Моделирование материальных ресурсов
Схема модели
3
Клиенты
detach
Att
S
4
AG
Man
T
Склад пункта
проката
Проверка наличия
ресурса
Пользование
прокатом
Возврат
1
2
5
Слайд 275Моделирование материальных ресурсов
Текст модели
#include
float T_Kl; /* Интервал прихода
клиентов */
float Max_T; /* Макс. время пользования ресурсом */
int Max_Q; /* Макс. число единиц выдаваемого ресурса */ int Q; /* Исходное число единиц ресурса на складе */ forward
{
modbeg("Пункт проката",...);
ag("Клиенты", 1, none, expo, T_Kl, zero, zero, 2);
supply(2, Q); /* Начальное помещение ресурса на склад */
network(...)
Слайд 276Моделирование материальных ресурсов
{
top(2): attach("Склад", rundum()*Max_Q, prty, 3); place;
top(3):
manage("Есть ресурс?", 4);
place;
top(4): serv("Пользование ресурсом", 32000, none, unif,
Max_T, Max_T/3, zero,5); place;
top(5): term("Возврат ресурса");
clcode
detach();
fault(123);
}
modend(...);
}
Слайд 277Моделирование материальных ресурсов
Пример моделирования
пополняемого невозвращаемого ресурса
В качестве ресурса рассматривается
семейный бюджет. Пополнение происходит за счет зарплаты. Из бюджета берутся
деньги на покупки. Если на покупку не хватает денег, семья копит средства и временно ничего не покупает.Построить модель, имитирующую движение ресурсов.
Слайд 279Моделирование материальных ресурсов
Схема модели
Решение сделать
покупку
supply
Att
AG
Man
T
Кошелек
Денег на покупку
достаточно?
Деньги взяты
AG
T
Выдача
зарплаты
Зарплата получена
Слайд 280Моделирование денежных ресурсов
Моделирование финансовых ресурсов
Денежные ресурсы представляют собой «емкость», в
которой содержится определенное количество ресурса. Обычно эту «емкость» отождествляют со
счетом бухгалтерского учета. Это счет описывается с помощью узла типа send.В узле send образуется очередь транзактов, в которых содержится запрос на перевод денежных средств с данного счета send на какой-либо другой.
Приоритеты платежей устанавливаются в соответствии с приоритетными принципами (например, сначала налоги, потом зарплата, потом все остальные платежи).






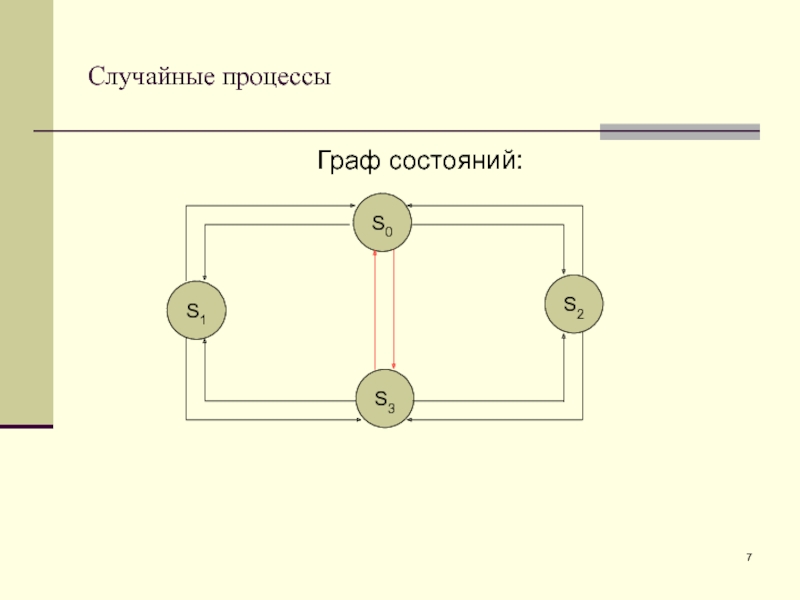

















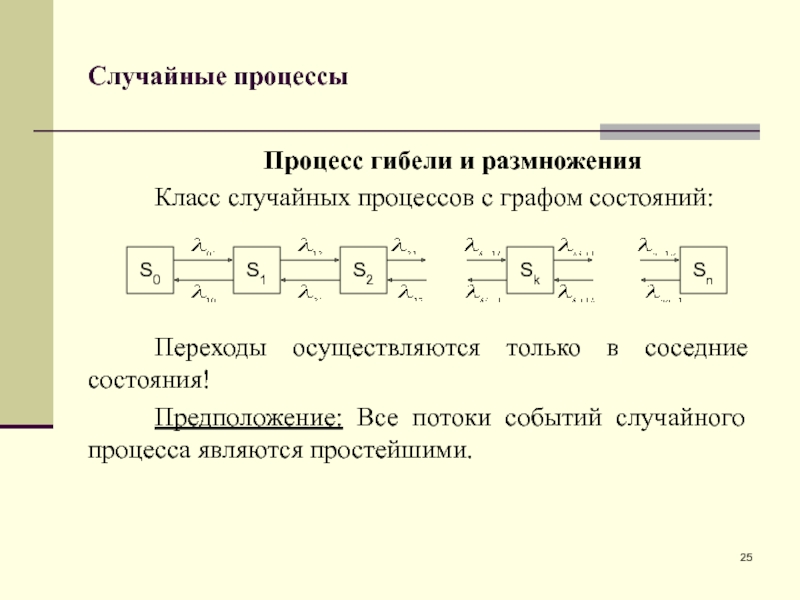





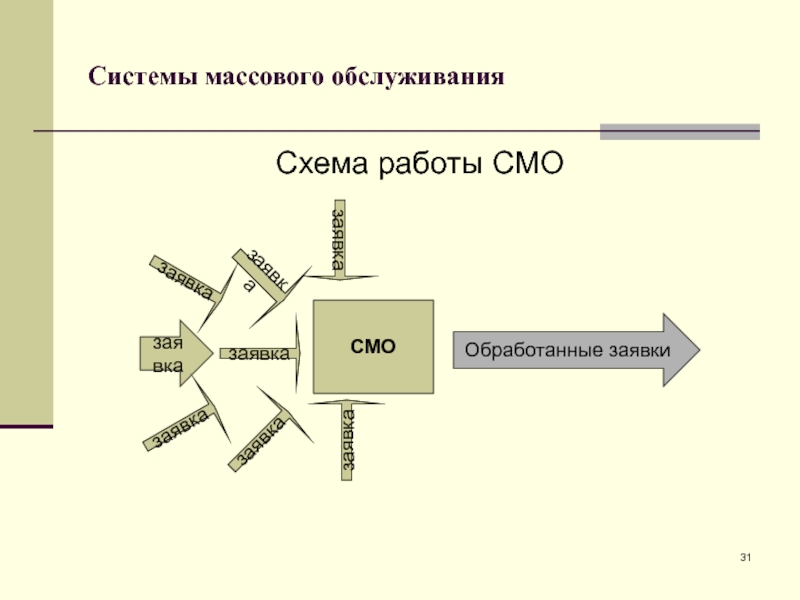


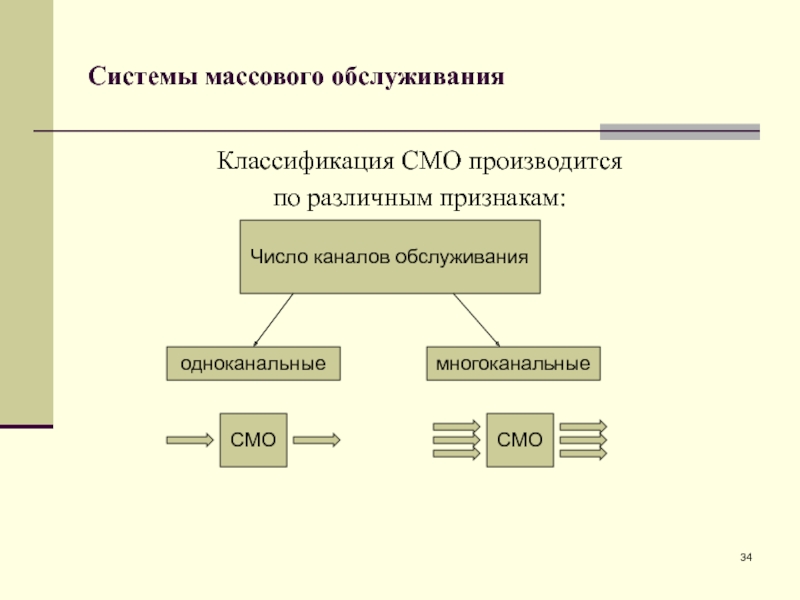
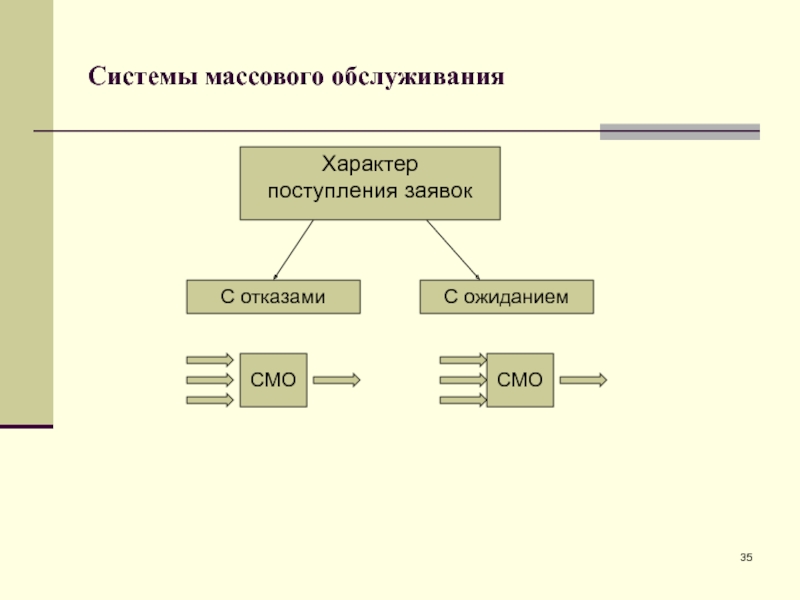
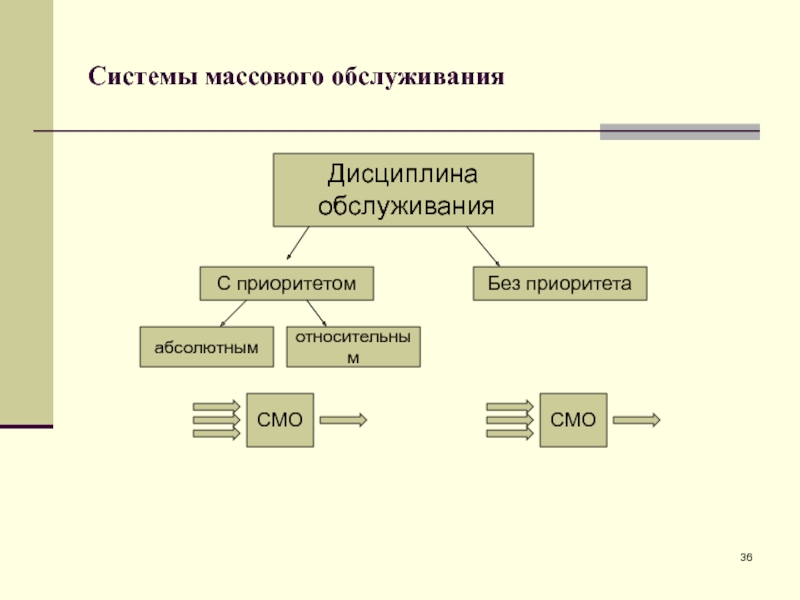
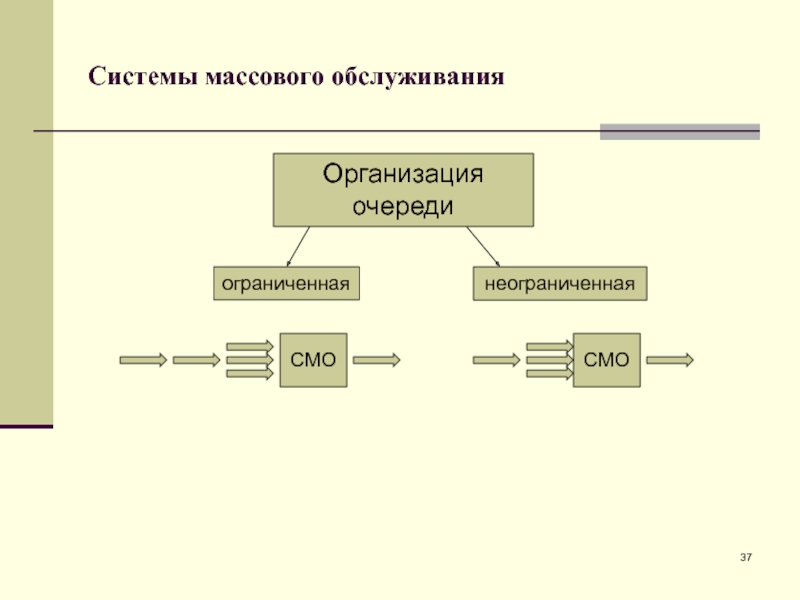
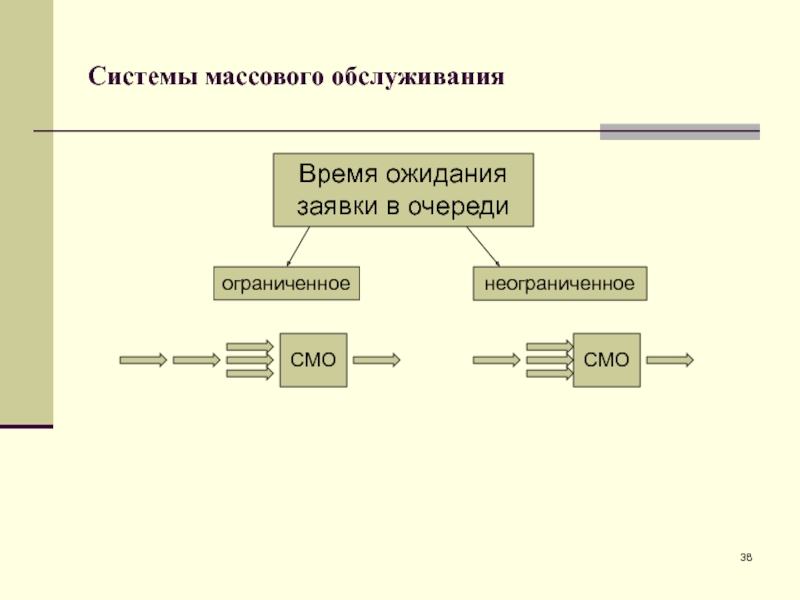








































































































































![Имитационное моделирование Параметры состояния узловaddr[n]→op – признак состояния узла типа KEY. Целочисленная переменная, Параметры состояния узловaddr[n]→op – признак состояния узла типа KEY. Целочисленная переменная, принимающая значение true, если клапан открыт,](/img/thumbs/6ce811362c549a6425ca084a69953e0b-800x.jpg)











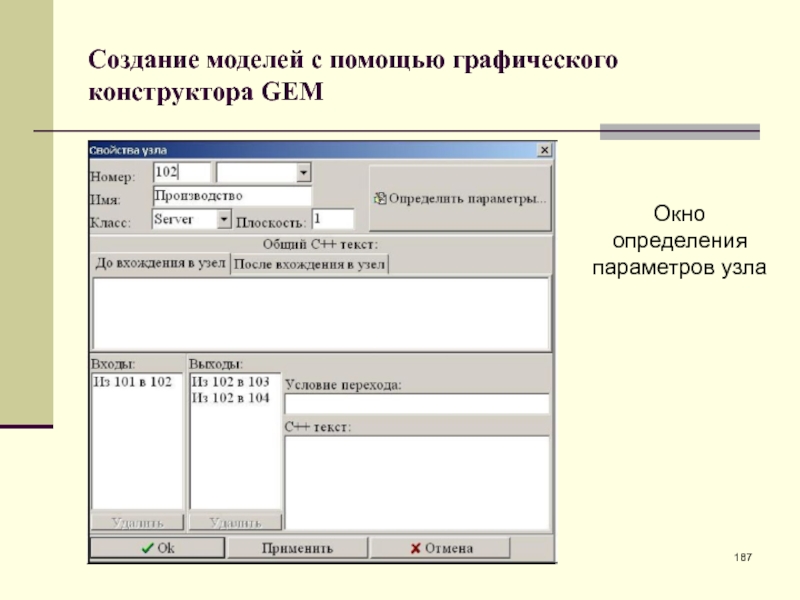



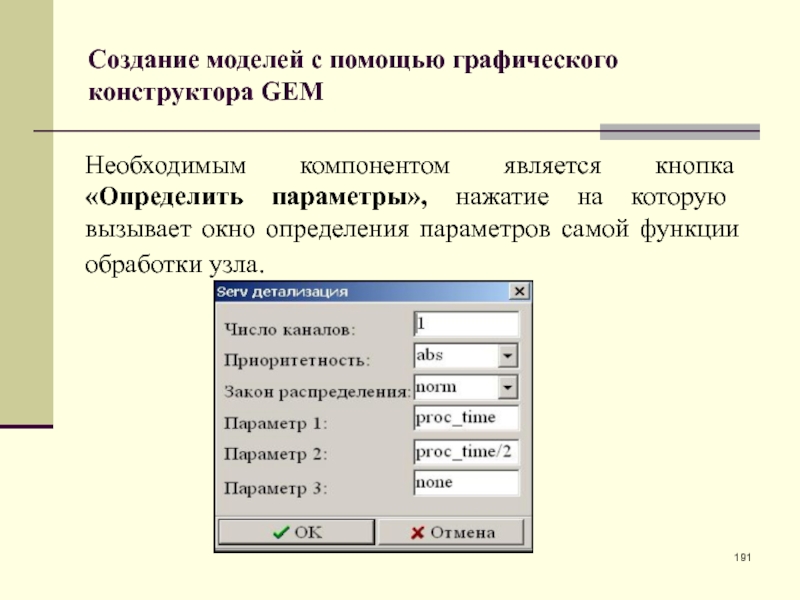

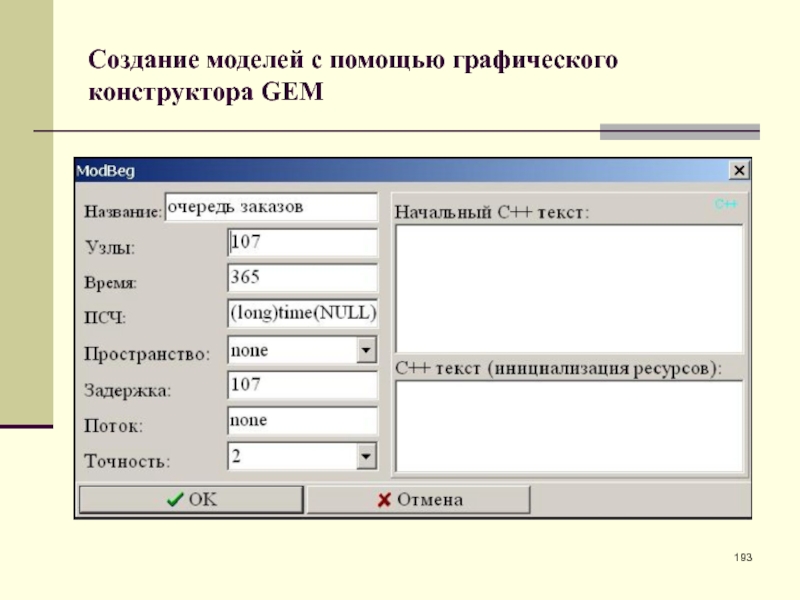

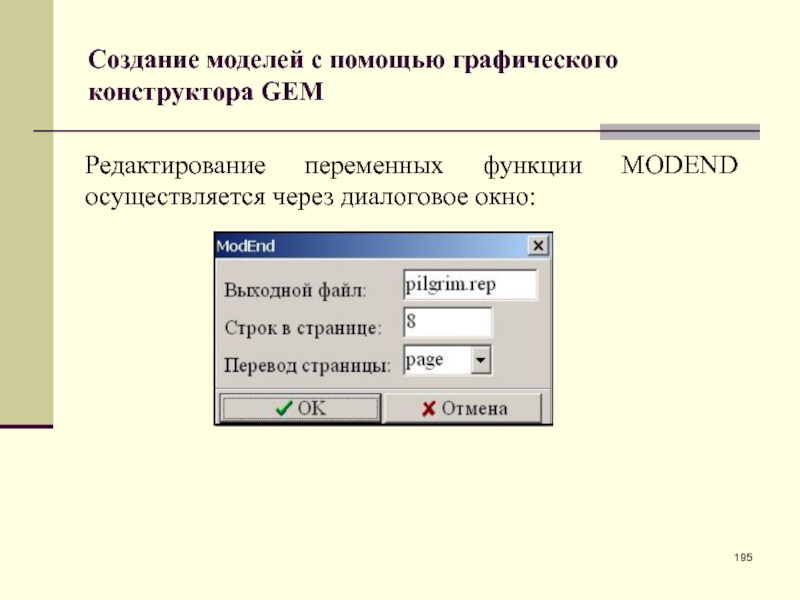



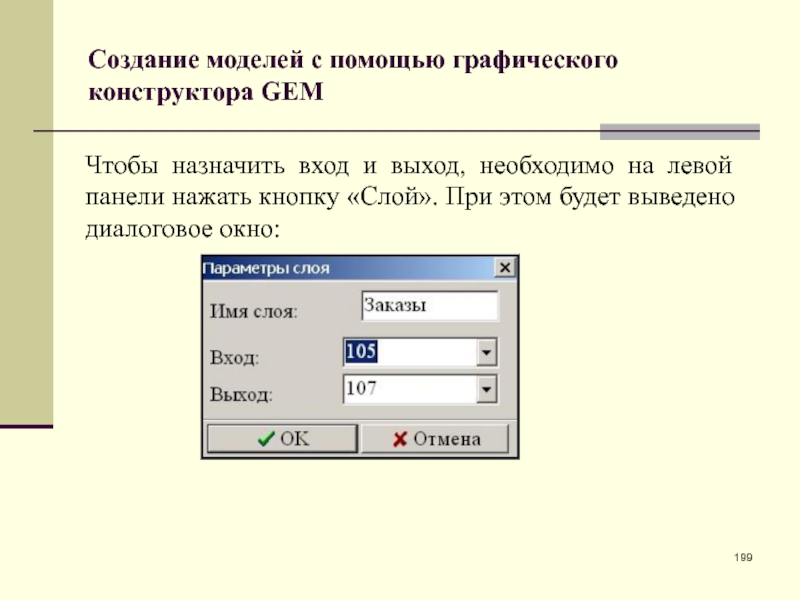
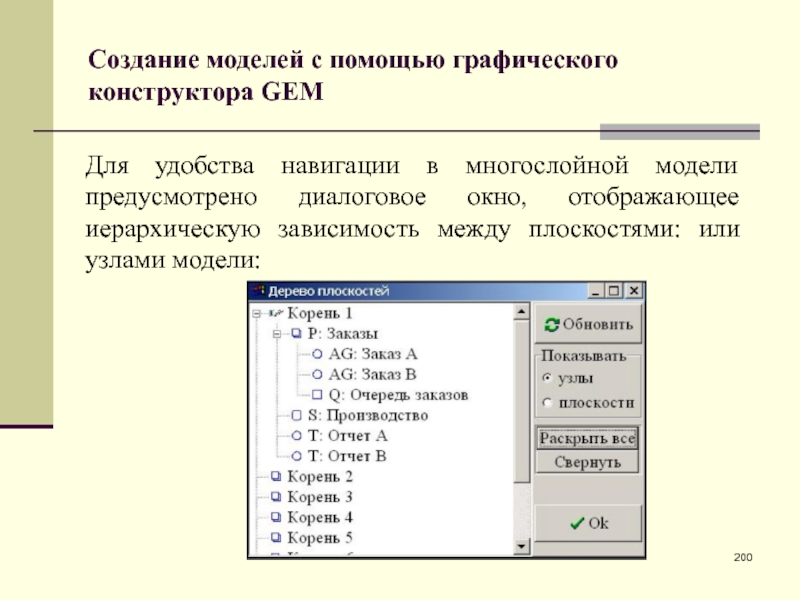
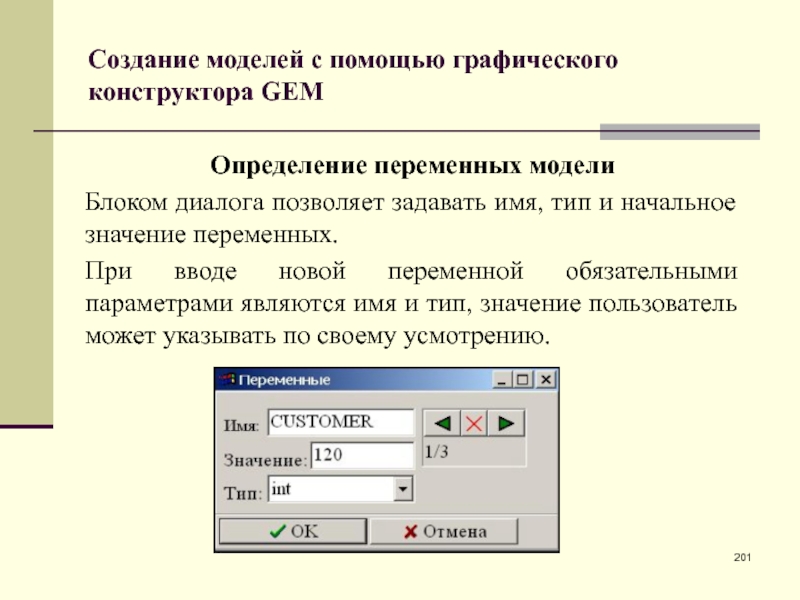



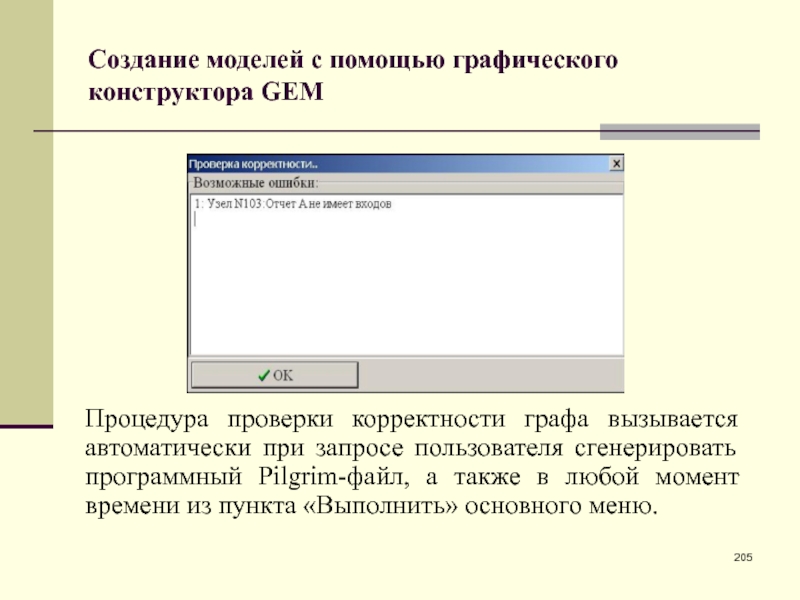


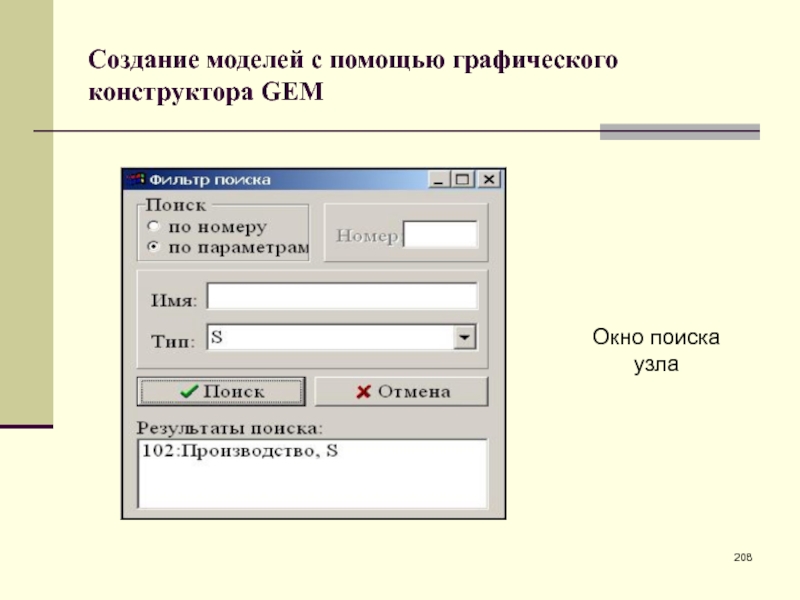








![Имитационное моделирование Обработка имитационной модели в системе Pilgrim7) M [t] среднее время. Среднее Обработка имитационной модели в системе Pilgrim7) M [t] среднее время. Среднее значение времени задержки транзакта в узле](/img/thumbs/41b23b5dcb8914e153e32715858ee315-800x.jpg)

![Имитационное моделирование Обработка имитационной модели в системе Pilgrim8) C2 [t] квадрат коэффициента вариации – Обработка имитационной модели в системе Pilgrim8) C2 [t] квадрат коэффициента вариации – отношение дисперсии временного интервала к квадрату](/img/thumbs/0fb2a55fa36021bcfd43813232db4369-800x.jpg)






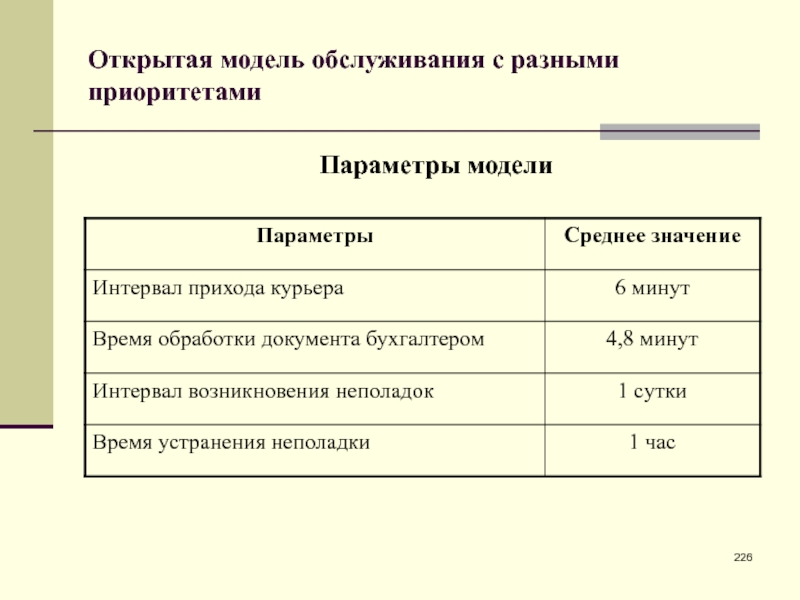
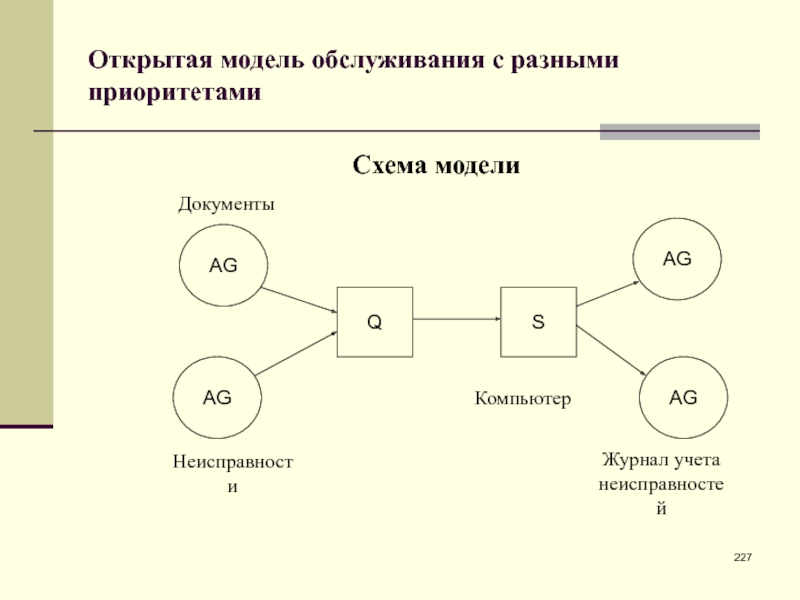

 pr ==">
pr ==">
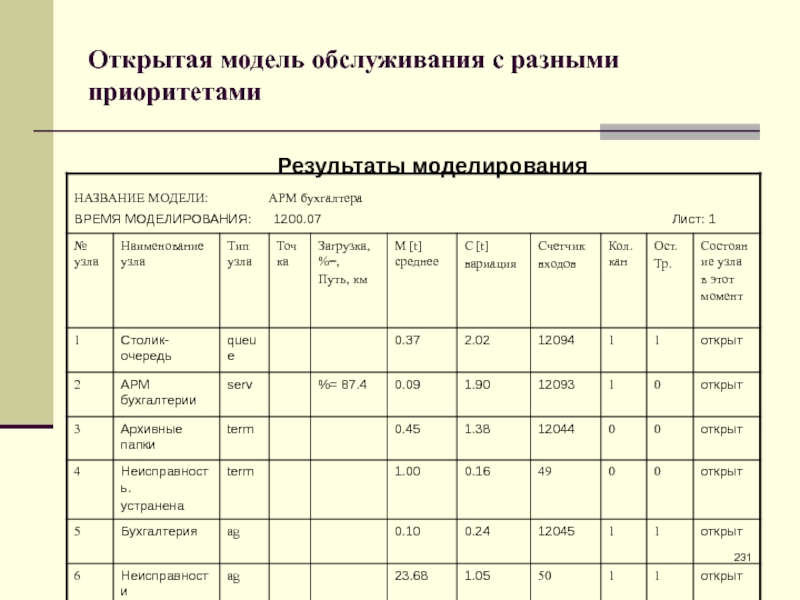

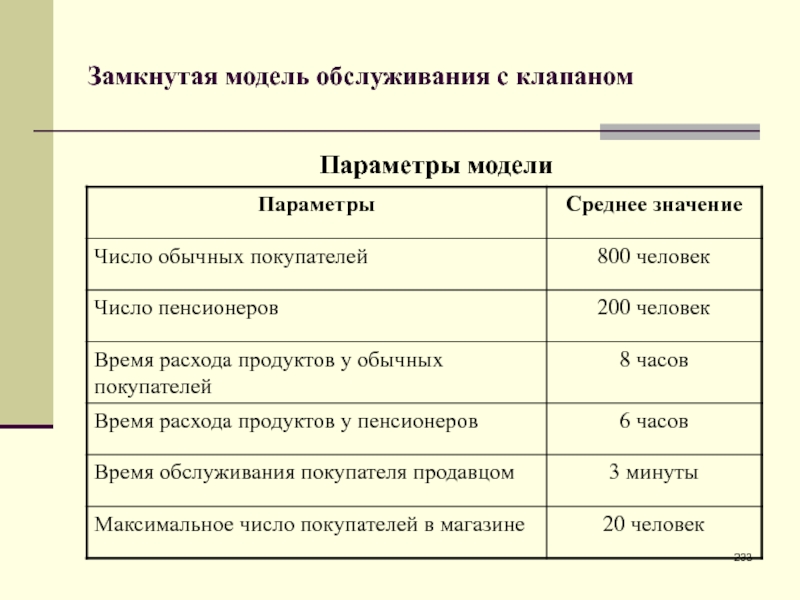
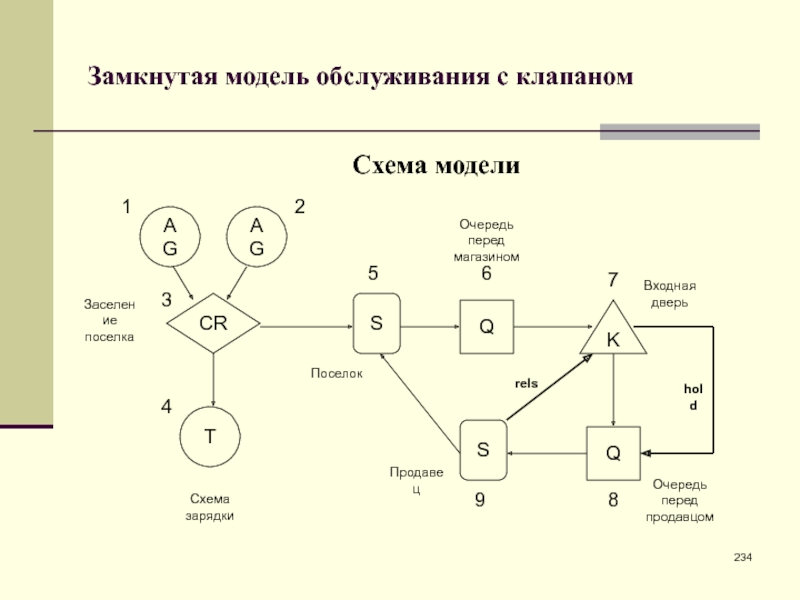



 ru0, t->ru0/3," alt="Замкнутая модель обслуживания с клапаномtop(5): serv("Поселок", N1+N2, none, norm, t->ru0, t->ru0/3, zero, 6); place; top(6): queue("Очередь перед">
ru0, t->ru0/3," alt="Замкнутая модель обслуживания с клапаномtop(5): serv("Поселок", N1+N2, none, norm, t->ru0, t->ru0/3, zero, 6); place; top(6): queue("Очередь перед">


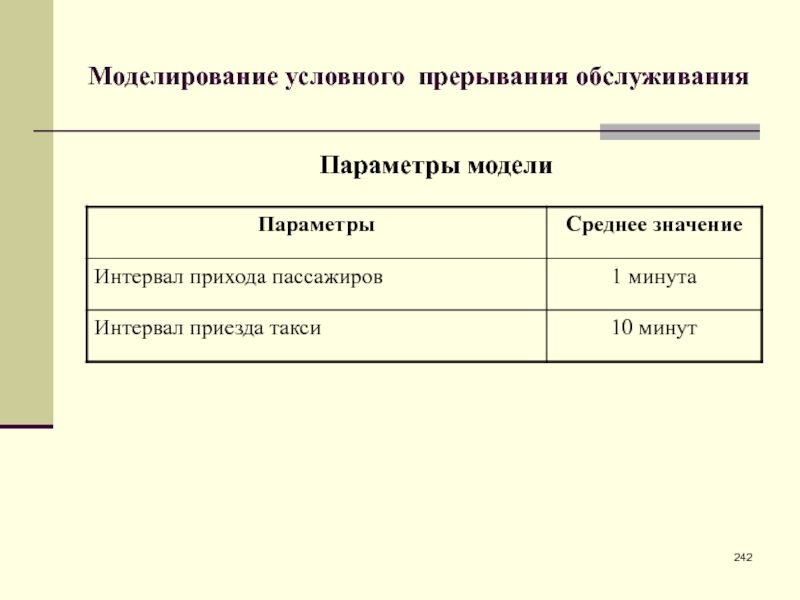
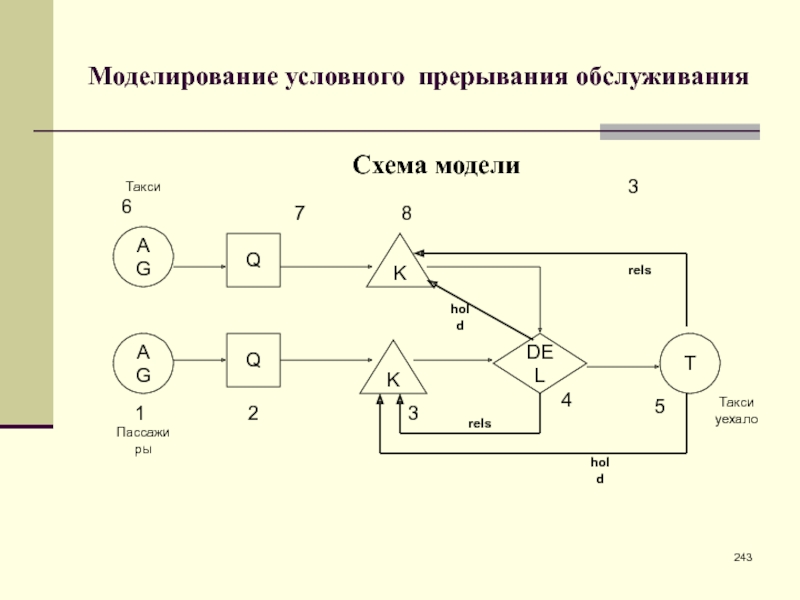

![Имитационное моделирование Моделирование условного прерывания обслуживания clcode if (addr[2]->na == Моделирование условного прерывания обслуживания clcode if (addr[2]->na == 1)](/img/thumbs/943159824ebcf25d0e08814c355490d6-800x.jpg)



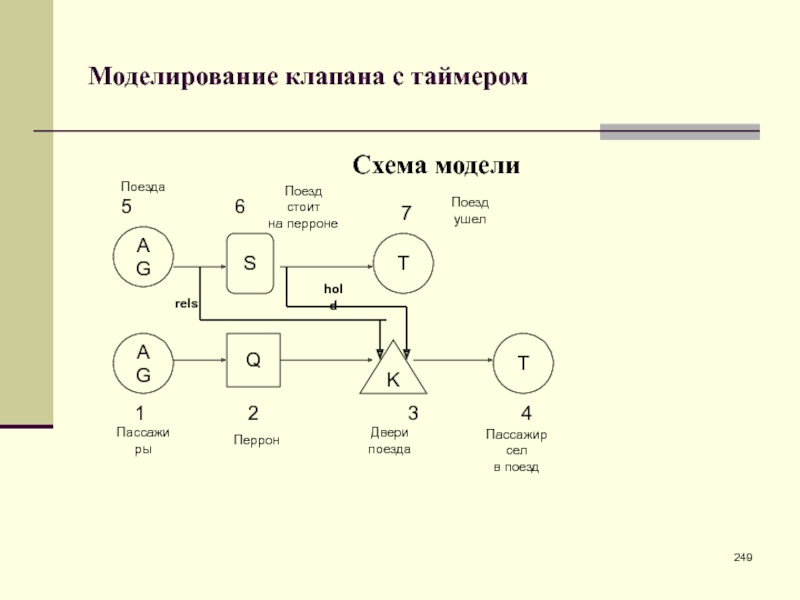

 na= =1) hold(3);" alt="Моделирование клапана с таймеромnetwork(dummy,dummy) { top(2): queue("Перрон",none,3); clcode if (addr[2]->na= =1) hold(3); place; top(3): key("Двери поезда",4); place; top(4): term("Пассажир сел в">
na= =1) hold(3);" alt="Моделирование клапана с таймеромnetwork(dummy,dummy) { top(2): queue("Перрон",none,3); clcode if (addr[2]->na= =1) hold(3); place; top(3): key("Двери поезда",4); place; top(4): term("Пассажир сел в">

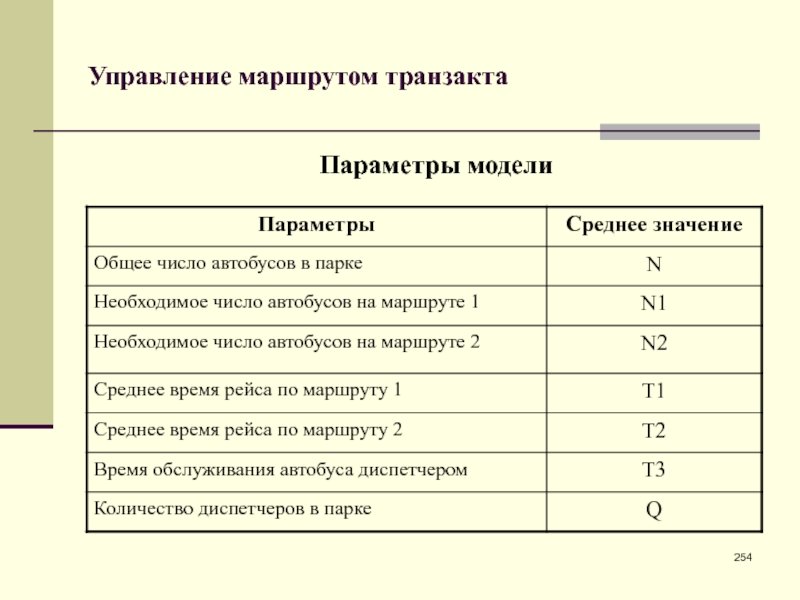
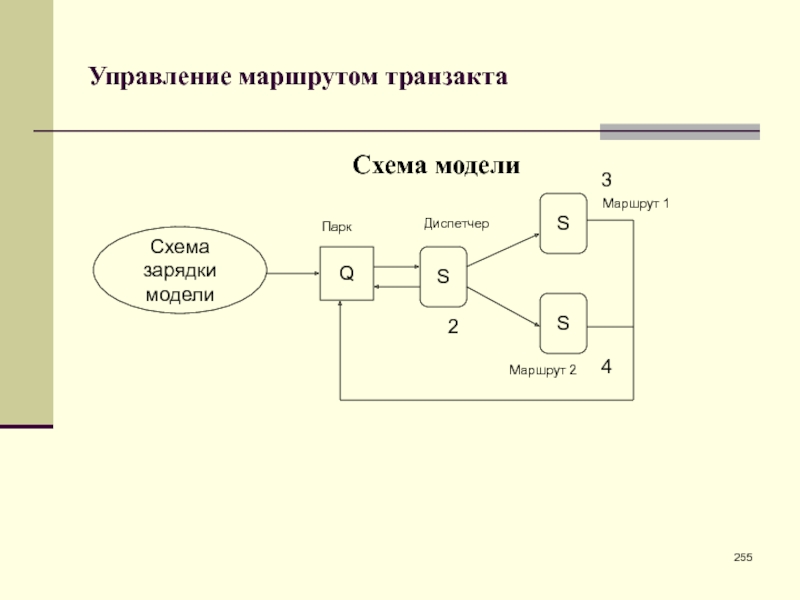

 tn" alt="Управление маршрутом транзактаТекст модели top(1): queue("Парк", prty, 2); place; top(2): if addr[3]->tn < N1 Forw=3; /* на маршрут">
tn" alt="Управление маршрутом транзактаТекст модели top(1): queue("Парк", prty, 2); place; top(2): if addr[3]->tn < N1 Forw=3; /* на маршрут">
 tn" alt="Управление маршрутом транзактаТекст модели top(1): queue("Парк", prty, 2); place; top(2): if addr[3]->tn < N1 Forw=3; /* на маршрут">
tn" alt="Управление маршрутом транзактаТекст модели top(1): queue("Парк", prty, 2); place; top(2): if addr[3]->tn < N1 Forw=3; /* на маршрут">