Слайд 1Индексный метод в статистике
Индекс – это относительный показатель, характеризующий соотношение
величин социально-экономических явлений.
Он может быть выражен в коэффициентах или
в процентах (умножением на 100 %).
В первом случае индекс показывает во сколько раз изменилась рассматриваемая характеристика экономического явления, во втором – на сколько процентов (предварительно из него следует вычесть единицу: отрицательное значение покажет процент снижения объема рассматриваемого показателя; положительное – процент увеличения этого объема).
Слайд 2В общем случае индексы используются для решения следующих задач:
выявления изменений
социально-экономических явлений во времени (индексы динамики), в пространстве – территориальные
индексы;
характеристики выполнения плановых заданий;
для изучения влияния различных факторов на изменение рассматриваемого явления.
Слайд 3Введем следующую систему обозначений:
q0, q1 – количество единиц данного вида
продукции в базисном (предыдущем) и отчетном периодах;
p0, p1 – цена
единицы продукции в базисном (предыдущем) и отчетном периодах;
z0, z1 – себестоимость единицы продукции в базисном (предыдущем) и отчетном периодах.
Слайд 4Все виды индексов подразделяются на две категории: индивидуальные индексы и
сводные (общие).
Индивидуальный индекс представляет собой относительный показатель, характеризующий изменение
(чаще всего во времени) отдельного элемента сложного экономического явления.
Математически расчет индивидуального индекса представляет собой частное от деления текущего и базисного абсолютных значений одного и того же элемента сложного экономического явления или значение текущего и значение предшествующего по времени элемента.
Слайд 5Индивидуальный индекс цен
Индивидуальный индекс
физического объема продукции
Индивидуальный индекс
себестоимости
Индивидуальный индекс
стоимости (товарооборота)
Индивидуальный индекс
затрат на производство
Слайд 6Сводный (общий) индекс представляет собой относительный показатель, отражающий изменение группы
однородных элементов изучаемого экономического явления непосредственно несоизмеримых из-за качественных различий.
Слайд 7Основной формой общего индекса является агрегатная: числитель и знаменатель представляют
собой сумму произведений двух величин, одна из которых является индексируемой
(изменение которой требуется проследить), а другая – постоянная, являющаяся весом индекса.
При построении индекса количественного показателя берут веса базисного периода, при построении индекса качественного показателя – используют веса отчетного периода.
Количественные показатели: физический объем продукции. Качественные: сводный индекс цен, сводный индекс себестоимости, сводный индекс трудоемкости.
Индексируемой величиной называется изучаемый с помощью индексного метода признак. Весом индекса – величина, выступающая соизмерителем индексируемых величин. Соизмеритель - это величина, переводящая значения индексируемых показателей к сопоставимому виду, чаще всего стоимостному.
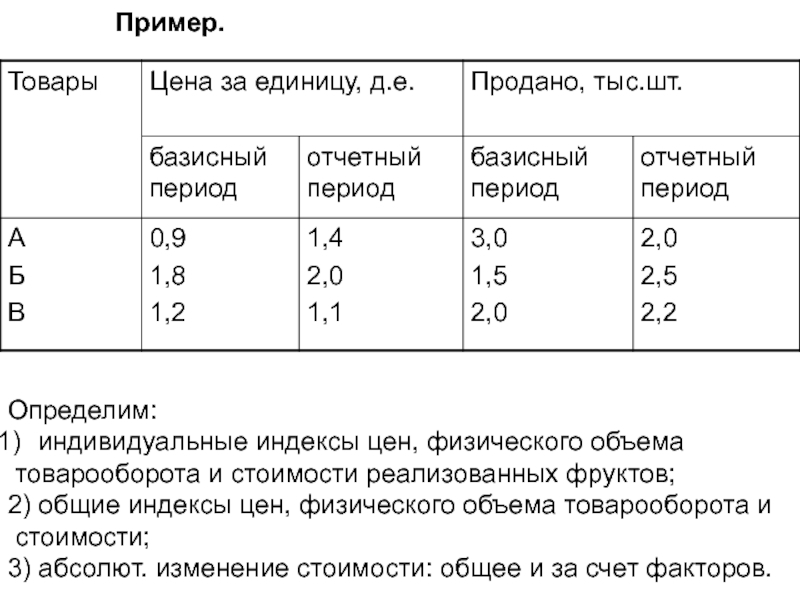
Слайд 13Пример.
Определим:
индивидуальные индексы цен, физического объема
товарооборота и стоимости реализованных фруктов;
2)
общие индексы цен, физического объема товарооборота и
стоимости;
3) абсолют. изменение
стоимости: общее и за счет факторов.
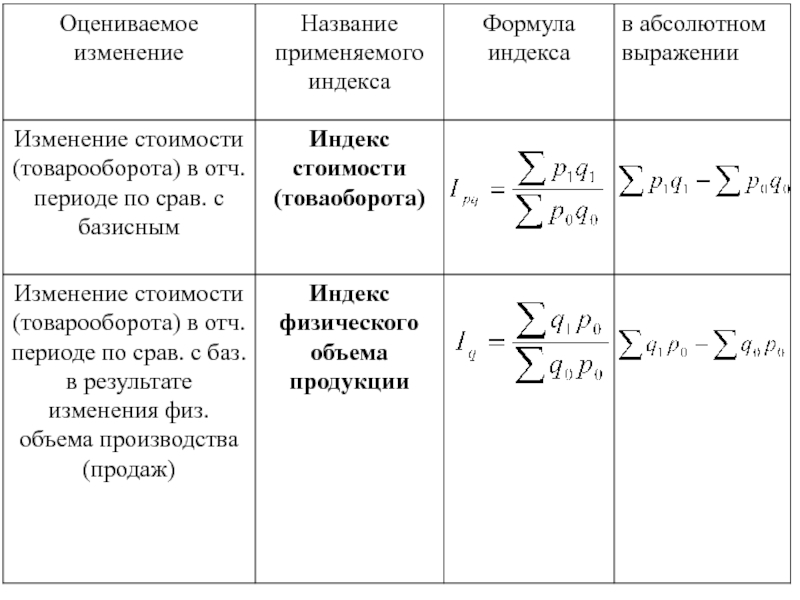
Слайд 17Изменение стоимости продукции (товарооборота) в отчетном периоде по сравнению с
базисным в результате изменения индивидуальных цен на товары:
Общее абсолютное изменение
стоимости (товарооборота) в отчетном периоде по сравнению с базисным:
Изменение стоимости (товарооборота) в отчетном периоде по сравнению с базисным в результате изменения физического объема производства (продаж):
Слайд 18Средние индексы
Если имеется информация по индивидуальным индексам, то вместо агрегатного
можно исчислить средний индекс, который даст эту же величину, но
другим расчетным путем.
Средние индексы получаются простым математическим преобразованием агрегатного индекса, поэтому их значения всегда равны.
Средний индекс – это сводный (общий) индекс, вычисленный исходя из значений индивидуальных индексов рассматриваемого показателя.
Слайд 19Формула среднего арифметического индекса физического объема продаж (товарооборота):
Формула среднего
гармонического индекса цен:
Слайд 20Пример.
Определите:
общий индекс цен;
общий индекс физического объема реализации с учетом
того,
что товарооборот октября возрос на 40 % по сравнению
с
июнем.
Слайд 21Средний гармонический индекс цен:
Слайд 22Формула среднего арифметического индекса физического объема производства:
Формула среднего гармонического
индекса себестоимости:
Слайд 23Факторный индексный анализ
Применяется только по отношению к качественным показателям.
На
формирование среднего уровня качественного показателя оказывают влияние несколько факторов, например,
на формирование средней цены – уровень индивидуальных цен на товары и структура продаваемой продукции.
При изучении динамики изменения средней цены определяют влияние на нее изменения индивидуальных цен на товары, изменения количеств проданных отдельных товаров и изменение структуры продаж. В какой мере каждый из этих факторов оказал свое влияние выясняется с помощью индексного факторного анализа.
Слайд 24Индекс переменного состава показывает общее изменение среднего уровня показателя отчетного
периода по сравнению с базисным, например при изучении изменения среднего
уровня цен:
То есть средняя цена, определяемая по формуле средней арифметической взвешенной по количеству проданных товаров, отчетного периода делится на среднюю цену базисного периода.
Слайд 25Индекс постоянного (фиксированного) состава показывает среднее изменение индексируемого показателя отчетного
периода по сравнению с базисным только за счет изменения аналогичных
показателей у единиц, участвующих в формировании его среднего значения.
Математически индекс постоянного состава совпадает с агрегатной формой индекса.
Слайд 26Индекс структурных сдвигов показывает влияние на формирование среднего значения индексируемой
величины изменения структуры изучаемого явления.
В случае анализа динамики средних цен
индекс покажет, как изменилась средняя цена на товары в отчетном периоде по сравнению с базисным, за счет того, что объемы продаж одних товаров увеличились, а других уменьшились, то есть за счет изменения структуры продаж без влияния изменения индивидуальных цен:
Слайд 27Так как индекс переменного состава показывает изменение исследуемого явления за
счет всех факторов, то между индексами существует следующая взаимосвязь: