Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интеллектуальные информационные системы
Содержание
- 1. Интеллектуальные информационные системы
- 2. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 3. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 4. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 5. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 6. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 7. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 8. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 9. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 10. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 11. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 12. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 13. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 14. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 15. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 16. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 17. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 18. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 19. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 20. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 21. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 22. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 23. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 24. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 25. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 26. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 27. Пример семантической сети для предложения типа «Поставщик
- 28. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 29. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 30. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 31. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 32. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 33. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 34. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 35. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 36. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 37. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 38. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 39. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 40. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 41. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 42. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 43. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 44. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 45. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 46. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Интеллектуальные информационные системы
Т.Ф. Лебедева
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КемИ РГТЭУ
Слайд 2ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.1 Исчисление высказываний
Исчисление – набор определенных действий по заданным
правилам над какими– либо элементами. Исчисление высказываний оперирует логическими высказываниями
Элементарным высказываниям – элементам исчисления высказывания сопоставляются латинские буквы. Логическая обработка высказываний заменяется обработкой этих букв.
Высказыванию «Автомобиль стоит у дома» сопоставим букву Р.
Если Р является формально правильным, то говорят, что оно принимает значение «истина», в противном случае – «ложь».
Если, например, шофер сидит в автомобиле, то высказывание «Шофер не сидит в автомобиле» - ложно.
Сопоставим этому высказыванию букву Q.
Сложное высказывание P и не Q или P Q означает при этом: Автомобиль стоит у дома и шофер сидит в автомобиле.
40
Слайд 3ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.1 Исчисление высказываний
Дадим формальное определение синтаксически правильной построенной формулы
(ППФ) исчисления высказываний:Каждое элементарное высказывание есть ППФ;
логические константы true и false также есть ППФ;
Если А – формула, то А также есть ППФ;
Если А и В – формулы, то АВ, АВ, АВ, АВ тоже ППФ;
других правил образования ППФ нет.
41
Слайд 4ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ 1
Логические модели
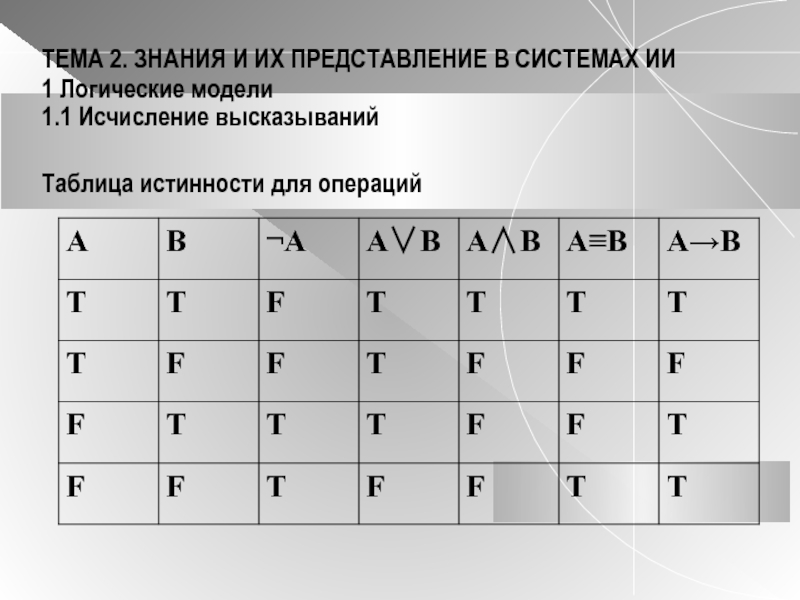
1.1 Исчисление высказываний
Таблица истинности для операций
Слайд 5ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.1 Исчисление высказываний
Приписывание логических значений true или false атомарным
формулам, входящим в формулу G называется интерпретацией формулы G. Задав интерпретацию, можно вычислить логическое значение формулы.
Формула называется истинной при некоторой интерпретации, если она имеет значение true в этой интерпретации.
Если формула G содержит n разных атомарных подформул, то она имеет 2 в степени n различных интерпретаций.
Если формула истинна при всех возможных интерпретациях, она называется общезначимой или тавтологией.
Обозначение -
Если формула ложна при всех возможных интерпретациях, то она называется противоречием или невыполнимой.
Обозначение -
Формулы G и H называются эквивалентными G H , если их логическое значение совпадает при любой интерпретации для G и H. Путем подбора всех возможных интерпретаций может быть доказана эквивалентность двух формул
43
Слайд 6ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
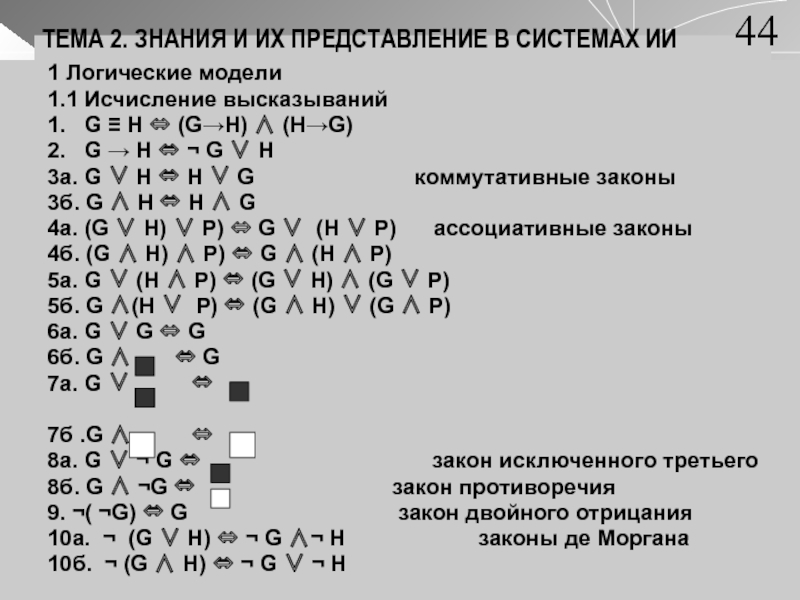
1.1 Исчисление высказываний
1. G H (GH)
(HG)2. G H G H
3а. G H H G коммутативные законы
3б. G H H G
4а. (G H) P) G (H P) ассоциативные законы
4б. (G H) P) G (H P)
5а. G (H P) (G H) (G P)
5б. G (H P) (G H) (G P)
6а. G G G
6б. G G
7а. G
7б .G
8а. G G закон исключенного третьего
8б. G G закон противоречия
9. ( G) G закон двойного отрицания
10а. (G H) G H законы де Моргана
10б. (G H) G H
44
Слайд 7ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.1 Исчисление высказываний
Чтобы на основе ряда истинных высказываний получить
новые истинные высказывания, составляются определенные правила формирования выводов.Наиболее известное Modus ponens (сокращенно MP) – правило дедуктивного вывода:
(1) р (посылка)
(2) Если р , то q (посылка)
(3 ) q (вывод:1:2, MP)
Этот вывод означает:
Если выражение р истинно и из р следует истинность высказывания q, то q также истинно.
Пример: а в
(1) «Шофер в автомобиле И автомобиль стоит у дома»
а в с
(2) «Если шофер в автомобиле И автомобиль стоит у дома, то шофер у дома»
с
(3) «Шофер у дома»
(Вывод: 1:2, MP)
45
Слайд 8ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.1 Исчисление высказываний
В основе правила MP лежит теорема о
дедукции:Пусть даны формулы G1,G2,G3,….Gn и формула Н.
Формула Н является логическим следствием G1,G2, ...Gn тогда и только тогда, когда формула G1G2…Gn H является общезначимой или тавтологией.
Следствие из теоремы:
Н является логическим следствием формул G1,G2,G3,….Gn , если формула вида G1G2…Gn Н является противоречием.
Таким образом, можно заключить, что
процесс решения задач, требующих логических рассуждений, может быть сведен к процедуре доказательства теорем.
При этом достаточно доказать либо общезначимость некоторой формулы, либо противоречивость отрицания этой формулы.
46
Слайд 9ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Логика предикатов – расширение логики
высказываний, которое позволяет учитывать структуру элементарных формул с точки зрения связей между субъектом и предикатом.Предикатом называется логическая функция, которая превращается в высказывание при фиксировании аргументов.
Высказывание в логике предикатов представляется следующим образом:
P (t1, t2,..,tn), где t1, t2,… tn - аргументы.
Р – n-местное отношение между этими аргументами или имя предиката.
Высказывание «Автомобиль стоит у дома» в логике предикатов -
стоять (автомобиль, дом)
Аргументы автомобиль и дом являются индивидуальными константами , которые соответствует некоторым понятиям. «стоять» означает отношение между домом и автомобилем.
К предикатам могут быть применены все операции исчисления высказываний и правило вывода MP.
47
Слайд 10ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Использование логики предикатов расширяет логику
высказываний благодаря введению множества констант для рассматриваемой предметной области (ПО) и множества переменных, принимающих значение на этой ПО, а так же благодаря введению кванторов: Квантора всеобщности
Квантора существования
Приведем формальное определение ППФ для логики предикатов, используя нотацию Бэкуса-Наура:
1) терм ::= константа | переменная | имя функции (терм [,терм] *)
2) атомарная_формула ::= имя_предиката | имя предиката (терм [,терм ]*)
3) ППФ ::=атомарная_формула |( ППФ) | (ППФ ППФ)| (ППФ ППФ)| (ППФ ППФ) | (ППФ ППФ) | ( (переменная) ППФ) |
( (переменная) ППФ)
4) других правил образования ППФ нет.
Приоритет выполнения операций: 1. 2. 3. 4. 5. 6. 7.
48
Слайд 11ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Рассмотрим некоторые примеры.
Высказывание «у
каждого человека есть отец» можно записать:( x) ( y) (ЧЕЛОВЕК(x) ОТЕЦ(y,x))
Выражение «Антон владеет красной машиной» записывается, например, так:
( x) (ВЛАДЕЕТ(АНТОН, x) МАШИНА(x) КРАСНЫЙ(x))
Областью действия квантора называется формула, в которой он применяется.
49а
Слайд 12ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Если существует некоторая предметная область
(ПО), то предикаты определяют отношения в этой предметной области, константы – элементы этой предметной области, функциональный символ – функцию.Интерпретация формулы G логики предикатов заключается в указании ПО D и в указании смысла всех встречающихся в формуле констант, функциональных и предикатных символов.
При этом:
Каждый константе из G ставится в соответствии некоторый определенный элемент из D.
Каждому n-местному функциональному символу fn из G ставится в соответствие отображение Dn на D, где Dn ={(x1,x2,….xn)},
xi D, i 1:n;
Каждому n-местному предикатному символу из G ставится в соответствие отображение вида Dn на {true, false};
49
Слайд 13ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Если задана интерпретация некоторой формулы
G на область D , то можно вычислить логическое значение этой формулы по следующим правилам:Значение атомарных подформул определяется, исходя из символов отображений, сопоставленных предикатным символам.
Если задано значение подформул А и В, то значение формул вида ( А), (АВ), (АВ), (АВ), (АВ) можно вычислить по таблице истинности.
Подформула вида (x) G принимает значение true, если G принимает значение true хотя бы для одного элемента из области D, в противном случае - false.
Подформула вида (x) G принимает значение true, если G принимает значение true для каждого элемента xD, в противном случае - false.
50
Слайд 14ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Вхождение переменной x в формулу
G называется связанным, если x является переменной, стоящей под знаком квантора и входит в область действия квантора, в противном случае - вхождение переменной называется свободным.Пример: H(x1) (x2) G(x1,x2), здесь x1 - свободная переменная, а x2 - связанная переменная.
Заметим, что если формула содержит свободные переменные, то вычислить логическое значение такой формулы нельзя.
Понятия истинной, ложной, общезначимой и противоречивой формул, понятие эквивалентности и логического следствия для логики предикатов формулируются точно также, как и в логике высказываний, но используемое при этом понятие интерпретации формул для логики предикатов является более сложным, чем для логики высказываний
51
Слайд 15ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Приведенный выше список пар эквивалентных
формул 1-10 б справедлив для логики предикатов, однако он может быть расширен с учетом действия кванторов.Пусть G, T – формулы, содержащие связанную переменную х или z, (обозначение G[x]), H - формула, не содержащая переменную х;
Q, Q1,Q2,Q3,Q4 – кванторы всеобщности или существования. Тогда имеют место следующие эквивалентности:
11а) (Qx) G[x] H (Qx) (G[x] H )
11b) (Qx) G[x] H (Qx) (G[x] H )
12a) (x) G[x ] (x) (G[x] )
12b) (x) G[x ] (x) (G[x] )
13a) (x) G[x ] (x) T[x ] (x) (G[x ] T[x ])
13b) (x) G[x ] (x) T[x ] (x) (G[x ] T[x ])
14a) (Q1x) G[x] (Q2z) T[z] (Q1x)(Q2z)(G[x] T[z])
14b) (Q3x) G[x] (Q4z) T[z] (Q3x)(Q4z)(G[x] T[z])
Соотношения 1-14b принято называть логическими законами
52
Слайд 16ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Формула логики предикатов F находится
в предваренной нормальной форме (ПНФ), если она имеет вид (Q1x)(Q2x)….(Qnx) M, где Qi – квантор существования или всеобщности; i 1:n; М – формула, которая не содержит кванторов и называется матрицей формулы F. Произвольную формулу логики предикатов можно преобразовать в ПНФ посредством следующего алгоритма:шаг_1: используя логические законы 1,2, исключаем логические связки , ;
шаг_2: используя логические законы 9-12b, проносим знак отрицания до атомарных формул;
шаг_3: переименовываем переменные так, чтобы разные кванторы связывали разные переменные;
шаг_4: выносим кванторы в начало, используя логические законы 11а-11b, 13a-13b.
53
Слайд 17ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Литералом будем называть атомарную формулу
или ее отрицание. Считается, что формула, не содержащая кванторов, находится в конъюнктивной нормальной форме (КНФ), если она имеет вид G1G2…Gn , где G1,G2, ...Gn – дизъюнкции литералов, которые принято называть дизъюнктами. Пусть G – некоторая формула логики предикатов. Она может быть подвергнута следующим изменениям:
формула может быть сведена к предваренной нормальной форме;
используя логические законы 5a,5b, матрица полученной формулы может быть сведена к конъюнктивной нормальной форме;
сохраняя свойство противоречивости формулы, в ней можно устранить кванторы существования.
54
Слайд 18ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.2 Исчисление предикатов (логика предикатов)
Согласно следствию теоремы о дедукции,
формула Н является логическим следствием формул G1,G2,G3,….Gn , если формула вида G1G2…Gn Н противоречива. В логике высказываний у каждой формулы имеется конечное число интерпретаций, поэтому выяснить, является ли формула противоречивой, можно путем перебора всех возможных интерпретаций и вычисления логического значения формулы в каждой интерпретации.
В логике предикатов интерпретаций для каждой формулы существует бесконечное множество, так как ПО можно придумать много. Алгоритм перебора всех интерпретаций будет работать бесконечно долго.
А. Черч и А.Тьюринг в 1936 году доказали, что не существует алгоритма, устанавливающего, является ли формула логики предикатов выполнимой или не выполнимой за конечное число шагов.
Тем не менее, Д. Эрбраном был разработан алгоритм, который за конечное число шагов устанавливает, что формула логики предикатов является противоречивой, если она на самом деле противоречива, в противном случае алгоритм Эрбрана «зацикливается».
Существенное улучшение этого алгоритма было предложено в 1965 г. Дж. Робинсоном, который разработал метод резолюции. Значительное повышение эффективности метода резолюций достигается за счет использования специальных эвристик, которые называются стратегиями резолюций.
55
Слайд 19ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.3 Формальное представление логических систем
В основе логических систем
лежит понятие формальной логической модели, заданной четверкой вида:M=
где Т – множество базовых элементов разной природы;
Р – множество синтаксических правил;
А – система аксиом;
В – семантические правила.
Множество Т - это как бы алфавит формальной системы, из которого строятся все остальные элементы. На элементы формальной системы не накладывается никаких ограничений.
Важно только , чтобы два любых элемента из Т чем-то отличались друг от друга, то есть должна существовать конструктивная процедура П1, применение которой к элементам множества Т дает ответ: одинаковы ли они или нет (например, если Т – множество букв русского алфавита, то отождествление различных написаний буквы А дело не такое простое).
Еще должна существовать конструктивная процедура П2, которая отвечает: принадлежит ли данный элемент к Т или нет.
56
Слайд 20ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
1
Логические модели
1.3 Формальное представление логических систем
Синтаксические правила Р используются
для того, чтобы из базовых элементов множества Т строить синтаксически правильные совокупности или ППФ. На множество правил также нет ограничений, только нужна конструктивная процедура П3, которая бы давала ответ: является ли данная совокупность базовых элементов синтаксически правильной.Систему аксиом - А образует любое множество синтаксически правильных совокупностей (например, законы 1-14b для логики предикатов).
Семантические правила - В или правила вывода расширяют, если это возможно, множество аксиом, добавляя к ним новые синтаксически правильные совокупности (например правило дедуктивного вывода МР).
Логические системы основаны на исчислении высказываний и исчислении предикатов. Наиболее известным языком программирования логических моделей является PROLOG .
57
Слайд 21ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
Модели, основанные на семантических сетях
Семантические сети (СС) являются исторически первым
классом моделей представления знаний.Здесь структура знаний ПО представляется в виде направленного графа, вершины (узлы) которого соответствуют объектам, понятиям, сущностям ПО, а дуги - отношениям или связям между ними.
Узлы и дуги имеют метки - имена. Имена вершин и дуг часто совпадают с именами соответствующих объектов и отношений ПО.
Объекты ПО, отображаемые в СС, можно условно разделить на группы:
обобщенные;
индивидные;
агрегатные.
58
Слайд 22ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
Модели, основанные на семантических сетях
Обобщенный объект соответствует некоторой собирательной абстракции
реально существующего объекта, процесса или явления ПО (например, «изделия», «предприятия», «сотрудники»).Индивидный объект – это, каким-то образом выделенный единичный представитель (экземпляр) класса (например, «сотрудник Иванов П.А.»).
Агрегатным объектом называется составной объект, образованный из других объектов, которые рассматривается как его составные части. Например, изделия состоят из совокупности деталей, предприятие - из совокупности служб, отделов, цехов.
Введенная классификация является относительной. В зависимости от решаемой задачи один и тот же объект может рассматриваться как обобщенный или индивидный, как агрегатный или неагрегатный.
59
Слайд 23ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
Модели, основанные на семантических сетях
Типы связей между объектами СС могут
быть любыми, но чаще всего применяются следующие основные связи: «род–вид» или АКО- a kind of
«является представителем» - is a
«является частью чего-либо» – a part of.
Наличие связи АКО между объектами А и В означает, что понятие А более общее, чем понятие В.
Связь «является представителем» - is a существует обычно между обобщенным и индивидным объектом, когда индивидный объект выступает в роли представителя некоторого класса, например, кошка Мурка является представителем класса кошек.
В ряде случаев между связями «род–вид» и «является представителем» не делают различий, отмечая, что эти связи задают отношение «общее-частное»
Все СС можно классифицировать по видам связи:
По количеству типов отношений:
однородные: один тип отношений
неоднородные: несколько типов
По количеству участников:
бинарные: 2 узла связываются.
N-арные: больше , чем 2.
60
Слайд 24ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
Модели, основанные на семантических сетях
Наиболее часто в семантических сетях используются
следующие группы отношений:Связи типа АКО (класс-подкласс).
Функциональные связи, определяемые глаголами (производит, выполняет, влияет и.т.д).
Количественные связи, задаваемые отношениями (больше, меньше, равно и.т.д).
Пространственные связи, определяющие размещение объектов по отношению друг к другу (далеко, близко, под, над, из-за, и.т.д).
Временные связи, задающие отношения во времени (раньше, позже, в течении, в одно время).
Атрибутивные связи - иметь свойство, иметь значение.
Логические связи, определяемые логическими операциями и, или, не.
Причинно-следственные связи.
61
Слайд 25ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
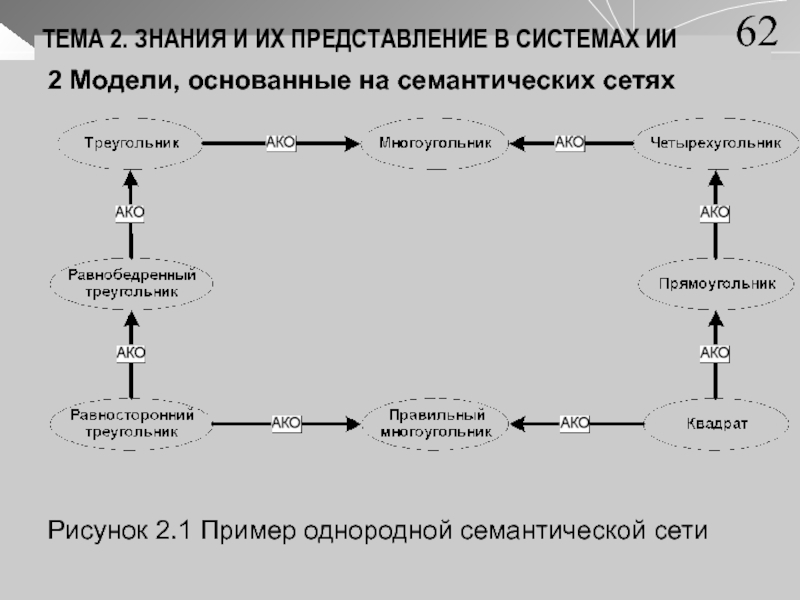
Модели, основанные на семантических сетях
Рисунок 2.1 Пример однородной семантической сети
62
Слайд 26ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
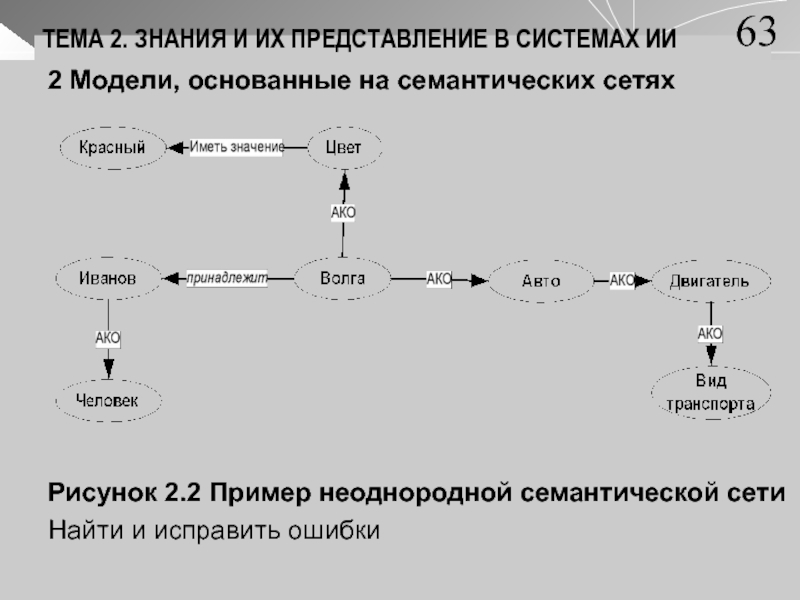
Модели, основанные на семантических сетях
Рисунок 2.2 Пример неоднородной семантической сети
Найти
и исправить ошибки63
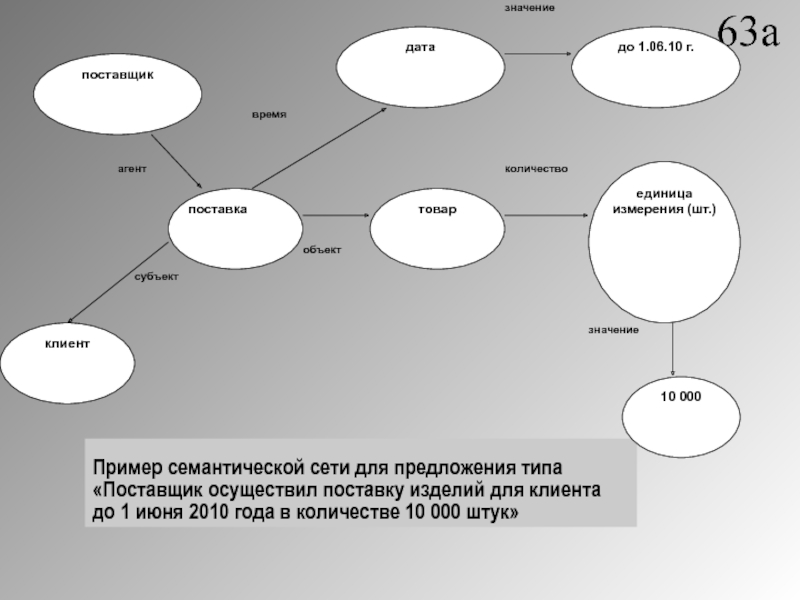
Слайд 27Пример семантической сети для предложения типа «Поставщик осуществил поставку изделий
для клиента до 1 июня 2010 года в количестве 10
000 штук»63а
Слайд 28ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
Модели, основанные на семантических сетях
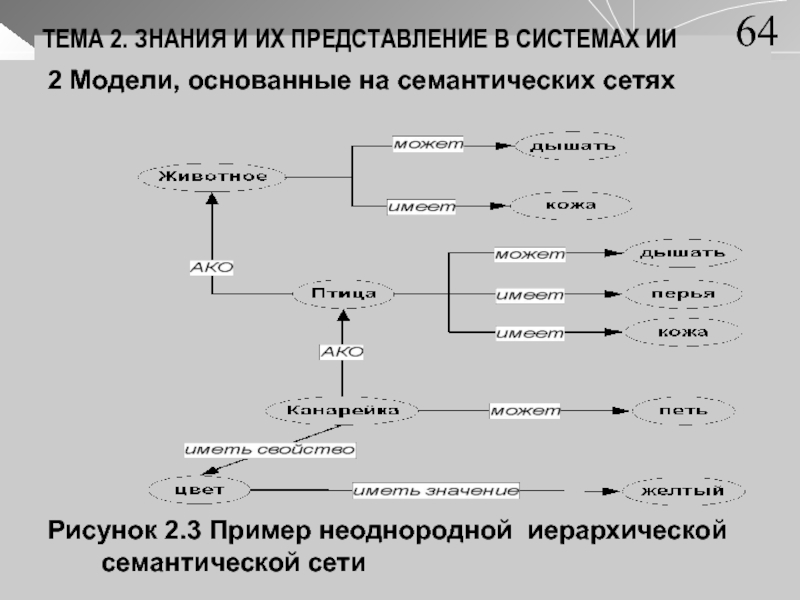
Рисунок 2.3 Пример неоднородной иерархической семантической
сети64
Слайд 29ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2 Модели, основанные на семантических сетях
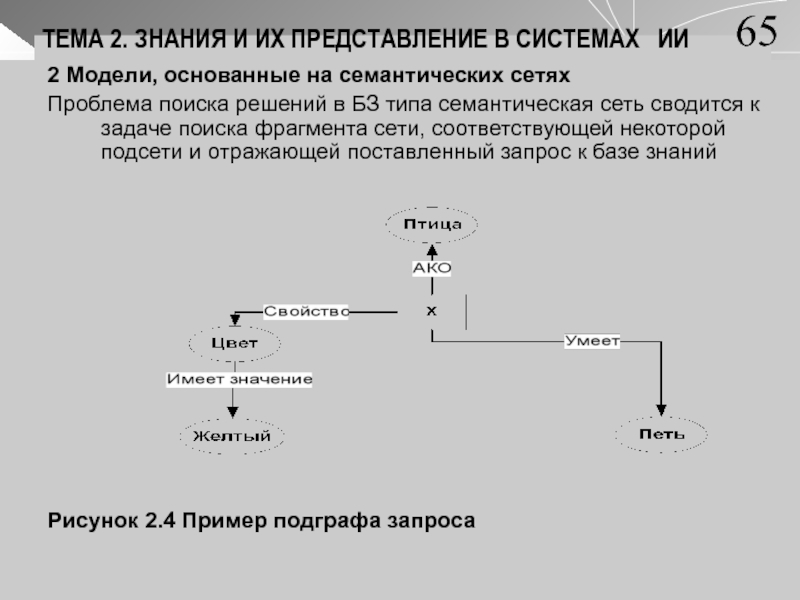
Проблема поиска решений в БЗ
типа семантическая сеть сводится к задаче поиска фрагмента сети, соответствующей некоторой подсети и отражающей поставленный запрос к базе знаний Рисунок 2.4 Пример подграфа запроса
65
Слайд 30ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2 Модели, основанные на семантических сетях
Поиск ответа на запрос реализуется
сопоставлением подграфа запроса (рис.2.4) с фрагментами СС. Для этого осуществляются наложение подграфа запроса на соответствующий фрагмент сети (рис 2.3).Успешным будет то наложение, в результате которого фрагмент сети оказывается идентичным подграфу запроса. При этом допускается использование в запросе переменных (х).
Переменная запроса сопоставляется с константой фрагмента сети. Словесное описание запроса:
«Существует ли такая птица Х, которая умеет петь и имеет желтый цвет»
Изоморфное наложение подграфа на семантическую сеть дает ответ: Х=канарейка.
Основное преимущество модели, основанной на СС - наибольшее соответствие современным представлением об организации долговременной памяти человека.
Модели используются при анализе текстов естественного языка.
66
Слайд 31ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2
Модели, основанные на семантических сетях
Операции в семантической сети:
создать элемент
удалить элемент
установить
связь с другими элементамизадать принадлежность элемента к классу
выбор всех элементов данного класса.
Проблемы и недостатки семантических сетей:
Наименование свойств и их принадлежность (свойство может принадлежать конкретной кошке Мурке, но не принадлежать кошке).
При возрастании размерности падает наглядность СС.
Отсутствие эффективных языков для реализации.
Сетевые модели не имеют общей теории.
Для работы с СС используется много эвристик.
Проблема эффективности процедур работы с сетью.
В чистом виде семантические сети редко используются на практике. При построении системы искусственного интеллекта с использованием семантической сети обычно накладываются ограничения на типы объектов и отношения.
Понятие СС получило дальнейшее развитие во фреймовых моделях.
67
Слайд 32ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Фреймы можно рассматривать как фрагменты семантической сети. Они были
предложены в 1975г. ученым Марвином Мински.Фрейм – это упорядоченная структура, оболочка или схема для представления стереотипных ситуаций.
Каждый фрейм описывает один концептуальный объект, а конкретные свойства этого объекта и факты, относящиеся к нему, описываются в слотах.
Слот – это незаполненный структурный элемент фрейма.
В психологии и философии известно понятие абстрактного образа. Например, «комната» - это жилое помещение с 4 стенами, окнами, дверями, потолком, полом, площадью 6-30 кв. метров. Но в этом определении есть дырки или слоты: количество окон, дверей, площадь и т.д.
Когда человек оказывается в новой ситуации, он извлекает из памяти ранее накопленные блоки знаний, имеющие отношение к текущей ситуации, и пытается применить их. Эти блоки знаний и представляют собой фреймы. Вероятно, знания человека организованы в виде сети фреймов, отражающих его прошлый опыт.
Фрейм задается как структура вида:
{N (ns1, vs1, ps1), (ns2, vs2, ps2)… (nsk, vsk, psk)}
где N –имя фрейма; nsi – имя слота; vsi – значение слота;
рsi – имя присоединенной процедуры.
68
Слайд 33ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
После заполнения слотов конкретными данными фрейм будет представлять ту
или иную ситуацию, явление или объект ПО.Процедуры являются необязательным элементом слота. В качестве значений слотов могут выступать имена других слотов или фреймов более высокого уровня, что обеспечивает возможность построения сети фреймов.
Пример фрейма, описывающего комнату (аудиторию):
{комната (дверь,1) , (окно, 5) , (длина, 15) , (ширина, 8) , (высота, 3), (площадь, РS6) , (объем, PS7))
Если значения слотов не определены, то фрейм называется фреймом – прототипом или образцом, если определены – фреймом – экземпляром или конкретным фреймом.
Фрейм может содержать специальный слот, в котором задается отношение данного фрейма с другими фреймами сети.
Часто используется отношения АКО и Is a (быть экземпляром).
Слот АКО указывает, что данный фрейм является прямым подклассом вышестоящего по иерархии фрейма.
Вышестоящий фрейм называется родительским фреймом или суперклассом.
69
Слайд 34ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Одноместный номер
АКО: гостиничный номер
Мебель: кровать «Эмилия», шкаф,
журнальный столик, кресло
Инвентарь: телевизор «JVC», холодильник
«Норд», телефон кнопочный,
пепельница, стакан, карниз, шторы
Санузел: душ, …………..
Оплата: Цена
…………………………………………………………….
Рисунок. 2.5 Пример фрейма, представляющего гостиничный номер
70
Слайд 35ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Важной характеристикой фреймов является возможность включения в слот присоединенных
процедур. Выделяют следующие виды процедур:1.Процедуры – демоны, которые активизируются автоматически при каждой попытке удаления или добавления данных в слот. Чаще всего используются демоны трех видов:
Процедура «если добавлено» выполняется, если новые данные помещаются в слот.
Процедура «если удалено» выполняется, когда данные удаляются из слота.
Процедура «если нужно» автоматически запускается, когда запрашивается информация из слота, а с ним не связаны никакие значения.
2. Процедуры – слуги активизируются только по запросу при обращении к слоту.
Например: при обращении к слоту «Оплата» будет активизирована процедура «Цена», которая определяет стоимость проживания в сутки.
71
Слайд 36ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Все фреймы можно классифицировать на 4 группы:
Фреймы – структуры,
которые используются для описания объектов, понятий (например, заем, комната)Фреймы – роли, например: менеджер, кассир, клиент, студент.
Фреймы – сценарии, например: банкротство, сдача экзаменов, защита дипломной работы. Здесь важна последовательность действий во времени.
Фреймы – ситуации, например: тревога, авария, рабочий режим устройства.
72
Слайд 37ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Запись структуры фрейма можно представить в виде таблицы:
Имя фрейма
Имя
слота Значение слота Способ получения значения Присоединенная процедура73
Слайд 38ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Существует несколько способов получения значений слотов во фреймах –
экземплярах:по умолчанию от фрейма-образца;
через наследование свойств от фрейма, указанного в слоте АКО;
по формуле, указанной в слоте;
через присоединенную процедуру;
явно из диалога с пользователем;
из БД.
Фреймовые системы представляют собой иерархически организованные структуры, реализующие принцип наследования информации. Наследование значений происходит в направлении «суперкласс-подкласс», «класс-экземпляр класса». Например, кровать «Эмилия» является экземпляром класса «кровать». Поэтому кровать «Эмилия» наследует все свойства своего суперкласса.
74
Слайд 39ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Рассмотрим примеры фреймовых систем:
Система FMS
В этой системе фрейм имеет
структуру:<фрейм>::=<имя фрейма><ссылка на суперкласс> <слот>*
<слот>::=<имя><указатель наследования>
<тип данных><значение>
[<процедуры-демоны>]
<указатель наследования>::= unique| same|range|override
<тип данных>::=INTEGER| REAL| BOOL| STRING| TEXT| TABLE| LIST| FRAME
<процедуры-демоны>::=<если-добавлено >|<если - удалено >|
<если-нужно>
Поясним значения указателей наследования:
Unique (уникальный) означает, слоты с одними и теми же именами во фреймах, находящихся на разных уровнях иерархии могут иметь разные значения (полиморфизм).
Same (такой же) показывает, что слоты должны иметь одинаковые значения на разных уровнях иерархии.
Range (диапазон) устанавливает некоторые границы, в которых может находиться значение слота фрейма нижнего уровня;
Override комбинирует свойства unique и same
75
Слайд 40ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Рассмотрим примеры фреймовых систем:
2) Язык FRL (Frame Representation Language)
В
этой системе каждый слот содержит несколько фацет (от англ. facet – грань, сторона, аспект), характеризующихся значением. Так, предложение «лошадь серого цвета» можно представить на языке FRL в виде:
Frame Лошадь, slot цвет, facet $ value, value серый.
В состав каждого слота может входить 6 фацет:
$ value –текущее значение слота;
$ require – допустимые значения фацета value;
$ default – значение по умолчанию фацета value;
$ if-added – процедура-демон «если добавлено»;
$ if-removed – процедура-демон «если удалено»;
$ if-needed – процедура-демон «если нужно».
Каждый фрейм, создаваемый на языке FRL, содержит предварительно определенный слот АКО, позволяющий наследовать значения слотов в соответствии с иерархией фреймов.
76
Слайд 41ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
В моделях представления знаний фреймами объединяются преимущества декларативного и
процедурного подходов представления знаний. Фреймовый подход широко используется на практике, о чем свидетельствует наличие развитых фреймовых языков FRL, GUS, KRL, CONSUL.Однако во фреймовых системах отсутствует специальный механизм управления выводом. Поэтому вывод обычно реализуется с помощью процедур, встроенных во фреймы.
Управление выводом
Во фреймовых системах используются три способа управления выводом:
с помощью механизма наследования.
с помощью процедур – демонов.
с помощью присоединенных процедур.
Механизм наследования
является встроенным средством вывода, которым оснащены все фреймовые системы. Он обеспечивает значительную экономию памяти и автоматическое определение значений для слотов фреймов нижних уровней.
Фреймовые системы также оснащается набором специальных процедур:
процедура конструирования класса;
процедура конструирования экземпляра класса;
процедура записи значения в слот;
процедура чтения слота.
77
Слайд 42ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Процедура конструирования класса формирует фрейм-прототип с необходимым набором слотов
и соответствующими ссылками на суперклассы. Фрейм может быть связан с несколькими суперклассами. Процедура конструирования экземпляра класса позволяет формировать фреймы-примеры. Она автоматически устанавливает связь всех таких фреймов с соответствующим классом посредством Is_a слота.
Процедуры записи и чтения значений слотов осуществляют доступ к слотам соответствующих фреймов и позволяют пользователю ввести или определить значение соответствующего слота. Для этого, при их вызове, им передается имя фрейма и имя соответствующего слота. В случае, если значение какого-либо слота при вызове соответствующей процедуры конструирования не задается, то автоматически вызывается процедура, позволяющая установить значение слота по умолчанию. Это часто выполняется с помощью механизма наследования.
78
Слайд 43ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
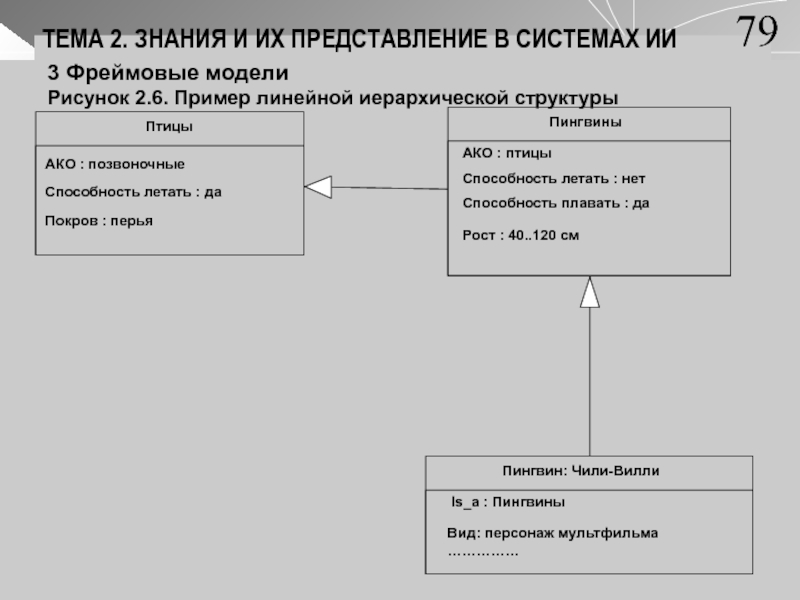
Рисунок 2.6. Пример линейной иерархической структуры
79
Слайд 44ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
На рис. 2.6 изображена простейшая иерархическая структура, в которой
каждый фрейм имеет только один суперкласс. Если подкласс (экземпляр класса) и суперкласс имеют слоты с совпадающими именами, то определения значений слотов, сделанные внутри подкласса (экземпляра класса), перекрывают определения суперкласса. Например, ответ на вопрос: «Может ли летать пингвин Чилли-Вилли?» будет отрицательным.
При поиске ответа фрейм–экземпляр («пингвин Чилли-Вилли») наследует все слоты фрейма «пингвины».
Значение слота «Способность летать» фрейма «Пингвины» перекрывает значение одноименного слота фрейма «Птицы».
В общем случае порядок наследования определяется с помощью списка предшествований. Для нашего примера его можно записать в виде:
(«пингвин Чилли-Вилли», «пингвины», «птицы»)
В реальных ситуациях взаимосвязь фреймов оказывается значительно сложнее, поэтому и правила формирования списка предшествований усложняются.
80
Слайд 45ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Использование процедур-демонов
Процедура «если нужно» вызывается, когда поступает запрос, требующий
установления значений соответствующего слота. Данная процедура наследуется подклассами и экземплярами класса. При этом процедура непосредственно не меняет значение слота, а каждый раз вычисляет его заново, учитывая определенные условия.
Например, для слота «Рост» экземпляра фрейма «Пингвин» (рис. 2.6) процедура может устанавливать рост в зависимости от значения слота «Вид». Если слот «Вид» принимает значение «Императорский» , то рост 100..120 см , иначе вернуть значение 40..50 см.
Процедуры «если добавлено» и «если удалено» активизируются при записи и удалении значений из слота.
81
Слайд 46ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
3
Фреймовые модели
Применение присоединенных процедур
Имя такой процедуры выступает в качестве значения
слота. Присоединенная процедура запускается по сообщению, переданному из другого фрейма. Для этого может использоваться специальная функция MSG, формат которой имеет вид:MSG(<имя фрейма>,<имя слота >, <параметры>).
Данная функция обеспечивает запуск присоединенной процедуры, находящейся в соответствующем слоте соответствующего фрейма. В свою очередь, вызванная процедура может также передать сообщение в другой фрейм и вызвать другую присоединенную процедуру и т.д. Возникает целая цепочка сообщений от одного фрейма к другому и возврат ответов. В итоге ответ возвращается в точку первоначального вызова и сообщается пользователю.
Если во фреймовой модели не используется процедуры – демоны и присоединенные процедуры, то фреймовые модели превращаются в семантические сети.
Использование процедурных значений во фреймовых системах повышает их гибкость, но усложняет управление.
Дальнейшее развитие фреймовые системы получили в системах объектно-ориентированного программирования.
Фреймовые модели эффективны для структурного описания сложных понятий и решения задач, в которых желательно применять различные способы вывода.
Фреймовую модель без механизма присоединенных процедур, а часто используют как базу данных системы продукций.
82