Временные ряды

Содержание

1. Временные ряды
2. План лекции:Виды временных рядовЧисловые характеристики стационарного временного рядаОсновные характеристики непрерывных случайных величинПрогнозирование временных рядов
3. Виды временных рядов Последовательность результатов наблюдений
4. Числовые характеристики стационарного временного рядаМатематическое ожидание: Дисперсия: Среднее квадратическое отклонение :
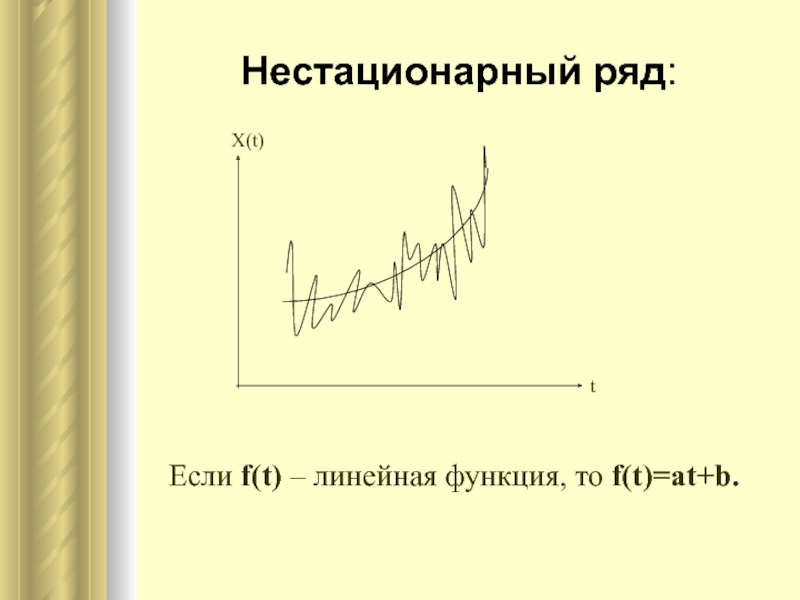
5. Нестационарный ряд:Значение х(t) определяют в виде суммы
6. Нестационарный ряд:Х(t)tЕсли f(t) – линейная функция, то f(t)=at+b.
7. Нахождение коэффициентовИспользуется метод наименьших квадратовРешение
8. ПРИМЕР: Данные о динамике роста объема
9. ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ Выявление основной
10. Для нашего примера прогнозирование заключается
11. БЛАГОДАРЮ ЗА ВНИМАНИЕ
12. Скачать презентанцию

План лекции:Виды временных рядовЧисловые характеристики стационарного временного рядаОсновные характеристики непрерывных случайных величинПрогнозирование временных рядов

Слайды и текст этой презентации

Слайд 1Временные ряды
Лекция 8

Слайд 2План лекции:
Виды временных рядов
Числовые характеристики стационарного временного ряда
Основные характеристики непрерывных

случайных величин
Прогнозирование временных рядов

План лекции:Виды временных рядовЧисловые характеристики стационарного временного рядаОсновные характеристики непрерывных случайных величинПрогнозирование временных рядов

Слайд 3 Виды временных рядов
Последовательность результатов наблюдений над некоторой величиной, полученных последовательно

во времени (интервал времени одинаков), называется временным рядом.
Временной ряд будет

детерминированным, если существует строгое функциональное соответствие х=f(t).
Все реальные ряды являются случайными.
Для произвольного ряда функция распределения зависит от времени. Такой ряд называется нестационарным.

Виды временных рядов Последовательность результатов наблюдений над некоторой величиной, полученных последовательно во времени (интервал времени одинаков),

Слайд 4Числовые характеристики стационарного временного ряда
Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение

:

Слайд 5Нестационарный ряд:
Значение х(t) определяют в виде суммы детерминированной f(t) и

случайной ζ(t) компоненты.
Детерминированная f(t) компонента характеризует основную тенденцию изменения временного

ряда, на которую накладываются случайные отклонения, определяемые случайной ζ(t) компонентой.
Основная задача практики – выявление тенденции изменения временного ряда (тренда), т.е. нахождение зависимости f(t).

Нестационарный ряд:Значение х(t) определяют в виде суммы детерминированной f(t) и случайной ζ(t) компоненты.Детерминированная f(t) компонента характеризует основную

Слайд 6Нестационарный ряд:
Х(t)
t
Если f(t) – линейная функция, то f(t)=at+b.

Слайд 7Нахождение коэффициентов
Используется метод наименьших квадратов

Решение

Слайд 8 ПРИМЕР: Данные о динамике роста объема производства некоторого препарата (в

т.) на фармацевтическом заводе за 10 лет представлены в таблице.

Составить уравнение тренда

f(t)=at+b

Уравнение тренда f(t) = 2,1·t+8,13

ПРИМЕР: Данные о динамике роста объема производства некоторого препарата (в т.) на фармацевтическом заводе за 10

Слайд 9ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ
Выявление основной тенденции изменения временного

ряда и нахождение его тренда называется прогнозированием временного ряда.

Ограничения:
между измерениями не происходит никаких принципиальных изменений в поведении ряда;
при увеличении временного интервала точность оценки снижается.

ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ Выявление основной тенденции изменения временного ряда и нахождение его тренда называется прогнозированием

Слайд 10 Для нашего примера прогнозирование заключается в попытке оценить

возможный объем производства на 11 год.
f(t) = 2,1·t+8,13

f(11) = 2,1·t+8,13= 2,1·11+8,13=31,23 (т)

Для нашего примера прогнозирование заключается в попытке оценить возможный объем производства на 11 год.

Слайд 11БЛАГОДАРЮ ЗА ВНИМАНИЕ

Скачать презентацию

Разделы презентаций

Временные ряды

Содержание

Слайды и текст этой презентации

Слайд 1Временные ряды
Лекция 8

Слайд 2План лекции:
Виды временных рядов
Числовые характеристики стационарного временного ряда
Основные характеристики непрерывных

случайных величин
Прогнозирование временных рядов

Слайд 3 Виды временных рядов
Последовательность результатов наблюдений над некоторой величиной, полученных последовательно

во времени (интервал времени одинаков), называется временным рядом.
Временной ряд будет

Слайд 4Числовые характеристики стационарного временного ряда
Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение

:

Слайд 5Нестационарный ряд:
Значение х(t) определяют в виде суммы детерминированной f(t) и

случайной ζ(t) компоненты.
Детерминированная f(t) компонента характеризует основную тенденцию изменения временного

Слайд 6Нестационарный ряд:
Х(t)
t
Если f(t) – линейная функция, то f(t)=at+b.

Слайд 7Нахождение коэффициентов
Используется метод наименьших квадратов

Решение

Слайд 8 ПРИМЕР: Данные о динамике роста объема производства некоторого препарата (в

т.) на фармацевтическом заводе за 10 лет представлены в таблице.

Слайд 9ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ
Выявление основной тенденции изменения временного

ряда и нахождение его тренда называется прогнозированием временного ряда.

Слайд 10 Для нашего примера прогнозирование заключается в попытке оценить

возможный объем производства на 11 год.
f(t) = 2,1·t+8,13

Слайд 11БЛАГОДАРЮ ЗА ВНИМАНИЕ

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Временные ряды

Содержание

Слайды и текст этой презентации

Слайд 1Временные рядыЛекция 8

Слайд 2План лекции:Виды временных рядовЧисловые характеристики стационарного временного рядаОсновные характеристики непрерывных

случайных величинПрогнозирование временных рядов

Слайд 3 Виды временных рядов Последовательность результатов наблюдений над некоторой величиной, полученных последовательно

во времени (интервал времени одинаков), называется временным рядом.Временной ряд будет

Слайд 4Числовые характеристики стационарного временного рядаМатематическое ожидание: Дисперсия: Среднее квадратическое отклонение

:

Слайд 5Нестационарный ряд:Значение х(t) определяют в виде суммы детерминированной f(t) и

случайной ζ(t) компоненты.Детерминированная f(t) компонента характеризует основную тенденцию изменения временного

Слайд 6Нестационарный ряд:Х(t)tЕсли f(t) – линейная функция, то f(t)=at+b.

Слайд 7Нахождение коэффициентовИспользуется метод наименьших квадратовРешение

Слайд 8 ПРИМЕР: Данные о динамике роста объема производства некоторого препарата (в

т.) на фармацевтическом заводе за 10 лет представлены в таблице.

Слайд 9ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ Выявление основной тенденции изменения временного

ряда и нахождение его тренда называется прогнозированием временного ряда.

Слайд 10 Для нашего примера прогнозирование заключается в попытке оценить

возможный объем производства на 11 год. f(t) = 2,1·t+8,13

Слайд 11БЛАГОДАРЮ ЗА ВНИМАНИЕ

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Временные ряды
Лекция 8

Слайд 2План лекции:
Виды временных рядов
Числовые характеристики стационарного временного ряда
Основные характеристики непрерывных

случайных величин
Прогнозирование временных рядов

Слайд 3 Виды временных рядов
Последовательность результатов наблюдений над некоторой величиной, полученных последовательно

во времени (интервал времени одинаков), называется временным рядом.
Временной ряд будет

Слайд 4Числовые характеристики стационарного временного ряда
Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение

Слайд 5Нестационарный ряд:
Значение х(t) определяют в виде суммы детерминированной f(t) и

случайной ζ(t) компоненты.
Детерминированная f(t) компонента характеризует основную тенденцию изменения временного

Слайд 6Нестационарный ряд:
Х(t)
t
Если f(t) – линейная функция, то f(t)=at+b.

Слайд 7Нахождение коэффициентов
Используется метод наименьших квадратов

Решение

Слайд 9ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ
Выявление основной тенденции изменения временного

возможный объем производства на 11 год.
f(t) = 2,1·t+8,13