Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Introduction to Continuous Mathematical Modeling
Содержание
- 1. Introduction to Continuous Mathematical Modeling
- 2. Математическая модельПРОСТЕЙШИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ОСНОВНЫЕ ПОНЯТИЯ
- 3. Математическая модельФормальная классификация моделейФормальная классификация моделей основывается
- 4. Математическая модельВ работе Р. Пайерлса (англ. R. Реiеrls) дана классификация математических моделей, используемых
- 5. Содержательная классификация моделейТип 2: Феноменологическая модель (ведем себя так,
- 6. Содержательная классификация моделейТип 4: Упрощение (опустим для ясности некоторые
- 7. Содержательная классификация моделейТип 5: Эвристическая модель (количественного подтверждения нет,
- 8. Содержательная классификация моделейТип 6: Аналогия (учтём только некоторые особенности)Р.
- 9. Содержательная классификация моделейТип 7: Мысленный эксперимент (главное состоит в
- 10. Содержательная классификация моделейТип 8: Демонстрация возможности (главное — показать внутреннюю
- 11. Содержательная классификация моделейВ основе содержательной классификации — этапы,
- 12. Элементарные математические модели Рассмотрим некоторые подходы к
- 13. Элементарные математические модели Законы сохранения Зако́ны
- 14. Законы сохраненияНекоторые из законов сохранения выполняются всегда
- 15. Законы сохранения Законы сохранения связаны с симметриями физических систем
- 16. Законы сохранения С фундаментальной точки зрения, согласно теореме
- 17. Ама́лия Э́мми НётерВ 1916 году Нётер переехала в Гёттинген,
- 18. Элементарные математические моделиДля каждого вида энергии закон
- 19. Элементарные математические моделиСохранение энергии. Этот закон известен
- 20. Элементарные математические моделиЭти трансформации описываются цепочкой равенств
- 21. Элементарные математические моделиЭта формула будет вполне точной,
- 22. Элементарные математические моделиПоэтому примененный для вычисления величины
- 23. Элементарные математические моделиСходные рассуждения может применить и
- 24. где — энергия, требуемая для
- 25. тратится энергия
- 26. где
- 27. Элементарные математические моделиВ действительности процесс сверления гораздо
- 28. Элементарные математические модели. Сохранение материиАнаксима́ндр Миле́тский
- 29. Элементарные математические модели. Сохранение материиЗакон сохранения массы —
- 30. Элементарные математические модели. Сохранение материиСовременное состояниеВ XX
- 31. Элементарные математические модели. Сохранение материиСовременное состояние(M2) Масса
- 32. Список использованной литературыhttp://ru.wikipedia.org/wiki/Математическая_модельСамарский А. А., Михайлов А.
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Introduction to Continuous Mathematical Modeling
Российский университет дружбы народов
Факультет физико-математических и
естественных наук
Слайд 2Математическая модель
ПРОСТЕЙШИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Рассмотрим
некоторые подходы к построению простейших математических моделей, иллюстрирующие применение фундаментальных
законов природы, вариационных принципов, аналогий, иерархических цепочек. Несмотря на простоту, привлекаемый материал даст возможность начать обсуждение таких понятий, как адекватность моделей, их «оснащение», нелинейность, численная реализация и ряда других принципиальных вопросов математического моделирования.Повторим подробнее формальную классификацию моделей
Слайд 3Математическая модель
Формальная классификация моделей
Формальная классификация моделей основывается на классификации используемых
математических средств. Часто строится в форме дихотомий. Например, один из популярных
наборов дихотомий:Линейные или нелинейные модели;
Сосредоточенные или распределённые системы;
Детерминированные или стохастические;
Статические или динамические;
Дискретные или непрерывные.
Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д.
Слайд 4Математическая модель
В работе Р. Пайерлса (англ. R. Реiеrls) дана классификация математических моделей, используемых в физике и, шире, в
естественных науках.
Содержательная классификация моделей
Тип 1: Гипотеза (такое могло бы быть)
Эти модели «представляют
собой пробное описание явления, причем автор либо верит в его возможность, либо считает его даже истинным». По Р. Пайерлсу это, например,
модель Солнечной системы по Птолемею и
модель Коперника (усовершенствованная Кеплером),
модель атома Резерфорда и модель Большого Взрыва.
Никакая гипотеза в науке не бывает доказана раз и навсегда. Очень чётко это сформулировал Ричард Фейнман:
«У нас всегда есть возможность опровергнуть теорию, но, обратите внимание, мы никогда не можем доказать, что она правильна. Предположим, что вы выдвинули удачную гипотезу, рассчитали, к чему это ведет, и выяснили, что все ее следствия подтверждаются экспериментально. Значит ли это, что ваша теория правильна? Нет, просто-напросто это значит, что вам не удалось ее опровергнуть.»[20]
Если модель первого типа построена, то это означает что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.
Слайд 5Содержательная классификация моделей
Тип 2: Феноменологическая модель (ведем себя так, как если бы…)
Феноменологическая
модель содержит механизм для описания явления. Однако этот механизм недостаточно
убедителен, не может быть достаточно подтверждён имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус вре́менных решений. Считается, что ответ всё ещё неизвестен и необходимо продолжить поиск «истинных механизмов». Ко второму типу Пайерлс относит, например, модели теплорода и кварковую модель элементарных частиц.Тип 3: Приближение (что-то считаем очень большим или очень малым)
Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди них модели линейного отклика. Уравнения заменяются линейными. Стандартный пример — закон Ома.
Слайд 6Содержательная классификация моделей
Тип 4: Упрощение (опустим для ясности некоторые детали)
В модели типа
4 отбрасываются детали, которые могут заметно и не всегда контролируемо
повлиять на результат. Одни и те же уравнения могут служить моделью типа 3 (приближение) или 4 (опустим для ясности некоторые детали) — это зависит от явления, для изучения которого используется модель. Так, если модели линейного отклика применяются при отсутствии более сложных моделей (то есть не производится линеаризация нелинейных уравнений, а просто ищутся линейные уравнения, описывающие объект), то это уже феноменологические линейные модели, и относятся они к типу 4 (все нелинейные детали «для ясности» опускаем).Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей и ядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям 4-го типа.
Слайд 7Содержательная классификация моделей
Тип 5: Эвристическая модель (количественного подтверждения нет, но модель способствует
более глубокому проникновению в суть дела)
Эвристическая модель сохраняет лишь качественное подобие
реальности и даёт предсказания только «по порядку величины». Типичный пример — приближение средней длины свободного пробега в кинетической теории. Оно даёт простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины.Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.
Слайд 8Содержательная классификация моделей
Тип 6: Аналогия (учтём только некоторые особенности)
Р. Пайерлс приводит историю
использования аналогий в первой статье В. Гейзенберга о природе ядерных сил. «Это
произошло после открытия нейтрона, и хотя сам В. Гейзенберг понимал, что можно описывать ядра состоящими из нейтронов и протонов, он не мог все же избавиться от мысли, что нейтрон должен в конечном счете состоять из протона и электрона. При этом возникала аналогия между взаимодействием в системе нейтрон — протон и взаимодействием атома водорода и протоном. Эта-то аналогия и привела его к заключению, что должны существовать обменные силы взаимодействия между нейтроном и протоном, которые аналогичны обменным силам в системе H − H + , обусловленным переходом электрона между двумя протонами. … Позднее было все-таки доказано существование обменных сил взаимодействия между нейтроном и протоном, хотя ими не исчерпывалось полностью взаимодействие между двумя частицами… Но, следуя все той же аналогии, В. Гейзенберг пришёл к заключению об отсутствии ядерных сил взаимодействия между двумя протонами и к постулированию отталкивания между двумя нейтронами. Оба последних вывода находятся в противоречии с данными более поздних исследований».Слайд 9Содержательная классификация моделей
Тип 7: Мысленный эксперимент (главное состоит в опровержении возможности)
А. Эйнштейн был одним
из великих мастеров мысленного эксперимента. Вот один из его экспериментов.
Он был придуман в юности и, в конце концов, привел к построению специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда юный Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость света не зависит от системы отсчета. Он выбрал второй — более красивый вариант. Другой знаменитый мысленный эксперимент Эйнштейна — Парадокс Эйнштейна — Подольского — Розена.Слайд 10Содержательная классификация моделей
Тип 8: Демонстрация возможности (главное — показать внутреннюю непротиворечивость возможности)
Это тоже
мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципам
и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.Один из самых знаменитых таких экспериментов — геометрия Лобачевского (Лобачевский называл её «воображаемой геометрией»). Другой пример — массовое производство формально — кинетических моделей химических и биологических колебаний, автоволн и др. Парадокс Эйнштейна — Подольского — Розена был задуман как модель 7 типа, для демонстрации противоречивости квантовой механики. Совершенно незапланированным образом он со временем превратился в модель 8 типа — демонстрацию возможности квантовой телепортации информации.
В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь типов исследовательских позиций при моделировании.
Слайд 11Содержательная классификация моделей
В основе содержательной классификации — этапы, предшествующие математическому анализу
и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь
типов исследовательских позиций при моделировании.Наиболее лаконичное определение математической модели:
«Уравнение, выражающее идею.»
Слайд 12Элементарные математические модели
Рассмотрим некоторые подходы к построению простейших математических моделей,
иллюстрирующие применение фундаментальных законов природы, вариационных принципов, аналогий, иерархических цепочек.
Несмотря на простоту, привлекаемый материал даст возможность начать обсуждение таких понятий, как адекватность моделей, их «оснащение», нелинейность, численная реализация и ряда других принципиальных вопросов математического моделирования.Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
Слайд 13Элементарные математические модели
Законы сохранения
Зако́ны сохране́ния — фундаментальные физические законы, согласно
которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую
физическую систему, не изменяются с течением времени.Философские предпосылки к открытию закона были заложены ещё античными философами, а также Декартом и М. В. Ломоносовым.
В письме к Эйлеру Ломоносов формулирует свой «всеобщий естественный закон» (5 июля 1748 года), повторяя его в диссертации «Рассуждение о твердости и жидкости тел» (1760)
...Все перемены, в натуре случающиеся, такого суть состояния, что сколько чего у одного тела отнимется, столько присовокупится к другому, так ежели где убудет несколько материи, то умножится в другом месте... Сей всеобщий естественный закон простирается и в самые правила движения, ибо тело, движущее своею силою другое, столько же оные у себя теряет, сколько сообщает другому, которое от него движение получает.
М. В. Ломоносов
Слайд 14Законы сохранения
Некоторые из законов сохранения выполняются всегда и при всех
условиях (например, законы сохранения энергии, импульса, момента импульса, электрического заряда), или, во всяком случае,
никогда не наблюдались процессы, противоречащие этим законам. Другие законы являются лишь приближёнными и выполняющимися при определённых условиях (например, закон сохранения массы выполняется в нерелятивистском приближении; закон сохранения чётности выполняется для сильного и электромагнитного взаимодействия, но нарушается в слабом взаимодействии).Закон сохранения энергии
Закон сохранения импульса
Закон сохранения момента импульса
Закон сохранения массы
Закон сохранения электрического заряда
Закон сохранения лептонного числа
Закон сохранения барионного числа
Закон сохранения чётности
Слайд 15Законы сохранения
Законы сохранения связаны с симметриями физических систем (теорема Нётер). Так,
законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных
симметрий (соответственно: однородности времени, однородности и изотропности пространства).При этом перечисленные свойства пространства и времени в аналитической механике принято понимать как инвариантность лагранжиана относительно изменения начала отсчета времени, переноса начала координат системы и вращения ее координатных осей.
Слайд 16Законы сохранения
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения
энергии является следствием однородности времени, то есть независимости законов физики от
момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.Ама́лия Э́мми Нётер (нем. Amalie Emmy Noether ; 23 марта 1882, Эрланген, Германия — 14 апреля 1935, Брин-Мор,Пенсильвания, США) — выдающийся немецкий математик, «самая крупная женщина-математик, когда-либо существовавшая»
Слайд 17Ама́лия Э́мми Нётер
В 1916 году Нётер переехала в Гёттинген, где знаменитые математики
Давид Гильберт и Феликс Клейн продолжали работы по теории относительности, и знания
Нётер в области теории инвариантов были им нужны. Гильберт оказал на Нётер огромное влияние, сделав её сторонницей аксиоматического метода. Он пытался сделать Нётер приват-доцентом Гёттингенского университета, но все его попытки провалились из-за предрассудков профессуры, в основном в области гуманитарных наук. Стала известна фраза Гильберта: Не понимаю, почему пол кандидата служит доводом против избрания её приват-доцентом. Ведь здесь университет, а не мужская баня!Нётер тем не менее, не занимая никакой должности, часто читала лекции за Гильберта. Лишь по окончании Первой мировой войны она смогла стать приват-доцентом в 1919 году, затем сверхштатным профессором (1922).
На протяжении 10 лет жизни она сотрудничала с математиками СССР; в 1928—1929 учебном году читала лекции в Московском университете, где она оказала влияние на Л. С. Понтрягина и особенно на П. С. Александрова, до этого часто бывавшего в Гёттингене.
Слайд 18Элементарные математические модели
Для каждого вида энергии закон сохранения может иметь
свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон
сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.
Классическая механика
В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом:
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда.
Слайд 19Элементарные математические модели
Сохранение энергии. Этот закон известен почти двести лет
и занимает, пожалуй, наиболее почетное место среди великих законов природы.
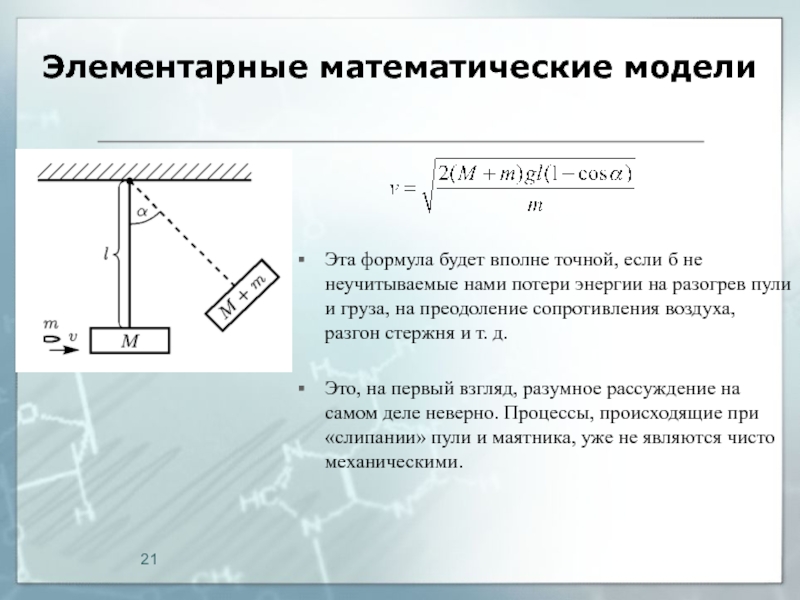
Полагаясь на него, эксперт по баллистике, желающий быстро определить скорость револьверной пули и не имеющий поблизости специальной лаборатории, может воспользоваться относительно простым устройством типа маятника — груза, подвешенного на легком жестком и свободно вращающемся стержне . Пуля, застрявшая в грузе, сообщит системе «пуля—груз» свою кинетическую энергию, которая в момент наибольшего отклонения стержня от вертикали полностью перейдет в потенциальную энергию системы.Слайд 20Элементарные математические модели
Эти трансформации описываются цепочкой равенств
Здесь
— кинетическая энергия пули массы
, имеющей скорость , - масса груза, — скорость системы «пуля—груз» сразу после столкновения, — ускорение свободного падения, — длина стержня, — угол наибольшего отклонения.Искомая скорость определяется формулой
Слайд 21Элементарные математические модели
Эта формула будет вполне точной, если б не
неучитываемые нами потери энергии на разогрев пули и груза, на
преодоление сопротивления воздуха, разгон стержня и т. д.Это, на первый взгляд, разумное рассуждение на самом деле неверно. Процессы, происходящие при «слипании» пули и маятника, уже не являются чисто механическими.
Слайд 22Элементарные математические модели
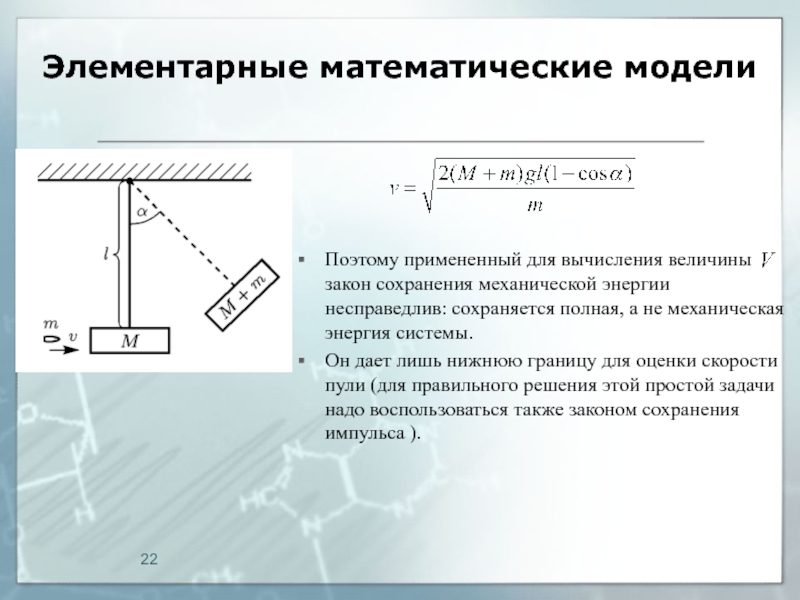
Поэтому примененный для вычисления величины закон сохранения механической
энергии несправедлив: сохраняется полная, а не механическая энергия системы.
Он
дает лишь нижнюю границу для оценки скорости пули (для правильного решения этой простой задачи надо воспользоваться также законом сохранения импульса ).Слайд 23Элементарные математические модели
Сходные рассуждения может применить и инженер для оценки
времени сверления слоя металла толщины
лазером с мощностью , излучение которого перпендикулярно поверхности материала.Слайд 24где — энергия, требуемая для испарения единицы массы.
Величина
имеет составную структуру:
, поскольку материал необходимо последовательно нагреть до температуры плавления, а затем расплавить и превратить в пар ( - исходная температура, - удельная теплоемкость и - соответственно удельная теплота плавления и парообразования).Элементарные математические модели
Если энергия лазера полностью идет на испарение столбика металла массы
( — облучаемая площадь, — объем столбика, — плотность вещества), то закон сохранения энергии выражается равенством
Слайд 25тратится энергия , равная
энергии , сообщаемой веществу лазером:
, откуда получается дифференциальное уравнениеЭлементарные математические модели
Изменение глубины выемки со временем определяется из детального баланса энергии в промежутке времени
от до . На испаренную за это время массу
Слайд 26где — вся энергия,
выделенная лазером к моменту времени . Следовательно, глубина
выемки пропорциональна затраченной энергии (причем величина , когда , совпадает с вычисленной по формулеЭлементарные математические модели
Его интегрирование (с учетом того, что начальная глубина выемки равна нулю) дает
Слайд 27Элементарные математические модели
В действительности процесс сверления гораздо сложнее рассмотренной схемы
— энергия тратится на нагрев вещества, на удаление паров из
выемки, которая может иметь неправильную форму. Поэтому уверенность в правильности предложенного математического описания значительно меньше, чем в случае с пулей. Вопрос о соответствии объекта и его модели — один из центральных в математическом моделировании.
Слайд 28Элементарные математические модели. Сохранение материи
Анаксима́ндр Миле́тский
( 610 — 547/540 до н. э.) древнегреческий философ, представитель милетской школы натурфилософии, ученик Фалеса
Милетского.Ввёл термин «закон», применив понятие общественной практики к природе и науке. Анаксимандру приписывают одну из первых формулировок закона сохранения материи:
«из тех же вещей, из которых рождаются все сущие вещи, в эти же самые вещи они разрушаются согласно предназначению».
Слайд 29Элементарные математические модели. Сохранение материи
Закон сохранения массы — исторический закон физики,
согласно которому масса как мера количества вещества сохраняется при всех природных процессах,
то есть несотворима и неуничтожима.Именно этим соображением руководствуются, решая задачу о заполнении бассейна водой, втекающей и вытекающей из двух труб.
В настоящее время известен ряд условий, при которых данный закон нарушается — например, при радиоактивном распаде совокупная масса вещества уменьшается. В современной физике закон сохранения массы является частным случаем закона сохранения энергии, и он выполняется только в консервативных физических системах, то есть при отсутствии энергообмена с внешней средой.
Слайд 30Элементарные математические модели. Сохранение материи
Современное состояние
В XX веке обнаружились два
новых свойства массы.
(M1) Масса физического объекта зависит от его внутренней
энергии (Эквивалентность массы и энергии). При поглощении внешней энергии масса растёт, при потере — уменьшается. Отсюда следует, что в общефизическом смысле закон сохранения массы неверен. Особенно ощутимо изменение массы при ядерных реакциях. Но даже при химических реакциях, которые сопровождаются выделением (или поглощением) тепла, масса не сохраняется, хотя в этом случае дефект массы ничтожен. Масса сохраняется только в консервативных системах, то есть при отсутствии обмена энергией с внешней средой. Академик Л. Б. Окунь пишет:Масса тела меняется всегда, когда меняется его внутренняя энергия, 1) при нагревании железного утюга на 200° его масса возрастает на величину ; 2) при полном превращении некоторого количества льда в воду .
Слайд 31Элементарные математические модели. Сохранение материи
Современное состояние
(M2) Масса не является аддитивной
величиной: масса системы не равна массе её составляющих. Примеры неаддитивности:
Электрон и позитрон,
каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).
Таким образом, при физических процессах, которые сопровождаются распадом или синтезом физических структур, общая масса не сохраняется.
Сказанное означает, что в современной физике закон сохранения массы является частным и ограниченным случаем закона сохранения энергии и не всегда выполняется.
Слайд 32Список использованной литературы
http://ru.wikipedia.org/wiki/Математическая_модель
Самарский А. А., Михайлов А. П. Математическое моделирование. Идеи.
Методы. Примеры. — 2-е изд., испр.. — М.: Физматлит, 2001. — ISBN 5-9221-0120-X.
Арнольд В.
И. Жёсткие и мягкие математические модели — М.: МЦНМО, 2004. — ISBN 5-94057-134-4.http://www.mccme.ru/edu/index.php?ikey=viarn-models