Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ И ГЕОИНФОРМАТИКА
Содержание
- 1. ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ И ГЕОИНФОРМАТИКА
- 2. Инженерная геодезия: учебник для студ. высш. учеб.
- 3. ВВЕДЕНИЕ Задачи геодезии в разных циклах строительного
- 4. ФИГУРА ЗЕМЛИ И МЕТОД ПРОЕКЦИЙ Общая фигура
- 5. ОБЩАЯ ФИГУРА ЗЕМЛИ, КАК ПЛАНЕТЫЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЯ ЛЮДЕЙО
- 6. ПЛАН И КАРТАПлан – уменьшенное изображение земной
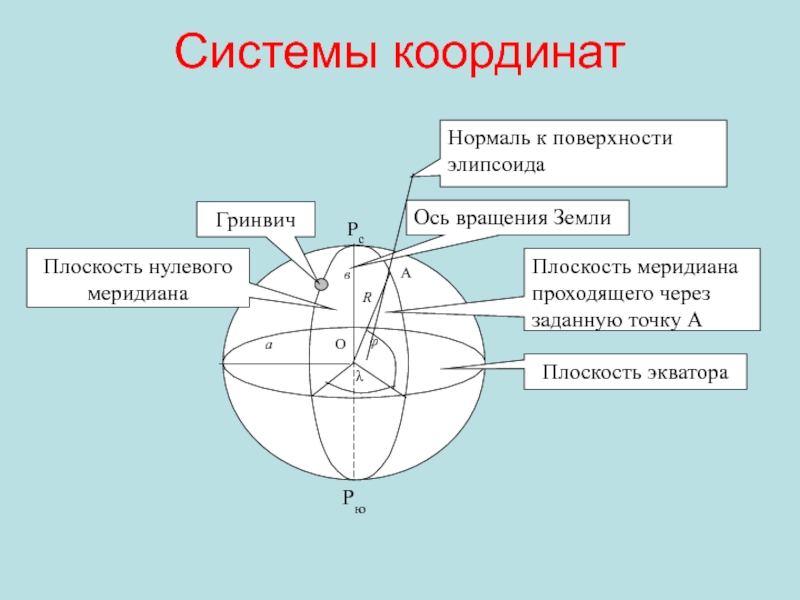
- 7. Системы координатРсНормаль к поверхности элипсоида
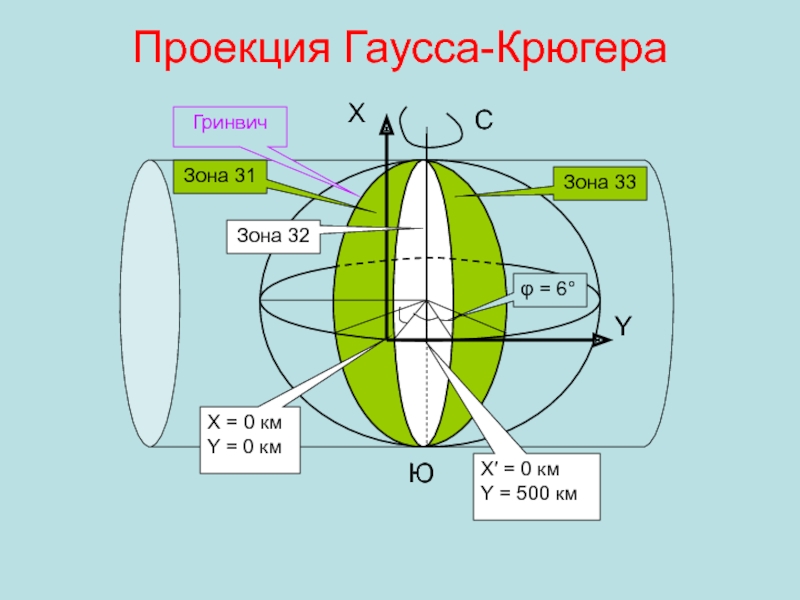
- 8. РАВНОУГОЛЬНАЯ ПОПЕРЕЧНО-ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ ЗЕМНОЙ ПОВЕРХНОСТИ (ПРОЕКЦИЯ ГАУССА-КРЮГЕРА)
- 9. Проекция Гаусса-Крюгераφ = 6°Зона 31Зона 32Зона 33
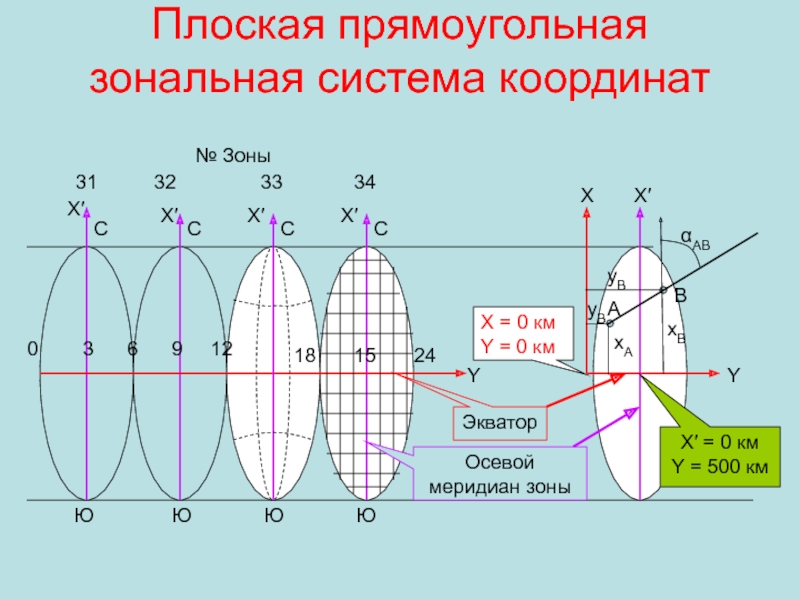
- 10. Плоская прямоугольная зональная система координат0
- 11. Ориентирование линий на Земной поверхностиистинным азимутом называют
- 12. Ориентирование линий на Земной поверхностиМагнитный азимут, склонение магнитной стрелки
- 13. Ориентирование линий на Земной поверхностиЮСАВDАи(А) < Аи(В)
- 14. Ориентирование линий на Земной поверхностиγ = (λВ – λА) Sin φСближение меридиановЮ
- 15. Ориентирование линий на Земной поверхности Понятие румбаЮСЗВX
- 16. Ориентирование линий на Земной поверхностиАВМагнитный меридианЛинии параллельные
- 17. Угловые измеренияЕдиницы измерения углов: Радиан, градус, град. Радиан
- 18. Угловые измерения Принцип измерения горизонтальных и вертикальных
- 19. Угловые измерения Прибор для измерения горизонтальных и
- 20. Угловые измерения Конструкция теодолита (тахеометра): Принцип устройстваОсь
- 21. Угловые измерения Поверки теодолита (тахеометра)Ось уровня
- 22. Угловые измерения Поверки теодолита (тахеометра)Вертикальная нить
- 23. Угловые измерения Способы измерения угловОт нуля;Приемов;Круговых приемовПовторений0° 00,0′АВСβАВСβАВСDE0° 17,0′
- 24. Угловые измерения Точность измерения угловβDβAβBβCACDβA1A1Погрешность центрированияПогрешность редукцииΔβA
- 25. Угловые измерения Точность измерения угловΔβ1, Δβ2, …, Δβn или x1, x2, …, xnx
- 26. Линейные измеренияНепосредственные: 20-и метровая стальная геодезическая
- 27. Линейные измерения Конструкция мерной ленты10,10,51,0РучкаШтрих начала счетаОтверстияЗаклепкаЗаклепка
- 28. Линейные измерения Косвенные. Оптические дальномерыС постоянным углом
- 29. Линейные измерения Косвенные. Светодальномер. Лазерный дальномерD =
- 30. +ΔL-ΔLЛинейные измерения Компарирование мерных приборовКомпарирование мерного прибора
- 31. Линейные измеренияМетодика измерения линий 20-и метровой стальной
- 32. Линейные измерения Геометрическое нивелирование из серединыh1
- 33. Линейные измерения Геометрическое нивелирование промежуточных точекАВСDEFУровень
- 34. Линейные измерения Тригонометрическое нивелированиеvvD = k n′nn′d
- 35. Съемка территории. Составление плана участка местностиПланово-высотное обоснование
- 36. Съемка территории. Составление плана участка местностиПолевые работыРекогносцировка
- 37. Съемка территории. Составление плана участка местностиСхема теодолитного хода2прим345Dср(1-2)Dср(2-3)Dср(3-4)Dср(4-5)Dср(5-1)Направление хода1Аxy1xy2345Направление на СеверXYαA-1X
- 38. 9 КЖ154,710,08,04,24,714,911,9Съемка территории. Составление плана участка местностиСпособы
- 39. Съемка территории. Составление плана участка местностиСпособы съемки
- 40. Съемка территории. Составление плана участка местностиКамеральные работыРешение
- 41. Съемка территории. Составление плана участка местностиОбратная геодезическая задачаАYXyАXАy1X1r = αА11dA1
- 42. Съемка территории. Составление плана участка местностиВычисления в
- 43. Съемка территории. Составление плана участка местностиВычисления в ведомости координат. Вычисление дирекционных угловС Северαпредαпослβправαпред180°С СеверАВDβлев
- 44. Съемка территории. Составление плана участка местностиВычисления в
- 45. Съемка территории. Составление плана участка местностиВычисление в ведомости координат. Уравнивание (сторон) приращений координат
- 46. Съемка территории. Составление плана участка местностиВычисление в
- 47. Съемка территории. Составление плана участка местностиВычисление в
- 48. Съемка территории. Составление плана участка местностиСъемка рельефаСъемочное обоснованиеГеометрическое нивелированиеТригонометрическое нивелированиеНивелирование застроенной территорииТахеометрическая съемкаРисовка рельефа на плане
- 49. Съемка рельефа. Балтийский футшток
- 50. Съемочное обоснованиеГеометрическое нивелированиеЖурнал технического нивелирования
- 51. Съемочное обоснованиеГеометрическое нивелированиеЖурнал технического нивелирования, Постраничный контроль:
- 52. Съемочное обоснование Геометрическое нивелирование Схема нивелирного ходаТ
- 53. Съемочное обоснование Геометрическое нивелирование Уравнивание превышенийИсходные данные:Средние
- 54. Съемка рельефа Абрис нивелирования застроенной территории9
- 55. Съемка рельефа Нивелирование застроенной территорииЖурнал нивелирования
- 56. Съемочное обоснование Тригонометрическое нивелирование Схема тахеометрического хода15432d12d51d45d34d23v12v43v51v34v32v23v21v54v45v15Превышения
- 57. Съемочное обоснование Тригонометрическое нивелированиеЖурнал тахеометрической съемкиСтанция №
- 58. Съемочное обоснование Тригонометрическое нивелирование Ведомость увязки
- 59. Съемка рельефа Абрис тахеометрической съемки0 00,01
- 60. Съемка рельефа Рисовка рельефа на плане33,2436,5932,1736,0934,8735,7737,1133,4534,2536,4535,1833,8932,1931,8835,6535,9734,3534,9833,9134,5533,1533,77
- 61. Трассирование и нивелирование Трассирование, Разбивка ключевых
- 62. Трассирование и нивелирование Трассирование, вычисление румбов
- 63. Трассирование и нивелирование Трассирование, вычисление румбовriCЮВЗθθCЮriri+1ri+1riCЮВЗCЮriθri+1θri+1ВЗ
- 64. Трассирование и нивелирование Трассирование и разбивка кривойΘТТΨ
- 65. ПК 2Трассирование и нивелирование Трассирование, вынос пикетов
- 66. Трассирование и нивелирование Трассирование, ведомость прямых и кривых
- 67. Трассирование и нивелирование Нивелирование, продольный профильСмотри файл в World
- 68. Элементы теории погрешностей геодезических измеренийСвойства измеренных величин
- 69. Элементы теории погрешностей равноточные измерения Распределение
- 70. Элементы теории погрешностей равноточные измерения Распределение
- 71. Элементы теории погрешностей Распределение вероятностей появления случайных
- 72. Элементы теории погрешностей Случайные погрешности обладают
- 73. Элементы теории погрешностей Оценка точности измеренийПо
- 74. Элементы теории погрешностей Оценка точности измеренийОтносительная погрешность
- 75. Элементы теории погрешностей неравноточные измерения
- 76. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ И ГЕОИНФОРМАТИКА
Кафедра
Геоэкологии и инженерной геологии
2013 – 14
уч. год
Слайд 2
Инженерная геодезия: учебник для студ. высш. учеб. заведений / Е.Б.
Клюшин, М.И. Киселев, Д.Ш. Михелев, В.Д. Фельдман; под ред. Д.Ш.
Михелева. – 8-е изд., стер. – М.: Изд. Центр “Академия”, 2008. – 480 с.Федотов Г.А. Инженерная геодезия: учебник / Г.А. Федотов. – 4-е изд. стер. – М.: Высш. шк., 2007. – 463 с.
Сборник задач и упражнений по геоинформатике: учеб. пособие / Е.Г. Капралов, и др.; под ред. В.С. Тикунова. – 2-е изд. Перераб и доп. – М.: Академия, 2009. – 512 с.
Интернет- ресурс
Михелев Д.Ш. Инженерная геодезия: учебник /Е.Б. Клюшин [и др.]; под ред. Д.Ш.Михелева, - 9-е изд. стер. – Электронные текстовые данные –М.: ИЦ «Академия», 2008.
ЛИТЕРАТУРА
Слайд 3ВВЕДЕНИЕ
Задачи геодезии в разных циклах строительного производства
В период проектирования:
сбор
исходной картографической информации для принципиального решения вопроса размещения объекта строительства;
съемочные
работы в крупном масштабе для детального проектирования элементов объекта строительства.В период строительства:
определение местоположения площадки строительства и пространственное размещение в плане и по высоте элементов запроектированного сооружения;
геодезическое сопровождение строительства объекта для контроля правильности возведения конструкции в целом и взаимного расположения его элементов.
В период эксплуатации:
исполнительная съемка для контроля правильности завершенного строительства и выявления отступлений от проекта;
геодезические работы по определению эксплуатационных сдвигов объекта в целом и смещений его элементов для контроля и прогноза устойчивости конструкции.
Слайд 4ФИГУРА ЗЕМЛИ И МЕТОД ПРОЕКЦИЙ
Общая фигура Земли, как планеты.
Географическая, геодезическая и астрономическая системы координат.
Равноугольная поперечно-цилиндрическая проекция Земной поверхности
(проекция Гаусса-Крюгера).Плоская прямоугольная зональная система координат.
Ориентирование линий на Земной поверхности. Истинный и магнитный азимут, дирекционный угол, румб.
Склонение магнитной стрелки. Сближение меридианов. Связь между истинным и магнитным азимутами, истинным азимутом и дирекционным углом.
Слайд 5ОБЩАЯ ФИГУРА ЗЕМЛИ, КАК ПЛАНЕТЫ
ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЯ ЛЮДЕЙ
О ФОРМЕ ЗЕМЛИ
первое –
Плоскость;
второе – Шар;
третье – Эллипсоид вращения;
четвертое – Геоид
Слайд 6ПЛАН И КАРТА
План – уменьшенное изображение земной поверхности выполненное в
ортогональной проекции:
без искажения расстояний и углов;
имеет место
подобие геометрических фигур;первое представление людей о форме Земли.
Карта - уменьшенное изображение земной поверхности выполненное в специальной картографической проекции:
искажаются либо расстояния либо углы;
отсутствует подобие геометрических фигур;
второе или третье представление людей о форме Земли.
Слайд 10Плоская прямоугольная зональная система координат
0 3
6 9 12
С
С
С
С
X′
X′
X′
X′
Y
Экватор
Ю
Ю Ю Ю18
24
15
№ Зоны
31
32
33
34
В
А
xB
yB
xA
yB
Y
X′
X
X′ = 0 км
Y = 500 км
X = 0 км
Y = 0 км
αАВ
Осевой меридиан зоны
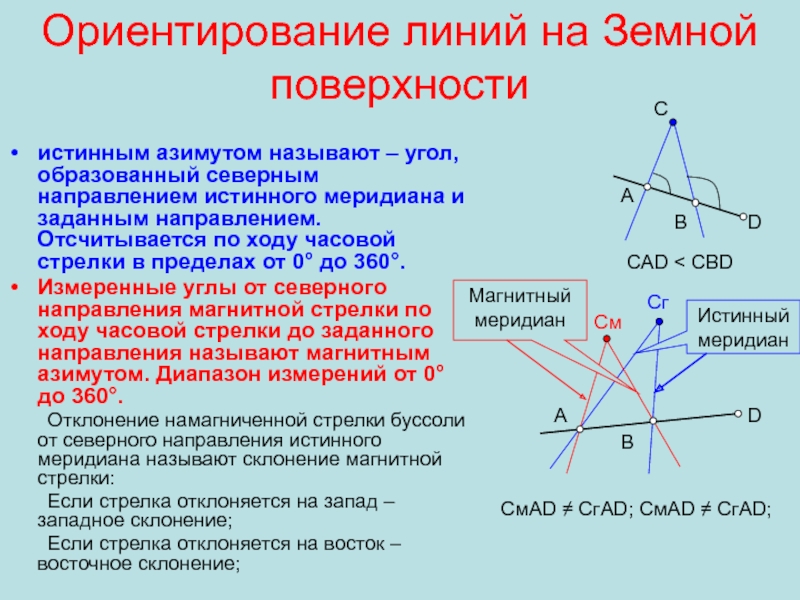
Слайд 11Ориентирование линий на Земной поверхности
истинным азимутом называют – угол, образованный
северным направлением истинного меридиана и заданным направлением. Отсчитывается по ходу
часовой стрелки в пределах от 0° до 360°.Измеренные углы от северного направления магнитной стрелки по ходу часовой стрелки до заданного направления называют магнитным азимутом. Диапазон измерений от 0° до 360°.
Отклонение намагниченной стрелки буссоли от северного направления истинного меридиана называют склонение магнитной стрелки:
Если стрелка отклоняется на запад – западное склонение;
Если стрелка отклоняется на восток – восточное склонение;
А
С
В
САD < CВD
D
Cг
См
А
В
D
CмАD ≠ CгАD; CмАD ≠ CгАD;
Магнитный меридиан
Истинный меридиан
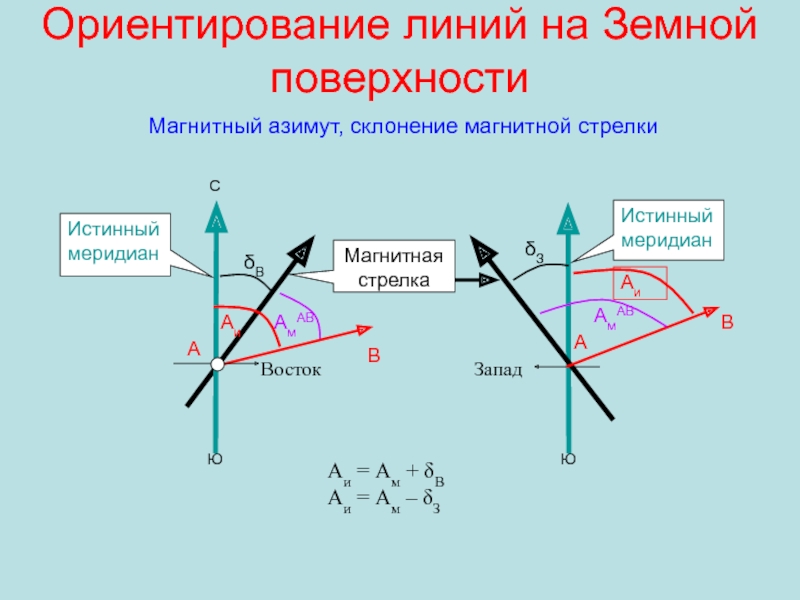
Слайд 13Ориентирование линий на Земной поверхности
Ю
С
А
В
D
Аи(А) < Аи(В) < Аи(D)
X
Y
Ю
С
А
В
D
X
Y
αB
αА =
αВ = αD
αD
αA
αА = Аи(А) + γз
γз
γв
αВ = Аи(В)
αD
= Аи(D) - γвК понятию дирекционного угла
Осевой меридиан
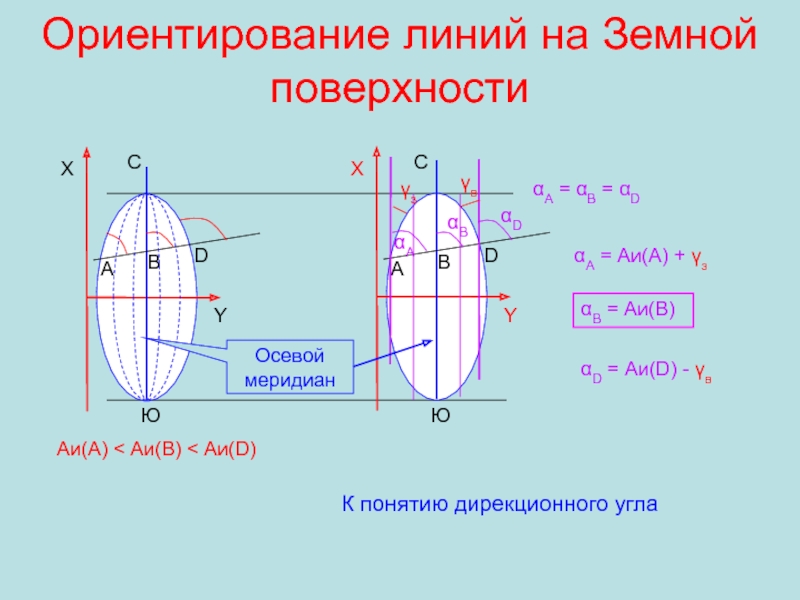
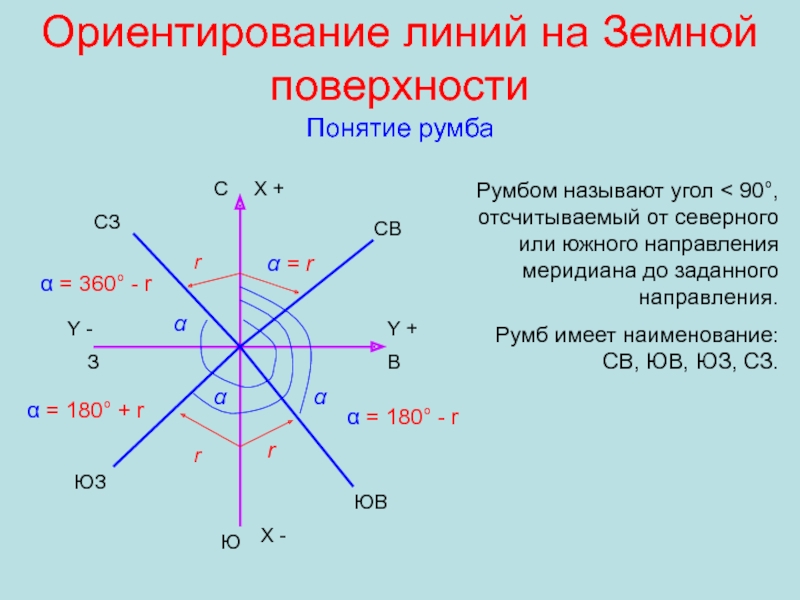
Слайд 15Ориентирование линий на Земной поверхности
Понятие румба
Ю
С
З
В
X +
Y +
СВ
α = r
ЮВ
α
r
α
= 180° - r
ЮЗ
α
r
α = 180° + r
СЗ
r
α
α = 360°
- rРумбом называют угол < 90°, отсчитываемый от северного или южного направления меридиана до заданного направления.
Румб имеет наименование: СВ, ЮВ, ЮЗ, СЗ.
X -
Y -
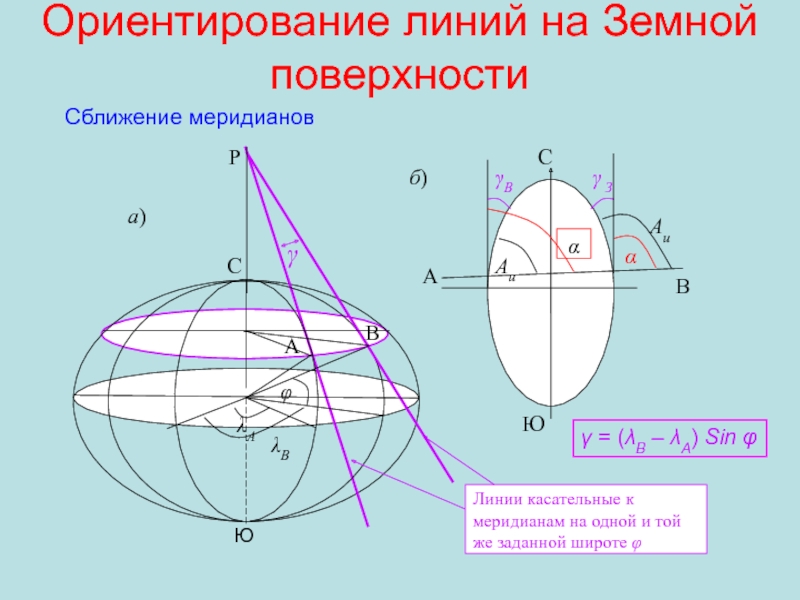
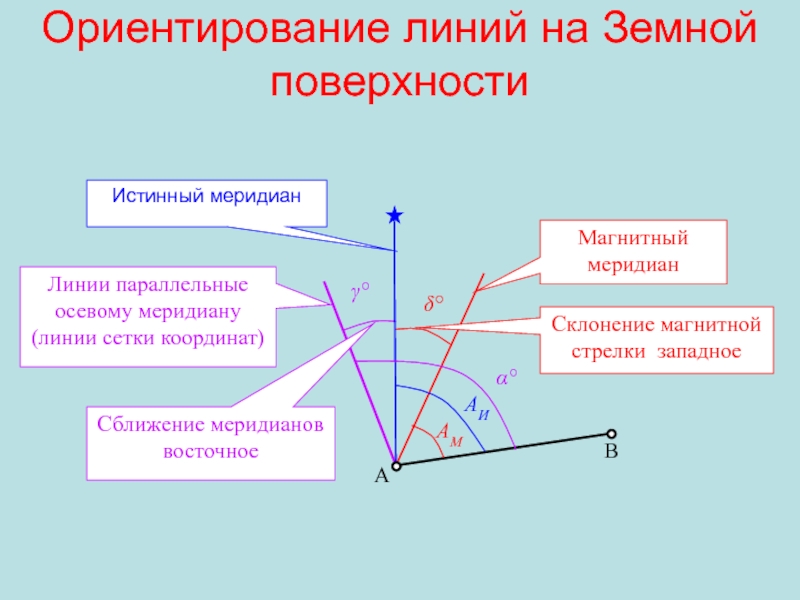
Слайд 16Ориентирование линий на Земной поверхности
А
В
Магнитный меридиан
Линии параллельные осевому меридиану
(линии
сетки координат)
АМ
АИ
α°
δ°
γ°
Сближение меридианов восточное
Склонение магнитной стрелки западное
Истинный меридиан
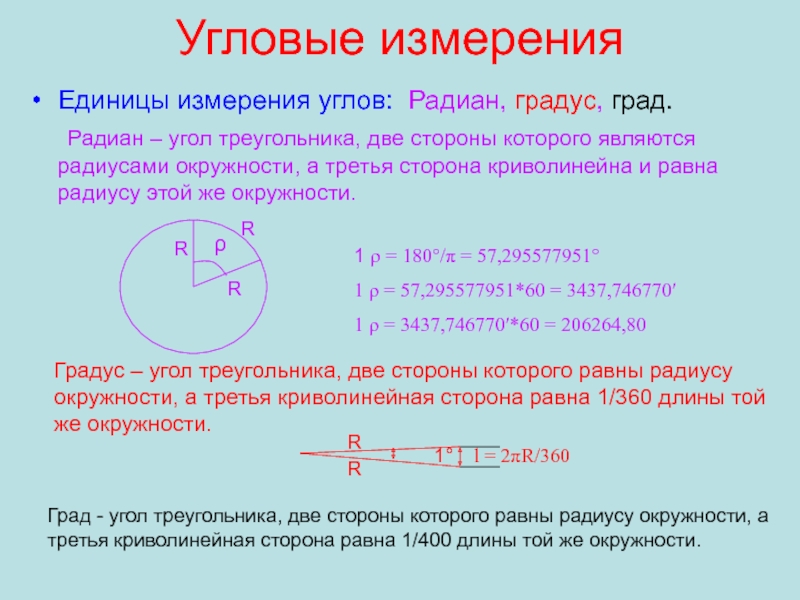
Слайд 17Угловые измерения
Единицы измерения углов: Радиан, градус, град.
Радиан – угол треугольника,
две стороны которого являются радиусами окружности, а третья сторона криволинейна
и равна радиусу этой же окружности.R
R
R
ρ
1 ρ = 180°/π = 57,295577951°
1 ρ = 57,295577951*60 = 3437,746770′
1 ρ = 3437,746770′*60 = 206264,80
Градус – угол треугольника, две стороны которого равны радиусу окружности, а третья криволинейная сторона равна 1/360 длины той же окружности.
1°
R
l = 2πR/360
R
Град - угол треугольника, две стороны которого равны радиусу окружности, а третья криволинейная сторона равна 1/400 длины той же окружности.
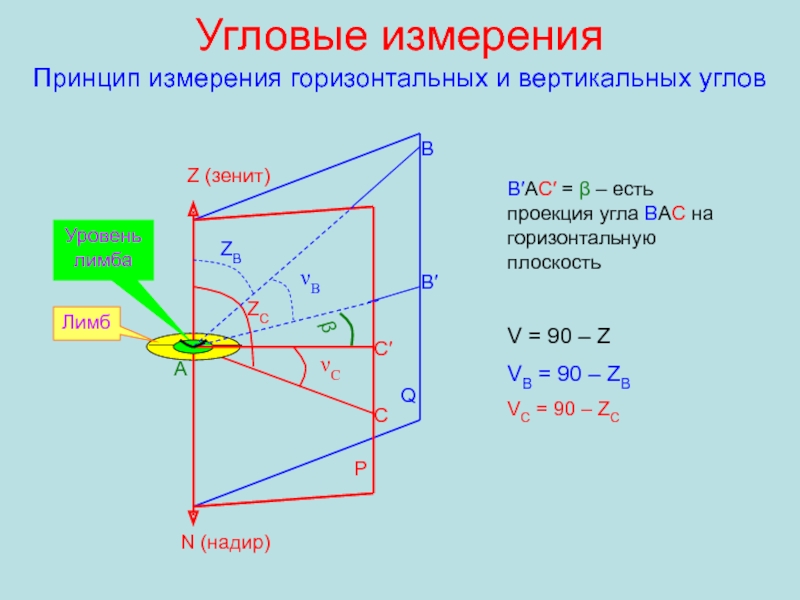
Слайд 18Угловые измерения
Принцип измерения горизонтальных и вертикальных углов
А
В
С
В′
β
νB
νC
P
Q
Лимб
Уровень лимба
С′
Z (зенит)
N (надир)
ZB
ZC
B′AC′
= β – есть проекция угла ВАС на горизонтальную плоскость
V
= 90 – ZVB = 90 – ZB
VC = 90 – ZC
Слайд 19Угловые измерения
Прибор для измерения горизонтальных и вертикальных углов
Основные части теодолита
2Т30
Подставка
Горизонтальный круг (лимб, алидада)
Визирная оптическая труба
Вертикальный круг
Отсчетное устройство (объектив, окуляр)
Слайд 20Угловые измерения
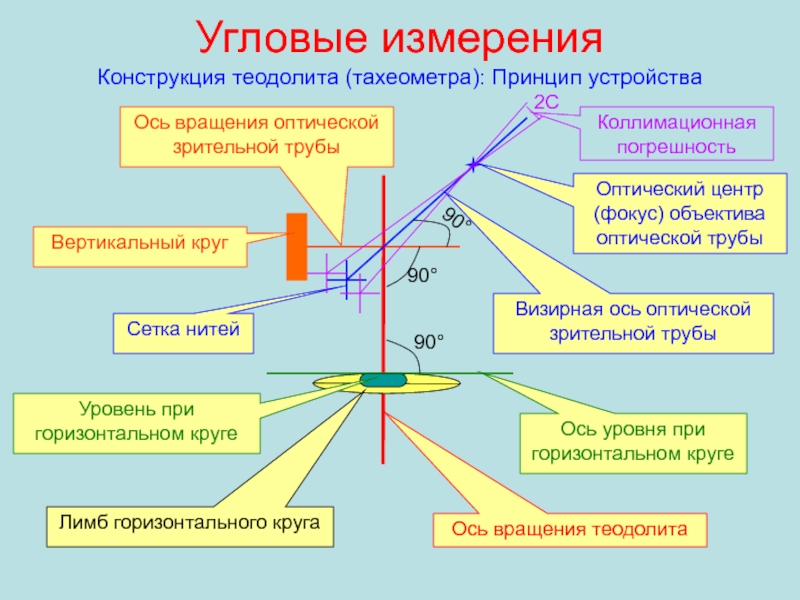
Конструкция теодолита (тахеометра): Принцип устройства
Ось вращения теодолита
Уровень при горизонтальном
круге
Лимб горизонтального круга
Ось уровня при горизонтальном круге
Оптический центр (фокус) объектива
оптической трубы Сетка нитей
Ось вращения оптической зрительной трубы
Визирная ось оптической зрительной трубы
90°
90°
90°
Вертикальный круг
Коллимационная погрешность
2С
Слайд 21Угловые измерения
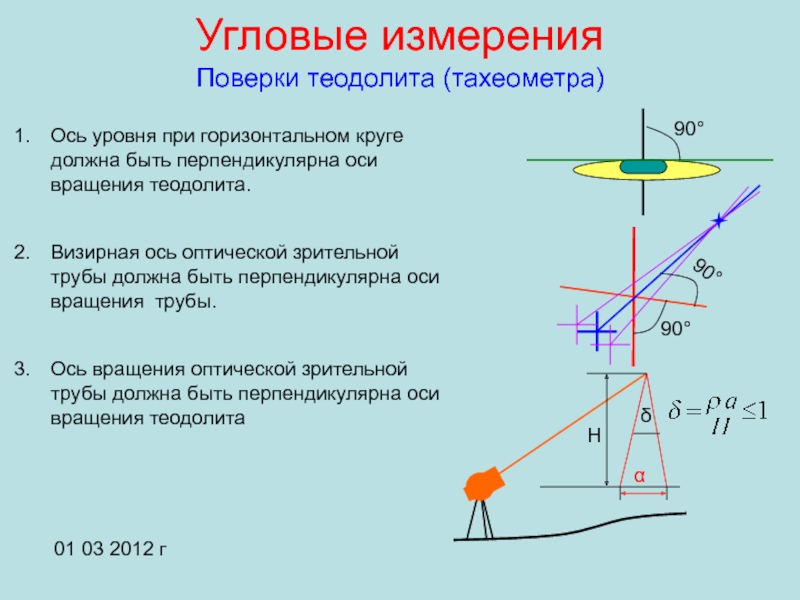
Поверки теодолита (тахеометра)
Ось уровня при горизонтальном круге должна
быть перпендикулярна оси вращения теодолита.
Визирная ось оптической зрительной трубы должна
быть перпендикулярна оси вращения трубы.Ось вращения оптической зрительной трубы должна быть перпендикулярна оси вращения теодолита
90°
90°
δ
α
Н
90°
01 03 2012 г
Слайд 22Угловые измерения
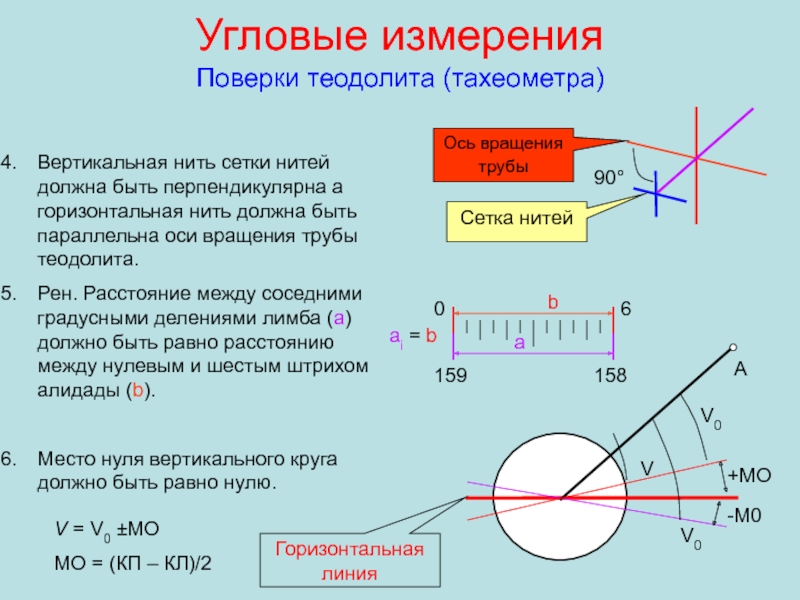
Поверки теодолита (тахеометра)
Вертикальная нить сетки нитей должна быть
перпендикулярна а горизонтальная нить должна быть параллельна оси вращения трубы
теодолита.Рен. Расстояние между соседними градусными делениями лимба (а) должно быть равно расстоянию между нулевым и шестым штрихом алидады (b).
Место нуля вертикального круга должно быть равно нулю.
V = V0 ±МО
МО = (КП – КЛ)/2
Слайд 23Угловые измерения
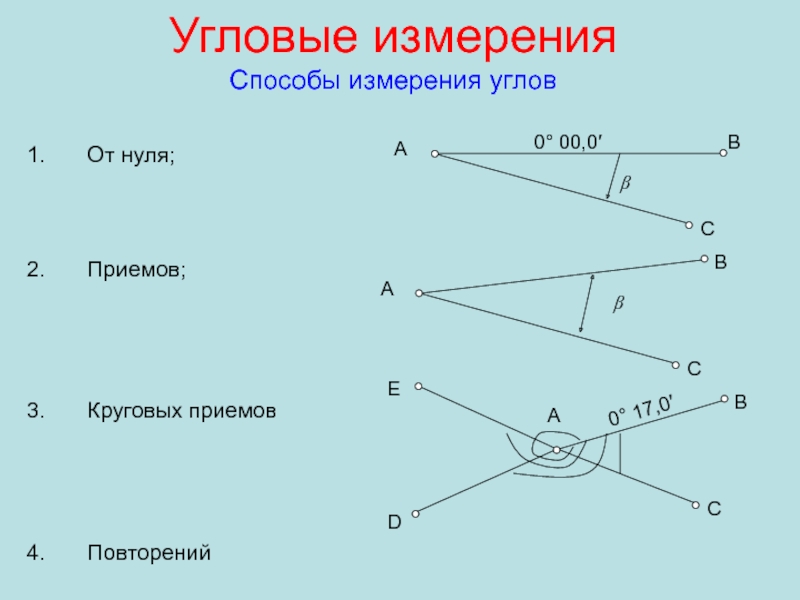
Способы измерения углов
От нуля;
Приемов;
Круговых приемов
Повторений
0° 00,0′
А
В
С
β
А
В
С
β
А
В
С
D
E
0° 17,0′
Слайд 24Угловые измерения
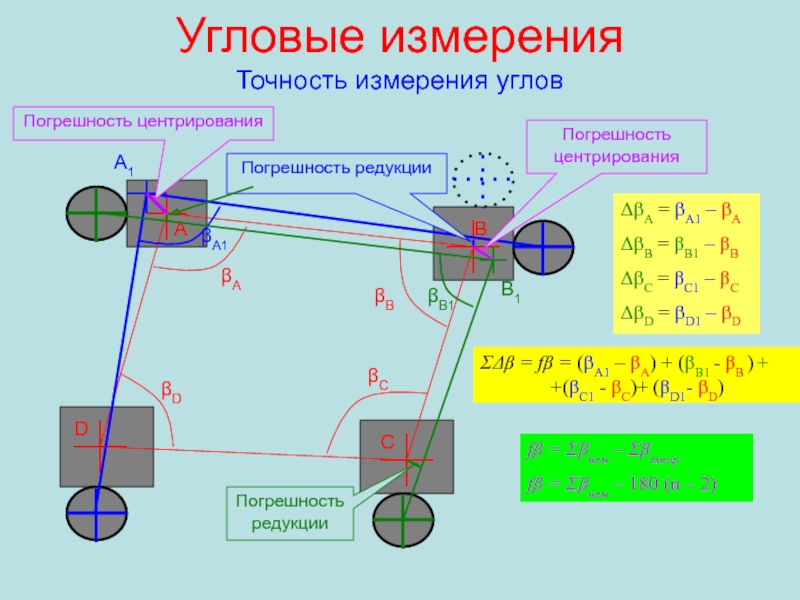
Точность измерения углов
βD
βA
βB
βC
A
C
D
βA1
A1
Погрешность центрирования
Погрешность редукции
ΔβA = βA1 – βA
ΔβB
= βB1 – βB
ΔβC = βC1 – βC
ΔβD = βD1
– βDB1
βB1
Погрешность центрирования
Погрешность редукции
ΣΔβ = fβ = (βA1 – βA) + (βB1 - βB ) + +(βC1 - βC)+ (βD1- βD)
fβ = Σβизм – Σβтеор
fβ = Σβизм – 180 (n – 2)
B
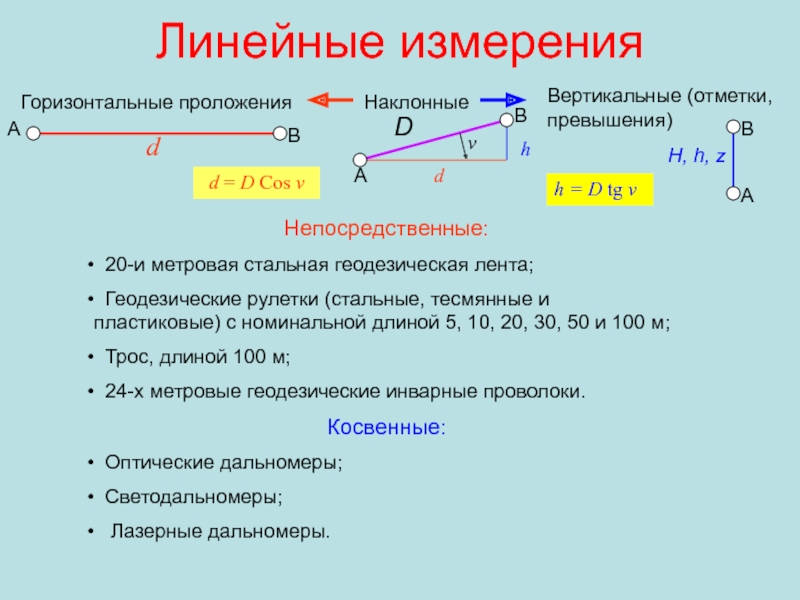
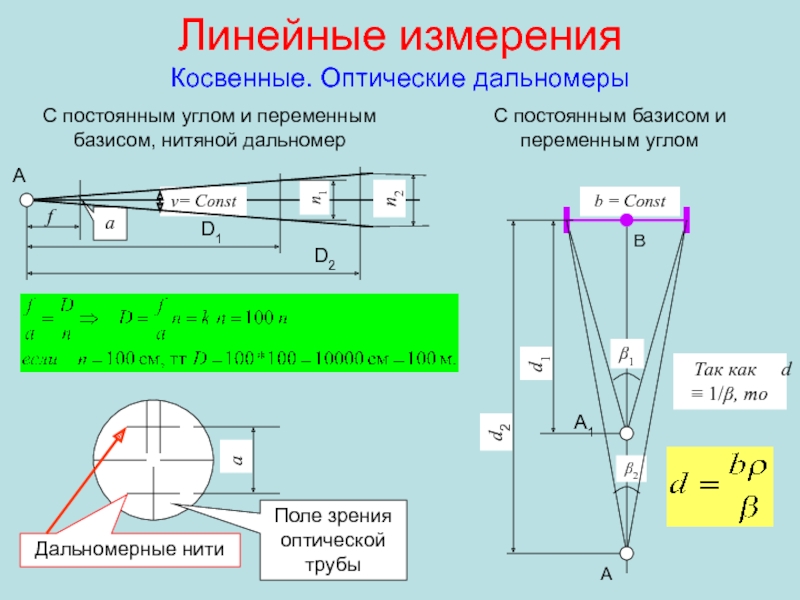
Слайд 26Линейные измерения
Непосредственные:
20-и метровая стальная геодезическая лента;
Геодезические рулетки
(стальные, тесмянные и пластиковые) с номинальной длиной 5, 10, 20,
30, 50 и 100 м;Трос, длиной 100 м;
24-х метровые геодезические инварные проволоки.
Косвенные:
Оптические дальномеры;
Светодальномеры;
Лазерные дальномеры.
Горизонтальные проложения
d
Наклонные
D
Вертикальные (отметки, превышения)
H, h, z
d = D Cos v
v
A
B
h = D tg v
h
d
А
В
А
В
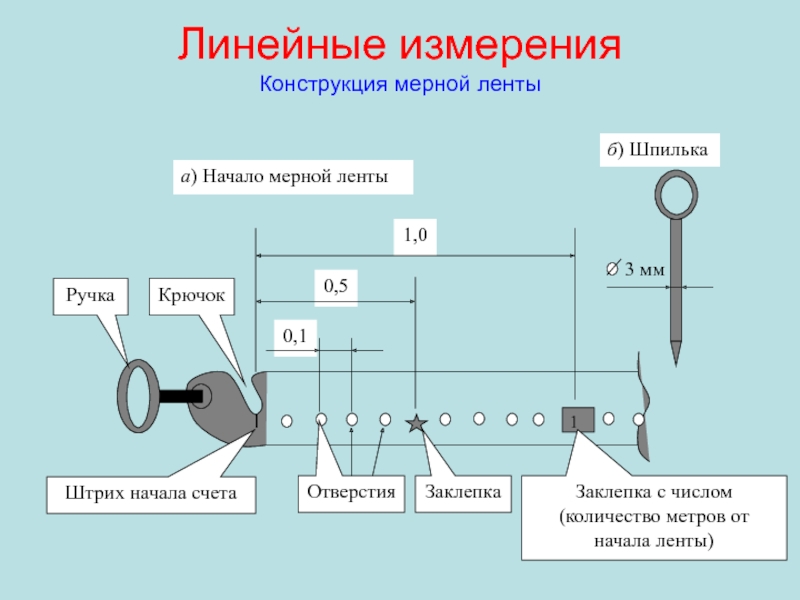
Слайд 27Линейные измерения
Конструкция мерной ленты
1
0,1
0,5
1,0
Ручка
Штрих начала счета
Отверстия
Заклепка
Заклепка с числом (количество метров
от начала ленты)
3 мм
а) Начало мерной ленты
б) Шпилька
Крючок
Слайд 28Линейные измерения
Косвенные. Оптические дальномеры
С постоянным углом и переменным базисом, нитяной
дальномер
С постоянным базисом и переменным углом
b = Const
β1
β2
d1
d2
Так как
d ≡ 1/β, то A
B
A
A1
Слайд 29Линейные измерения
Косвенные. Светодальномер. Лазерный дальномер
D = Vt/2
d = D Cos
v
v
А
В
15 03 2012
h′AB
h′AB = D Sin v
i
l
hAB = h′AB +
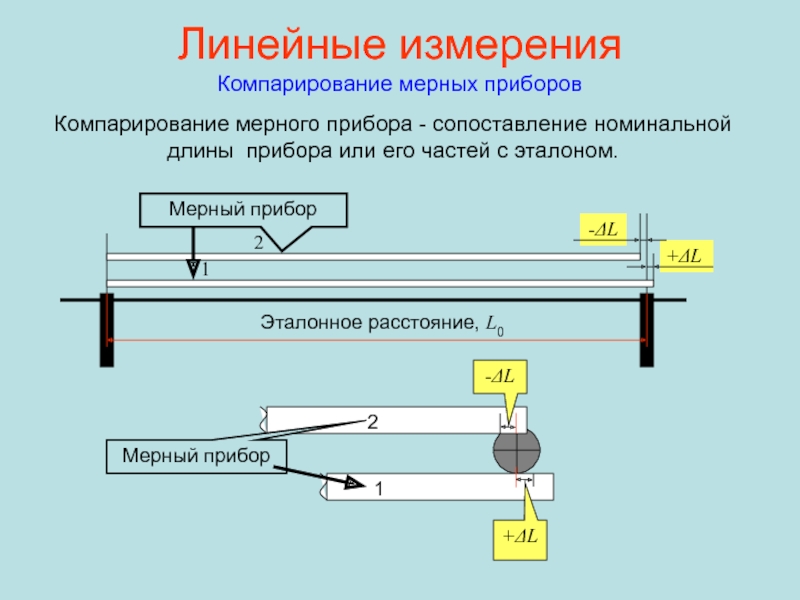
i - lСлайд 30+ΔL
-ΔL
Линейные измерения
Компарирование мерных приборов
Компарирование мерного прибора - сопоставление номинальной длины
прибора или его частей с эталоном.
Эталонное расстояние, L0
Мерный прибор
1
2
+ΔL
-ΔL
Мерный прибор
2
1
Слайд 31Линейные измерения
Методика измерения линий 20-и метровой стальной лентой
Lизм = N
*[(А- 1) * Lном] + (Lном *n) + D ±
[N (A-1) +n] ΔLLизм
D
20-и метровая стальная лента
20-и метровая стальная лента
d = Lизм Cos v
D
Слайд 32Линейные измерения
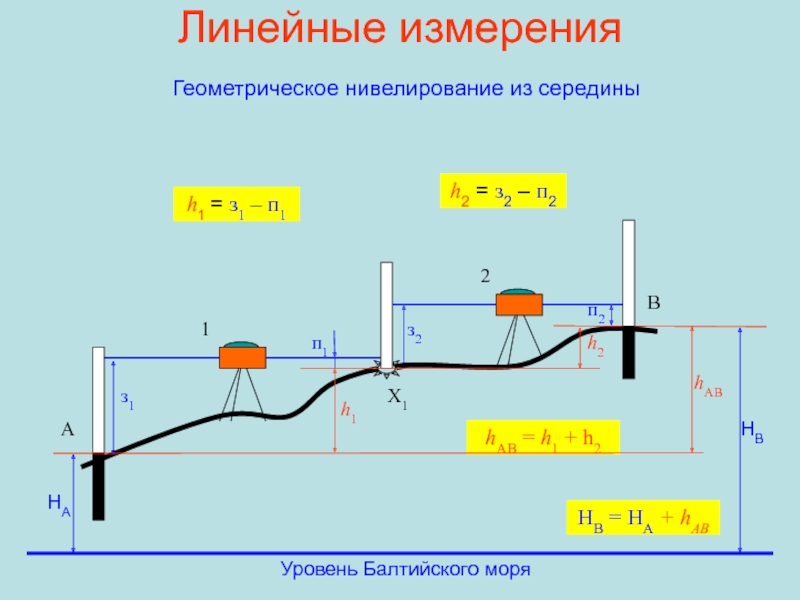
Геометрическое нивелирование из середины
h1 = з1 – п1
h2
= з2 – п2
hAB
A
B
h1
X1
з1
п1
1
2
з2
п2
h2
hAB = h1 + h2
Уровень Балтийского моря
HA
HB
HB
= HA + hABСлайд 33Линейные измерения
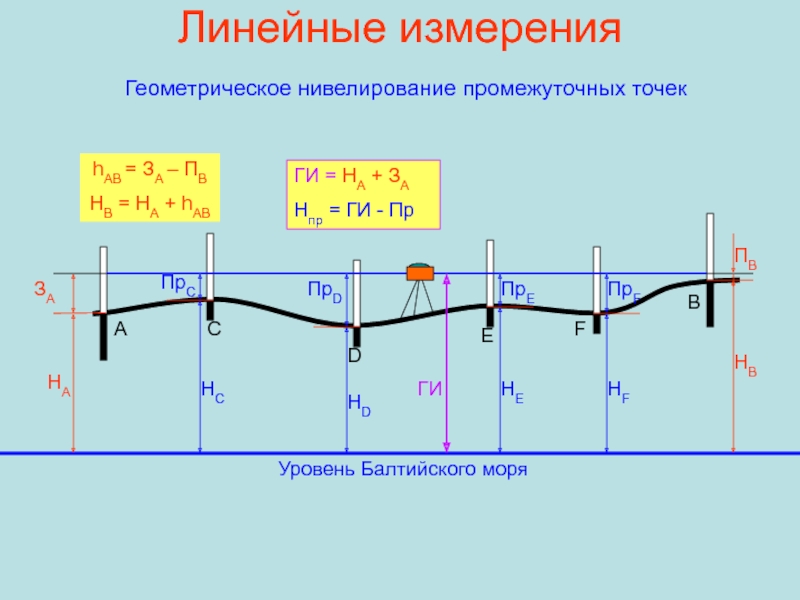
Геометрическое нивелирование промежуточных точек
А
В
С
D
E
F
Уровень Балтийского моря
ЗА
HA
ПВ
hАВ = ЗА
– ПВ
HB = HA + hAB
HВ
HС
HD
HE
HF
ГИ
ГИ = НА + ЗА
Hпр
= ГИ - ПрПрС
ПрD
ПрE
ПрF
Слайд 34Линейные измерения
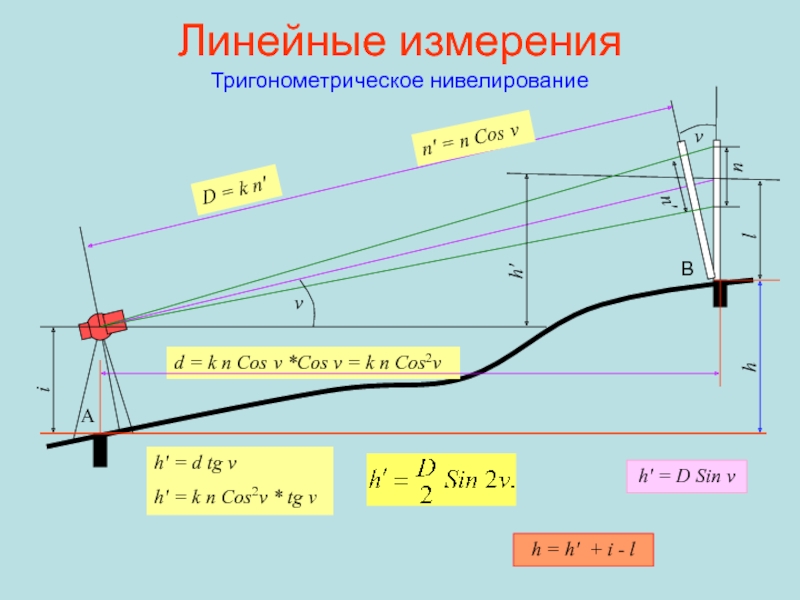
Тригонометрическое нивелирование
v
v
D = k n′
n
n′
d = k n Cos
v *Cos v = k n Cos2v
n′ = n
Cos vh′
h′ = d tg v
h′ = k n Cos2v * tg v
i
l
h
h = h′ + i - l
h′ = D Sin v
А
В
Слайд 35Съемка территории. Составление плана участка местности
Планово-высотное обоснование
Пункты триангуляции и
полигонометрии: точки обозначенные на местности постоянными специальными знаками, имеющими надземную
и подземную часть. Для таких точек установлены их координаты и высоты в единой государственной системе координат (X, Y, H):а) на незастроенной территории;
б) заделка в фасаде здания.
Съемочные точки теодолитных ходов: точки обозначенные на местности временными знаками (деревянные колышки, дюбель в асфальтовом покрытии, местные предметы точечного характера). Для таких точек устанавливают их координаты и высоты (X, Y, H) в процессе съемочных работ.
Слайд 36Съемка территории. Составление плана участка местности
Полевые работы
Рекогносцировка – осмотр территории
съемки;
Детальная рекогносцировка → закрепление точек временными знаками (колышки, дюбеля и
др.), составление схемы местоположения точек обоснования; Измерение горизонтальных и вертикальных углов между смежными точками;
Измерение расстояний между смежными точками;
Съемка горизонтальной ситуации (теодолитная съемка);
Геометрическое нивелирование по точкам теодолитного хода;
Съемка рельефа (нивелирование застроенной территории или тахеометрическая съемка)
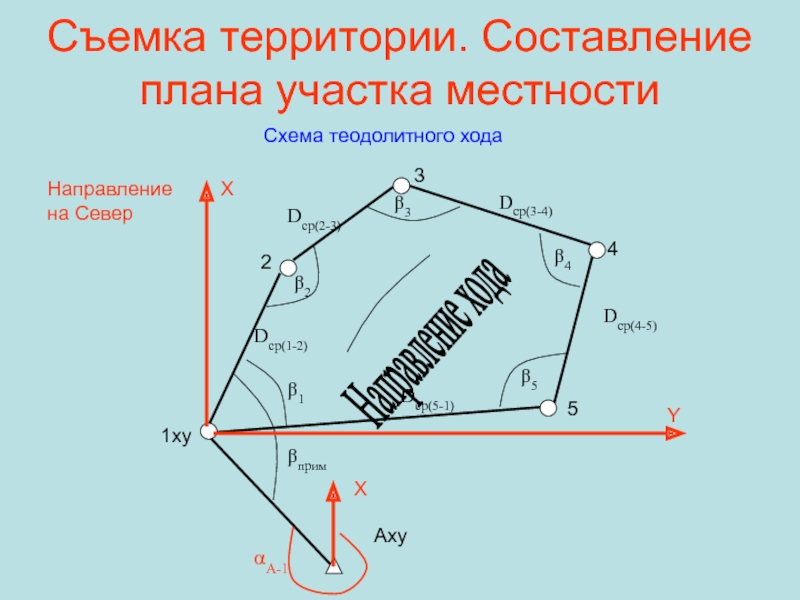
Слайд 37Съемка территории. Составление плана участка местности
Схема теодолитного хода
2
прим
3
4
5
Dср(1-2)
Dср(2-3)
Dср(3-4)
Dср(4-5)
Dср(5-1)
Направление хода
1
Аxy
1xy
2
3
4
5
Направление на
Север
X
Y
αA-1
X
Слайд 389 КЖ
154,7
10,0
8,0
4,2
4,7
14,9
11,9
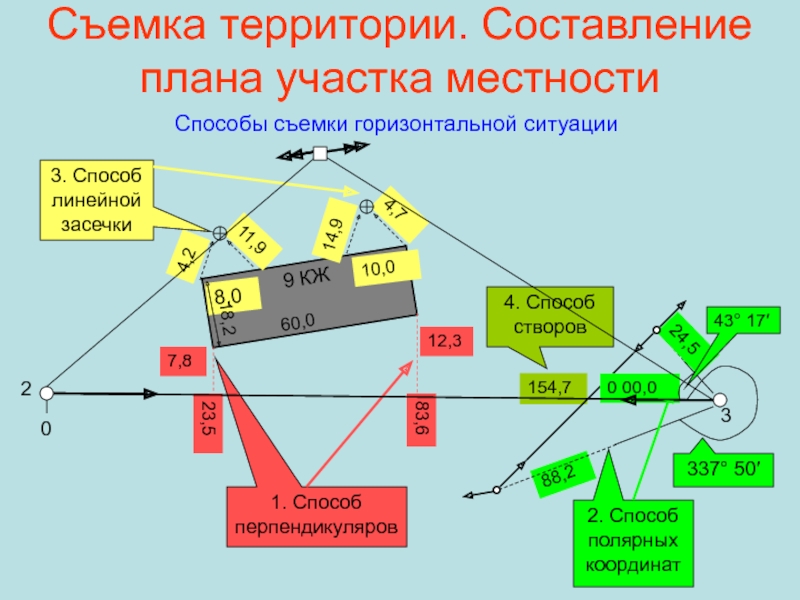
Съемка территории. Составление плана участка местности
Способы съемки горизонтальной ситуации
23,5
7,8
12,3
83,6
60,0
18,2
2
3
0
00,0
24,5
43° 17′
337° 50′
88,2
1. Способ перпендикуляров
3. Способ линейной засечки
2. Способ полярных
координат4. Способ створов
0
Слайд 39Съемка территории. Составление плана участка местности
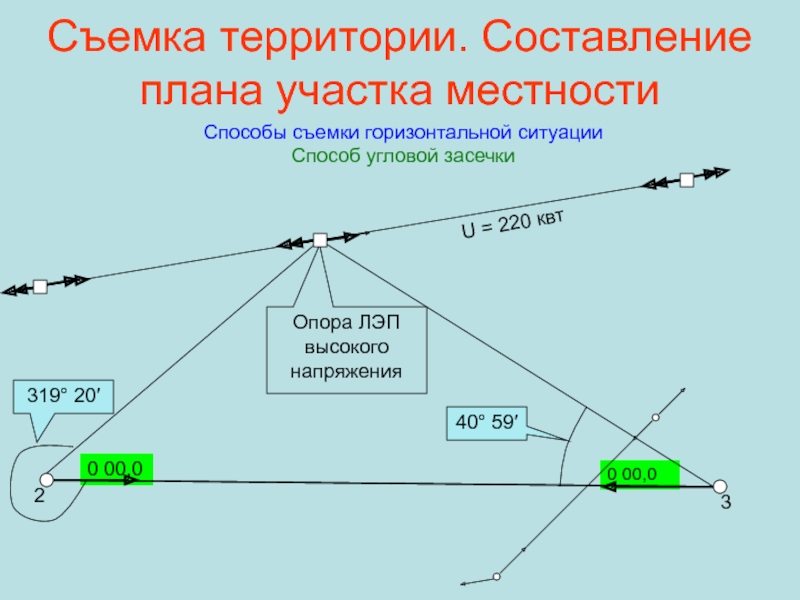
Способы съемки горизонтальной ситуации
Способ угловой
засечки
2
3
0 00,0
0 00,0
319° 20′
40° 59′
Опора ЛЭП высокого напряжения
U = 220
квтСлайд 40Съемка территории. Составление плана участка местности
Камеральные работы
Решение обратной геодезической задачи;
Вычисление
горизонтальных углов по результатам полевых измерений;
Вычисление горизонтальных проложений между смежными
точками;Вычисления в ведомости координат:
Исходные данные;
Уравнивание горизонтальных углов;
Вычисление дирекционных углов;
Вычисление приращений координат;
Уравнивание приращений координат;
Вычисление координат точек теодолитного хода.
Вычисления в ведомости геометрического нивелирования:
Исходные данные;
Уравнивание превышений
Вычисление отметок точек нивелирного хода.
Вычисления в журнале тахеометрической съемки:
Исходные данные;
Вычисление отметок пикетов.
Составление плана ситуации и рельефа:
Нанесение ситуации;
Нанесение пикетов и рисовка горизонталей.
Слайд 41Съемка территории. Составление плана участка местности
Обратная геодезическая задача
А
Y
X
yА
XА
y1
X1
r = αА1
1
dA1
Слайд 42Съемка территории. Составление плана участка местности
Вычисления в ведомости координат.
Исходные
данные:
1. Измеренные горизонтальные углы; 2. Исходный дирекционный угол;
3. Горизонтальные
проложения между смежными точками; 4. Координаты исходных точек.Уравнивание горизонтальных углов:
В разомкнутом теодолитном ходе угловая невязка равна:
В замкнутом теодолитном ходе так как αк = αн, то угловая невязка равна:
Допустимая угловая невязка равна:
Поправки в углы вычисляют по формуле:
Слайд 43Съемка территории. Составление плана участка местности
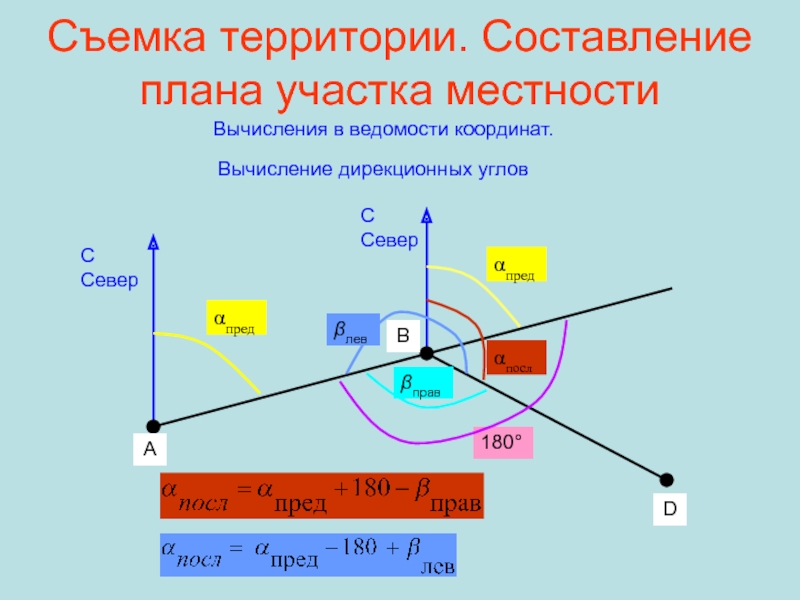
Вычисления в ведомости координат.
Вычисление
дирекционных углов
С Север
αпред
αпосл
βправ
αпред
180°
С Север
А
В
D
βлев
Слайд 44Съемка территории. Составление плана участка местности
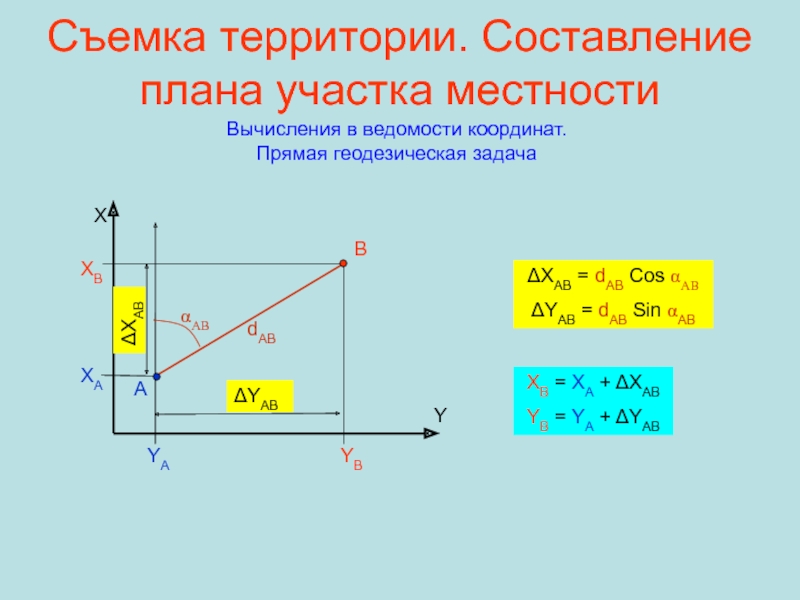
Вычисления в ведомости координат. Прямая
геодезическая задача
Y
X
YA
XA
A
B
YB
XB
dAB
αAB
ΔYAB
ΔXAB
ΔXAB = dAB Cos αAB
ΔYAB = dAB Sin αAB
XB
= XA + ΔXAB YB = YA + ΔYAB
Слайд 45Съемка территории. Составление плана участка местности
Вычисление в ведомости координат. Уравнивание
(сторон) приращений координат
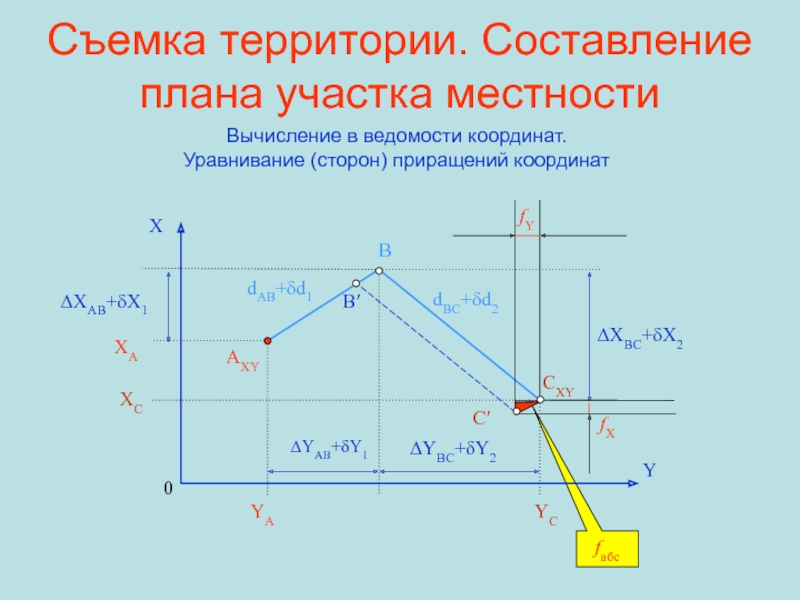
Слайд 46Съемка территории. Составление плана участка местности
Вычисление в ведомости координат. Уравнивание
(сторон) приращений координат
(∆XAB+δX1) + (∆XBC+δX2) = XC - XA;
(∆YAB+δY1) +
(∆YBC+δY2) = YC - YA.δX1 + δX2 = (XC - XA) – (∆XAB + ∆XBC)
δY1 + δY2 = (YC - YA) – (∆YAB + ∆YBC)
fx = -∑δX и fy = -∑δY
fx = ∑∆X – (Xк – Xн);
fy = ∑∆Y – (Yк – Yн),
Если Xк = Xн и Yк = Yн,
то
fx = ∑∆X;
fy = ∑∆Y.
Разомкнутый ход:
Замкнутый ход
Слайд 47Съемка территории. Составление плана участка местности
Вычисление в ведомости координат. Уравнивание
(сторон) приращений координат
Xпосл = Xпред + ΔXиспр
Yпосл = Yпред +
ΔYиспр ΔXиспр = ΔXвыч + vx
ΔYиспр = ΔYвыч + vy
Асолютная погрешность –
Допустимая погрешность –
Поправки в приращения координат –
Исправленные приращения координат –
Координаты точек теодолитного хода –
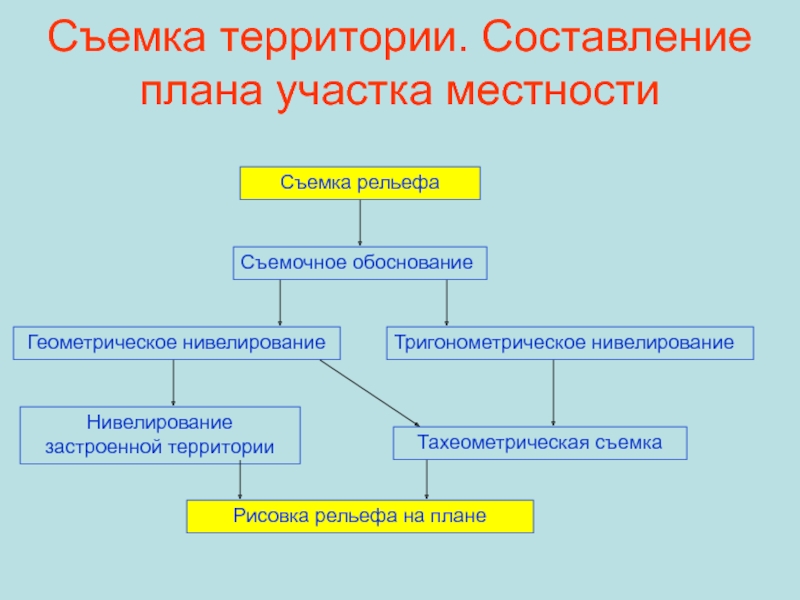
Слайд 48Съемка территории. Составление плана участка местности
Съемка рельефа
Съемочное обоснование
Геометрическое нивелирование
Тригонометрическое нивелирование
Нивелирование
застроенной территории
Тахеометрическая съемка
Рисовка рельефа на плане
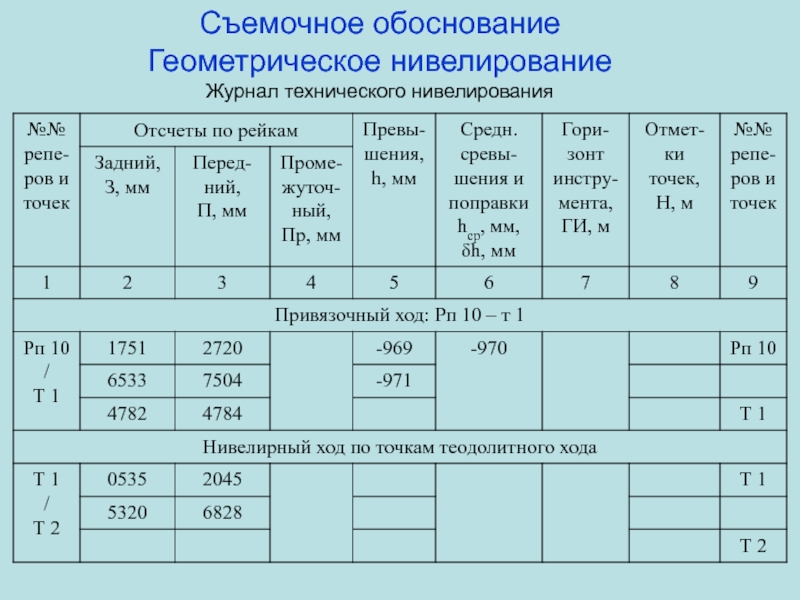
Слайд 51Съемочное обоснование
Геометрическое нивелирование
Журнал технического нивелирования,
Постраничный контроль: З - П
=
Сумма средних превышений от репера № 10 до репера
№ 11 → hср = окончание
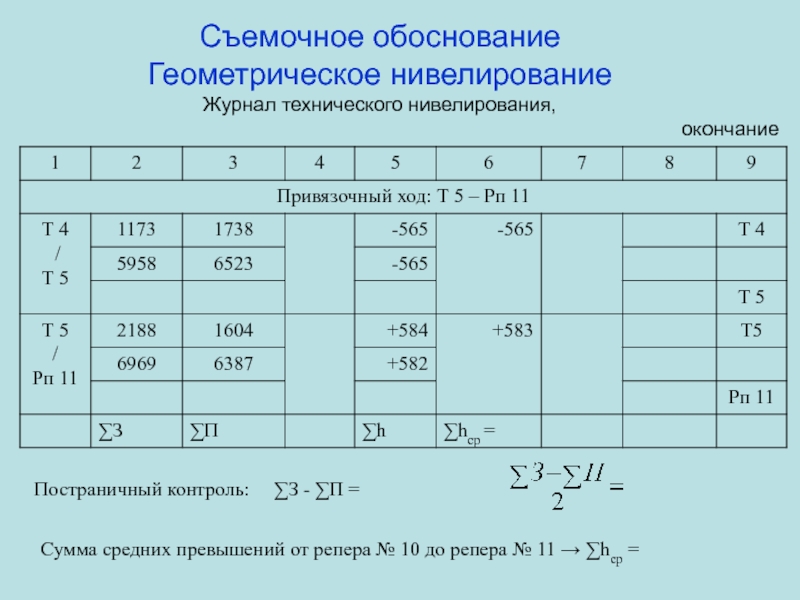
Слайд 52Съемочное обоснование
Геометрическое нивелирование
Схема нивелирного хода
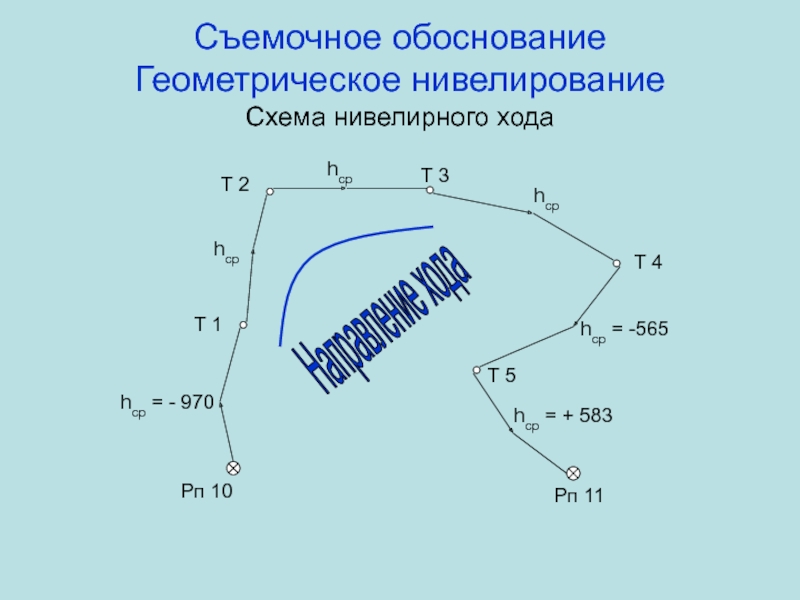
Т 1
Т 2
Т 3
Т 4
Т 5
Рп
10
Рп 11
Направление хода
hср = - 970
hср = -565
hср = +
583hср
hср
hср
Слайд 53Съемочное обоснование
Геометрическое нивелирование
Уравнивание превышений
Исходные данные:
Средние превышения между станциями hср
Сумма средних превышений
от репера № 10 до репера № 11 → hср
Отметки Реперов → Hрп10
→ Hрп11
2 Вычисления:
Фактической невязки: f hф= hср – (HK - HH )
f hф= hср – (Hрп11 - Hрп10 )
Допустимой невязки: fh(доп) =
Поправок в превышения: δh = - f hф/ n
Исправленных превышений: hиспр = hср + δh
Отметок точек: Hi+1 = Hi + hиспр
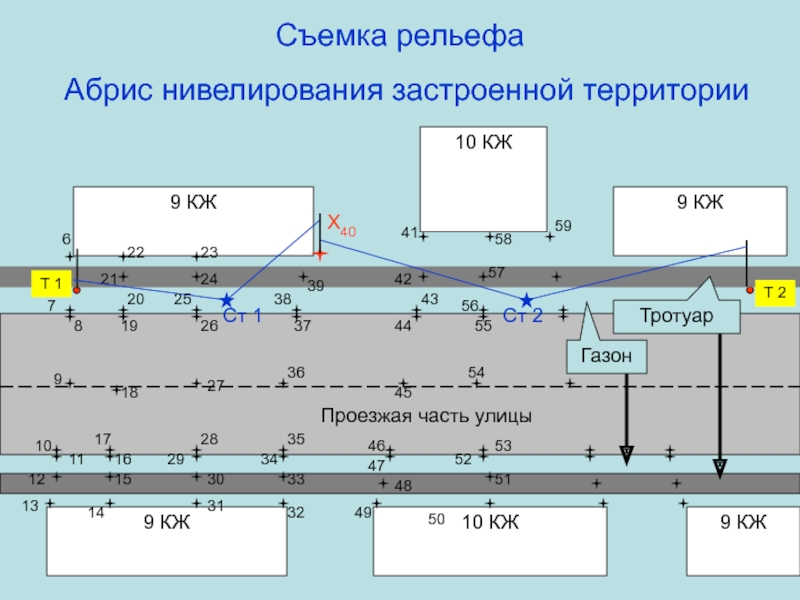
Слайд 54Съемка рельефа
Абрис нивелирования застроенной территории
9 КЖ
10 КЖ
9 КЖ
9 КЖ
10
КЖ
9 КЖ
Т 1
Т 2
8
7
10
9
13
12
11
6
14
19
18
17
16
15
23
22
21
20
Ст 1
25
26
27
28
29
30
31
24
34
33
32
35
36
37
38
39
X40
44
45
46
41
47
48
49
56
42
43
55
54
53
52
51
50
Ст 2
57
58
59
Тротуар
Газон
Проезжая часть улицы
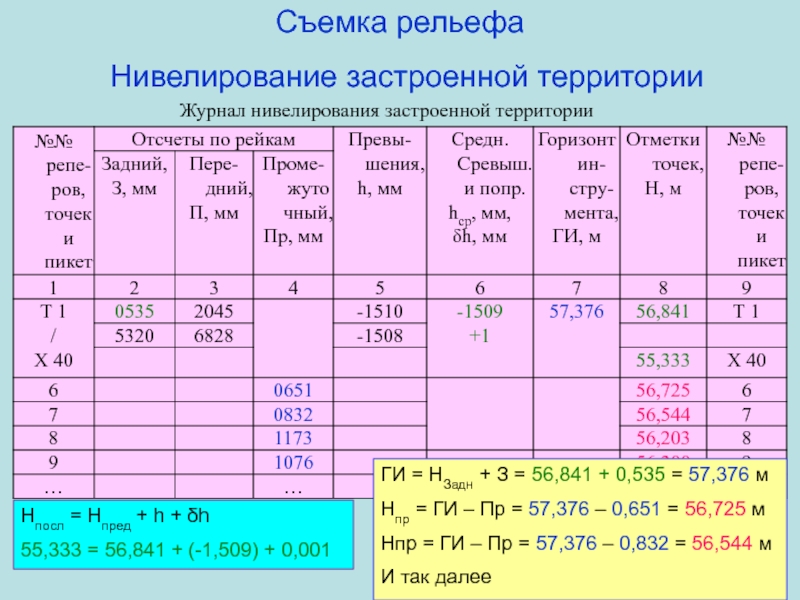
Слайд 55Съемка рельефа
Нивелирование застроенной территории
Журнал нивелирования застроенной территории
Нпосл = Нпред
+ h + h
55,333 = 56,841 + (-1,509) + 0,001
ГИ
= НЗадн + З = 56,841 + 0,535 = 57,376 мНпр = ГИ – Пр = 57,376 – 0,651 = 56,725 м
Нпр = ГИ – Пр = 57,376 – 0,832 = 56,544 м
И так далее
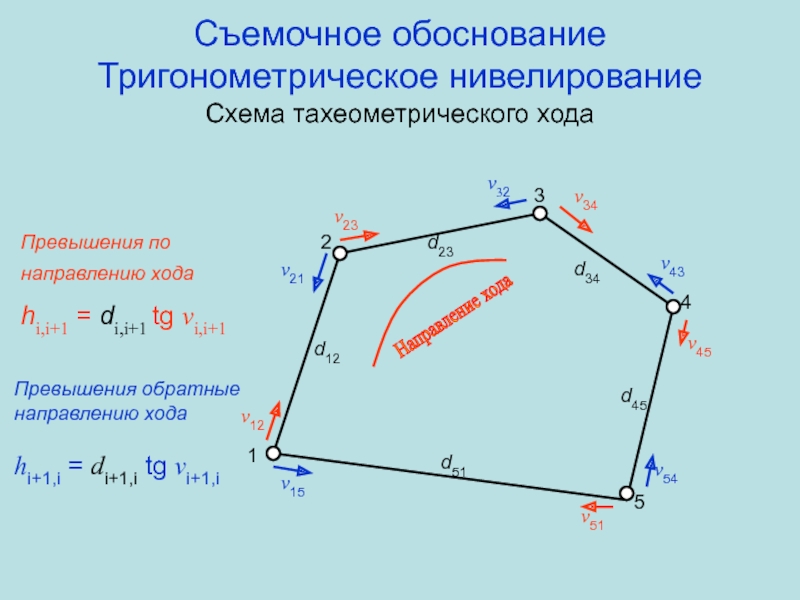
Слайд 56Съемочное обоснование
Тригонометрическое нивелирование
Схема тахеометрического хода
1
5
4
3
2
d12
d51
d45
d34
d23
v12
v43
v51
v34
v32
v23
v21
v54
v45
v15
Превышения по направлению хода
hi,i+1 =
di,i+1 tg vi,i+1
Направление хода
Превышения обратные направлению хода
hi+1,i = di+1,i tg
vi+1,iСлайд 57Съемочное обоснование
Тригонометрическое нивелирование
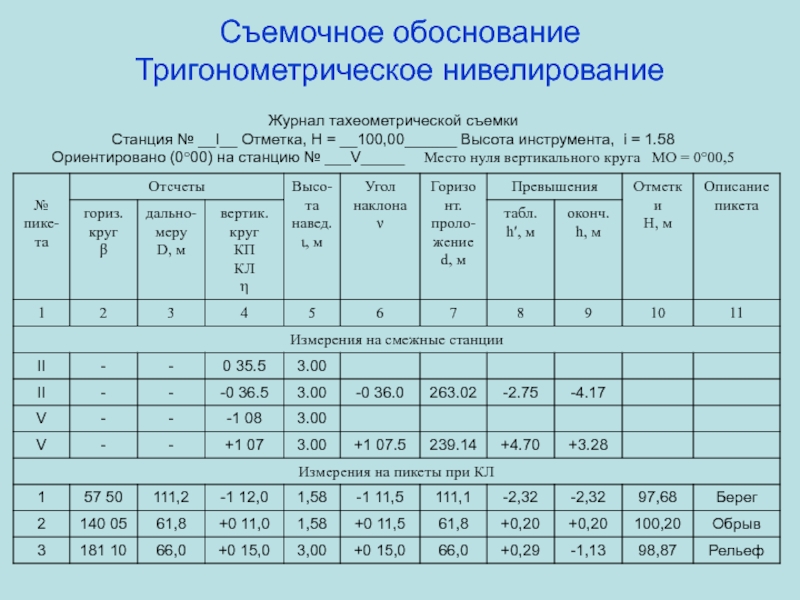
Журнал тахеометрической съемки
Станция № __I__ Отметка, H =
__100,00______ Высота инструмента, i = 1.58
Ориентировано (000) на станцию №
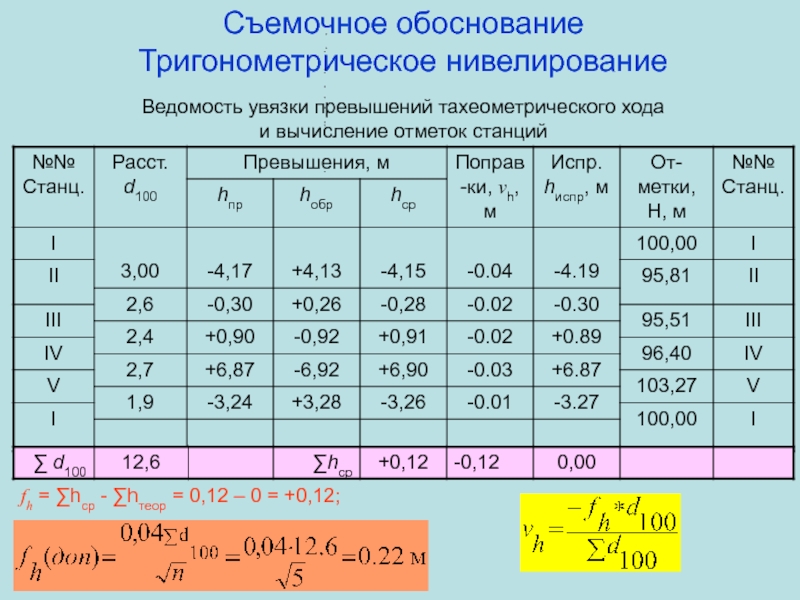
___V_____ Место нуля вертикального круга МО = 000,5Слайд 58Съемочное обоснование Тригонометрическое нивелирование Ведомость увязки превышений тахеометрического хода и вычисление отметок
станций
fh = ∑hср - ∑hтеор = 0,12 – 0
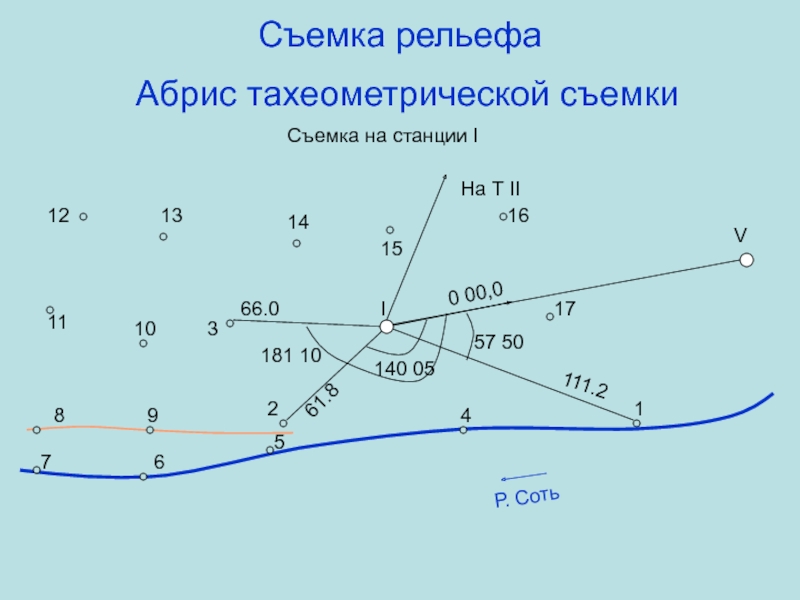
= +0,12;Слайд 59Съемка рельефа
Абрис тахеометрической съемки
0 00,0
1
7
3
I
V
57 50
181
10
140 05
Р. Соть
Съемка на станции I
6
5
4
2
10
8
9
11
13
12
14
15
17
16
111.2
61.8
66.0
На Т II
Слайд 60Съемка рельефа
Рисовка рельефа на плане
33,24
36,59
32,17
36,09
34,87
35,77
37,11
33,45
34,25
36,45
35,18
33,89
32,19
31,88
35,65
35,97
34,35
34,98
33,91
34,55
33,15
33,77
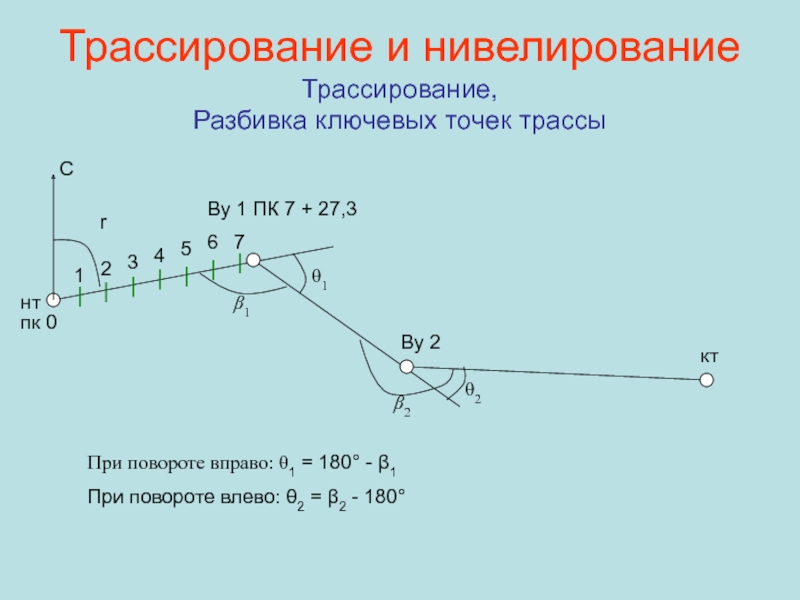
Слайд 61Трассирование и нивелирование
Трассирование,
Разбивка ключевых точек трассы
нт
Ву 1 ПК 7
+ 27,3
Ву 2
кт
θ1
θ2
β1
β2
При повороте вправо: θ1 = 180° - β1
При повороте влево: θ2 = β2 - 180°
2
1
пк 0
3
4
5
6
7
С
r
Слайд 63Трассирование и нивелирование
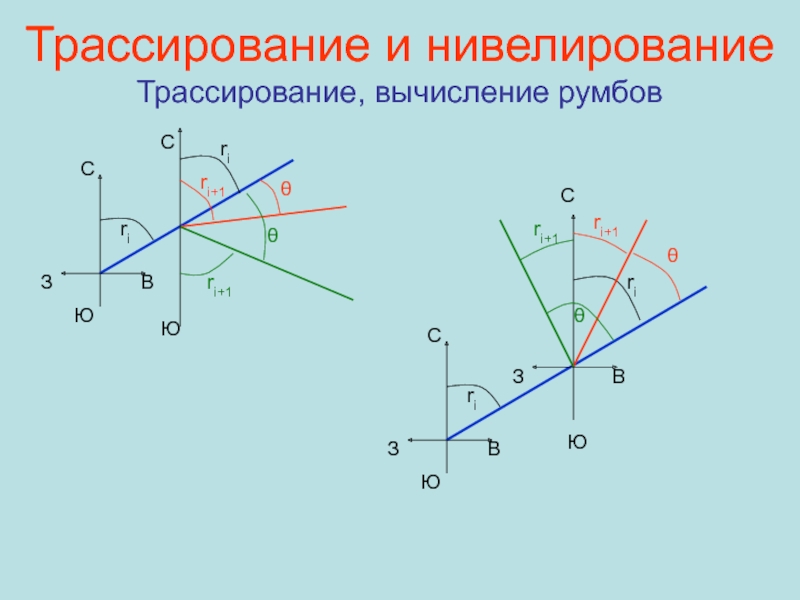
Трассирование, вычисление румбов
ri
C
Ю
В
З
θ
θ
C
Ю
ri
ri+1
ri+1
ri
C
Ю
В
З
C
Ю
ri
θ
ri+1
θ
ri+1
В
З
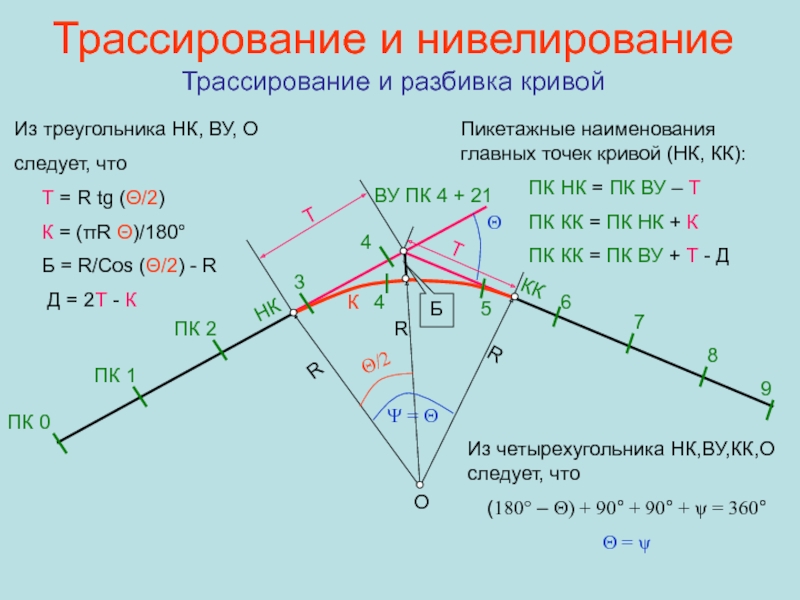
Слайд 64Трассирование и нивелирование Трассирование и разбивка кривой
Θ
Т
Т
Ψ = Θ
НК
КК
К
Б
ПК 0
ПК
1
ПК 2
3
4
ВУ ПК 4 + 21
Из четырехугольника НК,ВУ,КК,О следует, что
(180° – Θ) + 90° + 90° + ψ = 360°
Θ = ψ
О
Θ/2
Из треугольника НК, ВУ, О
следует, что
Т = R tg (Θ/2)
К = (πR Θ)/180°
Б = R/Cos (Θ/2) - R
Д = 2Т - К
R
R
R
Пикетажные наименования главных точек кривой (НК, КК):
ПК НК = ПК ВУ – Т
ПК КК = ПК НК + К
ПК КК = ПК ВУ + Т - Д
4
5
6
7
8
9
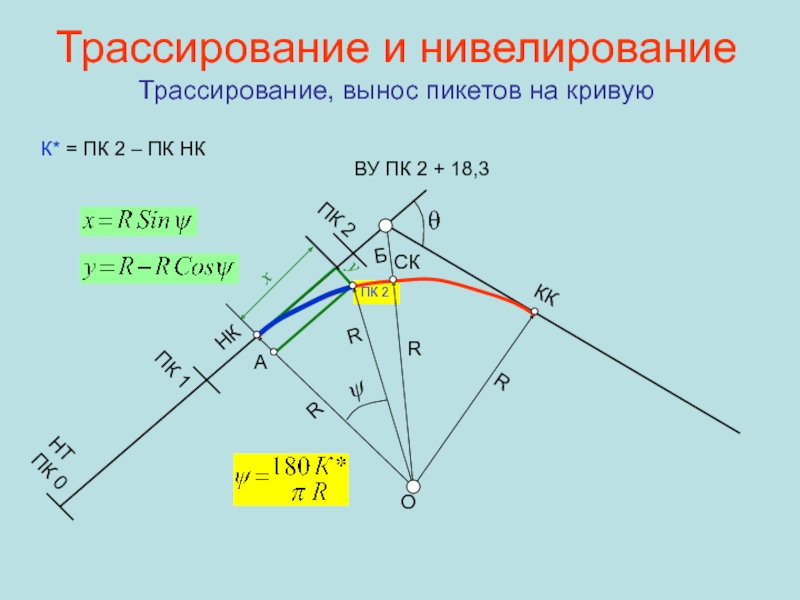
Слайд 65ПК 2
Трассирование и нивелирование Трассирование, вынос пикетов на кривую
x
y
НТ ПК
0
ПК 1
ПК 2
θ
НК
ψ
К* = ПК 2 – ПК НК
R
R
R
R
ВУ ПК
2 + 18,3О
Б
КК
СК
А
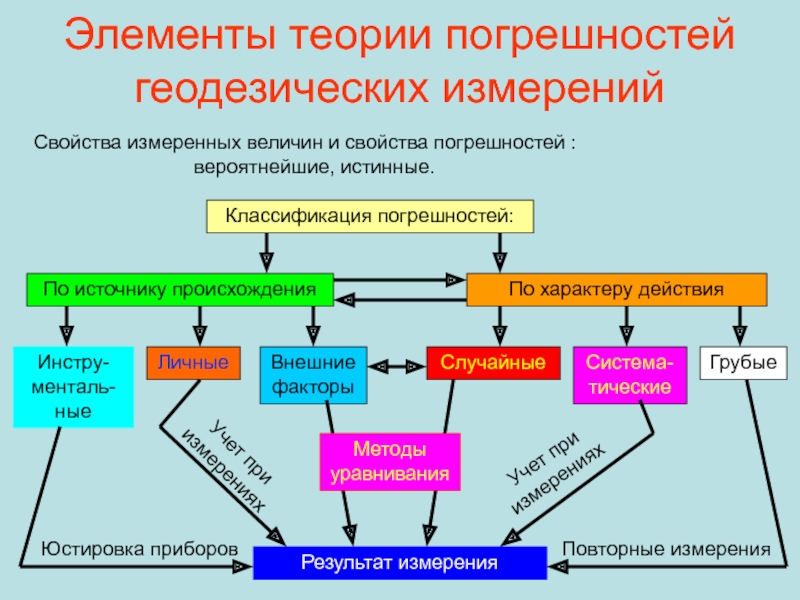
Слайд 68Элементы теории погрешностей геодезических измерений
Свойства измеренных величин и свойства погрешностей
: вероятнейшие, истинные.
Классификация погрешностей:
По источнику происхождения
По характеру действия
Инстру-менталь-ные
Внешние факторы
Личные
Грубые
Система-тические
Случайные
Результат
измеренияЮстировка приборов
Учет при измерениях
Повторные измерения
Учет при измерениях
Методы уравнивания
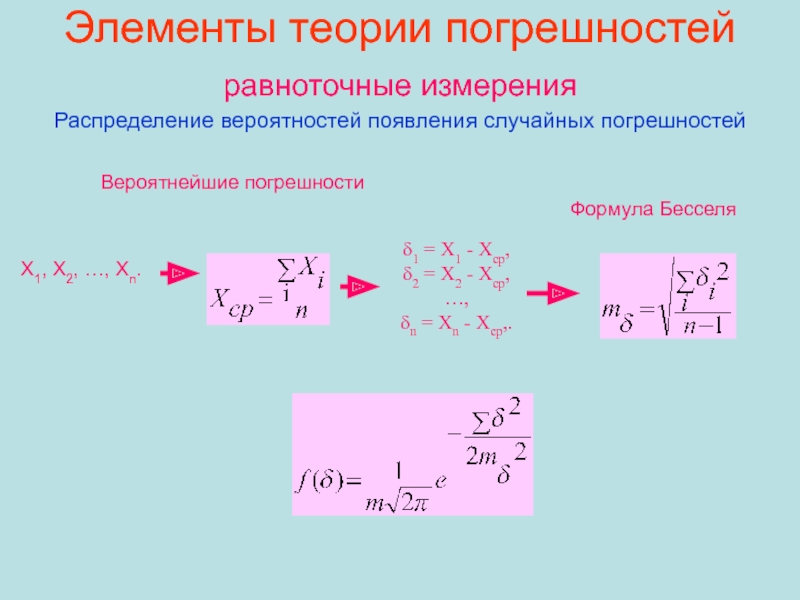
Слайд 69Элементы теории погрешностей
равноточные измерения
Распределение вероятностей появления случайных погрешностей
X1, X2,
…, Xn.
δ1 = X1 - Xср,
δ2 = X2 -
Xср, …,
δn = Xn - Xср,.
Формула Бесселя
Вероятнейшие погрешности
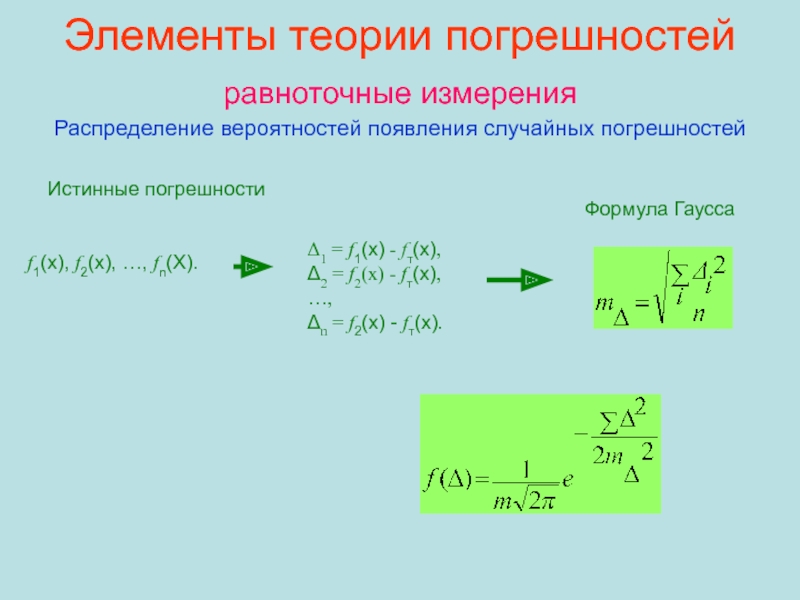
Слайд 70Элементы теории погрешностей
равноточные измерения
Распределение вероятностей появления случайных погрешностей
Истинные погрешности
f1(x),
f2(x), …, fn(X).
Δ1 = f1(x) - fт(x),
Δ2 = f2(x)
- fт(x), …,
Δn = f2(x) - fт(x).
Формула Гаусса
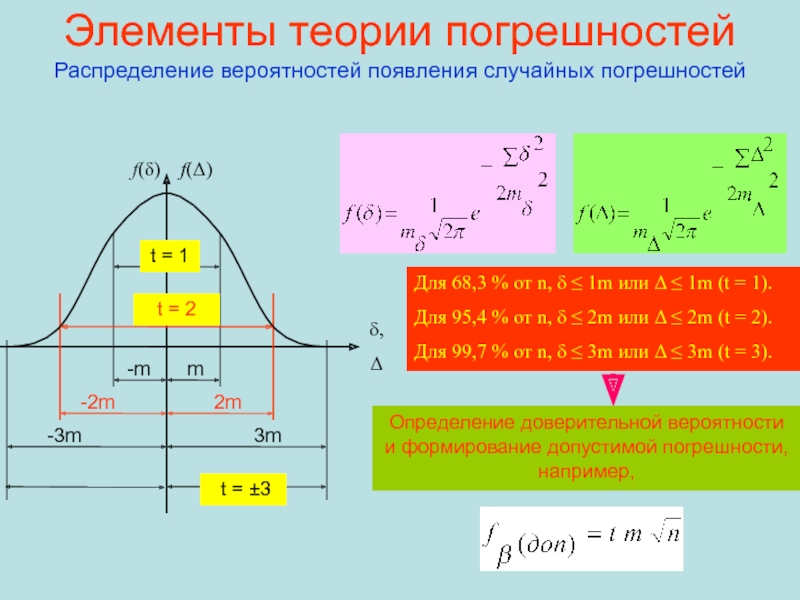
Слайд 71Элементы теории погрешностей Распределение вероятностей появления случайных погрешностей
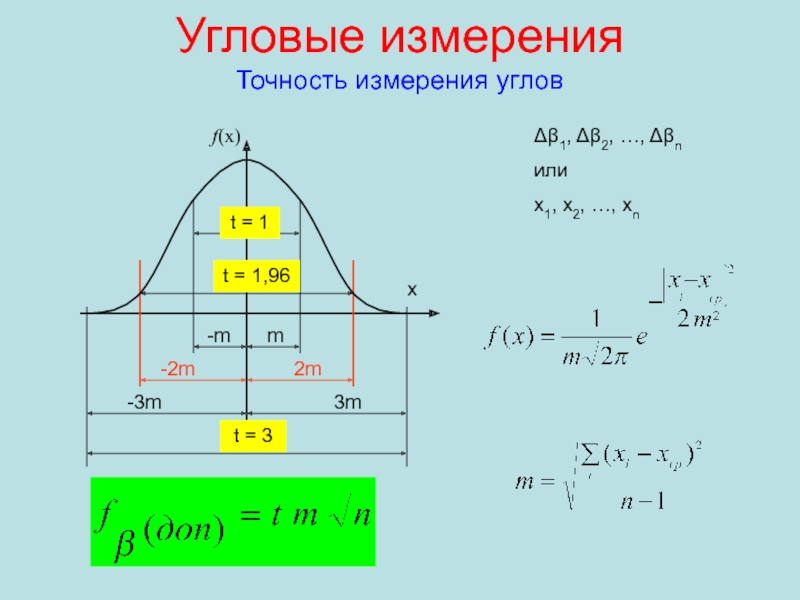
Для 68,3 %
от n, δ ≤ 1m или Δ ≤ 1m (t
= 1).Для 95,4 % от n, δ ≤ 2m или Δ ≤ 2m (t = 2).
Для 99,7 % от n, δ ≤ 3m или Δ ≤ 3m (t = 3).
Определение доверительной вероятности и формирование допустимой погрешности, например,
t = ±3
Слайд 72Элементы теории погрешностей
Случайные погрешности обладают следующими свойствами:
Предельного значения. Абсолютные
значения случайных погрешностей при заданных условиях измерений не могут превосходить
предельного значения. Это предельное значение является граничным, отделяющим случайные погрешности от грубых.Симметрии. Появление отрицательных и положительных случайных погрешностей равновероятно.
Обратной пропорциональности. Меньшим значениям случайных погрешностей соответствует большая вероятность их появления и наоборот, чем больше случайная погрешность, тем меньше вероятность ее появления.
Компенсации. Среднее арифметическое случайных погрешностей стремится к нулю при неограниченном увеличении количества измерений.
или
Слайд 73Элементы теории погрешностей
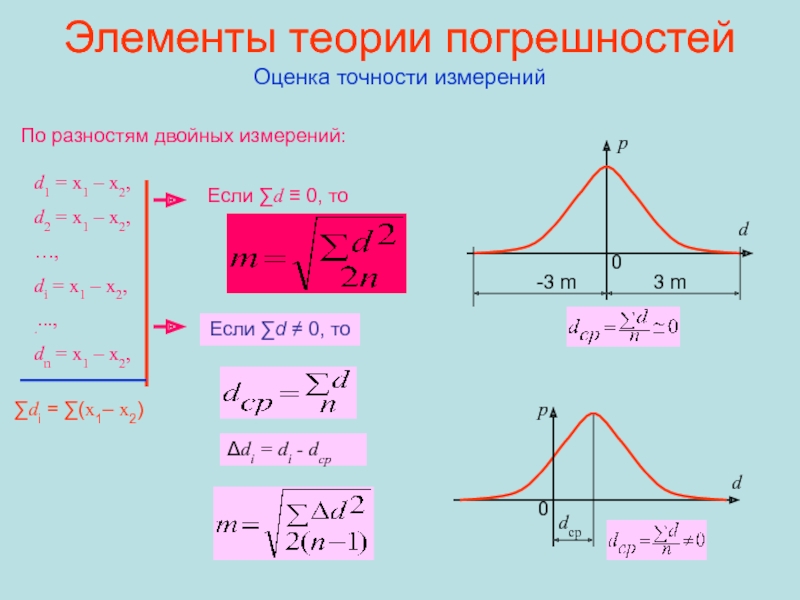
Оценка точности измерений
По разностям двойных измерений:
d1 =
x1 – x2,
d2 = x1 – x2,
…,
di = x1 –
x2,....,
dn = x1 – x2,
Если ∑d ≡ 0, то
Если ∑d ≠ 0, то
Δdi = di - dср
d
d
p
-3 m
3 m
0
0
dср
p
∑di = ∑(x1– x2)
Слайд 75Элементы теории погрешностей
неравноточные измерения
Оценка точности измерений
Понятие веса
измерения:
Степень доверия к измеренным параметрам:
1
2
3
L1 = 1 км, m1
= 17 ммL3 = 10 км, m3 = 53 мм
L2 = 2 км, m2 = 23 мм
Н1 = 10,021
Н2 = 10,044
Н3 = 10,068
P1 = 10/1 = 10
P2 = 10/2 = 5
P3 = 10/10 = 1
10,031
P1 = 532/172 = 10
P2 = 532/232 = 5
P3 = 532/532 = 1
10.031









![ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ И ГЕОИНФОРМАТИКА Линейные измеренияМетодика измерения линий 20-и метровой стальной лентойLизм = N *[(А- Линейные измеренияМетодика измерения линий 20-и метровой стальной лентойLизм = N *[(А- 1) * Lном] + (Lном *n)](/img/tmb/4/343499/99f32b47d753c1c7b4141296b1155faa-800x.jpg)