Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ
Содержание
- 1. ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ
- 2. ЛЕКЦИЯ 4 многогранники. Пересечение многогранника плоскостью.Взаимное пересечение многогранников.
- 3. Основные понятия Многогранной называется поверхность,
- 4. Правильные многогранники
- 5. По заданной горизонтальной проекции точки Е ,
- 6. Основные понятия При пересечении многогранника плоскостью
- 7. Пересечение многогранника проецирующей плоскостьюЕсли секущая плоскость проецирующая
- 8. Решение задачиЗадача: Построить сечение
- 9. Секущая плоскость R перпендикулярна фронтальной плоскости
- 10. Каждую из вершин сечения , отмеченную
- 11. Соединив полученные точки 1,2,3,4 в
- 12. Строим натуральную величину сечения 10-20-30-40
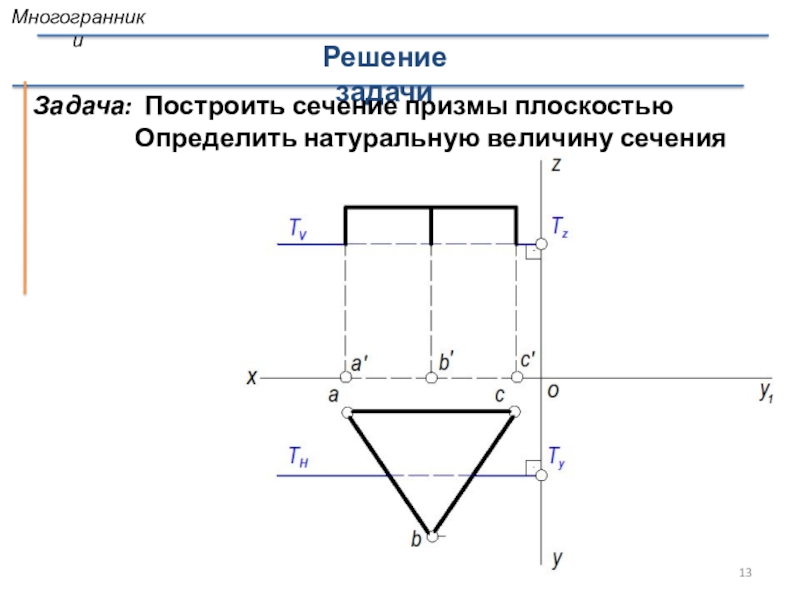
- 13. Решение задачиЗадача: Построить сечение призмы плоскостью
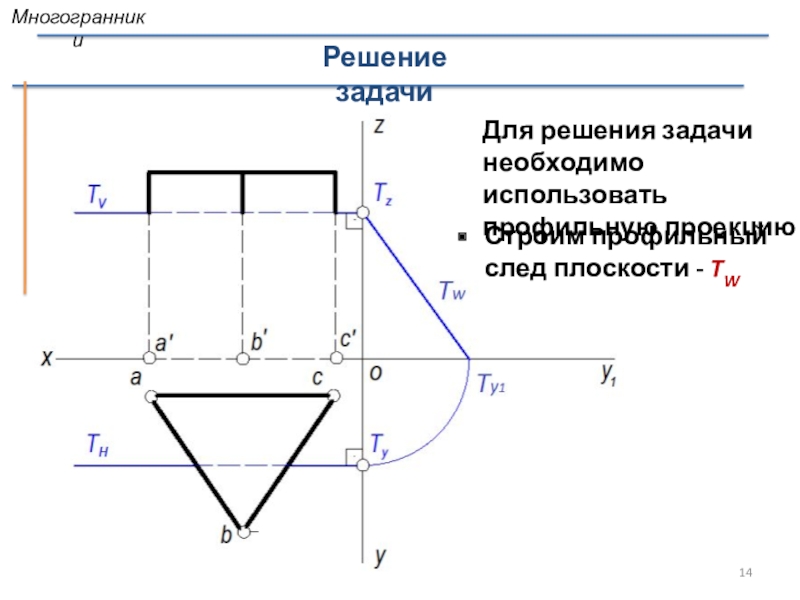
- 14. Для решения задачи необходимо использовать профильную проекциюРешение задачиСтроим профильный след плоскости - TWМногогранники
- 15. Строим профильную проекцию призмыРешение задачиМногогранники
- 16. Секущая плоскость T перпендикулярна профильной плоскости
- 17. Решение задачи МногогранникиСоединяем полученные точки в определенном порядке , получаем горизонтальную и фронтальную проекции сечения
- 18. Решение задачиНаходим недостающие координаты точек Х1 ,
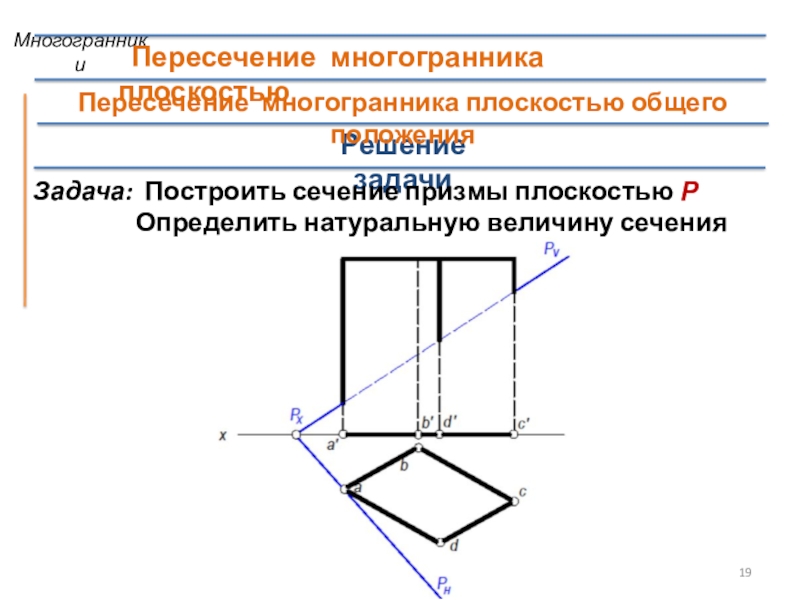
- 19. Решение задачиЗадача: Построить сечение призмы плоскостью Р
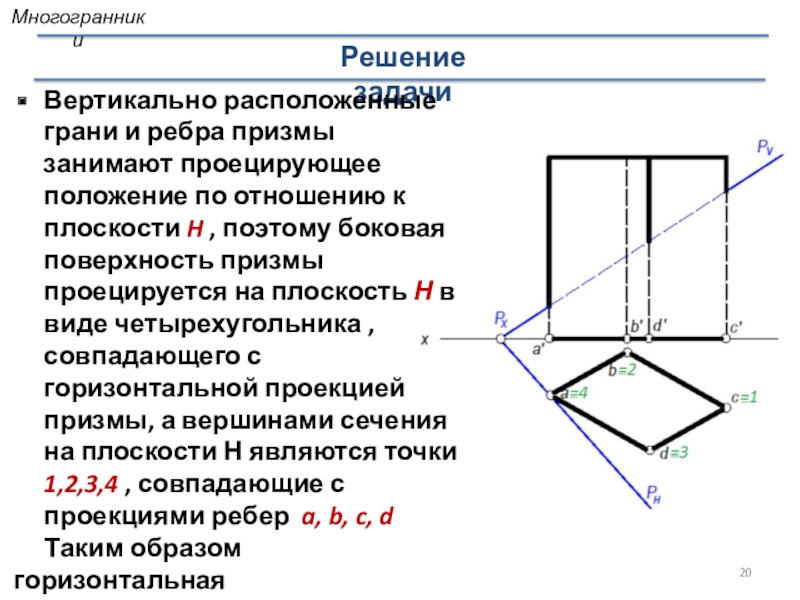
- 20. Решение задачиВертикально расположенные грани и ребра призмы
- 21. Решение задачиФронтальную проекцию сечения определяем из принадлежности
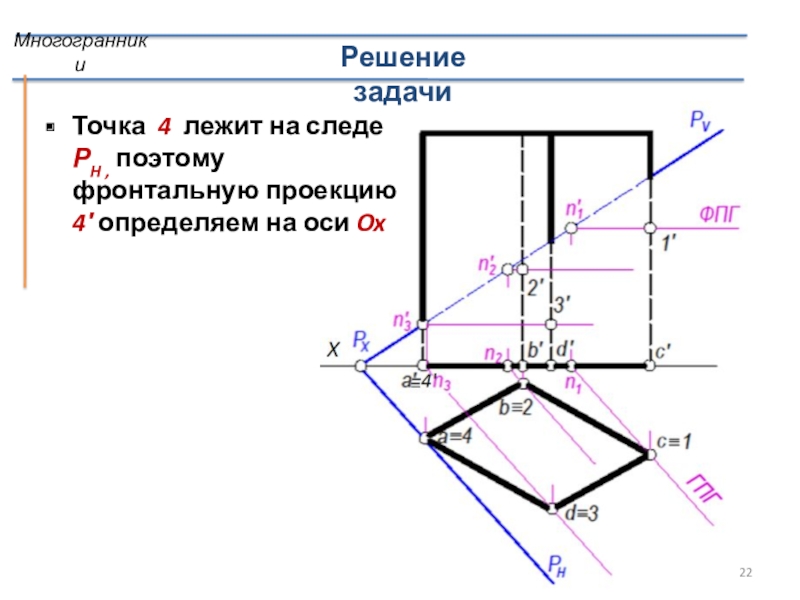
- 22. Решение задачиТочка 4 лежит на следе РH
- 23. Соединяя точки , получим фронтальную проекцию сечения
- 24. Строим натуральную величину сечения способом вращения плоскости
- 25. Точкам n'2 и n'3 , расположенным на
- 26. В совмещенном положении любая горизонталь плоскости окажется
- 27. Находим в совмещенном положении точки 20 и 30Решение задачиГ л а в а 4. Многогранники
- 28. Точка 4 расположена на оси вращения РH
- 29. Соединяя полученные точки, определяем натуральную величину сечения
- 30. 4.3. Пересечение прямой с поверхностью многогранникаЧерез прямую
- 31. Решение задачиЗадача: Построить точки пересечения прямой АВ
- 32. Решение задачиЗаключаем прямую АВ во фронтально проецирующую
- 33. Решение задачиНаходим проекции искомых точек пересечения прямой
- 34. 1 способОпределяем точки , в которых ребра
- 35. Задача: Построить линию пересечения
- 36. Находим точки пересечения ребер наклонной призмы с
- 37. Соединяя точки в определенной последовательности отрезками прямых
- 38. В данной задаче призма
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ
ГРАФИКА
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И
ГРАФИКИ
Слайд 2ЛЕКЦИЯ 4
многогранники.
Пересечение многогранника
плоскостью.
Взаимное пересечение многогранников.
Слайд 3Основные понятия
Многогранной называется поверхность, образованная отсеками пересекающихся
плоскостей (многоугольниками)
Многогранником называется тело , ограниченное многогранной
поверхностьюМногоугольники называются гранями , их общие стороны – ребрами, а точки пересечения ребер называются вершинами
Прямая шестигранная призма
Прямая шестигранная пирамида
МНОГОГРАННИКИ
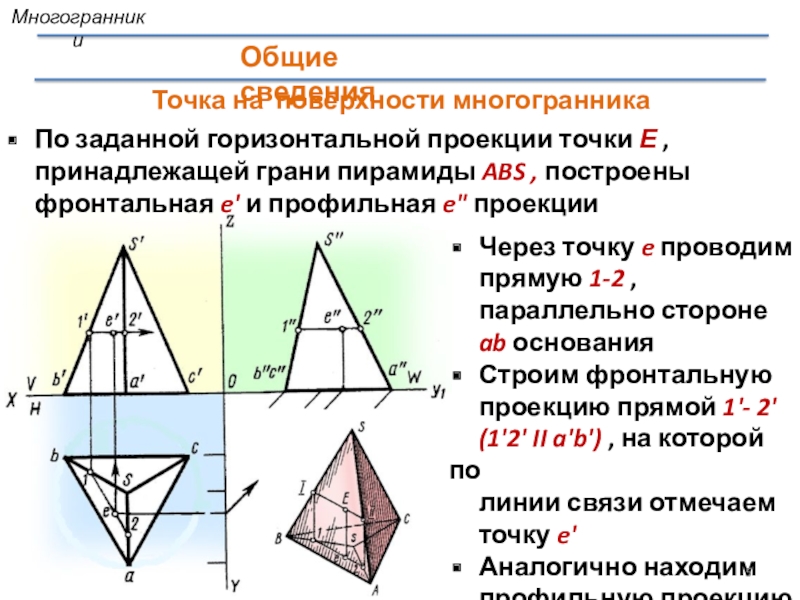
Слайд 5По заданной горизонтальной проекции точки Е , принадлежащей грани пирамиды
ABS , построены
фронтальная e' и профильная e"
проекцииТочка на поверхности многогранника
Через точку e проводим прямую 1-2 , параллельно стороне ab основания
Строим фронтальную проекцию прямой 1'- 2'
(1'2' II a'b') , на которой по
линии связи отмечаем
точку e'
Аналогично находим профильную проекцию e"
Многогранники
Общие сведения
Слайд 6Основные понятия
При пересечении многогранника плоскостью образуется замкнутая ломаная
линия (многоугольник). Плоская фигура, получаемая в результате пересечения, называется сечением
Решение задачи сводится к многократному пересечению прямой с плоскостью
Точки, в которых ребра многогранника пересекаются с заданной плоскостью, будут вершинами искомого сечения
Многогранники
Пересечение многогранника плоскостью
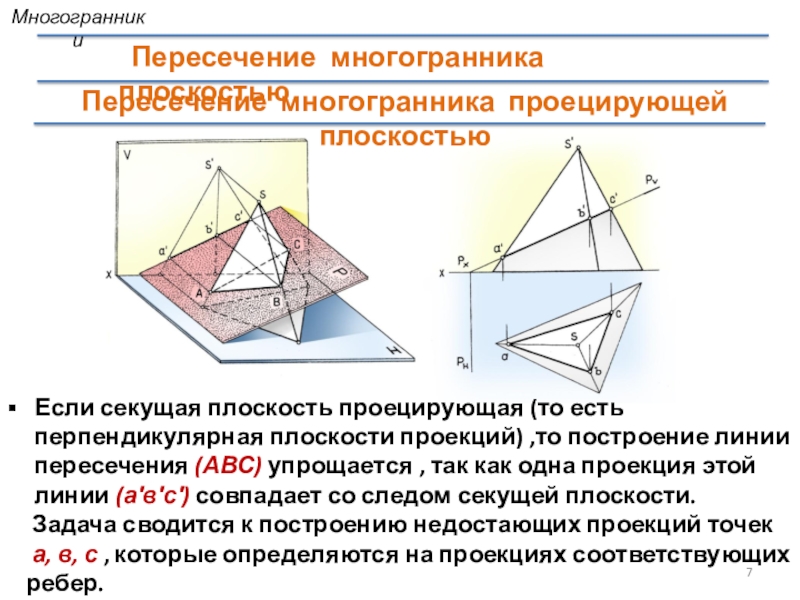
Слайд 7Пересечение многогранника проецирующей плоскостью
Если секущая плоскость проецирующая (то есть перпендикулярная
плоскости проекций) ,то построение линии пересечения (АВС) упрощается , так
как одна проекция этой линии (а′в′с′) совпадает со следом секущей плоскости.Задача сводится к построению недостающих проекций точек
а, в, с , которые определяются на проекциях соответствующих
ребер.
Многогранники
Пересечение многогранника плоскостью
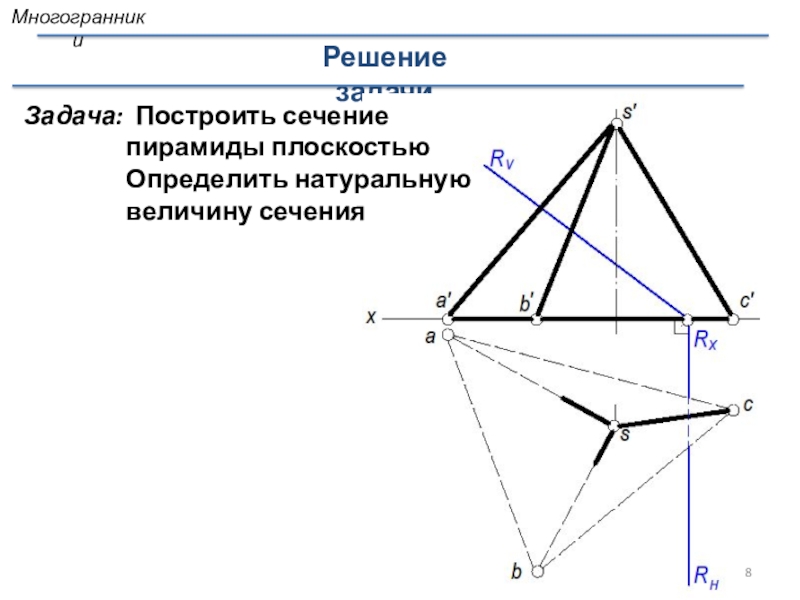
Слайд 8Решение задачи
Задача: Построить сечение
пирамиды плоскостью
Определить натуральную величину сечения
Многогранники
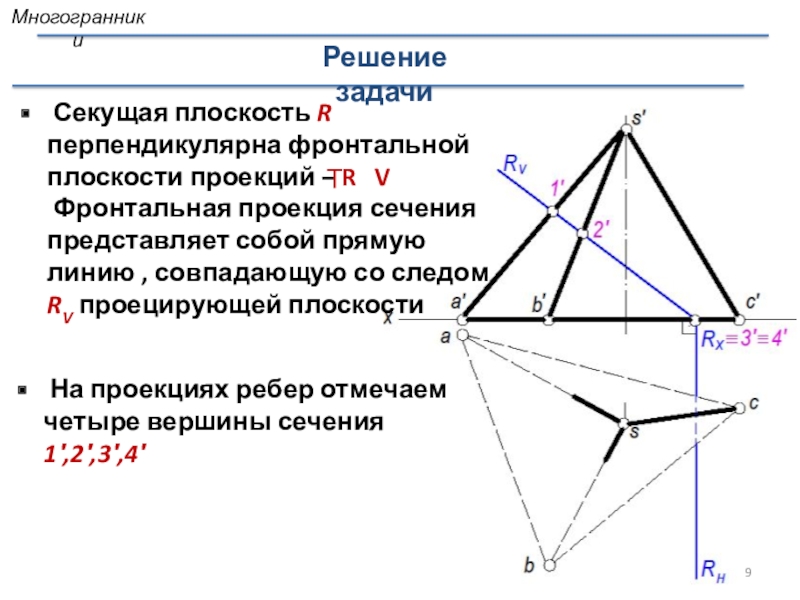
Слайд 9 Секущая плоскость R перпендикулярна фронтальной плоскости проекций – R
V
Фронтальная проекция сечения представляет собой прямую
линию , совпадающую со следом RV проецирующей плоскостиТ
На проекциях ребер отмечаем четыре вершины сечения 1′,2′,3′,4′
Решение задачи
Многогранники
Слайд 10 Каждую из вершин сечения , отмеченную на фронтальной плоскости
проекций 1′,2′,3′,4′,
находим на горизонтальной проекции - 1,2,3,4
Решение
задачи Многогранники
Слайд 11Соединив полученные точки
1,2,3,4 в определенном порядке
,
получаем горизонтальную проекцию
сечения - четырехугольник 1-2-4-3 Решение задачи
Многогранники
Слайд 12Строим натуральную
величину сечения 10-20-30-40
способом совмещения
Проекции сечения не определяют действительные размеры сечения , так
как секущая плоскость не параллельна ни одной из плоскостей проекцийРешение задачи
Многогранники
Слайд 13Решение задачи
Задача: Построить сечение призмы плоскостью
Определить натуральную величину сечения
Многогранники
Слайд 14Для решения задачи необходимо использовать профильную проекцию
Решение задачи
Строим профильный след
плоскости - TW
Многогранники
Слайд 16 Секущая плоскость T перпендикулярна профильной плоскости проекций, следовательно профильная
проекция сечения совпадает со следом TW проецирующей плоскости
Находим четыре вершины
сечения как точки пересечения соответствующих ребер с заданной плоскостью ТРешение задачи
Многогранники
Слайд 17Решение задачи
Многогранники
Соединяем полученные точки в определенном порядке , получаем
горизонтальную и фронтальную проекции сечения
Слайд 18Решение задачи
Находим недостающие координаты точек Х1 , X2 , X3
, X4 , с помощью которых получаем искомую натуральную величину
10-20-40-30Многогранники
Строим натуральную величину сечения способом перемены плоскостей проекций
Слайд 19Решение задачи
Задача: Построить сечение призмы плоскостью Р
Определить натуральную величину сечения
МногогранникиПересечение многогранника плоскостью общего положения
Пересечение многогранника плоскостью
Слайд 20Решение задачи
Вертикально расположенные грани и ребра призмы занимают проецирующее положение
по отношению к плоскости H , поэтому боковая поверхность призмы
проецируется на плоскость Н в виде четырехугольника , совпадающего с горизонтальной проекцией призмы, а вершинами сечения на плоскости Н являются точки 1,2,3,4 , совпадающие с проекциями ребер a, b, c, dТаким образом горизонтальная
проекция сечения 1-2-4-3 известна
без построения
Многогранники
Слайд 21Решение задачи
Фронтальную проекцию сечения определяем из принадлежности сечения плоскости Р.
Для этого через известные горизонтальные проекции точек 1,2,3,4 проводим в
плоскости Р прямые – горизонтали, с помощью которых находим фронтальные проекции точек 1′,2′,3′,4′Многогранники
Слайд 22Решение задачи
Точка 4 лежит на следе РH , поэтому фронтальную
проекцию 4′ определяем на оси Ox
Многогранники
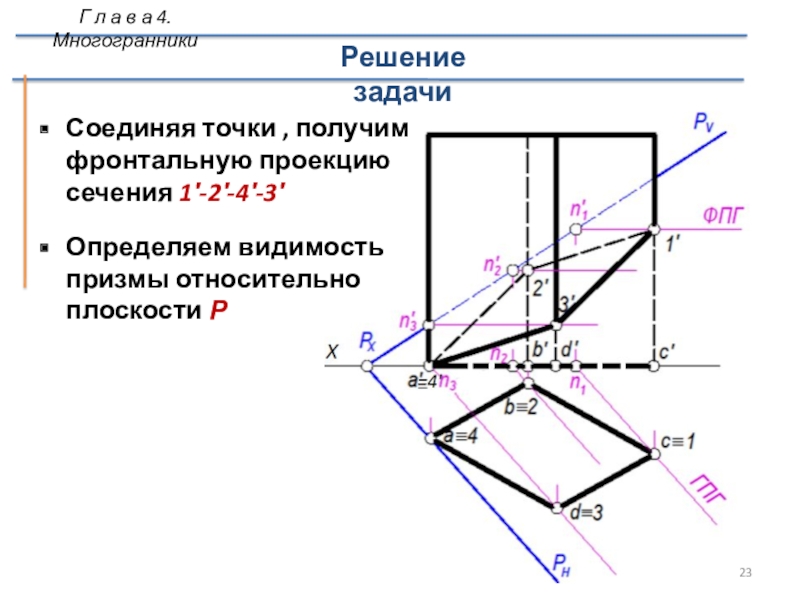
Слайд 23Соединяя точки , получим фронтальную проекцию сечения 1′-2′-4′-3′
Определяем видимость призмы
относительно плоскости Р
Решение задачи
Г л а в а 4. Многогранники
Слайд 24Строим натуральную величину сечения способом вращения плоскости Р вокруг следа
РH до совмещения ее с плоскостью проекций Н
Соединив точки
PX и N1,0 , определяем совмещенное
положение фронтального
следа - PV,0
Решение задачи
Г л а в а 4. Многогранники
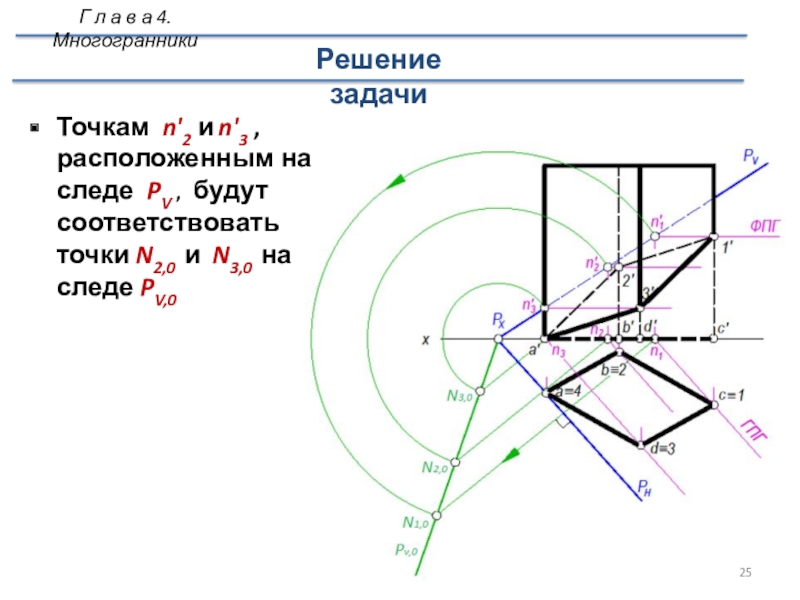
Слайд 25Точкам n'2 и n'3 , расположенным на следе PV ,
будут соответствовать точки N2,0 и N3,0 на следе PV,0
Решение задачи
Г
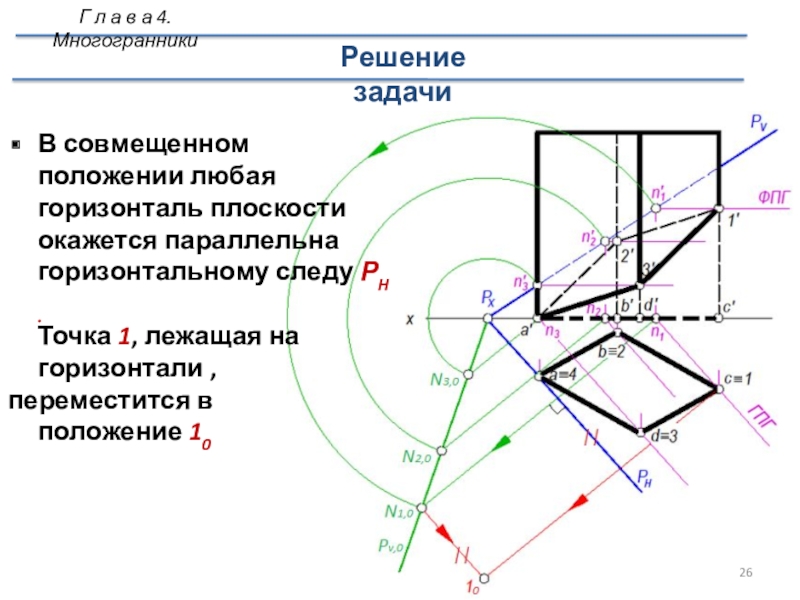
л а в а 4. МногогранникиСлайд 26В совмещенном положении любая горизонталь плоскости окажется параллельна горизонтальному следу
РH .
Точка 1, лежащая на
горизонтали , переместится в положение 10
Решение задачи
Г л а в а 4. Многогранники
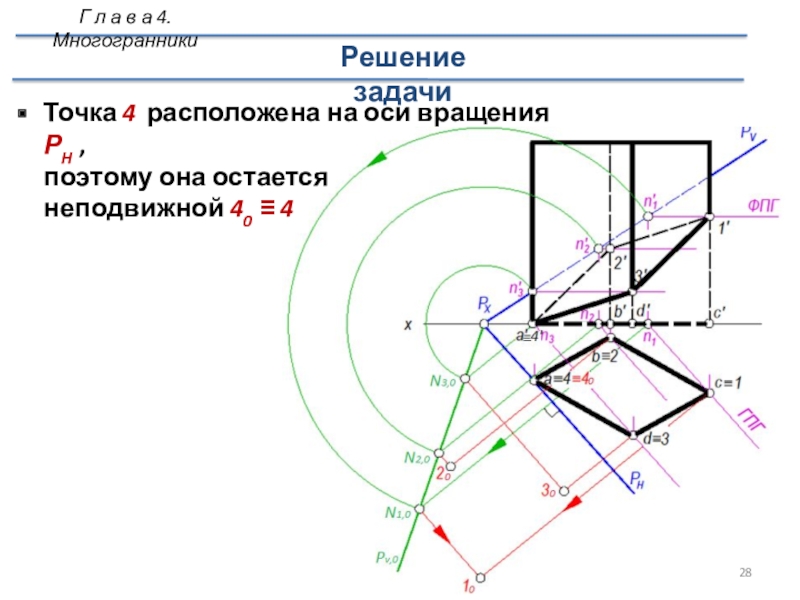
Слайд 28Точка 4 расположена на оси вращения РH ,
поэтому она остается
неподвижной 40 ≡ 4
Решение
задачиГ л а в а 4. Многогранники
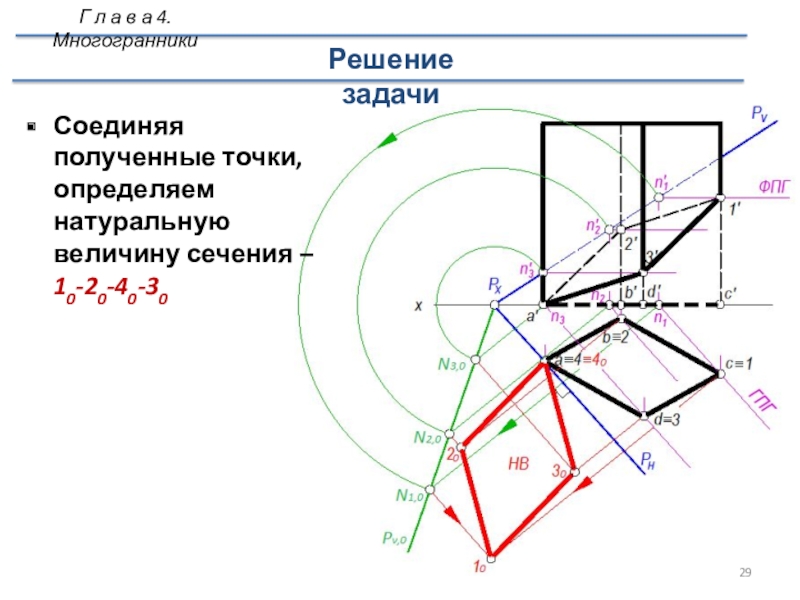
Слайд 29Соединяя полученные точки, определяем натуральную величину сечения –
10-20-40-30
Решение задачи
Г л а в а 4. Многогранники
Слайд 304.3. Пересечение прямой с поверхностью многогранника
Через прямую АВ проводим вспомогательную
секущую плоскость Р
Строим линию пересечения плоскости с поверхностью многогранника (треугольник)
Определяем
искомые точки I и II как точки пересечения данной прямой с линией пересечения Алгоритм решения аналогичен задаче на пересечение прямой с плоскостью
Г л а в а 4. Многогранники
Слайд 31Решение задачи
Задача: Построить точки пересечения прямой АВ
с поверхностью пирамиды
Г л а
в а 4. МногогранникиСлайд 32Решение задачи
Заключаем прямую АВ во фронтально проецирующую плоскость S
На
плоскости V каждую из вершин сечения 1′-2′-3′ определяем как точку
пересечения соответствующегоребра со следом SV
На плоскости Н определяем
горизонтальную проекцию линии
пересечения – треугольник 1-2-3
Г л а в а 4. Многогранники
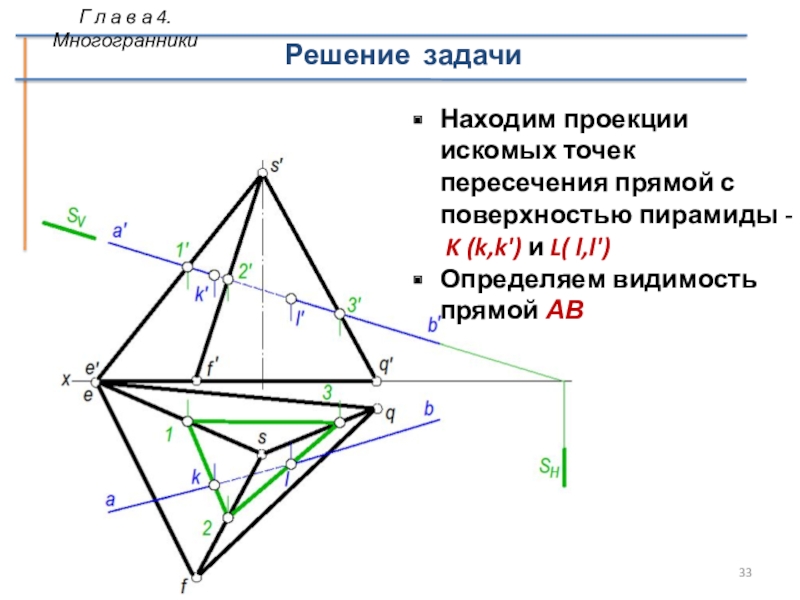
Слайд 33Решение задачи
Находим проекции искомых точек пересечения прямой с поверхностью пирамиды
-
K (k,k') и L( l,l')
Определяем видимость
прямой АВГ л а в а 4. Многогранники
Слайд 341 способ
Определяем точки , в которых ребра одного из многогранников
пересекают грани другого и ребра второго пересекают грани первого
Через полученные
точки в определенной последовательности проводим ломанную линию – линию пересечения данных многогранников (соединять можно только те точки, которые лежат в одной и той же грани)Способы построения линии пересечения многогранников
2 способ
Определяем отрезки прямых , по которым грани одного из многогранников пересекают грани другого
Отрезки являются звеньями ломанной линии пересечения данных поверхностей
Взаимное пересечение многогранников
Г л а в а 4. Многогранники
Слайд 36Находим точки пересечения ребер наклонной призмы с гранями прямой призмы
На
плоскости Н отмечаем :
- точки 1 и
8 пересечения ребра с с гранями km и kl
- точки 2 и 5 пересечения ребра b
с гранями km и ml
Точки 1′,8′ и 2′,5′ определяем на
проекциях соответствующих
ребер с′ и b′
Находим точки пересечения ребер
прямой призмы с гранями наклонной
Горизонтальные проекции точек 3Ξ4 и 6Ξ7 совпадают с горизонтальными проекциями ребер m и l
Фронтальные проекции 3',4',6‘,7'
определяем из принадлежности
точек соответствующим граням призмы
Решение задачи
Г л а в а 4. Многогранники
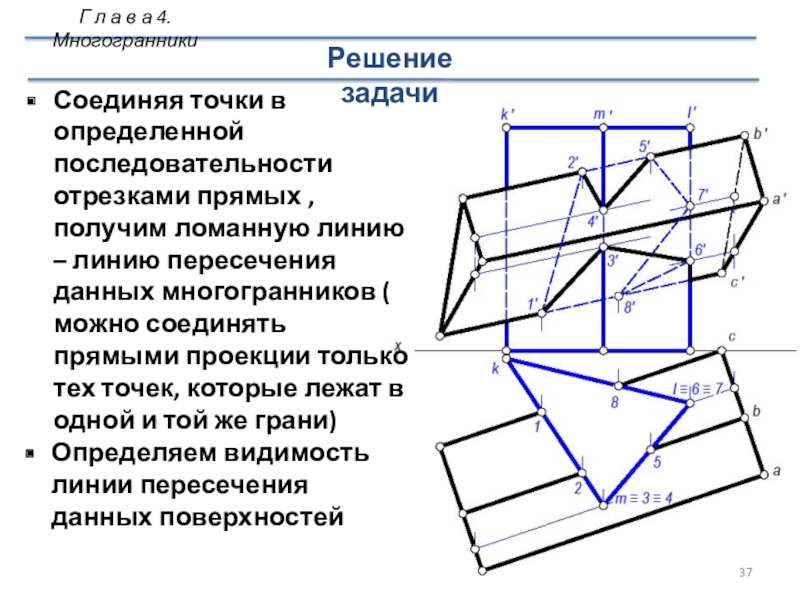
Слайд 37Соединяя точки в определенной последовательности отрезками прямых , получим ломанную
линию – линию пересечения данных многогранников ( можно соединять прямыми
проекции только тех точек, которые лежат в одной и той же грани)Определяем видимость линии пересечения данных поверхностей
Решение задачи
Г л а в а 4. Многогранники
Слайд 38 В данной задаче призма пересекает пирамиду насквозь
, в этом случае линия пересечения распадается на две замкнутые
ломанные линии. Это хорошо видно на профильной проекции. Кроме того ребра пирамиды не пересекаются с призмойЧерез ребра призмы проводим вспомогательные горизонтальные плоскости Q и Q1 , при пересечении этих плоскостей с пирамидой получаем треугольники , подобные основанию пирамиды , в которых на ребрах и определяются точки 1,2 и 3,5
Г л а в а 4. Многогранники
Решение задачи
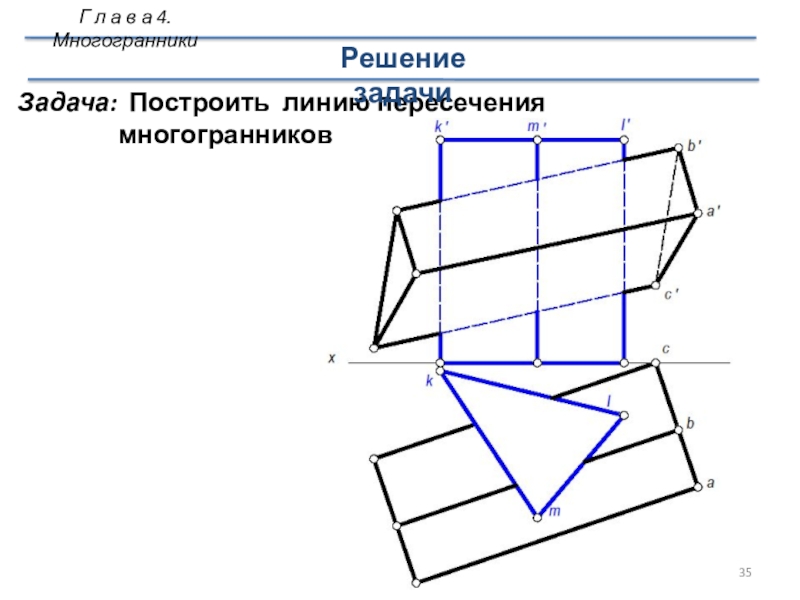
Задача: Построить линию пересечения многогранников