Слайд 1Использование деревьев в алгоритме Хаффмана
Слайд 2Алгоритм Хаффмана - адаптивный жадный алгоритм оптимального префиксного кодиро- вания алфавита с минимальной избыточностью. Был разработан
в 1952 году Дэвидом Хаффманом при написании им курсовой работы. В настоящее
время используется во многих программах сжатия данных.
Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.
Слайд 3Идея алгоритма состоит в следующем: зная вероятности символов в сообщении,
можно описать процедуру построения кодов переменной длины, состоящих из целого
количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т.е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
Слайд 4Алгоритм
Символы входного алфавита образуют список свободных узлов. Каждый лист имеет
вес, который может быть равен либо вероятности, либо количеству вхождений
символа в сжимаемое сообщение.
Выбираются два свободных узла дерева с наименьшими весами.
Создается их родитель с весом, равным их суммарному весу.
Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.
Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Слайд 5Чтобы получить код для каждого символа на основе его частотности,
нам надо построить бинарное дерево, такое, что каждый лист этого
дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов в экспериментальной строке «beep boop reeb!»
Слайд 6После вычисления частот мы создадим узлы бинарного дерева для каждого
знака и добавим их в очередь, используя частоту в качестве
приоритета:
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.
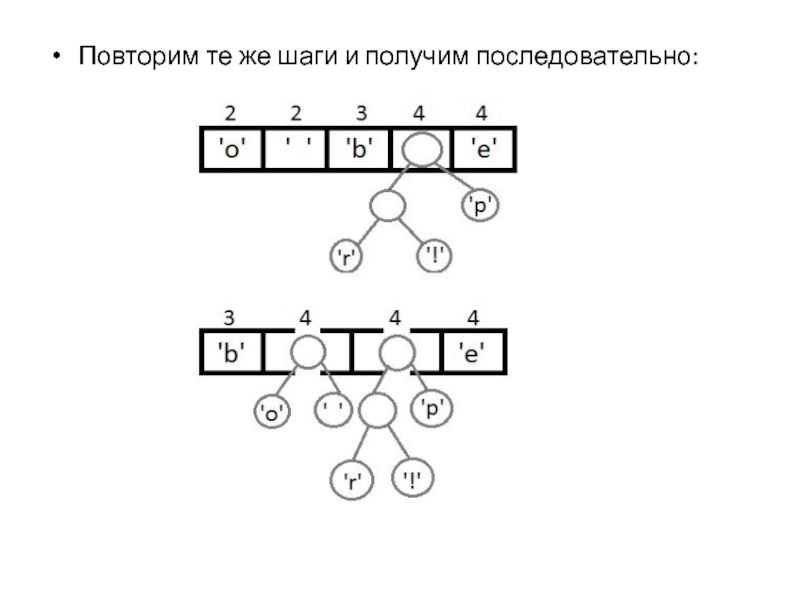
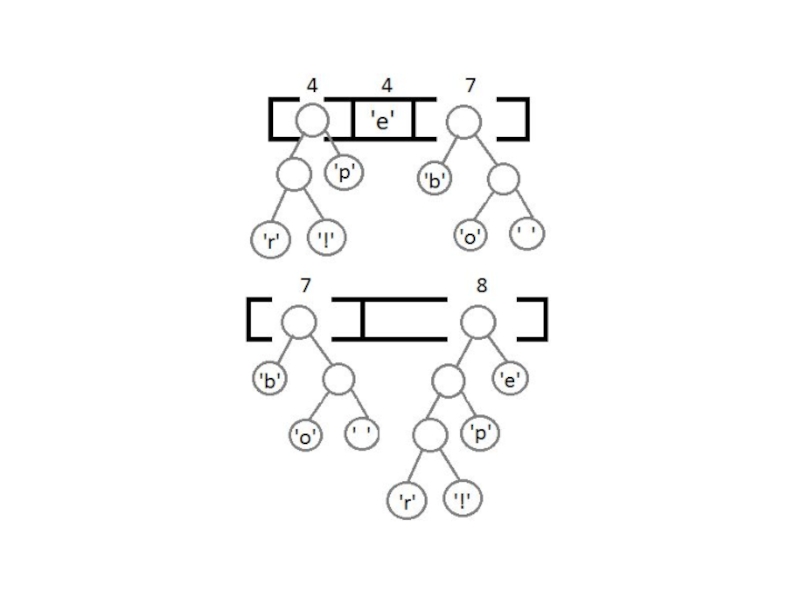
Слайд 7Повторим те же шаги и получим последовательно:
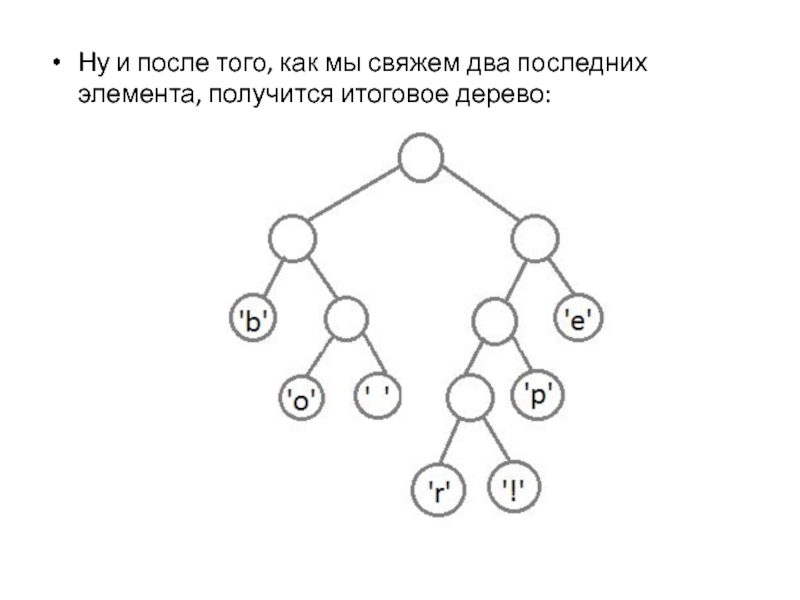
Слайд 9Ну и после того, как мы свяжем два последних элемента,
получится итоговое дерево:
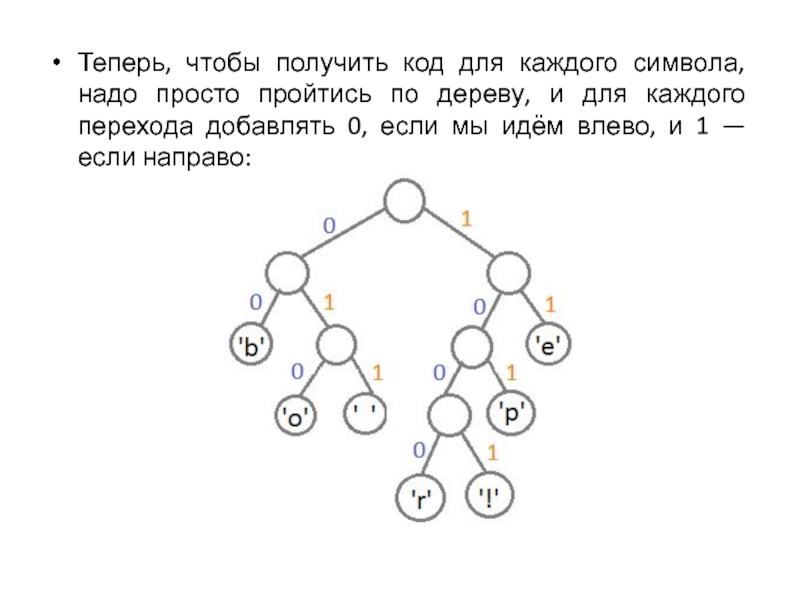
Слайд 10Теперь, чтобы получить код для каждого символа, надо просто пройтись
по дереву, и для каждого перехода добавлять 0, если мы
идём влево, и 1 — если направо:
Слайд 11Если мы так сделаем, то получим следующие коды для символов:
Чтобы
расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву,
сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для 'b', то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на 'b'.
Слайд 12На практике, при реализации данного алгоритма сразу после построения дерева
строится таблица Хаффмана. Данная таблица — это по сути связный
список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: «beep boop reeb!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.
Слайд 13Классический алгоритм Хаффмана имеет ряд существенных недостатков. Во-первых, для восстановления
содержимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался
кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и Н-дерева), другого для собственно кодирования. Во-вторых, избыточность кодирования обращается в ноль лишь в тех случаях, когда вероятности кодируемых символов являются обратными степенями числа 2. В-третьих, для источника с энтропией, не превышающей 1 (например, для двоичного источника), непосредственное применение кода Хаффмана бессмысленно.
Слайд 14В создании алгоритма адаптивного кодирования Хаффмана наибольшие сложности возникают при
разработке процедуры обновления модели очередным символом. Теоретически можно было бы
просто вставить внутрь этой процедуры полное построение дерева кодирования Хаффмана, однако, такой алгоритм сжатия имел бы неприемлемо низкое быстродействие, так как построение Н-дерева — это слишком большая работа, и производить её при обработке каждого символа неразумно. К счастью, существует способ модифицировать уже существующее Н-дерево так, чтобы отобразить обработку нового символа.
Слайд 15Обновление дерева при считывании очередного символа сообщения состоит из двух
операций.
Первая — увеличение веса узлов дерева. Вначале увеличиваем вес листа, соответствующего
считанному символу, на единицу. Затем увеличиваем вес родителя, чтобы привести его в соответствие с новыми значениями веса потомков. Этот процесс продолжается до тех пор, пока мы не доберемся до корня дерева. Среднее число операций увеличения веса равно среднему количеству битов, необходимых для того, чтобы закодировать символ.
Вторая операция — перестановка узлов дерева — требуется тогда, когда увеличение веса узла приводит к нарушению свойства упорядоченности, то есть тогда, когда увеличенный вес узла стал больше, чем вес следующего по порядку узла. Если и дальше продолжать обрабатывать увеличение веса, двигаясь к корню дерева, то дерево перестанет быть деревом Хаффмана.
Слайд 16Переполнение. В процессе работы алгоритма сжатия вес узлов в дереве
кодирования Хаффмана неуклонно растет. Первая проблема: вес корня дерева начинает
превосходить вместимость ячейки, в которой он хранится. Как правило, это 16-битовое значение и, следовательно, не может быть больше, чем 65535. Вторая проблема: размер самого длинного кода Хаффмана превосходит вместимость ячейки, которая используется для того, чтобы передать его в выходной поток. Декодеру все равно, какой длины код он декодирует, поскольку он движется сверху вниз по дереву кодирования, выбирая из входного потока по одному биту. Кодер же должен начинать от листа дерева и двигаться вверх к корню, собирая биты, которые нужно передать. Обычно это происходит с переменной типа «целое», и, когда длина кода Хаффмана превосходит размер типа «целое» в битах, наступает переполнение.
Слайд 17Масштабирование весов узлов дерева Хаффмана Принимая во внимание сказанное выше,
алгоритм обновления дерева Хаффмана должен быть изменен следующим образом: при
увеличении веса нужно проверять его на достижение допустимого максимума. Если мы достигли максимума, то необходимо «масштабировать» вес, обычно разделив вес листьев на целое число, например, 2, а потом пересчитав вес всех остальных узлов.
Однако при делении веса пополам возникает проблема, связанная с тем, что после выполнения этой операции дерево может изменить свою форму. Объясняется это тем, что мы делим целые числа и при делении отбрасываем дробную часть.
Слайд 18Правильно организованное дерево Хаффмана после масштабирования может иметь форму, значительно
отличающуюся от исходной. Это происходит потому, что масштабирование приводит к
потере точности нашей статистики. Но со сбором новой статистики последствия этих «ошибок» практически сходят на нет. Масштабирование веса — довольно дорогостоящая операция, так как она приводит к необходимости заново строить все дерево кодирования. Но, так как необходимость в ней возникает относительно редко, то с этим можно смириться.