минимуму
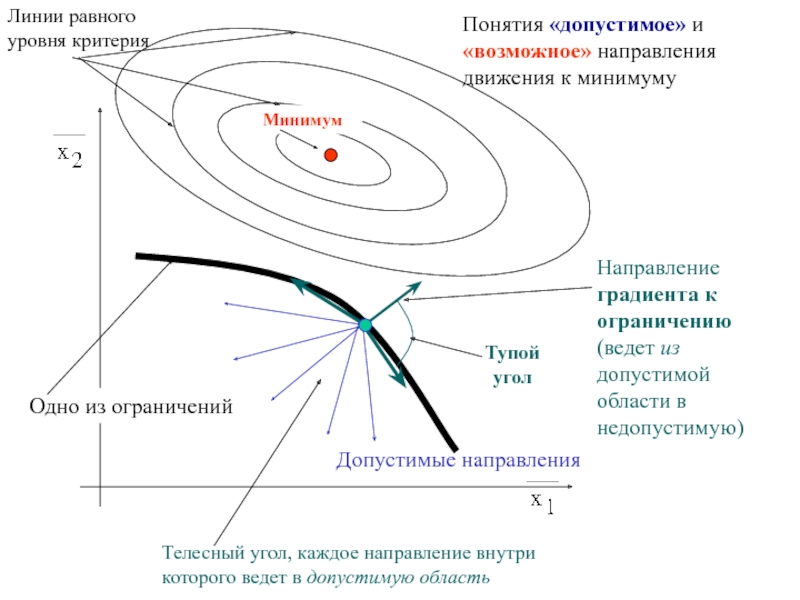
Одно из ограничений
Направление градиента к ограничению (ведет из допустимой области
в недопустимую)Тупой угол
Телесный угол, каждое направление внутри которого ведет в допустимую область
Допустимые направления