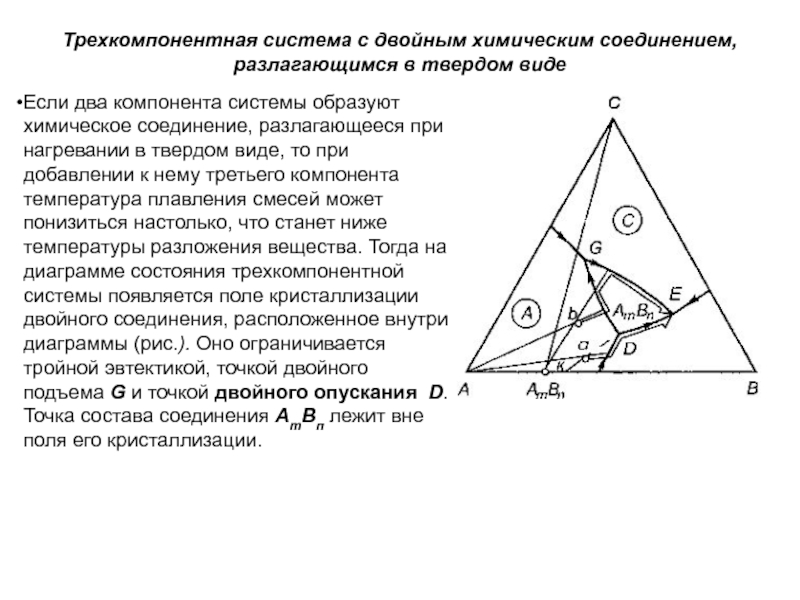
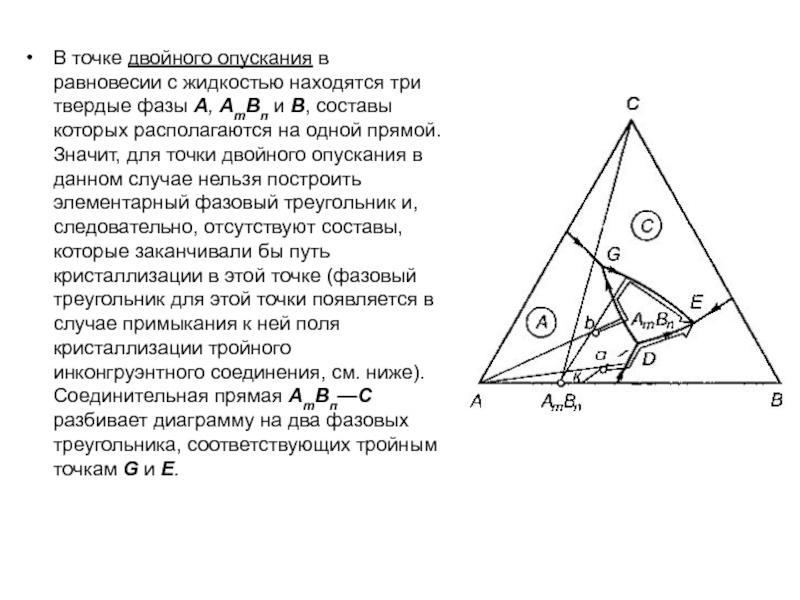
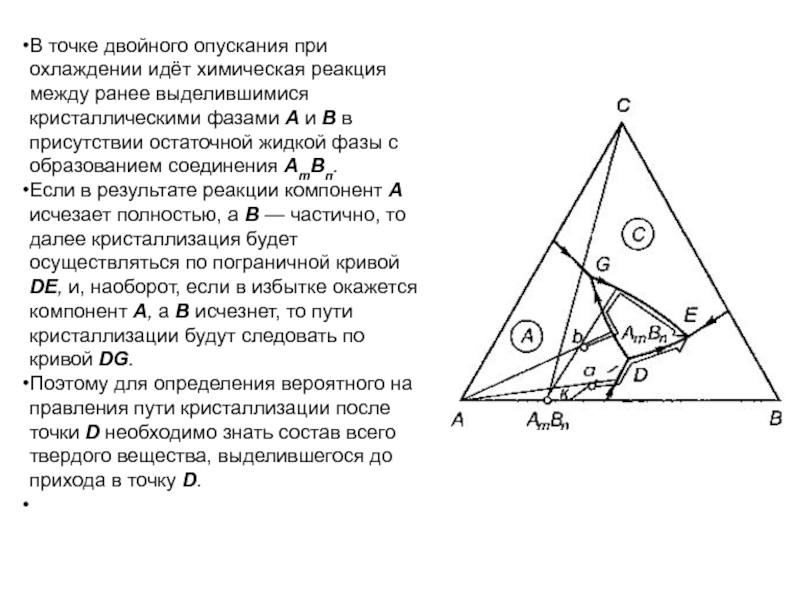
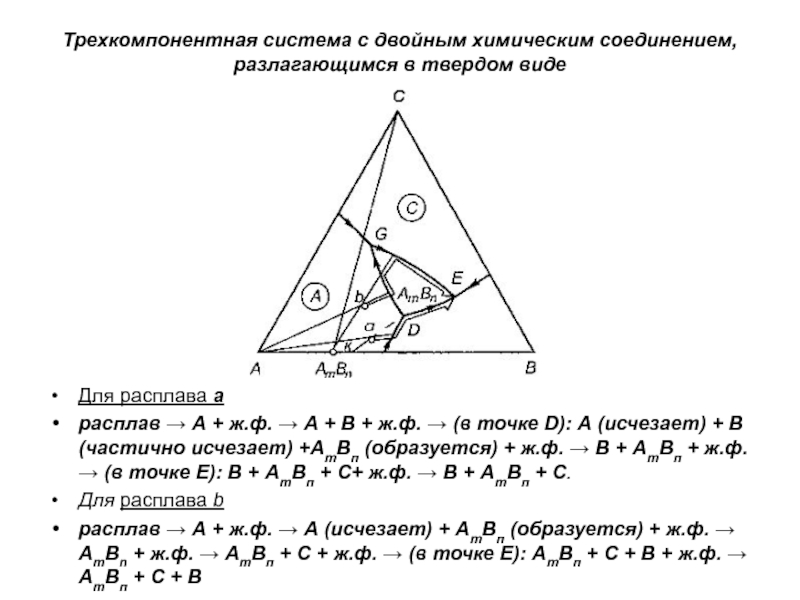
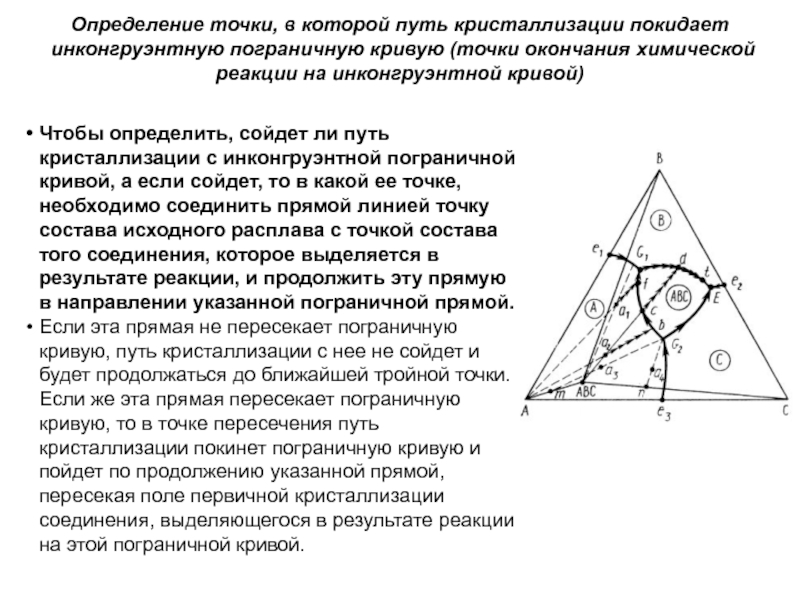
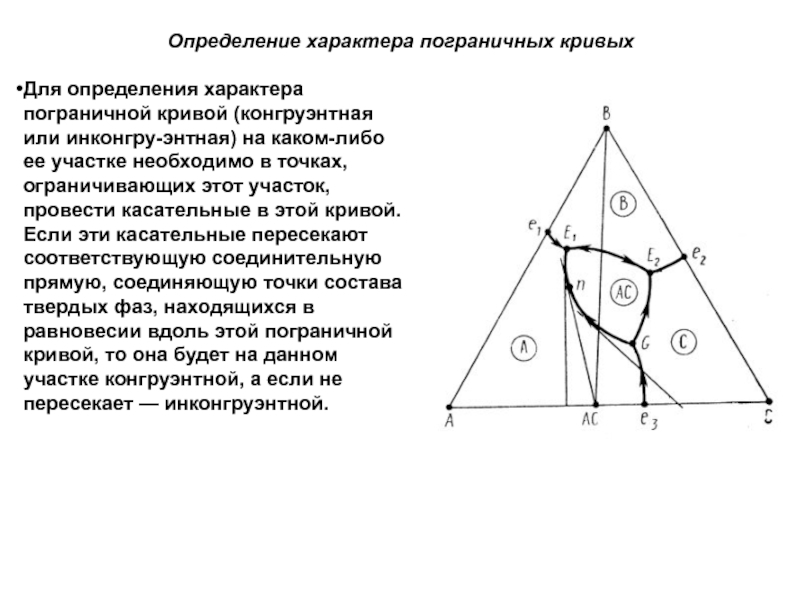
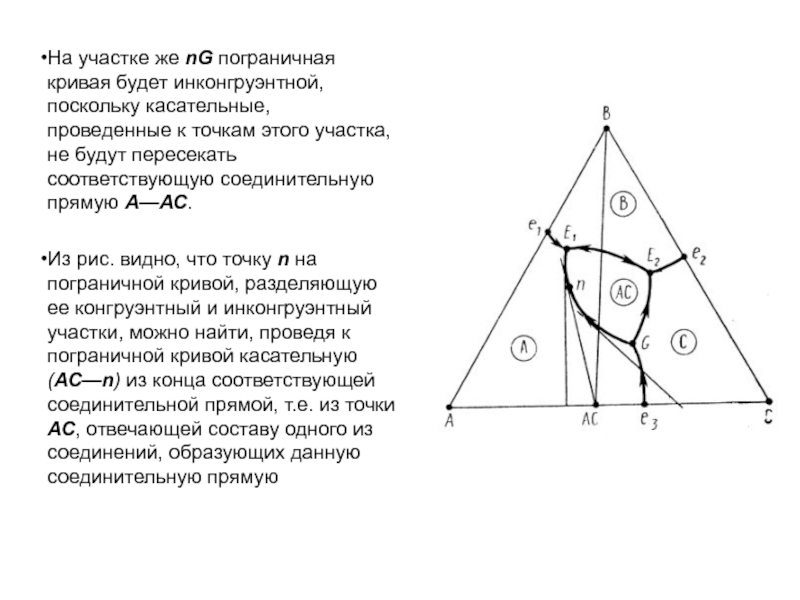
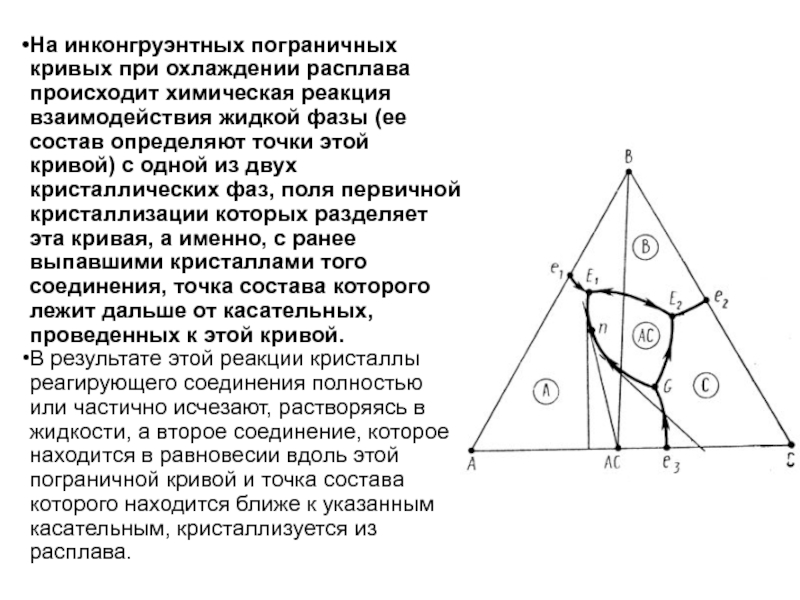
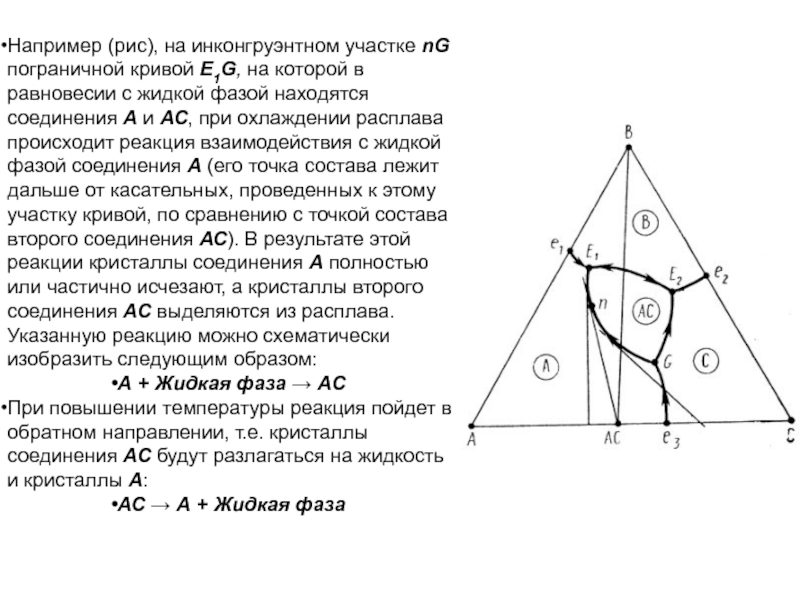
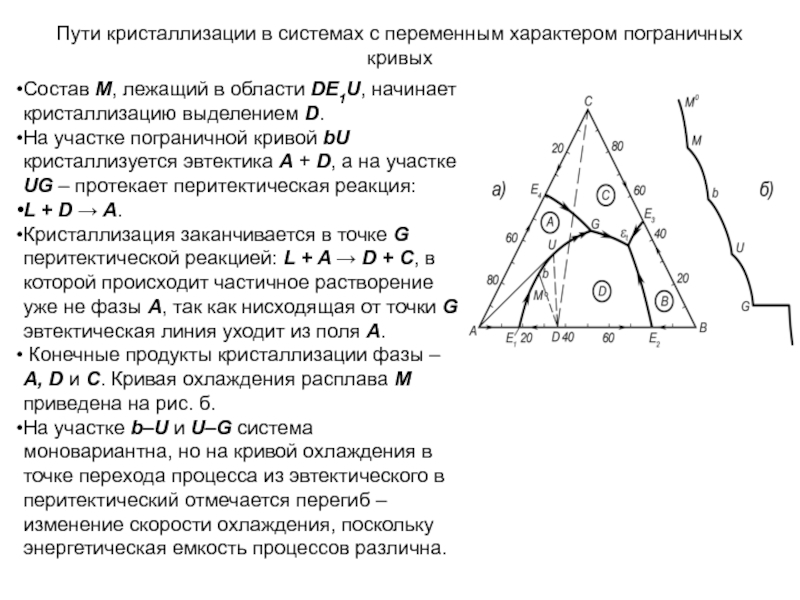
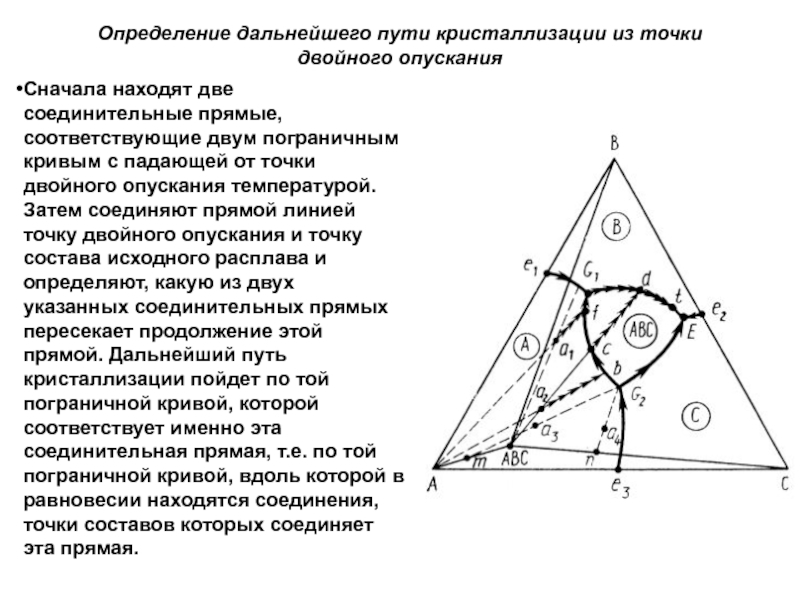
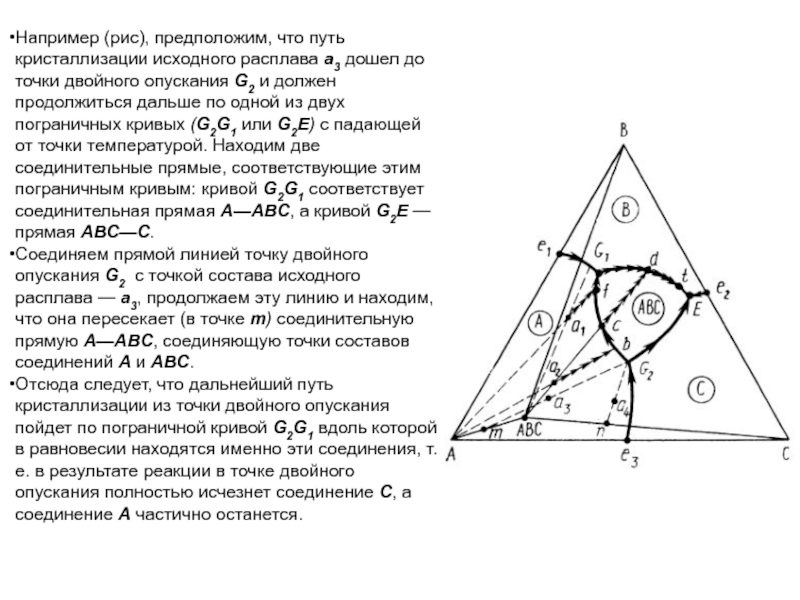
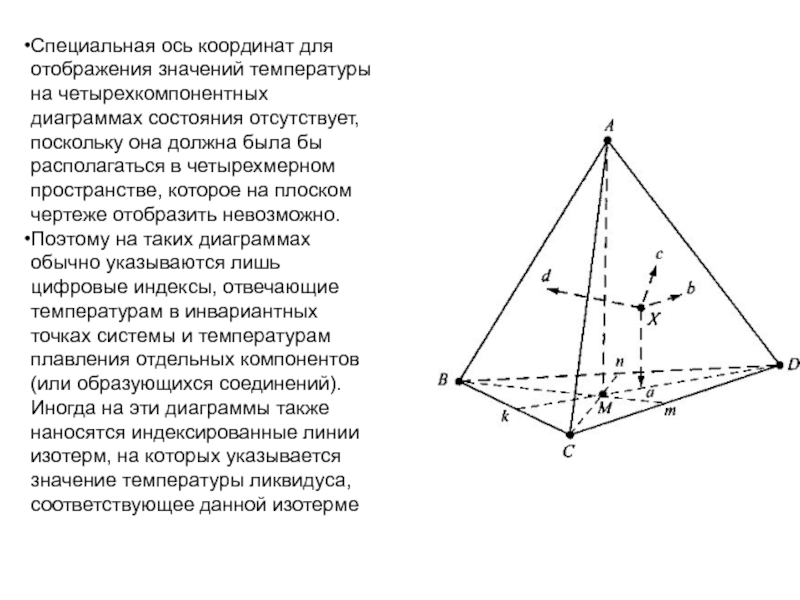
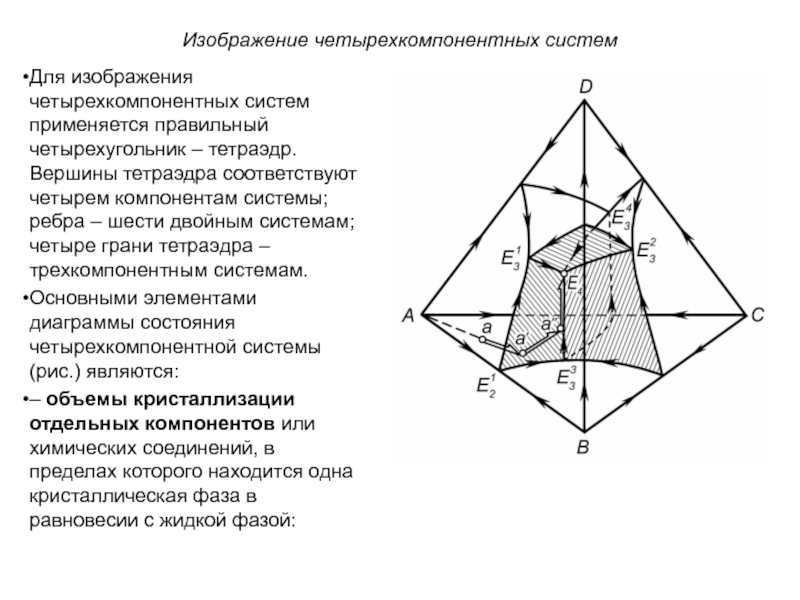
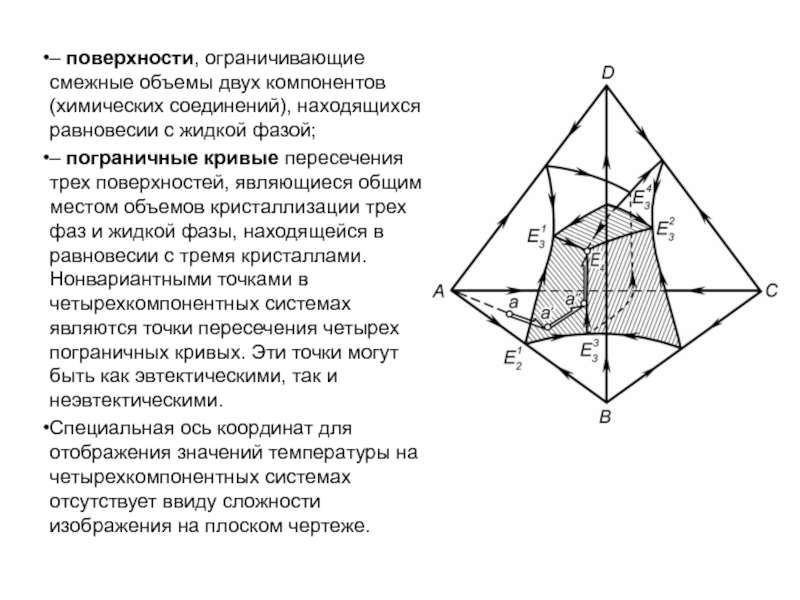
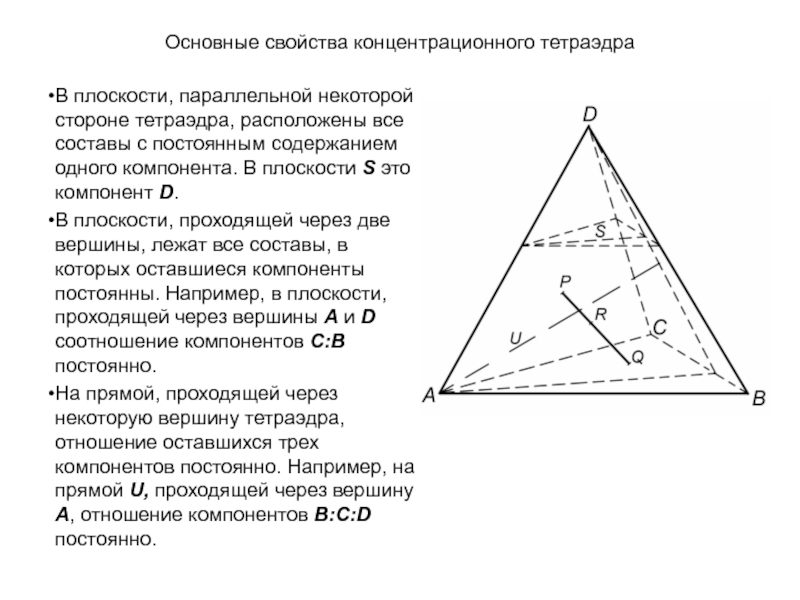
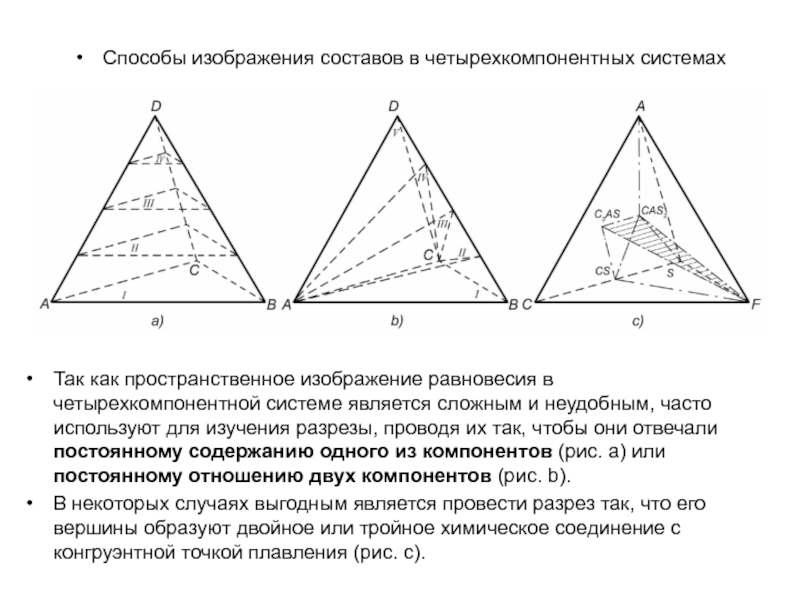
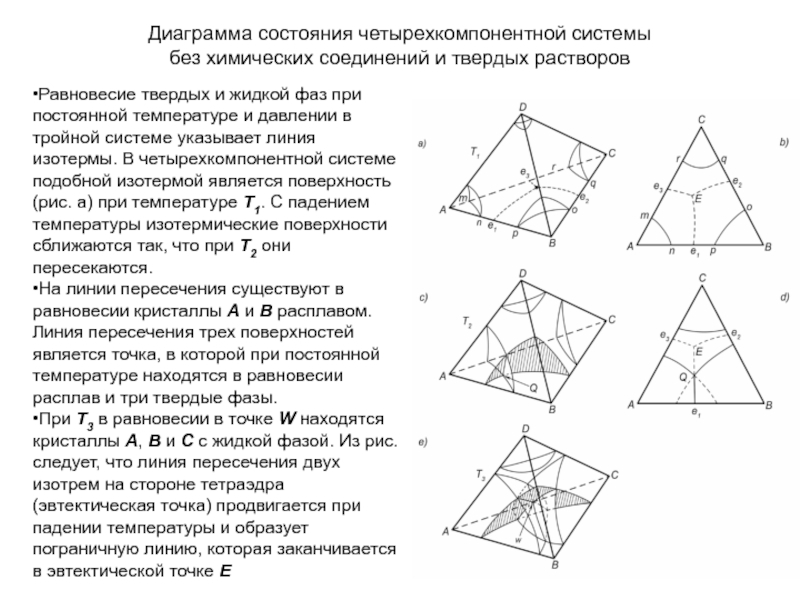
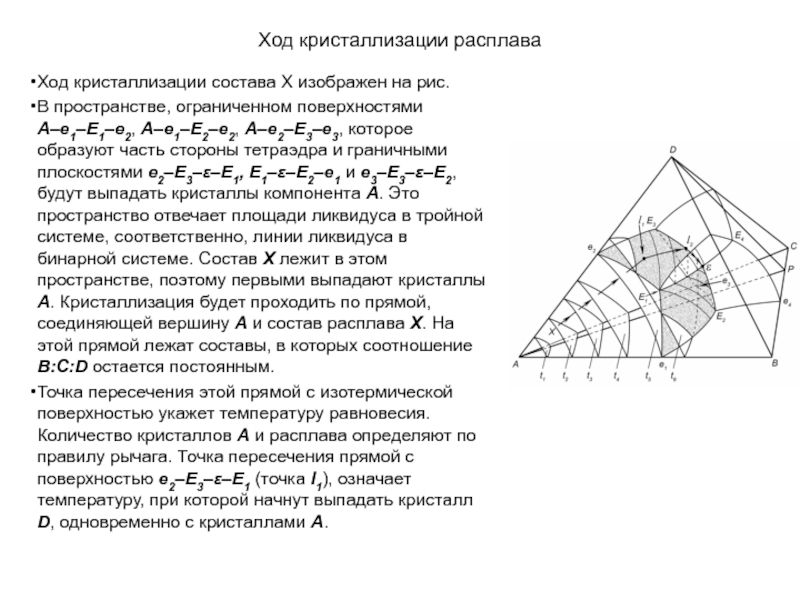
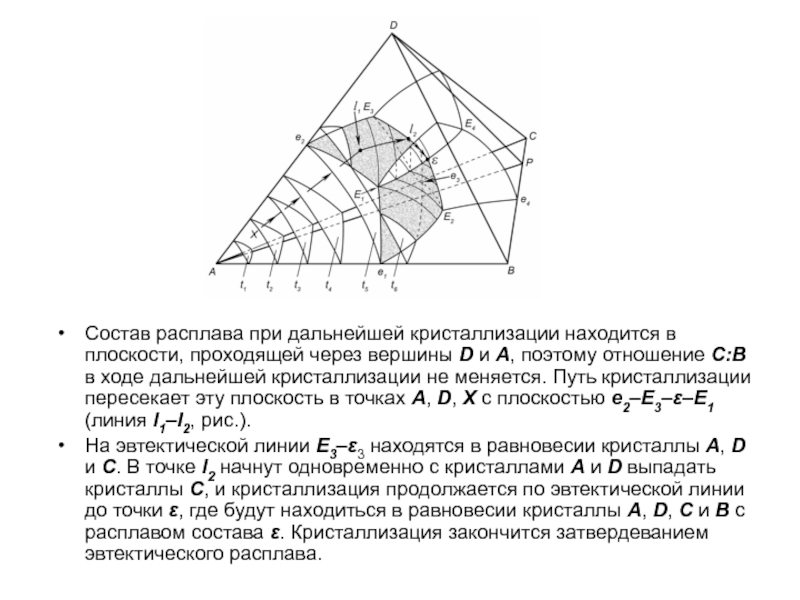
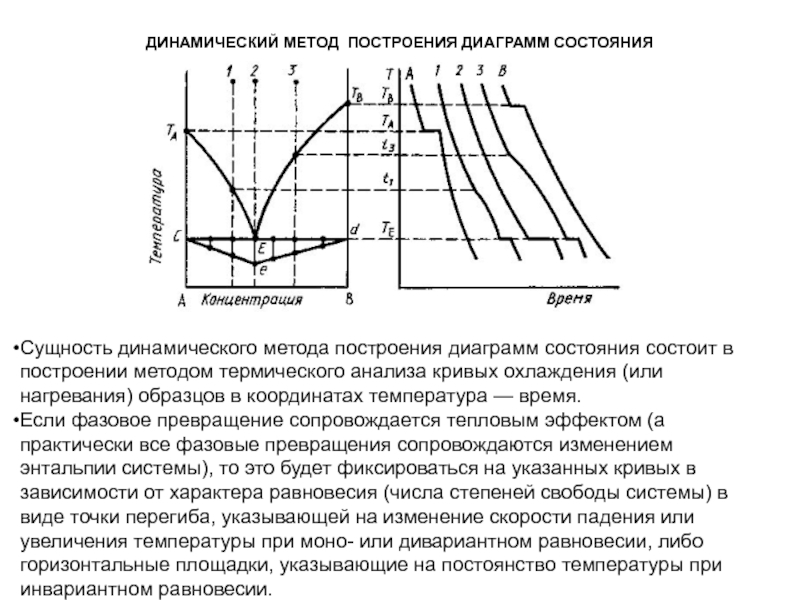
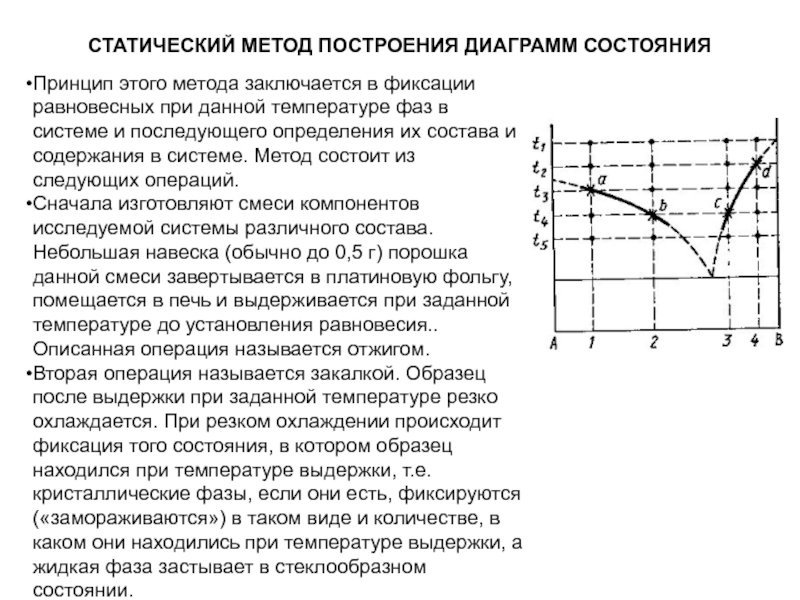
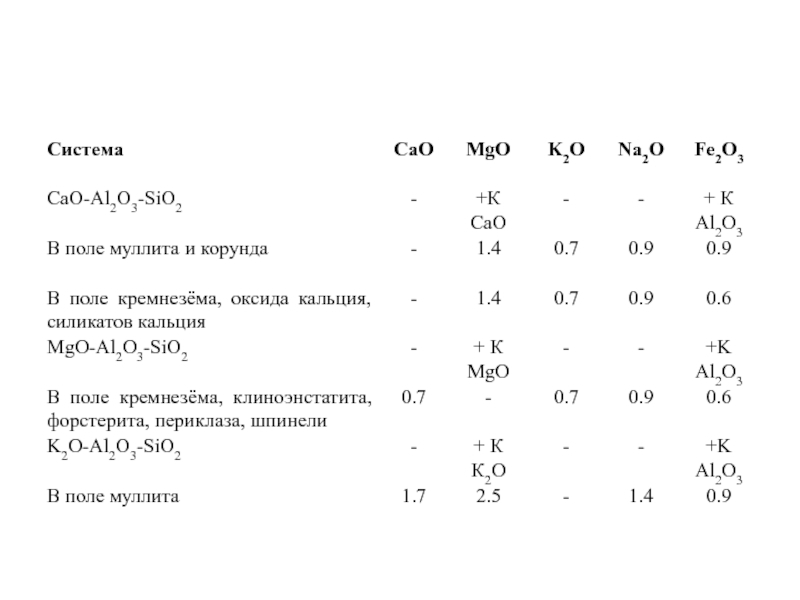
Слайд 1История учения о физико – химическом равновесии
Учение о фазовых
равновесиях – один из разделов классической термодинамики, в котором изучаются
условия равновесного сосуществования веществ в различных агрегатных состояниях, многообразные химические и физико – химические реакции, протекающие в многофазных системах при высоких температурах (плавление и кристаллизация, образование и разложение веществ и твёрдых растворов, полиморфные превращения и др.). Термодинамические данные о свойствах равновесных фаз могут быть представлены в виде математических уравнений, таблиц и диаграмм состояния.
Данные о термодинамических свойствах равновесных фаз представляют собой научный фундамент, основываясь на котором можно разрабатывать технологии, определять оптимальные параметры и направление течения процессов, определять состав и ожидаемые свойства продуктов в различных условиях эксплуатации.
Началом научного анализа в области химической термодинамики следует считать работы Рудольфа Юлиуса Клазиуса в 1857 - 1862 гг по формулированию второго закона термодинамики и работ по приложению термодинамики, в том числе к химическим процессам разложения и соединения.
Это новое направление не сразу было признано до 1873 гг, когда появились исследования Джозайя Уиллада Гиббса и его фундаментального труда "О равновесии гетерогенных систем".
Главный принцип, положенный Гиббсом в основу теории равновесия – после того, как энтропия системы достигнет максимума, система будет находиться в состоянии равновесия.
Рудольф Юлиус Клазиус
Джозайя Уиллад Гиббс

Слайд 2ОСНОВНЫЕ ПОНЯТИЯ УЧЕНИЯ О ФАЗОВЫХ РАВНОВЕСИЯХ
1.1. СИСТЕМА. ПАРАМЕТРЫ СИСТЕМЫ
Система
– часть вещества, выбранная и отделённая, физически или виртуально (математически),
таким образом, что в ней можно установить (наблюдать) изменения и конечные состояния при различных внешних условиях.
Изолированными являются системы, совершенно не взаимодействующие с окружающей средой, т.е. не обменивающиеся с ней ни веществом, ни энергией и, следовательно, имеющие постоянный объем.
К закрытым относятся системы, не обменивающиеся с окружающей средой веществом, но взаимодействующие с ней путем передачи энергии (в виде теплоты или работы).
Открытые системы — это системы, обменивающиеся с окружающей средой веществом (они могут, естественно, обмениваться и энергией).
Значения этих свойств, характеризующих состояние системы, называются ее параметрами состояния (термодинамическими параметрами).
В качестве параметров системы в общем случае могут выступать любые свойства системы — температура, давление, концентрация, удельный или молярный объем, в некоторых случаях — электрический потенциал, магнитное толе, поверхностное натяжение и пр.
К экстенсивным параметрам и определяемым ими свойствам (например, объем, масса, внутренняя энергия, энергия Гиббса) относятся параметры, значения которых пропорциональны массе системы и аддитивны, т.е. равны сумме значений таких же параметров отдельных частей системы.

Слайд 3Интенсивные параметры (например, температура, давление, концентрация, различные удельные и молярные
свойства) не зависят от массы системы, а определяются только ее
состоянием и характеризуют собой специфические свойства системы в данном состоянии. Величины интенсивных параметров не являются аддитивными.
Выбор тех или иных параметров зависит от конкретных условий. Чаще всего в качестве независимых выбирают такие параметры, которые поддаются непосредственному измерению — температуру, давление или упругость пара, концентрацию, молярный или удельный объем
Исключительно важную роль в учении о фазовых равновесиях и геометрической интерпретации фазовых равновесий имеет одна из характеристических функций состояния — G, называемая изобарно-изотермическим потенциалом или энергией Гиббса (характеристическими называются функции состояния, с помощью которых или их производных по соответствующим данной функции параметрам могут быть выражены в явном виде все термодинамические свойства системы). Энергия Гиббса для закрытых систем является функцией независимых параметров — температуры Т и давления р и определяется выражением
G = Н - TS = U - TS + pV,
где H — энтальпия; U —внутренняя энергия; S — энтропия.
Полный дифференциал энергии Гиббса по независимым переменным Т и р равен:
dG = — SdT + Vdp.

Слайд 4ФАЗА
Фазой называется часть или совокупность гомогенных частей системы, отделенных от
других частей системы поверхностью раздела и характеризующихся в отсутствие внешнего
поля сил одинаковыми во всех своих точках составом и свойствами.
Фаза – совокупность гомогенных частей системы, одинаковых по свойствам и физическому строению.
Следует отметить следующие особенности фазы как части гетерогенной термодинамической системы.
1. Фаза в термодинамическом смысле этого слова представляет собой часть системы, находящейся в равновесии, и, следовательно, сама должна находиться в равновесном состоянии. Поэтому применение термина "фаза" к веществу, находящемуся в метастабильном состоянии, является неправильным.
2. Каждая фаза обладает определенными индивидуальными свойствами и, следовательно, между фазами должна существовать межфазная граница — поверхность раздела, переход через которую от одной фазы к другой сопровождается резким скачкообразным изменением свойств. Каждую отдельную фазу условно можно рассматривать как самостоятельную систему, по отношению к которой все остальные фазы играют роль внешней среды.
3. Понятие фазы применимо только к макроскопическим объектам, для которых свойства вещества в его объеме являются определяющим по сравнению с поверхностными свойствами. Если часть системы находится в настолько высокой степени дисперсности, что поверхностными свойствами нельзя пренебречь, то классическое понятие фазы становится к такой части системы неприменимым

Слайд 5НЕЗАВИСИМЫЕ КОМПОНЕНТЫ
Простые или сложные вещества, наименьшее число которых необходимо
и достаточно для образования всех возможных фаз данной системы, находящейся
в равновесии, называются независимыми компонентами системы.
Число компонентов – наименьшее число веществ, достаточных для образования любой фазы равновесной системы.
Независимые компоненты представляют собой такие соединения данной системы, которые не превращаются друг в друга и общее содержание (концентрация) их в системе при данных параметрах не зависит от концентрации других составных частей системы. Концентрации могут изменяться только за счет введения этих соединений в систему или удаления из нее.
В общем случае число независимых компонентов К системы определяется по формуле
К = К0 - n,
где Kо — общее число соединений, существующих в системе; п — число независимых уравнений, с помощью которых можно связать концентрации веществ, составляющих фазы системы.
Характерной особенностью независимых компонентов является то, что количество каждого из них не зависит от количества остальных компонентов.
В зависимости от числа независимых компонентов системы делятся на одно-, двух-, трех-, четырехкомпонентные и т.д.

Слайд 6В чисто физических системах, т.е. в системах, в которых не
происходит никаких обусловленных химическими реакциями превращений одних составных частей системы
в другие, все соединения, образующие систему, являются независимыми компонентами, поскольку их концентрации не зависят друг от друга и могут изменяться независимо.
Следовательно, в таких системах п = 0 и К= К0, т.е. число независимых компонентов равно общему числу индивидуальных химических соединений, существующих в системе.
В химических системах, т.е. в системах, в которых между составными частями протекают обратимые химические реакции, концентрации лишь части соединений, входящих в систему, могут изменяться независимо. В этом случае концентрации участвующих в реакциях соединений количественно связаны друг с другом термодинамическими уравнениями химического равновесия, число которых равно числу независимо протекающих обратимых реакций.
Поэтому в химических системах число независимых компонентов будет меньше общего числа соединений, существующих в системе, и будет равняться разности между общим числом соединений и числом независимо протекающих реакций.

Слайд 7Рассмотрим систему, состоящую из четырех индивидуальных химических соединений:
MgO, SiO2,
MgO-SiO2 и 2MgO-SiO2.
В этой системе возможны две независимые химические
реакции:
MgO + SiО2 ↔MgO-SiО2
2MgO + SiО2↔2MgO-SiО2
Таким образом, для данной системы К0 = 4, п=2 и число независимых компонентов К=4—2 = 2, т.е. система двухкомпонентная.
В рассматриваемой системе возможна еще одна реакция:
MgO-SiО2 + MgО ↔ 2MgO-SiО2
Однако она будет зависимой, так как концентрация MgO*SiO2 определяется первой реакцией.
В качестве компонентов в этой системе будут выступать оксиды MgO и SiО2, общее содержание которых в закрытой системе не зависит от содержания других составных частей системы.
Слайд 8ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
Равновесным называется такое состояние системы, которое характеризуется при
постоянных внешних условиях неизменностью во времени термодинамических параметров и отсутствием
в системе потоков вещества и теплоты.
Для устойчивого (стабильного) равновесия всякое бесконечно малое воздействие на систему вызывает только бесконечно малое изменение ее состояния, но не может вызвать конечного изменения состояния. Общее условие устойчивого равновесного состояния системы при постоянных температуре, давлении и составе заключается в том, что система в этом состоянии обладает минимальной (по сравнению с другими возможными состояниями) энергией Гиббса G. Следовательно, при всех процессах, не нарушающих постоянства температуры, давления и состава системы, величина G остается постоянной или возрастает. Таким образом, для равновесных систем dG = 0 и d2G>0.
Устойчивое равновесие означает равновесие термическое, механическое и химическое. При термическом и механическом равновесиях соответственно температуры и давления во всех точках системы одинаковы. При химическом равновесии отсутствует движущая сила для переноса вещества внутри фаз и от одной фазы системы к другим фазам.

Слайд 9
Термодинамическое равновесие следует рассматривать как равновесие динамическое, т.е. такое состояние
системы, которое при неизменных параметрах сохраняется вследствие протекания в системе
обратимых фазовых и (или) химических превращений, идущих с одинаковой скоростью в двух противоположных направлениях.
Изменение параметров равновесной системы может вызывать протекание в системе различных фазовых и (или) химических процессов. Эти процессы следует рассматривать как непрерывную последовательность отдельных равновесных состояний, при которых система переходит из одного равновесного состояния в другое, наступающее после каждого малого изменения каждого из параметров.
В реальных, особенно силикатных, системах часто приходится встречаться с так называемым метастабильным равновесием. Это такое равновесие, при котором некоторые бесконечно малые воздействия не вызывают, а другие могут вызывать конечные изменения состояния системы, в результате которых система переходит в стабильное устойчивое состояние.
Термодинамическими параметрами называются величины, характеризующие состояние системы или термодинамического процесса

Слайд 10СТЕПЕНИ СВОБОДЫ
Термодинамическими степенями свободы f называются независимые параметры системы
находящейся в равновесии, изменение которых в определенных пределах не вызывает
нарушения фазового равновесия, т.е. не приводит к изменению природы и числа существующих фаз.
Степени свободы — это такие независимые переменные параметры, которые в известных пределах можно произвольно менять, не вызывая исчезновения одних и образование других фаз в системе.
Числом степеней свободы называется наименьшее число независимых параметров, характеризующих состояние системы.
Число степеней свободы равновесной системы характеризует ее вариантность – число степеней свободы, которые могут изменяться в определенных пределах, без изменения количества фаз - в зависимости от которой система может находиться в инвариантном (f =0), моновариантном (f =1), дивариантном (f =2) и т.д. состояниях.
В инвариантном состоянии система не имеет степеней свободы, все ее параметры (например, температура, давление, концентрация) фиксированы и ни один из них не может изменяться без нарушения равновесия, т.е. без исчезновения старых и появления новых фаз.
Моновариантное состояния системы означает, что в некоторых пределах можно произвольно изменять один параметр (все другие параметры в соответствии с этим будут принимать строго определенные значения) без изменения числа и природы фаз, при дивариантном состоянии системы можно изменять два параметра и т.д.

Слайд 11ХИМИЧЕСКИЙ ПОТЕНЦИАЛ
Молярный химический потенциал µi формально представляет собой частную производную
какой-либо характеристической функции (U, H, F, G) по количеству вещества
(молей) ni одного из компонентов i в данной фазе при постоянных соответствующих внешних параметрах состояния и количестве вещества (молей) остальных компонентов.
Наибольшее распространение получило выражение химического потенциала через энергию Гиббса G:
где индексы означают, что производная берется при постоянных температуре, давлении и количеству вещества (молей) всех других компонентов в данной фазе, кроме i-го компонента.
Молярный химический потенциал, являясь парциальной молярной энергией Гиббса, характеризует состояние какого-либо компонента i в фазе данного состава и зависит как от концентрации данного компонента, так и от вида и концентрации всех других компонентов данной фазы. По физическому смыслу µi выражает отнесенное к 1 моль компонента приращение энергии Гиббса данной фазы, находящейся при постоянных температуре и давлении, при введении дополнительного количества i-го компонента к такому большому ее количеству, что состав этой фазы не изменяется. Для фазы, состоящей только из одного компонента i, химический потенциал последнего в этой фазе равен его молярной энергии Гиббса
(µi = G/ni).

Слайд 12
Химический потенциал является интенсивной величиной и представляет собой движущую силу.
Он определяет количественное распределение (концентрации) компонентов по всем фазам равновесной
системы и характеризует способность компонента к выходу из данной фазы путем растворения, кристаллизации, химического взаимодействия и т.д. Причем переход компонента самопроизвольно может происходить только из той фазы, где его химический потенциал больше, в фазу, где он меньше.
Как известно, при постоянных температуре и давлении самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (dG<0), а поскольку (dG)r,p = ∑ µi/dni, критерием возможности таких процессов является неравенство
∑ µi/dni < 0.
Когда химический потенциал компонентов системы, во всех фазах окажется одинаковым, система приходит в состояние равновесия, условием которого является равенство
∑ µi/dni = 0,
т.е. алгебраическая сумма произведений химического потенциала компонентов на изменение количества вещества (молей) их в фазах системы равна нулю. Отсюда следует, что в системе, находящейся в равновесии, химический потенциал каждого данного компонента должен быть одинаковым во всех ее фазах.

Слайд 13ПРАВИЛО ФАЗ ГИББСА
Основным законом учения о фазовых равновесиях в
гетерогенных системах является правило фаз Гиббса (1876 г), определяющее условия
равновесия в таких системах.
Это правило устанавливает соотношение между числом степеней свободы, числом независимых компонентов и числом фаз для систем, находящихся в термодинамическом равновесии.
f – число степеней свободы системы
K – число независимых компонентов системы
m – число внешних параметров для системы
ρ – число фаз в системе
Уравнение f = К + т – ρ является общим математическим выражением правила фаз:
число степеней свободы равновесной системы равно числу независимых компонентов плюс число внешних параметров, влияющих на состояние системы, минус число фаз в системе.
Слайд 14Более конкретный вид уравнения правила фаз зависит от числа m,
т.е. числа внешних переменных параметров, определяющих состояние системы. Если в
качестве таких параметров выступают температура и давление, то т=2 и уравнение правила фаз принимает вид
f = К + 2 - ρ.
Очень часто для конденсированных систем давление может приниматься постоянным и не влияющим на состояние системы. При этом в качестве внешнего параметра будет выступать только температура и число т уменьшится на единицу, т. е. уравнение правила фаз приобретает вид
f = К + 1 – ρ
Правило фаз характеризует системы, находящиеся в термодинамическом равновесии
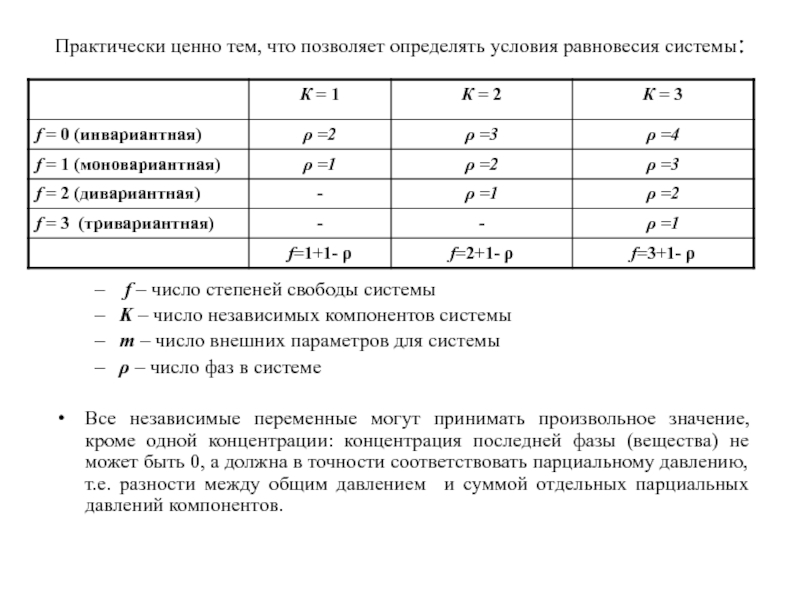
Слайд 15Практически ценно тем, что позволяет определять условия равновесия системы:
f
– число степеней свободы системы
K – число независимых компонентов системы
m
– число внешних параметров для системы
ρ – число фаз в системе
Все независимые переменные могут принимать произвольное значение, кроме одной концентрации: концентрация последней фазы (вещества) не может быть 0, а должна в точности соответствовать парциальному давлению, т.е. разности между общим давлением и суммой отдельных парциальных давлений компонентов.
Слайд 16Вывод правила фаз Гиббса
Во всех фазах равновесной гетерогенной системы t
и Р одинаковы и химические потенциалы каждого из компонентов равны
(определение состояния равновесия).
Тогда составим уравнения, выражающие эти условия равновесия для случая, когда система состоит из фаз, в каждую из которых входят все компоненты без исключения.
нижние индексы – компоненты (К), верхние – фазы (ρ)
Равенство (1) – тождества, т.к. давление и температура являются независимыми переменными. Равенство (2) – не тождество, т.к. потенциал одного и того же компонента в различных фазах описывается различными функциями концентрации, температуры и давления.
Слайд 17На основании этих равенств можно составить независимые уравнения.
Химический потенциал является
функцией не только t и Р, но и концентрации всех
веществ, образующих данную фазу. тогда вид этого уравнения в общем случае неизвестен, но учитывая разнообразие свойств реальных веществ можно утверждать, что при переходе от одной фазы к другой вид функции, выражающей зависимость потенциала от температуры, давления и состава изменяется и каждое из равенств μ1I = μ1II , μ1II = μ1III и т.д. является независимым уравнением.
Подставим число уравнение, составленных на основании рядов равенств (2) и число независимых переменных, охватываемых этими уравнениями. Каждая строка системы равенств (2) позволяет составить (ρ -1) независимое уравнение. Число строк равно К (числу компонентов системы), следовательно общее число уравнений
К*(ρ -1).
Независимые переменные в данной системе уравнений – температура, давление и концентрации компонентов.
Слайд 18Т.к. в каждой фазе К компонентов, но задавшись произвольными значениями
t и Р мы не можем произвольно выбирать концентрации всех
без исключения компонентов – концентрация одного из них должна принимать строго определённое значение (например при произвольных температуре и давлении концентрация газа в данной фазе м.б. произвольными коме одной концентрации последнего газа, которая должна в точности соответствовать парциальному давлению – разности между общим давлением в системе и суммой отдельных парциальных давлений всех остальных газов.
Т.о. число независимых компонентов в каждой
фазе = К-1, а общее число независимых концентраций
ρ *(К-1), но т.к. независимыми переменными являются, как правило давление и температура – Р и Т , общее число независимых переменных, полученных из правила фаз для конденсированных систем, ρ (К-1) +2.
Слайд 19Если число независимых переменных = числу уравнений, их связывающих, т.е.
К(ρ -1) = ρ (К-1)+2 ,
то каждая независимая переменная
принимает некоторое, строго определенное значение и вся система может существовать при этом единственно возможным сочетании Т, Р и концентрации.
Если же число уравнений меньше числа независимых переменных, то разность обозначаемая
F = ρ * (K-1) + 2 – K * (ρ -1) = K + 2 – ρ
представляет собой число переменных, которыми можно предавать произвольные значения при имеющемся числе уравнений, а следовательно и при имеющемся числе фаз (т.к. число уравнений определяется числом фаз).
F + ρ = K + 2
Если условия существования системы кроме температуры определяется ещё каким – либо переменным параметром, например электрическим потенциалом, то
F + ρ = K + 3
Если система конденсирована, т.е. Р – пренебрежимо мало, то
F + ρ = K +1
или
F = K + 1 - ρ
Слайд 20Закон Рауля – Вант-Гоффа
Температура застывания /плавления смеси веществ всегда ниже
температуры застывания / плавления индивидуальных веществ – это явление называют
депрессией.
Описывается депрессия законом Рауля - Вант-Гоффа, согласно которому
При концентрации Х2 растворённого вещества на 100 г растворителя
Этот закон действителен при небольших концентрациях растворённого вещества и при отсутствии в системе твёрдых растворов.
Слайд 21ОБЩИЕ СВЕДЕНИЯ О ДИАГРАММАХ СОСТОЯНИЯ ГЕТЕРОГЕННЫХ СИСТЕМ
При исследовании равновесных
систем конечной целью физико-химического анализа является установление зависимости между параметрами
системы, характеризующими ее состояние, и, в частности, определение составов равновесных фаз при тех или иных параметрах состояния. Данная зависимость наряду с аналитической формой описания в виде уравнений состояния может быть выражена графически в виде соответствующих термодинамических диаграмм. Такое графическое описание состояний равновесных систем отличается прежде всего компактностью и большой наглядностью, что и обусловливает широкое использование подобных диаграмм на практике.
Графическое толкование гетерогенных процессов и равновесий основано на строгих закономерностях изменения характеристик термодинамических функций в зависимости от параметров состояния и установления на этой основе графических соотношений между ними. Диаграммой фазового равновесия или диаграммой состояния называется графическое изображение соотношений между параметрами состояния.
Слайд 22Для многокомпонентных равновесных систем особое значение имеют диаграммы состав —
свойства, строящиеся в координатах концентрация компонентов — температура фазовых превращений.
Для однокомпонентных систем вместо параметра концентрация, который для таких систем теряет смысл, обычно используют давление (упругость пара) или свободную энергию.
Особенность диаграмм состояния заключается в том, что любая точка на диаграмме имеет строгий физико-химический смысл, так как характеризует определенное состояние вещества и численные значения параметров этого состояния.
Другими словами, каждое состояние системы изображается на диаграммах некоторой точкой, которая называется фигуративной точкой.
Слайд 24Диаграмма состояния позволяет установить:
- температуру начала и завершения процессов плавления
и кристаллизации при любом соотношении компонентов смеси;
- количество и состав
фаз в системе при любой температуре;
- количественное соотношение фаз при любой температуре и составе смеси;
- изменения в количестве и составе фаз, происходящие в смеси при повышении / понижении температуры;
- достигнуто ли состояние равновесия системы (по числу компонентов и фаз), а если не достигнуто – то определить степень и причины отклонения от равновесного состояния.
Диаграммы состояния описывают только системы, находящиеся в термодинамическом равновесии.
Большинство силикатных систем обладает особенностями, влияющими как на методику построения диаграмм состояния, так и на их оценку с точки зрения практического использования.
Слайд 25Однокомпонентные системы
Элементы строения однокомпонентных диаграмм
f + ρ =K +
2. при К = 1,
условия равновесного состояния в
системе
характер равновесия число фаз
Дивариантное 1
Моновариантное 2
Нонвариантное 3
Равновесие будет дивариантным тогда, когда имеется одна фаза: твердая, жидкая или газообразная (пар). При наличии нескольких твердых модификаций вещества, каждая модификация образует отдельную фазу.
При моновариантном равновесии имеет место сосуществование двух фаз: твердая — пар, жидкость — пар, твердая — жидкость, твердая — твердая.
В случае нонвариантного равновесия возможны следующие комбинации фаз: твердая — жидкость — пар, твердая — твердая — пар.
Больше трех фаз в однокомпонентной системе не могут находиться в равновесии друг с другом.
Однокомпонентные диаграммы строятся в координатах температура – давление (упругость пара над кристаллической или жидкой фазой)
Слайд 26Элементы строения однокомпонентных диаграмм
Линии упругости пара (KM, MM′, MN, NN′,
NL), которые разделяют диаграмму на области стабильного существования отдельных фаз.
Каждой фазе соответствует определенный графический образ – участок плоскости – поле стабильного существования. В пределах каждого поля система дивариантна, т.е. в пределах данного поля двум параметрам системы (P и T) можно придавать произвольные значения без нарушения равновесия (не изменяя число и природу фаз ρ = 1, f = 2).
Поля фаз отделены друг от друга пограничными линиями – это линии моновариантных равновесий. Равновесию двух фаз на пограничных кривых соответствуют вполне определенные значения P и T, т.е. без нарушения равновесия произвольно изменять можно только один параметр системы (например, P или T), при этом второй (зависимый) параметр системы будет принимать строго определенное значение (ρ = 2, f = 1).
Слайд 27Поля трех фаз сходятся в одной точке (M и N),
в которой сходятся и три линии моновариантных равновесий, разграничивающих попарно
эти три поля. Точка инвариантного равновесия трех сосуществующих фаз называется тройной точкой. Тройная точка вместе со сходящимися в ней линиями и полями образует фигуру, называемую трёхлучевой звездой, для которой она является вершиной.
Фазовые переходы в однокомпонентной системе зависят не только от температуры, но и от давления, поэтому линии MM' NN' имеют наклон к оси температур. Если угол наклона тупой (1), то высокотемпературная форма имеет объём меньший, чем низкотемпературная, если угол наклона – острый (2) – то наоборот.
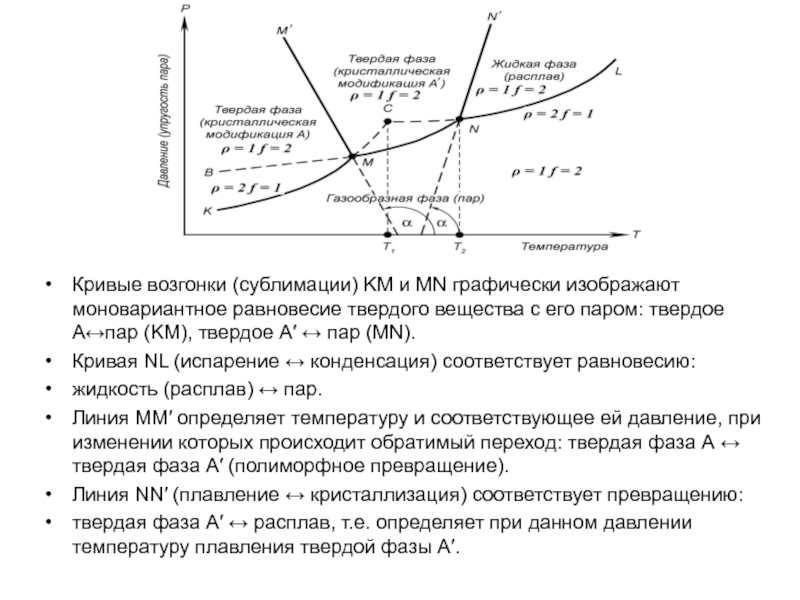
Слайд 28Кривые возгонки (сублимации) KM и MN графически изображают моновариантное равновесие
твердого вещества с его паром: твердое А↔пар (KM), твердое А
↔ пар (MN).
Кривая NL (испарение ↔ конденсация) соответствует равновесию:
жидкость (расплав) ↔ пар.
Линия MM′ определяет температуру и соответствующее ей давление, при изменении которых происходит обратимый переход: твердая фаза А ↔ твердая фаза А′ (полиморфное превращение).
Линия NN′ (плавление ↔ кристаллизация) соответствует превращению:
твердая фаза А′ ↔ расплав, т.е. определяет при данном давлении температуру плавления твердой фазы А′.
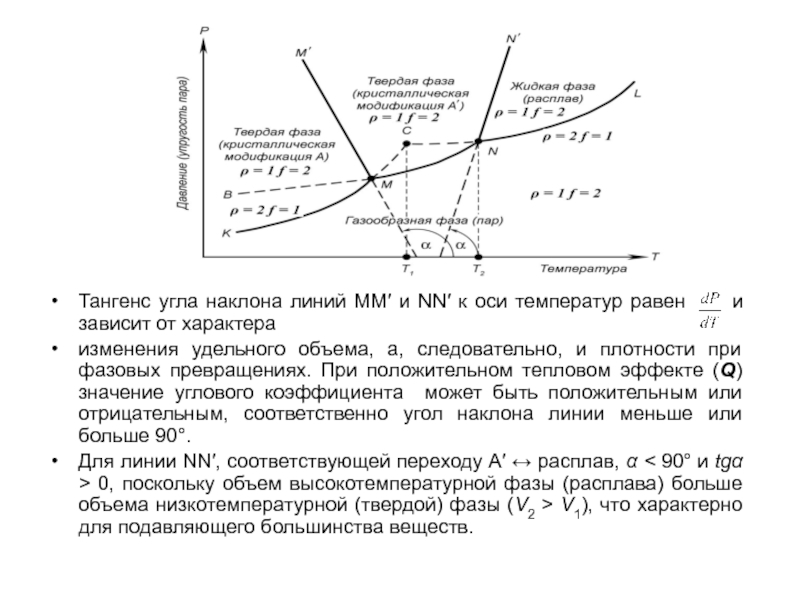
Слайд 29Тангенс угла наклона линий MM′ и NN′ к оси температур
равен и зависит от характера
изменения удельного объема,
а, следовательно, и плотности при фазовых превращениях. При положительном тепловом эффекте (Q) значение углового коэффициента может быть положительным или отрицательным, соответственно угол наклона линии меньше или больше 90.
Для линии NN′, соответствующей переходу А′ расплав, < 90 и tg > 0, поскольку объем высокотемпературной фазы (расплава) больше объема низкотемпературной (твердой) фазы (V2 > V1), что характерно для подавляющего большинства веществ.
Слайд 30Точка плавления при повышении давления повышается. Но поскольку, в случае
равновесия твердая фаза расплав, ΔV очень мало, влияние давления
на точку плавления невелико и линия плавления на диаграмме близка к вертикальной прямой.
Для линии MM′, соответствующей переходу твердое А твердое А′ угловой коэффициент отрицательный (tg1<90°) и угол 1>90, т.е., это может быть только в том случае, если удельный объем высокотемпературной фазы меньше, чем низкотемпературной (V2 < V1), а плотность соответственно, выше. При этом с повышением давления температура фазового перехода понижается, т.е. повышение давления ускоряет фазовый переход. Такая ситуация, однако, бывает редко.
Гораздо чаще высокотемпературная фаза имеет больший удельный объем и меньшую плотность, чем низкотемпературная и с повышением давления температура фазового перехода возрастает: при плавлении NN' V2 > V1, 2 < 90°, tg2 > 0. В случае равновесия ТВ – Ж ΔV очень мало и, чтобы добиться заметного изменения температуры плавления, нужно приложить высокие давления.
Слайд 31Ко всем моновариантным равновесиям применимо уравнение Клаузиуса‑Клайперона
где Q – скрытая теплота
перехода одной фазы в другую, находящуюся с ней в равновесии;
T
– абсолютная температура, при которой находятся эти фазы;
P – давление;
V1 – V2 = ΔV – изменение удельного объема при переходе от одной фазы к другой (от менее богатой энергией к более богатой).
Слайд 32полиморфизм
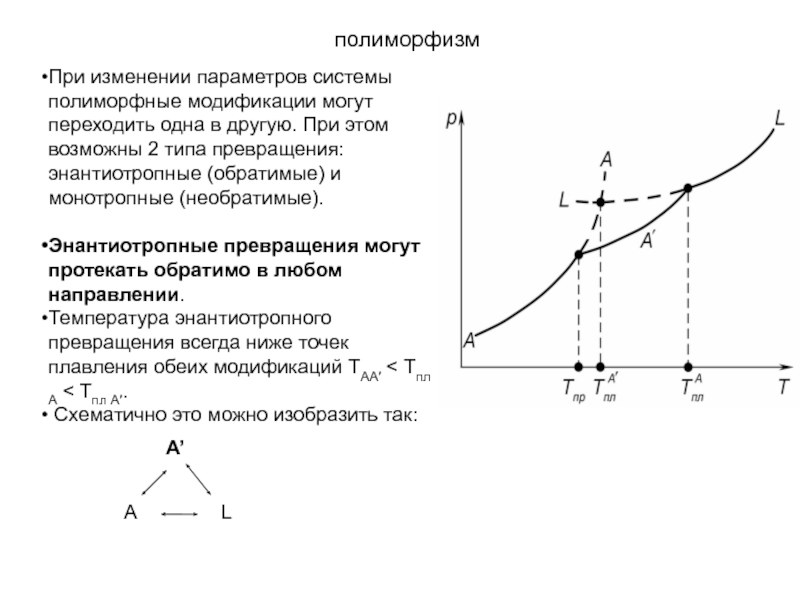
При изменении параметров системы полиморфные модификации могут переходить одна в
другую. При этом возможны 2 типа превращения: энантиотропные (обратимые) и
монотропные (необратимые).
Энантиотропные превращения могут протекать обратимо в любом направлении.
Температура энантиотропного превращения всегда ниже точек плавления обеих модификаций TAA′ < Tпл А < Tпл А′.
Схематично это можно изобразить так:
Слайд 33При монотропном превращении переход одной модификации в другую необратим
Это
имеет место, в случае если температура перехода одной модификации в
другую лежит выше точек плавления каждой из них, а одна из модификаций при данных условиях является метастабильной TAA′ < TА′ < TА.
Высокотемпературная модификация имеет более высокую температуру плавления.
Схематически это можно изобразить так:
Слайд 34Последовательность фазовых превращений регулируется правилом ступеней Оствальда:
образование вещества существующего
в нескольких модификациях протекает ступенчато таким образам, что сначала стремится
образоваться неустойчивая модификация, которая затем превращается в более устойчивую.
Слайд 35Система кремнезема
Система SiO2 является однокомпонентной со сложным полиморфизмом. Оксид кремния
может существовать в газообразном состоянии в виде SiO:
SiO2 + Si
2SiO (1250 – 1300 0C вакуум)
SiO2 + C SiO + CO (> 1000 0C)
SiO2 + H2 SiO + H2O (> 1000 0C)
Твёрдый SiO оседает и постепенно "сгорает" на воздухе с образованием SiO2.
Полиморфные превращения кремнезема в зависимости от температуры, давления и состава минерализатора
На рис. показана схема превращения одних кристаллических модификаций SiO2 в другие при атмосферном давлении, длительном нагревании и при применении в качестве минерализатора ускорителя превращений модификаций кремнезема – вольфрамо-кислого натрия Na2WO4·2H2O.
На диаграмме Феннера на оси ординат в произвольном масштабе отложено гипотетическое давление паров модификаций над их твердым состоянием, а по оси абсцисс – температура. Из химической термодинамики известно, что чем выше парциальное давление фазы, тем менее устойчиво вещество. Таким образом, диаграмма Феннера дает сравнительное представление об устойчивости модификаций в определенных температурных интервалах.

Слайд 36Все превращения форм кремнезема разделяют на две группы.
Как видно
из диаграммы, SiO2 образует три главные модификации:
кварц, тридимит и
кристобалит
(первая группа) – каждая из которых в свою очередь имеет несколько разновидностей модификаций второго порядка:
- и -кварц, -, - и -тридимит, - и -кристобалит.
а б
Диаграмма SiO2 по Феннеру (а) и по Прянишникову (б) в координатах:
гипотетическая упругость пара – температура.
Слайд 37Структура силикатов
а
б в
Соединение тетраэдров в кристаллических модификациях
Кремнекислородный тетраэдр
Соединение тетраэдров в аморфной модификации
(стекле)
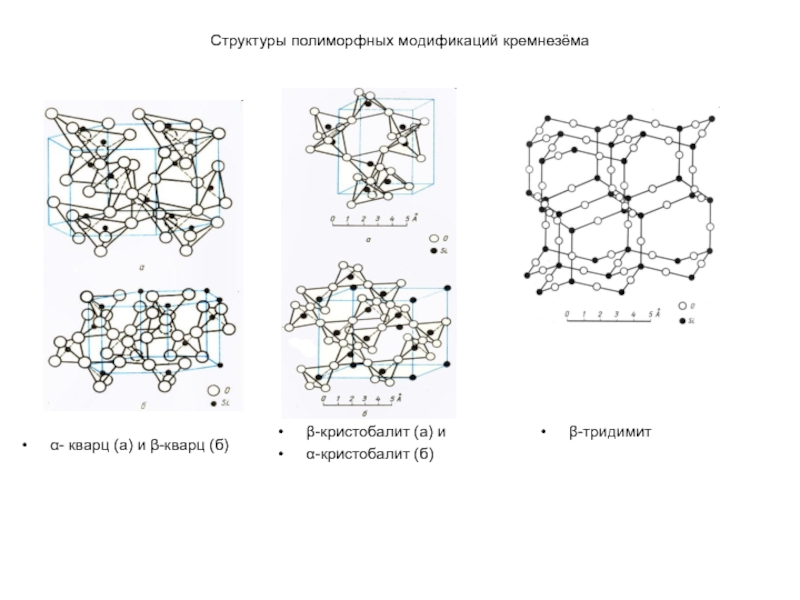
Слайд 38Структуры полиморфных модификаций кремнезёма
α- кварц (а) и β-кварц (б)
β-кристобалит (а)
и
α-кристобалит (б)
β-тридимит
Слайд 39Типы симметрий и параметры ячеек модификаций кремнезёма
Элементарные ячейки типов симметрии
а
- кубической;
б - гексагональной;
в - тригональной;
г -
тетрагональной;
д - ромбической;
е - моноклинной;
ж - триклинной
Слайд 40Фазовые превращения в системе кремнезёма
Превращение в вертикальных рядах относится к
полиморфным соединениям со смещением во вторичной координационной сфере, и оно
происходит очень быстро вследствие незначительности структурных изменений при этих переходах.
Наоборот горизонтальные превращения между главными модификациями, т.е. ‑кварц -тридимит -кристобалит, относятся к реконструктивным превращениям в первой координационной сфере и протекают при изменении температуры очень медленно, так как это связано со значительной перестройкой структуры.
Последовательность фазовых превращений в системе SiO2 по Феннеру в отсутствии минерализатора будет иной (по Прянишникову).
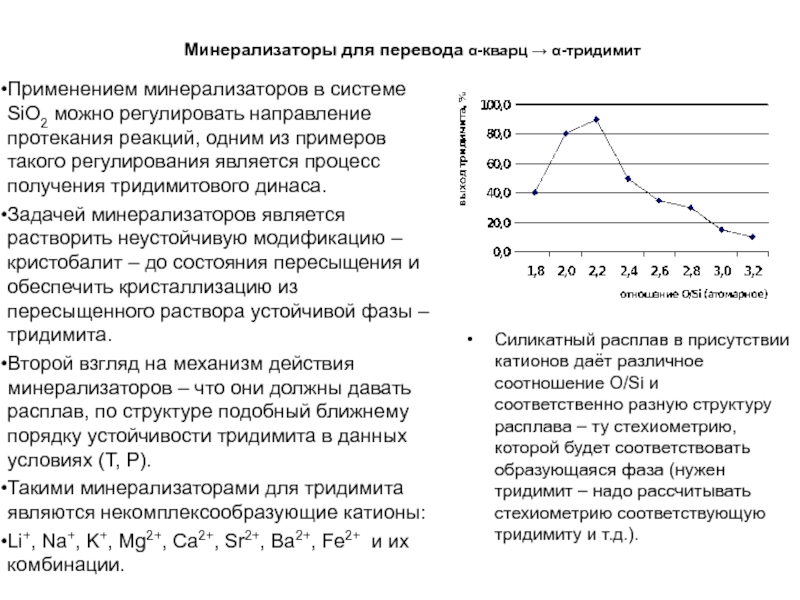
Слайд 41Минерализаторы для перевода -кварц -тридимит
Применением минерализаторов в системе SiO2
можно регулировать направление протекания реакций, одним из примеров такого регулирования
является процесс получения тридимитового динаса.
Задачей минерализаторов является растворить неустойчивую модификацию – кристобалит – до состояния пересыщения и обеспечить кристаллизацию из пересыщенного раствора устойчивой фазы – тридимита.
Второй взгляд на механизм действия минерализаторов – что они должны давать расплав, по структуре подобный ближнему порядку устойчивости тридимита в данных условиях (Т, Р).
Такими минерализаторами для тридимита являются некомплексообразующие катионы:
Li+, Na+, K+, Mg2+, Ca2+, Sr2+, Ba2+, Fe2+ и их комбинации.
Силикатный расплав в присутствии катионов даёт различное соотношение O/Si и соответственно разную структуру расплава – ту стехиометрию, которой будет соответствовать образующаяся фаза (нужен тридимит – надо рассчитывать стехиометрию соответствующую тридимиту и т.д.).
Слайд 42Превращение кварца при обжиге
С повышением температуры плотность модификаций SiO2 уменьшается
от 2,65 г/см3 у -кварца до 2,21 г/см3 у -кристобалита.
Изменение плотности происходит скачками в момент перехода, в связи с чем, иногда существенно изменяется объем при переходе из одной фазы в другую.
Величины объемных эффектов превращений
Слайд 43ДВУХКОМПОНЕНТНЫЕ СИСТЕМЫ
ЭЛЕМЕНТЫ СТРОЕНИЯ ДИАГРАММ СОСТОЯНИЯ
ДВУХКОМПОНЕНТНЫХ СИСТЕМ
В однокомпонентных системах с
изменением термодинамических параметров происходят либо полиморфные превращения, либо фазовые переходы
одного вещества.
В 2х компонентных системах наряду с этими процессами могут происходить и многие другие, что обуславливает большое разнообразие двухкомпонентных систем.
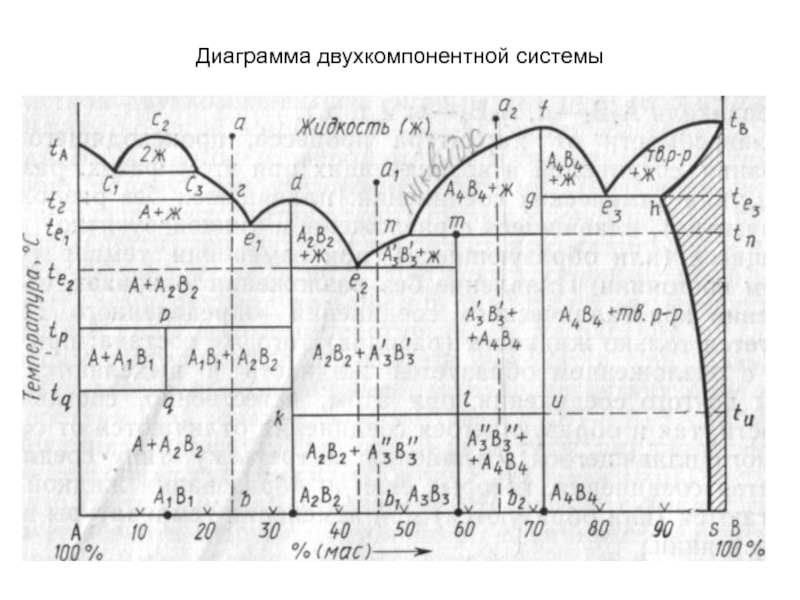
К основным элементам строения двухкомпонентных (бинарных) диаграмм состояния относятся: координатные оси, вертикали составов, изотермы, точки составов химических соединений, кривые ликвидуса и солидуса, точки эвтектики и перитектики, эвтектоидные точки, изотермы полиморфных превращений, бинодальные кривые.
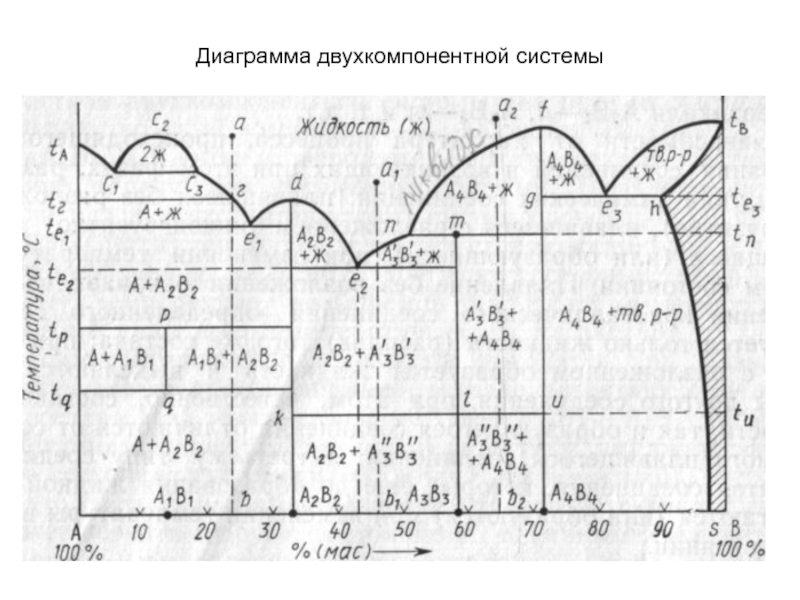
Слайд 44Диаграмма двухкомпонентной системы
Слайд 45
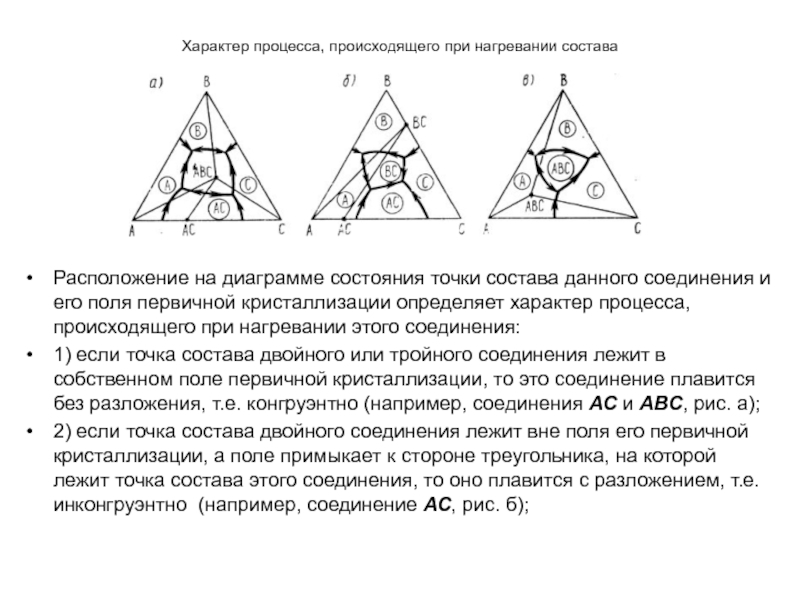
В зависимости от характера процесса, происходящего при нагревании соединений и
возникающих при этом фазах, различают три типа химических соединений:
1)
плавящиеся без разложения (конгруэнтно) А2В2, А4В4, - т.е. при плавлении кристаллического соединения определенного состава образуется только жидкость (расплав) того же состава
2) плавящиеся с разложением (инконгруэнтно), А3В3 – т.е. при плавлении образуется жидкость и выделяется кристаллы другого соединения, при этом, естественно, составы как жидкости, так и образующегося соединения отличаются от состава исходного плавящегося соединения
3) разлагающиеся (или образующиеся) при изменении температуры в твердом состоянии, А1В1 - соединения, которые еще до образования жидкой фазы разлагаются (или образуются) при изменении температуры в твердом состоянии.
Слайд 46Кривые ликвидуса и солидуса
Важнейшим элементом строения двухкомпонентных диаграмм состояния являются
кривые ликвидуса - от лат. liquidus жидкий - (например, кривые
tAc1, с3е1, e1d, de2, e2n, nf, fe3, е3tв на рис.). Точки кривых ликвидуса показывают состав жидкой фазы (расплава), насыщенной при соответствующей температуре (температуре ликвидуса) по отношению к одной твердой кристаллической фазе, т.е. существующей с ней в равновесии (например, на кривой с3е1 в равновесии с жидкой фазой находятся кристаллы соединения А, на кривой fе3 — кристаллы соединения А4В4 и т.д.). Точки кривых ликвидуса показывают также температуру начала кристаллизации расплава при его охлаждении или температуру конца плавления твердого вещества при его нагревании.
Кривые солидуса - лат. solidus — плотный, твёрдый - точки которых показывают состав твердой фазы, в частности насыщенного твердого раствора (например, кривая htв на рис.), находящейся в равновесии с жидкой фазой (состав которой показывают точки кривой ликвидуса), а также температуру начала плавления твердой фазы при ее нагревании или конца кристаллизации при охлаждении расплава. Солидус может быть представлен также и ломаной линией (например, fge3, htB на рис.).

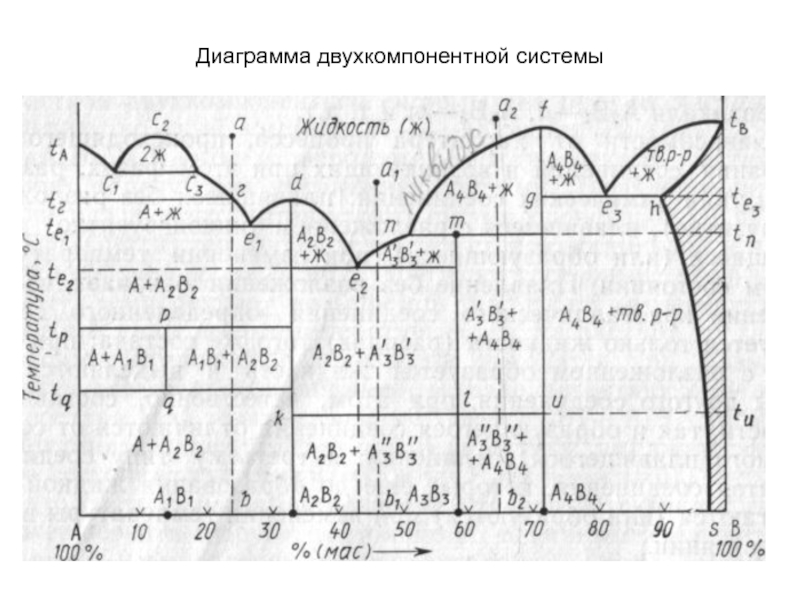
Слайд 47Диаграмма двухкомпонентной системы
Слайд 48Поскольку вдоль кривых ликвидуса и солидуса в равновесии находятся две
фазы — жидкая и одна твердая, по правилу фаз все
точки этих кривых (кроме тройных точек и точек, отвечающих составам индивидуальных химических соединений) выражают моновариантное состояние системы (f=K+ 1—Р=2+1—2 = 1).
Однофазная область жидкой фазы над кривыми ликвидуса является дивариантной.
Слайд 49Точки эвтектики и перитектики
Эвтектоидные точки. Ветви кривых ликвидуса пересекаются в
точках, называемых точками эвтектики (например, точки е1, е2, е3 и
т.д. на рис.), а составы, соответствующие этим точкам, называются эвтектическими.
Плавление или кристаллизация любого состава таких систем происходит (начинается и заканчивается) при одной и той же строго постоянной и наинизшей (по сравнению со всеми другими составами этой частной системы) температуре, называемой эвтектической температурой (например, температуры te1, te2 на рис.
В точках эвтектики в равновесии находятся три фазы: одна жидкая и две твердые (например, в точке эвтектики е2 — жидкая фаза состава этой точки и твердые фазы А2В2 и А3В3), поэтому в соответствии с правилом фаз точки эвтектики выражают инвариантное состояние системы
(f=K+1—Р = 2+1—3=0).
Слайд 50В точках эвтектики происходит только физический процесс кристаллизации (при охлаждении)
или плавления (при нагревании) и кристаллизация в этой точке всегда
заканчивается (т.е. жидкая фаза исчезает).
Точка перитектики является точкой химической реакции и в зависимости от исходного состава кристаллизация в этой точке перитектики может закончиться (жидкая фаза исчезнет) или продолжится дальше (исчезнет одна твердая фаза) до точки эвтектики.
Различие между точками эвтектики и перитектики заключается также в том, что первые всегда лежат ниже температур кристаллизации (или плавления) чистых компонентов, а вторые между указанными температурами
Слайд 51Служебные линии диаграмм
Изотермы полиморфных превращений. При наличии в двухкомпонентной системе
соединений, существующих в нескольких полиморфных модификациях (например, соединение А3В3 на
рис. существует в виде полиморфных форм А3'В3' и А3"В3"), на диаграмме состояния появляется изотерма (klи), разделяющая температурные области стабильного существования этих форм (выше температуры tu соединение А3В3 существует в виде А3'В3'-, а ниже - в виде А3"В3"-формы).
Бимодальные кривые. Если в двухкомпонентной системе имеет место явление ликвации (фазового разделения однородной жидкой фазы на две несмешивающиеся жидкости), то на кривой ликвидуса появляется характерная горбообразная кривая (например, с1с2с3 на рис.), называемая бинодальной кривой, ограничивающая область ликвации. Точки левой и правой ветвей этой кривой (c2с1 и с2сз) характеризуют составы двух жидких фаз, находящихся при данной температуре в равновесии. В области ликвации до начала кристаллизации расплава двухкомпонентная система моноварианта, а после начала кристаллизации — инвариантна.
В системах с образованием ограниченного твердого раствора бинодальными кривыми или линиями сольвуса называют также кривые (например, hs на рис.), характеризующие составы находящихся в равновесии твердых растворов ниже эвтектоидной температуры (te3).

Слайд 52Конноды. Коннодами на диаграммах состояния называются отрезки прямых, соединяющие своими
концами точки составов фаз, находящихся в равновесии при данной температуре.
На диаграммах двухкомпонентных систем коннодами являются отрезки прямых, параллельных оси концентраций, т.е. конноды совпадают с изотермами (например, коннода с1с3 лежащая своими концами на кривой ликвидуса, показывает, что при соответствующей температуре в равновесии находятся жидкие фазы, составы которых выражаются точками с1 и с3, коннода kl, лежащая своими концами на вертикалях состава соединений А2В2 и А3В3, показывает, что в равновесии находятся фазы, состав которых выражается точками k и l, а именно, соединения А2В2 и А3В3 и т. д
Слайд 53Диаграмма двухкомпонентной системы
Слайд 54ОСНОВНЫЕ ТИПЫ ДИАГРАММ СОСТОЯНИЯ ДВУХКОМПОНЕНТНЫХ СИСТЕМ И ПРАВИЛА РАБОТЫ С
НИМИ
Правило определения содержания компонентов в исходном составе и конечных фаз
кристаллизации
Для определения концентрации компонентов в жидкой фазе или их содержания в твердом веществе данного состава в двухкомпонентных диаграммах состояния необходимо из фигуративной точки, выражающей этот состав, опустить на ось концентраций вертикаль состава и отсчитать по этой оси содержание компонентов.
Диаграмма состояния дает возможность даже без построения пути кристаллизации сразу же определить конечные для данного состава фазы кристаллизации (под конечными фазами кристаллизации понимаются условно твердые кристаллические фазы, образующиеся не только после окончания кристаллизации расплава, но и после дальнейшего охлаждения твердой системы до минимальной температуры, обозначенной на диаграмме). Для определения конечных фаз кристаллизации необходимо из точки состава исходного расплава опустить вертикаль состава на ось концентраций.
Конечными фазами кристаллизации являются те кристаллические фазы (соединения), между точками составов которых (на оси концентраций) попадает указанная вертикаль состава.

Слайд 55Правило определения характера поведения химического соединения при нагревании
Положение на диаграмме
состояния вертикалей составов индивидуальных химических соединений по отношению к кривым
ликвидуса и изотермам определяют характер поведения этих соединений при нагревании или вообще при изменении температуры.
Если вертикаль состава (например, А2В2—d на рис.) соединения (А2В2) доходит до кривой ликвидуса, которая в точке их пересечения имеет максимум (точка d), то это соединение плавится без разложения (конгруэнтно).
Точка (d) температурного максимума на кривой ликвидуса называется дистектикой.
Если вертикаль состава (например, А3В3—m) соединения (А3В3) не доходит до кривой ликвидуса, а ограничена изотермой (tn), пересекающей кривую ликвидуса, которая имеет в точке пересечения n перегиб, то это соединение плавится с разложением (инконгруэнтно).
Если вертикаль состава (рq на рис.) соединения (А1B1) ограничена изотермами (tp и tq), лежащими ниже изотермы эвтектической температуры, то это соединение устойчиво только в интервале температур, соответствующих этим изотермам, т.е. при изменении температуры вне этого интервала оно разлагается в твердом состоянии

Слайд 56Правила определения путей кристаллизации и путей плавления в двухкомпонентной системе
с эвтектикой
На оси абсцисс нанесен состав системы в массовых процентах,
а на оси ординат – температуры. Линиями АE, BE и CD диаграмма делится на четыре поля. Верхнее поле – область жидкой фазы или расплава (L). Снизу оно ограничивается линиями ликвидуса AE и BE. AE – линия жидкой фазы предельно насыщенной компонентом A, BE компонентом B.
Понижение температуры ниже этих линий вызывает кристаллизацию твердой фазы, иногда эти линии называют линиями начала кристаллизации. Ниже линии AE кристаллизуется A, а ниже BE – B. Выделение из жидкой фазы только одной из этих первичных твердых фаз протекает в температурном интервале до линии CD..
Диаграмма состояния системы A—B (а) и кривая охлаждения (б)
Слайд 57При постоянной температуре линии CD кристаллизация жидкой фазы любого двойного
состава заканчивается одновременным выделением кристаллов A и B. Поэтому линия
CD называется линией солидуса.
Ниже линии CD присутствуют только эти две твердые фазы. Составы сосуществующих фаз в двухфазном поле определяются проведением в пределах этого поля изотермы, называемой коннодой.
Концы конноды показывают составы сосуществующих при данной температуре фаз
Диаграмма состояния системы A—B (а) и кривая охлаждения (б)
Слайд 58закон Рауля-Вант-Гоффа
для смесей веществ
Понижение температуры плавления при переходе от чистого
компонента к смеси происходит в соответствии с законом Рауля-Вант-Гоффа, согласно
которому при добавлении к любому веществу другого, не образующего с первым твердого раствора, наблюдается понижение температуры плавления:
,
где t0 – температура плавления чистого компонента;
tX – температура плавления смеси;
X – концентрация добавки (в г на 100 г основного вещества);
M – молекулярная масса добавки;
T – абсолютная температура плавления основного вещества;
Q – скрытая теплота его плавления;
R – газовая постоянная.
Однако, уравнение это применимо для расчета лишь в малых областях концентраций.
Слайд 59Правило рычага.
Расчеты по диаграммам состояния двойных систем
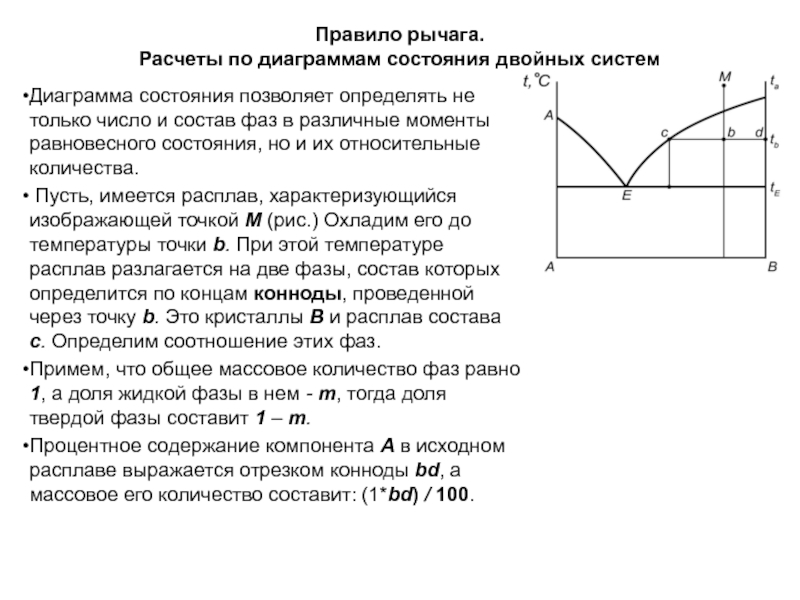
Диаграмма состояния позволяет
определять не только число и состав фаз в различные моменты
равновесного состояния, но и их относительные количества.
Пусть, имеется расплав, характеризующийся изображающей точкой M (рис.) Охладим его до температуры точки b. При этой температуре расплав разлагается на две фазы, состав которых определится по концам конноды, проведенной через точку b. Это кристаллы В и расплав состава с. Определим соотношение этих фаз.
Примем, что общее массовое количество фаз равно 1, а доля жидкой фазы в нем - m, тогда доля твердой фазы составит 1 – m.
Процентное содержание компонента A в исходном расплаве выражается отрезком конноды bd, a массовое его количество составит: (1*bd) / 100.
Слайд 60При температуре точки b компонент A полностью останется в расплаве
состава с. Процентное содержание A в нем выражается длиной конноды
cd, а массовое количество составит: m*cd /100.
Но , отсюда ,
а массовое количество твердой фазы
и массовое соотношение фаз
Это отношение называется правилом рычага, так как коннода подобна рычагу с опорой в точке b.
Правило рычага:
Если одна фаза разлагается на две фазы, то количество полученных фаз обратно пропорционально отрезкам конноды от точки состава исходной фазы до точек состава полученных фаз.
Слайд 61К выводу правила рычага
Пример
Для смеси: A – 20%, B –
80% определить состав и относительные количества фаз при температуре tb.
Через
точку b характеризующую состояние системы, проводим конноду и по концам ее определяем состав фаз.
Это расплав состава: A – 47%, B – 53% (точка с) и кристаллы B (точка d). Измеряем отрезки конноды bc и bd. Отрезок bc, соответствующий количеству твердой фазы, a bd, соответствующий количеству жидкой фазы. Общая длина конноды – cd.
Количество:
твердой фазы – (bc:cd)·100;
жидкой фазы – (bd:cd)·100.
Слайд 62Массовые и молярные проценты
Одной из актуальных задач расчетов по диаграммам
состояния является пересчёт составов из массовых процентов в молярные и
обратно
На рис. изображена диаграмма состояний SiO2—SnO, состав которой выражен в массовых процентах. Изобразить эту диаграмму при выражении состава в молярных процентах.
Произведем пересчет массовых процентов в молярные. При пересчете пользуемся формулой
Мол. масса SnO – 134,69, SiO2 – 60,09. Состав, эвтектической точки: SiO2 – 30,9% SnO – 69,1%.
20 масс. % SnO соответствуют:
10,0 мол. %;
40 масс. % SnO соответствуют:
22,9 мол. %.
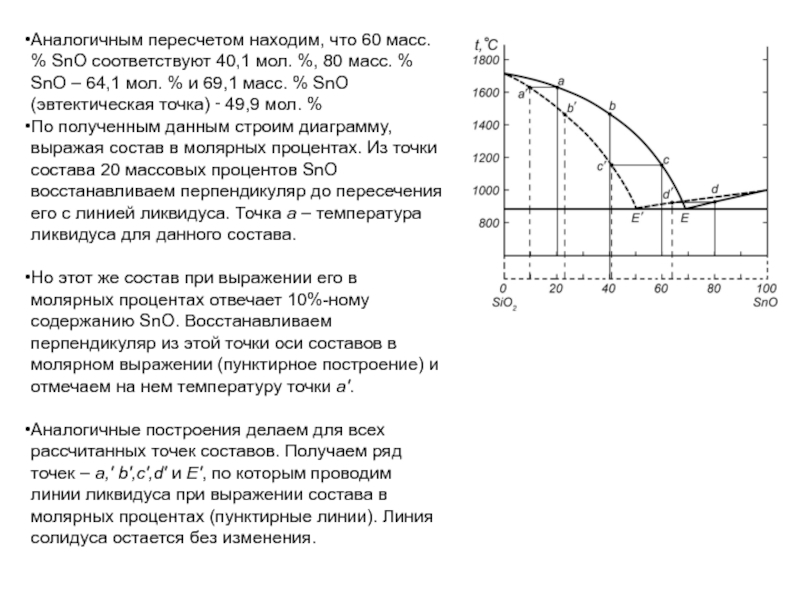
Слайд 63Аналогичным пересчетом находим, что 60 масс. % SnO соответствуют 40,1 мол.
%, 80 масс. % SnO – 64,1 мол. % и
69,1 масс. % SnO (эвтектическая точка) ‑ 49,9 мол. %
По полученным данным строим диаграмму, выражая состав в молярных процентах. Из точки состава 20 массовых процентов SnO восстанавливаем перпендикуляр до пересечения его с линией ликвидуса. Точка a – температура ликвидуса для данного состава.
Но этот же состав при выражении его в молярных процентах отвечает 10%-ному содержанию SnO. Восстанавливаем перпендикуляр из этой точки оси составов в молярном выражении (пунктирное построение) и отмечаем на нем температуру точки a.
Аналогичные построения делаем для всех рассчитанных точек составов. Получаем ряд точек – a,' b,c,d и E, по которым проводим линии ликвидуса при выражении состава в молярных процентах (пунктирные линии). Линия солидуса остается без изменения.
Слайд 64Аналитические методы расчета фазового состава
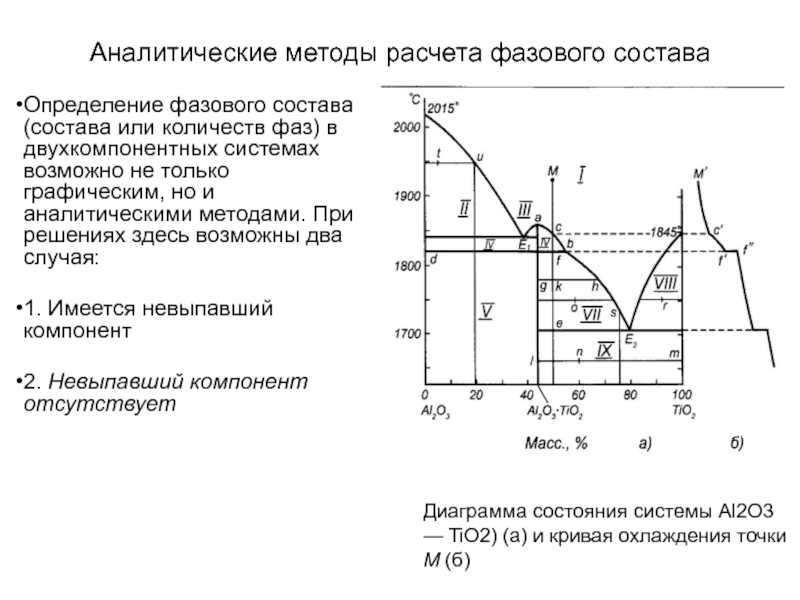
Определение фазового состава (состава или
количеств фаз) в двухкомпонентных системах возможно не только графическим, но
и аналитическими методами. При решениях здесь возможны два случая:
1. Имеется невыпавший компонент
2. Невыпавший компонент отсутствует
Диаграмма состояния системы Al2O3 — TiO2) (а) и кривая охлаждения точки M (б)
Слайд 65Имеется невыпавший компонент
Такое положение имеет место, например, в системе,
состояние которой на рис., а характеризуется изображающей точкой t. Невыпавшим
компонентом, находящимся только в жидкой фазе, является TiO2.
Для решения в общем виде невыпавший компонент обозначим А, его содержание в исходной смеси (в процентах) а1, а в жидкой фазе a2. Предположим, что вес исходной смеси составляет 100 г. Тогда количество A в ней будет a1 г. Но все это количество А как компонента невыпавшего, находится в жидкой фазе. Если количество жидкой фазы в граммах или процентах р, то количество в нем
компонента А составит . Но
Это уравнение связывает три величины. При двух известных оно позволяет определить любую третью неизвестную величину. Так количество фаз в процентах составит:
жидкая фаза – ;
твердая фаза (%) определится по разности 100 – p.
Слайд 66Невыпавший компонент отсутствует
Примером такого состояния системы может служить точка
k (рис.). Она характеризуется наличием твердой фазы в виде соединения
-Al2O3TiO2, содержащего оба компонента, и жидкой фазы также из обоих компонентов.
Как и в предыдущем случае, обозначим один из компонентов А, его содержание в процентах в исходной смеси a1, в жидкой фазе а2 и в твердой фазе a3. Количество исходной смеси примем также равным 100 г. Если количество жидкой фазы в граммах или в процентах примем равным p, то количество твердой фазы составит 100 – p.
Масса компонента А в исходной смеси, будет а1 г. Он распределится в жидкой и твердой фазах.
Вес А в жидкой фазе составит , а в твердой фазе
Следовательно
Слайд 67
Уравнение связывает четыре величины. Если известны три из них, любая
четвертая определятся из уравнения. Так, если известно количество фаз и
их составы, можно определить состав исходной смеси. Если же известны составы фаз и исходной смеси, то, решая уравнение относительно р, определяют количества фаз в процентах:
жидкая фаза (%) ;
твердая фаза (%) 100 – р.
При выводе формул принималось, что система содержит одну твердую и одну жидкую фазу. Они будут применимы и для случаев, когда система будет состоять из двух твердых или двух жидких фаз.
Слайд 68Пример
Для исходного состава: Al2O3 – 95%, TiO2 – 5% (рис.,
а) определить фазовый состав при температуре 1950 C.
Состояние системы на
диаграмме изображается точкой t.
По концам конноды, проведенной через эту точку, определяем состав фаз – это твердая фаза ‑Al2O3 и жидкая фаза состава: Al2O3 – 80%, TiO2 – 20% (точка u).
Слайд 69Инвариантные точки системы Al2O3—TiO2
Слайд 70Определим их относительные количества (случай с невыпавшим компонентом):
Жидкая фаза
;
твердая фаза 100 – p.
2. Из расплава состава: Al2O3 – 80%, TiO2 – 20% (рис., а) при кристаллизации выделилось 25% ‑Al2O3. Определить состав оставшегося расплава.
Количество жидкой фазы 100 – 25 = 75%. Содержание выпавшего компонента в оставшейся жидкой фазе составляет:
; Al2O3 = 100 – 26,7 = 73,3%.
Слайд 713. При кристаллизации исходного расплава (рис., а) из него выделилось
64,9% кристаллической фазы. Оставшийся расплав имеет состав: Al2O3 – 24,5%,
TiO2 – 75,5%. Определить температуру такого равновесия, фазовый состав системы и состав исходного расплава.
Из точки оси составов, отвечающей составу оставшегося расплава, восстанавливаем перпендикуляр до пересечения с линией ликвидуса в точке S.
Эта точка является одним концом конноды, другим ее концом будет точка на линии соединения -Al2O3TiO2. Это соединение и будет выпавшей твердой фазой. Состав его: Al2O3 – 56,1%, TiO2 – 43,9%. Температура точки s, равная 1730 C – температура равновесного состояния.
Количество оставшегося расплава 100 – 64,9 = 35,1%.
Поделим состав исходного расплава, так как здесь невыпавший компонент отсутствует.
;
Al2O3 = 100 – 55,0 = 45,0%.
Слайд 724. Определить состав и количество фаз в момент подхода кристаллизации
к эвтектической температуре расплава состава: Al2O3 – 50%, TiO2 –
50%.
Равновесными фазами в момент подхода кристаллизации к эвтектической температуре будут кристаллы -Al2O3TiO2 и расплав состава E2. (невыпавший компонент отсутствует).
;
-Al2O3TiO2 = 100 – 16,9 = 83,1%
Слайд 73Правила определения путей кристаллизации в двухкомпонентных системах с химическими соединениями,
плавящимися конгруэнтно
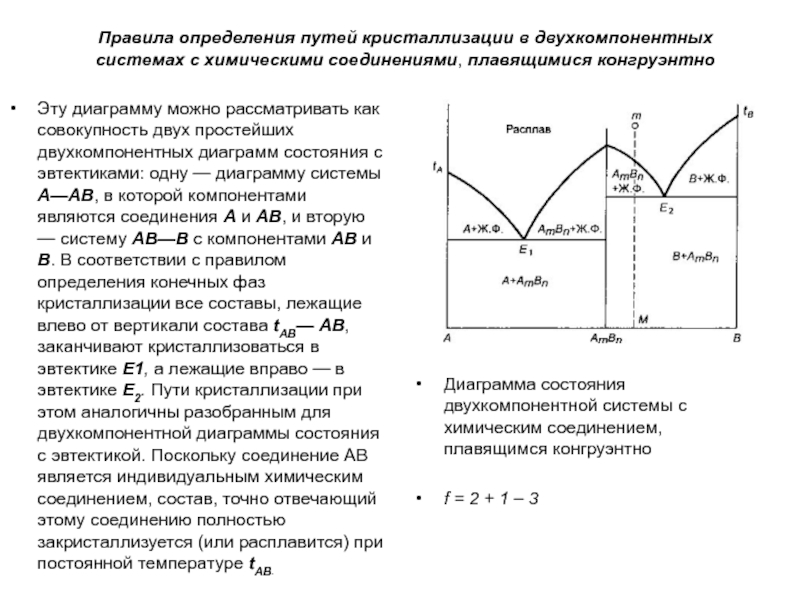
Эту диаграмму можно рассматривать как совокупность двух простейших двухкомпонентных
диаграмм состояния с эвтектиками: одну — диаграмму системы А—АВ, в которой компонентами являются соединения А и АВ, и вторую — систему АВ—В с компонентами АВ и В. В соответствии с правилом определения конечных фаз кристаллизации все составы, лежащие влево от вертикали состава tAB— АВ, заканчивают кристаллизоваться в эвтектике Е1, а лежащие вправо — в эвтектике Е2. Пути кристаллизации при этом аналогичны разобранным для двухкомпонентной диаграммы состояния с эвтектикой. Поскольку соединение АВ является индивидуальным химическим соединением, состав, точно отвечающий этому соединению полностью закристаллизуется (или расплавится) при постоянной температуре tAB.
Диаграмма состояния двухкомпонентной системы с химическим соединением, плавящимся конгруэнтно
f = 2 + 1 – 3
Слайд 74Правила определения путей кристаллизации в двухкомпонентных системах с химическими соединениями,
плавящимися инконгруэнтно
Характерной точкой этой диаграммы является инвариантная точка n перитектики
При
соответствующих этой точке составе жидкости и перитектической температуре tu при охлаждении или нагревании системы при постоянной температуре tu происходит химическая реакция, схему которой можно изобразить следующим образом:
т.е. при охлаждении расплава последний реагирует с ранее выпавшими кристаллами В с образованием соединения АВ (реакция идет слева направо), а при нагревании твердого вещества соединение АВ разлагается на жидкость состава n и кристаллы В (реакция идет справа налево).
В результате первой реакции кристаллы В полностью или частично исчезают (такое полное или частичное растворение ранее выделившейся твердой фазы называется резорбцией).
Слайд 75Правила определения путей кристаллизации в двухкомпонентных системах с соединением, разлагающимся
в твёрдом виде
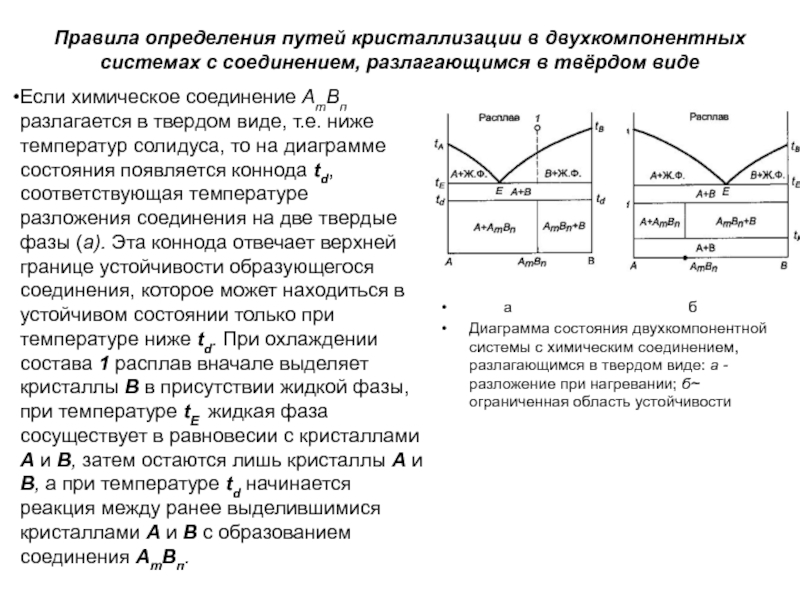
Если химическое соединение АтВп разлагается в твердом виде,
т.е. ниже температур солидуса, то на диаграмме состояния появляется коннода td, соответствующая температуре разложения соединения на две твердые фазы (a). Эта коннода отвечает верхней границе устойчивости образующегося соединения, которое может находиться в устойчивом состоянии только при температуре ниже td. При охлаждении состава 1 расплав вначале выделяет кристаллы В в присутствии жидкой фазы, при температуре tE жидкая фаза сосуществует в равновесии с кристаллами А и В, затем остаются лишь кристаллы А и В, а при температуре td начинается реакция между ранее выделившимися кристаллами А и В с образованием соединения АтВп.
a б
Диаграмма состояния двухкомпонентной системы с химическим соединением, разлагающимся в твердом виде: a - разложение при нагревании; б~ ограниченная область устойчивости
Слайд 76Соединение АтВп может иметь не только верхнюю, но и нижнюю
границу устойчивости (б). В этом случае на линии концентраций будет
лишь точка, отвечающая составу соединения, а вертикаль пойдет от температуры tK образования соединения АтВп в результате реакции в твердом состоянии между А и В при нагревании (или разложения АтВп на А и В при охлаждении).
Следует подчеркнуть, что при образовании исходными компонентами любого химического соединения на диаграмме состояния двухкомпонентной системы появляется вертикаль. По числу вертикалей на диаграмме можно определить количество соединений, образующихся в системе.
Слайд 77Правила определения путей кристаллизации в двухкомпонентных системах с ликвацией
На диаграмме
состояния такой системы (рис. ) на линии ликвидуса появляется горизонтальный
участок CD, в области которого не наблюдается эвтектического понижения температуры ликвидуса. Над участком CD формируется так называемый "купол" ликвации, ограничивающий область сосуществования двух несмешивающихся жидких фаз.
При охлаждении расплава, состав которого располагается между точками С и D на линии CКD одна жидкая фаза распадается на две, и составы этих фаз при понижении температуры скользят вдоль линий КС и KD. Так для расплава смеси d1, составы сосуществующих фаз при температуре tl будут отвечать точкам l'1 и l"1, а при температypе t2 - l'2 и l"2. Точки С и D соответствуют составам насыщенных жидких фаз с предельными значениями растворимости. Количественные соотношения между жидкими фазами определяются с помощью правила рычага.
Путь изменения состава жидкой фазы для состава 1 можно схематически изобразить следующим образом:
В области купола ликвации система одновариантна (f = 2+1—2=1), поскольку в равновесии находятся две фазы.
на линии CD система инвариантна
(f = 2+1—3=0)

Слайд 78Метастабильная ликвация
Метастабильная ликвация наблюдается только в подликвидусной области в отличие
от стабильной, всегда надликвидусной.
Если однофазный переохлажденный расплав 1, состав
которого лежит между точками С и D, выдерживать при температурах ниже tl (при tl), то вначале получим две несмешивающиеся между собой жидкости, и только потом начнут выделяться кристаллы В.
Явления расслаивания будут наблюдаться при tl и у состава 2, у которого путь кристаллизации пересекает область метастабильной ликвации, но не затрагивает купол стабильной ликвации.
В системах с пологим или S-образным ходом кривой ликвидуса купол стабильной ликвации отсутствует, но, как правило, обнаруживается купол метастабильной ликвации. Критическая точка К может располагаться вблизи кривой ликвидуса (при очень пологом ликвидусе) или в значительном отдалении от нее (при слабо выраженной пологости кривой ликвидуса) и даже ниже линии солидуса.
Появляется метастабильная ликвация в системах двух видов:
1) во всех системах со стабильной ликвацией - в виде продолжения области стабильной ликвации в подликвидусную область,
2) в системах, не проявляющих стабильной ликвации, но имеющих пологий или S-образный ход кривой ликвидуса
Области метастабильной ликвации в двухкомпонентных системах: со стабильной ликвацией (а); с пологим ходом кривой ликвидуса (б)

Слайд 79Термодинамические основы ликвационных явлений
Ликвация ление протекает в две стадии:
1)
химический распад, приводящий к возникновению зародышей новой фазы;
2) рост
частиц новой фазы с последующей переконденсацией, т.е. ростом крупных частиц за счет более мелких.
С позиций термодинамики любая система стремится перейти в равновесное состояние с минимумом свободной энергии. В двойной системе с ликвацией зависимость энергии Гиббса F от состава имеет вид кривой с максимумом (а). Рост концентрации компонента В на участке I—II или компонента А на участке VI—V повышает устойчивость системы, так как свободная энергия F npи этом понижается. Дальнейшее увеличение концентрации второго компонента на участках II—III и V-IV приводит к повышению энергии Гиббса, и система становится термодинамически неустойчивой.
Понижение свободной энергии на участке II—V достигается разделением на фазы разного состава. При распаде жидкости состава С на две фазы С' и С" свободная энергия уменьшается.
Следовательно, все составы в области С' — С" склонны к ликвации
Зависимость энергии Гиббса от концентрации в двухкомпонентной системе с ликвацией в случае однофазного (неустойчивого) состояния (а) и изменение энергии Гиббса в результате малых отклонений С1 и С2 от средних значений С на участках III—IV и II—III (б)

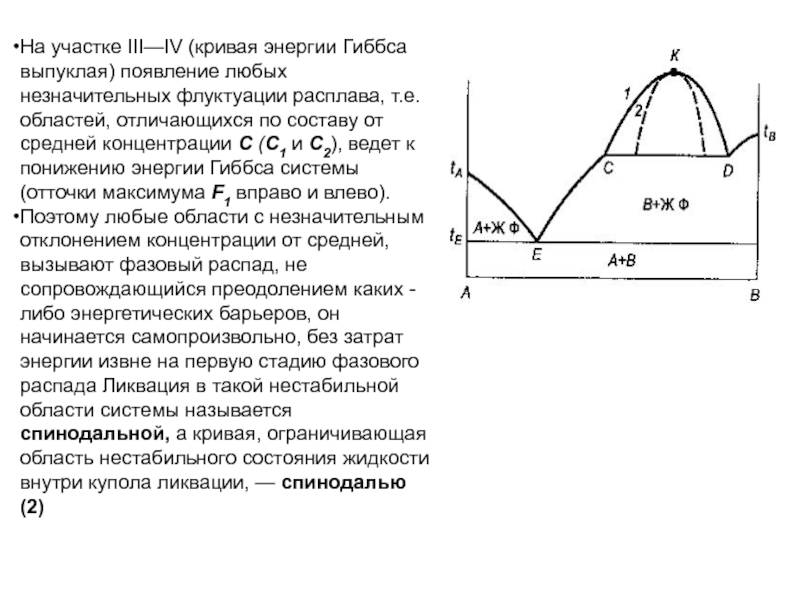
Слайд 80На участке III—IV (кривая энергии Гиббса выпуклая) появление любых незначительных
флуктуации расплава, т.е. областей, отличающихся по составу от средней концентрации
С (С1 и С2), ведет к понижению энергии Гиббса системы (отточки максимума F1 вправо и влево).
Поэтому любые области с незначительным отклонением концентрации от средней, вызывают фазовый распад, не сопровождающийся преодолением каких - либо энергетических барьеров, он начинается самопроизвольно, без затрат энергии извне на первую стадию фазового распада Ликвация в такой нестабильной области системы называется спинодальной, а кривая, ограничивающая область нестабильного состояния жидкости внутри купола ликвации, — спинодалью (2)
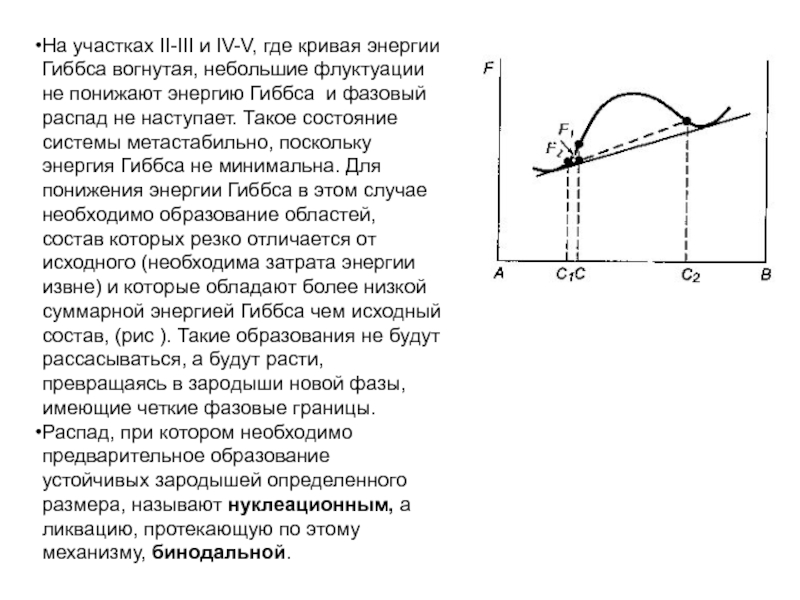
Слайд 81На участках II-III и IV-V, где кривая энергии Гиббса вогнутая,
небольшие флуктуации не понижают энергию Гиббса и фазовый распад не
наступает. Такое состояние системы метастабильно, поскольку энергия Гиббса не минимальна. Для понижения энергии Гиббса в этом случае необходимо образование областей, состав которых резко отличается от исходного (необходима затрата энергии извне) и которые обладают более низкой суммарной энергией Гиббса чем исходный состав, (рис ). Такие образования не будут рассасываться, а будут расти, превращаясь в зародыши новой фазы, имеющие четкие фазовые границы.
Распад, при котором необходимо предварительное образование устойчивых зародышей определенного размера, называют нуклеационным, а ликвацию, протекающую по этому механизму, бинодальной.
Слайд 82Обычно в области бинодальной ликвации образуется капельная структура с четко
оформленными границами раздела, а в спинодальной — взаимопроникающая, или двухкаркасная,
хотя возможны и отклонения от этих особенностей внешнего проявления ликвации в зависимости от условий охлаждения расплава
а б
Различные формы проявления ликвации в высоковязких системах
а – капельная,
б - двухкаркасная или взаимопроникающая
Слайд 83Вторичная ликвация
Вторичная ликвация — явление вторичного фазового распада в сформировавшихся
при ликвации фазах.
Возникает это при термической обработке предварительно ликвировавших
стекол и в соответствии со схемой, показанной на рис.
Если при температуре t1 в расплаве (стекле) образовались фазы l1 и l'1, то при резком снижении температуры до t2 и последующем выдерживании при ней фаз l1 и l'1 должны выделиться фазы l2 и l'2 При высокой вязкости расплавов полною перераспределения фаз до составов l2 и l'2 не происходит. В результате фаза 11 распадается на две фазы l2 и l'2, а фаза l'1 , в свою очередь, также самостоятельно распадается на те же две фазы l2 и l'2.
Слайд 84Правила определения путей кристаллизации в двух компонентных системах с полиморфными
превращениями компонентов
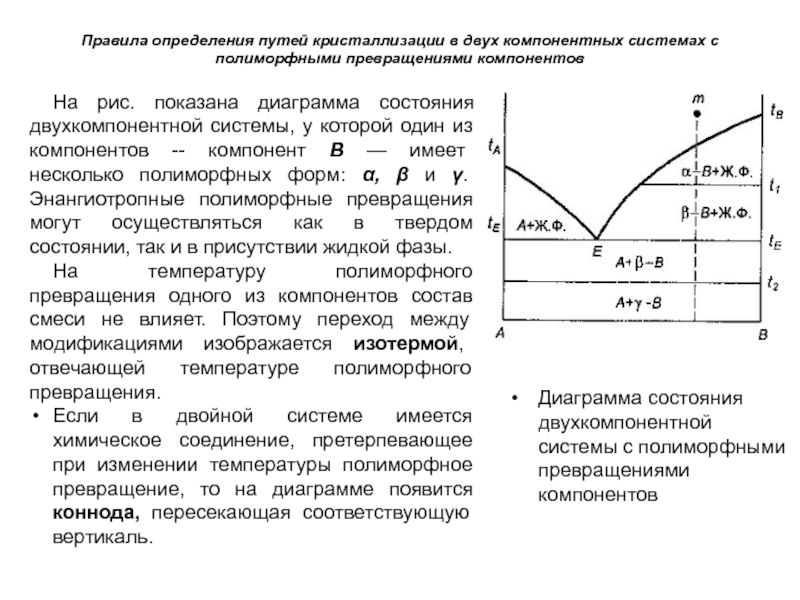
На рис. показана диаграмма состояния двухкомпонентной системы, у которой
один из компонентов -- компонент В — имеет несколько полиморфных форм: α, β и γ. Энангиотропные полиморфные превращения могут осуществляться как в твердом состоянии, так и в присутствии жидкой фазы.
На температуру полиморфного превращения одного из компонентов состав смеси не влияет. Поэтому переход между модификациями изображается изотермой, отвечающей температуре полиморфного превращения.
Если в двойной системе имеется химическое соединение, претерпевающее при изменении температуры полиморфное превращение, то на диаграмме появится коннода, пересекающая соответствующую вертикаль.
Диаграмма состояния двухкомпонентной системы с полиморфными превращениями компонентов
Слайд 85Таким образом, схему фазовых превращений при охлаждении расплава т можно
записать в следующем виде:
расплав → а-В + расплав →
β-В + расплав → (при температуре tЕ): β-В + А + расплав → А + β-В→ А + γ-В.
Однако если полиморфным превращениям подвергаются не чистые соединения, а твердые растворы, то температура полиморфных превращений не остается постоянной и зависит от состава твердого раствора. В этом случае линия полиморфного превращения не будет выражаться изотермой.
Слайд 86Правила определения путей кристаллизации в двухкомпонентных системах с образованием твердых
растворов
Рассмотрим путь кристаллизации расплава, состояние которого характеризуется точкой а.
При
температуре t1 однофазный расплав распадается на две фазы: жидкую состава l1 и твердый раствор состава S1. Составы фаз, находящихся в равновесии, определяются точками пересечения соответствующей конноды с линиями ликвидуса (l1) и солидуса (S1).
Понижение температуры до t2 приведет к изменению состава жидкой фазы до l2, а состава твердого раствора — до S2. Полное затвердевание произойдет при температуре t3, когда в смеси останется твердый раствор состава S3 и исчезающе малое количество жидкости l3.
Диаграмма состояния двухкомпонентной системы с непрерывным рядом твердых растворов
Слайд 87Когда состав твердого раствора окажется одинаковым с исходным составом жидкости,
т.е. когда точка состава твердого раствора, в данном случае точка
S3, окажется на вертикали исходного состава (al1S3) при температуре t3 произойдет окончательное затвердевание расплава, который в этот момент будет иметь состав S3.
Таким образом, путь изменения состава жидкой фазы изобразится как
а→l1→l2→l3,
а твердой — a→S1→S2→S3.
Следовательно, линии ликвидуса и солидуса можно назвать соответственно кривыми изменения составов жидких и твердых фаз, находящихся в равновесии
Слайд 88Двухкомпонентная система с ограниченной растворимостью компонентов в твердом состоянии
.
Обозначим раствор компонента В в компоненте А как SА(В) (твердый
раствор с преобладанием компонента А), а раствор компонента А в компоненте В — SB(A) (твердый раствор с преобладанием компонента В).
Кривая, соединяющая точки tA - с - а, определяет предельные концентрации компонента В, которые могут раствориться в компоненте А при различных температурах. Соответственно кривая tB – d - b относится к предельной растворимости компонента А в компоненте В. Эти линии представляют собой кривые составов насыщенных твердых растворов
Диаграмма состояния двухкомпонентной системы с ограниченной растворимостью в твердом состоянии
Слайд 89
расплав состава 1
расплав → SA(B) + расплав → SA(B).
расплав состава 2
расплав → SA(B) + расплав → SA(В)
→ SA(В) + SB(A).
расплав состава 3
расплав → SA(B) + расплав → при tE: SЕВ{А) + SЕА(В) + расплав → SA(B) + SB(A)
Эвтектическая смесь при кристаллизации также выделяет не чистые компоненты, а два твердых раствора, имеющих при tЕ составы SЕВ{А) и SЕА(В). Поэтому в отличие от обычной эвтектики точка Е В этой системе называют эвтектоидной.
Слайд 90Двухкомпонентная система с твердыми растворами
ограниченной растворимости и перитектикой
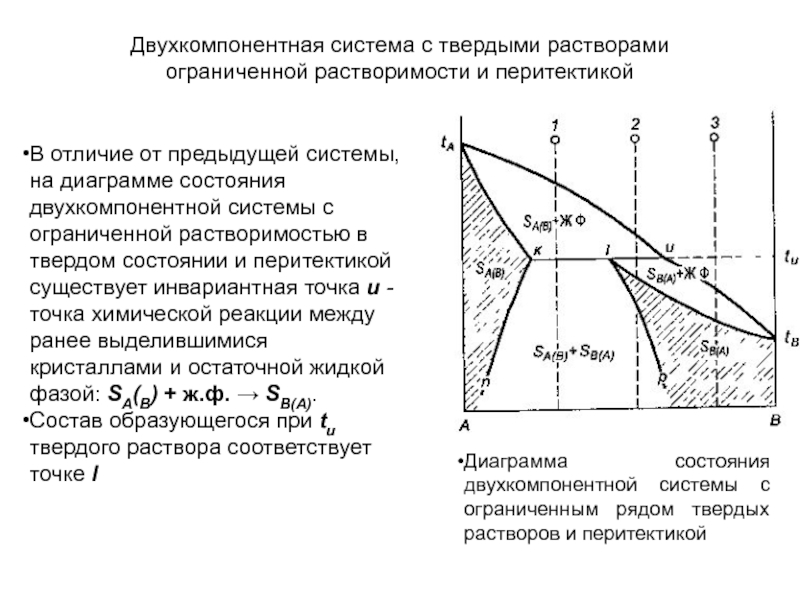
В отличие
от предыдущей системы, на диаграмме состояния двухкомпонентной системы с ограниченной
растворимостью в твердом состоянии и перитектикой существует инвариантная точка и - точка химической реакции между ранее выделившимися кристаллами и остаточной жидкой фазой: SA(B) + ж.ф. → SB(А).
Состав образующегося при tu твердого раствора соответствует точке l
Диаграмма состояния двухкомпонентной системы с ограниченным рядом твердых растворов и перитектикой
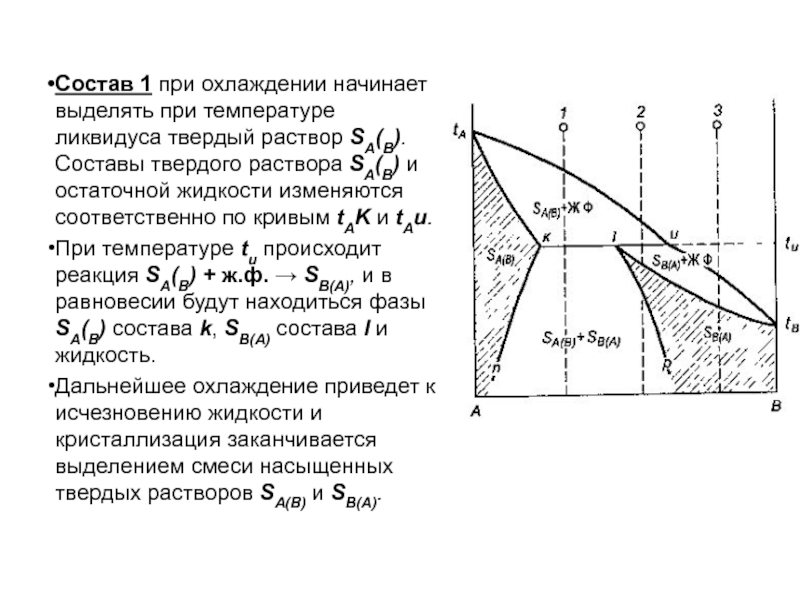
Слайд 91Состав 1 при охлаждении начинает выделять при температуре ликвидуса твердый
раствор SA(B). Составы твердого раствора SA(B) и остаточной жидкости изменяются
соответственно по кривым tAK и tAu.
При температуре tu происходит реакция SA(B) + ж.ф. → SB(А), и в равновесии будут находиться фазы SA(B) состава k, SВ(А) состава l и жидкость.
Дальнейшее охлаждение приведет к исчезновению жидкости и кристаллизация заканчивается выделением смеси насыщенных твердых растворов SA(B) и SB(A).
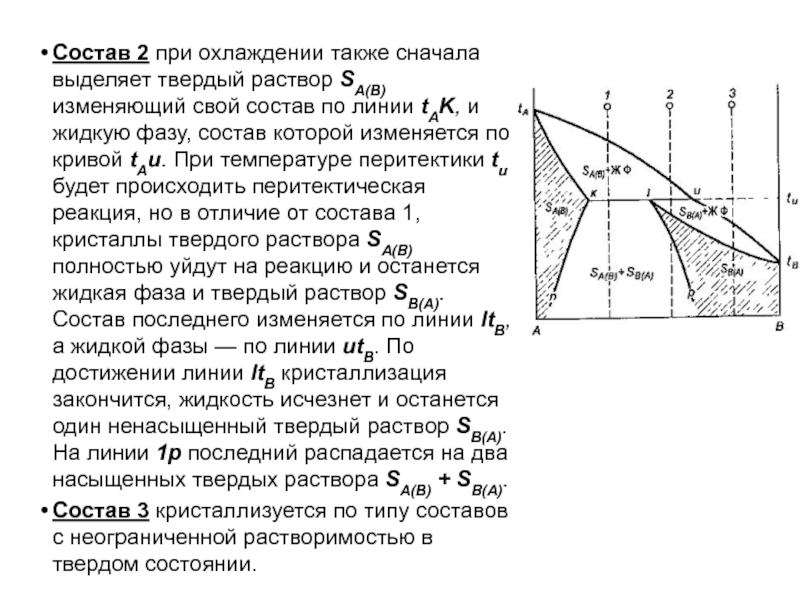
Слайд 92Состав 2 при охлаждении также сначала выделяет твердый раствор SA(B)
изменяющий свой состав по линии tAK, и жидкую фазу, состав
которой изменяется по кривой tAu. При температуре перитектики tu будет происходить перитектическая реакция, но в отличие от состава 1, кристаллы твердого раствора SA(B) полностью уйдут на реакцию и останется жидкая фаза и твердый раствор SB(A). Состав последнего изменяется по линии ltB, а жидкой фазы — по линии utB. По достижении линии ltB кристаллизация закончится, жидкость исчезнет и останется один ненасыщенный твердый раствор SB(A). На линии 1р последний распадается на два насыщенных твердых раствора SA(B) + SB(A).
Состав 3 кристаллизуется по типу составов с неограниченной растворимостью в твердом состоянии.
Слайд 93ТРЁХКОМПОНЕНТНЫЕ СИСТЕМЫ
ЭЛЕМЕНТЫ СТРОЕНИЯ ДИАГРАММ СОСТОЯНИЯ ТРЕХКОМПОНЕНТНЫХ СИСТЕМ
Правило фаз Гиббса
для трехкомпонентной конденсированной системы
при исключении парообразного состояния и давления
запишется в виде:
F + P = 3 + 1,
для которого условия равновесия:
Число фаз Характер равновесия
P = 1 F = 3
P = 2 F = 2
P = 3 F = 1
P = 4 F = 0
р – число фаз f – число параметров
Независимыми параметрами, определяющими состояние системы, являются температура и концентрации двух компонентов Х1 и Х2.
Концентрацию третьего компонента Х3 находят по разности 100 – Х1 – Х2.
Так как общее число параметров 3 – на диаграмме должно быть три оси, и она будет пространственной.
Слайд 94Концентрации компонентов в такой диаграмме обычно откладывают на стороне равностороннего
треугольника, называемого треугольником концентраций, а независимый параметр – температуру на
перпендикулярах, восстановленных к плоскости треугольника из его вершин.
Слайд 95Изображение концентраций (составов) в трехкомпонентных системах
Основой трехкомпонентной диаграммы состояния является
равносторонний треугольник концентраций. Длину стороны треугольника принимают за 100 частей
тройной системы. Каждая вершина треугольника означает 100% содержание того компонента, именем которого она обозначена. Каждая сторона треугольника – проекция частной двойной системы (A—B; B—C; A—C). Отсчет содержания данного компонента ведут по любой из двух сторон треугольника, образующих угол с его нулевым содержанием. Точки, лежащие на сторонах треугольника, выражают составы двухкомпонентных смесей.
Для определения состава трехкомпонентной смеси удобно пользоваться отрезками, отсекаемыми на сторонах треугольника линиями, проведенными через точку этого состава параллельно сторонам треугольника.
Слайд 96Для состава точки M через эту точку проводят линии ab,
cd и ef. Содержание компонента отсчитывается по отрезку на стороне
треугольника, отсеченному линией, противоположной вершине, обозначающей данный компонент. Для точки M содержание компонента A в смеси определяется отрезком Bd или Cc (20%), содержание B – отрезком Ab или Cd (50%), содержание C – отрезком Ae или Bf (30%). Но Ae = bd и, следовательно, сумма отрезков, выражающих состав смеси, равна стороне треугольника. Таким образом, для определения состава трехкомпонентной смеси достаточно через эту точку провести две прямые (ab и cd), параллельные каким-нибудь двум сторонам треугольника (AB и CD), тогда на третьей стороне можно прочитать состав смеси
Слайд 97Свойства некоторых линий в треугольнике составов
Прямая (например, ef), параллельная какой-нибудь
стороне треугольника, соответствующей содержанию двух компонентов (A и B), есть
геометрическое место точек составов смесей с постоянным содержанием третьего компонента (C), но с переменным соотношением двух других (A и B).
Если точка M движется по прямой ef вместе с прямыми Mb и Md, то отрезок bd, соответствующий содержанию C, будет перемещаться по AB без изменения, что означает постоянство содержания C на прямой ef. Соотношение же этих компонентов A и B при этом будет изменяться;
Слайд 98- Прямая Cg, исходящая из вершины треугольника, соответствующей 100 %
содержанию какого-либо компонента (C), есть геометрическое место точек составов, характеризующихся
постоянством соотношения двух других компонентов (при переменной их сумме). Это соотношение определяется как обратное отношение величин отрезков, образованных на стороне этих двух компонентов точкой пересечения с указанной прямой.
Так, например, на линии Cg расположены составы с переменным количеством C и постоянным соотношением A и B.
При C = 0, отношение . В составе, выраженном точкой D на
линии Cd, содержание компонента C соответствует отрезку Ae, а
отношение , но ,
т.е. отношение компонентов A и B остается постоянным.
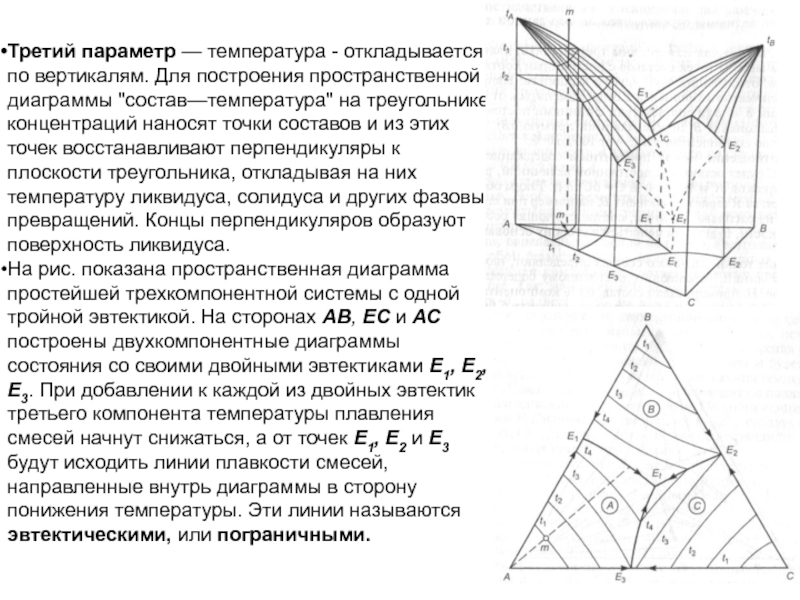
Слайд 99Третий параметр — температура - откладывается по вертикалям. Для построения
пространственной диаграммы "состав—температура" на треугольнике концентраций наносят точки составов и
из этих точек восстанавливают перпендикуляры к плоскости треугольника, откладывая на них температуру ликвидуса, солидуса и других фазовых превращений. Концы перпендикуляров образуют поверхность ликвидуса.
На рис. показана пространственная диаграмма простейшей трехкомпонентной системы с одной тройной эвтектикой. На сторонах АВ, ЕС и АС построены двухкомпонентные диаграммы состояния со своими двойными эвтектиками E1, Е2, Е3. При добавлении к каждой из двойных эвтектик третьего компонента температуры плавления смесей начнут снижаться, а от точек Е1, Е2 и Е3 будут исходить линии плавкости смесей, направленные внутрь диаграммы в сторону понижения температуры. Эти линии называются эвтектическими, или пограничными.
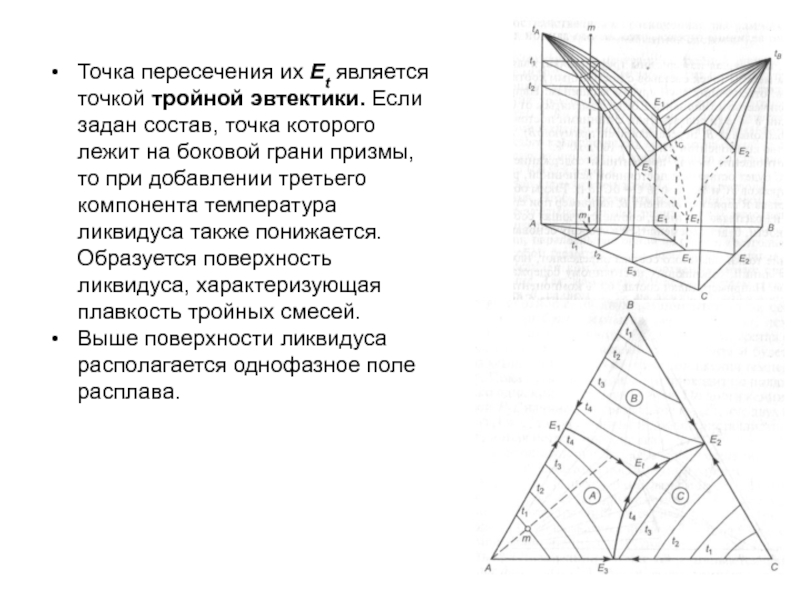
Слайд 100Точка пересечения их Et является точкой тройной эвтектики. Если задан
состав, точка которого лежит на боковой грани призмы, то при
добавлении третьего компонента температура ликвидуса также понижается. Образуется поверхность ликвидуса, характеризующая плавкость тройных смесей.
Выше поверхности ликвидуса располагается однофазное поле расплава.
Слайд 101Понятие о путях кристаллизации расплавов
Возьмем расплав состава т. Точка его
располагается в поле кристаллизации компонента А на изотерме t1. Это
означает, что при охлаждении расплава поверхность ликвидуса будет достигнута при температуре t1. С этого момента начнется кристаллизация расплава с выделением компонента А.
Чтобы далее проследить за фазовыми изменениями при охлаждении, необходимо построить путь кристаллизации. В данном случае путь кристаллизации означает геометрическое место точек, показывающих изменение состава остаточной жидкой фазы при кристаллизации.
Диаграмма состояния трехкомпонентной системы с эвтектикой.
Пути кристаллизации в системе
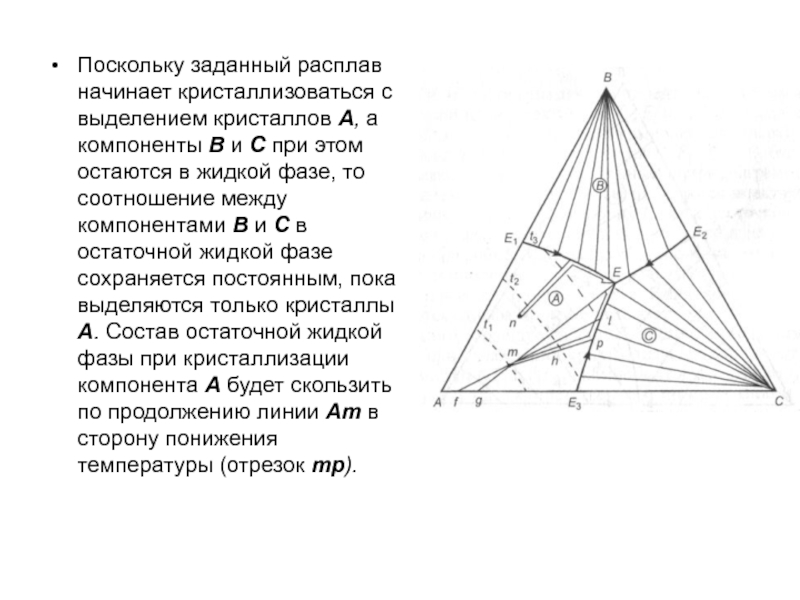
Слайд 102Поскольку заданный расплав начинает кристаллизоваться с выделением кристаллов А, а
компоненты В и С при этом остаются в жидкой фазе,
то соотношение между компонентами В и С в остаточной жидкой фазе сохраняется постоянным, пока выделяются только кристаллы А. Состав остаточной жидкой фазы при кристаллизации компонента А будет скользить по продолжению линии Am в сторону понижения температуры (отрезок тр).
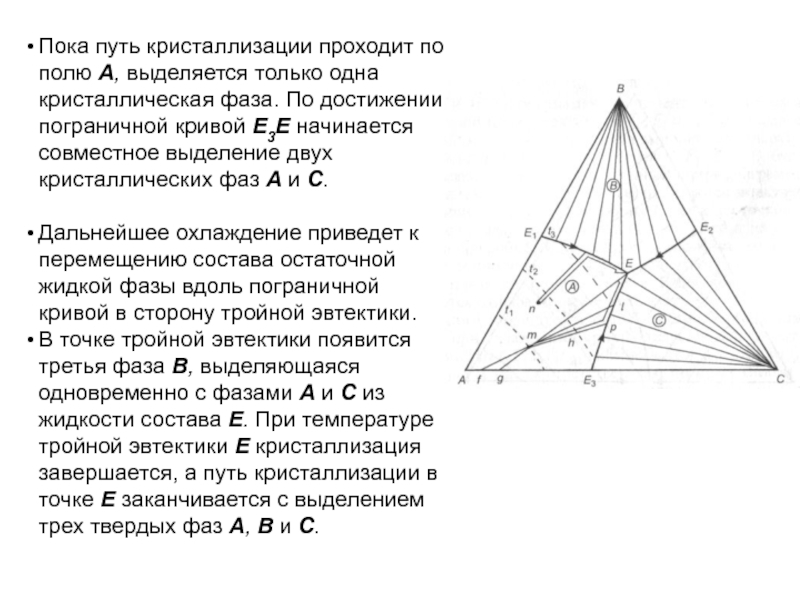
Слайд 103Пока путь кристаллизации проходит по полю А, выделяется только одна
кристаллическая фаза. По достижении пограничной кривой E3E начинается совместное выделение
двух кристаллических фаз А и С.
Дальнейшее охлаждение приведет к перемещению состава остаточной жидкой фазы вдоль пограничной кривой в сторону тройной эвтектики.
В точке тройной эвтектики появится третья фаза В, выделяющаяся одновременно с фазами А и С из жидкости состава Е. При температуре тройной эвтектики E кристаллизация завершается, а путь кристаллизации в точке Е заканчивается с выделением трех твердых фаз А, В и С.
Слайд 104Таким образом, температура полного затвердевания расплава будет отвечать температуре той
тройной эвтектики, где заканчивается путь кристаллизации.
Следовательно, фазовые превращения при охлаждении
расплава пройдут по схеме:
Расплав→А + ж.ф.→А + С + ж.ф.→в точке Е: А+ С+B + ж.ф.→A+ В+ С.
Слайд 105Правило рычага и центра тяжести в треугольнике концентраций
Если из двух
разных тройных смесей (или фаз) получается одна смесь (или фаза),
то точка состава последней лежит на прямой, соединяющей точки составов исходных смесей (фаз) и между ними. Отношение количеств двух исходных смесей обратно пропорционально отрезкам соединительной прямой от точек составов этих смесей до точки состава суммарной смеси или фазы.
На рис. суммарная смесь P получена смешением тройных составов M и N.
Тройная смесь M, в которой в количестве m г, содержит компонента A определяемого величиной отрезка a1%.
Тройная смесь N, в которой в количестве n г, содержит компонента A, определяемого величиной отрезка a2 %.
Суммарная смесь P в количестве (m + n) г, содержит x% компонента A.
Так как a1m + a2n = x(m + n), то m(a1 – x) = n(x – a2), и ;
из подобия треугольников MPR и MNS следует: ,
следовательно m/n = PN/PM.
Слайд 106Это отношение позволяет определить состав суммарной смеси.
Если одна фаза распадается
на две другие фазы, то точки составов исходной и вновь
образовавшихся фаз лежат на одной прямой.
Если известны состав Р и масса р исходной фазы и составы М и N, образовавшихся из неё фаз, то количества последних т и п определяется следующим образом:
в массовых единицах –
m = p * PN / MN, n = p* PM / MN;
и в массовых % –
m’ = 100 *p * PN / MN, n’ = 100 * p* PM / MN; .
Правило рычага позволяет определить суммарный состав не только двух, но и большего числа исходных смесей или фаз
Слайд 107Правило рычага позволяет определить суммарный состав не только двух, но
и большего числа исходных смесей или фаз.
Например, требуется определить суммарный
состав трех смесей состава: M, N и Р (рис.), массовые количества которых составляют соответственно т, n и р. Сначала находят суммарный состав двух смесей, например, М и N.
Соединив эти точки прямой и измерив ее длину, делит ее в соотношении n:m. Таким образом находят точку R суммарного состава для М и N. Массовое количество суммарной смеси будет m+n.
Затем, соединив прямой точки R и P, находят точку суммарного состава для R и P. Для этого прямую RP делят в соотношении (m + n):p. Точка S будет выражать суммарный состав всех трех смесей.
Количество суммарной смеси
s = m + n + p.
Слайд 108Развитием правила рычага является правило центра тяжести треугольника, которое позволяет
определить суммарный состав трех фаз, если известны их составы и
количества. Оно может быть выведено из правила рычага. Для этого определим суммарный состав трех смесей состава M, N и Р, количества которых составляют соответственно m, n и р (рис.)
По правилу рычага найдем суммарный состав R для смесей М и N, а затем, складывая R и P, определим суммарный состав S для всех трех смесей.
Можно эту задачу решить, начиная с определения суммарного состава Q смесей М и Р, а затем, складывая Q и N, найти суммарный состав трех смесей.
Слайд 109Он выразится той же точкой S. Эта точка, лежащая одновременно
на линиях PR и NQ, является точкой их пересечения. Аналогичные
результаты получаются, если начать сложение смесей P и N.
Описанный метод определения суммарного состава аналогичен методу определения центра тяжести треугольника масс MNP, в вершинах которого находятся массы m, n и p. Точка S является центром тяжести такого треугольника.
Этот случай называется схемой треугольника.
Слайд 110Если из смесей (или фаз) состава M, N, Q нужно
получить смесь (или фазу) состава P (рис.), схема для этого
случая называется положением оппозиции.
Смесь точки K может быть получена двумя способами:
M + N = K и P + Q = K,
тогда M + N = P + Q
и P = M + N – Q.
Т.е. для получения смеси P нужно от смеси (M + N) отнять некоторое количество смеси Q.
Если из смесей M, N и P нужно получить смесь Q, такой случай называют положением конъюнкции.
После проведения прямых NQ и MQ точка P находится внутри треугольника MQN. Тогда смесь P можно получить простым сложением P = M + N + Q и Q = P + (M + N), т.е. для получения смеси состава Q нужно от смеси P отнять некоторое количество смеси (M + N).
.
.
Слайд 111Правилом центра тяжести треугольника удобно пользоваться для решения обратной задачи
– определения количеств трех фаз, на которые распадется исходная фаза.
Такое положение имеет место, например, при кристаллизации жидкой фазы
Исходя из отношений (рис. 4.4): ; ; ,
количество фаз, образовавшихся из исходной в массовых единицах составят:
; ; ,
а относительные количества в процентах:
; ; .
Слайд 112Элементы строения тройных диаграмм
Элементы строения диаграмм состояния трехкомпонентных систем, показанные
на рис., включают в себя:
треугольник концентраций, изотермы, точки составов
химических соединений, пограничные кривые, поля первичной кристаллизации, тройные точки, соединительные прямые, элементарные треугольники, биноидальные кривые, кривые полиморфных превращений
Слайд 113Характер процесса, происходящего при нагревании состава
Расположение на диаграмме состояния точки
состава данного соединения и его поля первичной кристаллизации определяет характер
процесса, происходящего при нагревании этого соединения:
1) если точка состава двойного или тройного соединения лежит в собственном поле первичной кристаллизации, то это соединение плавится без разложения, т.е. конгруэнтно (например, соединения АС и ABC, рис. а);
2) если точка состава двойного соединения лежит вне поля его первичной кристаллизации, а поле примыкает к стороне треугольника, на которой лежит точка состава этого соединения, то оно плавится с разложением, т.е. инконгруэнтно (например, соединение АС, рис. б);
Слайд 1143) если точка состава двойного соединения лежит вне поля его
первичной кристаллизации, а последнее расположено внутри треугольника концентраций, не примыкая
к стороне треугольника, на которой лежит точка состава этого двойного соединения, то оно при нагревании разлагается в твердом состоянии (например, соединение ВС, рис. б);
4) если точка состава тройного соединения лежит вне поля его первичной кристаллизации, то это соединение плавится с разложением, т.е. инконгруэнтно (например, соединение ABC, рис. в).
Слайд 115На пограничных кривых, каждая из которых разделяет два поля первичной
кристаллизации, в равновесии находятся три фазы - жидкость и кристаллы
двух соединений, поля которых разделяет эта кривая (например, на пограничной кривой ab на рис. в равновесии с жидкостью находятся кристаллы соединений АВ и АС), т.е. система по правилу фаз в данном случае является моновариантной. Все точки пограничных кривых в процессе кристаллизации показывают состав жидкой фазы, находящейся в равновесии с кристаллами соответствующих соединений.
На пограничных кривых стрелками указывается направление падения температуры.
В зависимости от характера процесса, происходящего в системе при изменении температуры вдоль пограничных кривых, они разделяются на конгруэнтные и инконгруэнтные.
Слайд 116На конгруэнтных пограничных кривых происходит физический процесс кристаллизации (при понижении
температуры) или плавления (при повышении температуры).
Инконгруэнтные кривыми являются те,
на которых происходит химическая реакция, сопровождающаяся исчезновением одних и появлением других фаз в системе.
Конгруэнтные и инконгруэнтные пограничные кривые отличаются также тем, что путь кристаллизации с первых никогда не сходит, а со вторых может (хотя и не обязательно) сойти.
Слайд 117Тройные точки
Три сходящиеся пограничные кривые на диаграммах состояния образуют так
называемые тройные точки (например, точки b, e и т. д.
на рис.),
в которых, если кристаллизация не закончена, в равновесии находятся четыре фазы — жидкость состава этой точки и три кристаллических соединения, поля первичной кристаллизации которых сходятся в этой точке
(например, в тройной точке b на рис. в равновесии с жидкой фазой находятся кристаллы соединений АВ, АС и A1B1C1).
По правилу фаз система, параметры которой соответствуют этой точке, является инвариантной, т.е. не имеет степеней свободы p = 4, F = 0.
В зависимости от направления падения температуры на пограничных кривых тройные точки разделяются на точки эвтектики, точки двойного подъема и точки двойного опускания
Слайд 118Точка эвтектики является точкой, образованной тремя пограничными кривыми с падающей
по всем трем кривым к этой точке температурой (рис. а),
Точка двойного подъема образуется тремя пограничными кривыми, по двум из которых температура падает к точке, а по одной — от точки (рис. б),
Точка двойного опускания образуется, когда по одной пограничной кривой температура падает к точке, а по двум другим пограничным кривым — от точки (рис. в).
Тройные точки отличаются по характеру процессов, происходящих при постоянной температуре (система инвариантна) в системе, когда состав жидкой фазы соответствует этой точке.
В точке эвтектики при отводе теплоты происходит физический процесс кристаллизации твердых фаз (соединений),
Точки двойного подъема и опускания являются точками химической реакции, сопровождающейся исчезновением старых и появлением новых фаз.
Слайд 119Соединительные прямые и элементарные треугольники
Прямые линии на трехкомпонентных диаграммах состояния,
соединяющие точки составов индивидуальных химических соединений, имеющих смежные поля первичной
кристаллизации, называются соединительными прямыми (например, прямые АВ — A1B1C1, AB — АС и т.д. на рис. ).
Соединительные прямые можно проводить только между точками составов соединений со смежными полями первичной кристаллизации, т.е. поля кристаллизации которых соприкасаются по какой-либо пограничной кривой.
Каждой пограничной кривой на диаграмме состояния соответствует своя соединительная прямая, соединяющая составы кристаллических фаз (соединений), которые находятся в равновесии вдоль этой пограничной кривой, и, наоборот, каждой соединительной прямой соответствует своя пограничная кривая.
Слайд 120Определение количественного содержания твердых фаз, находящихся в равновесии вдоль данной
пограничной кривой с применением правила рычага производится с помощью именно
соединительных прямых.
При расчетах все графические построения на диаграммах надо относить только к соединительной прямой, соответствующей данной пограничной кривой
Слайд 121Элементарные треугольники
Соединительные прямые разбивают все поле треугольника концентраций на элементарные
треугольники, образуемые тремя соединительными прямыми (например, треугольник АВ—В— A1C1, AC—ABC—ВС,
АВ—A1B1C1—АС и т.д., рис.).
Элементарными являются только те треугольники, которые не содержат внутри себя других соединительных прямых и, следовательно, других треугольников.
Элементарные треугольники позволяют определять конечные фазы (соединения) кристаллизации, выделяющиеся из трехкомпонентного расплава любого состава, и на основании этого — конечную точку (температуру) кристаллизации.
Количества элементарных треугольников в системе определяется по формуле:
N = 1 + D + 2T,
где N – количество элементарных треугольников,
D – количество двойных соединений в системе,
T – количество тройных соединений в системе.
Слайд 122Биноидальные кривые и кривые полиморфных превращений
Если в одной из частных
двойных систем (например, А—С, рис.), составляющих трехкомпонентную систему, имеется область
ликвации, то она сохраняется и в тройной системе в виде примыкающей к соответствующей стороне (АС) треугольника концентраций области, ограниченной линией (mpl), которая, как и в двухкомпонентных системах, называется бинодальной кривой.
Точки ветвей этой кривой (рт и pl) показывают составы двух образующихся при расслоении жидких фаз, находящихся в равновесии при данной температуре. Составы этих фаз определяются экспериментально и точки этих составов соединяются прямыми — коннодами (например, m'l'), концы которых лежат на ветвях бинодальной кривой.
Слайд 123Кривые полиморфных превращений, происходящих в равновесных условиях при постоянной температуре,
совпадают с изотермой, соответствующей температуре полиморфного превращения.
Например (рис.), если
компонент В имеет две полиморфные модификации (В' и В") с температурой превращения 1500°С, то кривая полиморфного превращения будет совпадать на трехкомпонентной диаграмме состояния с линией изотермы qs, соответствующей 1500°С
Слайд 124Определение состава первично кристаллизующейся из расплава твердой фазы
Первично выпадающей при
кристаллизации фазой будут кристаллы того соединения, в поле первичной кристаллизации
которого лежит точка состава исходного расплава.
На рис. изображен тип трехкомпонентной диаграммы состояния с бинарным химическим соединением АmBn, плавящимся конгруэнтно. На диаграмме состояния появляется дополнительное поле кристаллизации этого соединения и возникают две тройные эвтектики.
Существование одной тройной эвтектики в такой системе невозможно, поскольку тогда к одной точке примыкали бы четыре поля кристаллизации и в равновесии должны были бы находиться четыре твёрдые фазы и расплав, что противоречит правилу фаз. Появляется новая пограничная кривая Е1Е2, разделяющая поля первичной кристаллизации АmBn и С.
Слайд 125Из расплава состава c первыми при соответствующей температуре будут выпадать
кристаллы соединения АmBn, поскольку точка этого состава лежит в поле
первичной кристаллизации этого соединения.
По пограничной кривой Е1Е2 кристаллизуются две твёрдые фазы – С и АmBn , но температуры падают и к Е1 и к Е2. Следовательно, между ними должна быть точка температурного максимума.
Её положение определяется правилом температурного максимума.
Слайд 126Определение направления падения температуры на пограничных кривых (правило температурного максимума)
Температура
на пограничной кривой всегда падает от точки пересечения этой пограничной
кривой или ее продолжения с соответствующей этой пограничной кривой соединительной прямой или ее продолжением (эта точка на пограничной кривой является точкой температурного максимума).
На рис. приведены возможные случаи взаимного расположения пограничной кривой тn и соответствующей ей соединительной прямой А—В: если пограничная кривая и соединительная прямая непосредственно пересекаются друг с другом (случай а), то температура падает в обе стороны от точки их пересечения s в направлениях, указанных стрелками; если же пограничная кривая и соединительная линии непосредственно не пересекаются, то, продолжив соединительную прямую до пограничной кривой (случай б), или пограничную кривую до соединительной прямой (случай в), или оба указанных элемента строения (случай г), находят точку tmax (s), от которой по пограничной кривой будет падать температура, причем в последних двух случаях температура падает на всем протяжении пограничной кривой в одну сторону

Слайд 127Определение конечных фаз и конечной точки кристаллизации на диаграммах состояния
При
заданном составе исходного расплава диаграмма состояния позволяет даже без построения
пути кристаллизации определить состав конечных кристаллических фаз после завершения кристаллизации расплава.
По конечным фазам можно определить на диаграмме конечную точку кристаллизации, которая характеризует температуру, при которой заканчивается кристаллизация, и состав жидкой фазы в последний момент кристаллизации.
При работе с диаграммами состояния это рекомендуется делать до построения пути кристаллизации, что позволяет ограничить этот путь начальной (она задается) и конечной точками и тем самым избежать ошибок при определении последовательности фазовых изменений.
Состав конечных кристаллических фаз после завершения кристаллизации трехкомпонентного расплава определяется по правилу элементарного треугольника.
Слайд 128Конечными продуктами кристаллизации являются те три соединения, точки составов которых
лежат в вершинах элементарного треугольника, внутри которого находится точка состава
исходного расплава.
Конечной же точкой кристаллизации трехкомпонентного расплава является та тройная точка, в которой сходятся поля первичной кристаллизации конечных фаз кристаллизации.
Слайд 129Определение первичного пути изменения состава жидкой фазы
после начала кристаллизации
При
кристаллизации из расплава одной твердой фазы состав жидкой фазы (расплава)
изменяется (т.е. путь кристаллизации проходит) от точки состава исходного расплава по продолжению прямой, проведенной через точку состава кристаллизующегося соединения и точку состава исходного расплава, в сторону понижения температуры.
Для исходного расплава а1 (рис.) состав жидкой фазы при кристаллизации соединения АС изменяется (т.е. путь кристаллизации проходит) по продолжению прямой АС—а1, соединяющей точки АС и а1, т.е. по прямой а1b в сторону понижения температуры. Если точка состава исходного расплава (например, а2) попадает на конгруэнтную пограничную кривую, то изменение состава жидкой фазы (путь кристаллизации) при одновременной кристаллизации двух твердых фаз (в данном случае А и АС) будет происходить в сторону понижения температуры по этой кривой.
Слайд 130Если же точка состава исходного расплава попадает на инконгруэнтную пограничную
кривую, то путь кристаллизации с нее сойдет и в этом
случае действует описанное выше правило определения первичного пути изменения состава жидкой фазы, т.е. путь кристаллизации проходит по продолжению прямой, соединяющей точку состава кристаллизующейся фазы и точку состава исходного расплава
Слайд 131Трехкомпонентная система с двойным химическим соединением,
плавящимся инконгруэнтно
На сторону
АВ проектируется уже не две двойные эвтектики, а одна эвтектика
E и перитектика G.
В двойной системе АВ, при температуре tu и охлаждении растворяются выделившиеся раньше кристаллы А с образованием соединения АтВп.
Этот же процесс идет и на пограничной кривой uG. Если путь кристаллизации расплава попадет на пограничную кривую uG, то будет происходить не одновременное выделение кристаллов А и АтВп, а растворение кристаллов А и образование соединения АтВп.
Соединив точки составов фаз, кристаллизующихся в точке G, получим элементарный фазовый треугольник А-С-АтВп, все составы которого будут заканчивать кристаллизацию в точке G c выделением твердых фаз А, С и АтВп. Как видно из рис., точка G лежит за пределами своего фазового треугольника. Это один из отличительных признаков точки двойного подъема, по которому она определяется на диаграмме.
Слайд 132Для эвтектической точки Е элементарным фазовым треугольником будет область АтВп-С—В,
и составы, попадающие в эту область, должны закончить кристаллизацию в
точке Е.
В поле кристаллизации АтВп пути кристаллизации пойдут по прямым, соединяющим заданные составы с точкой состава соединения АтВп. В соответствии с их направлением вторичной кристаллической фазой будут кристаллы В или С, а конечными продуктами кристаллизации В, С и АтВп.
Слайд 133Пути кристаллизации различных составов в системе
Для состава а:
расплав →
А + расплав → А + С + расплав →
в точке G: А (растворяется) + С + АтВп (образуется) + жидкость → А + С + АтВп, причем в точке G соединение АтВп будет образовываться вследствие лишь частичного растворения ранее выделившихся кристаллов А.
Для состава b:
расплав → А + расплав → А (растворяется) + АтВп (образуется) + расплав (АтВп образуется на пограничной кривой за счет частичного растворения кристаллов А) → (в точке G): А + АтВп + С + жидкость →А+ АтВп + С.
Для состава с
расплав → А + расплав → А (растворяется) + C (образуется) + расплав (C образуется на пограничной кривой за счет частичного растворения кристаллов А) → (в точке G): А (исчезает)+ АтВп + С + жидкость → АтВп + С + расплав → (в точке Е): АтВп + С + В
Слайд 134Для состава d
расплав → А + ж.ф. → А (растворяется)
+ АтВп (образуется) + ж.ф. → АтВп + ж.ф. →
АтВп + С + ж.ф. → (в точке Е): АтВп + С + В + жидкость → АтВп + С + В.
Если точка исходного состава попадает на соединительную прямую, то конечными фазами кристаллизации будут те два соединения, точки составов которых соединяет эта соединительная прямая (в подобных случаях исходный состав следует рассматривать как принадлежащий частной двухкомпонентной системе, образованной этими соединениями).
Если же точка состава исходного расплава точно соответствует составу какого-либо соединения, то конечным продуктом кристаллизации будет одна фаза — кристаллы этого соединения
Слайд 135Трехкомпонентная система с двойным химическим соединением,
разлагающимся в твердом виде
Если
два компонента системы образуют химическое соединение, разлагающееся при нагревании в
твердом виде, то при добавлении к нему третьего компонента температура плавления смесей может понизиться настолько, что станет ниже температуры разложения вещества. Тогда на диаграмме состояния трехкомпонентной системы появляется поле кристаллизации двойного соединения, расположенное внутри диаграммы (рис.). Оно ограничивается тройной эвтектикой, точкой двойного подъема G и точкой двойного опускания D. Точка состава соединения АтВп лежит вне поля его кристаллизации.
Слайд 136В точке двойного опускания в равновесии с жидкостью находятся три
твердые фазы А, АтВп и В, составы которых располагаются на
одной прямой. Значит, для точки двойного опускания в данном случае нельзя построить элементарный фазовый треугольник и, следовательно, отсутствуют составы, которые заканчивали бы путь кристаллизации в этой точке (фазовый треугольник для этой точки появляется в случае примыкания к ней поля кристаллизации тройного инконгруэнтного соединения, см. ниже). Соединительная прямая АтВп—С разбивает диаграмму на два фазовых треугольника, соответствующих тройным точкам G и Е.
Слайд 137В точке двойного опускания при охлаждении идёт химическая реакция между
ранее выделившимися кристаллическими фазами А и В в присутствии остаточной
жидкой фазы с образованием соединения АтВп.
Если в результате реакции компонент А исчезает полностью, а В — частично, то далее кристаллизация будет осуществляться по пограничной кривой DE, и, наоборот, если в избытке окажется компонент А, а В исчезнет, то пути кристаллизации будут следовать по кривой DG.
Поэтому для определения вероятного направления пути кристаллизации после точки D необходимо знать состав всего твердого вещества, выделившегося до прихода в точку D.
Слайд 138Но возможно также графическое определение вероятного пути кристаллизации после точки
D. Для этого точку двойного опускания соединяют с точкой состава
исходной смеси и продолжают до пересечения со стороной А—АтВn-В.
Если точка пересечения лежит между А и АтВп, то путь кристаллизации пойдет по пограничной кривой DG, равновесной но отношению к А и АтВп, а если эта точка оказывается между АтВп и В — по кривой DE.
Слайд 139Трехкомпонентная система с двойным химическим соединением,
разлагающимся в твердом виде
Для
расплава а
расплав → А + ж.ф. → А +
В + ж.ф. → (в точке D): А (исчезает) + В (частично исчезает) +АтВп (образуется) + ж.ф. → В + АтВп + ж.ф. → (в точке Е): В + АтВп + С+ ж.ф. → В + АтВп + С.
Для расплава b
расплав → А + ж.ф. → А (исчезает) + АтВп (образуется) + ж.ф. → АтВn + ж.ф. → АтВп + С + ж.ф. → (в точке Е): АтВп + С + В + ж.ф. → АтВп + С + В
Слайд 140Определение точки, в которой путь кристаллизации покидает инконгруэнтную пограничную кривую
(точки окончания химической реакции на инконгруэнтной кривой)
Чтобы определить, сойдет ли
путь кристаллизации с инконгруэнтной пограничной кривой, а если сойдет, то в какой ее точке, необходимо соединить прямой линией точку состава исходного расплава с точкой состава того соединения, которое выделяется в результате реакции, и продолжить эту прямую в направлении указанной пограничной прямой.
Если эта прямая не пересекает пограничную кривую, путь кристаллизации с нее не сойдет и будет продолжаться до ближайшей тройной точки. Если же эта прямая пересекает пограничную кривую, то в точке пересечения путь кристаллизации покинет пограничную кривую и пойдет по продолжению указанной прямой, пересекая поле первичной кристаллизации соединения, выделяющегося в результате реакции на этой пограничной кривой.
Слайд 141Для расплава состава а1 (рис) путь кристаллизации, можно условно изобразить
следующей схемой: a1fG1dE, он не сойдет с инконгруэнтной кривой G1G2,
поскольку продолжение прямой ABC—а1 соединяющей точку состава исходного расплава а1 и точку состава соединения ABC, кристаллизующегося в результате реакции:
А + жидкая фаза АBC, не пересекает указанную кривую.
Для расплава состава точки а2 путь кристаллизации, который условно можно изобразить схемой: a2bcdE, сойдет с пограничной кривой G1G2 в точке с, поскольку в этой точке продолжение прямой ABC—a2 пересекает эту пограничную кривую, и пойдет по продолжению cd этой прямой, пересекая поле первичной кристаллизации соединения ABC.
Слайд 142Определение характера пограничных кривых
Для определения характера пограничной кривой (конгруэнтная или
инконгру-энтная) на каком-либо ее участке необходимо в точках, ограничивающих этот
участок, провести касательные в этой кривой. Если эти касательные пересекают соответствующую соединительную прямую, соединяющую точки состава твердых фаз, находящихся в равновесии вдоль этой пограничной кривой, то она будет на данном участке конгруэнтной, а если не пересекает — инконгруэнтной.
Слайд 143На рис. представлен тип трехкомпонентной диаграммы состояния с бинарным химическим
соединением (АС), разлагающимся при нагревании в твердом состоянии, на которой
иллюстрируется правило определения характера пограничных кривых.
Пограничная кривая GE1, вдоль которой в равновесии находятся соединения А и АС, на участке Е1n будет иметь конгруэнтный характер, поскольку все касательные, проведенные к кривой из любой точки этого участка, пересекают соответствующую этой кривой соединительную прямую А—АС (совпадающую в данном случае с участком стороны треугольника концентраций).
Слайд 144На участке же nG пограничная кривая будет инконгруэнтной, поскольку касательные,
проведенные к точкам этого участка, не будут пересекать соответствующую соединительную
прямую А—АС.
Из рис. видно, что точку n на пограничной кривой, разделяющую ее конгруэнтный и инконгруэнтный участки, можно найти, проведя к пограничной кривой касательную (АС—n) из конца соответствующей соединительной прямой, т.е. из точки АС, отвечающей составу одного из соединений, образующих данную соединительную прямую
Слайд 145Определение характера процесса,
происходящего при изменении температуры вдоль пограничных кривых
При
движении фигуративной точки по конгруэнтной пограничной кривой при охлаждении расплава
происходит физический процесс совместной кристаллизации двух фаз — кристаллов соединений, поля первичной кристаллизации которых разделяет эта пограничная кривая.
Например (рис.), при понижении температуры на конгруэнтном участке Е1n пограничной кривой E1G происходит совместная кристаллизация соединений А и АС, а при повышении температуры — плавление этих соединений.
Слайд 146На инконгруэнтных пограничных кривых при охлаждении расплава происходит химическая реакция
взаимодействия жидкой фазы (ее состав определяют точки этой кривой) с
одной из двух кристаллических фаз, поля первичной кристаллизации которых разделяет эта кривая, а именно, с ранее выпавшими кристаллами того соединения, точка состава которого лежит дальше от касательных, проведенных к этой кривой.
В результате этой реакции кристаллы реагирующего соединения полностью или частично исчезают, растворяясь в жидкости, а второе соединение, которое находится в равновесии вдоль этой пограничной кривой и точка состава которого находится ближе к указанным касательным, кристаллизуется из расплава.
Слайд 147Например (рис), на инконгруэнтном участке nG пограничной кривой E1G, на
которой в равновесии с жидкой фазой находятся соединения А и
АС, при охлаждении расплава происходит реакция взаимодействия с жидкой фазой соединения А (его точка состава лежит дальше от касательных, проведенных к этому участку кривой, по сравнению с точкой состава второго соединения АС). В результате этой реакции кристаллы соединения А полностью или частично исчезают, а кристаллы второго соединения АС выделяются из расплава. Указанную реакцию можно схематически изобразить следующим образом:
А + Жидкая фаза АС
При повышении температуры реакция пойдет в обратном направлении, т.е. кристаллы соединения АС будут разлагаться на жидкость и кристаллы А:
АС А + Жидкая фаза
Слайд 148Пути кристаллизации в системах с переменным характером пограничных кривых
Состав M,
лежащий в области DE1U, начинает кристаллизацию выделением D.
На участке
пограничной кривой bU кристаллизуется эвтектика A + D, а на участке UG – протекает перитектическая реакция:
L + D A.
Кристаллизация заканчивается в точке G перитектической реакцией: L + A D + C, в которой происходит частичное растворение уже не фазы A, так как нисходящая от точки G эвтектическая линия уходит из поля A.
Конечные продукты кристаллизации фазы – A, D и C. Кривая охлаждения расплава M приведена на рис. б.
На участке b–U и U–G система моновариантна, но на кривой охлаждения в точке перехода процесса из эвтектического в перитектический отмечается перегиб – изменение скорости охлаждения, поскольку энергетическая емкость процессов различна.
Слайд 149На рис. изображена диаграмма состояния системы с двойным химическим соединением
D, плавящимся с разложением, и пограничной кривой UEt, переходящей из
перитектической в эвтектическую.
Точкой перехода является точка K – точка контакта касательной к линии UEt прямой, исходящей из точки D. На участке UK протекает перитектическая реакция, в которой растворяющейся фазой является A.
Пути кристаллизации составов данной системы не отличаются от ранее рассмотренных.
Так, при кристаллизации состава M первоначально выделяется фаза A. На участке пограничной кривой aK проходит перитектическая реакция: L + A D. Она заканчивается в точке K, хотя фаза A еще остается.
На участке KEt кристаллизуется эвтектика A + D. Кристаллизация заканчивается в точке Et выделением тройной эвтектики
Слайд 150Определение характера процесса, происходящего
в тройной точке
В точке эвтектики при
отнятии от системы теплоты при постоянной температуре (система инвариантна), отвечающей
этой точке, происходит физический процесс одновременной кристаллизации из жидкой фазы состава этой точки трех соединений, поля первичной кристаллизации которых сходятся в этой точке.
В точке двойного подъема при отнятии теплоты при постоянной температуре (система инвариантна), отвечающей этой точке, происходит химическая реакция взаимодействия жидкой фазы состава этой точки с одним из трех находящихся в равновесии с расплавом в этой точке кристаллических соединений. В результате этой реакции реагирующее соединение полностью или частично исчезает, а два других соединения кристаллизуются из расплава. С жидкостью взаимодействует то соединение, от поля первичной кристаллизации которого отходит единственная пограничная кривая с падающей от точки двойного подъема температурой, а два других соединения, находящихся в равновесии с жидкостью вдоль указанной пограничной кривой, кристаллизуются из расплава.
Слайд 151При этом в процессе охлаждения возможны следующие варианты:
1) исчезает
одна жидкая фаза — при этом кристаллизация в точке двойного
подъема закончится и конечными продуктами будут три кристаллические фазы, поля первичной кристаллизации которых сходятся в этой точке;
2) исчезает одна кристаллическая фаза — соединение, реагирующее с жидкостью, при этом кристаллизация при охлаждении продолжится дальше и путь кристаллизации уйдет из точки двойного подъема;
3) исчезают одновременно две фазы — жидкая и одна твердая (соединение, реагирующее с жидкостью) — при этом кристаллизация в точке двойного подъема закончится и конечными продуктами будут две кристаллические фазы, находящиеся в равновесии вдоль единственной пограничной кривой с падающей от точки двойного подъема температурой (этот частный случай имеет место, когда точка исходного состава попадает на соединительную прямую, соответствующую указанной пограничной кривой, т.е. в частную двойную систему).
Слайд 152В точке двойного опускания при постоянной температуре, отвечающей этой точке,
происходит химическая реакция взаимодействия жидкой фазы состава этой точки с
двумя из трех кристаллических соединений, находящихся в равновесии в этой точке, в результате чего эти реагирующие соединения полностью или частично исчезают, а третье соединение кристаллизуется из расплава. С жидкостью взаимодействуют те два соединения, которые находятся в равновесии с жидкостью вдоль единственной пограничной кривой с падающей к точке двойного опускания температурой, а выделяется из расплава то соединение, поле первичной кристаллизации которого граничит с двумя пограничными кривыми с падающей от точки двойного опускания температурой. При нагревании процесс идет в обратном направлении.
Слайд 153При этом возможны варианты:
1) исчезает одна жидкая фаза — при
этом кристаллизация в точке двойного опускания закончится и конечными продуктами
будут три кристаллические фазы — соединения, поля первичной кристаллизации которых сходятся в этой точке;
2) полностью исчезает одна из двух реагирующих с жидкостью кристаллических фаз — при этом путь кристаллизации продолжится дальше и уйдет из точки двойного опускания по одной из двух пограничных кривых с падающей от точки температурой;
3) исчезают одновременно и полностью две фазы — жидкая и одна из реагирующих с ней твердых фаз — при этом кристаллизация в точке двойного опускания заканчивается и конечными продуктами будут две оставшиеся кристаллические фазы (этот частный случай имеет место, когда точка состава исходного расплава попадает на соединительную прямую, т.е. в частную двойную систему, причем конечными продуктами кристаллизации будут именно те соединения, точки состава которых соединяет эта соединительная прямая);
4) исчезают одновременно и полностью три фазы (жидкая и реагирующие с ней две твердые фазы) — кристаллизация в точке двойного опускания заканчивается и конечным продуктом будет одна кристаллическая фаза — соединение, поле первичной кристаллизации которого граничит с двумя пограничными кривыми с падающей от точки температурой (это имеет место, когда точка состава исходного расплава точно соответствует составу тройного соединения в данной системе).

Слайд 154Определение дальнейшего пути кристаллизации из точки двойного опускания
Сначала находят две
соединительные прямые, соответствующие двум пограничным кривым с падающей от точки
двойного опускания температурой. Затем соединяют прямой линией точку двойного опускания и точку состава исходного расплава и определяют, какую из двух указанных соединительных прямых пересекает продолжение этой прямой. Дальнейший путь кристаллизации пойдет по той пограничной кривой, которой соответствует именно эта соединительная прямая, т.е. по той пограничной кривой, вдоль которой в равновесии находятся соединения, точки составов которых соединяет эта прямая.
Слайд 155Например (рис), предположим, что путь кристаллизации исходного расплава а3 дошел
до точки двойного опускания G2 и должен продолжиться дальше по
одной из двух пограничных кривых (G2G1 или G2E) с падающей от точки температурой. Находим две соединительные прямые, соответствующие этим пограничным кривым: кривой G2G1 соответствует соединительная прямая А—ABC, а кривой G2E — прямая ABC—С.
Соединяем прямой линией точку двойного опускания G2 с точкой состава исходного расплава — а3, продолжаем эту линию и находим, что она пересекает (в точке т) соединительную прямую А—ABC, соединяющую точки составов соединений А и ABC.
Отсюда следует, что дальнейший путь кристаллизации из точки двойного опускания пойдет по пограничной кривой G2G1 вдоль которой в равновесии находятся именно эти соединения, т.е. в результате реакции в точке двойного опускания полностью исчезнет соединение С, а соединение А частично останется.
Слайд 156Если же исходный расплав соответствует точке а4, то путь кристаллизации
из точки двойного опускания G2 пойдет по пограничной кривой G2E,
так как продолжение прямой линии, соединяющей точки G2 и а4, пересекает (в точке n) соединительную прямую ABC—С.
Слайд 157Система с полиморфными превращениями компонентов и ликвацией
При наличии у одного
из компонентов полиморфных превращений на диаграмме состояния трёхкомпонентной системы появляются
линии полиморфных превращений.
Они совпадают с изотермами, соответствующими температурам полиморфных превращений.
Так как на проекционной диаграмме тройной системы изображаются только те процессы, которые проявляются на поверхности ликвидуса, то на диаграмму состояния наносятся лишь изотермы полиморфных превращений, протекающих в присутствии жидкой фазы, т.е. на диаграмме показанны (рис.) полиморфные превращения компонента относящиеся к надсолидусной области.
В трехкомпонентной системе часто наблюдается расслоение в жидкой фазе.
Слайд 158На диаграмме (рис.) двухкомпонентная система ВС имеет область ликвации be,
прилегающую к вершине В.
С повышением температуры область ликвации трехкомпонентной системы
постепенно уменьшается и образуется объемный купол ликвации. Верхняя точка купола называется критической (по температуре). Выше этой точки жидкость не расслаивается.
На проекционной диаграмме изображается только линия пересечения куполом ликвации поверхности ликвидуса — линия скb, соответствующая изотермической плоскости. Она ограничивает ту область трехкомпонентных составов, которые расслаиваются в жидком состоянии, и называется бинодальной кривой. Составы сосуществующих фаз определяются точками пересечения коннод с данной кривой.
Слайд 159Если ликвация наблюдается не в одной, а в двух частных
двойных системах, то в этом случае возможно слияние двух областей
ликвации (если области ликвации примыкают к одной вершине). Такая общая область ликвации abcd в поле кристаллизации компонента В представлена на рис.
Составы сосуществующих фаз перемещаются с изменением температуры по линиям ab (обогащенная компонентом В) и dc (обедненная компонентом В). Между ними располагаются конноды, показывающие своими концами составы пар равновесных жидкостей.
Составы, точки которых лежат на одной конноде, разделяются на одни и те же фазы. Составы жидкостей в любой момент кристаллизации определяются концами той конноды, которую пересекает путь кристаллизации, построенный для исходной смеси.
Слайд 160В трехкомпонентных системах широко распространены явления метастабильной ликвации, развивающиеся в
переохлажденных расплавах в подликвидусиой части диаграмм состояния. Области метастабильной ликвации
могут простираться под куполом стабильной ликвации, являясь его продолжением ниже поверхности ликвидуса, но могут образовывать и самостоятельные подликвидусные или подсолидусные купола при отсутствии стабильной ликвации.
Примером такой диаграммы состояния с подликвидусной метастабильной ликвацией может служить диаграмма, приведенная на рис.. На ней изображены изотермы, получающиеся при пересечении купола метастабильной ликвации изотермическими плоскостями. Конноды, пересекающие разрезы купола ликвации, указывают на составы сосуществующих жидкостей.
Слайд 161Трехкомпонентная система с тройным химическим соединением,
плавящимся конгруэнтно
Если тройное соединение
(обозначим его АтВпСр) плавится без разложения, то на диаграмме состояния
появляется его поле кристаллизации, ограниченное тремя тройными эвтектиками Е1, Е2 и Е3 (рис.), а точка состава соединения АтВпСр (точка М) лежит в пределах своего поля кристаллизации. Соединительные прямые А-М, В-М и С- М делят эту диаграмму на три простейшие, из которых каждая имеет одну тройную эвтектику. Точки пересечения соединительных прямых А-М, В-М и С-М с пограничными кривыми Е1Е2, Е2Е3 и Е1Е3 отвечают температурным максимумам, и поэтому температуры падают по обе стороны отточек пересечения.
Составы, попадающие в элементарный фазовый треугольник А-М-В, закончат кристаллизацию в точке Е2 составы треугольника В-М-С - в точке Е3, и составы треугольника С-М-А - в точке Е1.
Слайд 162В поле кристаллизации соединения АтВпСр пути кристаллизации составов идут по
прямым, исходящим из точки М.
Состав, соответствующий точке а, при охлаждении
вначале выделит компонент С. Затем на пограничной кривой совместно с кристаллами С появится вторая твердая фаза А. В точке Е1 расплав полностью закристаллизуется с выделением фаз С, А и АтВпСр.
Составы, лежащие на соединительных прямых, будут относиться к истинным двойным системам. Поэтому их пути кристаллизации закончатся непосредственно на соединительных прямых в точках пересечения последних с пограничными кривыми, т.е. в точках температурных максимумов на пограничных кривых. Конечными фазами таких составов будут кристаллы лишь двух типов: соединения АтВпСр и одного из исходных компонентов.
Слайд 163Трехкомпонентная система с тройным химическим соединением,
плавящимся инконгруэнтно
На рис.
показана диаграмма состояния трехкомпонентной системы с тройным химическим соединением АтВпСр,
плавящимся с разложением. Соединение имеет внутри диаграммы свое поле кристаллизации, заключенное между двумя тройными эвтектиками Е1 и Е2 и точкой двойного подъема G. Точка М, отвечающая составу соединения АтВпСр, лежит за пределами его поля кристаллизации.
Так как точка М находится в поле устойчивости компонента А, то пограничная кривая E1G, разделяющая поля кристаллизации фаз А и АтВпСр, является инконгруэнтной. На этой кривой будет происходить реакция между ранее выделившимися кристаллами А и остаточной жидкой фазой с образованием соединения АтВпСр.
Слайд 164Соединительные прямые А—М, В—М, С—М разбивают диаграмму на три элементарных
фазовых треугольника, из которых два имеют тройную эвтектику, а третий
относится к точке двойного подъема, лежащей вне своего фазового треугольника. Пограничные кривые Е1G и E1E2 имеют температурные максимумы в точках пересечения с ними соединительных прямых А—М (продолжение ее) и С-М. Поэтому температуры падают по обе стороны от точек пересечения к точкам G и Е1 (кривая GE1), E1 и Е2 (кривая Е1Е2). У третьей пограничной кривой GE2 температурного максимума нет, и температуры вдоль нее падают от точки G к точке Е2.
В поле кристаллизации АтВпСр пути кристаллизации пойдут по прямым, исходящим из точки М, и закончатся в точке Е2 либо Е1, в зависимости от того, лежит ли точка состава исходной смеси в фазовом треугольнике С—М—В или С—М—А.
Слайд 165Точка а находится в поле кристаллизации компонента А и лежит
в элементарном фазовом треугольнике А—М—В. Следовательно, первичной кристаллической фазой будет
компонент А, а конечной точкой затвердевания расплава - точка G. Схема фазовых превращений для точки а будет выглядеть так:
расплав → А + ж.ф. → А + В + ж.ф. → (в точке G): А (частично растворяется) + В + АтВпСр (образуется) + ж.ф. → А + В + АтВпСр.
Состав точки b, первичной кристаллической фазой будут кристаллы В. Путь кристаллизации по продолжению линии Вb попадает в точку двойного подъема G. В этой точке кристаллы В находятся в равновесии с соединением АтВпСр и незначительным количеством кристаллов А в присутствии остаточной жидкой фазы. Кристаллы А практически сразу расходуются на реакцию образования химического соединения АтВпСр. Далее путь кристаллизации проследует по пограничной кривой GE2 в точку E2. Конечными твердыми фазами будут B АтВпСр и С.
Слайд 166Значительно сложнее протекают процессы кристаллизации составов, заключенных между пограничной кривой
Е1G и точкой состава соединения М. Они лежат в поле
кристаллизации компонента A. Однако количества кристаллов А, выделившихся до прихода пути кристаллизации на инконгруэнтную пограничную кривую E1G, не хватает для протекания реакции на всем протяжении пограничной кривой, и путь кристаллизации покидает эту кривую.
Так, для состава с путь кристаллизации вначале идет по продолжению линии Ас (выделяются кристаллы А), затем по пограничной кривой Е1G вверх до точки пересечения пограничной кривой с линией Мс (выделяются кристаллы АтВпСр, а кристаллы А исчезают) и по продолжению линии Мс через поле АтВпСр к пограничной кривой GE2. Проследовав по кривой GE2, путь кристаллизации закончится в точке Е2. Значит, для точки с схему фазовых превращений при охлаждении можно показать так:
расплав → А + ж.ф. → А (растворяется) + АтВпСр (образуется) + ж.ф. → АтВпСр + ж.ф. → АтВпСр + В + ж.ф, → (в точке Е2): АтВпСр + В+С + ж.ф.→АтВпСр +В+С
Слайд 167трёхкомпонентной системы с тройным химическим соединением,
плавящимся инконгруэнтно (тип II)
На
ней поле кристаллизации тройного соединения ограничено точками эвтектики, двойного подъема
и двойного опускания. Последняя в этом случае имеет свой элементарный фазовый треугольник, все составы которого заканчивают кристаллизацию в точке D.
В процессе кристаллизации в точке двойного опускания протекает реакция между двумя твердыми фазами А и С и жидкой фазой с образованием соединения М (т.е. А + С + жидкая фаза → М) и возможны следующие варианты:
- исчезает одна жидкая фаза, при этом кристаллизация закончится в точке двойного опускания (G);
- полностью исчезает одна из двух реагирующих с жидкостью кристаллических фаз, тогда путь кристаллизации пойдет дальше по одной из пограничных кривых с падающей от точки температурой;
Слайд 168- исчезают одновременно и полностью две фазы — жидкая и
одна из твердых, при этом кристаллизация закончится в точке двойного
опускания (G или E), а конечными продуктами кристаллизации будут две оставшиеся твердые фазы (исходный состав в этом случае лежит на соединительной прямой);
- исчезают одновременно и полностью три фазы — жидкая и две реагирующие с ней твердые фазы, кристаллизация в этом случае заканчивается в точке двойного опускания (G или E) с выделением одной кристаллической фазы — тройного соединения (точка исходного состава соответствует точке тройного соединения)
Слайд 169Трехкомпонентная система с твердыми растворами
При образовании в одной из частных
двойных систем непрерывного ряда твердых растворов трехкомпонентная система не будет
иметь тройной эвтектики. Есть только эвтектическая линия между двумя двойными эвтектиками, образованными составляющими твердого раствора с третьим компонентом.
На рис. 1 показана пространственная диаграмма системы, у которой компоненты А и С неограниченно растворимы друг в друге в твердом состоянии. На поверхности ликвидуса имеется единственная пограничная кривая Е1Е2 которая проектируется на основание призмы (рис. 2).
Слайд 170В чистом виде выделяется лишь компонент В. Поле его кристаллизации
- область ВЕ1Е2 (рис. 2). Вторая часть диаграммы – Е1САЕ2
— относится к области составов, выделяющих при кристаллизации в качестве первичной фазы твердые растворы SAC. Компоненты А и С выделяются при кристаллизации тройных смесей только в виде твердого раствора.
На пограничной линии Е1Е2 в равновесии с жидкостью будут находиться кристаллы компонента В и твердого раствора SAC.
Конечный состав кристаллизующегося твердого раствора имеет то же соотношение компонентов А и С, что и исходная смесь. Поэтому точки составов исходной смеси и выделяющегося при полной кристаллизации твердого раствора будут лежать на одной прямой, исходящей из вершины В.
Слайд 171Для состава т соединяя вершину В и продолжая прямую до
пересечения со стороной треугольника АС, находим состав конечных твердых растворов
S1 (по правилу рычага из соотношения отрезков, отсекаемых линией Вт на стороне АС).
Между стороной АС и пограничной кривой Е1Е2 наносятся конноды, указывающие своими концами конечные составы сосуществующих фаз соответственно твердого раствора и жидкости (для состава т – S1 и l1). Конец пути кристаллизации состава т будет в точке пересечения пограничной линии с коннодой, проведенной через точку конечного состава твердого раствора, т.е. в точке 11. Однако построение всего пути кристаллизации для точки т возможно лишь в том случае, если на диаграмме нанесены линии изменения состава жидкой фазы при кристаллизации.
Слайд 172Поскольку состав твердого раствора, выделяющегося из расплава т в процессе
кристаллизации, все время меняется, т.е. состав первичной твердой фазы не
остается постоянным, то не сохраняется и постоянство соотношения А и С в твердом растворе. Поэтому путь кристаллизации не может идти по линии, соединяющей составы конечного твердого раствора и исходной смеси. Линии изменения состава жидкой фазы наносятся на диаграмму по экспериментальным данным (см. кривые линии в поле кристаллизации твердых растворов SAC).
Возможное направление для пути кристаллизации состава т показано кривой ml1'. В точке l1' начинается совместное выделение кристаллов В и твердого раствора SAC точке l1 кристаллизация закончится. Фазовые превращения расплава состава т при охлаждении идут по схеме:
расплав → SAC + ж.ф. →+SAC+ B + ж.ф. → SAC + В.
Слайд 173Состав n лежит в поле кристаллизации компонента В поэтому первыми
при охлаждении расплава появятся кристаллы В. Путь кристаллизации расплава n
пойдет по продолжению линии Вn, а затем по пограничной кривой Е1Е2. Для определения конечной точки затвердевания расплава нужно найти конноду, проходящую через точку S4. Эта точка соответствует составу конечного твердого раствора, выделяющегося при кристаллизации расплава n, и получается пересечением прямой Вn со стороной АС.
Второй конец конноды S4l4 указывает конечную точку нуги кристаллизации расплава n.
Как и для состава т, в результате полной кристаллизации расплава n выделяются две фазы — В и SAC.
Слайд 174Следует отметить, что в сложных трехкомпонентных системах, характеризующихся наличием нескольких
химических соединений и имеющих значительное количество полей кристаллизации, нанесение полей
твердых растворов представляет большие трудности. Поэтому для удобства фазы, образующие между собой твердые растворы, соединяются только прямой линией, частично или полностью заштрихованной в зависимости от того, является ли ряд твердых растворов ограниченным или непрерывным.
Слайд 175Расчёт количества и состава фаз по тройным диаграммам
Найти соотношение между
равновесными фазами при охлаждении исходного расплава точка m, рис) до
температуры, определяемой изотермами t2, t3, и к моменту прихода пути кристаллизации точке эвтектики Е
Решение Точка т находится в поле кристаллизации фазы А, кристаллы которой выделяются в качестве первых при охлаждении расплава. Путь кристаллизации будет следовать по продолжению прямой, проходящей через точку составов фазы А и исходного расплава т до сечения с пограничной кривой ЕЕ'. При этом изотерма t2 пересекается в точке р, соответствующей составу остаточной жидкой фазы при температуре t2. Таким образом, из исходного расплава состава m при температуре t2 выделится две фазы: твёрдая А и жидкая состава р. Точки составов всёх трёх указанных фаз лежат на одной прямой Ар, а количественное соотношение между равновесными фазами согласно правилу рычага можно выразить соотношениями:
,
где хА и хЖ – содержание твёрдой фазы (кристаллов А) и остаточного расплава р, образовавшихся при температуре t2 из исходного расплава, соответственно, %.

Слайд 176При температуре t3 состав остаточной жидкой фазы соответствует точке пересечения
пути кристаллизации с изотермой t3 (точка l). В равновесии с
жидкой фазой в этот момент находятся кристаллы двух твёрдых фаз А и С. Суммарный состав твёрдой фазы, выделившейся к настоящему моменту, определяется точкой к, которая лежит на пересечении соединительной прямой АС, с продолжением прямой, соединяющей точки l и m. Содержание равновесных твёрдых и жидкой фаз (%) можно рассчитать по правилу рычага следующими соотношениями:
где хТв и хЖ – количество равновесных твёрдой (А + С) и жидкой (состава l) фаз при температуре t3, %.
В свою очередь твёрдая фаза состоит из кристаллических фаз А и С. Точка к делит линию АС на отрезки кА и кС, обратное соотношение между которыми пропорционально доле каждой из фаз: хА/хС = кС/АК. Следовательно
Слайд 177Аналогично определяются количественные соотношения между равновесными фазами в момент прихода
пути кристаллизации в тройную точку системы (рис. точка Е) до
начала кристаллизации эвтектики или появления третьей твердой фазы.
При этом суммарный состав выделившихся кристаллов в ходе охлаждения расплава М будет определяться точкой s, а фазовые соотношения – системой уравнений:
хЖ = (mk/kE) 100 %
xA = (sC/AC) (100-xЖ)
xC = (sA /AC) (100 – хЖ)
Во всех примерах устанавливается общее суммарное содержание кристаллических фаз, выделившихся с начала кристаллизации до заданной температуры.
Слайд 178Аналитический метод расчёта фазового состава
Рассмотрим наиболее общий случай, когда
исходный состав распадается на три фазы, каждая из которых содержит
все три компонента. Пусть процентное содержание компонентов A, B и C в исходном составе составляет соответственно a, b и c, содержание их в первой фазе, образовавшейся из исходного состава – a1, b1 и c1, во второй фазе – a2, b2 и c2 и в третьей фазе – a3, b3 и c3.
Примем массу исходного состав равным 100%, массу, образовавшейся из него первой фазы – X, второй – Y%. Тогда масса третьей фазы составит 100 – (X + Y), %.
Составим уравнение баланса по двум компонентам, например, по A и B. содержание компонентов A в % составляет: в исходном составе – a;
в первой фазе – ; во второй фазе – ;
в третьей фазе – .
Но .
Аналогично для компонента B получаем:
.
Удобнее этими уравнениями баланса пользоваться в таком виде:
100a = Xa1 + Ya2 + (100 – X – Y)a3;
100b = Xb1 + Yb2 + (100 – X – Y)b3.
Решение системы этих двух уравнений позволяет определить две неизвестные величины. Это или количество двух фаз, или содержание двух компонентов в фазе. Третья величина определяется по разности между 100 и суммой двух известных.

Слайд 179Определение количественного соотношения твердых фаз, выделяющихся из расплава в данный
момент кристаллизации
Количественное соотношение двух твердых фаз, кристаллизующихся из расплава при
его охлаждении вдоль конгруэнтной пограничной кривой, в общем случае не остается постоянным, а изменяется (постоянным это соотношение будет только в том случае, если пограничная линия является прямой).
Для определения указанного соотношения в каждый данный момент кристаллизации, т.е. при данных температуре и составе расплава, необходимо к пограничной кривой в точке, соответствующей этой температуре, провести касательную и продолжить ее до пересечения с соответствующей этой кривой соединительной линией. Точки пересечения делит соединительную линию на отрезки, длины которых (в обратной пропорциональности) будут характеризовать соотношение двух выделяющихся при кристаллизации твердых фаз.
Слайд 180Например (рис.), для определения количественного соотношения кристаллов АС и В,
выделяющихся при температуре t3 из расплава состава точки n, лежащей
на конгруэнтной пограничной кривой Е1Е2, проводим в точке n к этой кривой касательную и продолжаем ее до пересечения с соответствующей этой кривой соединительной линией АС— В (точка к').
Количественное соотношение выделяющихся твердых фаз определяем из выражения
Слайд 181ЧЕТЫРЕХКОМПОНЕНТНЫ СИСТЕМЫ
В соответствии с правилом фаз максимальное число степеней свободы
конденсированной четырехкомпонентной системы fмакс при минимальном числе присутствующих в ней
фаз pмин = 1 составляет:
fмакс = К+1-р = 4+1-1 = 4.
При этом в качестве четырех независимых параметров, отвечающих числу fмакс и оказывающих влияние на равновесие в системе, выступают температура и концентрации трех компонентов х1, х2, x3 (концентрацию четвертого компонента находят по разности 100 —х1— х2 — х3).
Для отображения концентраций на четырехкомпонентных диаграммах состояния используется концентрационный тетраэдр, представляющий собой правильную пирамиду с четырьмя плоскими гранями в виде равносторонних треугольников (рис.).
Слайд 182Специальная ось координат для отображения значений температуры на четырехкомпонентных диаграммах
состояния отсутствует, поскольку она должна была бы располагаться в четырехмерном
пространстве, которое на плоском чертеже отобразить невозможно.
Поэтому на таких диаграммах обычно указываются лишь цифровые индексы, отвечающие температурам в инвариантных точках системы и температурам плавления отдельных компонентов (или образующихся соединений). Иногда на эти диаграммы также наносятся индексированные линии изотерм, на которых указывается значение температуры ликвидуса, соответствующее данной изотерме
Слайд 183Изображение четырехкомпонентных систем
Для изображения четырехкомпонентных систем применяется правильный четырехугольник
– тетраэдр. Вершины тетраэдра соответствуют четырем компонентам системы; ребра –
шести двойным системам; четыре грани тетраэдра – трехкомпонентным системам.
Основными элементами диаграммы состояния четырехкомпонентной системы (рис.) являются:
– объемы кристаллизации отдельных компонентов или химических соединений, в пределах которого находится одна кристаллическая фаза в равновесии с жидкой фазой:
Слайд 184– поверхности, ограничивающие смежные объемы двух компонентов (химических соединений), находящихся
в равновесии с жидкой фазой;
– пограничные кривые пересечения трех поверхностей,
являющиеся общим местом объемов кристаллизации трех фаз и жидкой фазы, находящейся в равновесии с тремя кристаллами. Нонвариантными точками в четырехкомпонентных системах являются точки пересечения четырех пограничных кривых. Эти точки могут быть как эвтектическими, так и неэвтектическими.
Специальная ось координат для отображения значений температуры на четырехкомпонентных системах отсутствует ввиду сложности изображения на плоском чертеже.
Слайд 185Основные свойства концентрационного тетраэдра
В плоскости, параллельной некоторой стороне тетраэдра, расположены
все составы с постоянным содержанием одного компонента. В плоскости S
это компонент D.
В плоскости, проходящей через две вершины, лежат все составы, в которых оставшиеся компоненты постоянны. Например, в плоскости, проходящей через вершины A и D соотношение компонентов C:B постоянно.
На прямой, проходящей через некоторую вершину тетраэдра, отношение оставшихся трех компонентов постоянно. Например, на прямой U, проходящей через вершину A, отношение компонентов B:C:D постоянно.
Слайд 186Из тройных составов P и Q можно смешением получить все
составы, лежащие на прямой, соединяющей обе точки. Состав R найден
смешением составов P и Q в соотношении отрезков RQ:RP.
Из трех составов, если их составы не лежат на одной прямой, можно смешением получить составы, лежащие внутри треугольника.
Их четырех смесей можно смешением получить составы, лежащие внутри тетраэдра с вершиной данными сложением четырех исходных составов.
Слайд 187Так как пространственное изображение равновесия в четырехкомпонентной системе является сложным
и неудобным, часто используют для изучения разрезы, проводя их так,
чтобы они отвечали постоянному содержанию одного из компонентов (рис. а) или постоянному отношению двух компонентов (рис. b).
В некоторых случаях выгодным является провести разрез так, что его вершины образуют двойное или тройное химическое соединение с конгруэнтной точкой плавления (рис. с).
Способы изображения составов в четырехкомпонентных системах
Слайд 188Диаграмма состояния четырехкомпонентной системы
без химических соединений и твердых растворов
Равновесие
твердых и жидкой фаз при постоянной температуре и давлении в
тройной системе указывает линия изотермы. В четырехкомпонентной системе подобной изотермой является поверхность (рис. а) при температуре T1. С падением температуры изотермические поверхности сближаются так, что при T2 они пересекаются.
На линии пересечения существуют в равновесии кристаллы A и B расплавом. Линия пересечения трех поверхностей является точка, в которой при постоянной температуре находятся в равновесии расплав и три твердые фазы.
При T3 в равновесии в точке W находятся кристаллы A, B и C с жидкой фазой. Из рис. следует, что линия пересечения двух изотрем на стороне тетраэдра (эвтектическая точка) продвигается при падении температуры и образует пограничную линию, которая заканчивается в эвтектической точке E
Слайд 189Ход кристаллизации расплава
Ход кристаллизации состава X изображен на рис.
В
пространстве, ограниченном поверхностями A–e1–E1–e2, A–e1–E2–e2, A–e2–E3–e3, которое образуют часть стороны
тетраэдра и граничными плоскостями e2–E3–ε–E1, E1–ε–E2–e1 и e3–E3–ε–E2, будут выпадать кристаллы компонента A. Это пространство отвечает площади ликвидуса в тройной системе, соответственно, линии ликвидуса в бинарной системе. Состав X лежит в этом пространстве, поэтому первыми выпадают кристаллы A. Кристаллизация будет проходить по прямой, соединяющей вершину A и состав расплава X. На этой прямой лежат составы, в которых соотношение B:C:D остается постоянным.
Точка пересечения этой прямой с изотермической поверхностью укажет температуру равновесия. Количество кристаллов A и расплава определяют по правилу рычага. Точка пересечения прямой с поверхностью e2–E3–ε–E1 (точка l1), означает температуру, при которой начнут выпадать кристалл D, одновременно с кристаллами A.
Слайд 190Состав расплава при дальнейшей кристаллизации находится в плоскости, проходящей через
вершины D и A, поэтому отношение C:B в ходе дальнейшей
кристаллизации не меняется. Путь кристаллизации пересекает эту плоскость в точках A, D, X с плоскостью e2–E3–ε–E1 (линия l1–l2, рис.).
На эвтектической линии E3–ε3 находятся в равновесии кристаллы A, D и C. В точке l2 начнут одновременно с кристаллами A и D выпадать кристаллы C, и кристаллизация продолжается по эвтектической линии до точки ε, где будут находиться в равновесии кристаллы A, D, C и B с расплавом состава ε. Кристаллизация закончится затвердеванием эвтектического расплава.
Слайд 191Пути кристаллизации на диаграмме состояния четырехкомпонентной системы без химических соединений
и твердых растворов
Сформулируем правила рассмотрения путей кристаллизации на многокомпонентной диаграмме
состояния
Правило 1. Твердой фазой, первично кристаллизующейся в пространстве первичной кристаллизации при охлаждении, является та, которой принадлежит данное пространство.
Правило 2. Путь первичной кристаллизации, происходящей в пространстве первичной кристаллизации при охлаждении, проходит по продолжению прямой, соединяющей точку состава кристаллизующейся твердой фазы с точкой состава исходного расплава, а именно от последней до пересечения указанной линии с первым встречающимся элементом строения диаграммы, например пограничной поверхностью или пространственной пограничной кривой.
Правило 3. Кристаллизация, протекающая на пограничной поверхности, сопровождается выделением двух твердых фаз, пространства первичной кристаллизации которых разделены данной пограничной поверхностью. При этом соотношение между кристаллизующимися фазами остается постоянным и таким же, как и в бинарной эвтектике, с точкой которой контактирует данная пограничная поверхность.
Правило 4. Путь кристаллизации на пограничной поверхности проходит в направлении понижения температуры по линии, являющейся следом сечения данной пограничной поверхности плоскостью, проходящей через ребро тетраэдра и точку, в которой первичный путь кристаллизации попадает на данную поверхность.

Слайд 192
Правило 5. Точка бинарной эвтектики, с которой контактирует данная пограничная
поверхность, является для нее температурным максимумом, и температура падает от
указанной точки по линии, отображающей (в соответствии с Правилом 4) путь кристаллизации.
Правило 6. Кристаллизация, протекающая на пространственной пограничной кривой, сопровождается выделением трех твердых фаз, пространства первичной кристаллизации которых примыкают к данной пограничной кривой. При этом соотношение между кристаллизующимися фазами остается постоянным и таким же, как в тройной эвтектике, с точкой которой данная пограничная кривая контактирует на грани тетраэдра диаграммы.
Правило 7. Путь кристаллизации на пространственной пограничной кривой проходит от точки, в которой первичный путь кристаллизации попадает на данную пограничную кривую, в направлении понижения температуры, т.е. к точке четверной эвтектики системы
Слайд 193Пример пути кристаллизации в четырёхкомпонентной системе
Рассмотрим путь кристаллизации расплава состава
а (рис. на котором представлен фрагмент диаграммы состояния четырехкомпонентной системы,
отображающий пространство первичной кристаллизации компонента А).
Первичный путь кристаллизации пойдет по линии am (Правило 1) и будет сопровождаться выделением кристаллов А (Правило 2). В точке m (где первичный путь кристаллизации попадет на пограничную поверхность е4ε2Eε3) начнется одновременное выделение двух твердых фаз (А и В), причем их соотношение при кристаллизации будет оставаться постоянным и таким же, как и в бинарной эвтектике е4 (Правило 3). Дальнейший путь кристаллизации пройдет в направлении падения температуры по линии mn, являющейся следом от сечения поверхности е4ε2Еε3 плоскостью АВn, проходящей через ребро АВ и точку m (Правила 4 и 5), и будет сопровождаться одновременным выделением кристаллов А и B в соотношении, отвечающем эвтектике е4.
Слайд 194В точке n (где путь кристаллизации попадет на пространственную пограничную
кривую ε2Е) начнется одновременная кристаллизация трех твердых фаз (А, В
и С), причем их соотношение будет таким же, как и в тройной эвтектике е2 (Правило 6). Далее путь кристаллизации будет проходить по пространственной пограничной кривой ε2Е в направлении падения температуры от точки n до точки Е (Правило 7), в которой кристаллизация закончится в результате одновременного выделения четырех твердых фаз (А, В, С и D) и исчезновения жидкой фазы.
Слайд 195МЕТОДЫ ПОСТРОЕНИЯ ДИАГРАММ СОСТОЯНИЯ
Построение реальных диаграмм состояния сводится к определению
опытным путем температур фазовых превращений, характера и состава фаз, находящихся
в данной системе в равновесии при различных температурах. Эти исследования производятся различными методами химического и физико-химического анализа — термическим, микроскопическим, электронно-микроскопическим, рентгенографическим, электронографическим, локальным рентгено-спектральным и другими методами анализа. Иногда используют также дилатометрические исследования, изучение электросопротивления, твердости и других свойств материалов.
Правильность построения диаграмм состояния на основе экспериментальных данных контролируется правилом фаз и так называемыми принципами непрерывности и соответствия, сформулированными Н.С. Курнаковым, которым диаграмма не должна противоречить.
Слайд 196Принцип непрерывности заключается в том, что при непрерывном изменении параметров,
определяющих состояние системы, свойства отдельных фаз и системы в целом
изменяются также непрерывно, но при условии, что не изменяется фазовый состав системы, т.е. не возникают новые и не исчезают старые фазы.
Принцип соответствия заключается в том, что каждой фазе или совокупности фаз системы, находящейся в равновесии, соответствует на диаграмме определенный геометрический образ — точка, линия, область.
Наиболее распространенными методами экспериментального построения диаграмм состояния являются динамический метод (метод построения кривых охлаждения или нагревания) и статический метод (метод закалки)
Слайд 197ДИНАМИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ДИАГРАММ СОСТОЯНИЯ
Сущность динамического метода построения диаграмм состояния
состоит в построении методом термического анализа кривых охлаждения (или нагревания)
образцов в координатах температура — время.
Если фазовое превращение сопровождается тепловым эффектом (а практически все фазовые превращения сопровождаются изменением энтальпии системы), то это будет фиксироваться на указанных кривых в зависимости от характера равновесия (числа степеней свободы системы) в виде точки перегиба, указывающей на изменение скорости падения или увеличения температуры при моно- или дивариантном равновесии, либо горизонтальные площадки, указывающие на постоянство температуры при инвариантном равновесии.
Слайд 198СТАТИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ДИАГРАММ СОСТОЯНИЯ
Принцип этого метода заключается в фиксации
равновесных при данной температуре фаз в системе и последующего определения
их состава и содержания в системе. Метод состоит из следующих операций.
Сначала изготовляют смеси компонентов исследуемой системы различного состава. Небольшая навеска (обычно до 0,5 г) порошка данной смеси завертывается в платиновую фольгу, помещается в печь и выдерживается при заданной температуре до установления равновесия.. Описанная операция называется отжигом.
Вторая операция называется закалкой. Образец после выдержки при заданной температуре резко охлаждается. При резком охлаждении происходит фиксация того состояния, в котором образец находился при температуре выдержки, т.е. кристаллические фазы, если они есть, фиксируются («замораживаются») в таком виде и количестве, в каком они находились при температуре выдержки, а жидкая фаза застывает в стеклообразном состоянии.
Слайд 199Третьей операцией является определение состава и содержания фаз в закаленном
образце. Это производится обычно с помощью методов микроскопического, рентгенографического анализов
или другими методами.
Каждая смесь подвергается закалке от различных температур. Если, например, в смеси состава 1 (рис.), закаленной от температур t1 и t2, обнаружена только стекловидная фаза, то это означает, что кристаллизация расплава при температуре выдержки еще не началась и эта температура лежит выше температуры ликвидуса.
Тогда выдерживают эту же смесь при более низкой температуре, например t4. Если в закаленном при этой температуре образце обнаружено большое содержание кристаллической фазы, значит, указанная температура лежит ниже температуры ликвидуса. Повторяя аналогичные определения несколько раз и постепенно сужая интервал между температурами t2 и t4 находят ту температуру (t3), которой соответствует появление в образце первых кристаллов твердой фазы. Эта температура будет соответствовать точке а кривой ликвидуса. Проделывая то же самое с другими составами (например, 2, 5, 4), находят другие точки кривых ликвидуса (b, с, d и т.д.)

Слайд 200ПРИНЦИПЫ ТЕОРЕТИЧЕСКОГО РАСЧЕТА ДИАГРАММ СОСТОЯНИЯ
Фазовые диаграммы состояния представляют собой графическое
изображение всех возможных равновесных состояний в данной системе, соответствующих ее
определенным параметрам. Поскольку условием равновесия является минимум энергии Гиббса, каждая точка на диаграмме соответствует той фазе или совокупности фаз, энергия Гиббса которых меньше, чем у других возможных (конкурирующих) фаз в системе. Другими словами, для теоретического расчета и построения диаграмм состояния необходимо знание энергии Гиббса конкурирующих фаз при данных параметрах системы.
Современный уровень знаний пока что не позволяет, исходя из свойств реальных веществ, теоретически полностью предсказать характер взаимодействия компонентов и построить на основании этого диаграмму состояния. Сделать это теоретически в настоящее время можно только на основании определенных допущений, определенных модельных представлений о жидких и твердых растворах, упорядоченных фазах и соединениях. Наиболее простой моделью для теоретического расчета фазовых равновесий является модель (приближение) идеальных растворов.

Слайд 201Расчет диаграмм состояния заключается, во-первых, в предсказании типа диаграммы состояния
на основе свойств чистых компонентов и, во-вторых, в отыскании уравнений
линий равновесия сосуществующих фаз. Основой при этом является знание температурной и концентрационной зависимости энергии Гиббса (G), которая в приближении идеальных растворов для любой фазы двухкомпонентной системы, состоящей из компонентов i и j определяется в общем случае выражением:
G=(l—x)Gi+xGi+RTxlnx+RT(1—x) ln (1— x),
где Gt и Gi — энергии Гиббса чистых компонентов i и j; х — молярная доля компонента j в данной фазе.
Слайд 202Энергии Гиббса конкурирующих фаз определяются из выражения
ΔG = ΔH—TΔS
на основании известных значений энтальпий (ΔH) и энтропии (ΔS) фазовых
превращений компонентов, определяемых на основании экспериментального изучения термодинамических свойств веществ. Решая для различных задаваемых температур системы уравнений указанного типа для жидких и твердых фаз, находят их равновесные составы, т.е. геометрическое место точек кривых ликвидуса и солидуса на диаграмме Т—х.
Для бинарных систем с эвтектикой, когда из расплава кристаллизуются только чистые компоненты, для расчета диаграммы состояния в приближении идеальных растворов можно использовать уравнения Шредера, описывающие кривые ликвидуса:
Зная температуры (Тпл) и теплоты (ΔHПЛ) плавления компонентов, из этих уравнений для различных значений Т можно найти состав жидкой фазы (концентрации компонентов ХА и лев), насыщенной по отношению к компонентам А и В, т.е. построить ветви кривых ликвидуса и получить диаграмму состояния системы А—В.
Слайд 203Приведение многокомпонентных диаграмм состояния к трёхкомпонентным
Пользоваться на практике поликомпонентными диаграммами
состояния весьма затруднительно. В связи с этим в некоторых случаях
многокомпонентную диаграмму состояния с помощью пересчёта приводят к трёхкомпонентной диаграмме состояния.
Принцип пересчёта заключается в том, что все компоненты делятся на 3 или 4 группы по признаку химического подобия – щелочные (R+), щелочноземельные (R2+), полуторные (R3+) и кислые (R4+). Все оксиды приводятся внутри одной группы (щелочные – к щелочным или щелочноземельным, полуторные – к полуторным, кислые – к кислым).
Для пересчёта пользуются переходными коэффициентами, выведенными на основании правила Рихтерса, говорящего, что оксиды плавня влияют на температуру соответственно их эквивалентным массам, т.е молекулярным массам, отнесённым к количеству катионов в формуле.