Слайд 2Введение
Современный человек в повседневной жизни постоянно сталкивается с числами и
цифрами: мы запоминаем номера автобусов и телефонов, в магазине подсчитываем
стоимость покупок, ведем свой семейный бюджет и т.д. и т.п. Числа, цифры…они с нами везде. А две тысячи лет назад что знал человек о числах? А пять тысяч лет назад?
Сегодня, в 21 веке, человечество для записи чисел использует в основном десятичную систему счисления.
А что такое система счисления?
Слайд 3Из истории счета
Древние системы счисления отличаются большим разнообразием, поскольку привычный нам
способ записи чисел с помощью десяти знаков появился далеко не
сразу.
Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет не один,то говорили «много». Постепенно появилось слово для обозначения двух предметов.
Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», которая всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук,так и ног.
Записывали числа по началу совсем просто: делали зарубки на куске дерева или кости.
Одни пользовались для запоминания чисел камешками, зернами, другие палочками,зарубками. Это были первые счетные приборы, которые привели к образованию различных систем счисления.
Слайд 4Латинская (Римская) нумерация
Примером такой системы счисления является пришедшая из Древнего
Рима римская система.
С нею мы достаточно часто сталкиваемся
в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов.
О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа.
Слайд 5Новая, или арабская нумерация
В различных районах Индии существовали разнообразные системы
нумерации, но в какой-то момент среди них выделилась одна. В
ней цифры имели вид начальных букв соответствующих числительных на древнеиндийском языке - санскрите, использующем алфавит "Деванагари".
Первоначально этими знаками представлялись числа 1, 2, 3, … 9, 10, 20, 30, …, 90, 100, 1000; с их помощью записывались другие числа. Но в последствии был введен особый знак - жирная точка, или кружок, для указания пустующего разряда; и нумерация "Деванагари" превратилась в поместную десятичную систему. Как и когда совершился такой переход - до сих пор неизвестно. К середине VIII века позиционная система нумерации получает широкое применение. В это же время она проникает в соседние страны: Индокитай, Китай, Тибет, Среднюю Азию.
Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения.
Слайд 6
Египетская нумерация
Египтяне придумали эту систему около 5 000 лет тому
назад. Это одна из древнейших систем записи чисел, известная человеку.
Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
Слайд 7Славянская глаголическая нумерация
Эта нумерация была создана для переписки чисел в
священных книгах западных славян. Использовалась она нечасто, но достаточно долго.
Для того, чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.
Слайд 8Славянская кириллическая нумерация
Эта нумерация была создана вместе со славянской алфавитной
системой для переписки священных книг для славян греческими монахами братьями
Кириллом (Константином) и Мефодиев в IX веке. Если посмотреть внимательно, то увидим, что после "а" идет буква "в", а не "б" как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите.
Слайд 9Китайская нумерация
Эта нумерация одна из старейших и самых прогрессивных, поскольку
в нее заложены такие же принципы, как и в современную
арабскую, которой мы с Вами пользуемся. Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае.
Эта нумерация одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную арабскую, которой мы с Вами пользуемся. Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае.
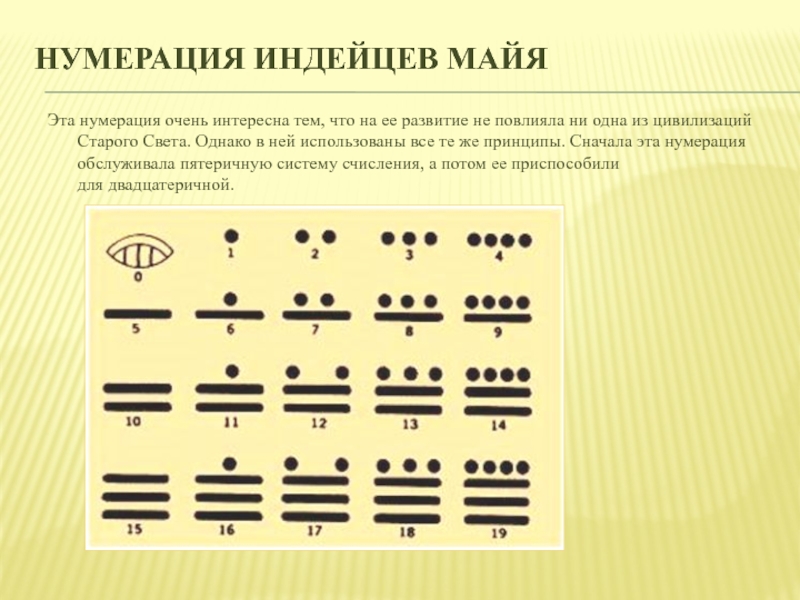
Слайд 10Нумерация индейцев Майя
Эта нумерация очень интересна тем, что на ее
развитие не повлияла ни одна из цивилизаций Старого Света. Однако в ней
использованы все те же принципы. Сначала эта нумерация обслуживала пятеричную систему счисления, а потом ее приспособили для двадцатеричной.
Слайд 11Древняя греческая нумерация
В древнейшее время в Греции была распространена так
называемая Аттическая нумерация. В этой нумерации числа 1, 2, 3,
4 изображались соответствующим количеством вертикальных полосок: I,II,III,IIII.
Число 5 записывалось знаком (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте". Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
Число 10 обозначалось - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000.
Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами
Слайд 12Обозначение чисел в древнеславянской системе счисления
Слайд 14В наше время используются: двоичная, восьмеричная, десятичная и шестнадцатеричная системы
счисления. Это связано с их использованием в математике и для
компьютерного представления информации.
Двоичная система счисления в вычислительной технике используется в связи с тем, что электронные элементы – триггеры (переключатели), из которых состоят микросхемы, могут находиться только в двух рабочих состояниях (включено или выключено – ноль или единица). Восьмеричная связана с основным кодированием символов восемью битами, а шестнадцатеричная – так как информация при хранении чаще укрупняется до двух байтов (16 бит) и из-за появления Unicode-шрифтов.
Слайд 15Двоичная система счисления
Двоичная система счисления является основной системой представления информации
в памяти компьютера.
В этой системе счисления используются две цифры: 0 и 1.
Двоичную цифру
называют битом.
Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.
Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово "килобайт", вообще говоря, означает "1000 байт". (Напомним, что приставка "кило" означает "тысяча".)
Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.
Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.
Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более
Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.
1 Мбайт = 1024 Кбайт = 1 048 576 байт.
Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт

Слайд 16Восьмеричная система счисления
Основание этой системы счисления равно восьми. Восьмеричную систему
счисления можно рассматривать как более короткий вариант записи двоичных чисел,
так как число восемь является степенью числа два. В этой системе счисления используется восемь цифр. Чтобы не выдумывать новых символов для обозначения цифр, в восьмеричной системе счисления были использованы символы десятичных цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для того чтобы не спутать систему счисления в записи числа используется индекс 8. Если же кроме восьмеричной формы записи чисел не предполагается использования никакой другой, то этот индекс можно опустить.
Число в этой системе счисления записывается как сумма единиц, восьмёрок, шестьдесят четвёрок и так далее. То есть веса соседних разрядов различаются в восемь раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как восьмые, шестьдесят четвёртые и так далее доли единицы.
Рассмотрим пример записи восьмеричного числа:
A8=125,468=1*82+2*81+5*80+4*8-1+6*8 -2=6410+1610+510+410/810+610/6410= 85,5937510
Во второй строке приведённого примера фактически осуществлён перевод числа, записанного в восьмеричной форме в десятичное представление того же самого числа. То есть мы фактически рассмотрели один из способов преобразования чисел из одной формы представления в другую.
Так как в формуле используются простые дроби, то возможен вариант, что точный перевод из одной формы представления в другую становится невозможным. В этом случае ограничиваются заданным количеством дробных разрядов.

Слайд 17Десятичная система счисления
Основание этой системы счисления равно десяти. В этой
системе счисления используется десять цифр. В настоящее время для обозначения
этих цифр используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число в десятичной системе счисления записывается как сумма единиц, десятков, сотен, тысяч и так далее. То есть веса соседних разрядов различаются в десять раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как десятые, сотые или тысячные доли единицы.
Здесь самый старший разряд числа будет называться сотнями. В приведённом примере сотням соответствует цифра 2. Следующий разряд будет называться десятками,десяткам соответствует цифра 4. Следующий разряд будет называться единицами, им соответствует цифра 7. Десятым долям соответствует цифра 5, а сотым – 6.
Например:
A10=247,5610=2*102+4*101+7*100+5*10-1 +6*10-2=20010+4010+710+0,510+0,0610
Слайд 18Шестнадцатеричная система счисления
Шестнадцатеричная система, или система с основанием 16. Поскольку
основание системы равно 16, то в ней должны существовать 16
различных цифр. У нас есть 10 цифр нашей десятичной системы счисления, их мы и используем в качестве первых 10 цифр шестнадцатеричной системы. В качестве остальных шести цифр мы используем буквы А, В, С, D, Е, F.
То, как мы представляем время на часах, это пример шестидесятеричной позиционной системы счисления. В представлении времени используется три позиции: для часов, минут и секунд; так как для каждой позиции приходится использовать 60 цифр, а у нас только десять цифр, то для каждой шестидесятиричной позиции используется две десятичные цифры (00, 01, 02, …, 59), а позиции разделяются двоеточием.
h: m: s
Чтобы получить время в секундах мы должны посчитать вот по такой формуле: