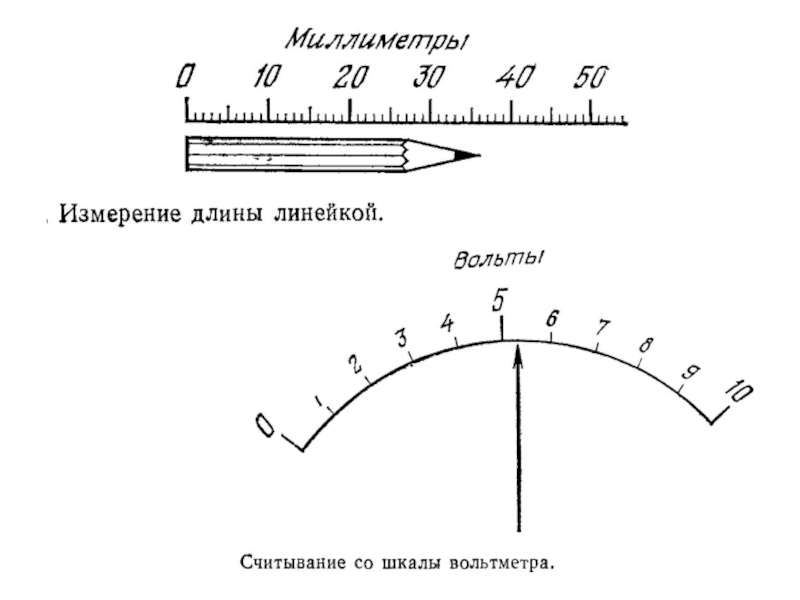
Измерительные приборы. Виды и предназначение

Содержание

1. Измерительные приборы. Виды и предназначение
2. Приведение и использование погрешностей
3. Слайд 3
4. Слайд 4
5. Слайд 5
6. Число δх называется погрешностью или ошибкой измерения в измерении х.
7. Абсолютная погрешность — понимают разность между точным
8. Относительная погрешность — погрешность измерения, выраженная отношением
9. Приведённая погрешность — погрешность, выраженная отношением абсолютной
10. Если шкала прибора односторонняя, то есть нижний
11. Значащие цифры
12. Слайд 12
13. Погрешность в любой измеренной величине имеет ту же размерность, что и сама измеренная величина.
14. Различие
15. Сравнение двух измеренных значений
16. Слайд 16
17. Относительные погрешностиКачество измерения характеризуется на только самой
18. Слайд 18
19. Погрешность в произведении
20. Слайд 20
21. Погрешности в косвенных измеренияхЕсли измеряются две величины
22. Слайд 22
23. Если измеряются две величины х и у
24. Слайд 24
25. Слайд 25
26. Слайд 26
27. Измеряем толщину Т 100 листов бумаги и получаем результат
28. Слайд 28
29. Слайд 29
30. Слайд 30
31. Независимые погрешности в сумме
32. Слайд 32
33. Слайд 33
34. Слайд 34
35. Слайд 35
36. Слайд 36
37. Слайд 37
38. Слайд 38
39. Слайд 39
40. тогда в соответствии с правилом погрешность равна
41. Степенная функция
42. Слайд 42
43. Слайд 43
44. Слайд 44
45. Слайд 45
46. Слайд 46
47. Слайд 47
48. Слайд 48
49. Слайд 49
50. Слайд 50
51. Общая формула для вычислениях погрешностей в косвенных измерениях
52. Скачать презентанцию

Приведение и использование погрешностей

Главная
Разное
Измерительные приборы. Виды и предназначение

Слайды и текст этой презентации

Слайд 1Измерительные приборы. Виды и предназначение.
Измерительные приборы. Контрольно-измерительные устройства. Классификация

приборов. Оптические, механические, электронные.

Измерительные приборы. Виды и предназначение. Измерительные приборы. Контрольно-измерительные устройства. Классификация приборов. Оптические, механические, электронные.

Слайд 2Приведение и использование погрешностей

Слайд 6Число δх называется погрешностью или ошибкой измерения в измерении х.

Слайд 7Абсолютная погрешность — понимают разность между точным (истинным) значением величины

xист и ее приближенным (измеренным) значением xизмер :
Абсолютная погрешность является

оценкой абсолютной ошибки измерения, поэтому абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина. Абсолютную погрешность применяют для сравнения точности измерения величин одного порядка и одной размерности.

Абсолютная погрешность — понимают разность между точным (истинным) значением величины xист и ее приближенным (измеренным) значением xизмер

Слайд 8Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерений

∆x к истинному значению xист измеряемой величины:

Относительная погрешность является безразмерной

величиной, либо измеряется в процентах. Поэтому относительная погрешность позволяет сравнивать разнородные величины.

Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерений ∆x к истинному значению xист измеряемой величины:Относительная

Слайд 9Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений

к условно принятому значению величины, постоянному во всем диапазоне измерений

или в части диапазона. Вычисляется по формуле

где xнорм– нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во

Слайд 10
Если шкала прибора односторонняя, то есть нижний предел измерений равен

нулю, то xнорм определяется равным верхнему пределу измерений;
Если шкала

прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.