Слайд 1Комбинаторные алгоритмы
Установочные лекции
Слайд 2Минимальный остов
Алгоритмы Борувки – Краскала,
Ярника – Прима – Дейкстры.
Слайд 3Минимальный остов
Остовом называется ацикличный связный подграф данного графа, содержащий все
его вершины.
Пусть G=(V,E,c) связный взвешенный неориенти-рованный граф. Под весом
с(H) произвольного ненулевого подграфа H будем понимать сумму весов всех ребер подграфа H.
Ацикличный остовный подграф (содержащий все вершины графа G) будем называть остовным лесом графа G.
Остов T называется минимальным, если для любого остова T’ выполняется неравенство c(T) c(T’).
Слайд 4Минимальный остов
Этот раздел посвящен решению следую-щей задачи: в данном связном
графе найти минимальный остов (задача о минимальном остове).
Слайд 5Предположим, что F остовный лес связного взвешенного графа G.
Будем говорить, что F продолжаем до мини-мального остова, если существует
такой минимальный остов T, что F T.
Минимальный остов
Слайд 6Минимальный остов
Справедлива следующая лемма.
Пусть остовный лес F продолжаем до минимального
остова и H одна из компонент связности леса F.
Если с ребро минимального веса из Ext(H) (т.е. внешнее по отношению к H: один его конец лежит в H, в другой – нет), то остовный лес F + c продолжаем до минимального остова.
Слайд 7Минимальный остов
Эта лемма позволяет сконструировать два алгоритма построения минимального остова
во взвешенном (n,m)-графе G.
Пусть F0 – тривиальный остовный лес (т.е.
остовный лес без ребер). Ясно, что F0 можно продолжить до минимального остова.
Оба алгоритма строят последовательность
F0, F1, …, Fn -1,
состоящую из остовных лесов, причем
Fi = Fi -1 + ei
где ei – ребро из Ext(Fi-1). Указанную после-довательность называют растущим лесом.
Слайд 8Минимальный остов
Последовательность строится таким образом, чтобы для каждого i (i[1,n-1])
остовный лес можно было бы продолжить до минимального остова. Ясно,
что тогда Fn-1 является минимальным остовом.
При переходе от Fi-1 к Fi (т.е. при выборе ребра ei) возможны две стратегии.
Слайд 9Минимальный остов
Стратегия 1. В качестве ei выбираем ребро минимального веса
среди всех ребер, внешних к остовному лесу Fi-1.
Пусть H –
одна из двух компонент связности, леса Fi-1, содержащая концевую вершину ребра ei. Если Fi-1 продолжаем до минималь-ного остова, то в силу леммы лес Fi = Fi-1 + ei обладает тем же свойством.
Слайд 10Минимальный остов
Стратегия 2. Здесь предполагается, что каждый остовный лес Fi
(i1) имеет только од-ну неодноэлементную компоненту связности Hi. Удобно считать,
что H0 состоит из не-которой заранее выбранной вершины графа G. Таким образом речь идет о построении последовательности
H0, H1, …, Hn -1,
состоящей из поддеревьев графа G, причем
Hi = Hi -1 + ei,
причем ei Ext(Fi-1). Указанную последователь-ность называют растущим деревом.
Слайд 11Минимальный остов
Стратегия 1 реализуется алгоритмом Борувки – Краскала, стратегия 2
– алгоритмом Ярника – Прима – Дейкстры.
Слайд 12Алгоритм
Борувки – Краскала
Минимальный остов
Слайд 13Отакар Борувка
(10 мая 1899 22 июля 1995)
Чешский математик, про-фессор
университета Брно.
Идея алгоритма построе-ния минимального остова была изложена в его
рабо-те в 1926 году. Однако, работа была практически забыта.
Слайд 14Джозеф Краскал
(29 января 1928 ― 19 сентября 2010 )
Американский
математик. Учился в Чикагском и в Принстонском университетах. В 1954
году получил степень PhD. Одним их его научных руководителей был Алберт Таккер (помните теорему Куна-Таккера о необходимых усло-виях экстремума в задаче ма-тематического программирова-ния?).
Член американской ассоциации статистики, ведущий ученый Bell Labs.
Алгоритм построения минималь-ного остова был опубликован в 1956 году.
Слайд 15Минимальный остов
Алгоритм Борувки – Краскала
Сортируем ребра графа по возрастанию весов.
Тривиальный
лес объявить растущим.
Проходим ребра в "отсортированном" порядке.
Для каждого
ребра выполняем:
если вершины, соединяемые данным ребром лежат в разных деревьях растущего леса, то объединяем эти деревья в одно, а ребро добавляем к строящемуся остову.
если вершины, соединяемые данным ребром лежат в одном дереве растущего леса, то исключаем ребро из рассмотрения.
Если есть еще нерассмотренные ребра и не все деревья объединены в одно, то переходим к шагу 3, иначе выход.
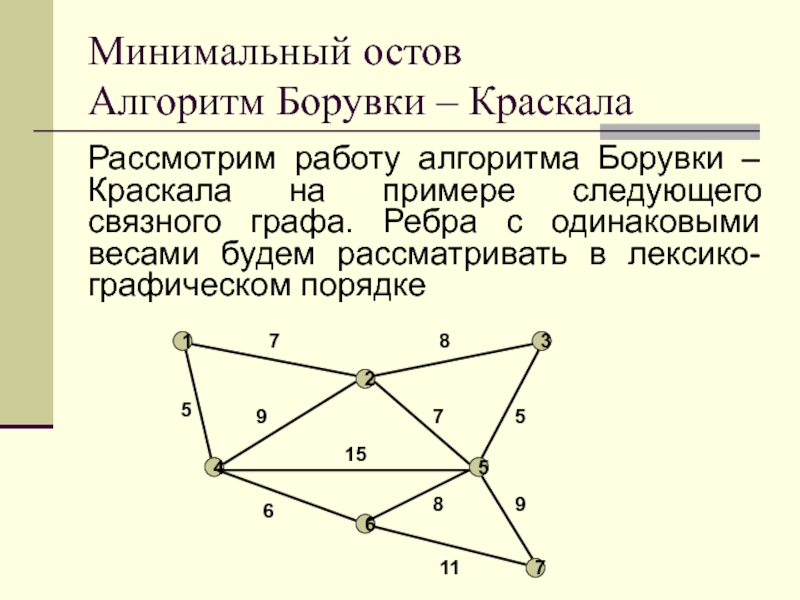
Слайд 16Рассмотрим работу алгоритма Борувки – Краскала на примере следующего связного
графа. Ребра с одинаковыми весами будем рассматривать в лексико-графическом порядке
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Минимальный
остов
Алгоритм Борувки – Краскала
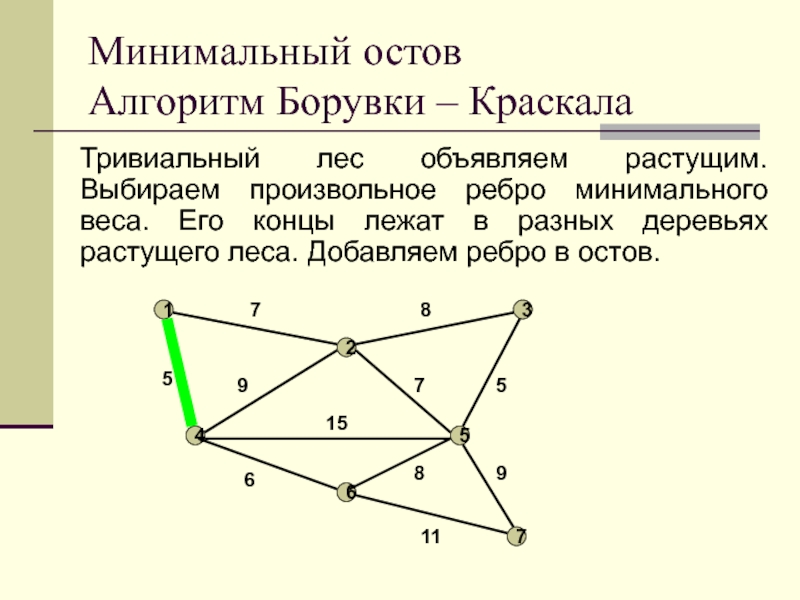
Слайд 17Тривиальный лес объявляем растущим. Выбираем произвольное ребро минимального веса. Его
концы лежат в разных деревьях растущего леса. Добавляем ребро в
остов.
Минимальный остов
Алгоритм Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
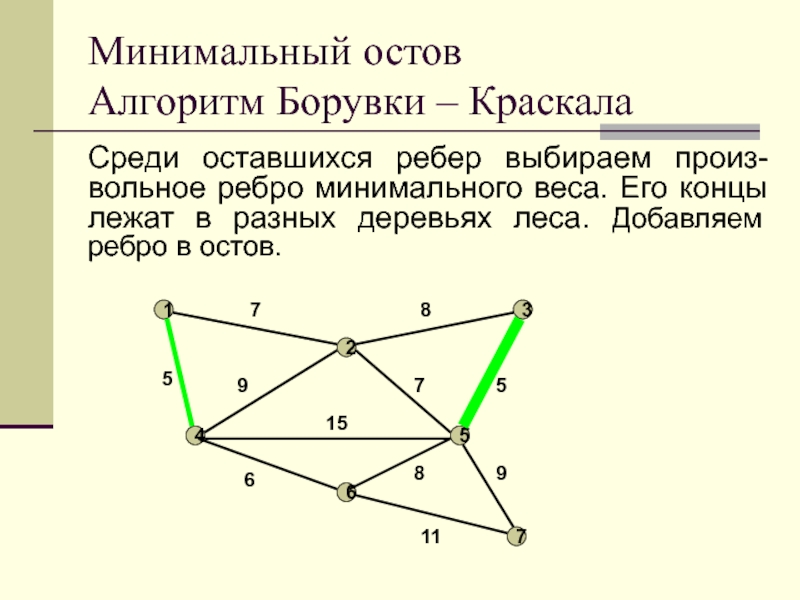
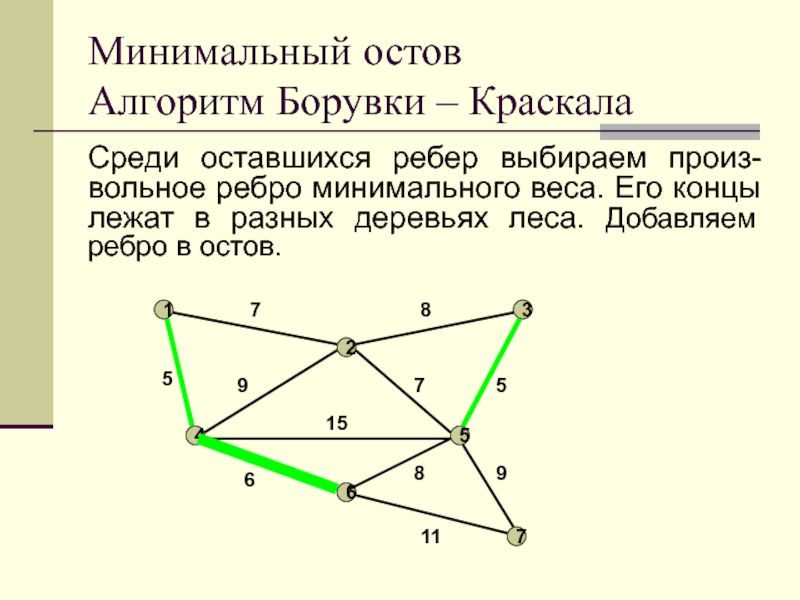
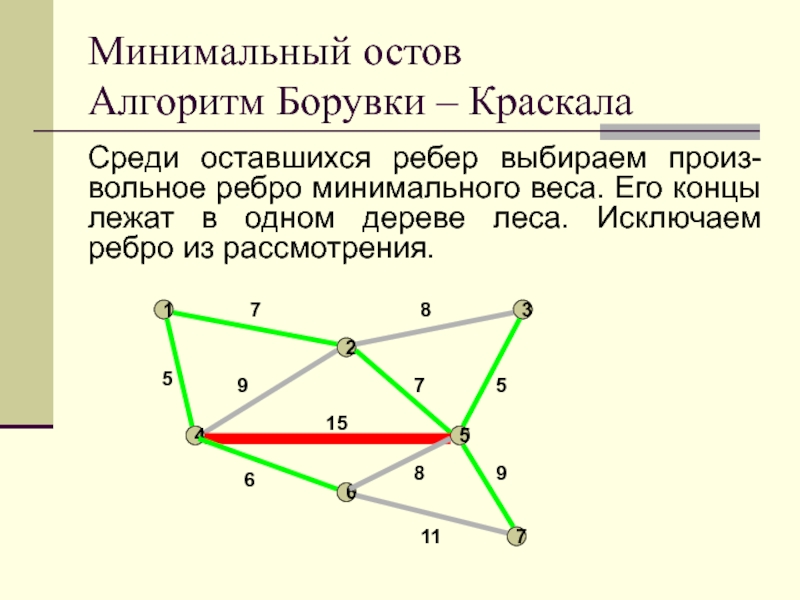
Слайд 18Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в разных деревьях леса. Добавляем ребро в остов.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 19Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в разных деревьях леса. Добавляем ребро в остов.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 20Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в разных деревьях леса. Добавляем ребро в остов.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 21Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в разных деревьях леса. Добавляем ребро в остов.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
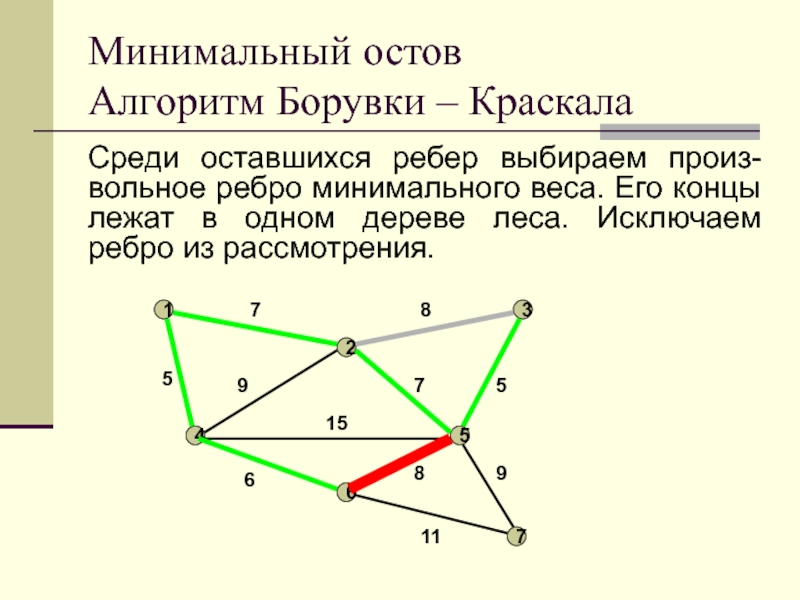
Слайд 22Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в одном дереве леса. Исключаем ребро из рассмотрения.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
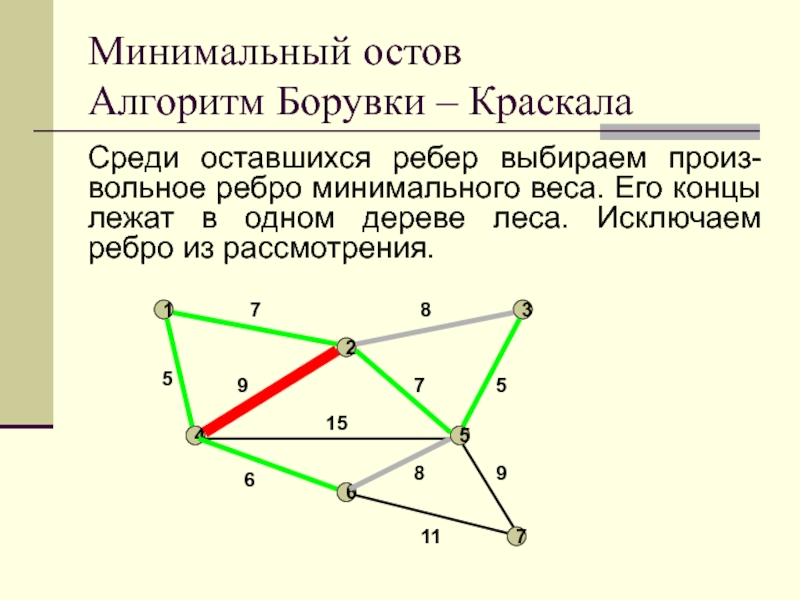
Слайд 23Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в одном дереве леса. Исключаем ребро из рассмотрения.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
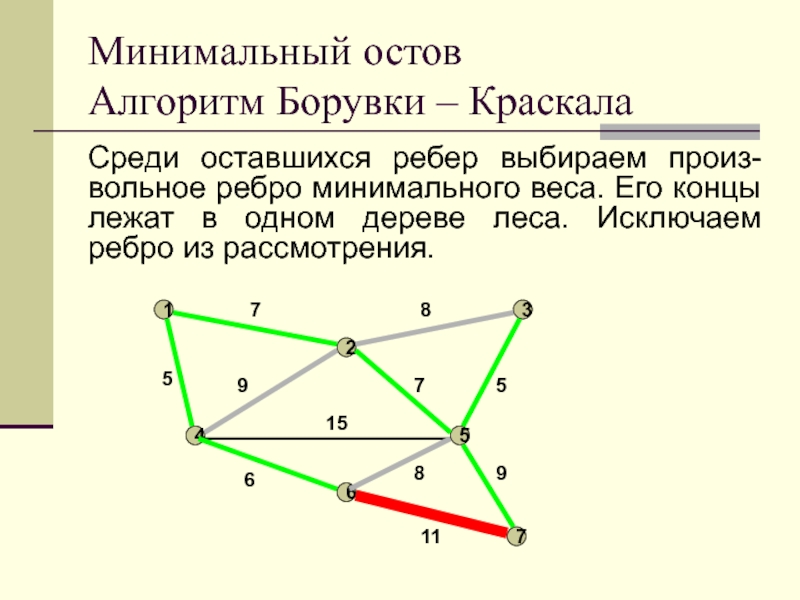
Слайд 24Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в одном дереве леса. Исключаем ребро из рассмотрения.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 25Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в разных деревьях леса. Добавляем ребро в остов.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 26Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в одном дереве леса. Исключаем ребро из рассмотрения.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 27Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы
лежат в одном дереве леса. Исключаем ребро из рассмотрения.
Минимальный остов
Алгоритм
Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 28Нерассмотренных ребер нет. Минимальный остов построен. Вес остова равен 39.
Минимальный
остов
Алгоритм Борувки – Краскала
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 29Алгоритм
Ярника – Прима – Дейкстры
Минимальный остов
Слайд 30Войтех Ярник
(22 декабря 1897 – 22 сентября 1970)
Чешский математик. Ос-новные
работы посвящены теории чисел и матема-тическому анализу.
В 1930 году разработал
алгоритм построения ми-нимального остова.
Слайд 31Роберт Прим
(род. в 1921 в Техасе, США)
Американский математик. Получил степень
PhD в Принстонском универси-тете в 1949. Позже рабо-тал вместе с
Джозефом Красаклом в Bell Labs.
Предложил алгоритм по-строения минимального остова в 1957 году.
Слайд 32Эдсгер Дейкстра
(11 мая 1930 – 6 августа 2002)
Голландский математик –
специалист в области компьютерных наук. В 1972 году стал лауреатом
премии Тьюринга за существенный вклад в развитие языков програм-мирования.
Разработал алгоритм построения минимального остова в 1959 году.
Слайд 33Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
Выбирается произвольная вершина –
она будет корнем остовного дерева.
Измеряется расстояние от нее до всех
внешних по отношению к растущему дереву вершин (расстояние от внешней вершины до ближайшей к ней вершины дерева)
До тех пор пока в дерево не добавлены все вершины делать:
Найти вершину, расстояние от дерева до которой минимально.
Добавить ее к дереву.
Пересчитать расстояния от вершин до дерева следующим образом: если расстояние до какой- либо вершины из новой вершины меньше текущего расстояния от дерева, то старое расстояние от дерева заменить новым.
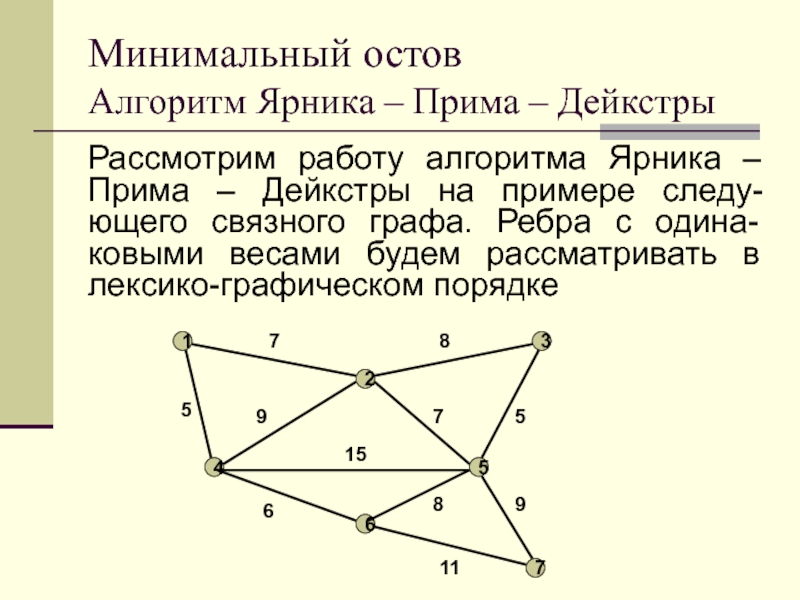
Слайд 34Рассмотрим работу алгоритма Ярника – Прима – Дейкстры на примере
следу-ющего связного графа. Ребра с одина-ковыми весами будем рассматривать в
лексико-графическом порядке
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
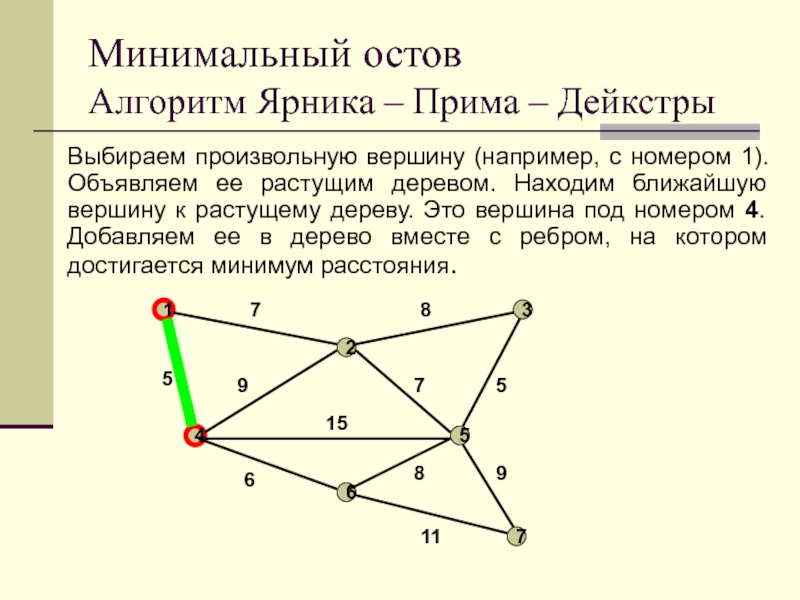
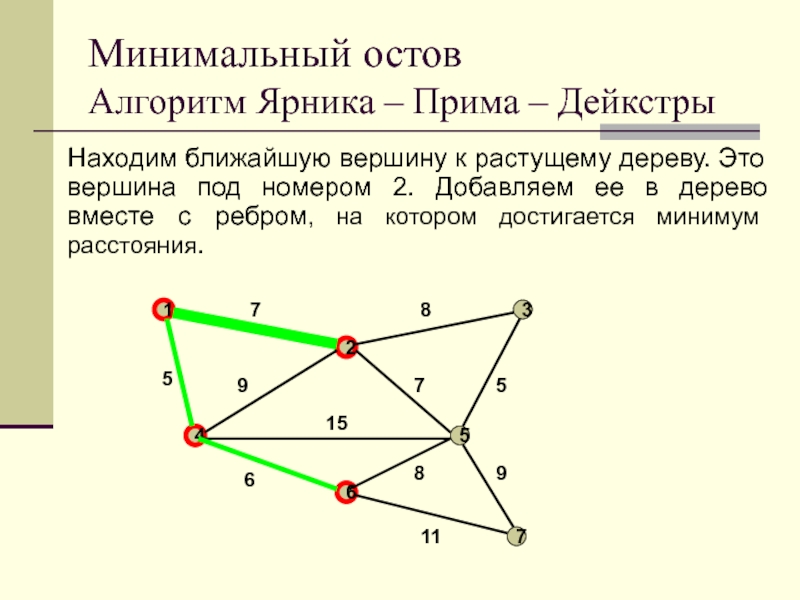
Слайд 35Выбираем произвольную вершину (например, с номером 1). Объявляем ее растущим
деревом. Находим ближайшую вершину к растущему дереву. Это вершина под
номером 4. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния.
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
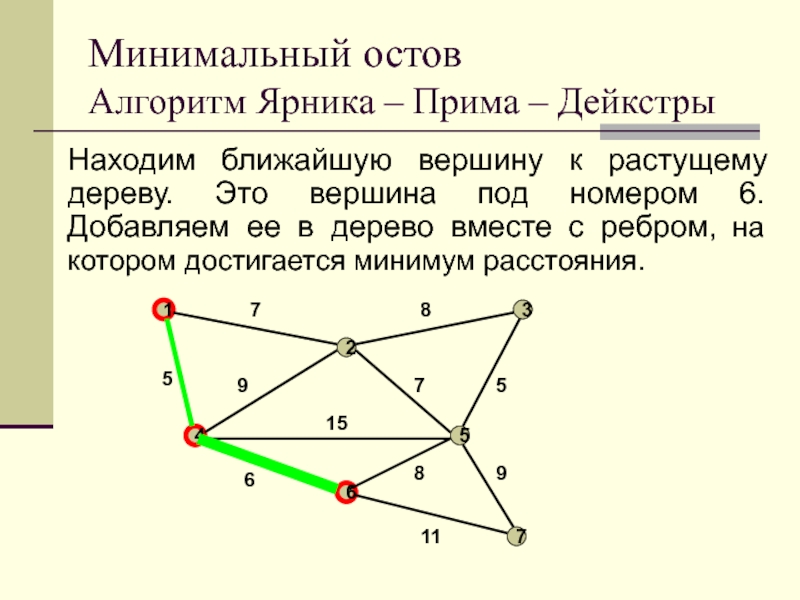
Слайд 36Находим ближайшую вершину к растущему дереву. Это вершина под номером
6. Добавляем ее в дерево вместе с ребром, на котором
достигается минимум расстояния.
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 37Находим ближайшую вершину к растущему дереву. Это вершина под номером
2. Добавляем ее в дерево вместе с ребром, на котором
достигается минимум расстояния.
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
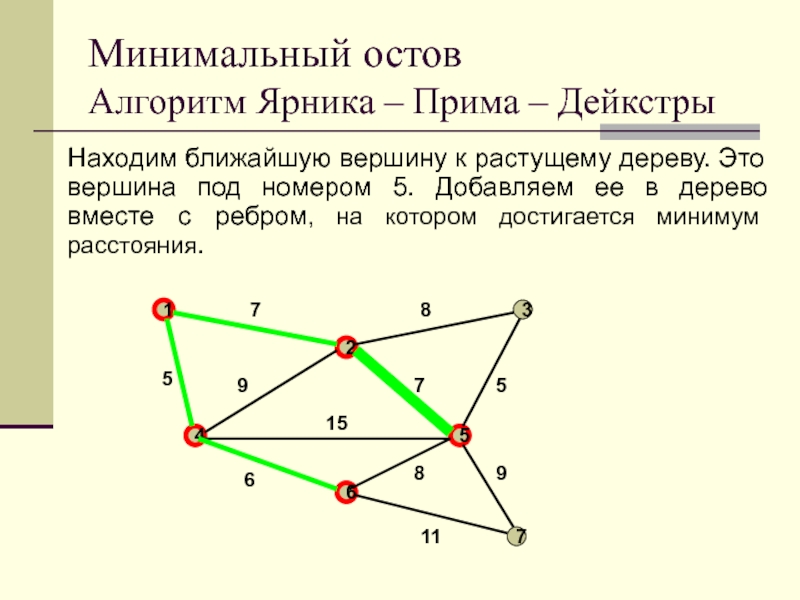
Слайд 38Находим ближайшую вершину к растущему дереву. Это вершина под номером
5. Добавляем ее в дерево вместе с ребром, на котором
достигается минимум расстояния.
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
Слайд 39Находим ближайшую вершину к растущему дереву. Это вершина под номером
3. Добавляем ее в дерево вместе с ребром, на котором
достигается минимум расстояния.
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
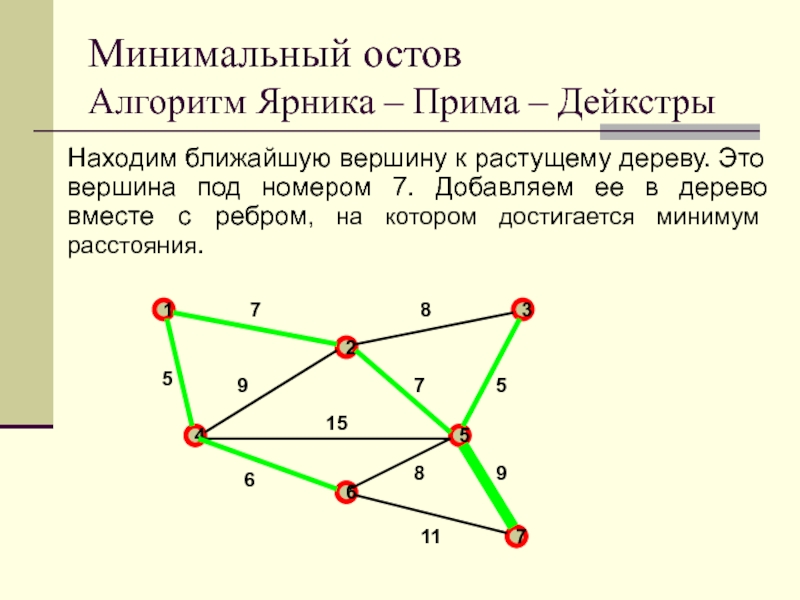
Слайд 40Находим ближайшую вершину к растущему дереву. Это вершина под номером
7. Добавляем ее в дерево вместе с ребром, на котором
достигается минимум расстояния.
Минимальный остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
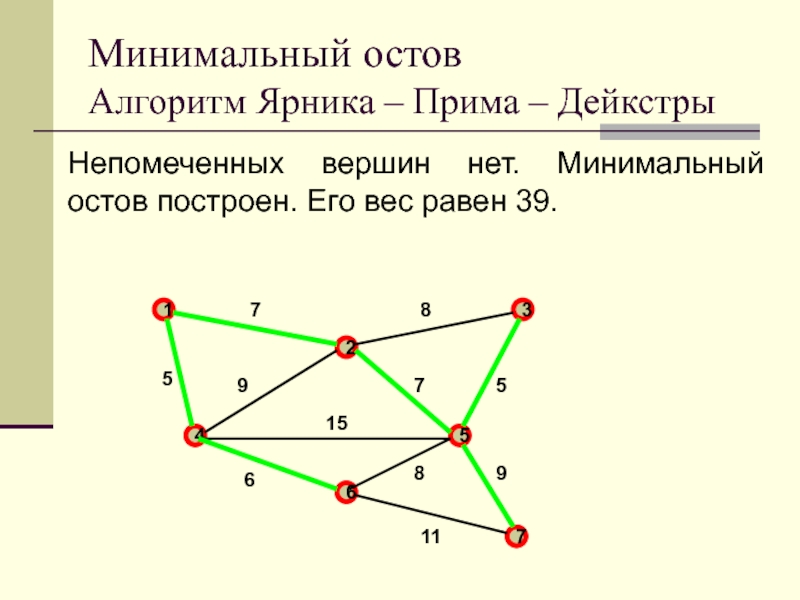
Слайд 41Непомеченных вершин нет. Минимальный остов построен. Его вес равен 39.
Минимальный
остов
Алгоритм Ярника – Прима – Дейкстры
1
2
3
4
5
6
7
7
8
9
7
5
5
15
6
11
8
9
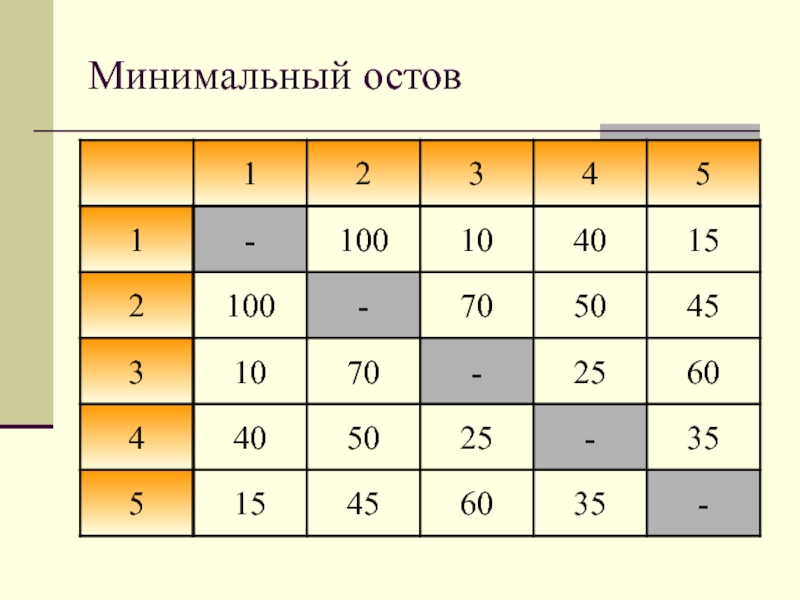
Слайд 42Рассмотрим следующую задачу.
Минимальный остов
Телефонная компания арендовала место, обозна-ченное узлом 1
для основного центра связи, и опре-делила расположение дополнительных центров (узлы
2,3, …5). Необходимо проложить кабель так, чтобы каждый дополнительный центр связи был связан с основным либо непосредственно, либо через другие дополнительные центры. В целях экономии компания стремиться израсходовать кабеля как можно меньше. Расстояния между центрами даны в таблице.
Слайд 44Пути в сетях
Алгоритмы Форда – Беллмана,
Дейкстры.
Слайд 45Пути в сетях
Взвешенный орграф G=(V,E,c) называется сетью.
Пусть P — некоторый
(v,w)–путь:
Положим
Величину с(P) назовем длиной пути P.
Слайд 46Пути в сетях
Наименьшую из длин (v,w)–путей назовем расстоянием от v
до w, …
… а тот (v,w)–путь, длина которого равна
расстоянию от v до w, будем называть кратчайшим (v,w)–путем.
Ясно, что расстояние от v до w может отличаться от рассто-яния от w до v.
!
!
Слайд 47Пути в сетях
Задача о кратчайшем пути между фикси-рованными вершинами формулируется
сле-дующим образом:
В заданной сети G с двумя выделен-ными вершинами s
и t найти кратчай-ший (s,t)–путь.
Слайд 48Пути в сетях
В этой задаче предполагается отсутствие циклов отрицательной длины
(иначе задача окажется некорректной).
Слайд 49Пути в сетях
Алгоритм
Форда – Беллмана
Слайд 50Лестер Рэндольф Форд младший
(род. 23 сентября 1927)
Американский математик.
В 1956 году
предложил алгоритм построения кратчайшего пути в сетях.
Слайд 51Ричард Беллман
(26 августа 1920 – 19 марта 1984)
Американский математик —
специалист по прикладной математике. Окончил Бруклин-ский колледж в 1941 году
(B.A.), универси-тет Висконсин–Мэдисон (M.A.). Работал в подразделении теоретической физики лаборатории в Лос–Аламос, где в 1946 году получил степень PhD. Награжден почетной медалью IEEE (Institute of Electrical and Electronics Engineers) за вклад в развитие теории принятия решений, теории управления и, в особенности, за создание и развития теории динамического програм-мирования. Был действительным членом Американской академии наук и искусств (с 1975 года), и Национальной инженерной академии США (с 1977 года).
Предложил алгоритм построения кратчай-шего пути в сетях в 1958 году.
Слайд 52Пути в сетях
Алгоритм Форда – Беллмана
Для описания алгоритма будем использовать
следующие обозначения:
D[v] – массив, в котором будет «накапли-ваться» расстояние от
выделенной верши-ныs до всех остальных вершин графа;
ПРЕДШ[v] – массив, в котором на месте v будет храниться номер вершины – предшест-венницы вершины v в кратчайшем (s,v)–маршруте.
Слайд 53Пути в сетях
Алгоритм Форда – Беллмана
Для всех вершин v из
V положить
D[v]:=c(s,v),
Если c(s,v)
n-2 раза:
для всех вершин v из V \ {s}
D[v]:=min{D[v],D[w]+c[w,v] | w из V}
ПРЕДШ [v]:=w* (та вершина, которая обеспечила минимум D[v]).
После выполнения этого алгоритма массив D содержит длины кратчайших (s,v)–путей, а по массиву ПРЕДШ[v] можно восстановить сам путь.
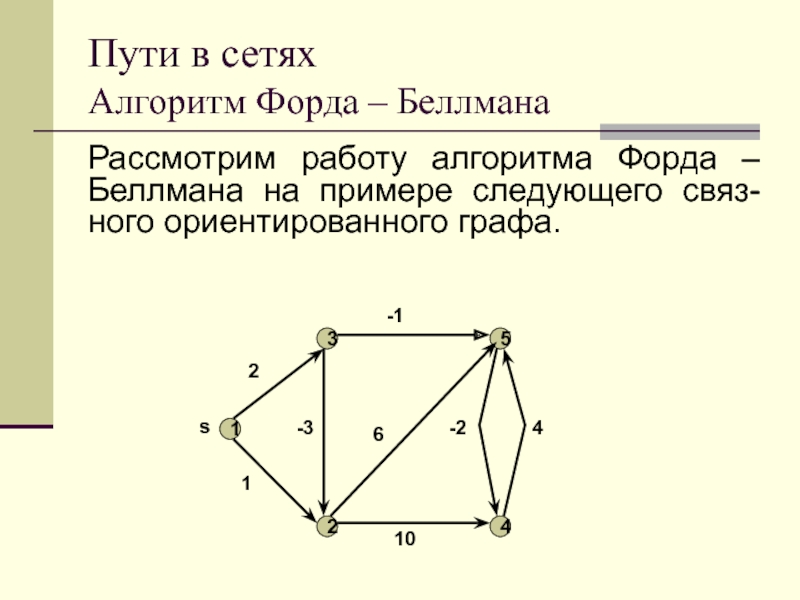
Слайд 54Рассмотрим работу алгоритма Форда – Беллмана на примере следующего связ-ного
ориентированного графа.
Пути в сетях
Алгоритм Форда – Беллмана
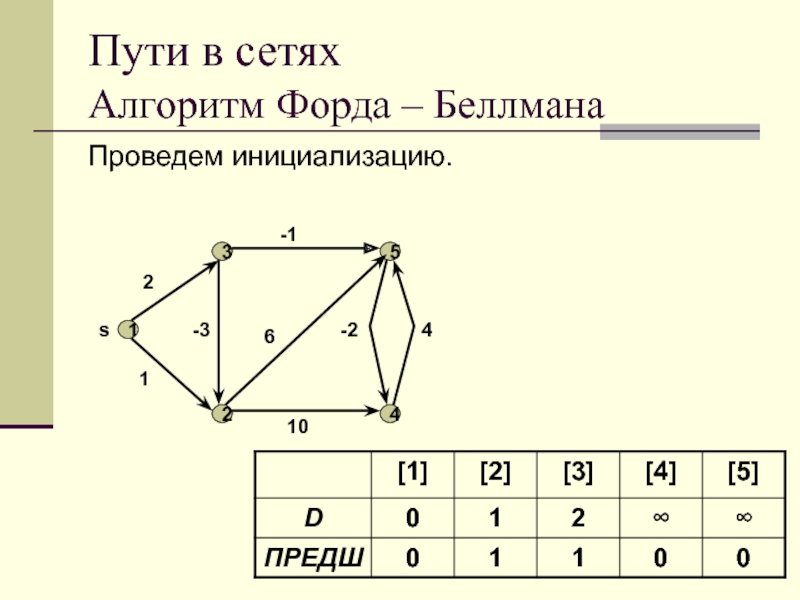
Слайд 55Пути в сетях
Алгоритм Форда – Беллмана
Проведем инициализацию.
Слайд 56Пути в сетях
Алгоритм Форда – Беллмана
Произведем перерасчет значений D[v] первый
раз.
Слайд 57Пути в сетях
Алгоритм Форда – Беллмана
Произведем перерасчет значений D[v] второй
раз.
Слайд 58Пути в сетях
Алгоритм Форда – Беллмана
Произведем перерасчет значений D[v] третий
и последний раз. Работа алгоритма закончена.
Слайд 59Случай неотрицательных весов.
Алгоритм Дейкстры
Пути в сетях
Слайд 60Пути в сетях
Алгоритм Дейкстры
Для описания алгоритма будем использовать следующие обозначения:
D[v]
– метки вершин, в которых будет «накапливаться» расстояние от выделенной
вершины s до вершины v графа;
ПРЕДШ[v] – массив, в котором на месте v будет храниться номер вершины – предшест-венницы вершины v в кратчайшем (s,v)–маршруте;
F – множество еще не просмотренных вершин.
Слайд 61Пути в сетях
Алгоритм Дейкстры
D[s]:=0; ПРЕДШ[s]:=0; F:=V\{s}
для всех v из F
положим
D[v]:=c[s,v];
ПРЕДШ[v]:=s;
n-1 раз делать
выбрать wF: D[w] = min{ D[u] |
uF }; F:=F\{w};
для всех vF делать
если (D[w]+c[w,v]
D[v]:=D[w]+c[w,v];
ПРЕДШ[v]:=w.
инициализация
Слайд 62Пути в сетях
Алгоритм Дейкстры
Рассмотрим работу алгоритма Дейкстры на примере следующего
графа.
1
2
3
4
5
s
6
1
3
10
4
2
2
3
12
5
Слайд 63Пути в сетях
Алгоритм Дейкстры
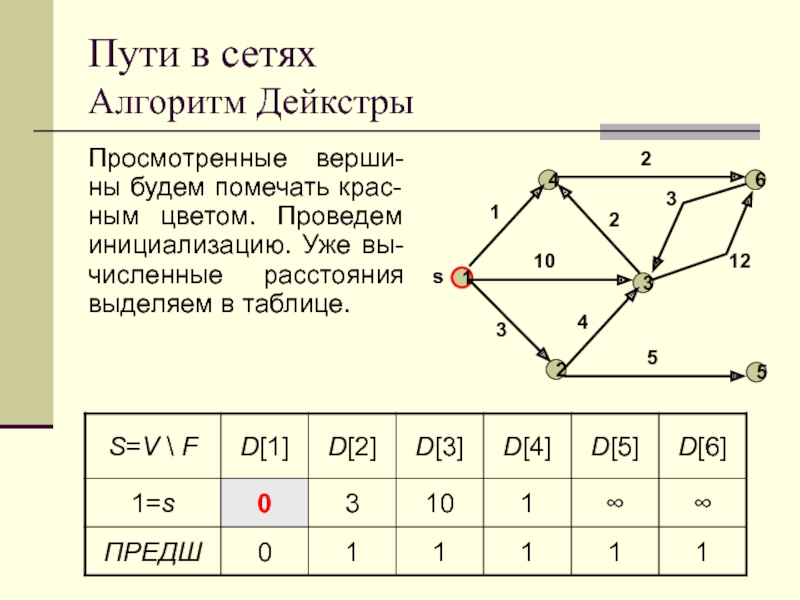
Просмотренные верши-ны будем помечать крас-ным цветом. Проведем
инициализацию. Уже вы-численные расстояния выделяем в таблице.
Слайд 64Пути в сетях
Алгоритм Дейкстры
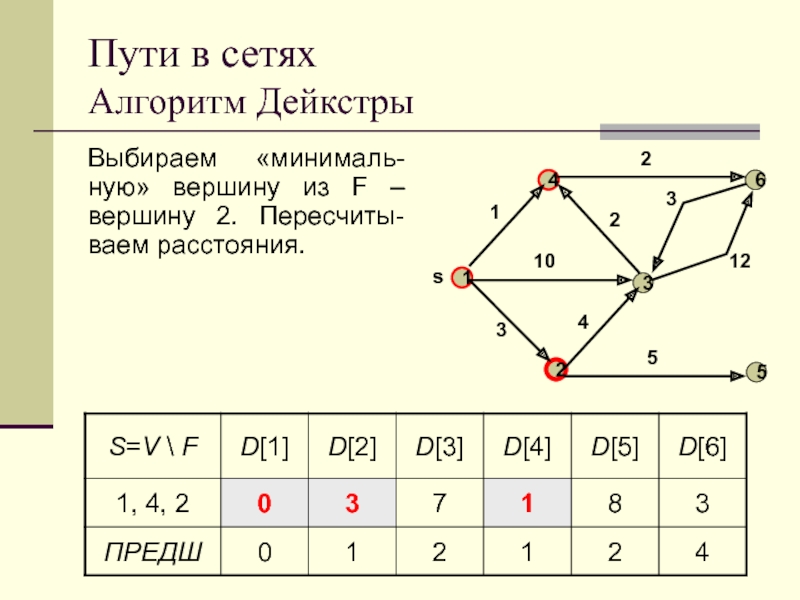
Выбираем «минималь-ную» вершину из F – вершину
4. Пересчиты-ваем расстояния.
1
2
3
4
5
s
6
1
3
10
4
2
2
3
12
5
Слайд 65Пути в сетях
Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину
2. Пересчиты-ваем расстояния.
1
2
3
4
5
s
6
1
3
10
4
2
2
3
12
5
Слайд 66Пути в сетях
Алгоритм Дейкстры
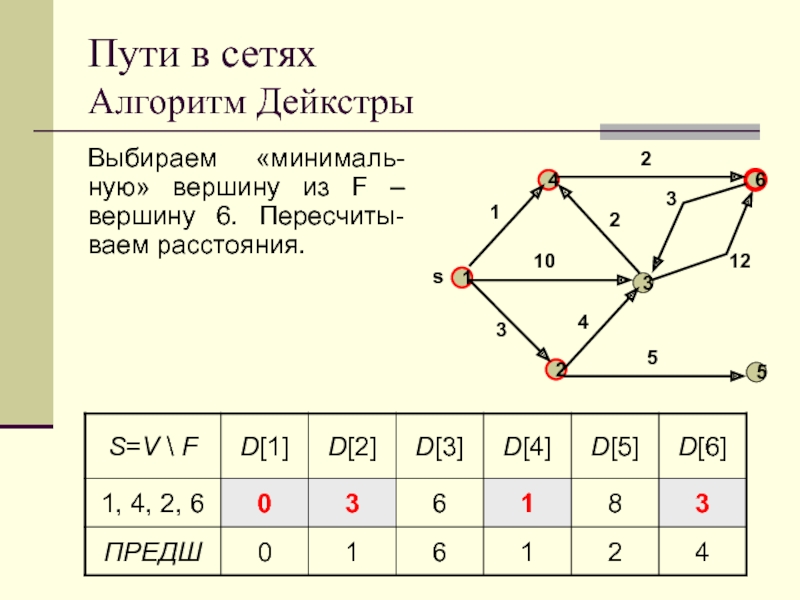
Выбираем «минималь-ную» вершину из F – вершину
6. Пересчиты-ваем расстояния.
1
2
3
4
5
s
6
1
3
10
4
2
2
3
12
5
Слайд 67Пути в сетях
Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину
3. Пересчиты-ваем расстояния.
1
2
3
4
5
s
6
1
3
10
4
2
2
3
12
5
Слайд 68Пути в сетях
Алгоритм Дейкстры
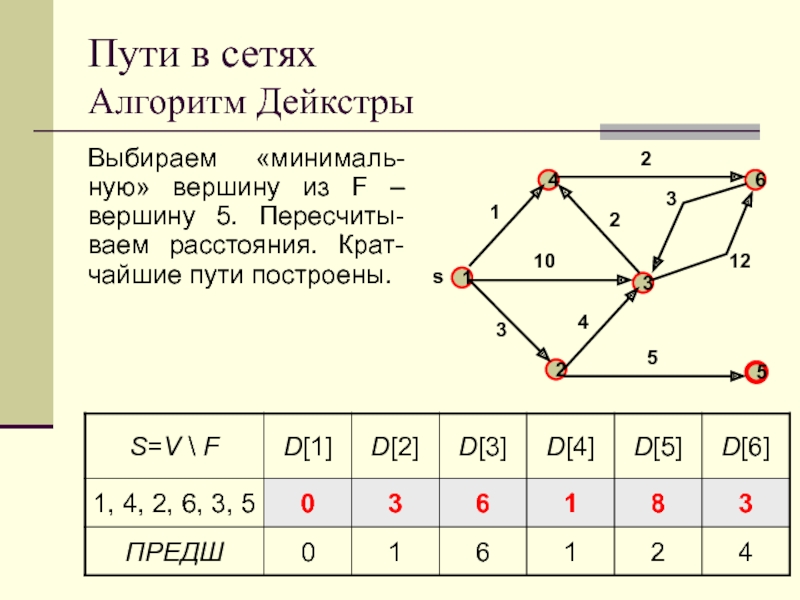
Выбираем «минималь-ную» вершину из F – вершину
5. Пересчиты-ваем расстояния. Крат-чайшие пути построены.
1
2
3
4
5
s
6
1
3
10
4
2
2
3
12
5
Слайд 69Потоки в сетях
Алгоритм Форда – Фалкерсона
Слайд 70Потоки в сетях
В этом разделе будем рассматривать сети G=(V,E,c;s,t), имеющие
единственную вершину с нулевой степенью захода (s) и единственную вершину
с нулевой степенью исхода (t).
Будем считать, что веса c(e) неотрицательны. Числа c(e) будем называть пропускной способностью дуги e.
Слайд 71Потоки в сетях
Потоком в сети G называется функция
f : ER,
удовлетворяющая условиям:
0f(e)c(e) для всех eE;
f(v-)=f(v+) для всех vV \ {s,t}
Здесь
, а
Слайд 72Потоки в сетях
Величиной потока называется число , рав-ное
f(s+).
Поток f называется максимальным, если для любого потока f* выполняется
неравенство:
Слайд 73Потоки в сетях
Задача о максимальном потоке: в заданной сети найти
поток максимальной величины.
Слайд 74Потоки в сетях
(s,t)–разрезом (в дальнейшем, просто разре-зом) (Vs,Vt) в сети
G называется пара множеств Vs и Vt, удовлетворяющих условиям:
sVs, tVt
;
Vs Vt = V;
Vs Vt = .
Слайд 75Потоки в сетях
Для разреза (Vs,Vt) через E(VsVt) обозначим множество всех
дуг e, начала которых лежат в Vs, а концы —
в Vt, т.е.
Аналогично,
Слайд 76Потоки в сетях
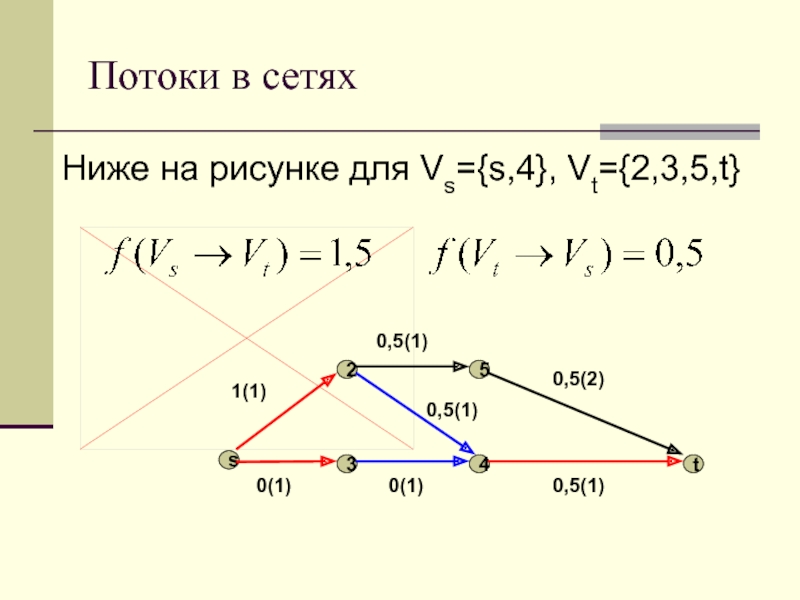
Ниже на картинке Vs={s,4}, Vt={2,3,5,t}.
На дугах указаны
поток и пропускная способ-ность (в скобках).
E(VsVt)={(s,2), (s,3), (4,t)};
E(VtVs)={(2,4), (3,4)}
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
Слайд 77Потоки в сетях
Для разреза (Vs,Vt)
Слайд 78Потоки в сетях
Ниже на рисунке для Vs={s,4}, Vt={2,3,5,t}
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
Слайд 79Потоки в сетях
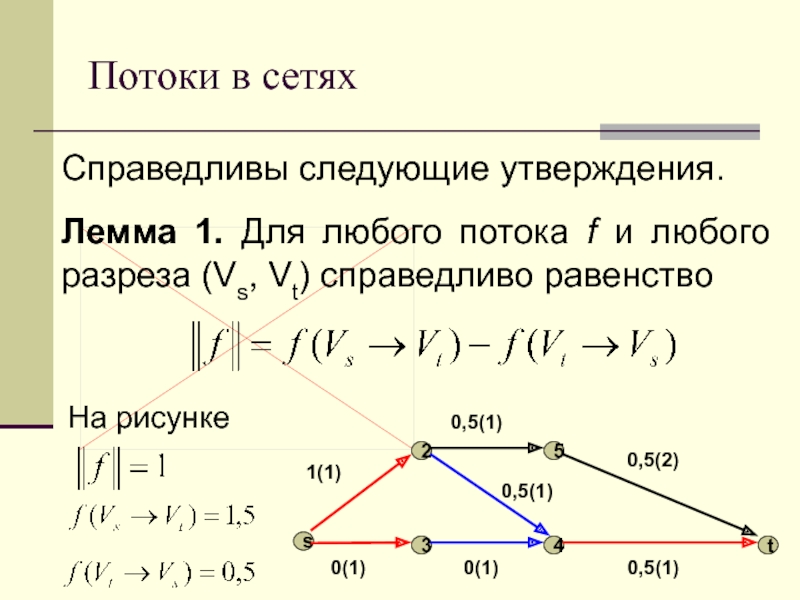
Справедливы следующие утверждения.
Лемма 1. Для любого потока f
и любого разреза (Vs, Vt) справедливо равенство
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
На рисунке
Слайд 80Потоки в сетях
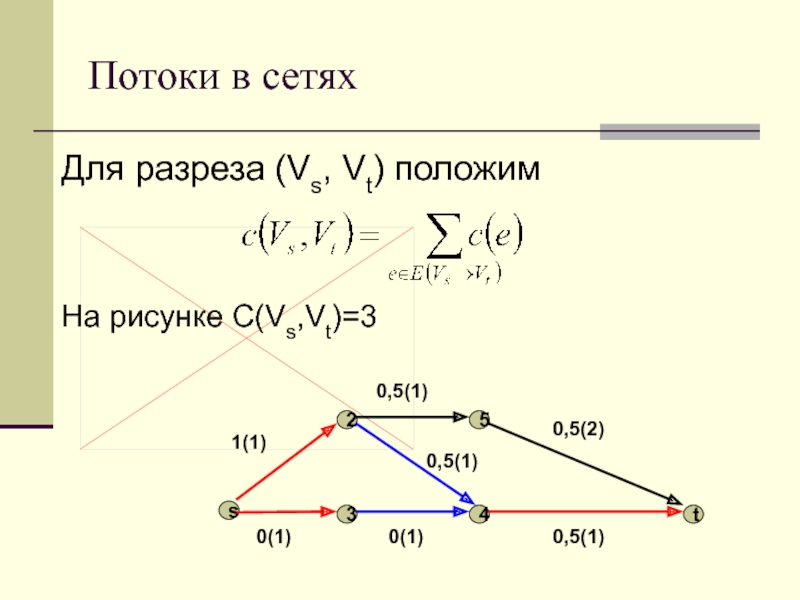
Для разреза (Vs, Vt) положим
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
На рисунке C(Vs,Vt)=3
Слайд 81Потоки в сетях
Справедливы следующие утверждения.
Следствие. Для любого потока f и
любого разреза (Vs, Vt) справедливо неравенство
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
На рисунке
Слайд 82Потоки в сетях
Разрез (Vs Vt) называется минимальным, если для любого
разреза (Vs*,Vt*) справедливо
Слайд 83Потоки в сетях
Лемма 2. Если для некоторого потока f* и
некоторого разреза (Vs*, Vt*) выполняется равенство то поток f* максима-лен, а
разрез (Vs*, Vt*) минимален.
s
4
3
2
5
t
1(1)
1(1)
1(2)
0(1)
1(1)
1(1)
1(1)
На рисунке
Слайд 84Потоки в сетях
Цепью из v в w в сети G
называется чередую-щаяся последовательность попарно различ-ных вершин и дуг
в которой
дуга er либо выходит из vr и входит в vr+1, либо, наоборот, выходит из vr+1 и входит в vr. В первом случае дуга называется прямой, во втором – обратной.
Слайд 85Потоки в сетях
Пусть P – цепь из v в w.
Для каждой дуги цепи P положим
Пусть
Цепь P из v в
w называется f-дополняющей, если h(P)>0.
Слайд 86Потоки в сетях
На рисунках цепи s-3-4-t и s-3-4-2-5-t являются f-дополняющими.
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
s
4
3
2
5
t
1(1)
0,5(1)
0,5(2)
0,5(1)
0(1)
0(1)
0,5(1)
Слайд 87Потоки в сетях
Лемма 3. Пусть f – поток в сети
G и P – f-до-полняющая (s,t)-цепь. Тогда в сети G
сущест-вует поток f* такой, что
Поток f* строится так:
Слайд 88Потоки в сетях
Теорема (Форда-Фалкерсона, 1956).
Для потока f в сети G
следующие условия эквивалентны:
поток f максимален;
не существует f-дополняющей цепи из s
в t;
существует разрез (Vs,Vt), для которого
Слайд 89Алгоритм
Форда-Фалкерсона
Потоки в сетях
Слайд 90Дэлберт Рей Фалкерсон
(14 августа 1924 10 января 1976)
Американский математик.
В
1956 году вместе с Лестером Рейнолдсом Фордом младшим разработал алгоритм
построения максимального потока в сетях.
Получил степень PhD в универси-тете Висконсин-Мэдисон в 1951.
В 1979 году была учреждена премия Фалкерсона, вручаемая каждые три года за выдающиеся достижения в области дискретной математики совместно матема-тико-программистским обществом и Американским математическим обществом.
Слайд 91Потоки в сетях
Алгоритм Форда-Фалкерсона
Работа алгоритма Форда-Фалкерсона базируется на идее, подсказанной
леммой 3.
положить f(e) = 0 для всех дуг eE;
для
текущего потока f искать f-дополня-ющую (s,t)-цепь;
если такая цепь P построена, то для всех прямых дуг цепи P положить
а для всех обратных и вернуться на шаг 2;
иначе СТОП.
Слайд 92Потоки в сетях
Алгоритм Форда-Фалкерсона
Однако, эффективность работы алгоритма зависит от способа
выбора f-дополняющих цепей. Ниже приведен пример, когда время работы алгоритма
не зависит от числа от размерности задачи, т.е. от m и n.
s
1
2
t
M
M
M
M
1
На дугах указаны их пропускные способнос-ти. Здесь M – достаточ-но большое целое чис-ло.
Слайд 93Потоки в сетях
Алгоритм Форда-Фалкерсона
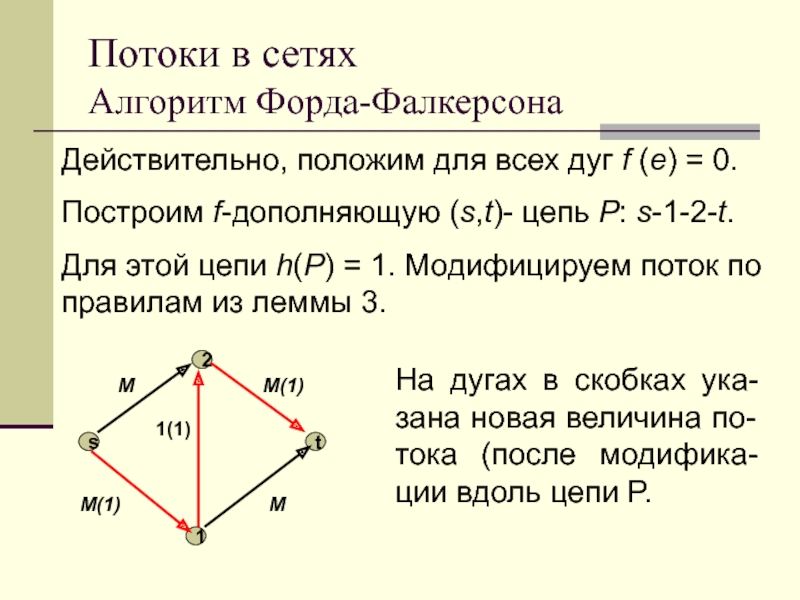
Действительно, положим для всех дуг f (e)
= 0.
Построим f-дополняющую (s,t)- цепь P: s-1-2-t.
Для этой
цепи h(P) = 1. Модифицируем поток по правилам из леммы 3.
s
1
2
t
M
M(1)
M(1)
M
1(1)
На дугах в скобках ука-зана новая величина по-тока (после модифика-ции вдоль цепи P.
Слайд 94Потоки в сетях
Алгоритм Форда-Фалкерсона
На следующем шаге построим f-дополняющую (s,t)-цепь P:
s-2-1-t.
Для этой цепи h(P) = 1. Модифицируем поток по
правилам из леммы 3.
s
1
2
t
M(1)
M(1)
M(1)
M(1)
1(0)
На дугах в скобках ука-зана новая величина по-тока (после модифика-ции вдоль цепи P.
Слайд 95Потоки в сетях
Алгоритм Форда-Фалкерсона
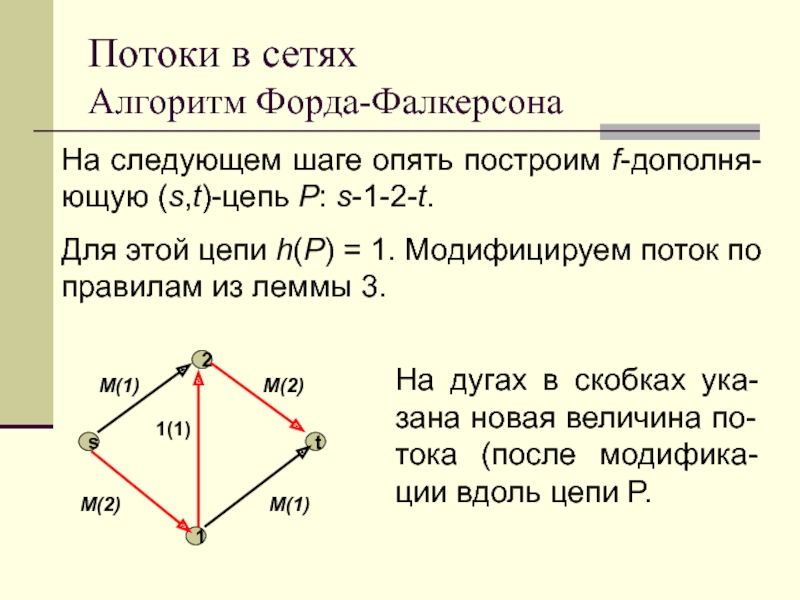
На следующем шаге опять построим f-дополня-ющую (s,t)-цепь
P: s-1-2-t.
Для этой цепи h(P) = 1. Модифицируем поток
по правилам из леммы 3.
s
1
2
t
M(1)
M(2)
M(2)
M(1)
1(1)
На дугах в скобках ука-зана новая величина по-тока (после модифика-ции вдоль цепи P.
Слайд 96Потоки в сетях
Алгоритм Форда-Фалкерсона
Далее на каждом нечетном шаге выбираем цепь
s-1-2-t, а на каждом четном шаге – цепь s-2-1-t. Каждый
раз поток увеличивается на единицу. Максимальный поток в этой сети равен 2M. Следовательно понадобится 2M итераций, т.е. их число не зависит от размерности задачи.
Слайд 97Потоки в сетях
Алгоритм Форда-Фалкерсона
На очередном шаге алгоритма следует отыскивать кратчайшие
по числу дуг f-дополняющие (s,t)- цепи!
Они могут быть найдены,
например, с помощью поиска в ширину.
Слайд 98Потоки в сетях
Алгоритм Форда-Фалкерсона
Отметим важное свойство:
если пропускные способности всех дуг
являются целочисленными, то как макси-мальный поток, так и все промежуточные
значения потока также являются цело-численными.
Слайд 99Потоки в сетях
Алгоритм Форда-Фалкерсона
Разберем пример. Пусть задана сеть (см. рисунок).
На дугах указаны их пропускные способности.
s
4
3
2
5
t
1
2
2
1
2
2
1
Слайд 100Потоки в сетях
Алгоритм Форда-Фалкерсона
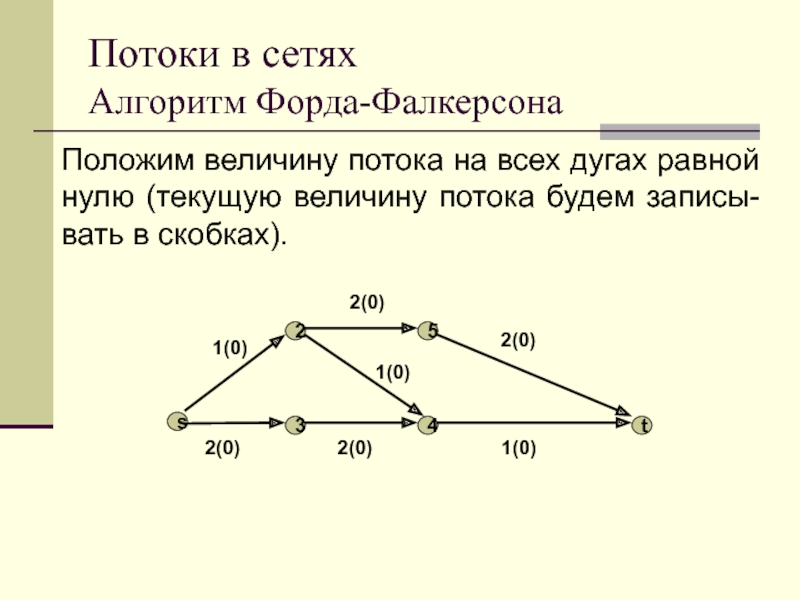
Положим величину потока на всех дугах равной
нулю (текущую величину потока будем записы-вать в скобках).
s
4
3
2
5
t
1(0)
2(0)
2(0)
1(0)
2(0)
2(0)
1(0)
Слайд 101Потоки в сетях
Алгоритм Форда-Фалкерсона
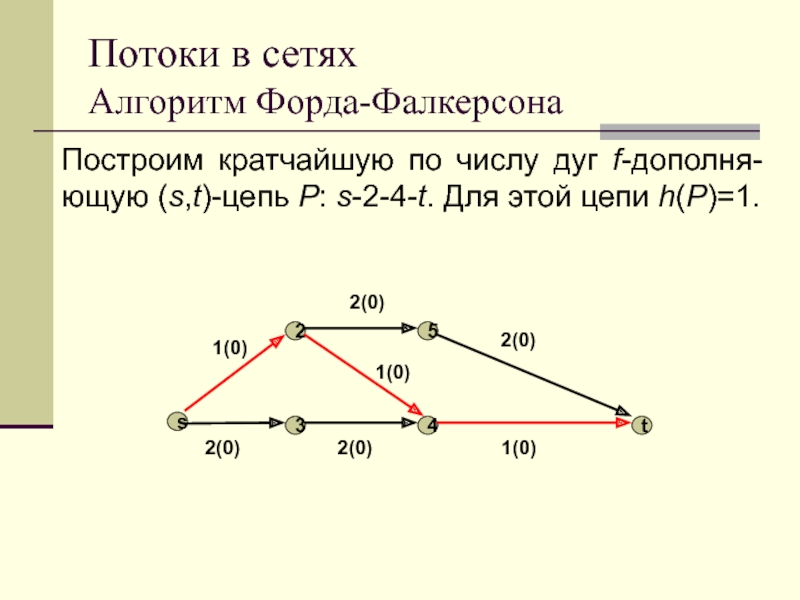
Построим кратчайшую по числу дуг f-дополня-ющую (s,t)-цепь
P: s-2-4-t. Для этой цепи h(P)=1.
s
4
3
2
5
t
1(0)
2(0)
2(0)
1(0)
2(0)
2(0)
1(0)
Слайд 102Потоки в сетях
Алгоритм Форда-Фалкерсона
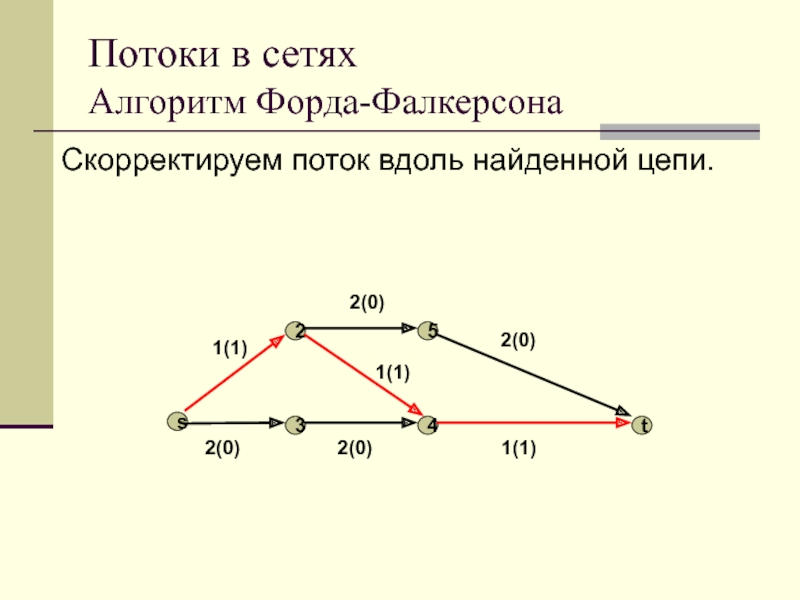
Скорректируем поток вдоль найденной цепи.
s
4
3
2
5
t
1(1)
2(0)
2(0)
1(1)
2(0)
2(0)
1(1)
Слайд 103Потоки в сетях
Алгоритм Форда-Фалкерсона
Построим кратчайшую по числу дуг f-дополня-ющую (s,t)-цепь
P: s-3-4-2-5-t. Для этой цепи h(P)=1. Дуга 4-2 ― обратная.
s
4
3
2
5
t
1(1)
2(0)
2(0)
1(1)
2(0)
2(0)
1(1)
Слайд 104Потоки в сетях
Алгоритм Форда-Фалкерсона
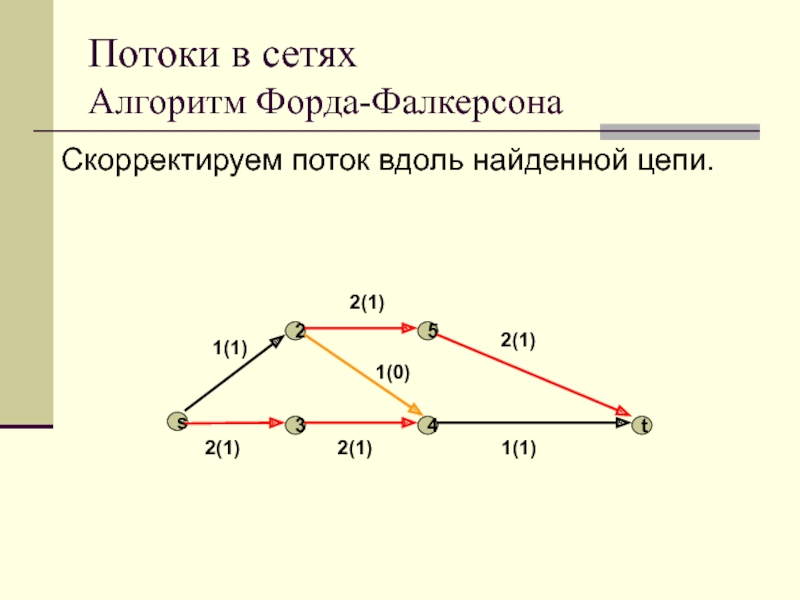
Скорректируем поток вдоль найденной цепи.
s
4
3
2
5
t
1(1)
2(1)
2(1)
1(0)
2(1)
2(1)
1(1)
Слайд 105Потоки в сетях
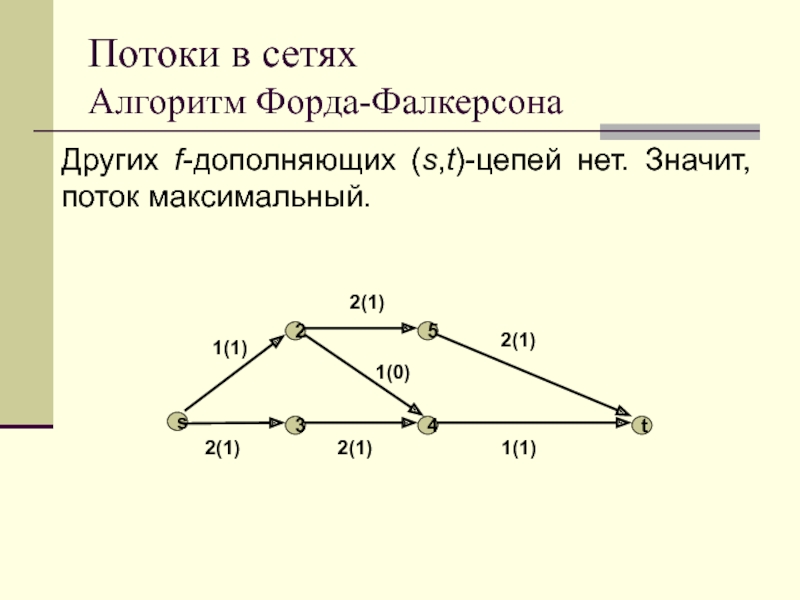
Алгоритм Форда-Фалкерсона
Других f-дополняющих (s,t)-цепей нет. Значит, поток максимальный.
s
4
3
2
5
t
1(1)
2(1)
2(1)
1(0)
2(1)
2(1)
1(1)
Слайд 106Потоки в сетях
Алгоритм Форда-Фалкерсона
Минимальный разрез строится так: Vs состоит из
концов всех f-дополняющих (s,v)-цепей. В данном случае Vs={s,3,4}, Vt={2,5,t}. Из
Vs в Vt ведут дуги (s,2) и (4,t). Значит, с(Vs,Vt)=1+1=2.
s
4
3
2
5
t
1(1)
2(1)
2(1)
1(0)
2(1)
2(1)
1(1)
Слайд 107Потоки в сетях
Алгоритм Форда-Фалкерсона
Задача. В стране имеется сеть железных дорог,
соединяющих M городов. Для двух заданных горо-дов A и B
требуется определить максимально воз-можное число поездов, которое можно пустить из A в B. Из-за конструктивных особенностей поездов и железных дорог никакие два поезда не могут про-езжать через один и от же город, исключая, конеч-но, города A и B. Железные дороги заданы парой городов, которые они соединяют. Проезд по ним возможен в любом направлении. Предложите ма-тематическую модель этой задачи как задачи опти-мизации на графе и опишите неформально алго-ритм ее решения.
Слайд 108Паросочетания в двудольных графах
Алгоритм Куна
Слайд 109Паросочетания в двудольных графах
Паросочетанием в графе называется произволь-ное множество его
ребер такое, что каждая вер-шина графа инцидентна не более, чем
одному реб-ру из этого множества.
Граф G=(V,E) называется двудольным, если мно-жество его вершин V можно разбить на непере-секающиеся множества X и Y такие, что каждое ребро eE имеет вид e=xy, где xX, yY.
Слайд 110Паросочетания в двудольных графах
Пусть M – паросочетание в графе G=(X,Y,E).
Говорят, что M сочетает x с y и y с
x, если xyM.
Вершины, не принадлежащие ни одному ребру из паросочетания, называют свободными относи-тельно M или просто свободными, а все прочие – насыщенными в M или просто насыщенными.
Удобно также все ребра, входящие в паросо-четание M называть M-темными или просто темными, а все прочие – M-светлыми или просто светлыми.
Слайд 111Паросочетания в двудольных графах
Паросочетание, содержащее наибольшее число ребер, называется наибольшим.
Паросочетание,
не содержащееся ни в каком дру-гом паросочетании, называется максимальным (по
включению).
Любое наибольшее паросочетание является ма-ксимальным. Обратное неверно.
Паросочетание, насыщающее все вершины дву-дольного графа, называется полным.
Слайд 112Паросочетания в двудольных графах
Пусть M – паросочетание в графе G.
M-чередующейся цепью называется такая последо-вательность вершин и ребер вида x0,
x0y1, y1, y1x2, x2, …, xk, xkyk+1, yk+1, где k > 0, что все вершины этой цепи различны, x0 и yk+1 – свободные, а все остальные вершины насыщенные в паросочетании M, причем каждое второе ребро принадлежит M (т.е. ребра вида yixi+1, i=1,…,k-1 входят в M), а остальные ребра в M не входят.
Слайд 113Паросочетания в двудольных графах
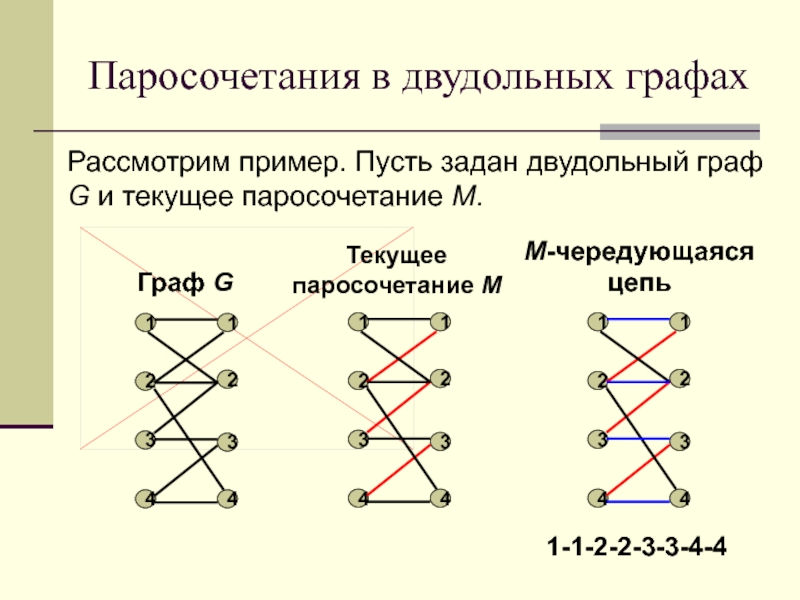
Рассмотрим пример. Пусть задан двудольный граф G
и текущее паросочетание M.
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
Граф G
Текущее
паросочетание M
1
2
3
4
1
2
3
4
1-1-2-2-3-3-4-4
M-чередующаяся цепь
Слайд 114Паросочетания в двудольных графах
Пусть M – текущее паросочетание и P
– построенная M-чередующаяся цепь. Операция MP определяется следующим образом: все
ребра из P, входившие в M из паросочетания исключаются, а все ребра из P, не входившие в M, в паросочетание добавляются. Другими словами,
В цепи P происходит «переключение цветов». Светлые ребра становятся темными и, наоборот, темные – светлыми.
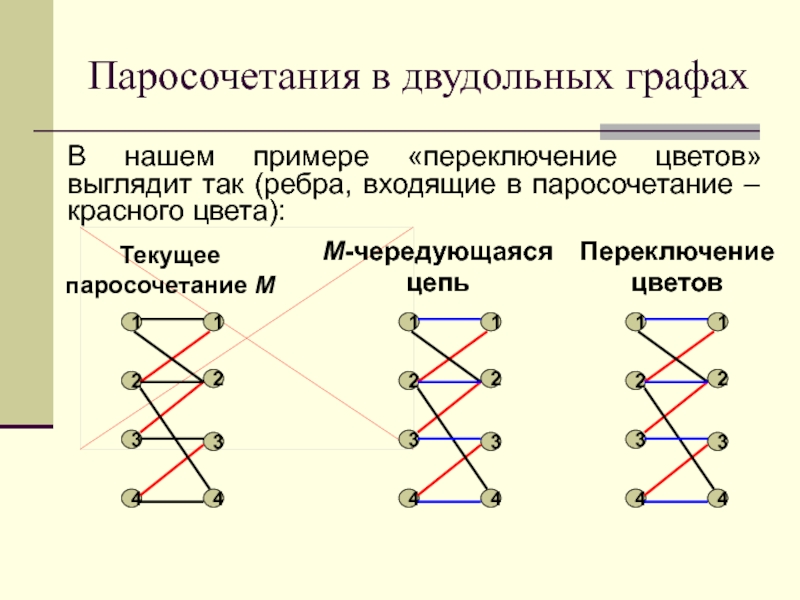
Слайд 115Паросочетания в двудольных графах
В нашем примере «переключение цветов» выглядит так
(ребра, входящие в паросочетание – красного цвета):
1
2
3
4
1
2
3
4
Текущее
паросочетание M
1
2
3
4
1
2
3
4
M-чередующаяся цепь
1
2
3
4
1
2
3
4
Переключение
цветов
Слайд 116Алгоритм Куна
Паросочетания в двудольных графах
Слайд 117Харольд Уиллиам Кун
(род. в 1925 году)
Американский математик. Специалист в области
теории игр. Профессор Принстонского университета. Автор Венгер-ского алгоритма (1955 год)
и соавтор теоремы Куна-Так-кера о необходимых условиях оптимальности в задаче мате-матического программирова-ния. В 1980 году удостоен приза Джона фон Неймана.
Слайд 118Неформально алгоритм может быть описан следующим образом.
Паросочетания в двудольных графах.
Алгоритм Куна
пустое паросочетание объявить текущим паросо-четанием M;
если все вершины из
X насыщены в M, то СТОП
(M – полное паросочетание);
иначе выбрать произвольную свободную вершину xX и искать M-чередующуюся цепь, начинающуюся в x;
если такая цепь P найдена, то положить M:=MP и вернуться на шаг 2;
иначе СТОП (полного паросочетания в заданном графе не существует).
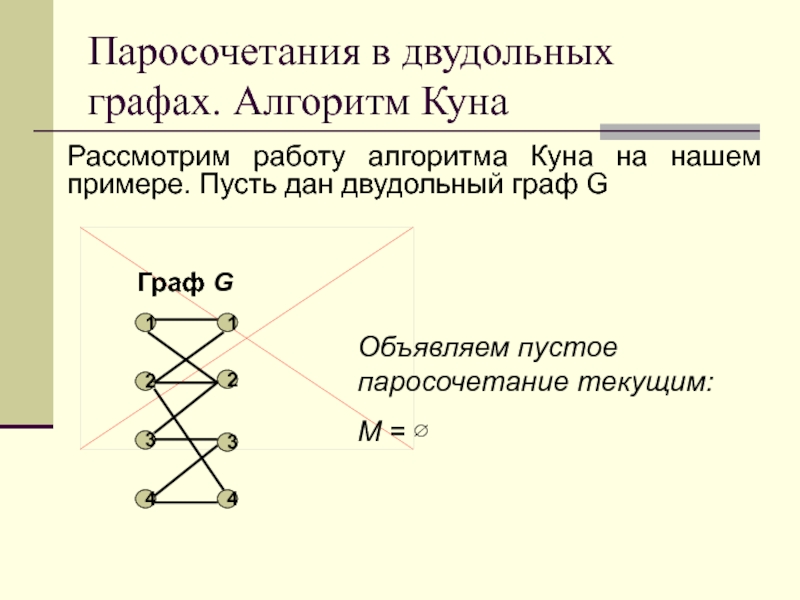
Слайд 119Паросочетания в двудольных графах. Алгоритм Куна
Рассмотрим работу алгоритма Куна на
нашем примере. Пусть дан двудольный граф G
1
2
3
4
1
2
3
4
Граф G
Объявляем пустое паросочетание
текущим:
M =
Слайд 120Паросочетания в двудольных графах. Алгоритм Куна
Будем просматривать вершины из доли
X в ес-тественном порядке. Находим первую M-чере-дующуюся цепь P: 1
– 1.
1
2
3
4
1
2
3
4
Граф G
Выполним операцию MP (переключаем цвета).
Новое текущее паросоче-тание
M={1-1}.
Слайд 121Паросочетания в двудольных графах. Алгоритм Куна
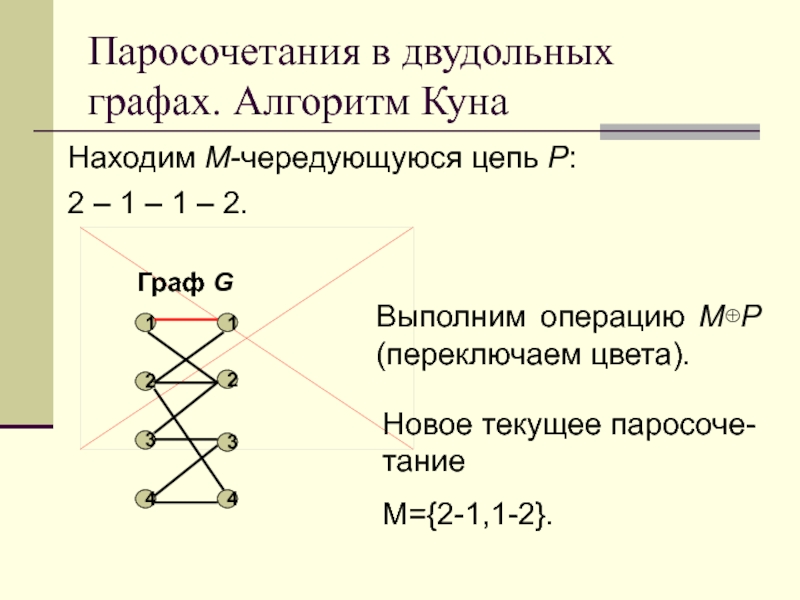
Находим M-чередующуюся цепь P:
2
– 1 – 1 – 2.
1
2
3
4
1
2
3
4
Граф G
Выполним операцию MP (переключаем
цвета).
Новое текущее паросоче-тание
M={2-1,1-2}.
Слайд 122Паросочетания в двудольных графах. Алгоритм Куна
Находим M-чередующуюся цепь P:
3 –
2 – 1 – 1 – 2 – 4.
1
2
3
4
1
2
3
4
Граф G
Выполним
операцию MP (переключаем цвета).
Новое текущее паросоче-тание
M={1-1, 2-4, 3-2}.
Слайд 123Паросочетания в двудольных графах. Алгоритм Куна
Находим M-чередующуюся цепь P:
4 –
4 – 2 – 1 – 1 – 2 –
3 – 3.
1
2
3
4
1
2
3
4
Граф G
Выполним операцию MP (переключаем цвета).
Новое текущее паросоче-тание
M={1-2, 2-1, 3-3, 4-4}.
Слайд 124Паросочетания в двудольных графах. Алгоритм Куна
Ненасыщенных вершин не осталось. Алгоритм
построил полное паросочетание.
1
2
3
4
1
2
3
4
Граф G
Слайд 125Задача о назначениях
Венгерский алгоритм
Слайд 126Задача о назначениях
Пусть G=(X,Y,E,c) – взвешенный двудольный граф, |X|=|Y|=n.
Весом паросочетания
M называется сумма весов входящих в него ребер.
Задача о назначениях:
в заданном взвешен-ном двудольном графе найти полное паросо-четание минимального веса (оптимальное паросочетание).
Слайд 127Задача о назначениях
Будем предполагать, что G – полный двудоль-ный граф
(т.е. любая пара вершин xX, yY соединена ребром). Это не
ограничивает общности, т.к. любую пару несмежных вершин можжно соединить ребром очень большого веса (например, большего суммы весов всех оставшихся ребер).
Слайд 128Венгерский алгоритм
Задача о назначениях
Слайд 129Задача о назначениях
Венгерский алгоритм
Идея работы венгерского алгоритма основана на нескольких
утверждениях.
Лемма 1. Если веса всех ребер графа, инци-дентных какой-либо вершине,
увеличить (уменьшить) на одно и то же число, то всякое оптимальное паросочетание в графе с новыми весами является оптимальным и в графе с исходными весами.
Слайд 130Задача о назначениях
Венгерский алгоритм
Эта лемма позволяет рассматривать только графы с
неотрицательными весами. Более того, каждой вершине этого графа оказывается инцидентна
хотя бы одна вершина нулевого веса.
Слайд 131Задача о назначениях
Венгерский алгоритм
Пусть X’X, Y’Y и d. Будем говорить,
что к графу G=(X,Y,E,c) применена операция (X’,d,Y’), если сначала из
веса каждого ребра, инцидентного вершине из X’, вычтено число d, а затем к весу каждого ребра, инцидентного вершине из Y’, прибавлено число d.
Слайд 132Задача о назначениях
Венгерский алгоритм
Справедлива следующая
Лемма 2. Пусть G=(X,Y,E,c) – двудольный
взвешенный граф с неотрицательными весами, X’X, Y’Y и d=min{c(x,y)|xX’, yY\Y’}.
Если к графу G применить операцию (X’,d,Y’), то
веса всех ребер G останутся неотрицатель-ными;
веса ребер вида xy, где xX’, yY’ или xX\X’, yY\Y’ не изменятся.
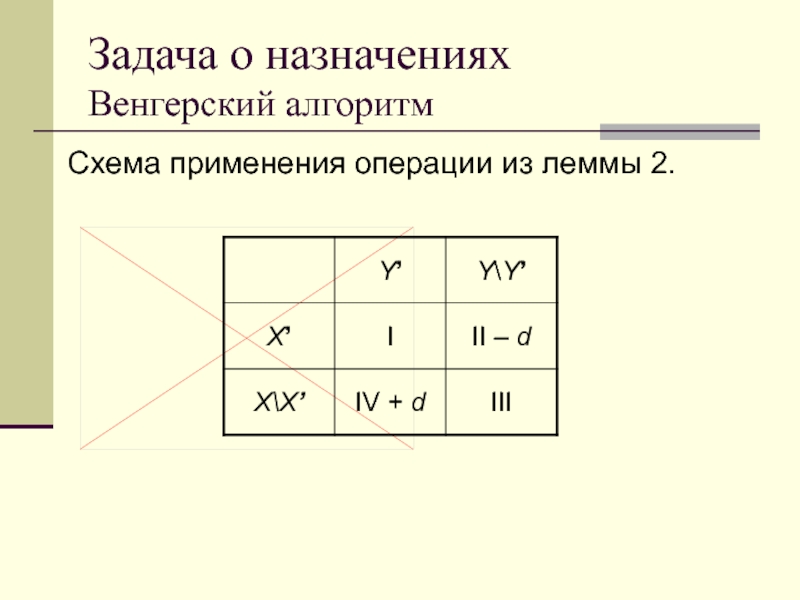
Слайд 133Задача о назначениях
Венгерский алгоритм
Схема применения операции из леммы 2.
Слайд 134Задача о назначениях
Венгерский алгоритм
Следующая лемма очевидна.
Лемма 3. Если веса всех
ребер графа неотри-цательны, и некоторое полное паросочетание состоит из ребер
нулевого веса, то оно явля-ется оптимальным.
Слайд 135Задача о назначениях
Венгерский алгоритм
В 1955 году Харольд Уиллиам Кун предложил
алгоритм решения задачи о назначениях, кото-рый принято называть Венгерским.
Слайд 136Задача о назначениях
Венгерский алгоритм
Преобразовать веса ребер так, чтобы веса всех
ребер стали неотрицательными и каждой вершине стало инцидентно хотя бы
одно ребро нулевого веса;
пустое паросочетание объявить текущим паросочетанием M;
если в графе все вершины насыщены относительно текущего паросочетания, то СТОП (текущее паросочетание оптимально);
иначе выбрать свободную вершину xX и искать M-чередующуюся цепь, начинающуюся в x, из ребер нулевого веса;
если такая цепь построена, то положить M:=MP и вернуться на шаг 3;
Слайд 137Задача о назначениях
Венгерский алгоритм
иначе для множества вершин X’X, Y’Y, помеченных
в ходе поиска (это вершины венгерского дерева), положить величину d
равной d=min{c(x,y)|xX’, yY\Y’} и применить к графу операцию (X’,d,Y’);
из тех вершин xX’, которым стало инцидентно хотя бы одно ребро нулевого веса, возобновить поиск M-чередующейся цепи по ребрам нулевого веса; если такая цепь P будет найдена, то положить M:=MP и вернуться на шаг 3; иначе вернуться на шаг 6 (множества X’ и Y’ при этом увеличатся).
Слайд 138Задача о назначениях
Венгерский алгоритм
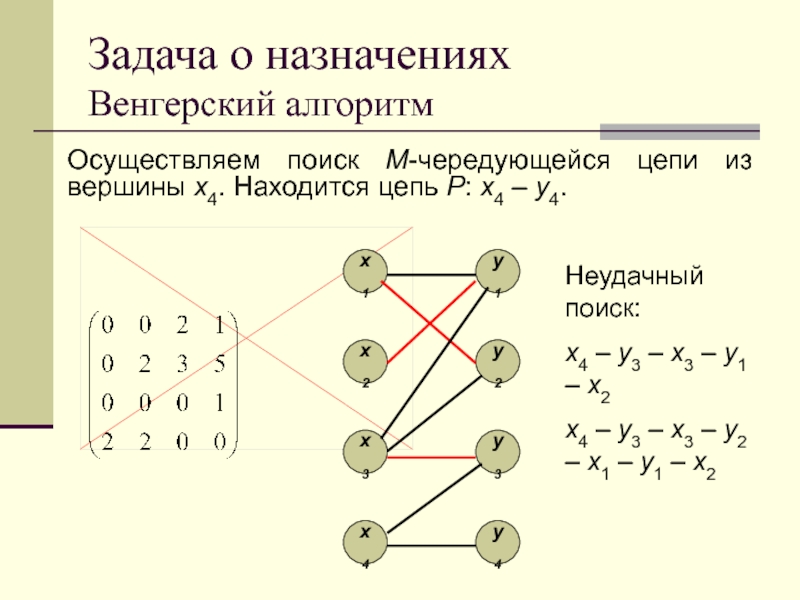
Рассмотрим пример работы венгерского алгоритма.
Пусть двудольный граф
задан своей матрицей весов:
На месте wij этой матрицы стоит вес
ребра, соединяющего верши-ны xi и yj.
Слайд 139Задача о назначениях
Венгерский алгоритм
Преобразуем веса так, чтобы каждой вершине оказа-лось
инцидентно ребро нулевого веса. Для этого из каждой строки матрицы
вычтем минимальный эле-мент строки.
Видим, что вершине y2 не инци-дентна ни одно ребро нулевого веса. Вычитаем из всех элемен-тов второго столбца его мини-мальный элемент.
Слайд 140Задача о назначениях
Венгерский алгоритм
Мы добились того, что каждой вершине инцидентно
как минимум одно ребро нулевого веса, и веса всех ребер
неотрицательны.
Слайд 141Задача о назначениях
Венгерский алгоритм
На рисунке будут отмечаться только ребра нулевого
веса.
x1
x2
x3
x4
y1
y2
y3
y4
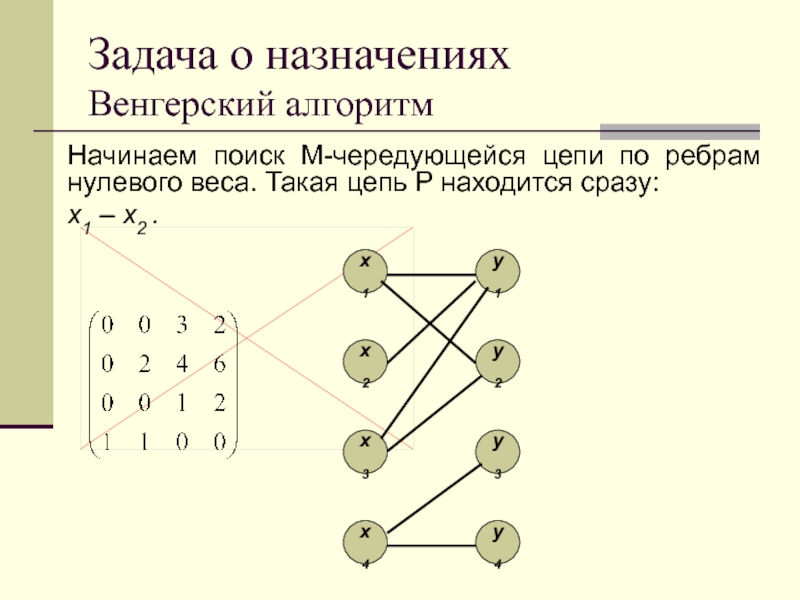
Слайд 142Задача о назначениях
Венгерский алгоритм
Начинаем поиск M-чередующейся цепи по ребрам нулевого
веса. Такая цепь P находится сразу:
x1 – x2 .
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 143Задача о назначениях
Венгерский алгоритм
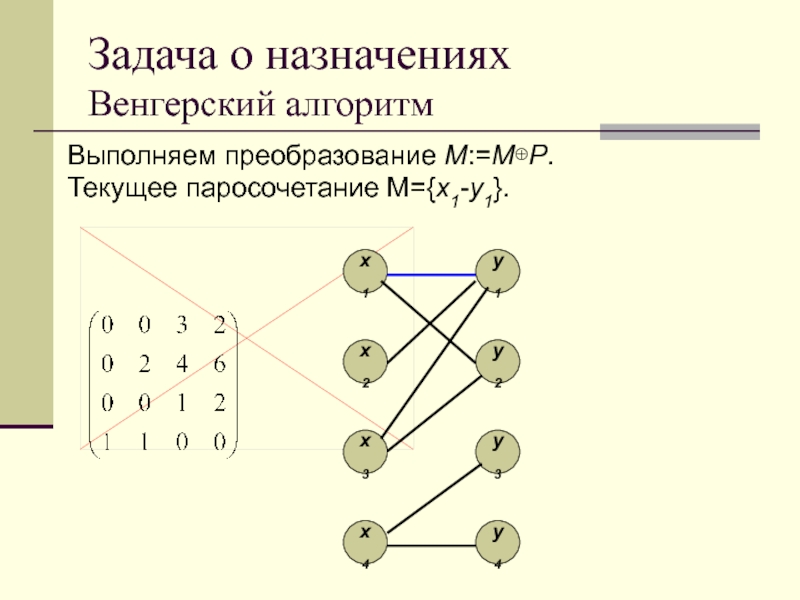
Выполняем преобразование M:=MP.
Текущее паросочетание M={x1-y1}.
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 144Задача о назначениях
Венгерский алгоритм
Ищем M-чередующуюся цепь из вершины x2 по
ребрам нулевого веса.
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 145Задача о назначениях
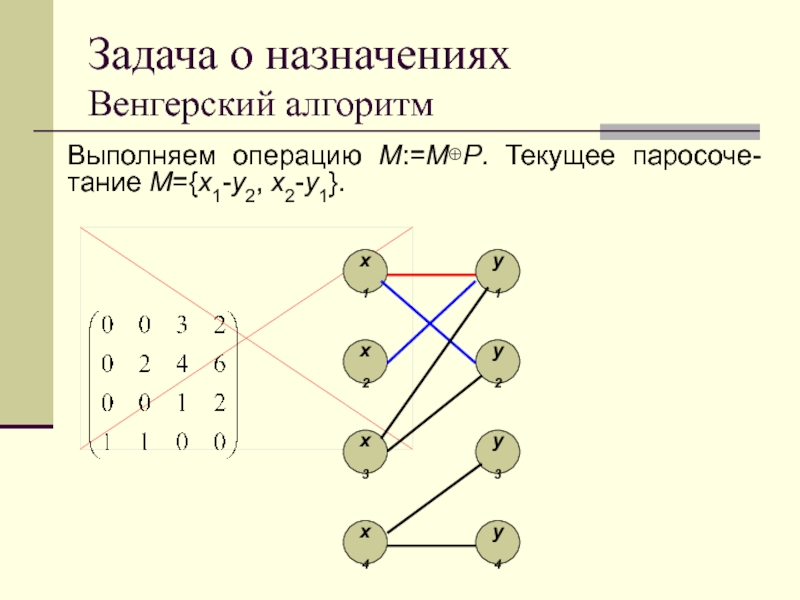
Венгерский алгоритм
Выполняем операцию M:=MP. Текущее паросоче-тание M={x1-y2, x2-y1}.
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 146Задача о назначениях
Венгерский алгоритм
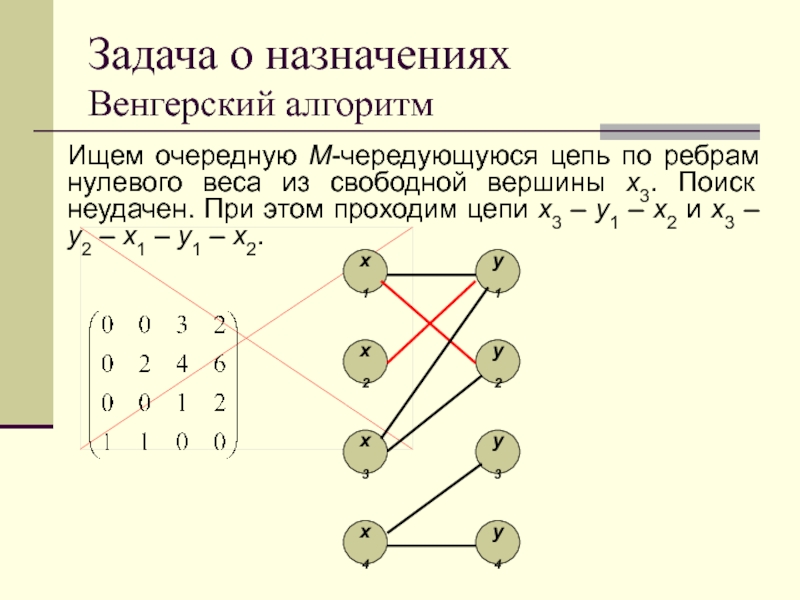
Ищем очередную M-чередующуюся цепь по ребрам нулевого
веса из свободной вершины x3. Поиск неудачен. При этом проходим
цепи x3 – y1 – x2 и x3 – y2 – x1 – y1 – x2.
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 147Задача о назначениях
Венгерский алгоритм
x1
x2
x3
x4
y1
y2
y3
y4
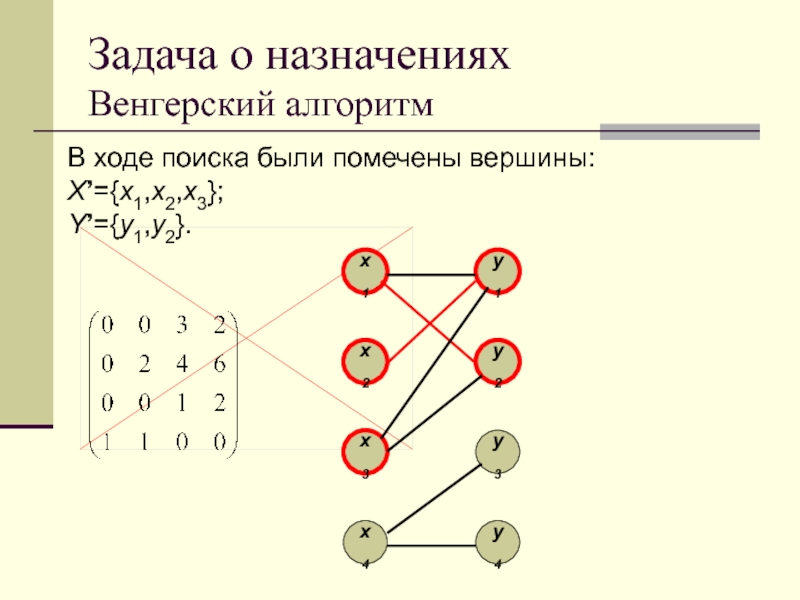
В ходе поиска были помечены вершины:
X’={x1,x2,x3};
Y’={y1,y2}.
Слайд 148Задача о назначениях
Венгерский алгоритм
x1
x2
x3
x4
y1
y2
y3
y4
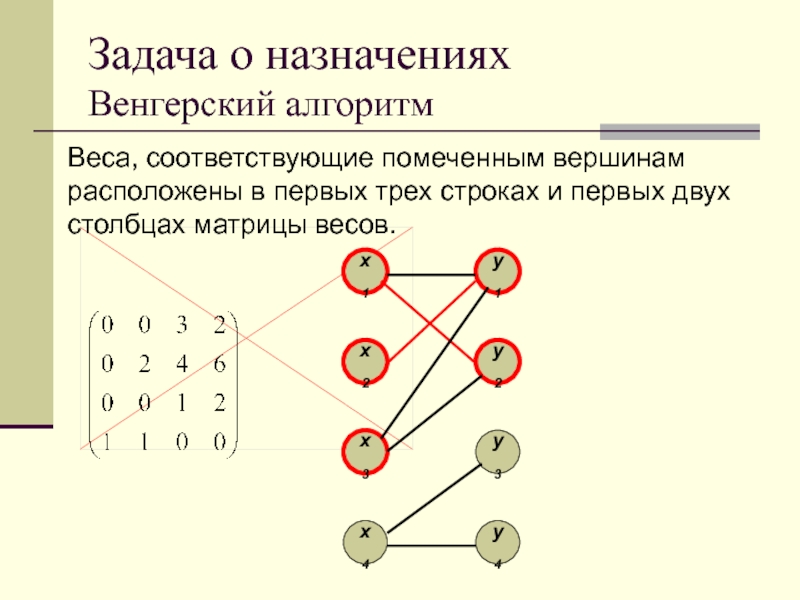
Веса, соответствующие помеченным вершинам расположены в первых
трех строках и первых двух столбцах матрицы весов.
Слайд 149Задача о назначениях
Венгерский алгоритм
x1
x2
x3
x4
y1
y2
y3
y4
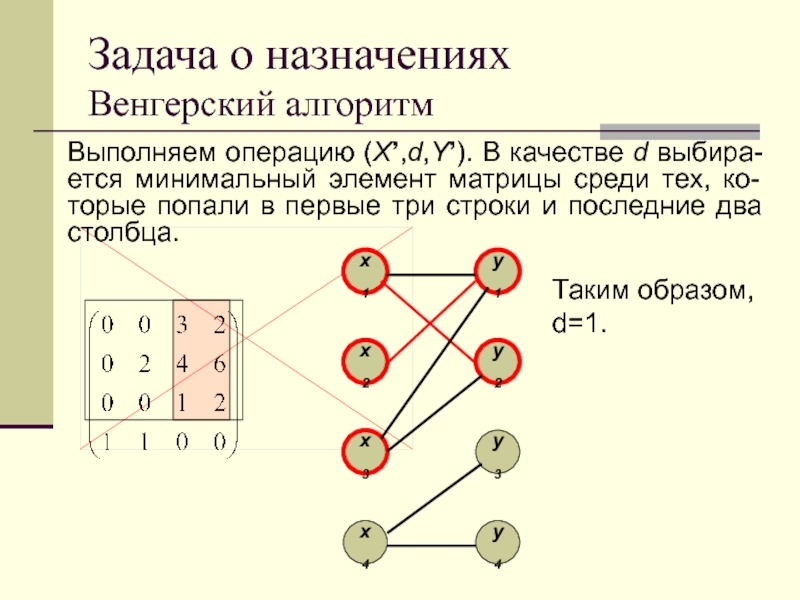
Выполняем операцию (X’,d,Y’). В качестве d выбира-ется
минимальный элемент матрицы среди тех, ко-торые попали в первые три
строки и последние два столбца.
Таким образом, d=1.
Слайд 150Задача о назначениях
Венгерский алгоритм
В результате применения операции (X’,d,Y’) матрица весов
преобразуется к следующему виду:
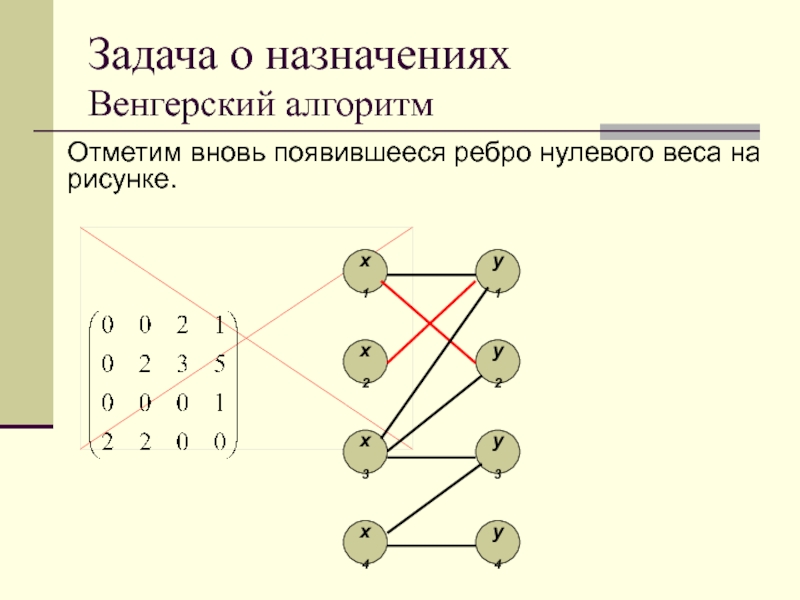
Множество ребер нулевого ве-са пополнилось. Появилось ребро
x3-y3.
Слайд 151Задача о назначениях
Венгерский алгоритм
Отметим вновь появившееся ребро нулевого веса на
рисунке.
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 152Задача о назначениях
Венгерский алгоритм
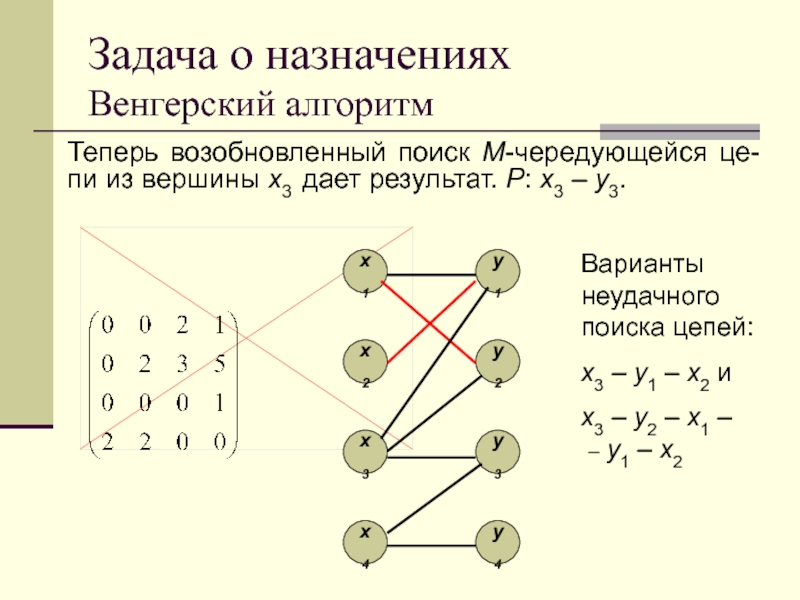
Теперь возобновленный поиск M-чередующейся це-пи из вершины
x3 дает результат. P: x3 – y3.
x1
x2
x3
x4
y1
y2
y3
y4
Варианты неудачного поиска цепей:
x3
– y1 – x2 и
x3 – y2 – x1 –
– y1 – x2
Слайд 153Задача о назначениях
Венгерский алгоритм
Преобразуем текущее паросочетание M:=MP.
Текущее паросочетание M={x1-y2, x2-y1,
x3-y3}.
x1
x2
x3
x4
y1
y2
y3
y4
Слайд 154Задача о назначениях
Венгерский алгоритм
Осуществляем поиск M-чередующейся цепи из вершины x4.
Находится цепь P: x4 – y4.
x1
x2
x3
x4
y1
y2
y3
y4
Неудачный поиск:
x4 – y3 –
x3 – y1 – x2
x4 – y3 – x3 – y2 – x1 – y1 – x2
Слайд 155Задача о назначениях
Венгерский алгоритм
Все вершины насыщены. Следовательно, перед на-ми полное
паросочетание наименьшего веса.
x1
x2
x3
x4
y1
y2
y3
y4
Его вес равен 12.
Слайд 156Задача о назначениях
Венгерский алгоритм
Рассмотрим задачу. Требуется выполнить n видов работ,
для выполнения которых имеется n видов станков . Каждая работа
должна быть выполнена на каком-нибудь одном станке, и на каждом станке можно выполнить не более одной работы. Для каждой пары (i-ая работа – j-ый станок) известно время выполнения cij.Требуется распределить работы по станкам так, чтобы все работы были выполнены, и суммарное время выполнения работ было минимальным.
Предложите математическую модель этой задачи как задачи оптимизации на графе и опишите в неформализованном виде алгоритм ее решения.
![Минимальный остовПоследовательность строится таким образом, чтобы для каждого i (i[1,n-1]) остовный лес можно было бы продолжить до](/img/thumbs/1f12fa441f01f2056e83d12fc53d066d-800x.jpg "Комбинаторные алгоритмы Минимальный остовПоследовательность строится таким образом, чтобы для каждого i (i[1,n-1]) остовный")
![Пути в сетях Алгоритм Форда – БеллманаДля описания алгоритма будем использовать следующие обозначения:D[v] – массив, в котором](/img/thumbs/013fe35d9f85f58e60928ce106f68053-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм Форда – БеллманаДля описания алгоритма будем использовать")
![Пути в сетях Алгоритм Форда – БеллманаДля всех вершин v из V положить D[v]:=c(s,v), Если c(s,v)](/img/thumbs/951eee4cfa64f5c3f0aca8d2bf87ac0f-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм Форда – БеллманаДля всех вершин v из V положить D[v]:=c(s,v), Если c(s,v)")
![Пути в сетях Алгоритм Форда – БеллманаПроизведем перерасчет значений D[v] третий и последний раз. Работа алгоритма закончена.](/img/thumbs/e9c23296e6701cd4a12d3f2f358d9c9e-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм Форда – БеллманаПроизведем перерасчет значений D[v] третий")
![Пути в сетях Алгоритм ДейкстрыДля описания алгоритма будем использовать следующие обозначения:D[v] – метки вершин, в которых будет](/img/thumbs/a68885cae8c3060b44b6b18b9c447a5c-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм ДейкстрыДля описания алгоритма будем использовать следующие обозначения:D[v]")
![Пути в сетях Алгоритм ДейкстрыD[s]:=0; ПРЕДШ[s]:=0; F:=V\{s}для всех v из F положим D[v]:=c[s,v]; ПРЕДШ[v]:=s;n-1 раз делать выбрать wF: D[w]](/img/thumbs/af15e0e46b7416500ff4ec1d614c09d9-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм ДейкстрыD[s]:=0; ПРЕДШ[s]:=0; F:=V\{s}для всех v из F")
![Пути в сетях Алгоритм Форда – БеллманаПроизведем перерасчет значений D[v] первый раз.](/img/thumbs/8941f0131d26d8e90993ed12eb493009-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм Форда – БеллманаПроизведем перерасчет значений D[v] первый раз.")
![Пути в сетях Алгоритм Форда – БеллманаПроизведем перерасчет значений D[v] второй раз.](/img/thumbs/8c4dd36dd6469c81f149e43d40d93403-800x.jpg "Комбинаторные алгоритмы Пути в сетях Алгоритм Форда – БеллманаПроизведем перерасчет значений D[v] второй раз.")
