Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм построения выпуклой оболочки
Содержание
- 1. Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм построения выпуклой оболочки
- 2. Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм
- 3. РАНДОМИЗИРОВАННЫЕ АЛГОРИТМЫ В ЗАДАЧАХ ВЫЧИСЛИТЕЛЬНОЙ ГЕОМЕТРИИРандомизированная пошаговая
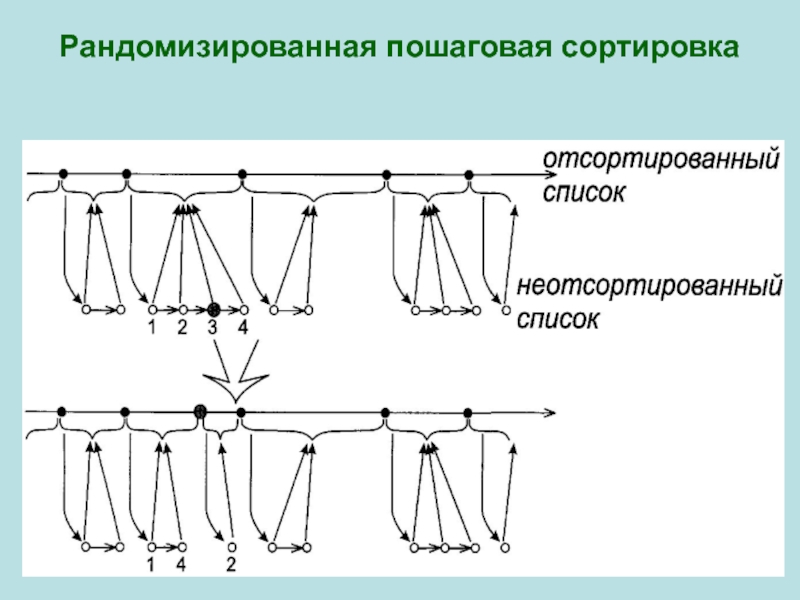
- 4. Рандомизированная пошаговая сортировка
- 5. Рандомизированная пошаговая сортировкаКакая работа требуется, чтобы сохранить
- 6. Рассмотрим работу, проделанную на i-ом шаге Обратный
- 7. Работана i-ом шаге Каково ожидаемое число указателей,
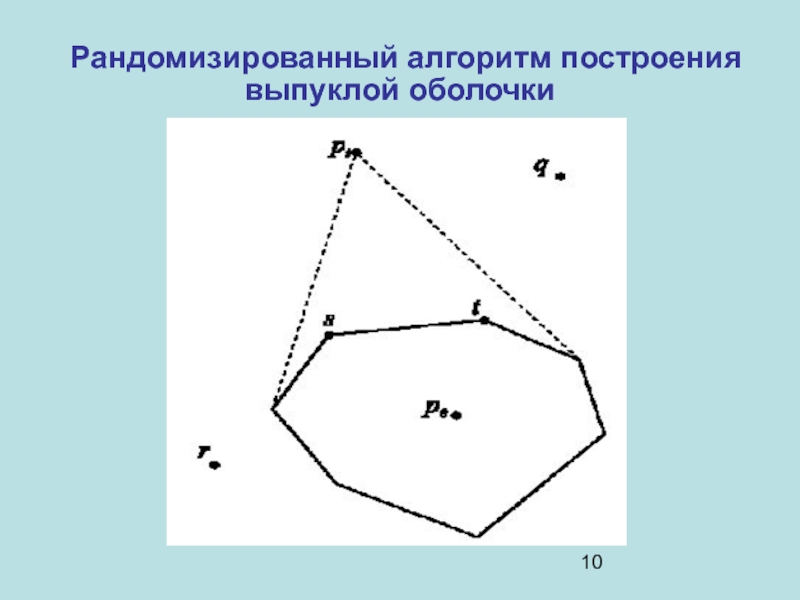
- 8. Рандомизированный алгоритм построения выпуклой оболочки S
- 9. Пример работы алгоритма1.
- 10. Рандомизированный алгоритм построения выпуклой оболочки
- 11. Пошаговое описание 1. Построить выпуклую оболочку из
- 12. 2.Построение произвольного треугольника
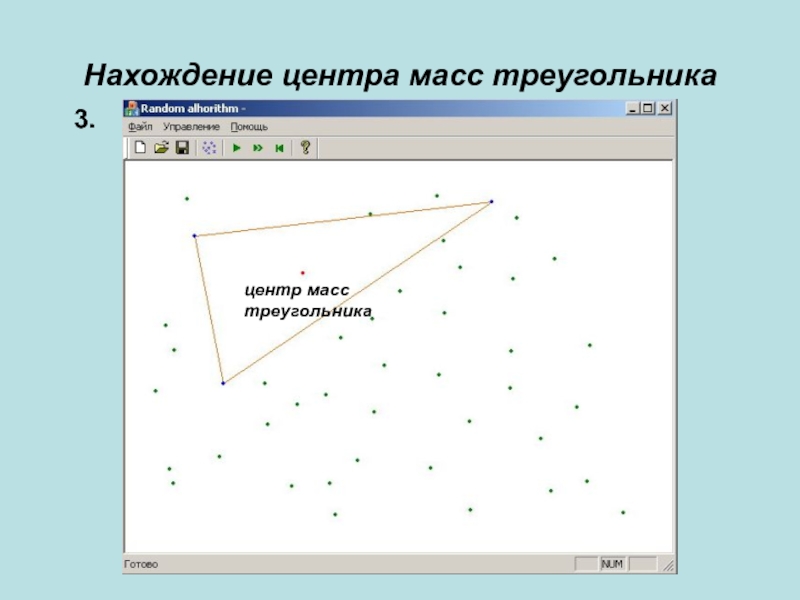
- 13. Нахождение центра масс треугольника3.центр масс треугольника
- 14. 4.
- 15. По шаговое описание (продолжение)4. ПОКА (S\Si-1 не
- 16. Нахождение соседних вершин для выбранной точки5.выбранная точкаправая соседняявершина левая соседняявершина
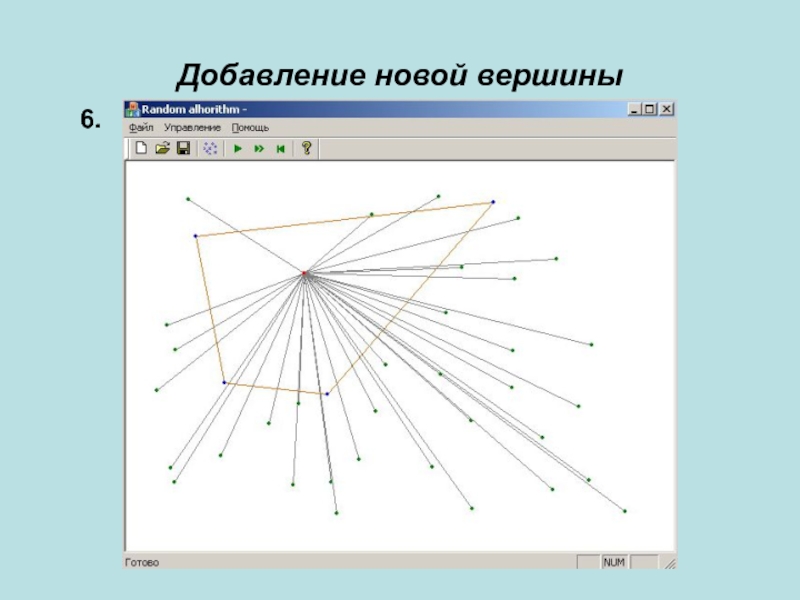
- 17. Добавление новой вершины6.
- 18. Построенная выпуклая оболочка7.
- 19. Теорема: Среднее время работы описанного выше рандомизированного
- 20. Скачать презентанцию
Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм построения выпуклой оболочки Рандомизированные геометрические алгоритмы Рандомизированная пошаговая конструкция: n объектов, составляющих входные данные к задаче, рассматриваются по одному в каждый момент времени
Слайды и текст этой презентации
Слайд 1Комбинаторные алгоритмы вычислительной геометрии
Рандомизированный алгоритм построения выпуклой оболочки
Слайд 2Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм построения выпуклой оболочки Рандомизированные геометрические
Слайд 3РАНДОМИЗИРОВАННЫЕ АЛГОРИТМЫ В ЗАДАЧАХ ВЫЧИСЛИТЕЛЬНОЙ ГЕОМЕТРИИ
Рандомизированная пошаговая сортировка
Дано n чисел,
которые нужно отсортировать.
Схема сортировки:
После i-ого из n шагов (1
< i < n) имеем i вставленных чисел в отсортированном списке. Эти i отсортированных чисел разобьют ранги (n-i) еще не отсортированных чисел на (i+1) интервалов.
(i+1)-ый шаг состоит в выборе одного из (n-i) еще не отсортированных чисел случайным образом и вставки его в отсортированный список.
Слайд 5Рандомизированная пошаговая сортировка
Какая работа требуется, чтобы сохранить указатели на каждое
число?
Мы вставляем число х, указатель которого указывает на интервал
I. При вставке х, мы имеем три задачи:
найти все числа, указатели которых указывают на I;
(2) обновить указатели всех чисел, чьи указатели указывают на I;
(3) удалить указатель от х к I.
Слайд 6Рассмотрим работу, проделанную на i-ом шаге
Обратный анализ:
представим, что
алгоритм выполняется назад, начиная с того,
что уже имеется отсортированный
список. При анализе i-ого шага прямого алгоритма мы представляем, что удаляется одно из i чисел в
отсортированном списке и обновляются указатели.
Работа по обновлению указателей в этом случае такая же, как если бы алгоритм выполнялся вперед как обычно.
Ключевой момент в обратном анализе:
так как в первоначальном алгоритме числа были добавлены в произвольном порядке,
то в обратном анализе мы можем принять, что каждое число в отсортированном списке равновероятно может быть удалено на этом шаге.
Рандомизированная пошаговая сортировка
Слайд 7Работана i-ом шаге
Каково ожидаемое число указателей, которые должны быть
обновлены на этом шаге?
Так как у нас i интервалов
и (n-i+1) указателей, оставшихся после удаления, то ожидаемое число указателей, которые были изменены на i-ом шаге - О((n-i)/i), которое есть О(n/i).Просуммируем проделанную работу по всем шагам и получим верхнюю границу математического ожидания полной работы. Так как
где γ - константа Эйлера, то получаем O( ) =
= О(n lоg n).
Рандомизированная пошаговая сортировка
Слайд 8 Рандомизированный алгоритм построения выпуклой оболочки
S – множество всех
точек на плоскости;
conv(S) – выпуклая оболочка множества S;
Для упрощения
предполагаем, что в S нет трех точек лежащих на одной прямой Слайд 11Пошаговое описание
1. Построить выпуклую оболочку из трех точек conv(S3).
2.
Найти точку р0 во внутренней области conv(S) - это центр
масс треугольника conv(S3).3. Для каждой точки p определить ребро conv(S3), пересекаемое отрезком pp0, и сформировать двунаправленный указатель от р на ребро и обратно. При это исключить из дальнейшего рассмотрения точки, находящиеся внутри conv(S3).
Рандомизированный алгоритм построения выпуклой оболочки
Слайд 15По шаговое описание (продолжение)
4. ПОКА (S\Si-1 не пусто) {
Выбрать случайным
образом точку pi из S\Si-1;
Найти в conv(Si-1) вершину v1, которая
является левой соседней (опорной) для pi в conv(Si). В процессе поиска запомнить в списке recheck указатели от удаляемых ребер;Найти в conv(Si-1) вершину v2, которая является правой соседней (опорной) для pi в conv(Si), дополнив при этом список recheck указателями от удаляемых ребер;
Вставить pi в выпуклую оболочку, сформировав conv(Si);
Для каждой точки , указатель на которую содержится в списке recheck, обновить её указатель на ребро conv(Si), пересекаемое отрезком рр0, указав его на [pi,v1] или [pi,v2]. При этом исключить из дальнейшего рассмотрения точки, которые попадают внутрь conv(Si);
}