Комбинация круглых тел и многогранников ( часть2)

Содержание

1. Комбинация круглых тел и многогранников ( часть2)
2. Матрица комбинаций
3. Конус вписан в пирамидуКонус называется вписанным в
4. Конус вписан в пирамиду 1.Конус с образующей
5. 3. В пирамиду, в основании которой
6. 4. В треугольную пирамиду, стороны основания которой
7. Цилиндр вписан в конусhH-hrRSOACh- высота цилиндраH-
8. hH-hrRSODCh- высота призмыH- высота конусаr –
9. hH-hrRSOEKh- высота цилиндраH- высота пирамидыr –
10. Матрица комбинаций
11. Скачать презентанцию

Матрица комбинаций

Главная
Разное
Комбинация круглых тел и многогранников ( часть2)

Слайды и текст этой презентации

Слайд 1Комбинация круглых тел и многогранников ( часть2)

Слайд 2Матрица комбинаций

Слайд 3Конус вписан в пирамиду
Конус называется вписанным в пирамиду,
если его

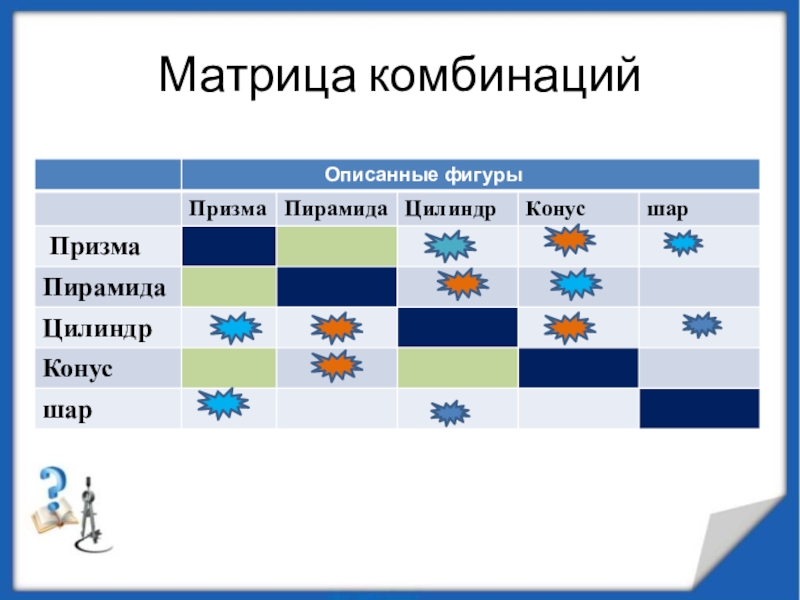
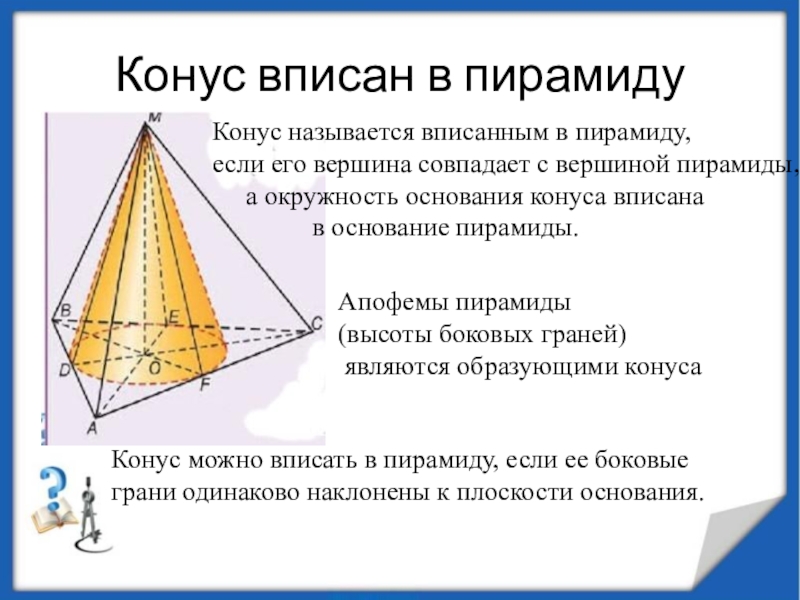
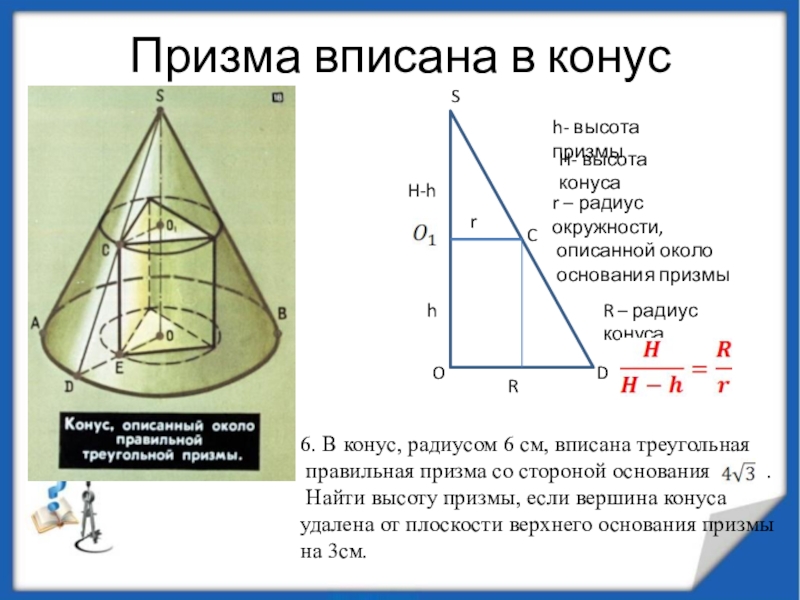
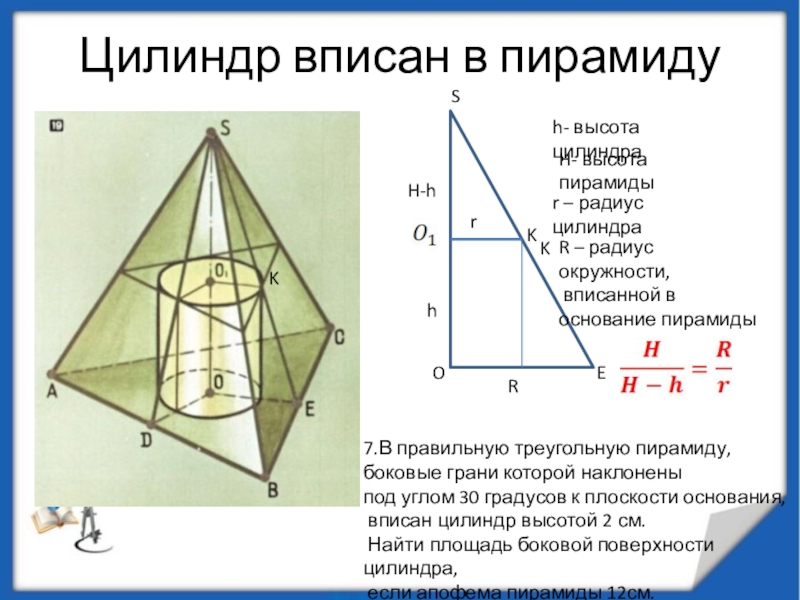
вершина совпадает с вершиной пирамиды,
а окружность

основания конуса вписана
в основание пирамиды.

Апофемы пирамиды
(высоты боковых граней)
являются образующими конуса

Конус можно вписать в пирамиду, если ее боковые грани одинаково наклонены к плоскости основания.

Конус вписан в пирамидуКонус называется вписанным в пирамиду, если его вершина совпадает с вершиной пирамиды,

Слайд 4Конус вписан в пирамиду
1.Конус с образующей 5 см, вписан

в правильную треугольную пирамиду со
стороной основания .

Найти высоту конуса.

2. Образующая конуса наклонена к плоскости основания под углом 45 градусов. Конус вписан в правильную четырехугольную пирамиду со стороной основания 10 см. Найти высоту пирамиды.

Конус вписан в пирамиду 1.Конус с образующей 5 см, вписан в правильную треугольную пирамиду со стороной основания

Слайд 53. В пирамиду, в основании которой ромб с диагоналями 30

и 40 см, вписан конус с образующей 20 см. Найти

высоту пирамиды.

Радиус окружности, вписанной в основание пирамиды

3. В пирамиду, в основании которой ромб с диагоналями 30 и 40 см, вписан конус

Слайд 64. В треугольную пирамиду, стороны основания которой 7, 24 и

25 см, вписан конус с высотой 4 см. Найти образующую

этого конуса, если двугранные углы при основании пирамиды равны.

MF- апофема пирамиды
и образующая конуса
OF- радиус конуса и радиус окружности, вписанной в основание пирамиды.
Площадь треугольника
p- полупериметр треугольника,
r – радиус окружности, вписанной в треугольник
Формула Герона для площади треугольника

4. В треугольную пирамиду, стороны основания которой 7, 24 и 25 см, вписан конус с высотой 4

Слайд 7 Цилиндр вписан в конус
h
H-h
r
R
S
O
A
C
h- высота цилиндра
H- высота конуса
r –

радиус цилиндра
R – радиус конуса
5. Высота конуса 4см, а высота

вписанного в него цилиндра – 3см.
Образующая конуса 5 см.
Найдите площадь боковой поверхности цилиндра

Цилиндр вписан в конусhH-hrRSOACh- высота цилиндраH- высота конусаr – радиус цилиндраR – радиус конуса5. Высота конуса

Слайд 8
h
H-h
r
R
S
O
D
C
h- высота призмы
H- высота конуса
r – радиус окружности,
описанной

около
основания призмы

R – радиус конуса
6. В конус, радиусом 6

см, вписана треугольная
правильная призма со стороной основания .
Найти высоту призмы, если вершина конуса
удалена от плоскости верхнего основания призмы
на 3см.

Призма вписана в конус

hH-hrRSODCh- высота призмыH- высота конусаr – радиус окружности, описанной около основания призмыR – радиус конуса6. В

Слайд 9
h
H-h
r
R
S
O
E
K
h- высота цилиндра
H- высота пирамиды
r – радиус цилиндра

R –

радиус окружности,
вписанной в
основание пирамиды
7.
Цилиндр вписан в пирамиду
K
K
7.В правильную

треугольную пирамиду,
боковые грани которой наклонены
под углом 30 градусов к плоскости основания,
вписан цилиндр высотой 2 см.
Найти площадь боковой поверхности цилиндра,
если апофема пирамиды 12см.