Комплексные числа и действия над ними

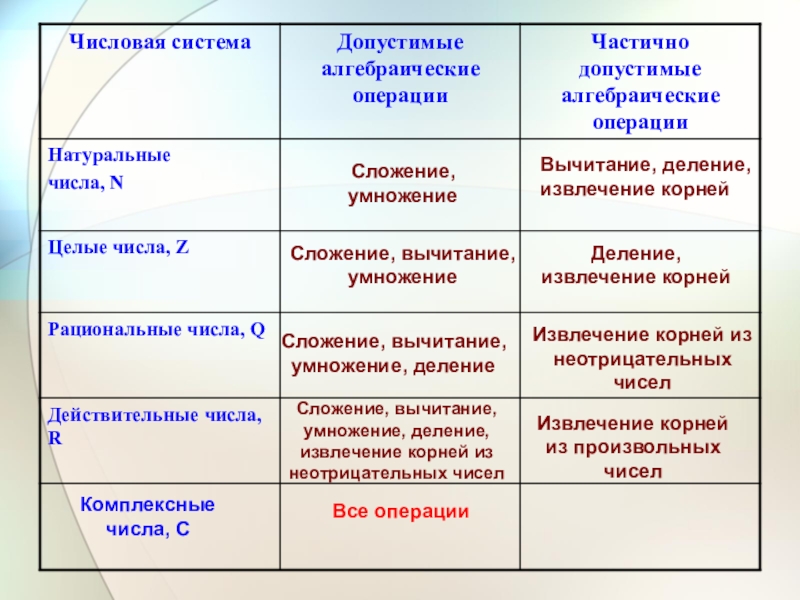
умножение, деление
Извлечение корней из неотрицательных чисел

Сложение, вычитание, умножение, деление, извлечение

Извлечение корней из произвольных чисел

Комплексные числа, C

Все операции

известная величина. Решение этого
уравнения можно записать как:

x = 0.

Здесь возможны три случая:

два значения: одно положительное, другое отрицательное; например, уравнение x 2

2 случай:

решений среди известных нам положительных и отрицательных чисел, потому что

3 случай:

a также и для отрицательных значений а , мы вынуждены

Согласно этому определению мнимых чисел мы можем определить и мнимую

два мнимых корня:

— чисто мнимые числа
Арифметические операции над чисто мнимыми числами выполняются

где a и b — действительные числа.

В общем виде правила арифметических операций с чисто мнимыми числами таковы:

чисто мнимого числа.
Определение 2. Два комплексных числа называют равными,

a + b i ,

где a, b – действительные числа,

≠ o
Рациональные
числа

Иррациональные
числа

Мнимые числа с
ненулевой
действительной
частью
a ≠

Чисто
мнимые
числа
a = 0, b ≠ 0.

об алгебраических правилах» Кардано (1545), который счёл их
непригодными к

в так называемом неприводимом случае впервые
оценил Бомбелли (1572). Он

, появляющиеся при решении квадратных и
кубических уравнений, стали

лат. imaginarius. Он же распространил все стандартные функции, включая логарифм,

a и b – действительные числа, i – мнимая единица,

При этом число a называется действительной частью числа z
, а b - мнимой частью.

Числа z=a+ib и называются комплексно – сопряженными.

Два комплексных числа z1=a1+ib1 и z2=a2+ib2 называются равными, если соответственно равны их действительные и мнимые части:

a1=a2; b1=b2

Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части
a=b=0.
Также комплексные числа можно записывать, например, в виде z=x+iy, z=u+iv.

содержание

M(a;b) или как вектор ОМ с началом в точке O(0;0)

z с положительным направлением оси абсцисс. Обозначение:,argz.

- модуль комплексного

di) = (а + с) + (b + d)i
(а

(а + bi)·(с + di) = (ac - bd) + (ad + bc)i

и поменять знак у мнимой части, то получится комплексное число,

:

.

Из всех комплексных чисел действительные числа (и только они) равны своим сопряженным числам.

Числа a + bi и a - bi называются взаимно сопряженными комплексными числами.

форме
Сложение комплексных чисел

Суммой двух комплексных чисел z1=x1+y1i и z2=x2+y2i

1. z1+z2= z2+z1,
2. (z1+z2)+z3=z1+(z2+z3),
3. z+0=z.

Вычитание комплексных чисел

Вычитание определяется как действие, обратное сложению.

Разностью двух комплексных чисел z1=x1+y1i и z2=x2+y2i называется такое комплексное число z, которое, будучи сложенным с z2, дает число z1 и определяется равенством
z=z1 – z2=(x1 – x2)+i(y1 – y2).

содержание

число, определяемое равенством

z=z1 z2=(x1 x2 –y1 y2 )+i(x1 y2 –x2

Свойства операции умножения:
1. z1z2= z2z1,
2. (z1z2)z3=z1(z2z3),
3. z1(z2+z3 ) =z1z2+z1z3,
4. z∙1=z.

содержание

чисел z1 и z2≠0 называется комплексное число z, которое будучи

содержание

целые степени мнимой единицы:
содержание

и знаменатель дроби на число, сопряженное знаменателю («избавляются

Пример 2. Даны комплексные числа 10+8i, 1+i. Найдем их сумму, разность, произведение и частное.

Решение.

а) (10+8i)+(1+i)=(10+1)+(8+1)i=11+9i;

б) (10+8i)–(1+i) =(10–1)+(8–1)i=9+7i;

в) (10+8i)(1+i) =10+10i+8i+8i2=2+18i;

г)

содержание

извлечения корней) комплексных чисел, заданных в тригонометрической форме;
первый стал использовать

Абрахам де Муавр (1667 – 1754) – английский математик французского происхождения.

комплексное число, п — любое целое число. Тогда