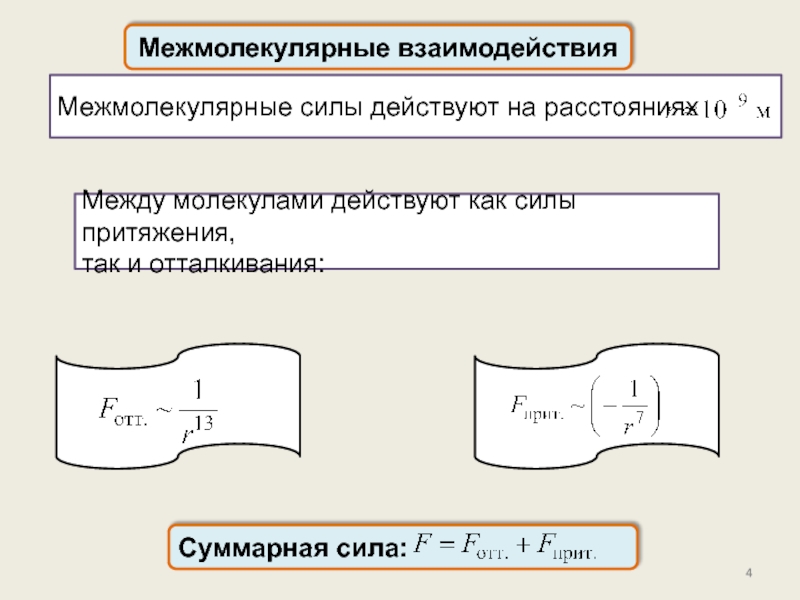
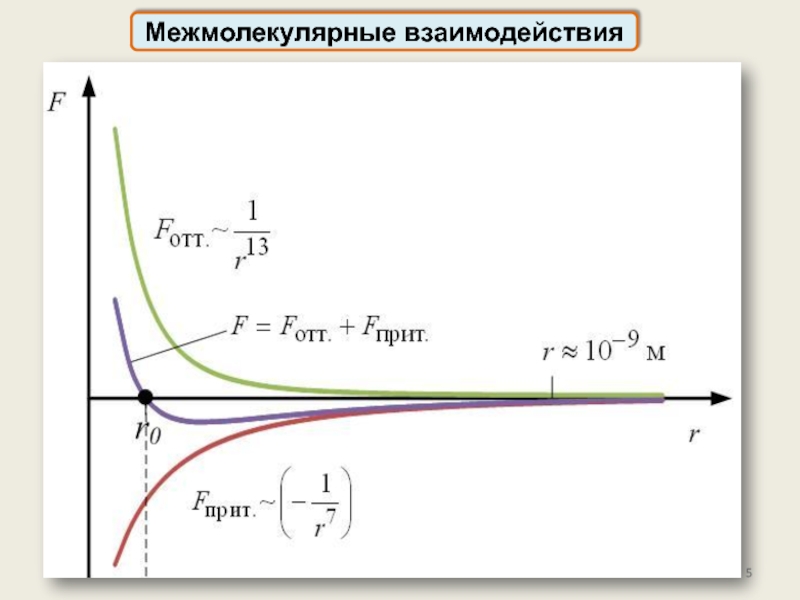
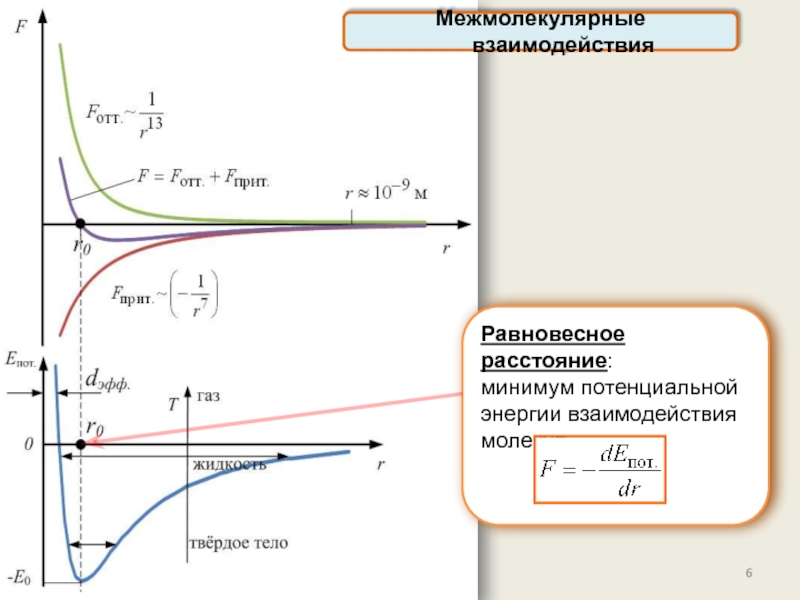
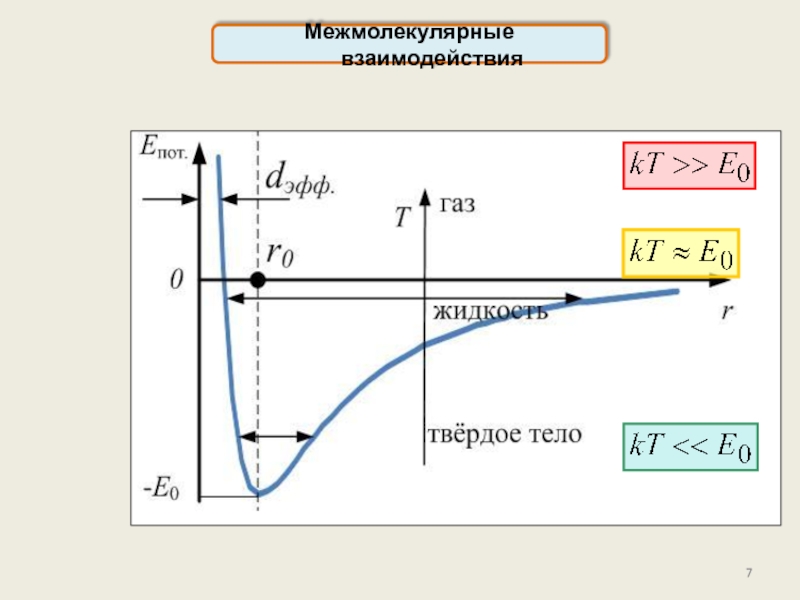
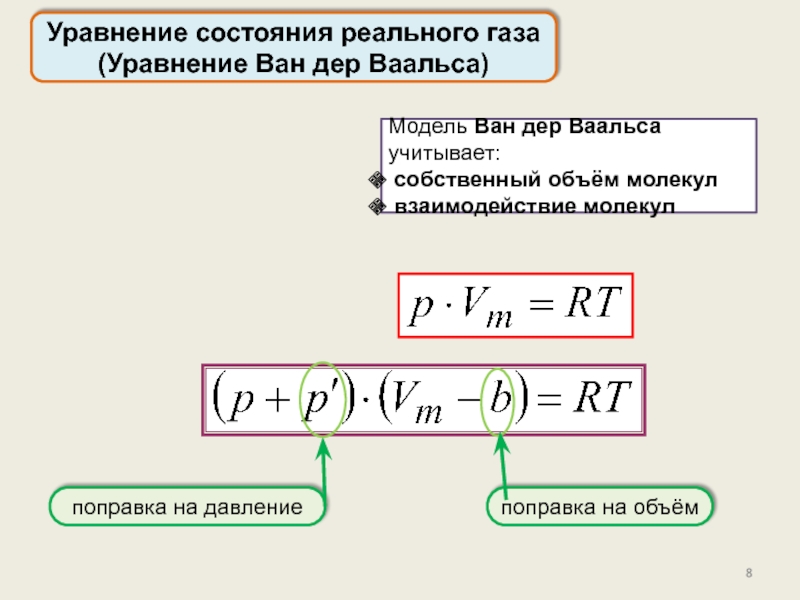
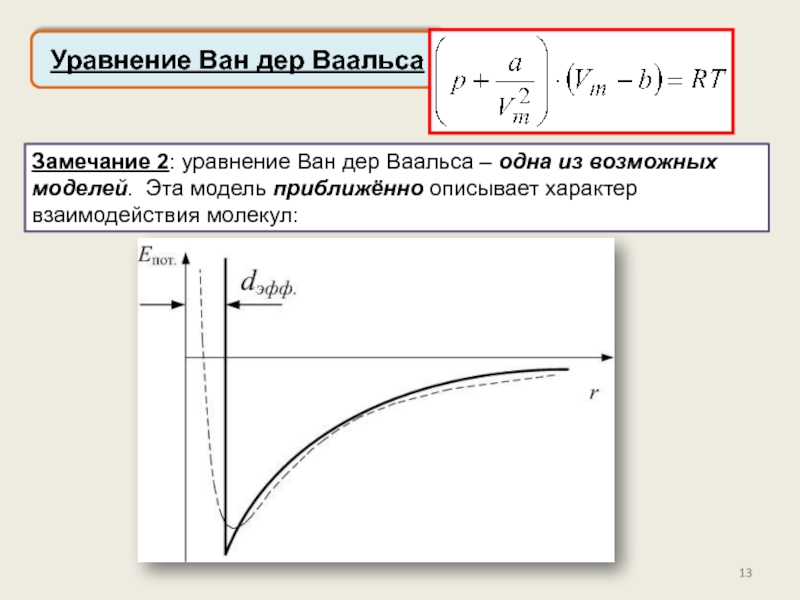
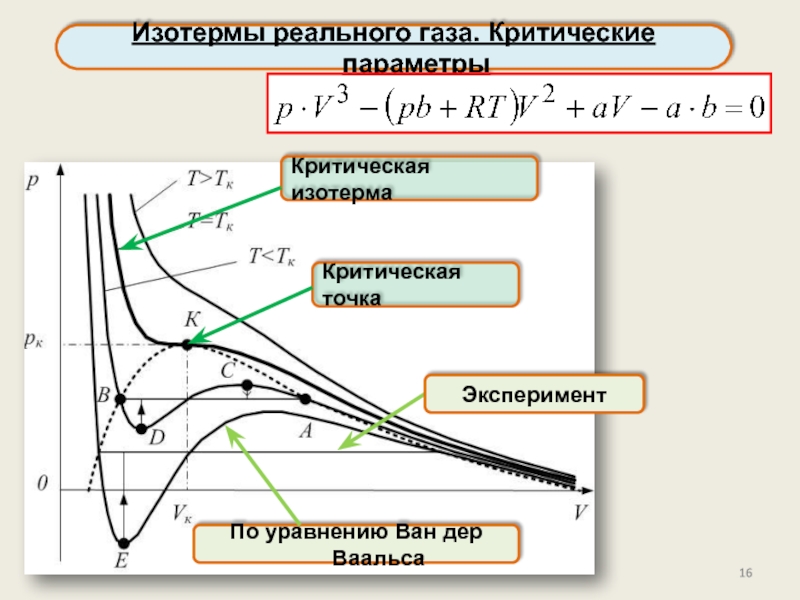
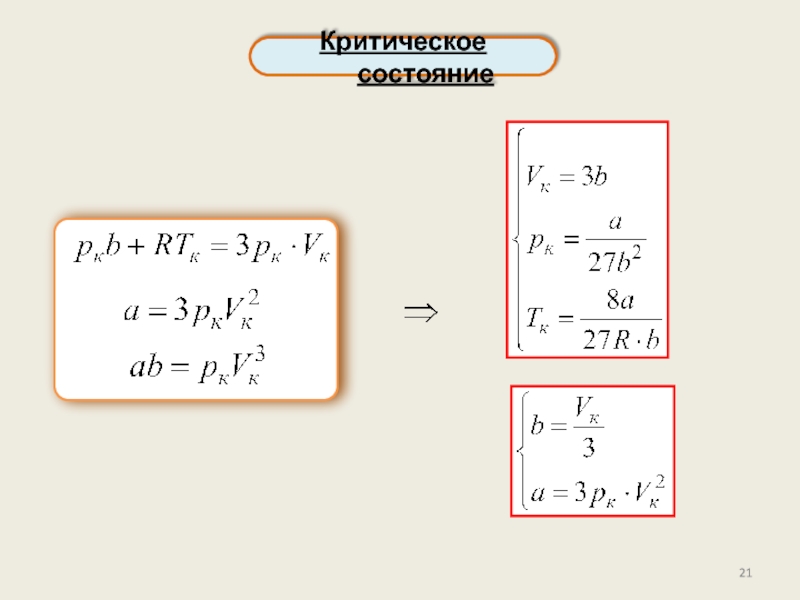
реального газа. Критические параметры.
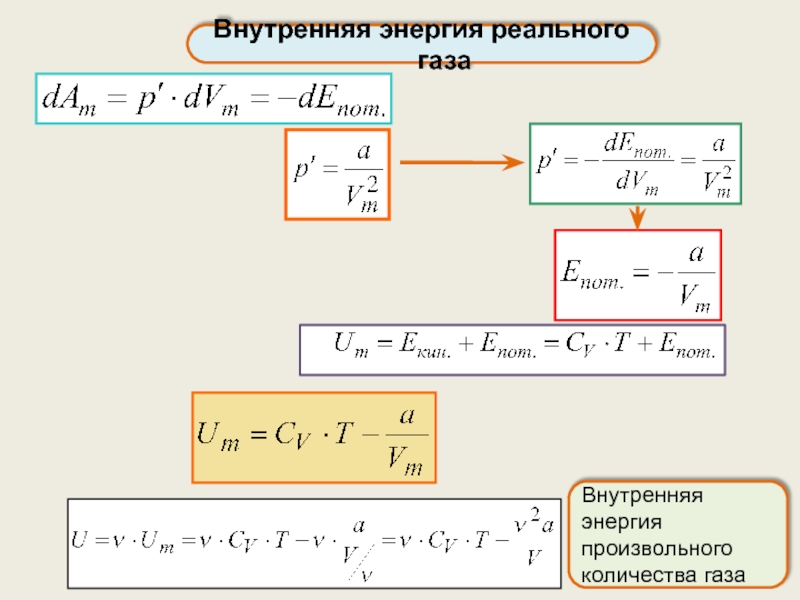
Внутренняя энергия реального газа
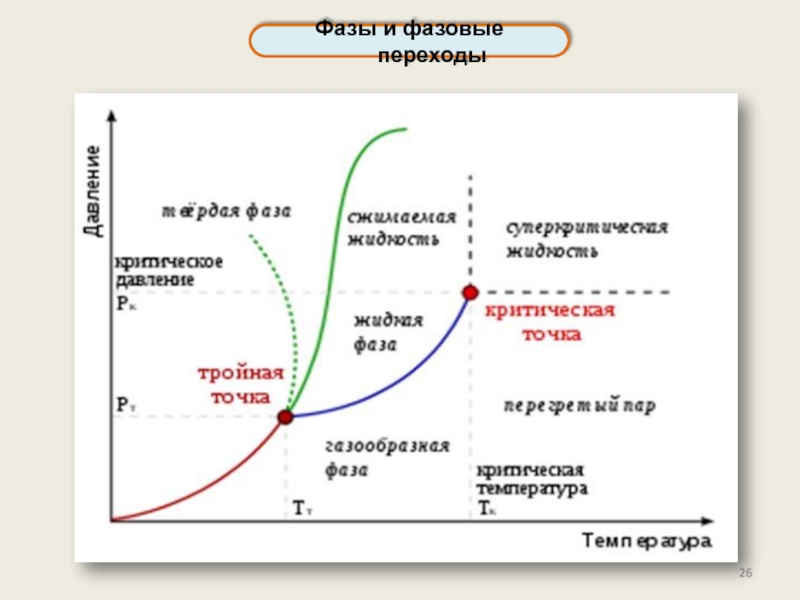
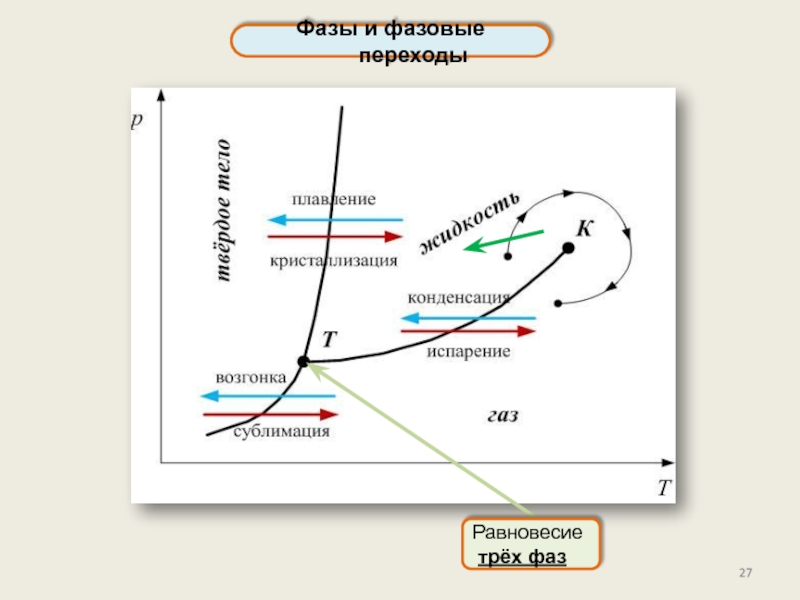
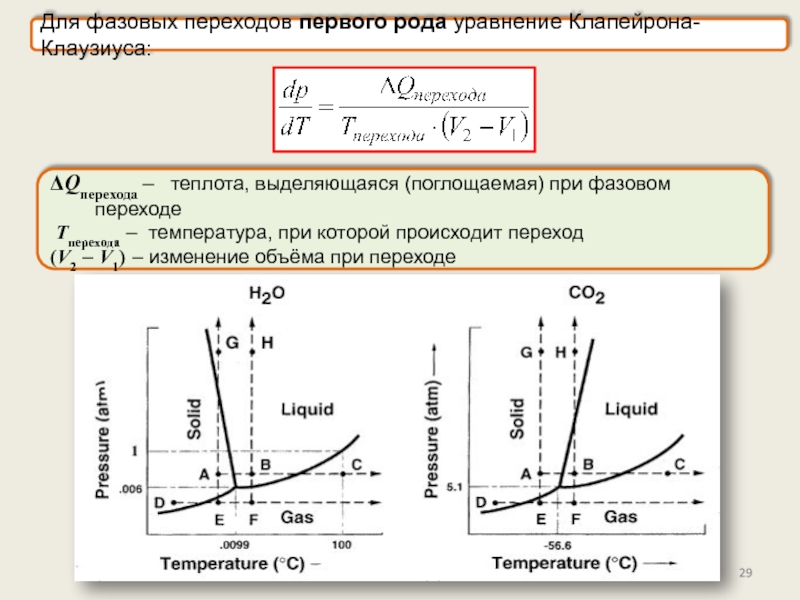
Фазы и фазовые переходы
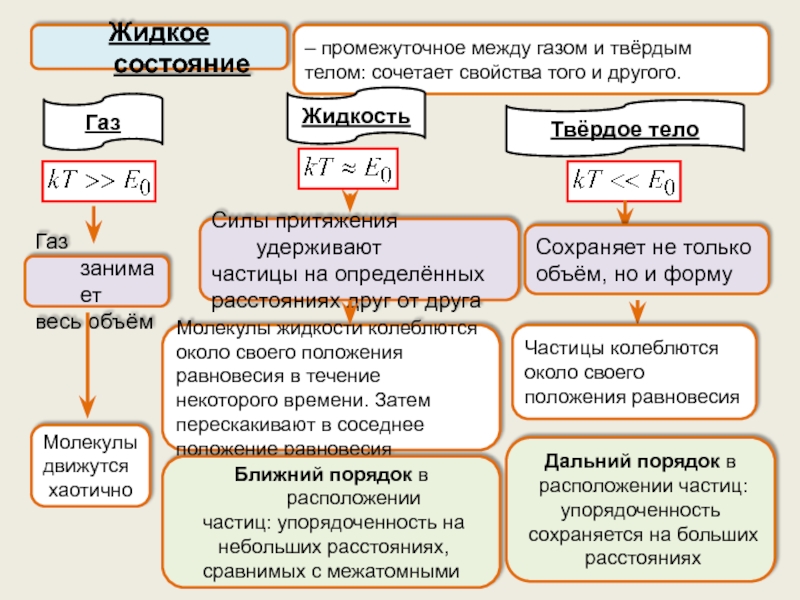
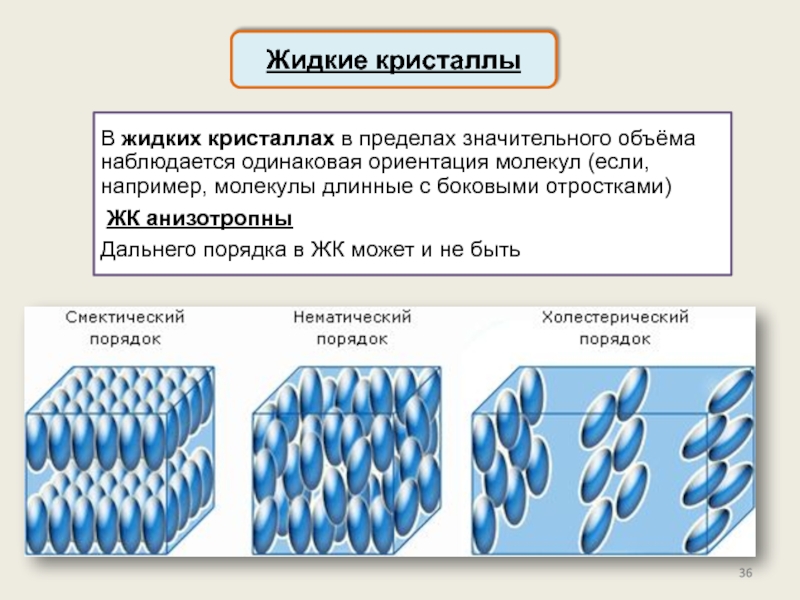
Жидкое
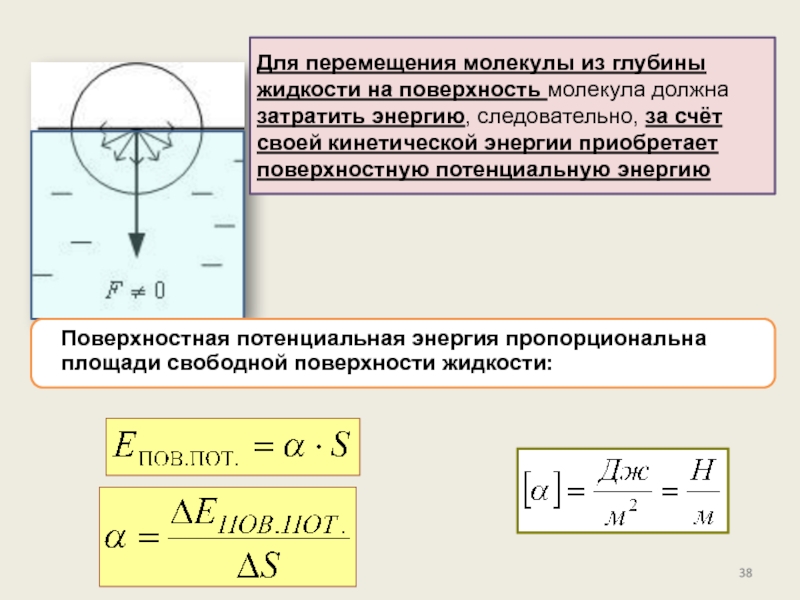
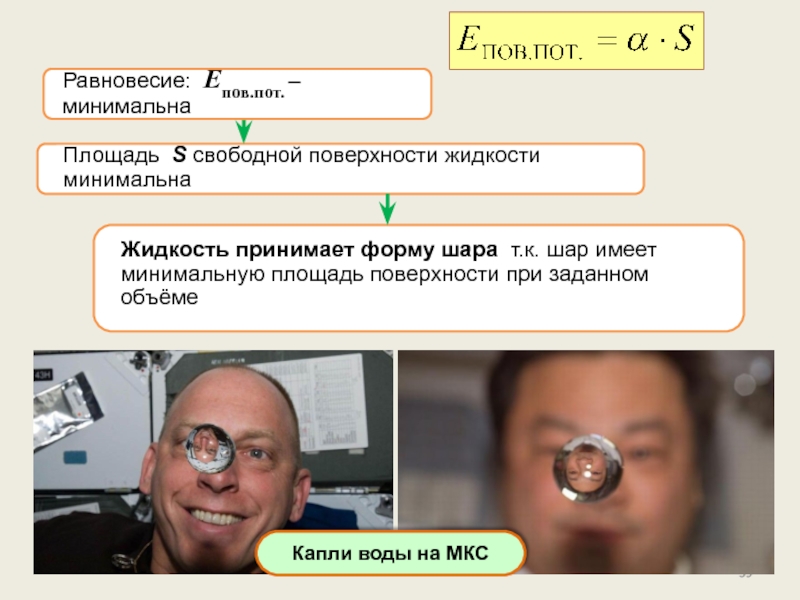
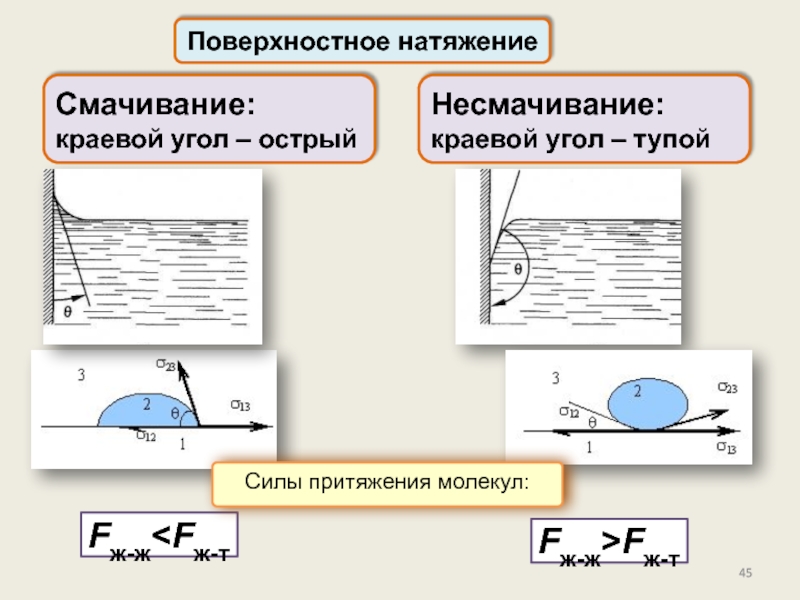
состояние, его характеристикиПоверхностное натяжение
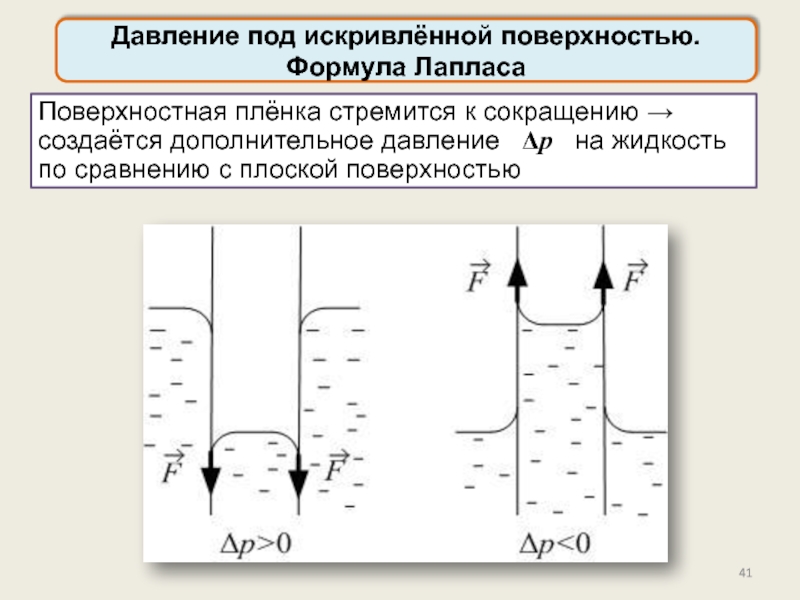
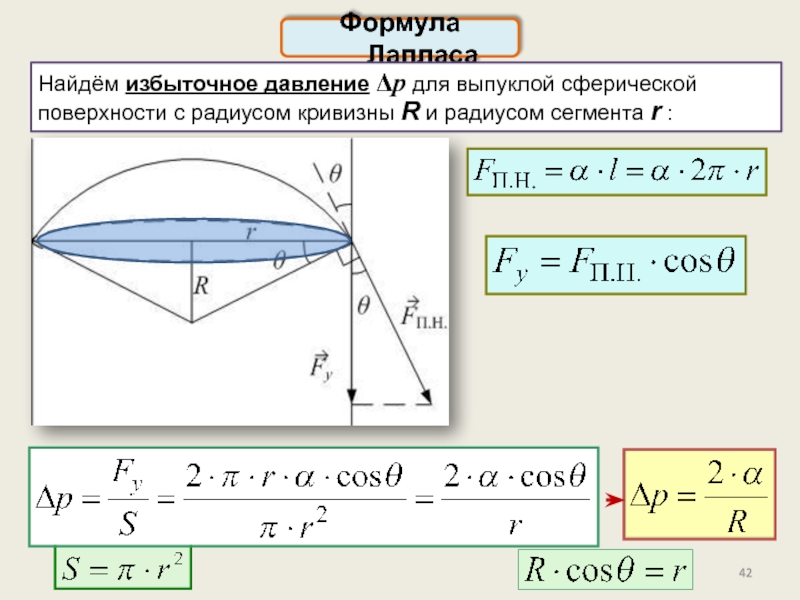
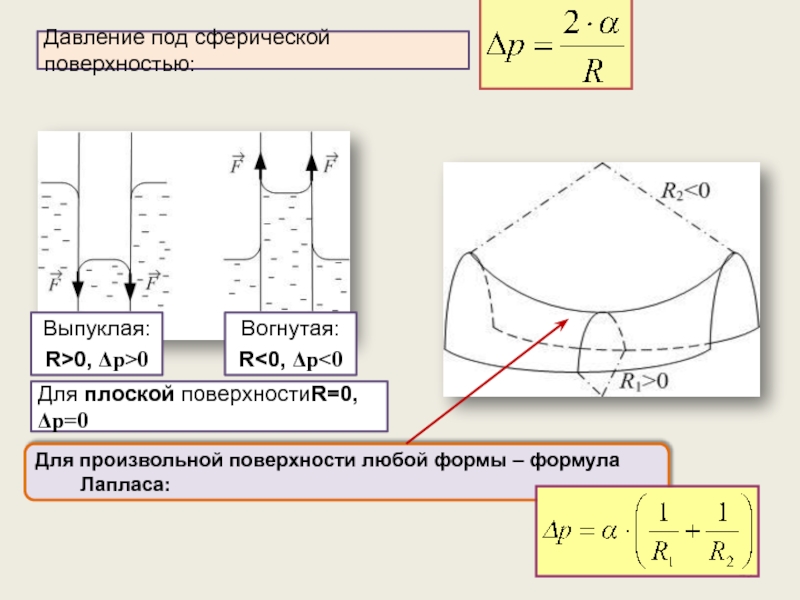
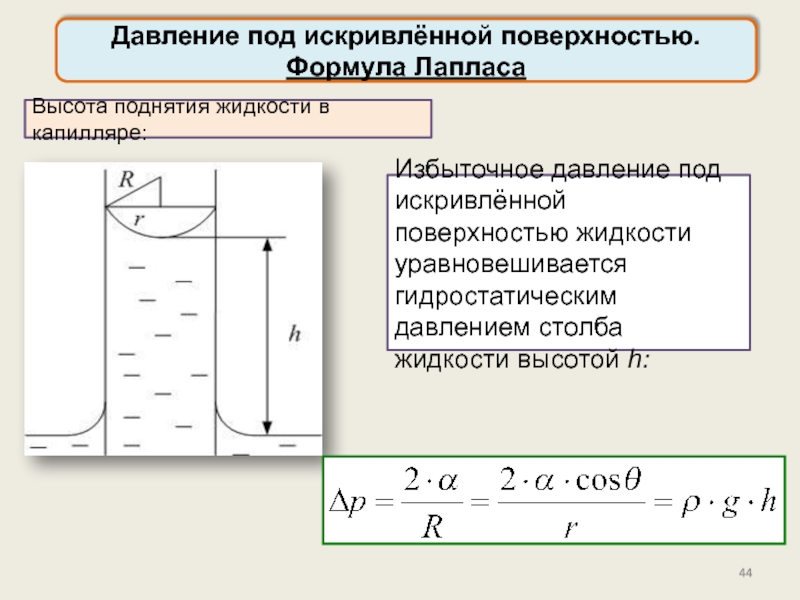
Давление под искривлённой поверхностью. Формула Лапласа
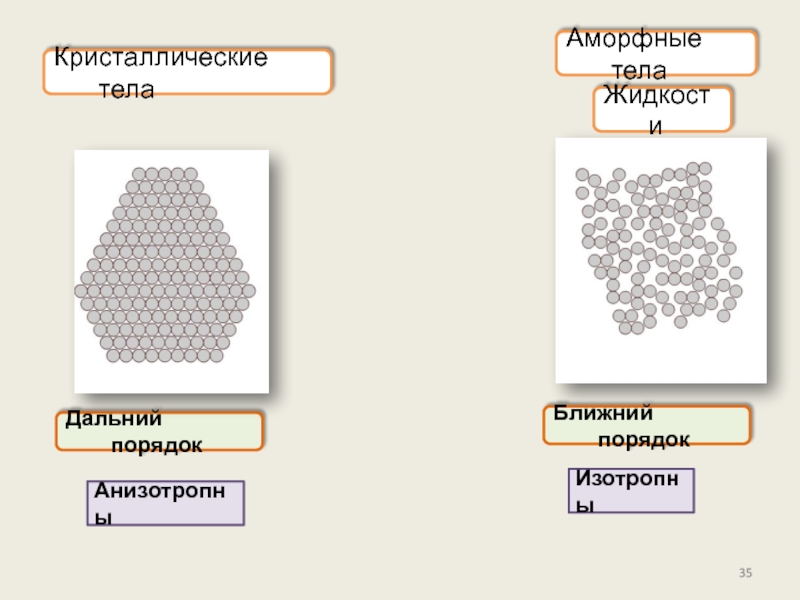
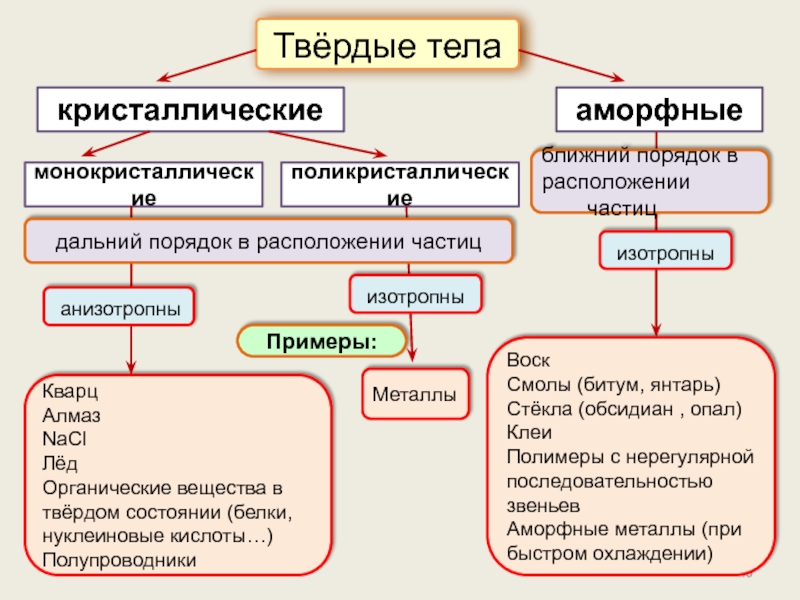
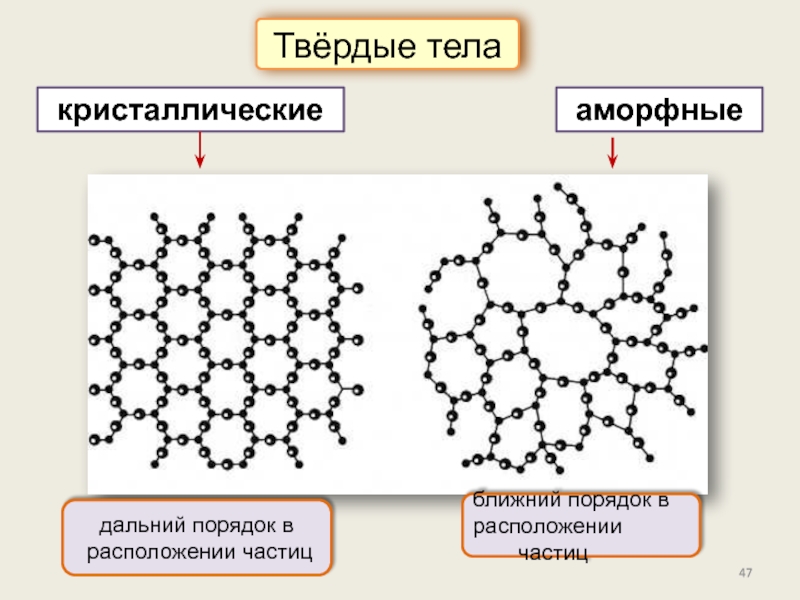
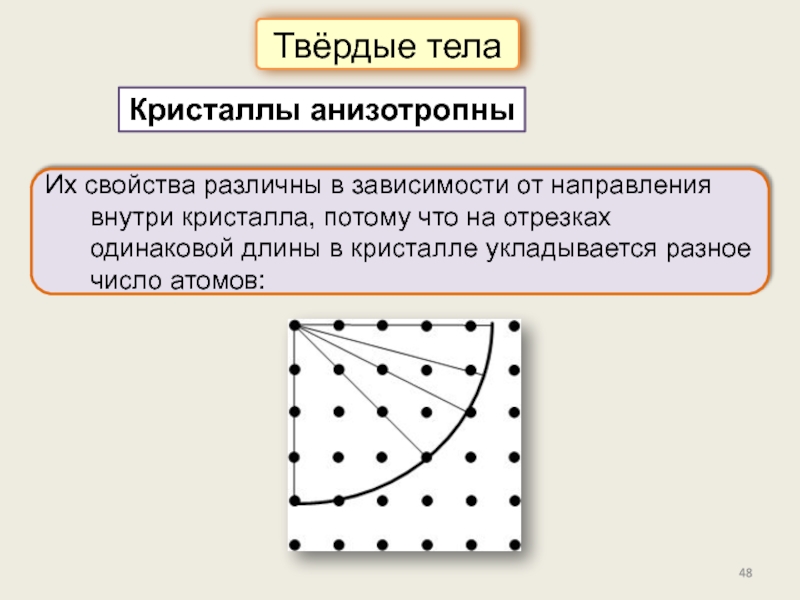
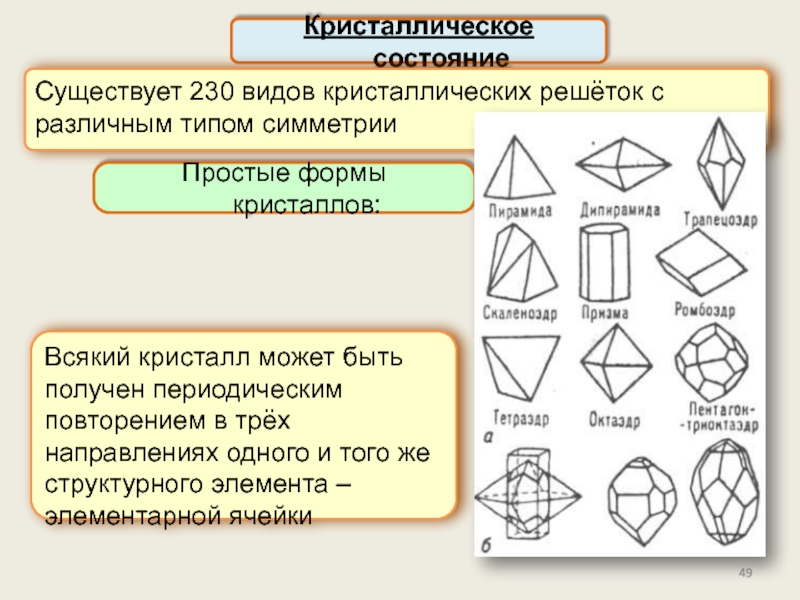
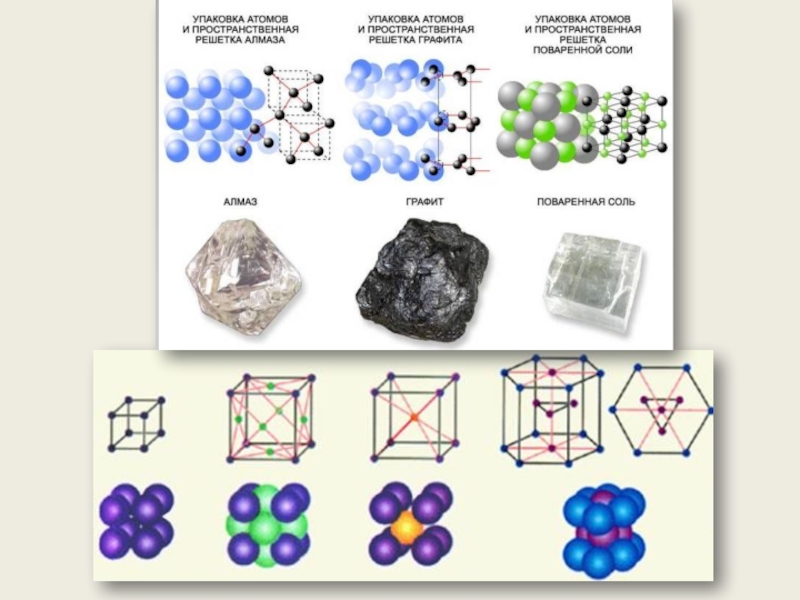
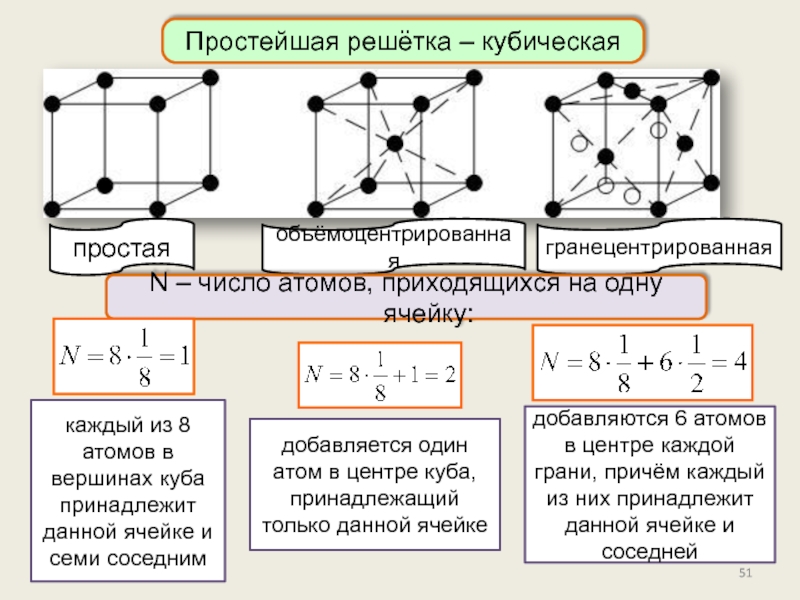
Кристаллическое состояние
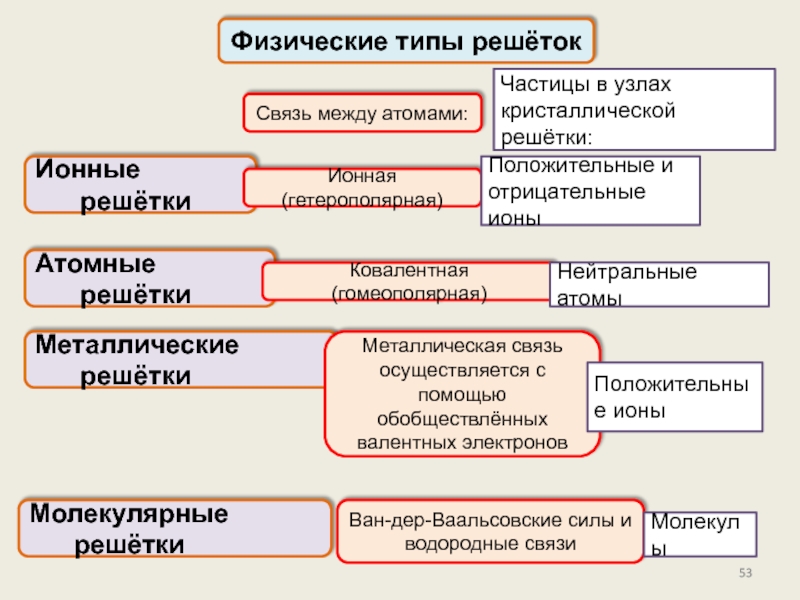
Физические типы решёток
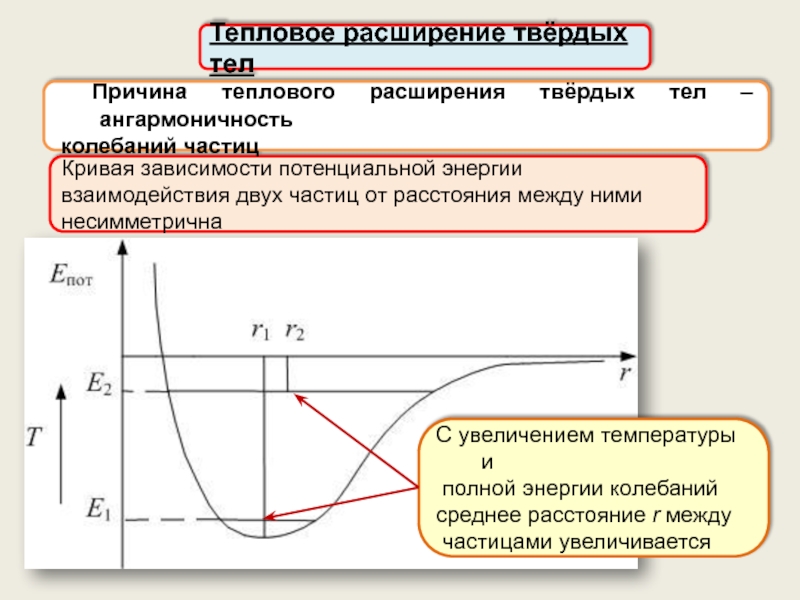
Тепловое расширение твёрдых тел
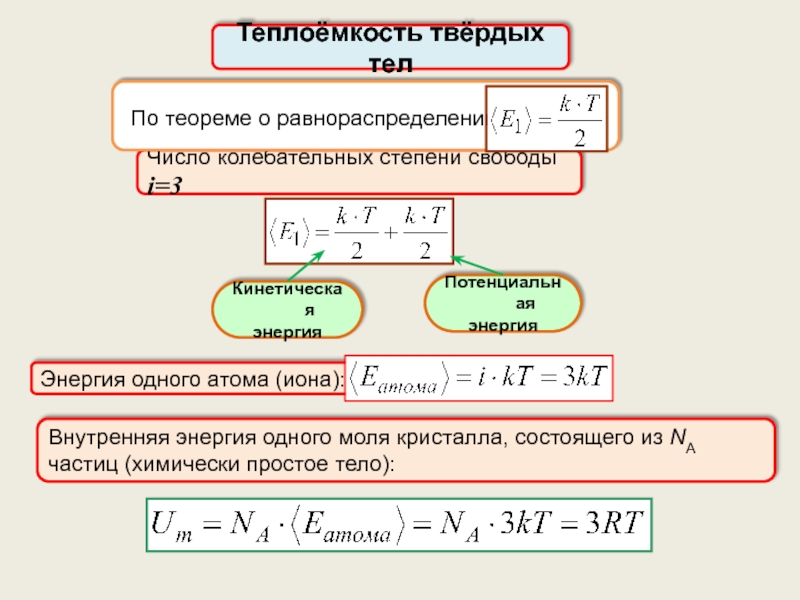
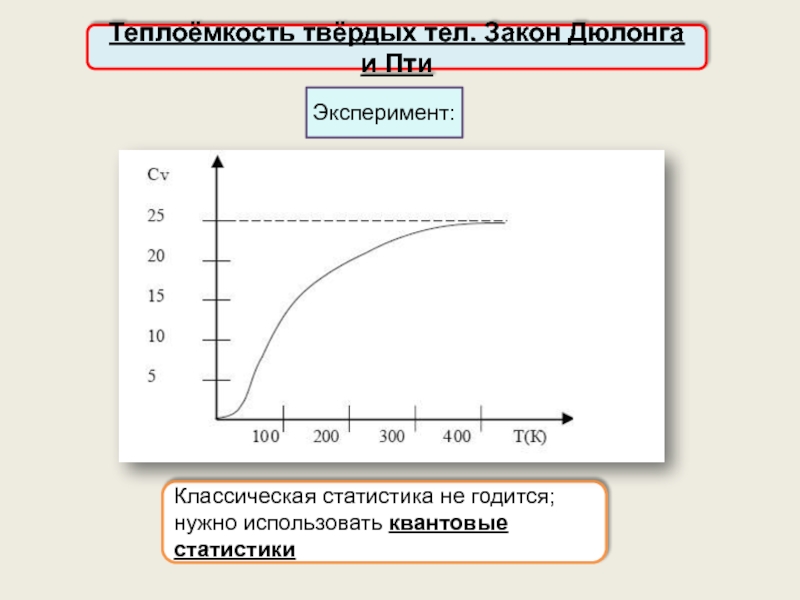
Теплоёмкость твёрдых тел. Закон Дюлонга и Пти
План