Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координаты вектора Л.С. Атанасян "Геометрия 10-11" Савченко Е.М., учитель
Содержание
- 1. Координаты вектора Л.С. Атанасян "Геометрия 10-11" Савченко Е.М., учитель
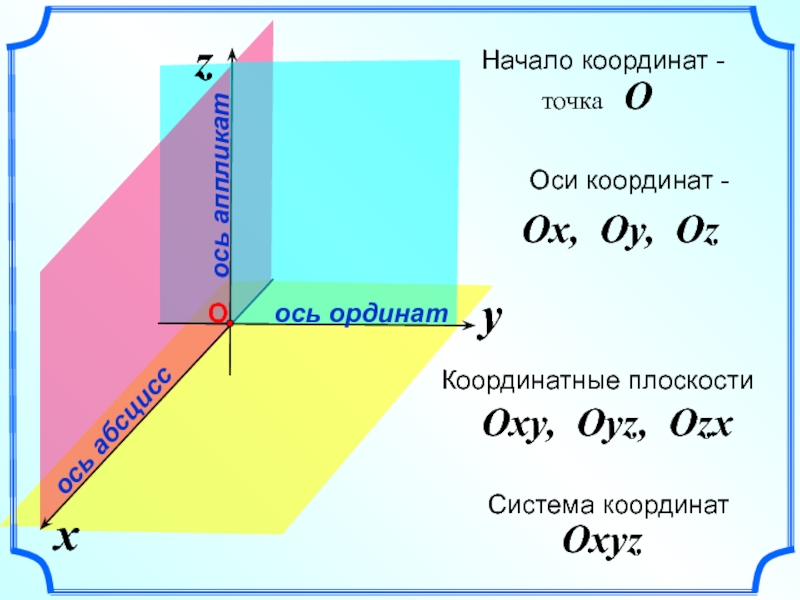
- 2. Слайд 2
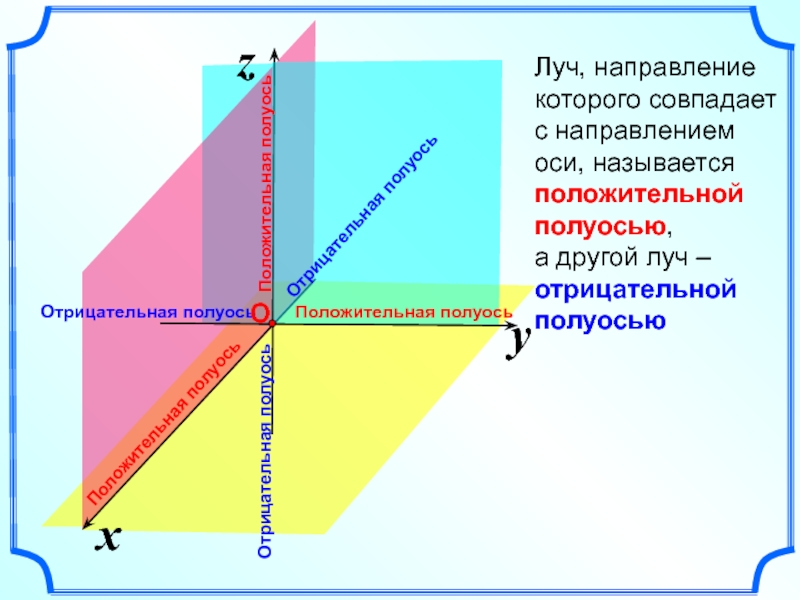
- 3. xzyЛуч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью
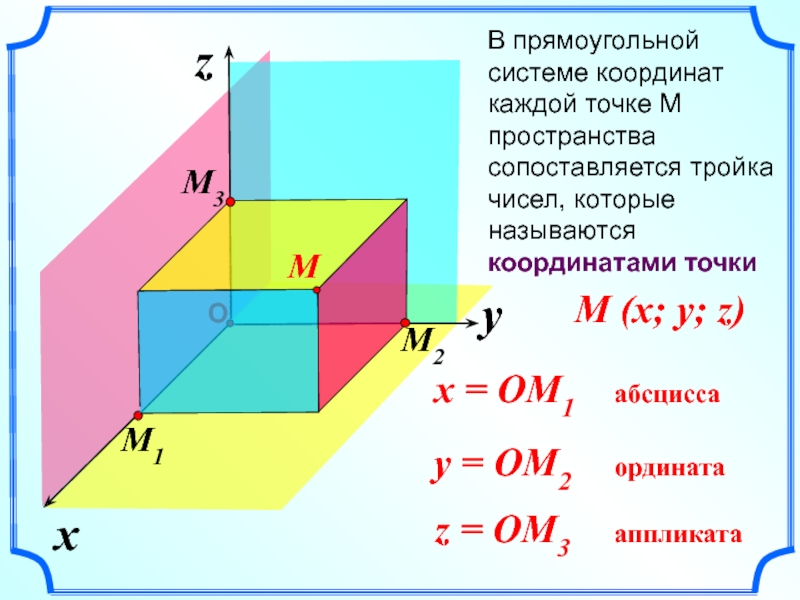
- 4. xzВ прямоугольной системе координат каждой точке М
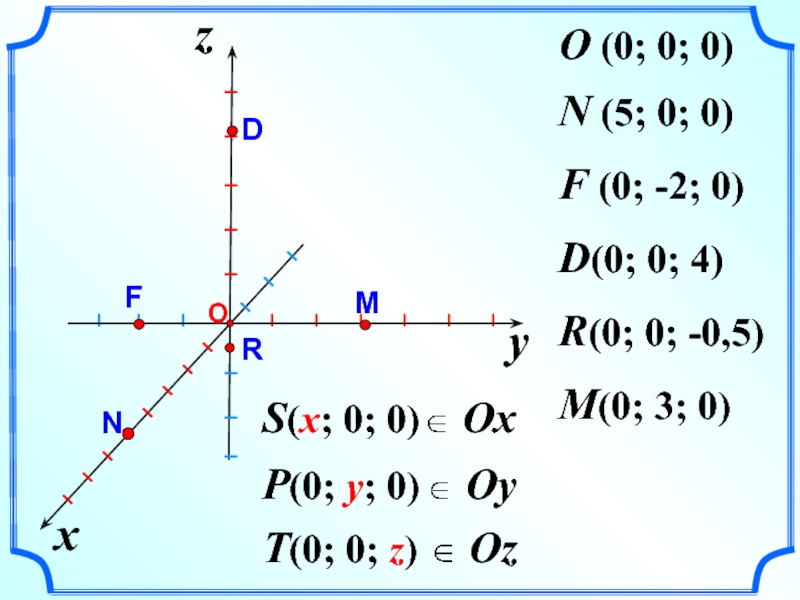
- 5. yxzO (0; 0; 0)N (5; 0; 0)I
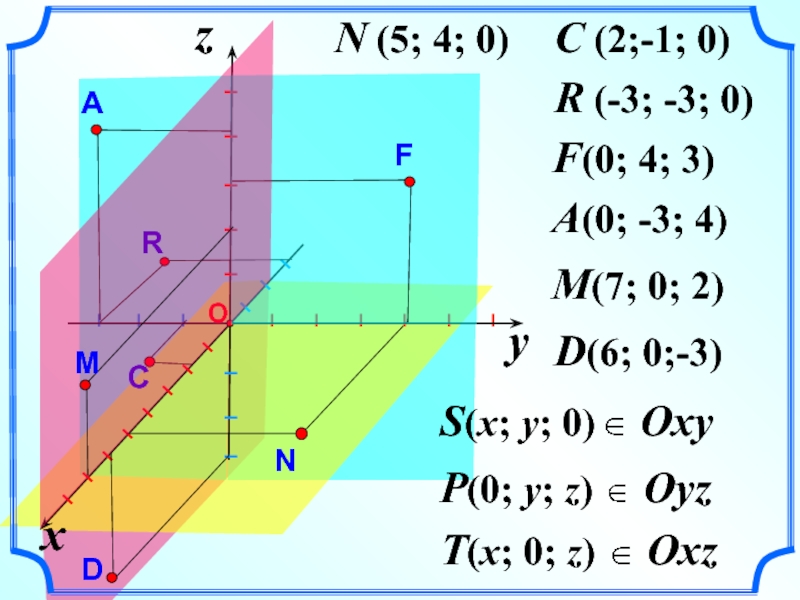
- 6. zN (5; 4; 0)C (2;-1; 0)I
- 7. В координатной плоскостиOxy (x; y; 0)Oyz
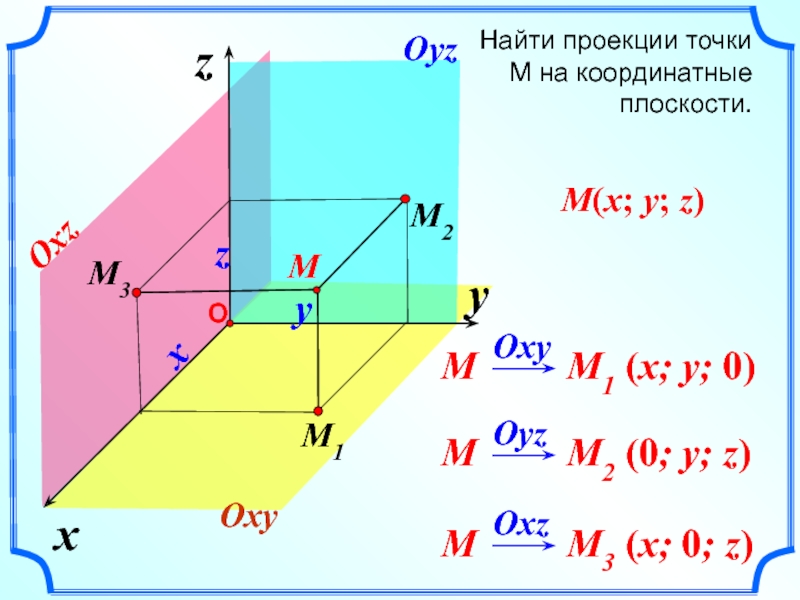
- 8. xzНайти проекции точки М на координатные плоскости.yMxyzOxyOyzOxzM(x; y; z)
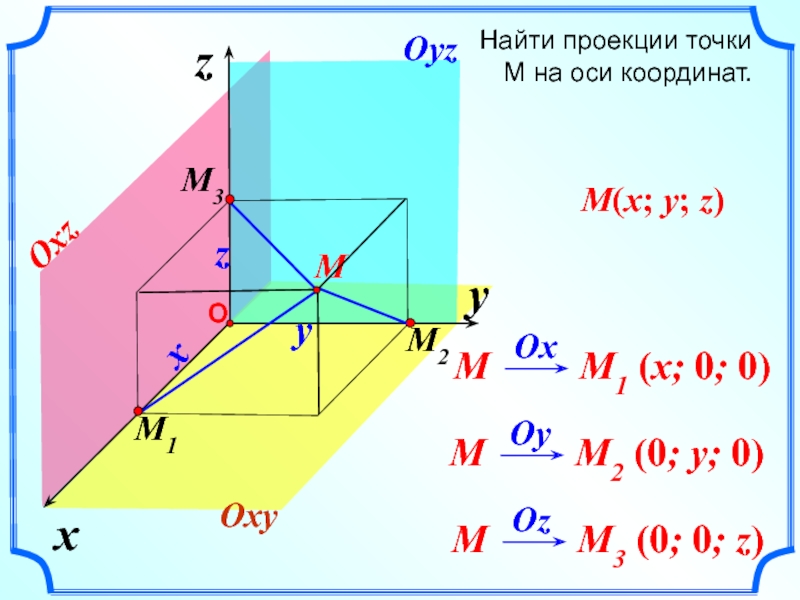
- 9. xzyMxzOxyOyzOxzНайти проекции точки М на оси координат.yM(x; y; z)
- 10. yxz I I
- 11. Вектор, начало которого совпадает с началом координат
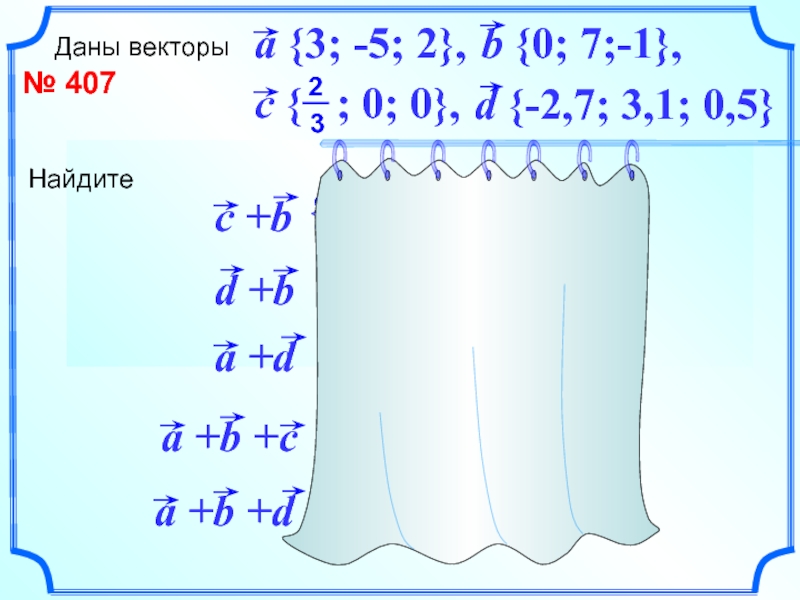
- 12. № 407Даны векторыd {-2,7; 3,1; 0,5}
- 13. 1 способ2 способ
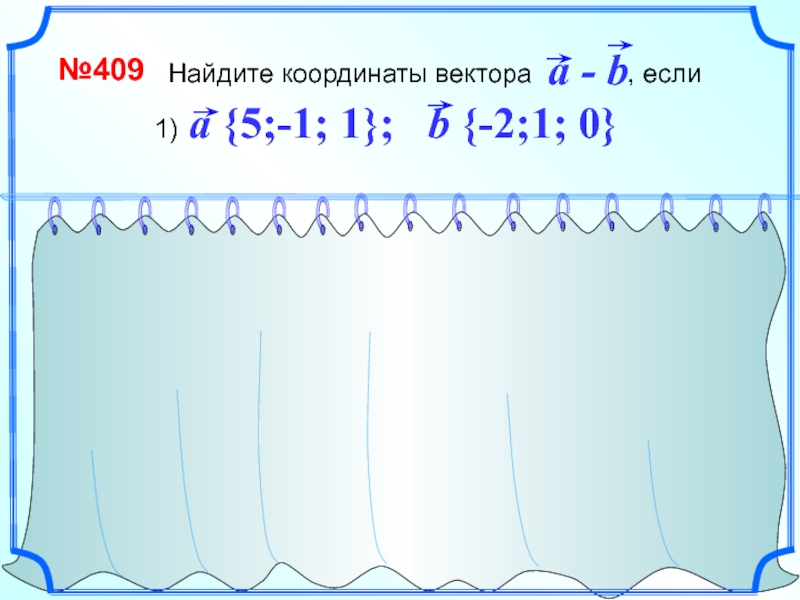
- 14. Найдите координаты вектора , если№409
- 15. Скачать презентанцию
xzyЛуч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью
Слайды и текст этой презентации
Слайд 3x
z
y
Луч, направление которого совпадает с направлением оси, называется положительной полуосью,
Слайд 4x
z
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка
чисел, которые называются координатами точки
y
M (x; y; z)
M
Слайд 5y
x
z
O (0; 0; 0)
N (5; 0; 0)
I
I I
I I I I II I I I I I I I I I I
F (0; -2; 0)
D(0; 0; 4)
R(0; 0; -0,5)
M(0; 3; 0)
S(x; 0; 0)
P(0; y; 0)
T(0; 0; z)
Слайд 6z
N (5; 4; 0)
C (2;-1; 0)
I I
I I I
I I I I I IR (-3; -3; 0)
F(0; 4; 3)
A(0; -3; 4)
M(7; 0; 2)
S(x; y; 0)
P(0; y; z)
T(x; 0; z)
y
I I I I I I I I
x
D(6; 0;-3)
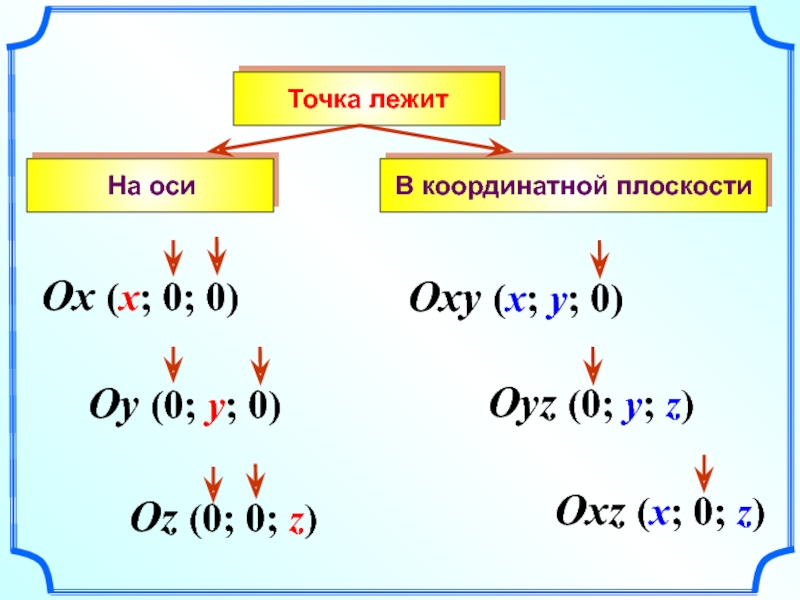
Слайд 7 В координатной плоскости
Oxy (x; y; 0)
Oyz (0; y; z)
Oxz
(x; 0; z)
Ox (x; 0; 0)
Oy (0; y; 0)
Oz (0;
0; z)На оси
Слайд 10y
x
z
I I
I I
I I I II I I I I I I I
I I I I I I I I
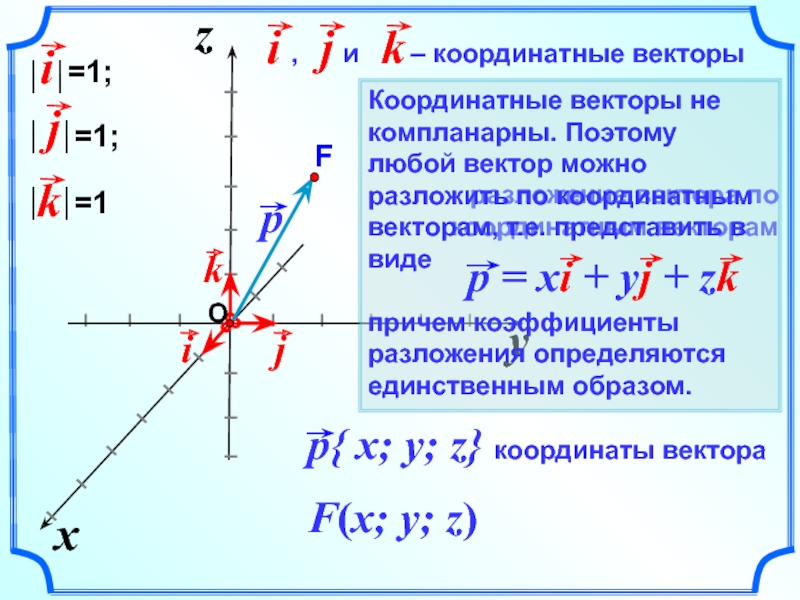
разложение вектора по координатным векторам
F(x; y; z)
O
Координатные векторы не компланарны. Поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде
причем коэффициенты разложения определяются единственным образом.
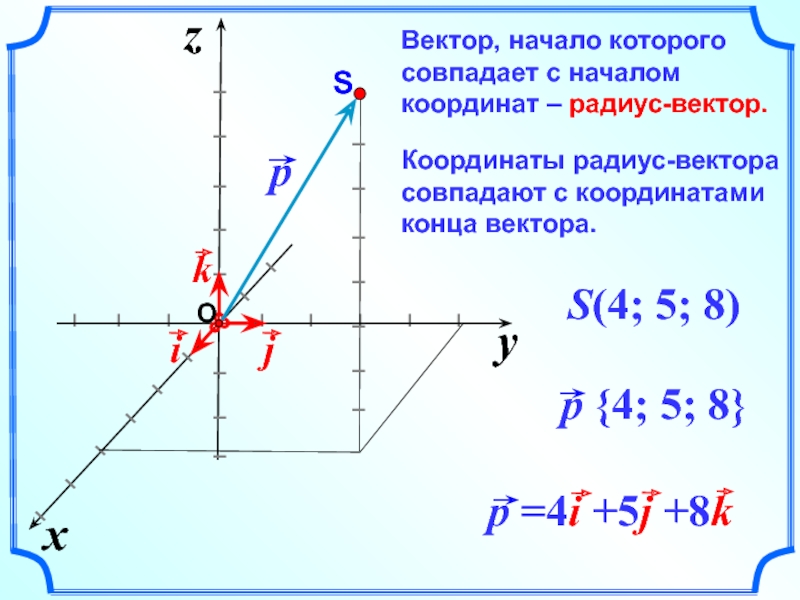
Слайд 11Вектор, начало которого совпадает с началом координат – радиус-вектор.
Координаты радиус-вектора
совпадают с координатами конца вектора.
y
x
z
I I
I I I I I I I I I I I I I I
I I I I I I I I
S(4; 5; 8)
O
